Localization of Vibration Weak Position of Composites Based on Weighted Modal Strain Energy Summation

Abstract

In this paper, two typical examples are used to illustrate the weak position of aircraft structure in the process of vibration. Through the modal analysis of the typical composite plate and I-shaped beam, the first 20-order modal strain energy of the plate is extracted, which is difficult to locate the weak spot due to the highly scattered location of the higher modal strain energy. The modal participation factor is introduced as the weight factor of the summation of the modal strain energy. The modal participation factor is large, the weighting factor is large, and the high modal strain energy of the composite plate moves diagonally in the 45° direction of the composite plate and the high strain energy region is consistent with the previous modes of the plate. This is the result of the weak in-plane shear stiffness of the composite panel, which shows the effectiveness of the mode weighted summation method. The I-shaped composite beam uses the modal strain energy summation of the weight factor, and the higher modal strain energy is concentrated on the middle part of the beam and at 1/4 and 3/4 of it. Therefore, the weak part of the vibration can be clearly identified. The higher modal strain energy is extracted by the method proposed to this paper, which can be used as a reference to structural design and dynamic on-line monitoring.

1. Introduction

The composite material is a new one made from two or more materials (such as reinforcing fiber and its adhesive matrix) by proper processing. At first, the engineers did not have high utility rate and high confidence in the use of composites, but only used them for secondary load-bearing structures. Over the years, people gradually realized the advantages of composite materials, which were more involved in more types of aircraft or structures of an increasing proportion. Composites have unique characteristics, such as low density, high specific strength and stiffness, low coefficient of thermal expansion, excellent fatigue resistance, corrosion resistance, shock absorption, and so on. With the increase in human’s understanding of it, its manufacturing technology tends to be mature and perfect, so it has been more and more widely used in aerospace, automotive, civil engineering and etc.

The carbon fiber reinforced resin composite sheet [1] is of great use for aerospace structural components, such as aircraft wing skin and fuselage skin, because of its mechanical properties and light weight. However, due to the impact of objects on the structure, such as hail impact, lightning strike, or vibration in flight, the inner changes (damage) of the material are not easy to detect.

The dynamic characteristic [2] is the inherent property of structure, which is reflected by the physical parameters such as modal stiffness, modal frequency, modal shape and so on. If the structure vibration is monitored in real time, the working state of the structure can be monitored. In on-line monitoring, the modal strain energy is one of the most easily obtained modal parameters and the precision is high, so it is most practical to identify the load-bearing and working condition of the structure by the change of modal strain energy.

Güemes, A., Fernandez-Lopez, A., Pozo, A.R., and Sierra-Pérez, J. [3] summarized structural health monitoring modes and methods for Advanced Composite Structures. Ashory, M.R., Ghasemi-Ghalebahman, A., and Kokabi, M.J. [4] dealt with an investigation into performing a damage identification technique using a finite element model updating based on genetic algorithm, and providing an evaluation approach from improved sensitivity for detection of quantitative parameters. Finally, an appropriate objective function had been developed based on weighted strain energy, exhibiting the highest level of sensitivity compared to the other methods of damage diagnosis. Hu, H., Lee, C.H., Wu, C.B., Lu, W.J. [5] showed detection of matrix cracks in composite laminates by using the modal strain energy method. Huiwen Hu and Jieming Wang [6] indicated damage detection of a woven fabric composite laminate using a modal strain energy method. Trung Vo-Duy, Vinh Ho-Huu, Hau Dang-Trung, Du Dinh-Cong, and Trung Nguyen-Thoi [7] introduced a model strain energy-based method and an improved differential evolution algorithm used to locate and quantify damage on the laminate composite plate. Huiwen Hu, Bor-Tsuen Wang, Cheng-Hsin Lee, and Jing-Shiang Su [8] presented an approach to detect surface cracks in various composite laminates. In the last two-year, Hui Liu, Wenyu Wang, and etc. [9,10,11,12] had deeply studied the nonlinear vibration analysis of composite structures and the effective measures to suppress the vibration, which provides good ideas and measures to reduce the vibration damage.

The whole plane was vibrating during the flight. The higher the vibration modal strain energy is, the weaker part of the structure it is. All sorts of failure modes and damage [13] are easy to detect, in order to ensure the good serviceability and safety of the composites. A virtual experiment (simulation analysis) is carried out to find the component of the highest modal strain energy, so that the strain gauges, sensors, etc., carry out health monitoring and management of aircraft’s structures. It can also effectively extract the modal strain energy in the vibration process and design the shock absorption of the region.

Considering the anisotropy of the composite material, the vibration shape of the composite plate is seldom symmetrical because of the difference in the ply angles and ply sequence. In this paper, the summation of the modal strain energy of the structure is used as the monitoring position, which can truly reflect the weak part of the structure vibration.

Based on the natural vibration modal analysis of the composite plate and I-shaped beam, which are typical components of the composite wing skin of airplanes, the free vibration modal strain energy of each order is extracted. The weak links with vibration of composites can be obtained by weighted sum of every modal participation factor, which can find out the position of health monitoring and anti-vibration design of aircraft’s structures.

In this paper, a method is proposed to identify the weak part of aircraft structure in the vibration process by introducing the modal participation factor as the weight factor so that the summation of modal strain energy can be calculated. In addition, the higher modal strain energy is extracted by the proposed method, which can be used as a reference for structural design and dynamic on-line monitoring.

2. Basic Principles

2.1. Modal Strain Energy

The free vibration equation is,

$$\left[M\right]\left\{\ddot{x}\right\}+\left[K\right]{\left\{x\right\}}_{}=0$$

(1)

where [M] is the structure mass matrix; [K] is the structure stiffness matrix; {x} is the displacement vector; $\left\{\ddot{x}\right\}$ is the acceleration vector.

In i-order mode of the structure, the modal strain energy of j element is defined as,

$$MS{E}_{ij}={\left\{{\phi }_i\right\}}^T\left[K_j\right]\left\{{\phi }_i\right\}$$

(2)

where [K_j] is j element stiffness Matrix, which is the extendable order of the total stiffness, and {φ_i} is the mode shape of i-order mode. This parameter is used to evaluate the strength of the structure vibration in the later section of this paper.

2.2. Modal Participation Factor

It is difficult to predict the dominant mode of the structure of the transient or frequency response analysis during the loading process. One Way to estimate the modes that play an important role is to calculate the modal participation factors [14], which also reflect the importance of different modes.

Firstly, a rigid body vector is defined as {D}_R

$${\left\{D\right\}}_R=[\varphi ]\left\{\epsilon \right\}$$

(3)

where [$\varphi$] is the modal eigenvector and {$\epsilon$} is the scaling factor of the EIGENVECTOR.

Multiply {D}_R by [$\varphi$]^T[M],

$${[\varphi ]}^T[M]{\left\{D\right\}}_R={[\varphi ]}^T[M][\varphi ]\{\epsilon \}$$

(4)

$${[\varphi ]}^T[M]{\left\{D\right\}}_R=[m]\{\epsilon \}$$

(5)

where [m] is the diagonal of the modal generalized mass matrix.

[$\varphi$]^T[M]{D}_R is called participation factor {$\mathsf{\Gamma }$}.

$$\begin{array}{l}\{\mathsf{\Gamma }\}={[\phi ]}^T[M]{\left\{D\right\}}_R=[m]\{\epsilon \}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \hspace{0.17em}=>\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\Gamma }}_i=m_{ii}{\epsilon }_i\end{array}$$

(6)

Scaling factor $\epsilon$_i times the generalized mass m_ii, which defines the first order modal participation factor $\mathsf{\Gamma }$_i.

3. Case Studies

3.1. Finite Element Models

3.1.1. Composite Plate

Composite Plate is divided into 8 layers and ply angle is 0₂°/45₂°/90₂°/−45₂°. The thickness of each two plies is 0.0025 m. The ratio of the thickness of each angle is 1:1:1:1. The length or width is 1 m, respectively, and the thickness is 0.01 m. The material is T300. In MSC.Patran, the establishment of finite element model was carried out. The number of nodes was 51005, the hexahedral element number was 40,000 and the plate had four-sided simple support constraints. The X and Y axes of the coordinate in Figure 1 are along the length and width of the plate, respectively, and the Z axis is determined by the right-hand rule to be perpendicular to and outward from the plate surface.

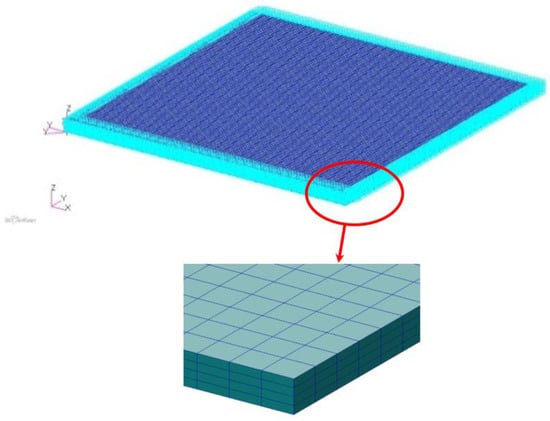
Figure 1. Mesh and boundary condition.

3.1.2. I-Shaped Beam

The composite I beam was divided into upper fringe (26 mm × 3.885 mm), lower fringe (46 mm × 3.33 mm), Middle Web (30 mm × 2.96 mm). The ply angle consists of 0°/45°/90°/−45°. The length and width of the beam are both 620 mm. The material is T300. In MSC.Patran, the finite element model was set up. The finite element model is shown in Figure 2. The number of nodes is 18,038, the number of 2D elements is 17,670, and both ends of the beam were fixed.

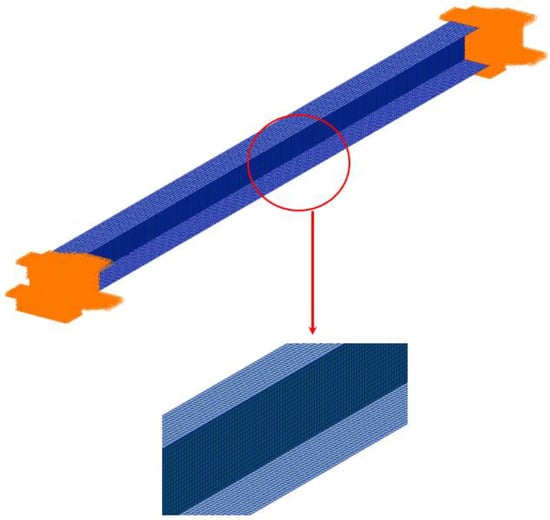
Figure 2. Mesh and boundary condition.

3.2. Analysis Results

After modal analysis and calculation in MSC.Nastran Sol103, the first 20 order vibration modes and vibration frequencies are obtained. The results are input into MSC. PATRAN interface, some typical important vibration modes are listed from Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

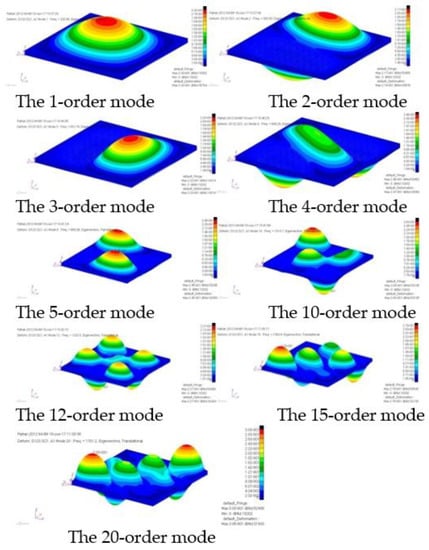
Figure 3. The typical modes of the composite plate.

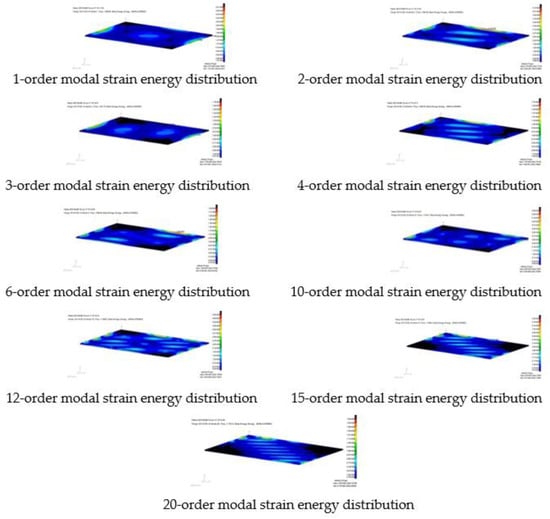
Figure 4. The typical strain energy of the composite plate.

Figure 5. The equal proportion linear summation strain energy of the first 20 modes of the composite plate.

Figure 6. The weighted summation strain energy of the first 20 modes of the composite plate.

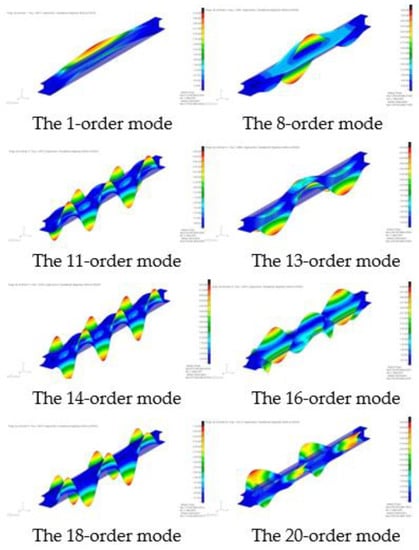
Figure 7. The typical modes of the I-shape composite beam.

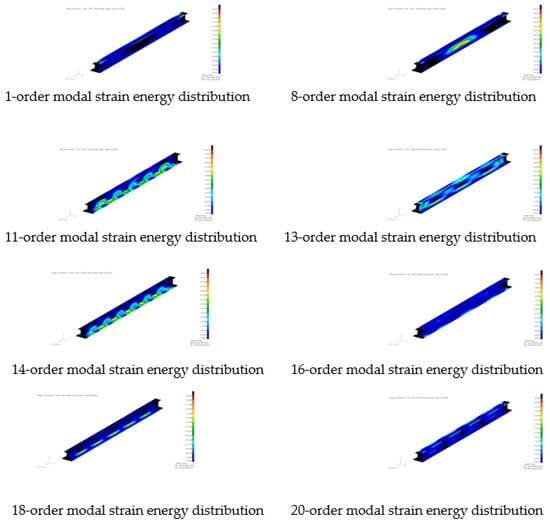
Figure 8. The typical strain energy of the composite I-shape beam.

Figure 9. The equal proportion linear summation strain energy of the first 20 modes of the composite beam.

Figure 10. The weighted summation strain energy of the first 20 modes of the composite beam.

Results of the Composite Plate

The modes of the composite plate are shown in Figure 3.

A typical modal strain energy distribution diagram is also extracted, as shown in Figure 4.

Figure 3 and Figure 4 show the vibration characteristics of the composite plate. It can be seen that the peak displacement and the distribution of the vibration strain are not regular. In MSC.Patran, PCL (Patran Command Language) functions were written for the linear summation of the first 20 order modal strain energy. The distribution of modal strain energy is indicated in Figure 5.

As can be seen from Figure 5, there are six high strain energy regions on the bottom left corner and upper right corner of the composite plate in the direction of 45° where the Red Circle is the weak part of the plate for vibration (or dynamic load). It can be seen that the vibration high strain energy of the structure is scattered because the modal participation is not considered.

Next, the modal proportion factor of each order mode is calculated and analyzed according to the modal participation factor of six directions. The FAC_i of each mode is as follows:

$$FA{C}_i=\sqrt{T{X}_i{}^2+T{Y}_i{}^2+T{Z}_i{}^2+R{X}_i{}^2+R{Y}_i{}^2+R{Z}_i{{}^2}_{}}$$

(7)

Among them, Tx_i, Ty_i, Tz_i, Rx_i, Ry_i, and Rz_i are the modal participation factors of each order mode in each direction, and i is the i-order mode. The weight coefficients of each mode in the summation of strain energy are defined as:

$$facto{r}_i=\frac{FA{C}_i}{{\displaystyle \sum _{i=1}^{20}FA{C}_i}}$$

(8)

The modal Frequencies, modal participation factors and weight coefficients of each order are shown in Table 1.

Table 1. Each order modal frequency, modal participation factor and weight coefficient.

Order	Frequency (Hz)	FACi	Factor
1	226.65	9.144539551	0.277780667
2	380.83	1.733514953	0.052658413
3	501.79	1.861333173	0.056541105
4	598.29	3.403887627	0.103398774
5	653.17	0.011237891	0.00034137
6	665.98	2.104142126	0.063916833
7	827.89	0.962315817	0.029231951
8	883.77	3.975252433	0.120754934
9	961.24	0.7609795	0.023116024
10	1019.73	0.937197945	0.028468953
11	1094.96	1.292080659	0.039249109
12	1232.55	0.291156127	0.008844354
13	1339.63	1.398832706	0.04249188
14	1353.44	2.657591204	0.080728773
15	1389.37	0.486192536	0.014768911
16	1458.25	0.125286375	0.003805783
17	1543.43	0.203094962	0.006169349
18	1666.48	0.509496781	0.015476816
19	1679.48	0.00491114	0.000149184
20	1701.20	1.056859506	0.032103873

According to the weight factor of the table above, in MSC. Patran post-processing, the PCL function is reprogrammed, which is weighted to sum the modal strain energy distribution graph shown in Figure 6.

As can be seen from the diagram above, when the factors of the modal participation factor (i. e. the contribution degree of each mode) are taken into account, the larger the modal participation factor is, the larger the proportion is (i.e., the larger the weighting factor is) in the process of summing the modal strain energy. Finally, a reasonable weak part of the plate for vibration is obtained. The weak link with the vibration moves from the bottom left corner and upper right corner position in the 45° direction of Figure 6 to the central position in the 45° direction of the composite plate. The high strain energy region in Figure 6 is consistent with the previous modes of the plate. That is to say, the shear stiffness of the composite panel is weak.

3.3. Results of the I-Shape Beam

The modes of the composite I-shape beam are shown in Figure 7.

A typical modal strain energy distribution diagram is also extracted, as shown in Figure 8.

Figure 7 and Figure 8 show the vibration characteristics of the beam. It can be seen that the peak displacement appears on the top and bottom edges and webs and the distribution of vibration strain is irregular. There is no way to know for sure whether it is the weak part of the vibration that we are looking at. In MSC.Patran, PCL functions were written for the linear summation of the first 20 order modal strain energy. The distribution of modal strain energy is indicated in Figure 9.

From Figure 9, it can be seen that the high strain energy zone is located at the junction between the lower flange and the web, and the high strain energy of the structure is located along the connection line between the lower flange and the web. According to the formula in Section 3.2 (Equations (7) and (8)), the modal frequencies, modal participation factors and weight coefficients of each order are given in Table 2.

Table 2. Each order modal frequency, modal participation factor and weight coefficient.

Order	Frequency (Hz)	FACi	Factor
1	4.67 × 102	3.67 × 10−1	1.76 × 10−1
2	7.49 × 102	3.15 × 10−1	1.51 × 10−1
3	7.95 × 102	4.90 × 10−1	2.35 × 10−1
4	1.19 × 103	4.42 × 10−2	2.11 × 10−2
5	1.87 × 103	6.70 × 10−2	3.21 × 10−2
6	1.88 × 103	4.50 × 10−2	2.16 × 10−2
7	1.89 × 103	7.07 × 10−2	3.38 × 10−2
8	1.94 × 103	5.25 × 10−2	2.51 × 10−2
9	2.22 × 103	1.51 × 10−2	7.24 × 10−3
10	2.34 × 103	7.52 × 10−3	3.60 × 10−3
11	2.70 × 103	5.92 × 10−3	2.83 × 10−3
12	2.74 × 103	1.38 × 10−1	6.63 × 10−2
13	2.90 × 103	1.86 × 10−1	8.92 × 10−2
14	3.07 × 103	4.17 × 10−3	2.00 × 10−3
15	3.45 × 103	5.30 × 10−2	2.54 × 10−2
16	3.48 × 103	8.36 × 10−2	4.00 × 10−2
17	3.50 × 103	3.24 × 10−2	1.55 × 10−2
18	3.81 × 103	7.48 × 10−2	3.58 × 10−2
19	3.85 × 103	8.60 × 10−3	4.12 × 10−3
20	3.87 × 103	2.78 × 10−2	1.33 × 10−2

According to the weight factor of the table above, in MSC. Patran post-processing, the PCL function is reprogrammed, which is weighted to sum the modal strain energy distribution graph shown in Figure 10.

As can be seen from the diagram above, when the factors of the modal participation factor (i. e. the contribution degree of each mode) are taken into account, the larger the modal participation factor is, the larger the proportion is (i.e., the larger the weighting factor is) in the process of summing the modal strain energy. Finally, a reasonable weak part of vibration is obtained. The weak link with the vibration is transferred from one of the boundary lines in Figure 9 to the upper edges and boundary of the 1/2, 1/4 and 3/4 beam. The high strain energy region in Figure 10 is consistent with the previous modes of the beam. This is the inherent property of vibration of it.

4. Conclusions

Through the modal analysis method of the composite plate and beam, the characteristics of the main modes of every order for a susceptible frequency range are made clear. The distribution of the modal strain energy and the sensitive location of the actual vibration damage are predicted. According to the results of modal strain energy analysis, the weak links with the composite structures are located by weighted summation method, which provides theoretical basis and direction for the design and dynamic modification of them. The results of this round of calculation and analysis show that the weak parts of the structure can be roughly located by the method of weighted summation of modal strain energy, which provides a reference for the vibration reduction of the active vibration control part and a basis for increasing material damping. These parts are also the focus of on-line monitoring, which can further predict the changes and failures of the bearing capacity of the key components of the aviation structures, so as to take accurate and effective measures to prevent structural failure and ensure the safe operation and work of them.