Identification and Mapping of Manufacturability Constraints for Extrusion-Based Additive Manufacturing

Abstract

This article develops and demonstrates a set of design-focused manufacturability constraints for the fused deposition modeling/fused filament fabrication (FDM/FFF) process. These can be mapped from the basic behavior and process characteristics and formulated in terms of implicit or explicit design constraints. When the FDM/FFF process is explored and examined for its natural limitations and behavior, it can provide a set of manufacturing considerations (advantages, limitations, and best practices). These can be converted into manufacturing constraints, which are practical limits on the ability of the process. Finally, these can be formulated in terms of design–useful manufacturability constraints. Many of the constants and parameters must be determined experimentally for specific materials. The final list of 54 major manufacturability constraints presented in this work will better inform designers considering using FDM/FFF as a manufacturing process, and help guide design decisions. After derivation and presentation of the constraint set, extensive discussion about practical implementation is provided at the end of the paper, including advice about experimentally determining constants and appropriate printing parameters. Finally, three case studies are presented which implement the constraints for simple design problems.

1. Introduction

One of the most well-developed and mature additive manufacturing (AM) processes designed for polymer and polymer-composite materials is the fused deposition modeling (FDM) process; this process is also sometimes called fused filament fabrication (FFF), or simply material extrusion AM [1,2,3]. The process typically works by extruding a molten bead (sometimes also called a “road”) of thermoplastic material into elements to selectively trace out the layers of the part. The fusion between the previous layer and the neighboring elements is accomplished via a polymer melt reaction [4,5,6,7,8]. The extruder position and path are driven using g-code (similar to a CNC milling machine); the process is typically monitored by an open-loop control system based on stepper motor position encoders, but other control systems exist [6,7,9,10,11]. The essential hardware components of an FDM machine are the extruder (for melting and depositing the molten raw material), the frame, and the build plate (Figure 1). A number of configurations are available (some examples are shown in Figure 2a–d), each with its own set of advantages and disadvantages; there are others (such as delta robots and robotic arm printers), but the ones shown are the most common 3-degrees-of-freedom configurations. For the purposes of this article, it is assumed that the design process for printed parts is the same regardless of the hardware configuration.

Figure 1. Typical hardware for the FDM process.

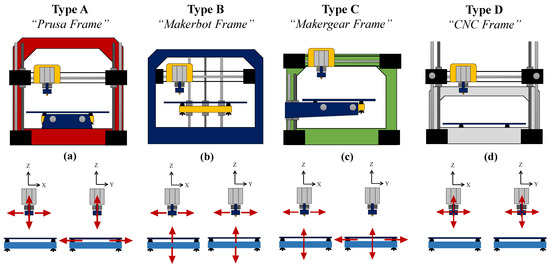
Figure 2. Most common 3-degree-of-freedom (DoF) hardware configurations ((a) Prusa-type frame, (b) Makerbot-type frame, (c) Makergear-type frame, and (d) CNC-type frame), with the degrees of freedom for the extruder and build plate shown in each case. Others exist, such as those built around delta robots and higher-DoF robotic arms.

FDM is a scanning-type AM (ST-AM) process, building each layer as a series of elements laid out in a pattern, typically bounded by a solid shell of elements printed on the outside boundary of each layer. Examples of other ST-AM processes include most laser powder bed fusion processes and laser-based stereolithography. ST-AM is the most common type of AM process, but others exist based on full-layer projection (such as digital light processing) and inkjet-like printing (such as Polyjet and binder jetting processes).

For ST-AM processes, especially FDM, the final bulk material contains small voids/inclusions and is highly anisotropic [12]; however, the pattern of the laid out elements is designable, allowing FDM to be used to create structured and tailored materials by controlling or optimizing the layout of the elements [13,14,15,16]. Effective design of the FDM structure requires knowledge and control of a variety of parameters, the most commonly studied of which are the nominal density, element layout (typically raster angle), layer thickness, print orientation, deposition speed, and processing temperature. A sampling of 30 recent papers related to FDM and discussing manufacturing parameters was collected to determine which parameters are considered most often; the results are shown in Table 1. Material choice was not considered as a parameter in this table, as the best ranges and limits on parameters are dependent on material choice. In most FDM studies, the materials under considerations are treated as separate problems, since each material will have different optimal parameters and constraints. Some FDM materials are amorphous (such as acrylonitrile butadiene styrene (ABS) and polycarbonate) and some are semi-cystalline (such as polylactic acid (PLA) and polyamides (nylon)).

Table 1. Example parameter control/optimization studies from a review of 30 recent papers on FDM.

Refs	Parameters from Sampled Literature
	Density	Infill Pattern	Print Speed	Print Temp	Layer Height	Orientation	Nozzle Size	Shells	Variance Compensation
[17]	▪	▪	▪	▪
[18]		▪
[15]	▪	▪	▪	▪	▪	▪
[19]	▪	▪		▪	▪
[20]	▪
[21]	▪	▪			▪
[22]	▪	▪			▪
[23]	▪	▪				▪
[24]	▪			▪	▪	▪
[25]	▪		▪	▪	▪		▪	▪
[26]	▪	▪					▪
[27]	▪	▪			▪		▪
[28]		▪	▪		▪	▪
[29]	▪	▪			▪			▪
[30]	▪	▪			▪	▪		▪
[31]		▪				▪
[32]	▪			▪	▪
[33]		▪				▪
[8]		▪				▪
[5]	▪	▪			▪	▪	▪	▪
[34]		▪	▪	▪	▪
[35]	▪	▪			▪	▪	▪
[36]		▪				▪
[37]			▪		▪				▪
[38]			▪	▪	▪			▪
[39]		▪
[40]	▪	▪	▪		▪	▪	▪		▪
[41]	▪	▪			▪		▪
[42]			▪	▪	▪		▪
[43]			▪		▪				▪

This concept paper explores the manufacturability constraints (and some related mechanics) for the FDM process. First, the basic, high-level, set of manufacturability constraints specifically for the FDM process is derived. Section 3 refines the constraint set relative to some common materials (ABS, PLA, and polycarbonate) selected for demonstration purposes; this included experimental determination of some of the constraints and sensitivity analysis of the stated assumptions. Finally, three case studies are presented in Section 4 to better demonstrate the concepts presented in this work.

2. FDM Manufacturability Constraints: Concepts

2.1. Parameters vs. Constraints

The printing parameters, being the main drivers for the final material properties for FDM-processed materials, can provide design variables and aid in the development of objective functions [17,22,24] during design. However, the constraints on and between these parameters is an important area which has received little to no attention in the AM literature thus far. Simple example constraints for the parameters shown in Table 1 are given in Table 2. Others certainly exist (including some complex equality constraints that describe relationships between the parameters); however, these provide excellent conceptual examples to demonstrate some kind of relationship between manufacturing parameters and manufacturability constraints. The realistic constraints that will be explored by this concept paper will be far more detailed and specific than the examples shown in Table 2.

Table 2. Example constraints for the general parameters found during the survey presented in Table 1.

Parameter	Example Simple Constraints
Nominal density	Maximum realistic density (<100%), minimum stable density
Raster angle	Minimum and maximum raster angle
Print speed	Minimum and maximum print speed for polymer rheology, minimum and maximum print speed for hardware stability/vibration, limits on motor performance
Extruder temperature	Minimum and maximum temperature for polymer rheology, minimum and maximum temperature for proper hardware function
Layer thickness	Minimum and maximum layer thickness for polymer rheology, minimum and maximum thickness for print time requirements, minimum and maximum thickness for surface quality
Printing orientation	Printing orientation limited by the number of degrees of freedom (DoF) for printing hardware (most printers limited to three DoF)
Nozzle size	Maximum nozzle size ≤ filament size, minimum nozzle size dependent on polymer melt behavior and temperature
Number of shells/contours	Minimum number of shells = minimal stable layer boundary, maximum number of shells ≤ smallest layer dimension divided by $2\times$ nozzle size
Compensation for filament	Minimum = no compensation, maximum extra material that will not disturb surface finish or create nodules/strings during printing

The proper formulation of any design problem requires at least one design objective and a design space to explore for answers which satisfy the objective [44]. In most problem formulations, this involves the identification of decision or design variables, formulation of an objective function, and definition of the design space via a set of constraints. Some toy problems and cases with obvious optima or single global solutions do not need constraints [45,46], but most practical problems will. While the objective function will always be a function of the decision variables, the constraints may take two forms: (1) a function of decision variables or (2) simple bounds on the possible values of each decision variable. For manufacturing-related problems, the bounds will be more commonly encountered [16,47,48,49]. As previously discussed, the various manufacturing parameters provide excellent objective functions and design variables, but do not provide rigorous constraints. In order to avoid manufacturability problems with the final designs [48,50,51] and avoid simplifying the design too much (as is often done in traditional design-for-manufacturing techniques [52,53,54]), it is vital that accurate and useful constraints are generated.

2.2. Mapping Manufacturing Knowledge to Design Constraints

The advantages, limitations, and best practices related to specific manufacturing processes are vital considerations during product design. This is especially true when using complex design methods (e.g., those generated using algorithms, such as topology optimization), as the final design may not actually be manufacturable without the imposition of the manufacturability constraints. This requires a rigorous process of mapping the useful manufacturing knowledge into design-focused manufacturability constraints; the purpose of these is to limit the design candidates to those which are manufacturable using a particular process or series of processes [55,56,57,58,59,60]. Different design scales must also be considered during this mapping; the basic scales referred to in this paper are defined in Figure 3.

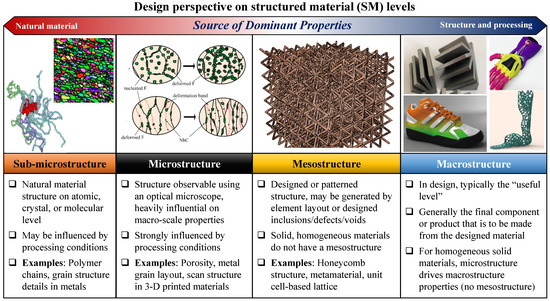
Figure 3. Design scales for materials and parts/products referred to throughout this paper. The mesostructure level will be the most often used and discussed. This chart shows examples of non-polymer materials for completeness, but it should be noted that nearly all FDM materials are thermoplastic polymers.

Manufacturing processes can be classified according to type (subtractive, additive, formative), family (e.g., machining processes), and individual process mechanics [61]. At each of these classifications, a list of process characteristics can be made; the items on this list may overlap heavily with other processes of the same type or family or may be unique to a single process. These characteristics can be divided into advantages, disadvantages, and best practices. The advantages provide some kind of clear cost or schedule benefit or open up the list of possible designs and design features the process can fabricate. The disadvantages do the opposite, helping decrease the size of the design space or increasing cost and schedule issues. Best practices are effectively “soft constraints” which could be either an advantage or disadvantage in particular cases and must be evaluated. The list of manufacturing considerations can cover a very large domain, as shown in Figure 4.

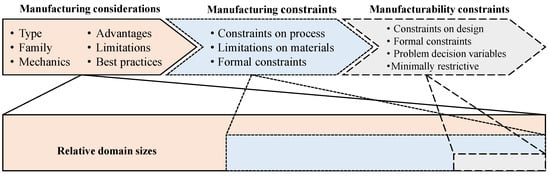
Figure 4. Basic mapping and domain sizes for general manufacturing processes.

Once the set of manufacturing considerations is established (at least conceptually), a set of manufacturing constraints arise naturally. For example, a manufacturing consideration for a machining process is that the cutting tool will generate both force and heat during operation. This naturally implies two manufacturing constraints: (1) that a machined feature must be thick enough to withstand the cutting force from the tool and (2) a feature must be large enough to dissipate heat without damaging the feature or material microstructure. The manufacturing constraints should be more formal than the manufacturing considerations and may require some expert intuition and experience to fully translate in some cases. The manufacturing constraints are also related to the material choice, but whether they are depending on the material selection or vice-versa will be depend on the problem at hand. Since these constraints are based on a specific process and specific set of conditions, the domain is contained within but significantly smaller than that of the manufacturing considerations (Figure 4).

The term “manufacturing” can have a variety of meanings, but one that is widely used and relevant to this work is the definition given by DeGarmo’s Materials and Processes in Manufacturing. Paraphrased, manufacturing is the performance of a series of operations on a product, raw material, or other item such that the successful completion of each operation or step increases its utility or monetary value [61]. With this in mind, the steps to manufacture a product will require a subset of the possible steps that a particular process or set of processes are capable of taking. Therefore, the domain (Figure 4) for the manufacturability constraints (imposed on the design, not the manufacturing process) will be the smallest of the three; this makes sense when considering that the set of relevant constraints bounds the design space for a specific design or design family. In summary:

• The manufacturing considerations are observed or collected by designers and/or experts in manufacturing science. These may be quite conceptual and may be at the level of process type (subtractive (SM), additive (AM), formative (FM)), process family, or specific process and material combination. Manufacturing considerations may provide advantages (e.g., AM increases possible design complexity over machining), limitations (e.g., in machining, features must be reachable by cutting tools), or guidelines/soft constraints (e.g., it is better to machine metal and mold engineering plastics when possible);
• The manufacturing considerations can (typically) be easily converted into manufacturing constraints (i.e., bounds on the applicability of the process);
• The manufacturability constraints on the design itself result directly from the limitations of the manufacturing process and material used.

2.3. FDM: Manufacturing Considerations

The four basic levels of analysis (system, extruder, element design, and element extrusion/fusion) for the FDM process are shown in Figure 5, from which the basic manufacturing considerations can be collected. Assuming a standard FDM machine design with three degrees of freedom, eight essential manufacturing considerations apply (Figure 6):

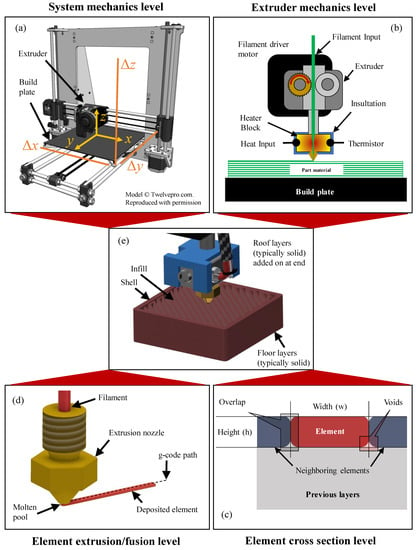
Figure 5. Levels of analysis for FDM. (a) System level, (b) extruder level, (c) element geometry level, and (d) element deposition/fusion level. Panel (e) shows the full process.

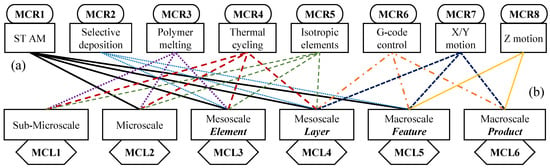
Figure 6. Mapping from the (a) basic eight manufacturing considerations to the (b) six sets of manufacturing constraints at each level of analysis for FDM.

• MCR1—ST-AM: FDM is a scanning-type AM process, where each layer is built from a series of elements (typically of uniform cross-section) which do not fully merge into each other and form an anisotropic material with natural voids and inclusions which may be designed or optimized (Figure 5a,d,e) [8,12,13,14,16,20,49,62,63];
• MCR2—Selective Deposition: Deposition of the raw material is accomplished by extruding a filament through a heated die and selectively depositing it to form the essential elements (Figure 5b–e) [12,20,49,63,64,65];
• MCR3—Polymer Melting: The fusion is accomplished via polymer melting (Figure 5b–d) [63,66,67,68,69,70,71,72];
• MCR4—Thermal Cycling: The bulk material is subjected to uneven thermal cycling during operations (Figure 5b) [66,67,68,70,73,74];
• MCR5—Isotropic Elements: Each element is approximately isotropic or transversely isotropic in terms of mechanical properties (Figure 5b–d) [12,63,75,76,77,78,79,80];
• MCR6—G-Code Control: The extruder die is controlled (generally using an open-loop controller or step counting in the motors) using g-code (Figure 5a,d) [12,49,63,67,81,82,83,84];
• MCR7—X/Y Motion: Motion of the extruder in X or Y directions builds each layer (Figure 5a) (definition for standard 3 DoF system);
• MCR8—Z Motion: Motion of the extruder in Z adds more layers (Figure 5a) (definition for standard three DoF system).

It should be noted here that this model and understanding of FDM is somewhat idealized in order to better understand the process from the perspective of a designer. While the mechanics are the same, the are some considerations that must be taken into account for very detailed and specific studies, say, for example, modeling the melt pool itself as a function of polymer rheology properties. As the material is interacting with the nozzle, there will be small wall slip effects and pressure drop effects, among other things. From the perspective of the product designer, these may or may not be important. This determination will need to be made by each designer, as it is impossible to create a perfect model and the more complex the model is, the more expensive it is.

2.4. FDM: Manufacturing Constraints

Given the manufacturing considerations from the previous section, the manufacturing constraints may be derived. In order to do this in a consistent and useful way, it is important to recognize that the bulk parts or products fabricated via FDM are structured materials, whether or not they are designed [12,13,14,20,62,63]. As such, it is necessary to examine FDM at several scales, which correspond to specific levels of analysis, shown in Figure 3. As demonstrated in Figure 6, FDM can be analyzed at the macro-level (e.g., a small part or large feature), the meso-level (e.g., the “structured” level of the part or product), the micro-level, and the sub-micro-level. It is assumed in this section that the reader has a basic understanding of polymer material behavior and the mechanics of the FDM process. In case of doubt, refer to an earlier section of the paper or one of the references.

2.4.1. Sub-Microstructure Level

At the sub-micro level, the basic material properties of the polymers in use determine the manufacturing constraints (Figure 7). The homogeneity of the local material units (driven often by the quality of the filament used) and the rheology of the polymer determine the manufacturing constraints at this level. These things, in general, must be determined experimentally for each polymer or polymer composite used, and limited choices are currently available since most FDM materials are thermoplastics. It is difficult to impossible to design the specific properties at this level, so the designer is typically required to consider these as fixed parameters (if a material is specified) or criteria for material selection (if not pre-selected). The rheological parameters (including the polymerization behavior and state) are mainly determined by the operating temperature and associated rheological properties for thermoplastics at this level [4,85], so temperature must be carefully specified or established when taking property data or observing behavior. At the sub-micro level, the processing conditions have little to no direct influence, so the experiments used do not have to be directly related to FDM to draw useful conclusions. As shown in Figure 7, seven basic manufacturing constraints directly from FDM can be mapped from the manufacturing considerations at this level.

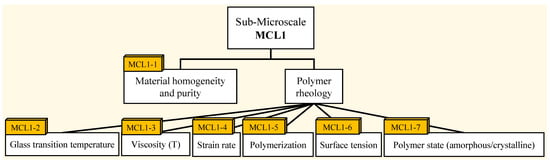
Figure 7. Essential manufacturing constraints at the sub-microscale level.

2.4.2. Microstructure Level

For the micro level (Figure 8), the material properties and processing conditions both influence the manufacturing constraints. Things such as the quality of the polymer chain reformulation (i.e., bonding) after extrusion and fusion, the amount of residual stress in and between each element, the state of the polymer chain (amorphous or semi-crystalline), and the amount of shrinkage (which may be related to residual stresses) after cooling drive the manufacturing constraints at this level. As with the sub-micro level, the values of the resulting manufacturing constraints must be determined experimentally.

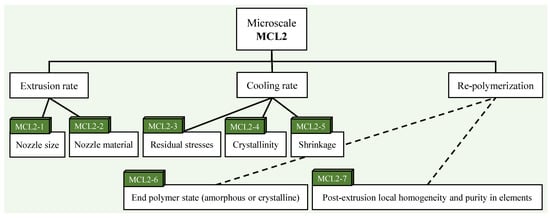
Figure 8. Essential manufacturing constraints at the microscale level.

2.4.3. Mesostructure Level

Using the definition for “meso level” given in Figure 3, FDM will have two levels of mesostructure, one at the individual element level (Figure 9) and one at the layer level (Figure 10). This is due to its nature as a scanning-type AM (ST-AM) process (Figure 5) and the fact that both the element geometry and the layout of the elements (i.e., the layer) can be designed in a simple mechanical way. These two sub-levels will have the largest set of manufacturing constraints of all the levels, but most of these will be simple bounds and inequality constraints. For these levels, the processing conditions and layout of the elements has a much larger impact on the final bulk properties of the part or product than the basic material properties. Of course, the constraints from the sub-micro and micro levels also impact the problem at the meso level through the properties of each element:

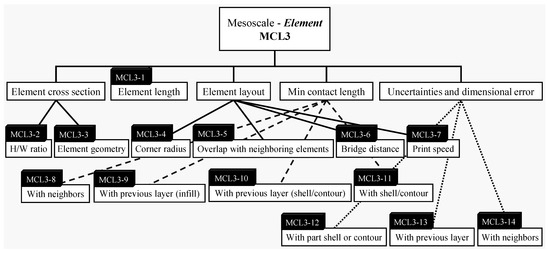
Figure 9. Essential manufacturing constraints at the single-element mesoscale level.

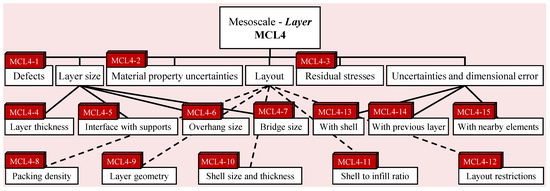
Figure 10. Essential manufacturing constraints at the single-layer mesoscale level.

• Single element mesostructure: As seen in Figure 5c, the element cross section and length can be designed in a similar way to a simple beam or truss member. The major manufacturing constraints at this level (Figure 9) are the selected geometry, height-to-width ratio, minimum length, minimum corner radius, minimum connection length with the last layer and neighboring elements, and a number of other constraints including the various dimensional errors. Given that FDM elements are produced via extrusion, selectively laid out, and are approximately isotropic or transversely isotropic, they can often be seen and treated similarly to beams in design problems;
• Single layer mesostructure: Similar to the single element mesostructure, the single layer element layout can be designed to have controllable (to some degree) mechanical properties. The most important of the manufacturing constraints for this level are restrictions on layer geometry, print direction, position accuracy uncertainties, element packing density, minimum useful layer thickness, the number of shells (“contours” in some of the literature), and the ratio of the shell area to the infill area for the layer. There are a number of others, as shown in Figure 10, which may be relevant. Following on from the discussion concerning the treatment of elements as beams in design problems, the layers may often be designed similarly to 2-D or 2.5D truss problems in practice.

2.4.4. Macrostructure Level

At the macro (“useful”) level, it is assumed that many layers of printed material are present. The size of macroscale features can range from an individual feature to the whole final part or product. In the case of FDM, this level can be further divided into two regions:

• Feature-level macrostructure: Manufacturing constraints at this level (Figure 11) include things like the printing orientation, the minimum layers to be printed, the roof and flood thickness, and interfaces with support material and other features on the part or product. Most of the existing feature catalogs and feature-level design for additive manufacturing guidelines focus on this level; examples include [86,87,88,89,90,91];
  

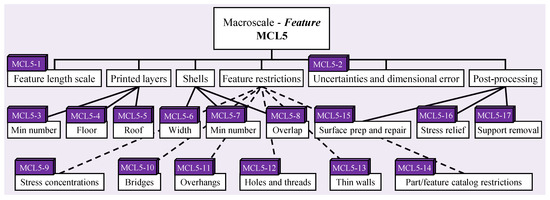  Figure 11. Essential manufacturing constraints at the macroscale (feature) level.
• Part/product-level macrostructure: This level (Figure 12) is the one that will be directly observed or tested by most users and product/part designers and so the manufacturing constraints are mainly concerned with final appearance, post-processing, dimensional accuracy, and interfaces/tolerances with other parts. General product design and success criteria mainly apply to this level. If the additively manufactured product is to be post-processed, it will typically be done with the product-level macroscale in mind.
  

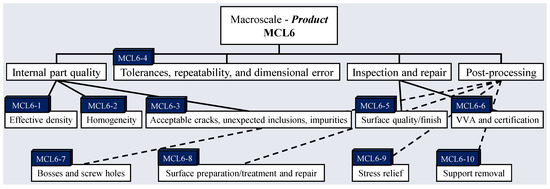  Figure 12. Essential manufacturing constraints at the macroscale (product) level.

2.5. FDM: Manufacturability Constraints

Given the large set of derived manufacturing constraints (i.e., limits on the process capabilities) explored in the previous section, a set of manufacturabilty constraints (i.e., on the design of a product to be fabricated using FDM) can be found. The step of mapping from the process limits to the design limits is a much more simple task than defining or finding all of the relevant process limits. Essentially, for each limit or set of limits, an equivalent design limit must exist to accommodate the parent process limit(s). These design limits (manufacturability constraints) can be used directly in design problems to guarantee (or at least better ensure) that that the final product is indeed manufacturable using FDM.

Compiling all of the process constraints discussed in Section 2.4 (and combining/ refining as needed), the set of design constraints at each level can be found, as shown in Table 3. Finding these constraints is fairly straightforward given the information from Section 2.4 and no special processes are required. In most cases, each of the manufacturability constraints will have more than one parent manufacturing constraint; likewise, a manufacturing constraint may drive more than one manufacturablity constraint. For thermoplastic FDM, all of the constraints directly drive the design decisions; however, in practice, some of the constraints simply drive the selection of materials, some of them limit the printing parameters, and some directly impact the design. Notes are given in the table for each case. Note that exact constraints cannot be derived without selecting a material and possibly collecting some experimental data, due to the different behavior of each of the FDM polymers. In addition, the constraints may not be independent of each other.

Table 3. Manufacturability constraints mapped from the manufacturing constraints and manufacturing consideration for the FDM process. These constraints are subject to three major assumptions: (1) The system has three degrees of freedom, (2) the extruder has a fixed round extrusion nozzle, and (3) the printer hardware is properly tuned. Definitions for the terms in the type, form, parent(s), and method columns are provided, mainly in Section 2.5.

Constraint	Type	Form	Parent(s)	Method	Notes
1. Acceptable material purity and quality	CN	MS	MCL1-1	SD	Usually need the highest quality material possible, but may be traded off for some other objective such as cost or order time
2. Filament additives and colors	CF-CN	MS	MCL1-1 MCL2-6 MCL2-7	PO ${}^1$	For most open-source materials, the presence of additives and dyes is not a major concern, with the exception of PLA [92]. Most commercial or proprietary filaments contain additives, which may or may not be known the to the designer. Flag 1: It is often only possible to obtain partial information regarding this constraint.
3. Environmental conditions	PP-CN	BP	MCL1-1 MCL2-6 MCL2-7	OB	Standard environmental conditions such as temperature, humidity, and air pressure
4. Minimum and maximum extruder temperature	PP-CN	BP	MCL1-2 MCL1-3 MCL1-4 MCL1-5 MCL1-6 MCL4-3	FE, M&S, HL	Common printing parameter that can be used as a constraint. The minimum temperature cannot be lower than the glass transition temperature or higher than the boiling point of the polymer material. However, typically, it is a much more narrow range in which the material flows effectively and can re-polymerize quickly once deposited.
5. Ambient temperature	CF-CN	BP	MCL1-2 MCL1-3 MCL1-4 MCL1-5 MCL1-6 MCL4-3	OB	The ambient temperature may be the temperature around the working environment or may be the local surrounding temperature only (in the case where an enclosure is used).
6. Minimum and maximum print speed	PP-CN	BP	MCL1-2 MCL1-3 MCL1-4 MCL1-5 MCL1-6 MCL3-7 MCL4-3	FE, M&S, HL	Common printing parameter that can be used as a constraint. Print speed is a function of the system dynamics and the molten polymer rheology. In general, faster print speed will result in faster completion but also rougher surface finish, lower dimensional accuracy, and increased incidences of defects in the final part. This is a trade-off that must be found for every material used.
7. Minimum and maximum build plate temperature	PP-CN	BP	MCL1-2 MCL1-3 MCL1-4 MCL1-5 MCL1-6 MCL4-3	FE, M&S, HL	Common printing parameter that can be used as a constraint. For many materials (particularly amorphous glassy polymers such as ABS and polycarbonate), the build plate heater helps keep a large section of the part at a temperature close to (but below) that of the glass transition temperature of the material. This helps to naturally dissipate residual stresses (for polymer materials) and prevent warping and premature bed detachment. Heating above glass transition temperature can cause melting/drooping of features and reduce dimensional accuracy.
8. Jerk and acceleration settings	CF-CN	BP	MCL1-2 MCL1-3 MCL1-4 MCL1-5 MCL1-6 MCL3-7 MCL4-3	SD, FE, CA, HL	Jerk and acceleration settings are not commonly considered by designers but are the best way to control/mitigate system vibration without modifying the basic hardware. Higher settings allow faster printing but decrease dimensional accuracy and increase the probability of print defects.
9. Crystallinity after printing	CF-CN	MS/BP ${}^2$	MCL1-7 MCL4-3	FE, M&S	The final polymer structure of the engineering plastic used has a lot of influence on the final mechanical properties, the degree of anisotropy, and the recyclability of the material. For many crystalline and semi-crystalline polymers, this can be controlled by controlling the cooling rate and with additives. Flag 2: Typically an amorphous or naturally semi-crystalline material will be selected for use, but can also be partially controlled when setting the printing parameters, so could be defined in the form of either material selection or build parameters.
10. Maximum % shrinkage allowed on cooling	CF-CN	MS	MCL2-3 MCL2-4 MCL2-5	SD, FE, M&S, CA	Stakeholder requirement
11. Defect % tolerance	CF-CN	BP	MCL4-1 MCL6-2 MCL6-3	SD	Stakeholder requirement
12. Degree of homogeneity in structure	CF-CN	BP/MS ${}^3$	MCL6-1 MCL6-2	FE, M&S	The higher the degree of homogeneity, the lower the anisotropy in the final part [93,94]. Flag 3: Usually going to be determined by the build parameters but material choice may also have a significant influence.
13. Realistic minimum and maximum element packing density	PP-CN	BP/MS ${}^4$	MCL4-8 MCL2-3 MCL2-4 MCL2-5 MCL2-6 MCL2-7 MCL4-3 MCL6-1	FE, M&S	Flag 4: Typically set using a combination of density and overlap parameters during printing setup, but can also be dependent on material choice. For example, amorphous materials such as ABS and PC can have regular packing densities greater than 99% while the same print settings produce 94–95% density for PLA [36]
14. Support available when needed?	PP-CN	GS	MCL4-5 MCL5-17 MCL6-10	GC	Basic requirement
15. Support removable?	PP-CN	GS	MCL4-5 MCL5-17 MCL6-10	GC	Basic requirement
16. Support does not interfere with function?	PP-CN	GS	MCL4-5 MCL5-17 MCL6-10	GC	Basic requirement
17. Minimum and maximum extruder nozzle size	PP-CN	BP	MCL1-3 MCL1-4 MCL1-6 MCL2-1	HL, FE, M&S	Common printing parameter that can be used as a constraint.
18. Nozzle material	CF-CN	BP ${}^5$	MCL2-2	SD, FE	Nozzle material is often a confounding factor that is not considered during print setup. However, the choice of nozzle material (typically brass or stainless steel, but can include others) can influence how much heat is retained in the immediate area of the extrusion, which can affect the rheological properties of the melt pool. Flag 5: Really can only be controlled as a build parameter.
19. Minimum and maximum deposited element width	PP-CN	BP	MCL3-2 MCL3-3	HL, FE, M&S	In most pre-processing software packages such as Ultimaker Cura, the element width can be varied significantly by over- or under-extruding out of the given nozzle. While calculating the nozzle diamater and the air gap/overlap between elements is the best way (in general) to lay out the elements, varying the element width here can be useful for materials which shrink rapidly (such as PLA with metal powder). This can also be used to improve the effective packing density (and homogeneity) in a part.
20. Minimum and maximum layer/element height	PP-CN	BP	MCL3-2 MCL4-4	HL, FE, M&S	Common printing parameter that can be used as a constraint.
21. Variability in layer height	CF-CN	GS ${}^6$	MCL3-2 MCL4-4	SD, HL, FE, CA	Generally, the layer height is consistent for a single part or at least within each layer. However, this is not necessary, since some freedom is available here even when using a standard 3 degrees-of-freedom (DoF) system. Flag 6: It probably is better to consider this a geometric constraint (due to its influence on the rest of the part) instead of a printing parameter even though it can be accomplished with custom g-code.
22. [Element] Height to width ratio	CN	GS	MCL3-2	FE, M&S	Function of the layer height and nozzle size in most cases. The ideal ratio depends on the material choice but should never be larger than H/W = 2/3 in the experience of the authors. When higher print speed is not available or too risky (due to vibration), using larger elements will decrease manufacturing time; however, this may require a trade-off with surface finish and internal void size.
23. [Element] Element layout restrictions (for non-raster infill layout)	PP-CN	BP/GS ${}^7$	MCL3-4 MCL3-5 MCL3-6 MCL4-9 MCL4-12	HL, FE, M&S, GC	When not using a raster-based layout for the infill, various constraints may be necessary to ensure that the infill is stable. Generally, this will include all of the parameters as a raster-based layout (gaps/overlaps, max and min element lengths, element size, etc.) except the minimum and maximum raster angles. Flag 7: Depending on the layout and parameters, this could be considered either a printing parameter constraint or a geometric constraint.
24. [Element] Minimum and maximum raster angle (for raster layout)	PP-CN	BP	MCL4-9 MCL4-12	HL, FE, M&S, GC	Common printing parameter that can be used as a constraint. It is almost always set as part of the build parameters.
25. [Element] Minimum stand-alone element length	CF-CN	GS/BP ${}^8$	MCL3-1	HL, FE, M&S	The minimum length of a single element so that it is stable and does not warp or curl. It may or may not be attached to another polymer element. Flag 8: This may be a geometric constraint (i.e., determine the minimum length scale for the part or feature) or may be set during the printing parameters.
26. [Element] Minimum and maximum element corner/turn radius	CF-CN	GS/BP ${}^8$	MCL3-4	HL, FE, M&S	The minimum turn radius of a single element so that it is stable and does not warp or curl. It may or may not be attached to another polymer element. See #25, Table 3 for flag.
27. [Element] Minimum contact length with shell/contour	CF-CN	GS/BP ${}^8$	MCL3-11	HL, FE, M&S	Same as #25 except based on a single element in contact with other printed material. See #25, Table 3 for flag.
28. [Element] Minimum contact length with previous layer (infill)	CF-CN	GS/BP ${}^8$	MCL3-9	HL, FE, M&S	Same as #25 except based on a single element in contact with other printed material. See #25, Table 3 for flag.
29. [Element] Minimum contact length with previous layer (shell/contour)	CF-CN	GS/BP ${}^8$	MCL3-10	HL, FE, M&S	Same as #25 except based on a single element in contact with other printed material. See #25, Table 3 for flag.
30. [Element] Limits on overlap or air gap with neighboring elements	PP-CN	BP	MCL3-5	HL, FE, M&S	Common printing parameter that can be used as a constraint. Generally, positive values represent air gaps and negative values represent overlaps.
31. [Element] Maximum bridge distance	CF-CN	GS	MCL3-6	HL, FE, M&S	The maximum distance that a single element can bridge an unsupported gap without collapsing.
32. Shell thickness	PP-CN	BP	MCL4-10 MCL5-6 MCL5-7 MCL5-8	SD, HL, FE, M&S	Common printing parameter that can be used as a constraint. May be a single shell with a fixed width or several shells with an overlap or air gap between them. Two times the minimum shell thickness plus the minimum infill distance for a design defines the lower bound on the length scale for a feature.
33. Shell–infill ratio	CF-CN	GS ${}^9$	MCL4-11	SD, FE, M&S	Common printing parameter that can be used as a constraint. The shell–infill ratio will determine the directional strengths in the FDM structure, especially in cases with large gaps or low-density infill. Flag 9: Best considered a geometric constraint. If control of this is desired during the design, the ratio between the two areas will be specified instead of being automatically generated based on build parameters.
34. [Layer] Maximum bridge distance	CF-CN	GS	MCL4-7	HL, FE, M&S	The maximum unsupported distance between two edges which can be bridged by a single layer.
35. [Layer] Max overhang distance	CF-CN	GS	MCL4-6	HL, FE, M&S	The maximum unsupported overhang distance from a single edge. This is heavily dependent on the material properties and rheology of the polymer, as well as the printing parameters [95]. The overhang angle is important as well, but usually addressed by Constraint #40, Table 3 and similar.
36. Minimum number of layers	PP-CN	BP	MCL5-3	HL, FE, M&S	Standard build parameter which may be used as a constraint
37. Minimum floor and roof thickness	PP-CN	BP	MCL5-4	HL, FE, M&S	Standard build parameter which may be used as a constraint. Only relevant if (1) the infill used is not the same density as the roof and floor or (2) a different infill pattern is used. If 100% density is used and/or a consistent infill pattern is used throughout the printed height, the floor and roof are not needed.
38. Feature geometry: Stress concentrations	CF-CN	GS	MCL5-9 MCL5-14	M&S, GC	Geometric constraints based on modeling, material properties, and design rules developed for specific AM processes. For example, sets of rules which would govern such a feature can be found in works by [87,88,89,96]
39. Feature geometry: Bridges	CF-CN	GS	MCL5-10 MCL5-14	M&S, GC	See #38, Table 3.
40. Feature geometry: Overhangs	CF-CN	GS	MCL5-11 MCL5-14	M&S, GC	See #38, Table 3.
41. Feature geometry: Holes and threads	CF-CN	GS	MCL5-12 MCL5-14 MCL6-7	M&S, GC	See #38, Table 3.
42. Feature geometry: Thin walls	CF-CN	GS	MCL5-13 MCL5-14	M&S, GC	See #38, Table 3.
43. Dimensional error [Element with shell or contour]	CF-CN	BP	MCL3-12	HL, FE, CA	Allowable dimensional error could be based on the size of the part being made, the expected tolerances and repeatability, and other considerations. This is an important consideration for design and one that may drive build parameters and design decisions directly. One of the weaknesses of FDM is the vibration during mechanical motion, as well as the open-loop position control system. The exact amount of error can be calculated using simple experiments for a specific machine and material, but may also include effects from material shrinkage and software/g-code errors [8,97,98,99].
44. Dimensional error [Layer with shell or contour]	CF-CN	BP	MCL4-13	HL, FE, CA	See #43, Table 3.
45. Dimensional error [Element with previous layer]	CF-CN	BP	MCL3-13	HL, FE, CA	See #43, Table 3.
46. Dimensional error [Layer with previous layer]	CF-CN	BP	MCL4-14	HL, FE, CA	See #43, Table 3.
47. Dimensional error [Element with neighboring element]	CF-CN	BP	MCL3-14	HL, FE, CA	See #43, Table 3.
48. Dimensional error [Layer with other out-of-layer elements]	CF-CN	BP	MCL4-15	HL, FE, CA	See #43, Table 3.
49. Dimensional error [Features]	CF-CN	BP	MCL5-2	HL, FE, CA	See #43, Table 3.
50. Allowable uncertainty in essential material properties	CF-CN	MS	MCL4-2	SD, FE	Stakeholder decision which may be the driver of some disparity between modeled and realistic performance for some parts.
51. Min feature length scale to dissipate heat/stress stably	CN	GS	MCL5-1 MCL4-3 MCL2-3 MCL2-4 MCL2-5 MCL5-1	FE, GC	For many design problems using FDM, this is the most important but most different constraint to figure out. In most cases, it is best to use physical experiments to determine the smallest length scale [94,100,101]. In general, the smaller the length scale, the larger the possible design space becomes. The rule of thumb (in the experience of the authors) is to use two shells around a feature plus a single shell-width worth of infill; given a nozzle size of 0.5 mm, the length scale is then 2.5 mm for any standard features. In some cases, particularly when using well-supported thin walls [102,103,104], it may be much smaller and still be stable.
52. Surface prep and repair access	CN	GS	MCL5-15 MCL6-5 MCL6-8	M&S, GC	Basic requirement
53. Allowable surface roughness	CF-CN	BP/MS ${}^{10}$	MCL5-15 MCL6-5 MCL6-8	SD, HL, FE, M&S	Basic requirement. Flag 10: Typically would be controlled via the build parameters (and post-processing, if needed), but could also be influenced by material selection.
54. Inspection, VV&A + Certification	CF-CN	MS/GS ${}^{11}$	MCL6-5 MCL6-6	SD, OB, HL, FE, M&S, CA, GC	Basic requirement for any part that will be used for a practical or real use beyond a prototype. Flag 11: In most cases, will require consideration of both material choice and geometric constraints; for a complete job, both destructive and non-destructive evaluation methods are needed.

The mapped conceptual manufacturability constraints for FDM are shown in Table 3. A total of 54 were identified, but not all of them will apply to all design problems. The large majority of these fall into two categories when not used as constraints:

• Build parameters: Designated as “PP-CN” type constraints in Table 3, these may be used as print parameters or constraints, depending on the objectives and needs of the design. In practice, a mix of constraints and parameters will likely be used;
• Confounding factors: Confounding factors are those which have some influence on a model or system, but the influence is not necessarily known or understood when these are not directly controlled. Designated as “CF-CN” type constraints in Table 3, these could be considered as largely “noise” variables in FDM processes, but could also be controlled or used as constraints in design problems.

The remaining constraints (“CN” in Table 3) are simple constraints (generally generated by the stakeholders as part of the project requirements). The type and form of the constraints should be considered separately in order to best formulate them and use them effectively in the design problem at hand. Just as the type of constraint may be simple (CN), parameter (PP-CN), or confounding factor (CF-CN), the form of the constraints may also be divided into three major categories (Table 3), depending on its main source:

• Build parameters (BP): Constraints directly on the build parameters. These will almost always be simple bounds (e.g., minimum and maximum raster angle) on the parameter in question;
• Material selection (MS): Constraints either driven by or driving material selection (depending on the progress of the design process). These may take the form of bounds, inequality constraints, and equality constraints, depending on what is considered. In the experience of the authors, the more complex constraint equations (e.g., the equality constraints) can be simplified dramatically by setting some variable values to fixed parameters;
• Geometric constraints (GS): These constraints may be driven by design rules (e.g., [87,88]) or by looking at geometric relationships in the design. While any non-bound functions are likely to be simple continuous functions, the possibility of having both inequality and equality constraints often necessesitates simplification, similar to what is done for material selection.

The realistic determination of the constraints may be done in eight major ways in practice (Table 3), namely:

• Stakeholder decision (SD): A value or limit decided and enforced by the designers and other stakeholders. These constraints typically deal with things such as manufacturing time, cost, safety, aesthetics and ergonomics, and the final verification/validation and accreditation process for the part or system being designed. These constraints may have little to no direct input from the process mechanics or material selection;
• Observation (OB): For parameters and constraints that are difficult to control (or simply not of interest to control for the present design problem—the ambient air temperature is a good example), simple observation may provide the needed values;
• Partial observation (PO): Similar to observation but when only partial or incomplete information is available to the designer and other stakeholders. Good examples would be the properties of proprietary filaments with unknown dyes and additives and the exact parameters for proprietary “plug and play” FDM systems;
• Formal experiments (FE): The vast majority of the constraint values and relationships for FDM can be found from simple formal experiments or from reviewing the experimental literature for some common materials;
• Modeling and simulation (M&S): Some of the boundaries and relationships needed can be found using modeling and simulation (for example, finding unhelpful stress concentrations using finite element modeling);
• Hardware limitations (HL): Hardware limitations can be a major source of constraints for FDM and these can usually be easily observed or measured;
• Calculations (CA): Some constraints may be able to calculated directly, such as ratios and relationships between geometric elements;
• Geometry check (GC): Given the numerous excellent sets of design feature catalogs and experimental testing methods, checking that geometry meets the constraints is not difficult to accomplish. This may be done automatically during design or the check may be formulated as a constraint.

To be useful in design, the constraints must be formulated in terms of the problem requirements. For mathematical optimization problems, these could be formulated as mathematical inequality and equality constraints and included in the problem directly. For other kinds of design problems, the constraints may be used to develop or refine design rules, guide requirement definition, and help drive success criteria for the project. Using the generated constraints in Table 3 as a checklist, an effective approach to formulating and using valuable FDM manufacturability constraints is:

• Collection: Note all of the relevant manufacturability constraints, their type, and their form. Formulate or define them in the same form as the rest of the problem.;
• Refinement: Decide which constraints may be simplified and which require additional information (such as material properties or machine performance behavior);
• Completion: For the constraints which require additional information, perform the tests or collect data from the published literature;
• Condensation: Remove all the duplicate, redundant, and inactive constraints;
• Application: Apply to the problem at hand;
• Sensitivity analysis: For any simplifications or assumptions, a sensitivity analysis should done in some form.

3. FDM Manufacturability Constraints: Determination

3.1. General Constraint Set

Table 4 shows the 54 identified constraints and how they are or can be satisfied using a mixture of assumptions, literature review, and physical experiments. For the purposes of this article, three materials were selected as the basis for refining the constraints: ABS, PLA, and polycarbonate. Measurements taken during experiments were done using a digital optical microscope and a Rexbeti (Amazon.com, accessed on 20 February 2021) digital micrometer with a 0.001 mm resolution

Table 4. FDM manufacturability constraint refinement for selected materials (ABS, PLA, and polycarbonate).

Constraint	Values/How Met
1. Acceptable material purity and quality	For the work presented, only pure ABS, PC, and PLA sourced from a reputable company with a good track record should be used. When possible, rolls should be purchased in groups (same filament size, color, etc.) to reduce possible batch variability.
2. Filament additives and colors	See #1, Table 4
3. Environmental conditions	Environmental conditions should follow typical ASTM/ISO standards (e.g., 22–24 °C and 40–60% relative humidity). Any deviation should be carefully recorded and reported with experimental results.
4. Min. and max. extruder temperature	The configuration of the FDM hardware will mainly drive this.
5. Ambient temperature	See #3, Table 4. When possible, printing should be done inside of an enclosure which may or may not be heated directly. It will prevent the spread of toxins in the air and provided a more consistent environment.
6. Minimum and maximum print speed	Similarly to the extrusion temperature, the values are determined by the hardware configuration used.
7. Minimum and maximum build plate temperature	Like the extrusion temperature and print speed, the build plate temperature is driven both by the hardware configuration and the choice of material and bed treatment (in most cases, a treatment is required).
8. Jerk and acceleration settings	Jerk and acceleration settings can be traded off with print speed and other settings to optimize the process. Partially dependent on material choice and hardware configuration.
9. Crystallinity after printing	Of the three materials used to complete the work presented here, ABS and PC are known to be amorphous, while PLA can vary from partially amorphous to semi-crystalline depending on the printing parameters [105,106,107,108,109,110].
10. Maximum % shrinkage allowed on cooling	The manufacturer of the filament used in the presented studies promised an error of less than $2.86\%$ including cooling-related shrinkage. The true rate of shrinkage will be explored in terms of dimensional accuracy later in this section. The true rate of shrinkage should be the value given by the manufacturer or less, or a new filament source should be found.
11. Defect % tolerance	This should be a major consideration for some problems and none at all for others; it depends heavily on the type of problem. For example, fracture testing specimens most likely will have a large notch or designed void which will effectively dominate any small material defect.
12. Degree of homogeneity in structure	Ideally, all variations in homogeneity are designed and contribute to the properties of the natural AM material. However, some random and uncontrollable about of non-homogeneity will remain with current technology.
13. Realistic minimum and maximum element packing density	The packing density should be no less than 95% for the amorphous materials and 90% for semi-crystalline materials.
14. Support available when needed?	Support any parts of the build that need it.
15. Support removable?	See #14, Table 4
16. Support does not interfere with function?	See #14, Table 4
17. Minimum and maximum extruder nozzle size	The constraint for this can be set by the available nozzle sizes. The standard sizes range from $0.2$ mm to $1.0$ mm in increments of $0.05$ mm. Nozzle size choice is a trade-off between print speed and degree of homogeneity/defect tolerance. 0.4–0.6 mm nozzles are the most commonly used sizes.
18. Nozzle material	When possible, only steel nozzles should be used. While more expensive, they have excellent heat distribution and do not wear out via expanding extrusion holes the way brass nozzles do.
19. Minimum and maximum deposited element width	In the experience of the authors, the element width can be up to $0.05$ mm wider or more narrow than the nozzle size on each side of the element without affecting printability. Over-extrusion can help with effective density, but this also reduces the control of the internal structure and diminishes surface finish.
20. Minimum and maximum layer (and element) height	For the materials in use, experience of the author and common best practice directs that the element height-to-width ratio should not be larger than 2/3. Element width is determined mainly the nozzle size.
21. Variability in layer height	When a designed operation, constraints should be places. However, there will be some small variability in layer height from the mechanics of the process and variability in the machine structure. Keeping machines well-tuned and lubricated and replacing worn parts regularly greatly reduces the risk of this.
22. [Element] Height to width ratio	See #20, Table 4
23. [Element] Element layout restrictions (for non-raster infill layout)	For the standard materials used here, no specific layout restrictions were anticipated beyond what will be imposed by other constraints.
24. [Element] Minimum and maximum raster angle (for raster layout)	Raster angle for the work described in this dissertation was limited to range from $0^{\circ }$ to ${90}^{\circ }$.
25. [Element] Minimum stand-alone element length	Minimum element print distance for stable print on a clean polished glass plate with no adhesive or contact with other polymer material. Experimentally determined; see Section 3.
26. [Element] Minimum and maximum element corner/turn radius	Since the radius will be determined by the mechanics of the process and not the adhesion to the build plate, this value is assumed to be valid for first-layer print and printing on top of existing polymer materials. Experimentally determined; see Section 3.
27. [Element] Minimum contact length with shell/contour	Measured as the minimum printed distance needed to ensure stable printing on top of existing polymer material. Experimentally determined; see Section 3.
28. [Element] Minimum contact length with previous layer (infill)	Since the printing is being done on top of existing material, it is assumed that this value will be the same as that determined for #27, Table 4
29. [Element] Minimum contact length with previous layer (shell/contour)	Since the printing is being done on top of existing material, it is assumed that this value will be the same as that determined for #27, Table 4
30. [Element] Limits on overlap or air gap with neighboring elements	Since almost all of the printed parts presented in this dissertation are presented full-density, the maximum air gap will be zero. A small 2% overlap is often used for all printing.
31. [Element] Maximum bridge distance	Assumed to be the same as the maximum bridge length for a layer or better. See #34, Table 4
32. Shell thickness	At least one shell is required but more than one is often used. The choice depends on the application and goals of the design. However, the design of the shell should definitely not be ignored as it is a large driver of the directional properties often seen in FDM materials.
33. Shell-infill ratio	See #32, Table 4
34. [Layer] Maximum bridge distance	Experimentally determined; see Section 3
35. [Layer] Max overhang distance	It is reasonable to assume that the maximum unsupported overhangs with the three standard, non-reinforced materials in question is zero; for a supported overhang, the support material would create a bridge and so not would not longer be an overhang design problem.
36. Minimum number of layers	Based on the experience of the author, a minimum of 5 layers should be printed for structural parts. Soft constraint for most FDM cases.
37. Minimum floor and roof thickness	With the designed element layouts for most of the work presented in this dissertation, floor and roof layers will not be used. However, when they are, it is best to use at least three layers for each in the experience of the author.
38. Feature geometry: Stress concentrations	Should be checked and addressed in the design stage
39. Feature geometry: Bridges	See #34, Table 4
40. Feature geometry: Overhangs	See #35, Table 4
41. Feature geometry: Holes and threads	Should be checked and addressed in the design stage
42. Feature geometry: Thin walls	Should be checked and addressed at the design stage
43. Dimensional error [Element with shell or contour]	It is assumed for this work that the expected dimensional error will be the same percentage as that which was experimentally determined for macro-scale features. See #49, Table 4
44. Dimensional error [Layer with shell or contour]	See #49, Table 4
45. Dimensional error [Element with previous layer]	See #49, Table 4
46. Dimensional error [Layer with previous layer]	See #49, Table 4
47. Dimensional error [Element with neighboring element]	See #49, Table 4
48. Dimensional error [Layer with other out-of-layer elements]	See #49, Table 4
49. Dimensional error [Features]	Experimentally determined, see Section 3.
50. Allowable uncertainty in essential material properties	See #1, #2, and #3, Table 4.
51. Min feature length scale to dissipate heat/stress stably	Based on author experience and previous work [8,56,57], the minimum macro-scale feature scale should be $2.5$ times the nozzle diameter for any parts which are taller than the part length scale. An exception to this is for thin-walled structures which do not need the same support due to their geometry, which keeps the part stable during printing [102] or 2.5D parts with stable features.
52. Surface prep and repair access	Standard design check
53. Allowable surface roughness	Determined by the final application, the interaction of the part with any others in a system, and the desired tolerances
54. Inspection, VV&A + Certification	Process and criteria established during the design phase

3.2. Detailed Constraint Determination

In this section, the experimental determination of constraints 25, 26, 27, 31, 34, and 35 is presented. In addition, dimensional error (constraints 10 and 49) analysis of a previously published dataset [8] is completed to find the values and confidence intervals for the material used in this work. In all cases, the print bed was heated (80 °C for ABS and PC and 60 °C for PLA—pre-heated for 10 min before printing). The extrusion temperatures were 230 °C for ABS, 250 °C for PC, and 210 °C for PLA).

3.2.1. Minimum Element Length on Glass Plate

In order to establish the minimum printed element length needed to securely print on a non-polymer surface, a series or prints were done on a clean, polished glass plate (Figure 13a). The length of any curled or separated material was measured. The test was repeated four times for each material, with the results shown in Figure 13b. The element width was $0.6$ mm and height was $0.2$ mm. No adhesive or other aid was used on the bed; the only treatment was a careful cleaning with isopropyl alcohol between runs. Note the significant difference in performance between the amorphous and semi-crystalline materials.

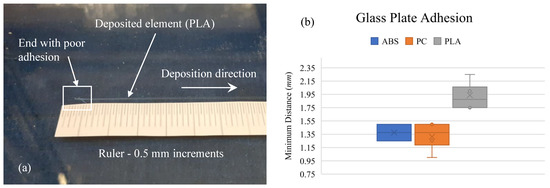
Figure 13. (a) Printed element on glass plate (PLA shown) and (b) minimum printed distance needed for adhesion to glass plate.

3.2.2. Minimum Element Corner Radius

To identify the minimum corner radius possible with the FDM, a 25-mm square film consisting of two printed layers and a single shell printed at 50 mm/s was examined under a microscope. Each corner of each film was examined, for a total of four observations for each material. The results are shown in Figure 14; it was observed for all cases that the corner radii were approximately the same size as the nozzle radii; therefore, a reasonable conclusion is that the lower limit of corner radii is the width of the extrusion nozzle. The element width was $0.6$ mm and height was $0.2$ mm.

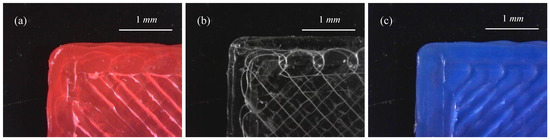
Figure 14. Example corners for printed samples of (a) ABS, (b) PC, and (c) PLA.

3.2.3. Minimum Element Length on Previous Material

A single thin wall, 25-mm high and wide, was printed to estimate the minimum length of adhesion between the deposited and previously printed material. In all cases, the adhesion was excellent and any observed error was much smaller than the nozzle with (Figure 14). The element width was $0.6$ mm and height was $0.2$ mm.

From the presented cases (Figure 15), it is reasonable to conclude that setting the minimum polymer–polymer contact length as the nozzle width would give a conservative constraint. For the specific materials here, a value 0.10–0.25 times the nozzle width would also likely be a valid constraint.

Figure 15. Edge samples to estimate the gap (if any) at the end of each layer of (a) ABS, (b) PC, and (c) PLA.

3.2.4. Maximum Element Bridge Distance

The maximum element bridge distance was estimated using the geometry shown in Figure 16a, where the gap varied from 1 mm to 10 mm in 1-mm increments. Two different print speeds were used (10 mm/s and 50 mm/s) for each material. The bridge length was examined in several studies, which were reviewed in Table 5 in order to compare with the results found here. Note the very wide variance between materials, even when controlling for the print speed. As seen in Figure 16, the longest stable bridge was taken as the maximum approximate bridge length for that material/speed combination.

Figure 16. Bridge length test setup and results. (a) Sample geometry, (b) results for ABS, (c) results for PC, and (d) results for PLA.

Table 5. Some reported bridge lengths from the FDM literature compared with results found in this work. Note that only PLA-based studies were found in the literature, while studies for all three materials under consideration were completed.

Study	Material	Stable Bridge Length
[111]	PLA	0.5–5.5 mm
[112]	PLA	0.5–4.0 mm
[113]	PLA	0.5–5.5 mm
Current (70 mm/s)	ABS	3.0 mm
Current (70 mm/s)	PC	7.0 mm
Current (70 mm/s)	PLA	3.0 mm
Current (20 mm/s)	ABS	6.0 mm
Current (20 mm/s)	PC	8.0 mm
Current (20 mm/s)	PLA	4.0 mm

3.2.5. Dimensional Error

To find the expected dimensional error, a dataset published previously by the author and colleagues [8,114] was analyzed (Figure 17). Note that this data analysis is new and was not part of the original studies that reported the dataset. It was based on the measurement of ASTM-specified IZOD testing samples, with the nominal Z, C, and E dimensions coming from ASTM-D256-10(2018) (Figure 17). Note that the printing parameters were slightly different (most importantly, the element width was $0.4$ mm with a height of $0.2$ mm) from what is used elsewhere in this paper, but it is assumed that the error between what is reported in this study and the current conditions is trivial; see the discussion on sensitivity analysis later in this paper. For the three materials examined, the observed errors (both raw and root mean squared (RMS) error) were equal to or smaller than the nozzle size.

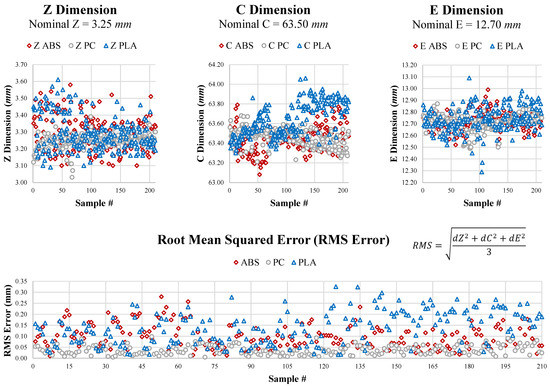
Figure 17. True vs. nominal dimensions for Z, C, and E as well as the root mean squared error [8,114].

3.3. Sensitivity Analysis

In this sensitivity analysis (Table 6), the assumptions and simplifications from Table 4 and elsewhere in this work are formally laid out. In each case, the consequences and impact of a particular assumption or simplification being incorrect or poor is presented.

Table 6. Sensitivity analysis on assumptions for the presented constraint set to be applied to the work in this paper. If a mitigation strategy has been put in place for the work presented, it will be specified in the table. If not (mitigation not needed or not possible), the entry for that assumption will be “None”.

Assumption	Risk if Wrong	Likelihood	Mitigation
1. The material used in this work is of good, consistent quality	Small increase in variability and error in the final results of any study	Low to moderate	Select material colors and brands with good historical behavior
2. Using the same color and brand of filament for all cases in this dissertation will eliminate or minimize dye and manufacturing impacts on the rolls of raw filament	Small increase in uncertainty about measured properties	Low	None
3. Environmental conditions required for standardized printing and testing can be accomplished	Increase in uncertainty concerning measured properties and behavior	Moderate	Careful conditioning of specimens and monitoring of environmental conditions
4. Jerk and acceleration can be treated as parameters and controlled during process	Effects on material placement, increase of dimensional error, poorer surface finish, more uncertainty in final material properties	Low	Careful settings and regular setting checks during printing
5. Amorphous materials will not fundamentally change their structure before and after printing	Material properties can change and become unpredictable	Very low	None
6. Semi-crystalline materials will not fundamentally change their structure before and after printing	Material properties can change and become unpredictable	Moderate to high	Careful process parameter selection, as well as full description of risk to reader of described results.
7. The expected shrinkage of the material on cooling is no more than that reported by the filament manufacturer	Less control over element geometry and repeatabilty and lower effective bulk density	Low	The manufacturer-given value is likely conservative, so no mitigation taken in this work.
8. There is no statistically significant variability in layer height unless specifically designed into the final g-code	Decreased control of structure and increased likelihood of cracks forming between layers	Low	Careful machine tuning, with regular lubrication and bearing and belt inspections.
9. The minimum print stable print length on any existing material is the same as estimated for a single element in Section 3.2.3	Less control over material structure and increased chance of unplanned voids and cracks	Very low	None
10. Bridge and overhang distances are similar for both individual elements and whole layers	Failed bridges and overhangs	Low	None
11. For fracture testing samples, no significant stress concentrations exist except those specifically designed into the structure to produce a controlled fracture	Unpredictable and unstable testing results	Very low	All parts and specimens inspected for obvious defects before being tested
12. Expected dimensional error (in terms of %) the same for all parts, scales, and areas of print	Reduced control of element geometry and placement	Moderate	Print with internal overlap of 2%, carefully maintain hardware, and reduce print speed and jerk when possible.
13. Roof and floor thickness should be at least three layers	Wasted material and print time	Low to moderate	None
14. Minimum length scale (for part or feature) is 2.5 times nozzle diameter (except self-supporting thin walled structures) to allow for two shells and some infill	Slightly reduced design freedom, wasted material, and longer printing time	Low to moderate	None

4. Case Studies

4.1. Case Study 1: 2.5D Designs with Stable Features

The first case study explores three simple problems (Figure 18) that could be represented as 2-D or 2.5-D (2-D + thickness) design representations subject to the constraints developed in this paper. In the first case, (Designs 1a and 1b), a simple fan cover was designed with manually laid out features. For Design 1a, a deposition nozzle of w = 0.4 mm was used with a layer thickness of h = 0.2 mm (h/w = 0.5), with each of the thicker features being two elements wide for stability and one element wide for the smaller features. For design 1b, a nozzle of w = 1.0 mm (h/w = 0.2) was used, with resulting changes in the design.

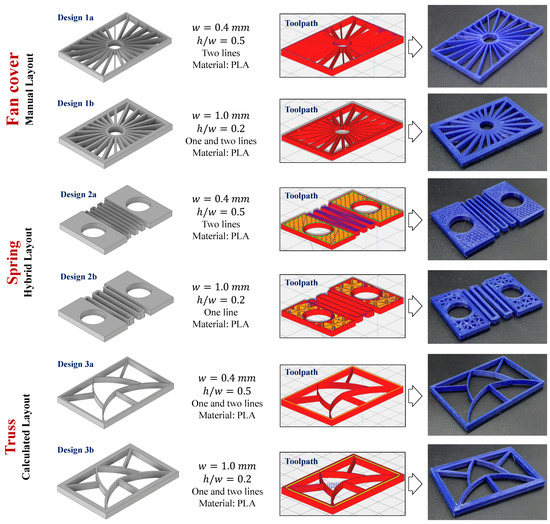
Figure 18. Results of Case Study 1.

In the case of Design 2, a hybrid design method was used, with the spring coil being manually laid out and the infill for the solid area being calculated and laid out in a series of triangles. The last problem dealt with a truss, where the layout could be calculated in response to a specific mechanical problem. This case study demonstrated that the imposition of effective constraints on the parameters heavily influenced the designs. In addition, it showed that all of the constrained designs, regardless of complexity, were manufacturable on the first attempt.

4.2. Case Study 2: Designed Infill Geometry in Defined Space

In this case study, the computational layout of a 20-mm cubic shell with a low-density designed core was generated using Ultimaker Cura from PLA. All of the FDM constraints generated in this paper were applied to ensure manufacturability, even on areas with bridges and very thin features. In addition to the objectives (lay out the elements efficiently based on inputs) and constraints, the major design inputs to the software tool were:

• The geometry within the shell was only allowed to be a single element thick, so the designed core only presented one level of designable mesostructure;
• The deposition nozzle used was 0.5 mm in diameter and the deposition width was defined as 0.505 mm to account for material shrinkage. This setting was found to be the best for the transparent PLA used in the study after several trials;
• The w/h ratio was selected to be 5/2. An overlap setting was not needed, since the designed area was only allowed to be one element thick.

Four basic layouts were selected, specifically 3D cross, quarter cubic, gyroid, and standard raster lines. Figure 19 shows the layouts for Layer 10, Layer 25, Layer 50, and Layer 90 for each of the cases. Only the gyroid contained an unsupported bridge, so a maximum unsupported bridge length was set at 3 mm (see Section 3.2.4) before the design generation. Since it was impractical to use support material for these designs, this was used to limit the size of the gyroid elements. The layouts were driven by the requirement that the 3-D cross and quarter cubic cases were to occupy a total of 10% of the open space, the gyroid was to be close to 15% dense with the bridge requirement (so the density is slightly higher), and the elements in raster case were to have a diagonal (corner-to-corner) length of approximately 4 mm. Note that all of the cases could easily have been printed without the outer shell (or had the shell removed after printing). Including the shell was a design choice, as the concept could be explored with or without the shell. This case study did not solve a specific design problem and was focused on demonstrating that that the designed structures (with several different layouts, including those that varied significantly between layers) could be accurately manufactured, since the design parameters were based on the mechanics of the selected process. As shown in Figure 19, the manufacturing was successful, with no significant manufacturing defects noted upon examination under a microscope.

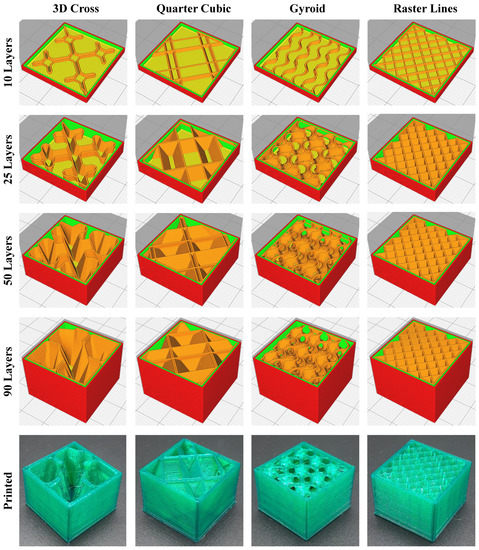
Figure 19. Results of Case Study 2.

4.3. Case Study 3: Minimal Surfaces with Second Mesostructure

In this case study, the design of two mesostructure levels is explored for two basic minimal surfaces (gyroid—a triply-periodic surface and a Scherk tower—a singly-periodic structure) which are given a wall thickness. The internal structure (the lower mesostructure level) for each case is designed the same way as described in Case Study 2.

In these cases, the gyroid (defined within a 125-mm cubic design space) is given a wall thickness of 5 mm, while the Scherk surface is given a wall thickness of 2 mm and calculated within a design space with a 50-mm square base and 160-mm height (Figure 20). The basic surface figures, generating functions, and Matlab code for generating the surfaces came from a technical report on generating minimal surface models by Muna & Patterson [115]. There are numerous ways to translate the surface model into a solid STL file, the best of which is to use the surf2solid tool in Matlab with the surface generation code published in [115]. The functions used to generate the minimal surfaces were:

$$f_{gyroid}=sin\left(x\right)cos\left(y\right)+sin\left(y\right)cos\left(z\right)+sin\left(z\right)cos\left(x\right)[x,y,z\in [0,125]\mathrm{mm}]$$

(1)

$$f_{scherk}=sinh\left(x\right)sinh\left(y\right)-sinh\left(z\right)[x,y\in [0,50]\mathrm{mm},z\in [0,160]\mathrm{mm}]$$

(2)

Figure 20. Case Study 3. (a) Mathematical model of the gyroid, (b) mathematical model of the Scherk surface, (c) g-code for final gyroid model, (d) g-code for final Scherk surface model, and (e–f) successfully manufactured designs.

Example surfaces are shown in Figure 20a,b, while the g-code for the generated surfaces for this case study can be seen in Figure 20c,d. Partial prints (to show the internal mesostructure) of each can be seen the last two panels of the figure. Both were printed from PLA using FDM and used the same settings as Case Study 1, with the exception that the Scherk surface was printed at nearly 100% density (so only natural voids determined meso-scale properties). In this case, the internal mesostructure was a series of concentric rings. The internal mesostructure for the gyroid (clearly seen in Figure 20e), was identical to that of the raster case in Case Study 2, with the exception that the diagonal dimension of the resulting squares was 5 mm.

5. Closing Remarks

In this article, the manufacturability constraints for the fused deposition modeling (FDM) process are mapped, defined, refined, and presented. While some of the constraints and parameters presented here may be somewhat idealized, this is best for developing a good design perspective on the process as it requires much less technical background knowledge and expertise to understand and used.

The results of the mapping and constraint generation were carefully tabulated and presented in such a way that the are useful for a variety of design problems. Whether using classic design-for-manufacturing or one of the more modern approaches, these constraints will aid in problem formulation and process understanding. Having well-defined manufacturability constraints will aid designers in making good decisions, which will result in higher-quality designs with a much lower risk of design-process mismatch. Careful definition of the process in terms of it manufacturability constraints will also help anyone using the process for design or manufacturing to better understand its capabilities, limitations, and the best practices for using it.