Collaborative Vehicle-Mounted Multi-UAV Routing and Scheduling Optimization for Remote Sensing Observations
Highlights
- A multi-UAV routing and scheduling framework for remote sensing observation tasks is proposed, and comparative experiments with classical algorithms demonstrate the superiority of the proposed method.
- A Multi-Region Edge Recombination Crossover operator and an Adaptive Hybrid Mutation mechanism are designed to enhance the genetic algorithm’s performance in multi-UAV task scheduling and routing optimization.
- The routing and scheduling schemes of vehicle-mounted multi-UAV systems are optimized, significantly reducing the coverage cost of remote sensing observations.
- The proposed framework provides practical scheduling guidance for large-scale remote sensing applications using vehicle-mounted multi-UAV systems, effectively minimizing task redundancy.
Abstract
1. Introduction
2. Related Work
2.1. Problem Description
- Prior to mission execution, the control system has complete knowledge of all task regions, including their number, locations, and boundaries.
- For remote-sensing mapping, orthophotos are used for wide-area coverage. Thus, each UAV flies at a fixed altitude and constant speed, maintaining constant forward and side overlap rates within each region. The ground sampling distance (GSD) is computed automatically from the flight altitude.
- UAV energy consumption is modeled as proportional to flight time, and aerodynamic models are not considered. UAVs are assumed to remain undamaged throughout the mission.
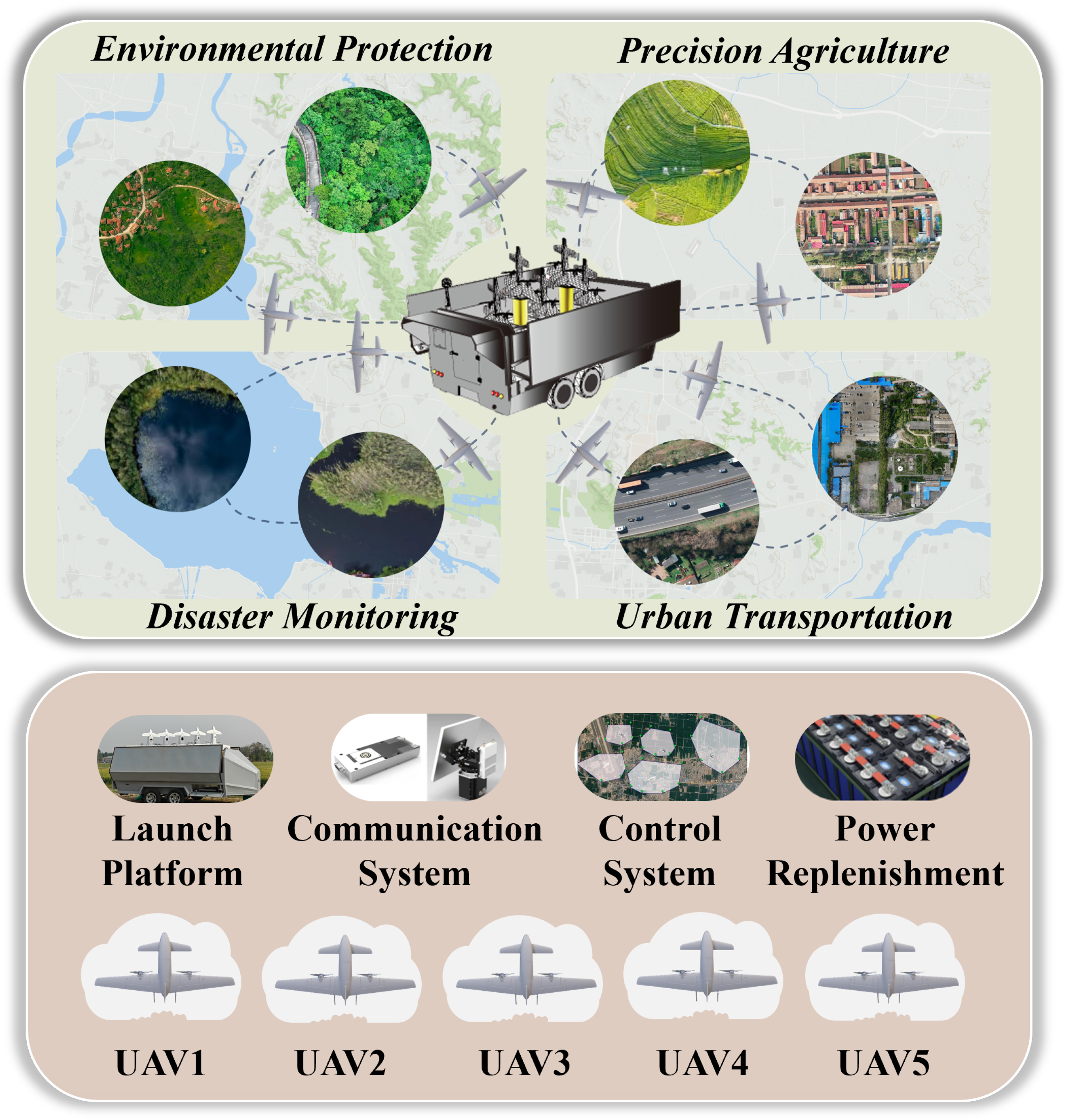
- UAVs are launched from the vehicle and are required to return to the vehicle upon mission completion.
2.2. Scheduling and Coverage Model Formulation
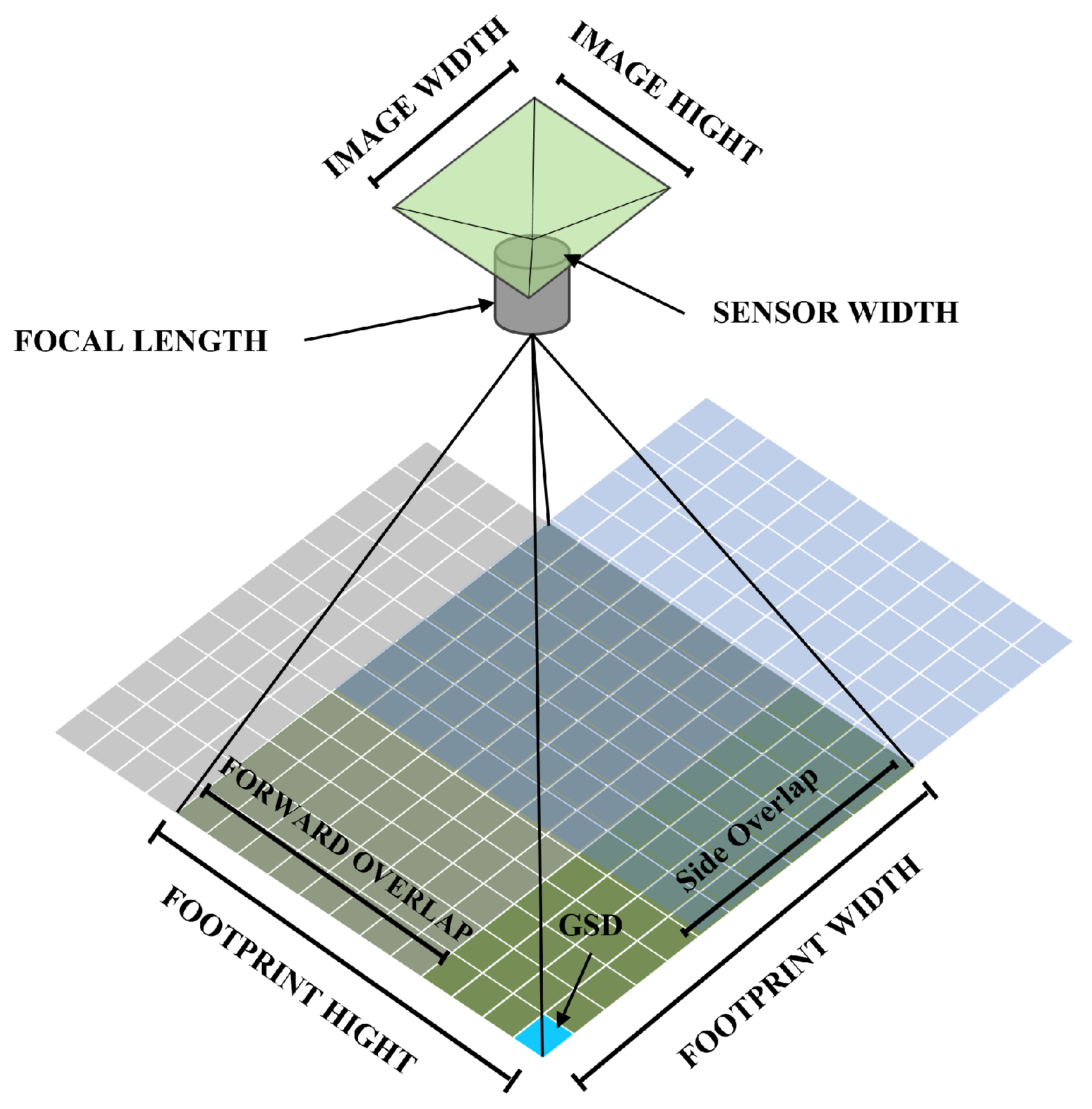
2.3. Camera Model
3. Energy-Optimal Coverage Planning Model
3.1. Area Discretization and Value Estimation
3.2. Linear Relaxation Solving
3.3. Atomic Strips Selection
3.4. Constructing Cycle Cover
3.5. Path Connection and Optimization
4. Multi-UAV Scheduling and Routing
4.1. Chromosome Encoding
4.2. Population Selection
4.3. Multi-Region Edge Recombination Crossover
- Identify all neighbors of from the adjacency list that are in and have not yet been visited.
- If there are candidate neighbors, select next based on the following priority:
- (a)
- Prefer a neighbor that forms a common edge with .
- (b)
- If there are multiple common-edge neighbors or none, prefer the neighbor connected by the shortest edge distance.
- (c)
- If ties still exist, prefer the neighbor that has the fewest unvisited neighbors itself. This heuristic reduces the risk of isolating other nodes later.
- If there are no such neighbors (i.e., is an isolated node), randomly select an unvisited node from the remainder of to be next.
- Add next to mark it as visited, and update .
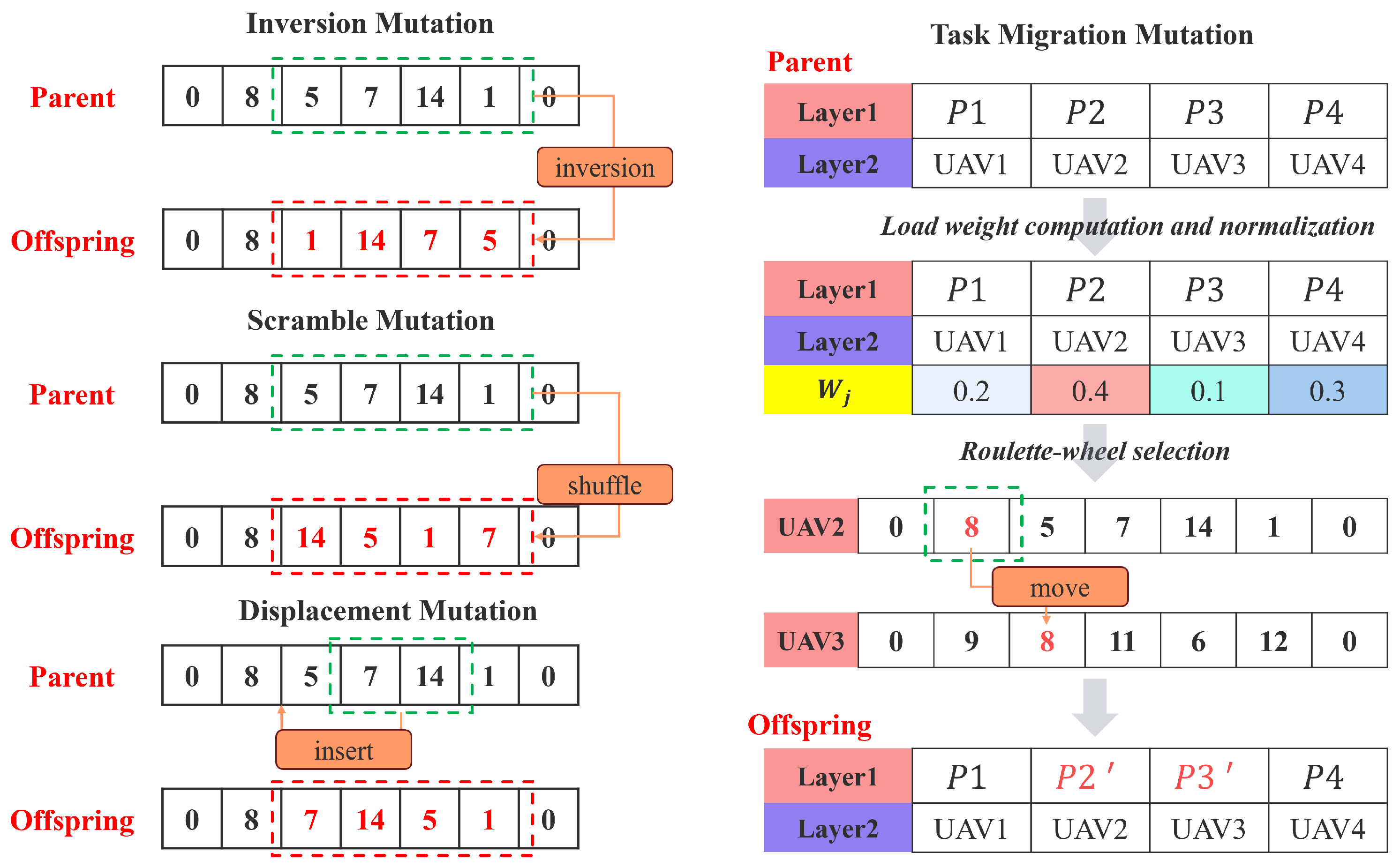
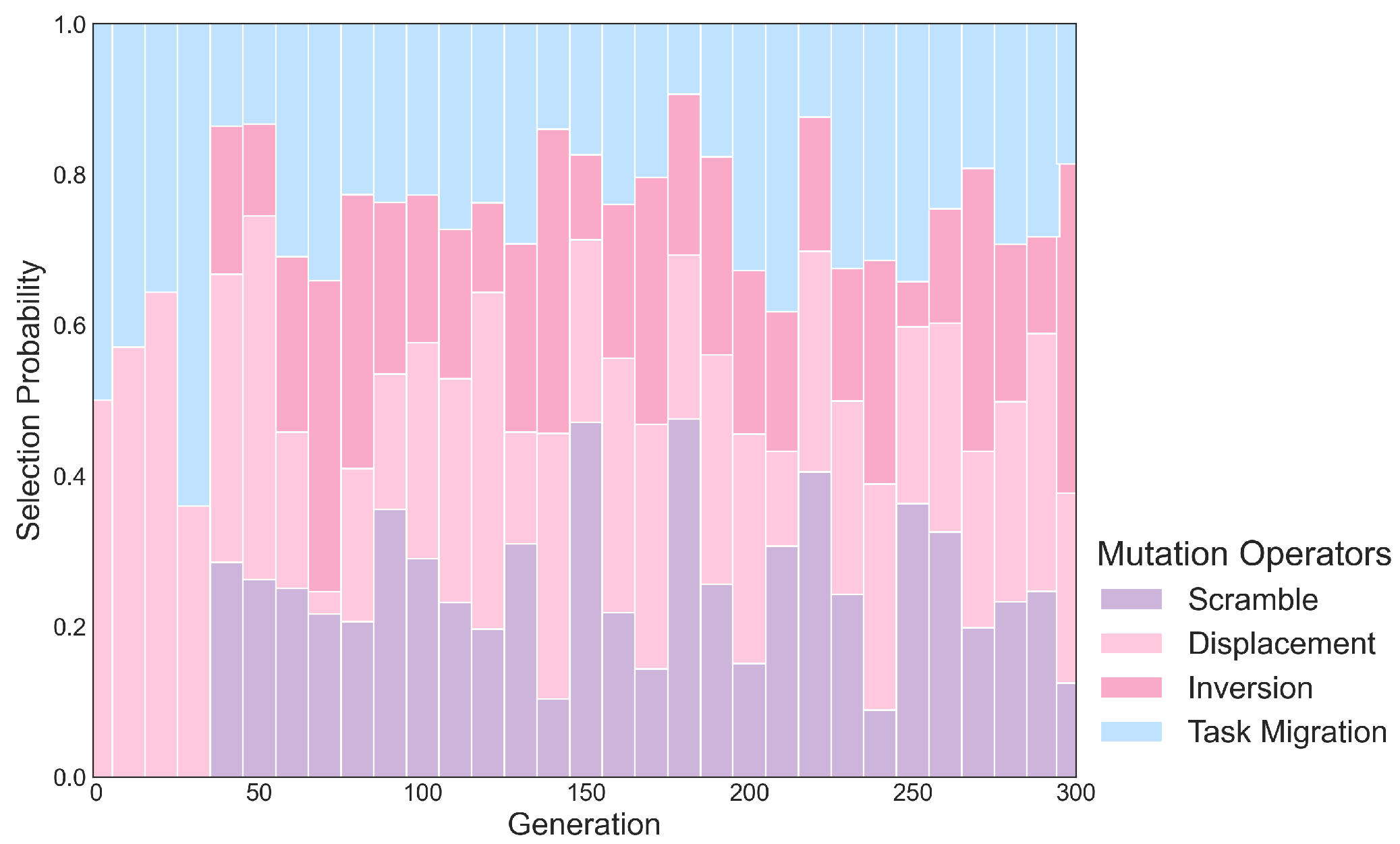
4.4. Adaptive Hybrid Mutation Mechanism
- For each route , load weight is calculated, which synthesizes the total intrinsic weight of tasks in the route and its expected execution cost, and is then normalized.
- Source route is selected from all routes using roulette wheel selection based on the load weights . Routes with higher loads have a greater chance of being selected.
- The route with the current minimum load weight is chosen as the target route , ensuring .
- If both and contain a sufficient number of tasks (at least two), a region is randomly removed from .
- The region is then added to . The insertion position is determined by a greedy best-insertion strategy, which tries all possible insertion points and selects the one that results in the minimum increase in the estimated cost of .
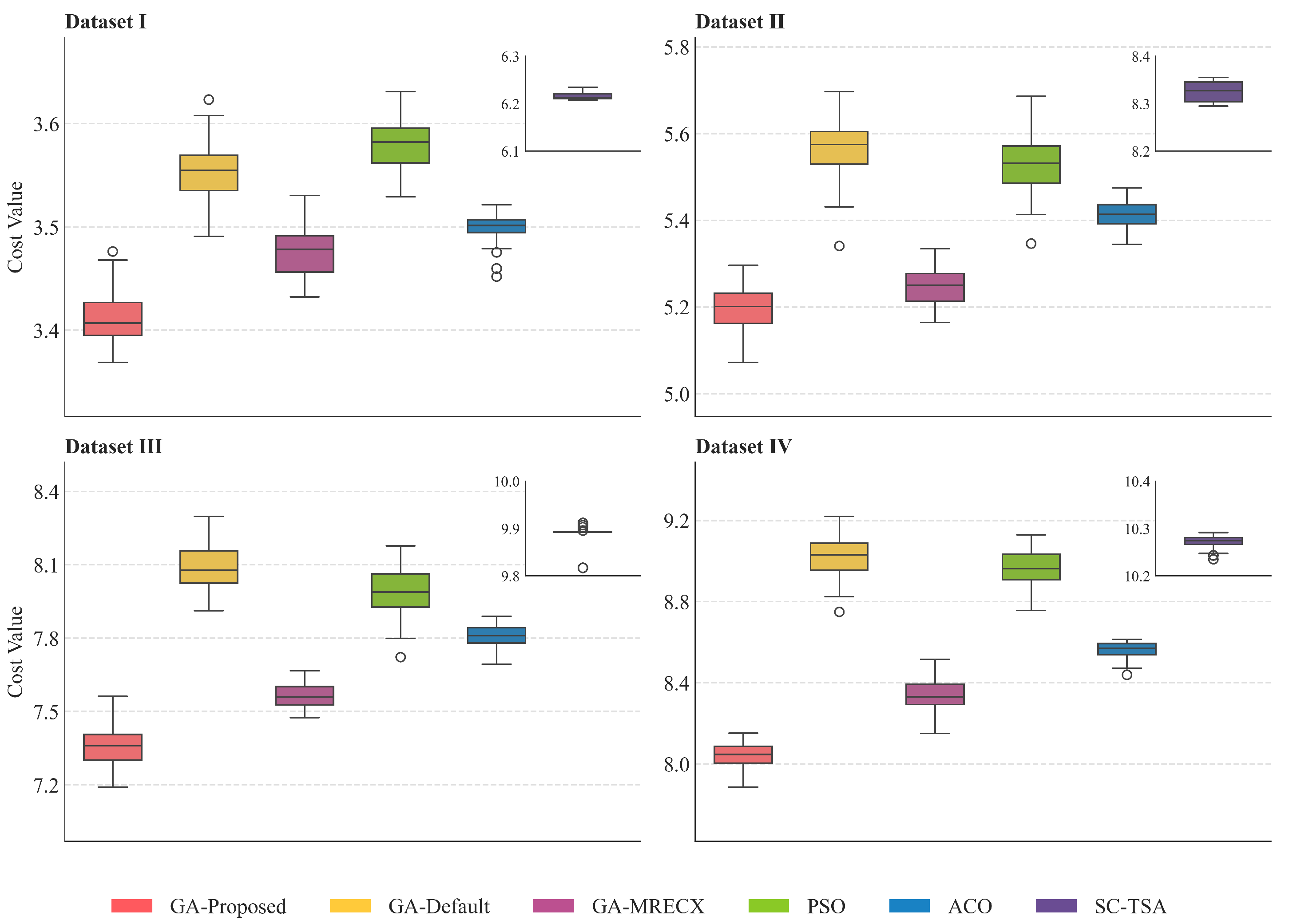
5. Experimental Results and Analysis
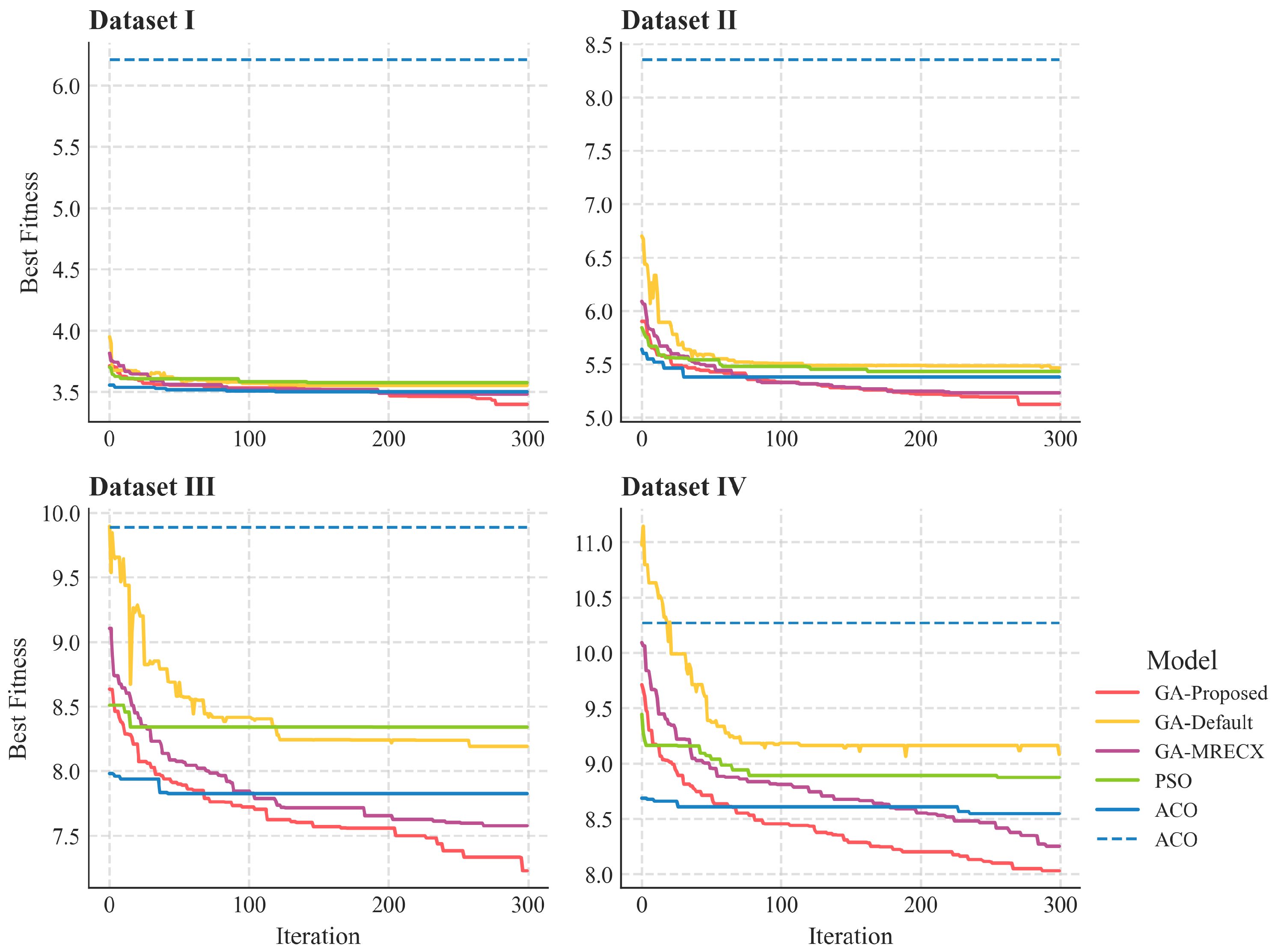
5.1. Numerical Simulation
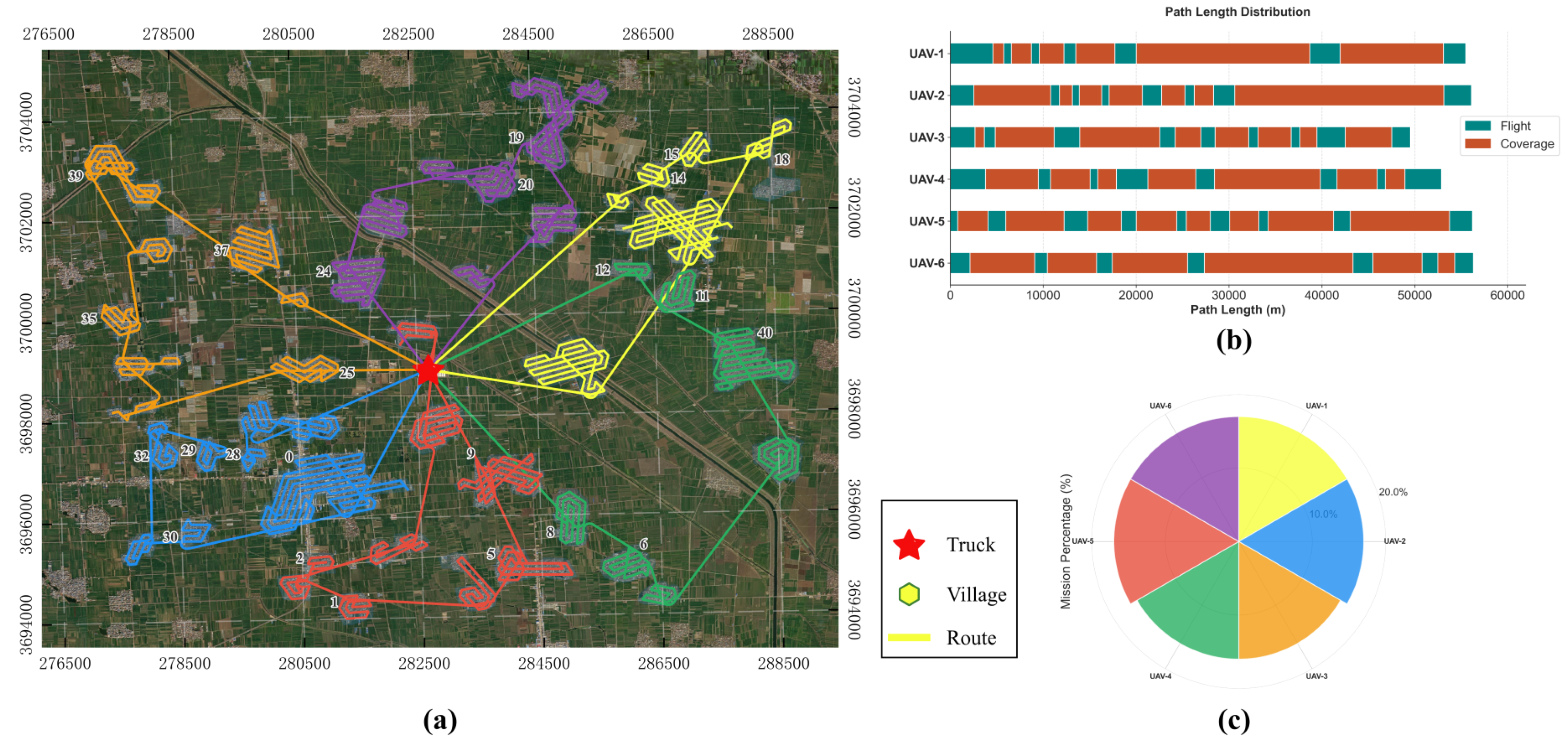
5.2. Collaborative Trajectories
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Model | Parameters |
|---|---|
| GA-Default | , , , |
| GA-MRECX | , , , |
| GA-Proposed | , , , |
| PSO | , , , , |
| ACO | , , , , |
| SC-TSA | , , , |
References
- Ji, R.; Tan, K.; Wang, X.; Tang, S.; Sun, J.; Niu, C.; Pan, C. PatchOut: A novel patch-free approach based on a transformer-CNN hybrid framework for fine-grained land-cover classification on large-scale airborne hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2025, 138, 104457. [Google Scholar] [CrossRef]
- La Salandra, M.; Nicotri, S.; Donvito, G.; Italiano, A.; Colacicco, R.; Miniello, G.; Lapietra, I.; Roseto, R.; Dellino, P.; Capolongo, D. A paradigm shift in processing large UAV image datasets for emergency management of natural hazards. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 103996. [Google Scholar] [CrossRef]
- Qin, K.; Li, J.; Zlatanova, S.; Wu, H.; Gao, Y.; Li, Y.; Shen, S.; Qu, X.; Yang, Z.; Zhang, Z.; et al. Novel UAV-based 3D reconstruction using dense LiDAR point cloud and imagery: A geometry-aware 3D gaussian splatting approach. Int. J. Appl. Earth Obs. Geoinf. 2025, 140, 104590. [Google Scholar] [CrossRef]
- Guo, X.; Cheng, J.; Yin, C.; Li, Q.; Chen, R.; Fang, J. The extraordinary Zhengzhou flood of 7/20, 2021: How extreme weather and human response compounding to the disaster. Cities 2023, 134, 104168. [Google Scholar] [CrossRef]
- Apostolidis, S.D.; Kapoutsis, P.C.; Kapoutsis, A.C.; Kosmatopoulos, E.B. Cooperative multi-UAV coverage mission planning platform for remote sensing applications. Auton. Robot. 2022, 46, 373–400. [Google Scholar] [CrossRef]
- Liao, X.; Yue, H.; Liu, R.; Luo, X.; Luo, B.; Lu, M.; Ryan, B.; Ye, H. Launching an unmanned aerial vehicle remote sensing data carrier: Concept, key components and prospects. Int. J. Digit. Earth 2020, 13, 1172–1185. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Yakushiji, K.; Fujita, H.; Murata, M.; Hiroi, N.; Hamabe, Y.; Yakushiji, F. Short-range transportation using unmanned aerial vehicles (UAVs) during disasters in Japan. Drones 2020, 4, 68. [Google Scholar] [CrossRef]
- Dong, Y.; Din, M.U.; Lagala, F.; Kuang, H.; Sun, J.; Yang, S.; Hussain, I.; He, S. Drone Carrier: An Integrated Unmanned Surface Vehicle for Autonomous Inspection and Intervention in GNSS-Denied Maritime Environment. arXiv 2025, arXiv:2501.12869. [Google Scholar] [CrossRef]
- Tahir, A.; Böling, J.; Haghbayan, M.H.; Toivonen, H.T.; Plosila, J. Swarms of unmanned aerial vehicles—A survey. J. Ind. Inf. Integr. 2019, 16, 100106. [Google Scholar] [CrossRef]
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-art and future research challenges in uav swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Liu, J.; Liao, X.; Ye, H.; Yue, H.; Wang, Y.; Tan, X.; Wang, D. UAV swarm scheduling method for remote sensing observations during emergency scenarios. Remote Sens. 2022, 14, 1406. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Yang, Y.; Liu, X. Cooperative mapping task assignment of heterogeneous multi-UAV using an improved genetic algorithm. Knowl.-Based Syst. 2024, 296, 111830. [Google Scholar] [CrossRef]
- Muñoz, A.; Rubio, F. Evaluating genetic algorithms through the approximability hierarchy. J. Comput. Sci. 2021, 53, 101388. [Google Scholar] [CrossRef]
- Pasha, J.; Elmi, Z.; Purkayastha, S.; Fathollahi-Fard, A.M.; Ge, Y.E.; Lau, Y.Y.; Dulebenets, M.A. The drone scheduling problem: A systematic state-of-the-art review. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14224–14247. [Google Scholar] [CrossRef]
- Hu, M.; Liu, W.; Peng, K.; Ma, X.; Cheng, W.; Liu, J.; Li, B. Joint routing and scheduling for vehicle-assisted multidrone surveillance. IEEE Internet Things J. 2018, 6, 1781–1790. [Google Scholar] [CrossRef]
- Kim, S.; Moon, I. Traveling salesman problem with a drone station. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 42–52. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Chen, J.; Xie, J. Joint task scheduling, routing, and charging for multi-UAV based mobile edge computing. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Hong, D.; Lee, S.; Cho, Y.H.; Baek, D.; Kim, J.; Chang, N. Energy-Efficient Online Path Planning of Multiple Drones Using Reinforcement Learning. IEEE Trans. Veh. Technol. 2021, 70, 9725–9740. [Google Scholar] [CrossRef]
- Mao, X.; Wu, G.; Fan, M.; Cao, Z.; Pedrycz, W. DL-DRL: A Double-Level Deep Reinforcement Learning Approach for Large-Scale Task Scheduling of Multi-UAV. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1028–1044. [Google Scholar] [CrossRef]
- Panowicz, R.; Stecz, W. Robust Optimization Models for Planning Drone Swarm Missions. Drones 2024, 8, 572. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, Z.; Li, Y.; Xiao, B.; Xun, Y. Multi-UAV Adaptive Cooperative Formation Trajectory Planning Based on an Improved MATD3 Algorithm of Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 12484–12499. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S.J.; Sparks, A.G. UAV cooperative multiple task assignments using genetic algorithms. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 2989–2994. [Google Scholar]
- Zhu, W.; Li, L.; Teng, L.; Yonglu, W. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double-chromosome encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar]
- Yan, F.; Chu, J.; Hu, J.; Zhu, X. Cooperative task allocation with simultaneous arrival and resource constraint for multi-UAV using a genetic algorithm. Expert Syst. Appl. 2024, 245, 123023. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Zhu, S.; Sun, Y. Multi-UAV task allocation based on improved algorithm of multi-objective particle swarm optimization. In Proceedings of the 2018 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Zhengzhou, China, 18–20 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 443–4437. [Google Scholar]
- Li, Y.; Zhang, Z.; Sun, Q.; Huang, Y. An improved ant colony algorithm for multiple unmanned aerial vehicles route planning. J. Frankl. Inst. 2024, 361, 107060. [Google Scholar] [CrossRef]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 203–209. [Google Scholar]
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Shah, K.; Ballard, G.; Schmidt, A.; Schwager, M. Multidrone aerial surveys of penguin colonies in Antarctica. Sci. Robot. 2020, 5, eabc3000. [Google Scholar] [CrossRef] [PubMed]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide areas algorithm for optimal multi-robot coverage path planning. J. Intell. Robot. Syst. 2017, 86, 663–680. [Google Scholar] [CrossRef]
- Cao, Y.; Cheng, X.; Mu, J. Concentrated coverage path planning algorithm of UAV formation for aerial photography. IEEE Sensors J. 2022, 22, 11098–11111. [Google Scholar] [CrossRef]
- Krupke, D. Near-optimal coverage path planning with turn costs. In Proceedings of the 2024 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX), SIAM, Alexandria, VA, USA, 7–8 January 2024; pp. 118–132. [Google Scholar]
- Kolmogorov, V. Blossom V: A new implementation of a minimum cost perfect matching algorithm. Math. Program. Comput. 2009, 1, 43–67. [Google Scholar] [CrossRef]
- Whitley, L.D.; Starkweather, T.; Fuquay, D. Scheduling problems and traveling salesmen: The genetic edge recombination operator. In Proceedings of the 3rd International Conference on Genetic Algorithms, Fairfax, VA, USA, 2–9 June 1989; pp. 133–140. [Google Scholar]
- Goldberg, D.E.; Lingle, R. Alleles, loci, and the traveling salesman problem. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications; Psychology Press: London, UK, 2014; pp. 154–159. [Google Scholar]
- Zhang, C.; Jiang, Z.; Tang, H.; Song, G. Path Planning for Multi-UAV Target Coverage via Improved GA-PSO Algorithm. In Proceedings of the 2024 6th International Conference on Robotics, Intelligent Control and Artificial Intelligence (RICAI), Nanjing, China, 6–8 December 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 304–310. [Google Scholar]
- Shafiq, M.; Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M.; Jussila, J.J. Convergence analysis of path planning of multi-UAVs using max-min ant colony optimization approach. Sensors 2022, 22, 5395. [Google Scholar] [CrossRef] [PubMed]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]







| Parameters | Attribute | Description |
|---|---|---|
| Number of Regions | The total number of task regions. | |
| Region Location | The geographic centroid of each region. | |
| Region Shape | A sequence of polygons defining the boundary of each region. | |
| Number of UAVs | The number of UAVs available for mission execution. | |
| Vehicle Deployment Location | Initial deployment position of the vehicle and UAVs (take off point). | |
| h | Flight Altitude | UAV flight altitude above ground level (m). |
| Side Overlap | Lateral overlap percentage between adjacent aerial images. | |
| Forward Overlap | Longitudinal overlap percentage between consecutive aerial images. | |
| Endurance Range | Maximum flight range of the UAV (km). | |
| Coordinates | Current three dimensional spatial coordinates of the UAV. | |
| Raw Heading | UAV’s heading angle relative to true north. | |
| Yaw Angle | UAV’s rotation around the vertical axis. | |
| Pitch Angle | UAV’s rotation around the lateral axis. | |
| f | Focal Length | Camera lens focal length determining image scale (mm). |
| v | Cruise Speed | UAV’s average cruising speed (m/s). |
| W | Image Width | Number of pixels in the horizontal direction of the captured image. |
| H | Image Height | Number of pixels in the vertical direction of the captured image. |
| Datasets | I | II | III | IV |
|---|---|---|---|---|
| UAVs | 4 | 8 | 12 | 16 |
| Regions | 30 | 50 | 70 | 100 |
| Area | 4 | 16 | 36 | 64 |
| Complexity | 0.9 | 0.8 | 0.7 | 0.6 |
| Coverage Cost | ||||
| Endurance | 50 km | 70 km | 70 km | 100 km |
| 1 | 1 | 1 | 1 | |
| 4 | 8 | 12 | 16 |
| Datasets | Model | ||||
|---|---|---|---|---|---|
| I | GA-Default | 3.493 | 0.011 | 3.539 | 1.858 |
| GA-MRECX | 3.432 | 0.011 | 3.476 | 2.10 | |
| GA-Proposed | 3.395 | 0.01 | 3.435 | 3.10 | |
| PSO | 3.542 | 0.009 | 3.577 | 1.807 | |
| ACO | 3.452 | 0.013 | 3.502 | 6.186 | |
| SC-TSA | 3.37 | 0.71 | 6.21 | 1.565 | |
| II | GA-Default | 5.347 | 0.015 | 5.466 | 2.326 |
| GA-MRECX | 5.129 | 0.013 | 5.233 | 3.915 | |
| GA-Proposed | 5.07 | 0.018 | 5.215 | 4.38 | |
| PSO | 5.357 | 0.011 | 5.443 | 2.137 | |
| ACO | 5.229 | 0.019 | 5.38 | 10.026 | |
| SC-TSA | 4.915 | 0.43 | 8.355 | 2.1970 | |
| III | GA-Default | 7.928 | 0.022 | 8.191 | 4.47 |
| GA-MRECX | 7.37 | 0.021 | 7.622 | 5.349 | |
| GA-Proposed | 6.983 | 0.017 | 7.186 | 6.868 | |
| PSO | 7.975 | 0.031 | 8.346 | 3.533 | |
| ACO | 7.384 | 0.037 | 7.826 | 12.423 | |
| SC-TSA | 6.762 | 0.261 | 9.892 | 3.457 | |
| IV | GA-Default | 8.521 | 0.038 | 9.126 | 4.735 |
| GA-MRECX | 8.017 | 0.015 | 8.257 | 6.664 | |
| GA-Proposed | 7.949 | 0.007 | 8.064 | 8.216 | |
| PSO | 8.504 | 0.023 | 8.875 | 4.253 | |
| ACO | 8.074 | 0.03 | 8.548 | 14.671 | |
| SC-TSA | 7.062 | 0.201 | 10.273 | 4.437 |
| Dataset | H | p-Value | Significant | Better Than |
|---|---|---|---|---|
| I | 219.3347 | Yes | ACO, GA-Default, PSO, SC-TSA | |
| II | 217.8611 | Yes | ACO, GA-Default, PSO, SC-TSA | |
| III | 224.9819 | Yes | ACO, GA-Default, PSO, SC-TSA | |
| IV | 226.1704 | Yes | ACO, GA-Default, PSO, SC-TSA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Tang, A.; Ye, H.; Yue, H.; Xu, C.; Hao, L.; He, H.; Liao, X. Collaborative Vehicle-Mounted Multi-UAV Routing and Scheduling Optimization for Remote Sensing Observations. Drones 2025, 9, 783. https://doi.org/10.3390/drones9110783
Du B, Tang A, Ye H, Yue H, Xu C, Hao L, He H, Liao X. Collaborative Vehicle-Mounted Multi-UAV Routing and Scheduling Optimization for Remote Sensing Observations. Drones. 2025; 9(11):783. https://doi.org/10.3390/drones9110783
Chicago/Turabian StyleDu, Bing, Anqi Tang, Huping Ye, Huanyin Yue, Chenchen Xu, Lina Hao, Hongbo He, and Xiaohan Liao. 2025. "Collaborative Vehicle-Mounted Multi-UAV Routing and Scheduling Optimization for Remote Sensing Observations" Drones 9, no. 11: 783. https://doi.org/10.3390/drones9110783
APA StyleDu, B., Tang, A., Ye, H., Yue, H., Xu, C., Hao, L., He, H., & Liao, X. (2025). Collaborative Vehicle-Mounted Multi-UAV Routing and Scheduling Optimization for Remote Sensing Observations. Drones, 9(11), 783. https://doi.org/10.3390/drones9110783









