Drone-Derived Nearshore Bathymetry: A Comparison of Spectral and Video-Based Inversions
Highlights
- Wave signal tracking using drone-captured video achieves suitable bathymetry estimation.
- Field comparisons show wave tracking performs better than spectral depth inversions under specific conditions.
- Wave signal tracking for depth inversions extends opportunities in nearshore regions where optical spectral methods may struggle such as in turbid waters.
- Results support drone use as a suitable method for collecting coastal monitoring data.
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Remotely Piloted Aircraft in Coastal Monitoring
1.3. Aims
2. Review of Bathymetry Inversion Approaches
3. Materials and Methods
3.1. Study Site
3.2. Data Acquisition
3.3. Data-Analysis
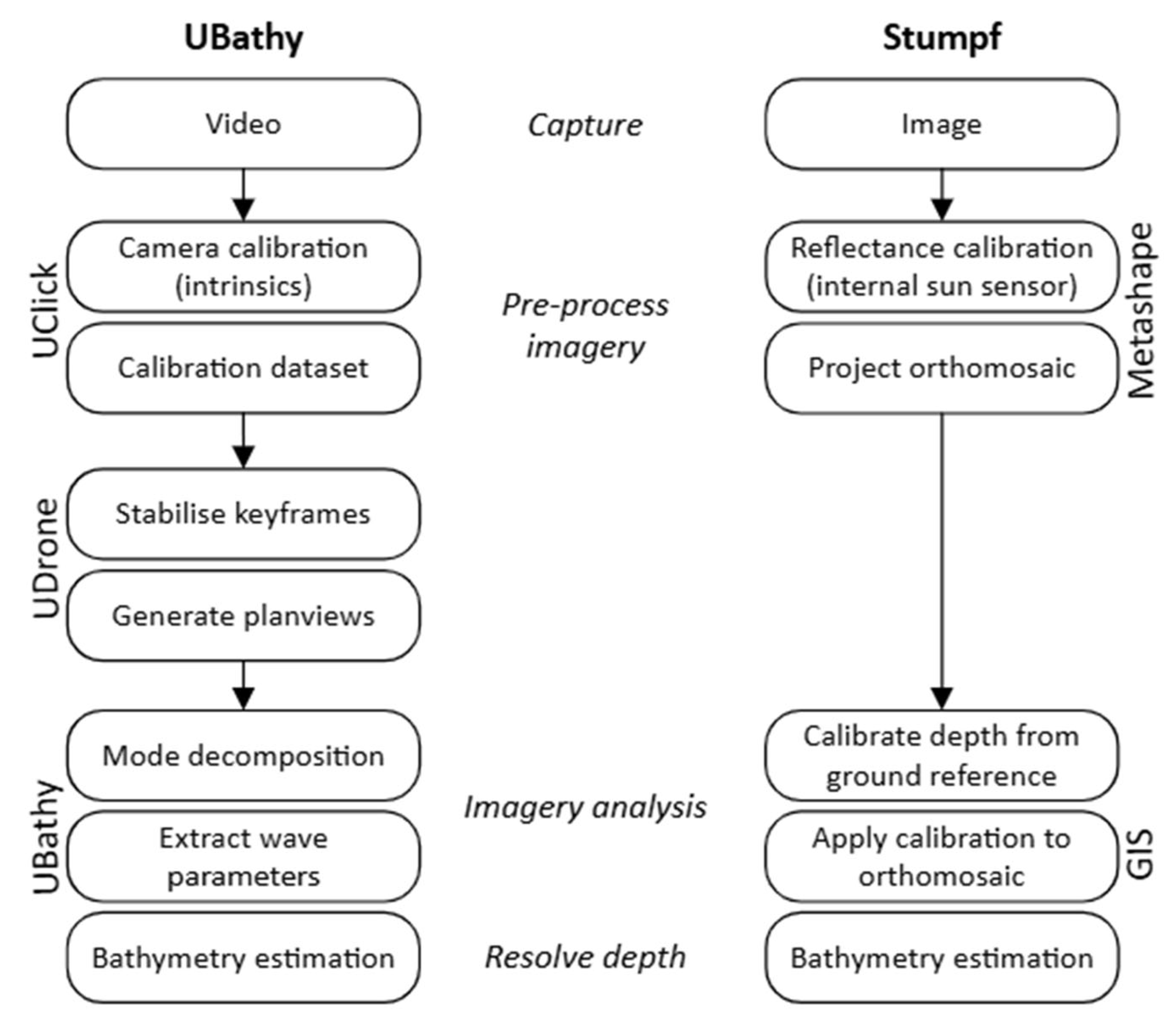
3.3.1. Video-Based Bathymetry Inversion
3.3.2. Spectral Inversion
4. Results
4.1. Overview of Bathymetric Model Performance
4.2. Model Accuracy and Bias by Depth
5. Discussion
5.1. Prediction Performance
5.2. Morphological Influences
5.3. Limitations of Research in Energetic Zones
5.4. Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLRM | Classical linear ratio model |
| DMD | Dynamic mode decomposition |
| EOF | Empirical orthogonal function |
| IHO | International Hydrographic Organisation |
| RPA | Remotely piloted aircraft |
| SDB | Satellite derived bathymetry |
| Sfm | Structure from motion |
| UAV | Unmanned aerial vehicle |
References
- Davidson, M.; Van Koningsveld, M.; de Kruif, A.; Rawson, J.; Holman, R.; Lamberti, A.; Medina, R.; Kroon, A.; Aarninkhof, S. The CoastView project: Developing video-derived Coastal State Indicators in support of coastal zone management. Coast. Eng. 2007, 54, 463–475. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D.; Luque, P.; Orfila, A.; Ribas, F. UBathy: A New Approach for Bathymetric Inversion from Video Imagery. Remote. Sens. 2019, 11, 2722. [Google Scholar] [CrossRef]
- Herrera, C.; Connolly, R.M.; Rasmussen, J.A.; McNamara, G.; Murray, T.P.; Lopez-Marcano, S.; Moore, M.; Campbell, M.D.; Alvarez, F. Drone Insights: Unveiling Beach Usage through AI-Powered People Counting. Drones 2024, 8, 579. [Google Scholar] [CrossRef]
- Wright, L.D.; Thom, B.G. Coastal depositional landforms: A morphodynamic approach. Prog. Phys. Geogr. Earth Environ. 1977, 1, 412–459. [Google Scholar] [CrossRef]
- Cabezas-Rabadán, C.; Pardo-Pascual, J.E.; Palomar-Vázquez, J.; Fernández-Sarría, A. Characterizing beach changes using high-frequency Sentinel-2 derived shorelines on the Valencian coast (Spanish Mediterranean). Sci. Total Environ. 2019, 691, 216–231. [Google Scholar] [CrossRef]
- Felix, R.; Hubbard, J.; Wilson, K.; Switzer, A. Heatmap analysis of modeled coastal tsunamis using different bathymetry data resolutions. Geosci. Lett. 2024, 11, 47. [Google Scholar] [CrossRef]
- Leon, J.X.; Phinn, S.R.; Hamylton, S.; Saunders, M.I. Filling the ‘white ribbon’—A multisource seamless digital elevation model for Lizard Island, northern Great Barrier Reef. Int. J. Remote Sens. 2013, 34, 6337–6354. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. Oceans 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Bak, A.S.; Durkin, P.; Bruder, B.; Saenz, M.J.; Forte, M.F.; Brodie, K.L. Amphibious Uncrewed Ground Vehicle for Coastal Surfzone Survey. J. Surv. Eng. 2023, 149, 04023011. [Google Scholar] [CrossRef]
- Thom, B.; Eliot, I.; Eliot, M.; Harvey, N.; Rissik, D.; Sharples, C.; Short, A.; Woodroffe, C. National sediment compartment framework for Australian coastal management. Ocean Coast. Manag. 2018, 154, 103–120. [Google Scholar] [CrossRef]
- Guillén, J.; Simarro, G.; Calvete, D.; Ribas, F.; Fernández-Mora, A.; Orfila, A.; Falqués, A.; de Swart, R.; Sancho-García, A.; Durán, R. Sediment leakage on the beach and upper shoreface due to extreme storms. Mar. Geol. 2024, 468, 107207. [Google Scholar] [CrossRef]
- Oliver, T.S.; Tamura, T. The relevance of coastal sediment budgets to management of sandy wave-dominated shorelines, a case study of Twofold Bay, southeastern Australia. Ocean Coast. Manag. 2022, 228, 106311. [Google Scholar] [CrossRef]
- Kennedy, D.M.; McCarroll, R.J.; Provis, D.; McCowan, A.; Zavadil, E. Delineating sediment compartment boundaries in an urbanised embayment for geomorphic management of decadal-scale coastal dynamics. Geomorphology 2025, 477, 109702. [Google Scholar] [CrossRef]
- Kroon, A.; Davidson, M.; Aarninkhof, S.; Archetti, R.; Armaroli, C.; Gonzalez, M.; Medri, S.; Osorio, A.; Aagaard, T.; Holman, R.; et al. Application of remote sensing video systems to coastline management problems. Coast. Eng. 2007, 54, 493–505. [Google Scholar] [CrossRef]
- Sherwood, C.R.; van Dongeren, A.; Doyle, J.; Hegermiller, C.A.; Hsu, T.-J.; Kalra, T.S.; Olabarrieta, M.; Penko, A.M.; Rafati, Y.; Roelvink, D.; et al. Modeling the Morphodynamics of Coastal Responses to Extreme Events: What Shape Are We In? Annu. Rev. Mar. Sci. 2022, 14, 457–492. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.A.; Splinter, K.D. Data-driven shoreline modelling at timescales of days to years. Coast. Eng. 2025, 197, 104685. [Google Scholar] [CrossRef]
- Joyce, K.E.; Fickas, K.C.; Kalamandeen, M. The unique value proposition for using drones to map coastal ecosystems. Camb. Prism. Coast. Futures 2023, 1, e6. [Google Scholar] [CrossRef]
- Angnuureng, D.; Brempong, K.; Jayson-Quashigah, P.; Dada, O.; Akuoko, S.; Frimpomaa, J.; Mattah, P.; Almar, R. Satellite, drone and video camera multi-platform monitoring of coastal erosion at an engineered pocket beach: A showcase for coastal management at Elmina Bay, Ghana (West Africa). Reg. Stud. Mar. Sci. 2022, 53, 102437. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R.; de Almeida, L.P.M.; Sall, M. On the operational use of UAVs for video-derived bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Matsuba, Y.; Sato, S. Nearshore bathymetry estimation using UAV. Coast. Eng. J. 2018, 60, 51–59. [Google Scholar] [CrossRef]
- Gao, M.; Hugenholtz, C.H.; Fox, T.A.; Kucharczyk, M.; Barchyn, T.E.; Nesbit, P.R. Weather constraints on global drone flyability. Sci. Rep. 2021, 11, 12092. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.; Westoby, M.J.; James, M.R. Low-budget topographic surveying comes of age: Structure from motion photogrammetry in geography and the geosciences. Prog. Phys. Geogr. Earth Environ. 2019, 43, 163–173. [Google Scholar] [CrossRef]
- Bergsma, E.; Conley, D.; Davidson, M.; O’Hare, T. Video-based nearshore bathymetry estimation in macro-tidal environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef]
- Casella, E.; Drechsel, J.; Winter, C.; Benninghoff, M.; Rovere, A. Accuracy of sand beach topography surveying by drones and photogrammetry. Geo-Mar. Lett. 2020, 40, 255–268. [Google Scholar] [CrossRef]
- Rossi, L.; Mammi, I.; Pelliccia, F. UAV-Derived Multispectral Bathymetry. Remote. Sens. 2020, 12, 3897. [Google Scholar] [CrossRef]
- Harris, L.R.; Defeo, O. Sandy shore ecosystem services, ecological infrastructure, and bundles: New insights and perspectives. Ecosyst. Serv. 2022, 57, 101477. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Demir, B. Deep learning-based bathymetry retrieval without in-situ depths using remote sensing imagery and SfM-MVS DSMs with data gaps. ISPRS J. Photogramm. Remote. Sens. 2025, 225, 341–361. [Google Scholar] [CrossRef]
- Agrafiotis, P.; Skarlatos, D.; Georgopoulos, A.; Karantzalos, K. DepthLearn: Learning to Correct the Refraction on Point Clouds Derived from Aerial Imagery for Accurate Dense Shallow Water Bathymetry Based on SVMs-Fusion with LiDAR Point Clouds. Remote Sens. 2019, 11, 2225. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Towards routine mapping of shallow bathymetry in environments with variable turbidity: Contribution of sentinel-2A/B satellites mission. Remote. Sens. 2020, 12, 451. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Emery, K.O. A Simple Method of Measuring Beach Profiles. Limnol. Oceanogr. 1961, 6, 90–93. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Theberge, A.E.; Wang, Y. Bathymetry: History of Seafloor Mapping. Encycl. Nat. Resour. 2014, 2, 564. [Google Scholar]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. Assessment and integration of conventional, RTK-GPS and image-derived beach survey methods for daily to decadal coastal monitoring. Coast. Eng. 2011, 58, 194–205. [Google Scholar] [CrossRef]
- Moulton, M.; Elgar, S.; Raubenheimer, B. A surfzone morphological diffusivity estimated from the evolution of excavated holes. Geophys. Res. Lett. 2014, 41, 4628–4636. [Google Scholar] [CrossRef]
- Carlson, D.F.; Fürsterling, A.; Vesterled, L.; Skovby, M.; Pedersen, S.S.; Melvad, C.; Rysgaard, S. An affordable and portable autonomous surface vehicle with obstacle avoidance for coastal ocean monitoring. HardwareX 2019, 5, e00059. [Google Scholar] [CrossRef]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of near-shore satellite derived bathymetry: Classification and account of five decades of coastal bathymetry research. J. Ocean Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Leder, T.D.; Baučić, M.; Leder, N.; Gilić, F. Optical Satellite-Derived Bathymetry: An Overview and WoS and Scopus Bibliometric Analysis. Remote. Sens. 2023, 15, 1294. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote. Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters I A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote. Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. CBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Ocean. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D.; Plomaritis, T.A.; Moreno-Noguer, F.; Giannoukakou-Leontsini, I.; Montes, J.; Durán, R. The influence of camera calibration on nearshore bathymetry estimation from UAV videos. Remote. Sens. 2021, 13, 150. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D. UBathy (v2.0): A Software to Obtain the Bathymetry from Video Imagery. Remote. Sens. 2022, 14, 6139. [Google Scholar] [CrossRef]
- Lumban-Gaol, Y.; Ohori, K.A.; Peters, R. Extracting Coastal Water Depths from Multi-Temporal Sentinel-2 Images Using Convolutional Neural Networks. Mar. Geod. 2022, 45, 615–644. [Google Scholar] [CrossRef]
- Lv, J.; Gao, C.; Qi, C.; Li, S.; Su, D.; Zhang, K.; Yang, F. Arctic supraglacial lake derived bathymetry combining ICESat-2 and spectral stratification of satellite imagery. EGUsphere 2025, 2025, 1–22. [Google Scholar] [CrossRef]
- Chen, A.; Ma, Y.; Zhang, J. Partition satellite derived bathymetry for coral reefs based on spatial residual information. Int. J. Remote. Sens. 2021, 42, 2807–2826. [Google Scholar] [CrossRef]
- Lee, J.; DeVore, K.; Hesser, T.; Bak, A.S.; Brodie, K.; Bruder, B.; Farthing, M. Blending bathymetry: Combination of image-derived parametric approximations and celerity data sets for nearshore bathymetry estimation. Coast. Eng. 2024, 192, 104546. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2 Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef]
- Hamylton, S.M.; Hedley, J.D.; Beaman, R.J. Derivation of high-resolution bathymetry from multispectral satellite imagery: A comparison of empirical and optimisation methods through geographical error analysis. Remote. Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef]
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote. Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S.; et al. Vegetation Indices Combining the Red and Red-Edge Spectral Information for Leaf Area Index Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef]
- Cao, B.; Deng, R.; Xu, Y.; Cao, B.; Liu, Y.; Zhu, S. Practical Differences Between Photogrammetric Bathymetry and Physics-Based Bathymetry. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 8016705. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Haidar, M.; Hartuti, M.; Kresnawati, D.K. Determination of the Best Methodology for Bathymetry Mapping Using Spot 6 Imagery: A Study Of 12 Empirical Algorithms. Int. J. Remote. Sens. Earth Sci. 2018, 14, 127–136. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef]
- Jawak, S.D.; Vadlamani, S.S.; Luis, A.J. A Synoptic Review on Deriving Bathymetry Information Using Remote Sensing Technologies: Models, Methods and Comparisons. Adv. Remote. Sens. 2015, 4, 147–162. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Confronting turbidity, the major challenge for satellite-derived coastal bathymetry. Sci. Total. Environ. 2023, 870, 161898. [Google Scholar] [CrossRef]
- Bruder, B.; Brodie, K.; Hesser, T.; Spore, N.; Farthing, M.; Renaud, A. guiBathy: A Graphical User Interface to Estimate Nearshore Bathymetry from Hovering Unmanned Aerial System Imagery. In Coastal and Hydraulics Laboratory; United States Army Corps of Engineers: Washington, DC, USA, 2021. [Google Scholar]
- Brodie, K.L.; Bruder, B.L.; Slocum, R.K.; Spore, N.J. Simultaneous Mapping of Coastal Topography and Bathymetry from a Lightweight Multicamera UAS. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 6844–6864. [Google Scholar] [CrossRef]
- Holman, R.; Bergsma, E.W.J. Updates to and performance of the cbathy algorithm for estimating nearshore bathymetry from remote sensing imagery. Remote. Sens. 2021, 13, 3996. [Google Scholar] [CrossRef]
- Lange, A.M.; Fiedler, J.W.; Merrifield, M.A.; Guza, R. UAV video-based estimates of nearshore bathymetry. Coast. Eng. 2023, 185, 104375. [Google Scholar] [CrossRef]
- Queensland Government. Noosa River Environmental Values and Water Quality Objectives; State of Queensland: Brisbane, QLD, Australia, 2022. [Google Scholar]
- Wishaw, D.; Leon, J.; Fairweather, H.; Crampton, A. Influence of wave direction sequencing and regional climate drivers on sediment headland bypassing. Geomorphology 2021, 383, 107708. [Google Scholar] [CrossRef]
- Salim, D.H.C.; Andrade, G.R.; Assunção, A.F.; Cosme, P.H.D.M.; Pereira, G.; Amorim, C.C. Assessing the Impact of Environmental Conditions on Reflectance Values in Inland Waters Using Multispectral UAS Imagery. Limnol. Rev. 2024, 24, 466–490. [Google Scholar] [CrossRef]
- Joyce, K.E.; Duce, S.; Leahy, S.M.; Leon, J.; Maier, S.W. Principles and practice of acquiring drone-based image data in marine environments. Mar. Freshw. Res. 2018, 70, 952–963. [Google Scholar] [CrossRef]
- Said, N.M.; Mahmud, M.R.; Hasan, R.C. Satellite-derived bathymetry: Accuracy assessment on depths derivation algorithm for shallow water area. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, XLII-4/W5, 159–164. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Chollett, I.; Harborne, A.R.; Heron, S.F.; Weeks, S.; Skirving, W.J.; Strong, A.E.; Eakin, C.M.; Christensen, T.R.L.; et al. Remote Sensing of Coral Reefs for Monitoring and Management: A Review. Remote. Sens. 2016, 8, 118. [Google Scholar] [CrossRef]
- Casal, G.; Harris, P.; Monteys, X.; Hedley, J.; Cahalane, C.; McCarthy, T. Understanding satellite-derived bathymetry using Sentinel 2 imagery and spatial prediction models. GIScience Remote. Sens. 2020, 57, 271–286. [Google Scholar] [CrossRef]







| Family | Method/Sub-Type | Platform/Tool | Principle |
|---|---|---|---|
| Traditional physical/field based | Lead line | Vessel | Manual depth sounding with a weighted line |
| Single-beam/multi-beam echo sounder | Vessel/RPA | Acoustic travel time, single or multiple beams | |
| Active remote sensing | Airborne bathy LiDAR [38] | Aircraft/RPA | Laser penetration through the water column |
| Radar altimetry | Satellite | Radar pulse travel time | |
| Microwave/SAR (spacebourne) | Coastal station/Vessel | Image backscatter, surface roughness, and wave fronts | |
| Spectral-derived optical | Physics-based—Radiative Transfer Models [39,40] | Satellite/RPA | Light/water interactions using radiative transfer equations |
| Empirical log-ratio [30] | Satellite/RPA | Log-linear ratio against in-situ depth | |
| Semi-empirical [41,42] | Satellite/RPA | Depth-invariant transform with regression | |
| Wave-based/computer vision | Wave speed from video [8] | Fixed camera | Wave phase speed inversion via linear wave theory |
| cBathy [43] | Fixed camera/RPA | Wave celerity tracking—PCA and filtering | |
| UBathy [44,45] | Fixed camera/RPA | Wave feature tracking—EOF/DMD wave decomposition | |
| Machine learning/computer vision/hybrid | Neural network [46] | Satellite | Predicts depth from multispectral image features using machine learning |
| SfM—spectral hybrid frameworks [27,28] | Satellite/RPA | Fuses SfM-MVS DSMs with multispectral imagery, correcting refraction and filling gaps | |
| Transformer deep learning architecture [47] | Satellite | Uses transformer architecture with high-resolution multispectral imagery for data-driven depth retrieval |
| Parameter | Noosa Main Beach | Burgess Creek |
|---|---|---|
| Orientation | North-facing, headland-protected embayment | East-facing, open coast |
| Wave exposure | Low-energy, highly refracted east–northeast swell | Low–high energy, direct exposure to ENE–SE swell |
| Dominant wave direction | Oblique ENE swell wrapping around Noosa Headland | ENE–SE swell, occasional northerly swell in spring/summer |
| Morphodynamic state | Intermediate classification, generally exhibiting a longshore bar trough. Stable to erosional depending on nourishment regime; influenced by groynes and structures. | Intermediate classification generally fluctuates between a low tide terrace and rhythmic longshore bar trough. Dynamic and seasonally variable; rapid erosion is possible during high-energy events. The area features a highly variable dry beach profile and bar trough system, influenced by the creek and moderate wave conditions. |
| Platform | Sensor | Mode | Flight Altitude |
|---|---|---|---|
| DJI Phantom 4 RTK (P4) | 1″ CMOS, 20 MP RGB | 4 K (3840 × 2160, 30 p) video | 50 m |
| DJI Phantom 4 Multispectral RTK (P4MS) | 6 sensors: Blue (B) 450 nm ± 16 nm; Green (G) 560 nm ± 16 nm; Red (R) 650 nm ± 16 nm; Red Edge (RE) 730 nm ± 16 nm; Near-Infrared (NIR) 840 nm ± 26 nm; integrated RGB sensor | Still imagery, 80/80% overlap front/side | 90 m (GSD 5 cm) |
| Site | Date | Tidal Level (mLAT) | Estimated Breaking Wave Height (m)/Period (s) | Wind Speed (kts)/Peak Direction |
|---|---|---|---|---|
| Burgess | 22 April 2025 | 1.1 | 1.0/11 | 20 SSW |
| Noosa | 28 April 2025 | 0.6 | 0.6/9 | 31 SE |
| Depth Bin (m) | n (Burgess) | n (Noosa) |
|---|---|---|
| −1 to −2 | 465 | 151 |
| −2 to −3 | 648 | 105 |
| −3 to −4 | 365 | 26 |
| −4 to −5 | 114 | 10 |
| Total | 1592 | 292 |
| Site | Method | RMSE (m) | Bias | R2 |
|---|---|---|---|---|
| Burgess | UBathy | 0.40 | −0.18 | 0.79 |
| Stumpf | 0.55 | 0.03 | 0.58 | |
| Noosa | UBathy | 0.26 | 0.02 | 0.90 |
| Stumpf | 0.45 | 0.00 | 0.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goessling, I.P.; Leon, J.X. Drone-Derived Nearshore Bathymetry: A Comparison of Spectral and Video-Based Inversions. Drones 2025, 9, 761. https://doi.org/10.3390/drones9110761
Goessling IP, Leon JX. Drone-Derived Nearshore Bathymetry: A Comparison of Spectral and Video-Based Inversions. Drones. 2025; 9(11):761. https://doi.org/10.3390/drones9110761
Chicago/Turabian StyleGoessling, Isaac P., and Javier X. Leon. 2025. "Drone-Derived Nearshore Bathymetry: A Comparison of Spectral and Video-Based Inversions" Drones 9, no. 11: 761. https://doi.org/10.3390/drones9110761
APA StyleGoessling, I. P., & Leon, J. X. (2025). Drone-Derived Nearshore Bathymetry: A Comparison of Spectral and Video-Based Inversions. Drones, 9(11), 761. https://doi.org/10.3390/drones9110761











