Fixed-Time Formation Control for MAV/UAVs with Switching Threshold Event-Triggered Strategy

Highlights

What are the main findings?

• Develops a fixed-time back-stepping formation control strategy for MAV/UAV systems.
• Introduces a novel switching threshold event-triggered mechanism.

What is the implication of the main finding?

• Designs a fixed-time filter to deal with the ‘explosion of complexity’ problem and improves the system’s stability.
• Switches the trigger conditions for controller updates according to the system state, which reduces conservatism while ensuring safety.

Abstract

The cooperative flight of manned and unmanned aerial vehicles (MAV/UAVs) has recently become a focus in the research of civilian and humanitarian fields, in which formation control is crucial. This paper takes the improvement of convergence performance and resource conservation as the entry point to study control problems of cooperative formation configuration of MAV/UAVs. Following the backstepping recursive design procedures, an event-triggered fixed-time formation control strategy for MAV/UAVs operating under modeling uncertainties and external disturbances is presented. Moreover, a novel switching threshold event-triggered mechanism is introduced, which dynamically adjusts control signal updates based on system states. Compared with periodic sampling control (Controller 1), fixed threshold strategies (Controller 2) and relative threshold strategies (Controller 3), this mechanism enhances resource efficiency and prevents Zeno behavior. On the basis of Lyapunov stability theory, the closed-loop system is shown to be stable in the sense of the fixed-time concept. Numerical simulations are carried out in Simulink to validate the effectiveness of the theoretical findings. The results show that compared with the three comparison methods, the proposed control method saves 86%, 34%, and 43% of control transmission burden respectively, which significantly reduces the number of triggered events.

1. Introduction

Multi-agent collaborative flight has extensive applications in both civilian and humanitarian fields. Among these, the collaborative formation of manned and unmanned aerial vehicles (MAV/UAVs) holds great significance in humanitarian operations. In international humanitarian relief operations, the collaborative flight of MAV/UAVs can efficiently accomplish tasks such as delivering relief supplies and assessing the conditions of disaster - stricken areas. This collaborative formation ensures a more efficient and targeted response to humanitarian crises.

MAV/UAV collaborative flight is a complex process where formation control is crucial [1,2]. In such formations, the MAV follows a desired trajectory while each UAV tracks the MAV’s trajectory and maintains a specific distance to achieve the desired formation [3]. Numerous studies have focused on multi-aircraft cooperative formation control [4,5], leading to several typical methods, such as leader–follower [6,7], potential field [8], behavior-based [9], and virtual structure approaches [10]. However, it is worth mentioning that current research on multi-agent formation control mainly focuses on multi UAV systems [11,12,13]. In [14], the author developed formation-keeping strategies and corresponding control methods for manned/unmanned aerial vehicle missions. Building on the leader–follower concept, a two-level hierarchical framework control strategy was proposed for MAV/UAV groups, offering greater efficiency and flexibility [3]. Furthermore, a three-dimensional cluster space formation control method was introduced to enable MAV pilots to simultaneously supervise and control UAVs [15]. However, as a part of IoD networks [16], the integration of security, privacy, and resource efficiency in MAV/UAVs emerges as a critical challenge [17]. Despite these aforementioned existing works, research on MAV/UAVs collaborative formation control with the dual objectives of enhancing security and conserving resources remains limited.

In actual flight control systems, limited computing and communication resources are a common challenge. Traditional formation cooperative control typically employs periodic sampling, which involves taking system state samples and updating control instructions at fixed intervals. However, this continuous high-frequency sampling and communication can lead to significant computational resource consumption and unnecessary actuator wear and tear [18]. Event-triggered control, on the other hand, dynamically triggers sampling and controller updates based on state errors or preset thresholds, effectively reducing the load on computational and communication resources [19,20,21]. To date, two primary event-triggered adaptive controller design strategies have been developed: the fixed threshold strategy [22,23] and the relative threshold strategy [24,25]. The fixed threshold strategy determines the event triggering condition using a predetermined value, irrespective of the system’s current state. In contrast, the relative threshold strategy bases its event triggering condition on an expression linked to the control signal. This means that when the system control signal is strong, the event triggering condition is heightened. Conversely, when the control signal is weak, a fixed value in the expression prevents the Zeno phenomenon from occurring [26,27]. However, when the control signal is too strong, it can result in excessive control errors. Therefore, combining these two strategies to design a switching threshold strategy for MAV/UAVs is crucial for maintaining a balance between event triggering intervals and system performance.

In collaborative formation scenarios, manned and unmanned aerial vehicles must complete trajectory tracking or formation reconstruction within specific time constraints. Early research achieved asymptotic stability in multi-agent control systems as time approached infinity [28,29,30]. To improve transient performance, finite-time control designs were proposed [31,32,33,34], enabling systems to converge within a finite time. However, since the settling time for finite-time stability depends on the initial state, convergence may be slower when the initial state is large. To address this, fixed-time control was developed to achieve faster consensus in a fixed time [35]. In [36], a fixed-time integral terminal sliding mode controller was designed to ensure the convergence rate of UAV systems and enhance disturbance rejection. A fixed-time disturbance observer-based robust fault-tolerant tracking control scheme for UAVs was proposed in [37]. Morever, [38] designed an appointed-fixed-time terminal sliding mode control strategy independent of initial states. Notably, the works in [35,36,37,38] primarily focus on UAV systems. Therefore, a fixed-time formation tracking strategy is needed for MAV/UAVs.

Motivated by the discussions above, this paper proposes a fixed-time control method for MAV/UAVs with switched-threshold event-triggered strategy. This method is designed to improve the formation tracking convergence, reduce computational resource consumption, and minimize unnecessary actuator losses. Compared with the aforementioned existing works, the main contributions of this article are stated as follows:

• Different to prior works [3,14,15], which neglect convergence performance in MAV/UAV formation control, this paper proposes a fixed-time backstepping formation controller for MAV/UAV systems under external disturbances and modeling uncertainties. The stability of the closed-loop system is rigorously proven using Lyapunov-based analysis.
• Compared with event-triggered control schemes that use fixed threshold strategies [22,23] or relative threshold strategies [24,25], this paper proposes a novel switching threshold event-triggered mechanism. This approach enhances resource efficiency by more effectively conserving system resources.
• By proposing a novel fixed-time command filtered backstepping approach, this paper effectively addresses the “explosion of complexity” problem while enhancing system stability.

To achieve fixed-time tracking for MAV/UAVs formations, the proposed control strategy is systematically designed as follows: First, define the system dynamics model. Then, based on the topology structure, obtain the tracking errors of the MAV and the UAV, respectively. Next, design a switching threshold event-triggered strategy according to the controller input. This strategy can effectively guarantee certain system performance metrics. Finally, taking external disturbances and model uncertainties into account, introduce neural networks. Based on the fixed-time convergence rule, design a formation consensus tracking control strategy to ensure the fixed-time convergence of the tracking error in the MAV/UAVs system.

The rest of this paper is organized as follows:

In Section 2, the dynamic model of MAV/UAVs is developed, and necessary preliminaries along with problem formulations are provided. Section 3 presents the design of the event-triggered fixed-time control and its corresponding stability analysis. Simulation results are showcased in Section 4, while Section 5 concludes the paper.

2. Preliminaries and Problem Formulation

2.1. Notations

Throughout this paper, ${\mathfrak{R}}^{n\times n}$ denotes real $m\times n$ matrices, sign $(·)$ is the signum function. $|·|$ denotes the absolute value, $\parallel ·\parallel$ represents the Euclidean 2-norm of a vector or matrix. ${\lambda }_{min}\left(D\right)$ is the minimum eigenvalues of the matrixD.

2.2. MAV/UAVs Dynamic Model

Suppose that the MAV/UAVs formation consisting of N aircrafts. The connections among aircraft are described as an undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$. The nodes $\mathcal{V}=\{v_1,\dots v_n\}$ being connected by edges $\mathcal{E}=\left\{\right(i,j),i,j\in \mathcal{V},$ and $i\ne j\}$. The Laplacian matrix is defined by $\mathcal{L}=\mathcal{D}-\mathcal{A}$, where $\mathcal{D}=\mathrm{diag}\{d_1,\dots d_n\}$ with $d_i={\sum }_{j=1}^n{a}_{ij}$. Let $\mathcal{A}=\left[a_{ij}\right]\in {\mathfrak{R}}^{n\times n}$ denotes the weighted adjacency matrix of $\mathcal{G}$, if jth aircraft receives the information from ith aircraft, then $a_{ij}>0$, and otherwise $a_{ij}=0$. When there exists a path from every node to every other node, $\mathcal{G}$ is connected.

Given that the dynamics of MAVs and UAVs are identical, their control mechanisms differ: MAVs are controlled via direct pilot operation of cockpit controls, whereas UAVs are typically managed by transmitting instructions through ground stations or remote controllers. Consequently, the dynamic model for the ith aircraft within the MAV/UAV system is provided in [39].

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\mathit{p}}}_i={\mathit{v}}_i\hfill \\ {\dot{\mathit{v}}}_i={\mathit{R}}_i{\mathit{\tau }}_i+\mathit{G}+{\mathit{\alpha }}_i+{\mathit{D}}_i,\end{array}\right.\end{array}$$

(1)

where ${\mathit{p}}_i={[x_i,y_i,z_i]}^{\mathrm{T}}$ represent the position of ith aircraft, ${\mathit{v}}_i={[u_i,v_i,w_i]}^{\mathrm{T}}$ is the non-inertial (body fixed frame coordinates) expression of the linear speed, $\mathit{G}={[0,0,-g]}^{\mathrm{T}}$ is the gravity acceleration. ${\mathit{D}}_{\mathit{i}}\in {\Re }^3$ denotes external disturbances. ${\mathit{\tau }}_i={[a_{ti},a_{yi},a_{pi}]}^{\mathrm{T}}$ denotes the control variable, ${\mathit{\alpha }}_i={[-{\displaystyle \frac{B_i}{m_i}}cos{\theta }_{i}cos{\psi }_i,-{\displaystyle \frac{B_i}{m_i}}cos{\theta }_{i}sin{\psi }_i,-{\displaystyle \frac{B_i}{m_i}}sin{\theta }_i]}^{\mathrm{T}}$, $B_i$ presents the drag force effect. The rotation matrix ${\mathit{R}}_i$ is

$$\begin{array}{c}\hfill {\mathit{R}}_i=\left[\begin{array}{ccc}cos{\theta }_{i}cos{\psi }_i& -sin{\psi }_i& -sin{\theta }_{i}cos{\psi }_i\\ cos{\theta }_{i}sin{\psi }_i& cos{\psi }_i& -sin{\theta }_{i}sin{\psi }_i\\ sin{\theta }_i& 0& cos{\theta }_i\end{array}\right].\end{array}$$

(2)

Considering the coefficient uncertainties, the accurate information of $B_i$ is unknown. In this sense, $B_i$ is decomposed into a known componet $B_{i0}$ and an uncertain one $\Delta B_{i0}$. Therefore, ${\mathit{\alpha }}_i$ can be decomposed into a known componet ${\mathit{\alpha }}_{i0}$ and an uncertain one $\Delta {\mathit{\alpha }}_i$.

Then, the speed kinematics is reformulated as

$$\begin{array}{c}\hfill {\dot{\mathit{v}}}_i={\mathit{R}}_i{\mathit{\tau }}_i+\mathit{G}+{\mathit{\alpha }}_{i0}+\Delta {\mathit{\alpha }}_{\mathit{i}}+{\mathit{D}}_i.\end{array}$$

(3)

Assumption 1.

The external disturbance ${\mathit{D}}_i$ is bounded and satisfying $d_{ij}\le d_0$, where $d_0$ is a positive constant.

In (3), the 3-degree-of-freedom (3-DOF) point mass model mainly consists of four parts: the control input vectora ${\mathit{R}}_i{\mathit{\tau }}_i$, the constant gravity acceleration $\mathit{G}$, the known and unknown part of the ${\mathit{\alpha }}_0$, and the external disturbance ${\mathit{D}}_i$. Here, ${\mathit{\tau }}_i$ is the control input designed later. The uncertain part $\Delta {\mathit{\alpha }}_{\mathit{i}}$ is approximated via a Radial Basis Function (RBF) neural network, while the external disturbance ${\mathit{D}}_i$ is handled through bounding.

2.3. Problem Statement

Given a virtual leader, when the position of the MAV converges to the reference value relative to it, and each UAV’s position also converges to the corresponding reference value relative to the MAV, the desired formation geometry is established. As illustrated in Figure 1, we define the formation tracking problem as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{p}}_i-{\mathit{p}}_r=\Delta {\mathit{p}}_{ir}\hfill \\ {\mathit{p}}_i-{\mathit{p}}_j=\Delta {\mathit{p}}_{ij},\end{array}\right.\end{array}$$

(4)

where ${\mathit{p}}_r={\left[x_r,y_r,z_r\right]}^{\mathrm{T}}$ represents the position of virtual leader, ${\mathit{p}}_i={\left[x_i,y_i,z_i\right]}^{\mathrm{T}}$ represents the ith aircraft, $\Delta {\mathit{p}}_{ir}={[\Delta x_{ir},\Delta y_{ir},\Delta z_{ir}]}^{\mathrm{T}}$, represents the relative position between the ith aircraft and virtual leader, $\Delta {\mathit{p}}_{ij}={[\Delta x_{ij},\Delta y_{ij},\Delta z_{ij}]}^{\mathrm{T}}$, represents the relative position between the ith aircraft and other aircraft. Then, the following equations hold

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \underset{t\to \infty }{lim}}\left({\mathit{p}}_i-{\mathit{p}}_r-\Delta {\mathit{p}}_{ir}\right)=0\hfill \\ {\displaystyle \underset{t\to \infty }{lim}}\left({\mathit{p}}_i-{\mathit{p}}_j-\Delta {\mathit{p}}_{ij}\right)=0,\end{array}\right.\end{array}$$

(5)

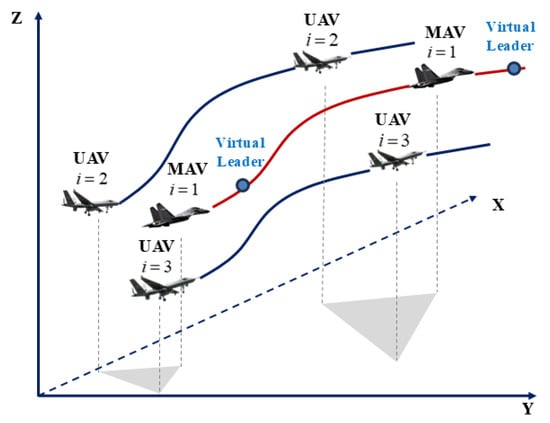
Figure 1. Geometrical formation illustration of MAV/UAVs.

According to (5), the formation tracking error is defined as

$$\begin{array}{c}\hfill {\mathit{e}}_{pi}={\xi }_{1i}{b}_i\left({\mathit{p}}_i-{\mathit{p}}_r-\Delta {\mathit{p}}_{ir}\right)+{\xi }_{2i}\sum _{j\in N_i}{a}_{ij}\left({\mathit{p}}_i-{\mathit{p}}_j-\Delta {\mathit{p}}_{ij}\right),\end{array}$$

(6)

If the ith aircraft is MAV, $b_i=1$, the tracking error is ${\mathit{e}}_{pi}={\xi }_{1i}\left({\mathit{p}}_i-{\mathit{p}}_r-\Delta {\mathit{p}}_{ir}\right)+{\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}\left({\mathit{p}}_i-{\mathit{p}}_j-\Delta {\mathit{p}}_{ij}\right)$. If the ith aircraft is UAV, $b_i=0$, the tracking error is ${\mathit{e}}_{pi}={\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}\left({\mathit{p}}_i-{\mathit{p}}_j-\Delta {\mathit{p}}_{ij}\right)$, where ${\mathit{e}}_{pi}={[e_{pi}^x,e_{pi}^y,e_{pi}^z]}^{\mathrm{T}}$, $e_{pi}^x={\xi }_{1i}{b}_i\left(x_i-x_r-\Delta x_{ir}\right)+{\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}\left(x_i-x_j-\Delta x_{ij}\right)$, $e_{pi}^y={\xi }_{1i}{b}_i\left(y_i-y_r-\Delta y_{ir}\right)+{\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}\left(y_i-y_j-\Delta y_{ij}\right)$, $e_{pi}^z={\xi }_{1i}{b}_i\left(z_i-z_r-\Delta z_{ir}\right)+{\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}\left(z_i-z_j-\Delta z_{ij}\right)$. ${\xi }_{1i}$ and ${\xi }_{2i}$ are positive design parameters.

Remark 1.

The relative position between MAV and virtual leader $\Delta {\mathit{p}}_{ir}$ can be set to 0, which means that the UAV follows the reference value. Then, the desired geometric pattern can be achieved by adjusting the relative position between MAV and UAV $\Delta {\mathit{p}}_{ij}$, where $\Delta x_{ij}$, $\Delta y_{ij}$, $\Delta z_{ij}$ are set according to task requirements.

2.4. Control Objective

This study aims to design an event-triggered fixed-time tracking controller that ensures the designed formation geometry is well-maintained for the MAV/UAV system under external disturbances and modeling uncertainties.

To design the fixed-time formation tracking controller, several lemmas are introduced.

Lemma 1

([40]). Consider the system

$$\dot{x}\left(t\right)=f\left(x\left(t\right)\right),x_0=x\left(0\right),$$

(7)

suppose that there exit a radially unbounded Lyapunov function $V\left(x\right)$ so that

$$\begin{array}{c}\hfill \dot{V}\left(x\right)\le -{\sigma }_1{V}^{\alpha }\left(x\right)-{\sigma }_2{V}^{\beta }\left(x\right)+\varsigma ,\end{array}$$

(8)

where ${\sigma }_1>0$, ${\sigma }_2>0$, $\alpha >0$, $0<\beta <1$, $0<\varsigma <+\infty$, then the system is practically fixed-time stable, and the residual set of the solution of system(7) can be given by

$$\begin{array}{c}\hfill V\left(x\right)\le min\left\{{\left({\displaystyle \frac{\varsigma }{\left(1-o\right){\sigma }_1}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{\varsigma }{\left(1-o\right){\sigma }_2}}\right)}^{{\displaystyle \frac{1}{\beta }}}\right\},\end{array}$$

(9)

where $o\in (0,1)$, the settling time is given by $T\le T_{max}:={\displaystyle \frac{1}{{\sigma }_{1}o\left(\alpha -1\right)}}+{\displaystyle \frac{1}{{\sigma }_{2}o\left(1-\beta \right)}}$.

Lemma 2

([41]). For $x\in \mathbb{R},\iota \in \mathbb{R},$ and $\iota >0$, then

$$0\le \left|x\right|-{\displaystyle \frac{x^2}{\sqrt{x^2+\iota }}}\le \sqrt{\iota }.$$

(10)

Lemma 3

([42]). For $x\in \mathbb{R},y\in \mathbb{R},c_1,c_2,c_3$ are positive constants, then

$${\left|x\right|}^{c_1}{\left|y\right|}^{c_2}\le {\displaystyle \frac{c_1}{c_1+c_2}}{c}_3{\left|x\right|}^{c_1+c_2}+{\displaystyle \frac{c_2}{c_1+c_2}}{c}_3^{-{\displaystyle \frac{c_1}{c_2}}}{\left|y\right|}^{c_1+c_2}.$$

(11)

Lemma 4

([43]). For $x_i\in \mathbb{R},i\in \mathcal{N}$, then

$${\left(\sum _{i=1}^n\left|x_i\right|\right)}^b\le \sum _{i=1}^n{\left|x_i\right|}^b\le n^{1-b}{\left(\sum _{i=1}^n\left|x_i\right|\right)}^b,$$

(12)

if $b\ge 1$, then

$$\sum _{i=1}^n{\left|x_i\right|}^b\ge n^{1-b}{\left(\sum _{i=1}^n\left|x_i\right|\right)}^b.$$

(13)

3. Event-Triggered Fixed-Time Formation Tracking Control Design

This section is devoted to developing an event-triggered fixed-time formation tracking control machine for the purpose of guaranteeing fixed-time formation tracking under modeling uncertainties and external disturbances. The proposed control frame-work is shown in Figure 2.

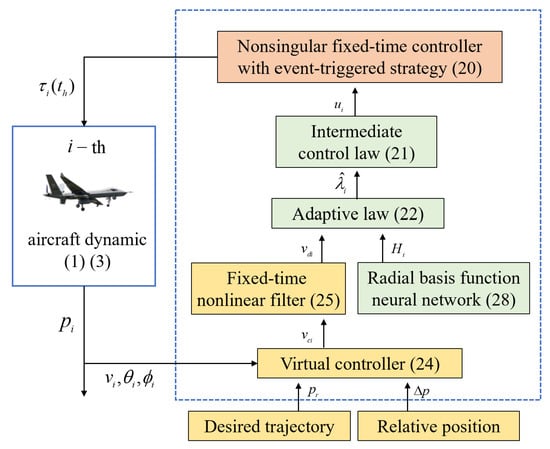
Figure 2. Proposed framework of the controller design.

To reduce the communication burden, a new switching threshold event-trigger strategy is designed as follows:

$$\begin{array}{c}\hfill {\mathit{\tau }}_i\left(t\right)={\mathit{\tau }}_i^{\prime }\left(t_h\right),\forall t\in \left[t_h,t_{h+1}\right),\end{array}$$

(14)

$$t_{h+1}=inf\left\{t\in R\left|\left|e_{{\tau }_{ti}}\right|\ge a_{1ti}+a_{2ti}or\left|e_{{\tau }_{yi}}\right|\ge a_{1yi}+a_{2yi}or\left|e_{{\tau }_{pi}}\right|\ge a_{1pi}+a_{2pi}\right.\right\},$$

(15)

$$\begin{array}{c}\hfill a_{1ji}=\left\{\begin{array}{cc}\varphi \left|{\tau }_{ji}\right|,\hfill & \left|{\tau }_{ji}\right|<D,\\ m_1,\hfill & \left|{\tau }_{ji}\right|\ge D,\end{array}\right.\end{array}$$

(16)

$$a_{2ji}={\displaystyle \frac{a_{i0}+{\lambda }_{i1}{e}^{-{\lambda }_{i2}t}}{\left|e_{{\tau }_{ji}}\left(t\right)\right|+k_{i0}}},$$

(17)

where ${\mathit{\tau }}_i\left(t\right)={[{\tau }_{ti}\left(t\right),{\tau }_{yi}\left(t\right),{\tau }_{pi}\left(t\right)]}^{\mathrm{T}}$, ${\mathit{\tau }}_i^{\prime }\left(t\right)={[{\tau }_{ti}^{\prime }\left(t_h\right),{\tau }_{yi}^{\prime }\left(t_h\right),{\tau }_{pi}^{\prime }\left(t_h\right)]}^{\mathrm{T}}$, ${\mathit{e}}_{{\tau }_i}={\mathit{\tau }}_i^{\prime }\left(t\right)-{\mathit{\tau }}_i\left(t\right)$ is measure error, ${\tau }_i^{\prime }\left(t\right)$ is control law, which will be defined later. D is user-designed parameter, $j\in [t,y,p]$. $\varphi$, $m_1$, $a_{i0}$, ${\lambda }_{i1}$, ${\lambda }_{i2}$, $k_{i0}$ are positive design parameters.

According to (17), we have

$$a_{2ji}\le {\displaystyle \frac{1}{k_{i0}}}\left(a_{i0}+{\lambda }_{i1}\right),$$

(18)

It follows from (14)–(18) that we arrive at

$${\mathit{\tau }}_i={\mathbf{\Gamma }}_i{\mathit{\tau }}_i^{\prime }+{\delta }_i,$$

(19)

where ${\mathbf{\Gamma }}_i=\mathrm{diag}\{{\left(1+{\eta }_1\varphi \mathrm{sign}\left({\tau }_{ti}\right)\right)}^{-1},{\left(1+{\eta }_2\varphi \mathrm{sign}\left({\tau }_{yi}\right)\right)}^{-1},{\left(1+{\eta }_3\varphi \mathrm{sign}\left({\tau }_{pi}\right)\right)}^{-1}\}$, ${\delta }_i=[-{\eta }_{1}m/\left(1+{\eta }_1\varphi \mathrm{sign}\left({\tau }_{ti}\right)\right), -{\eta }_{2}m/(1+{\eta }_2\varphi \mathrm{sign}\left({\tau }_{yi}\right)),-{\eta }_{3}m /(1+{\eta }_3\varphi \mathrm{sign}\left({\tau }_{pi}\right)){]}^{\mathrm{T}}$. $|{\eta }_1| <1$, $|{\eta }_2|$$<1$, $|{\eta }_3| <1$. When $\left|{\tau }_{ji}\right|<D$, $m={\displaystyle \frac{1}{k_{i0}}}\left(a_{i0}+{\lambda }_{i1}\right)$, when $\left|{\tau }_{ji}\right|\ge D$, $\varphi =0$, $m=m_1+{\displaystyle \frac{1}{k_{i0}}}\left(a_{i0}+{\lambda }_{i1}\right)$.

In (19), ${\mathit{\tau }}_i^{\prime }$ is a control variable that will be designed later, and ${\mathit{\tau }}_i$ is the control input of the system. When ${\mathit{\tau }}_i$ satisfies the event-triggering conditions specified in (14) and (15), the current ${\mathit{\tau }}_i$ is applied as the control input of the system at time $t_h$, denoted as ${\mathit{\tau }}_i^{\prime }\left(t_h\right)$. The control input of the system remains ${\mathit{\tau }}_i^{\prime }\left(t_h\right)$ until the next event-triggering condition is met, at which point the control input is updated to ${\mathit{\tau }}_i^{\prime }\left(t_{h+1}\right)$.

Remark 2.

Different from the triggering mechanisms in [22,23,24,25], our proposed switching threshold strategy combines the fixed threshold strategy and the relative threshold strategy. Specifically, when the control signal ${\tau }_{ij}$ is relatively small, the relative threshold strategy is employed; otherwise, the fixed threshold strategy is applied. This hybrid approach effectively ensures certain system performance metrics. Moreover, by incorporating $a_{2ji}$ into this technique, we guarantee that the event-triggered time interval $t^{*}$ remains lower bounded, even when $e_{\tau ji}$ converges to zero.

A nonsingular fix-time control law is developed as

$$\begin{array}{c}\hfill {\mathit{\tau }}_i^{\prime }=-{\displaystyle \frac{{\widehat{\mathbf{\Gamma }}}_i^{-1}{\mathit{R}}_i^{-1}{\mathit{e}}_{vi}\left({{\mathit{u}}_{\mathit{i}}}^{\mathrm{T}}{\mathit{u}}_{\mathit{i}}\right)}{\sqrt{{\mathit{e}}_{vi}^T{\mathit{e}}_{vi}{{\mathit{u}}_{\mathit{i}}}^{\mathrm{T}}{\mathit{u}}_{\mathit{i}}+\epsilon }}},\end{array}$$

(20)

where $e_{vi}=v_i-v_{di}$ is speed tracking error, $u_i$ is defined as

$$\begin{array}{cc}\hfill u_i=& {\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}+{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}+{\xi }_i{\mathit{e}}_{pi}+\mathit{G}\hfill \\ & +{\mathit{\alpha }}_{i0}-{\dot{\mathit{v}}}_{di}+{\displaystyle \frac{{\widehat{\lambda }}_i{\mathit{H}}_i}{2}}+{\displaystyle \frac{{\mathit{e}}_{vi}}{2}}+{\mathit{R}}_i{\delta }_{max},\hfill \end{array}$$

(21)

where ${\mathit{K}}_{3i}=\mathrm{diag}\{k_{31i},k_{32i},k_{33i}\},k_{3ji}\ge 0,{\mathit{K}}_{4i}=\mathrm{diag}\{k_{41i},k_{42i},k_{43i}\},k_{4ji}\ge 0, \alpha >0$, $0<\beta <1$, ${\mathit{H}}_i={\left[e_{vi1}{h}_{i1}^{\mathrm{T}}{h}_{i1},e_{vi2}{h}_{i2}^{\mathrm{T}}{h}_{i2},e_{vi3}{h}_{i3}^{\mathrm{T}}{h}_{i3}\right]}^{\mathrm{T}}$, $h_{ij}$ is basis function in radial basis function neural networks, ${\delta }_{max}={\left[{\displaystyle \frac{m}{1-\varphi }},{\displaystyle \frac{m}{1-\varphi }},{\displaystyle \frac{m}{1-\varphi }}\right]}^{\mathrm{T}}$, ${\widehat{\mathbf{\Gamma }}}_i=\mathrm{diag}\{{\left(1-\varphi \right)}^{-1},{\left(1-\varphi \right)}^{-1},{\left(1-\varphi \right)}^{-1}\}$.

The adaptive update law is designed as

$$\begin{array}{c}\hfill {\dot{\widehat{\lambda }}}_i={\displaystyle \frac{{\gamma }_i{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{H}}_i}{2}}-{\chi }_i{\gamma }_i{\widehat{\lambda }}_i,\end{array}$$

(22)

where ${\gamma }_i,{\chi }_i$ are positive design parameters.

In (20), the control variable ${\mathit{\tau }}_i^{\prime }$ is designed based on the proposed switching threshold event-triggered fixed-time convergence control strategy. By substituting it into (19), the control input ${\mathit{\tau }}_i$ of the system can be obtained.

Theorem 1.

Given dynamic models (1) and (3), dynamic controller (20), intermediate control law (21), parameter adaptation laws (22) and switching threshold event-triggered mechanism (15), all signals remain bounded and the formation tracking error converges to the origin within a fixed time, even in the presence of modeling uncertainties and external disturbances.

Proof. 

step 1: From (6), its time derivative is

$$\begin{array}{c}\hfill {\dot{\mathit{e}}}_{pi}={\xi }_i{\mathit{v}}_i-{\xi }_{1i}{b}_i{\dot{\mathit{p}}}_r-{\xi }_{1i}{b}_i\Delta {\dot{\mathit{p}}}_{ir}-{\xi }_{2i}\sum _{j\in N_i}{a}_{ij}\left({\dot{\mathit{p}}}_j+\Delta {\dot{\mathit{p}}}_{ij}\right),\end{array}$$

(23)

Design the virtual control signal ${\mathit{v}}_{ci}$ as

$$\begin{array}{cc}\hfill {\mathit{v}}_{ci}& =-{\displaystyle \frac{1}{{\xi }_i}}(\left({\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}+{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\right)\hfill \\ & +{\xi }_{1i}{b}_i{\dot{\mathit{p}}}_r+{\xi }_{1i}{b}_i\Delta {\dot{\mathit{p}}}_{ir}+{\xi }_{2i}\sum _{j\in N_i}{a}_{ij}\left({\dot{\mathit{p}}}_j+\Delta {\dot{\mathit{p}}}_{ij}\right)),\hfill \end{array}$$

(24)

where ${\mathit{K}}_{1i}=\mathrm{diag}\{k_{11i},k_{12i},k_{13i}\},k_{1ji}\ge 0,{\mathit{K}}_{2i}=\mathrm{diag}\{k_{21i},k_{22i},k_{23i}\},k_{2ji}\ge 0,{\xi }_i={\xi }_{1i}{b}_i+{\xi }_{2i}{\displaystyle \sum _{j\in N_i}}{a}_{ij}$.

To avoid the explosion of complex ${\mathit{v}}_{ci}$, a nonlinear filter ${\mathit{v}}_{di}$ is introduced to guarantee the overall fixed-time convergence as

$${\dot{\mathit{v}}}_{di}=-{\kappa }_i\left({\mathit{y}}_{vi}{∥{\mathit{y}}_{vi}∥}^{2\alpha -2}+{\mathit{y}}_{vi}{∥{\mathit{y}}_{vi}∥}^{2\beta -2}\right),$$

(25)

where $\alpha >0,0<\beta <1$ is fixed-time constants of fixed-time filter. ${\kappa }_i=\mathrm{diag}\{{\kappa }_{1i},{\kappa }_{2i},{\kappa }_{3i}\}$, ${\kappa }_{ji}\ge 0$, ${\mathit{v}}_{di}$ is filter output, the filter error is defined as $y_{vi}=v_{di}-v_{ci}$.

• Remark 3.The novel fixed-time command filter helps avoid the issue of complexity explosion. Meanwhile, according to (24), $v_{ci}$ is related to the formation tracking error $e_{pi}$. When $e_{pi}$ is large, $v_{ci}$ undergoes significant oscillations, which affects the stability of the system. By using the fixed-time filter, the impact of $e_{pi}$ on the system can be avoided, making the system more stable.

Let ${\mathit{e}}_{vi}={\mathit{v}}_i-{\mathit{v}}_{di}$. By using (24) and (25), we have

$$\begin{array}{cc}\hfill {\mathit{e}}_{pi}^{\mathrm{T}}{\dot{\mathit{e}}}_{pi}& ={\mathit{e}}_{pi}^T\left({\xi }_i{\mathit{v}}_i-{\xi }_{1i}{b}_i{\dot{\mathit{p}}}_r-{\xi }_{1i}{b}_i\Delta {\dot{\mathit{p}}}_{ir}-{\xi }_{2i}\sum _{j\in N_i}{a}_{ij}\left({\dot{\mathit{p}}}_j+\Delta {\dot{\mathit{p}}}_{ij}\right)\right)\hfill \\ & ={\mathit{e}}_{pi}^T\left({\xi }_i\left({\mathit{e}}_{vi}+{\mathit{v}}_{ci}+{\mathit{y}}_{vi}\right)-{\xi }_{1i}{b}_i{\dot{\mathit{p}}}_r-{\xi }_{1i}{b}_i\Delta {\dot{\mathit{p}}}_{ir}-{\xi }_{2i}\sum _{j\in N_i}{a}_{ij}\left({\dot{\mathit{p}}}_j+\Delta {\dot{\mathit{p}}}_{ij}\right)\right)\hfill \\ & =-{\mathit{e}}_{pi}^{\mathrm{T}}\left({\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}+{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\right)+{\xi }_i{\mathit{e}}_{pi}^{\mathrm{T}}\left({\mathit{e}}_{vi}+{\mathit{y}}_{vi}\right).\hfill \end{array}$$

(26)

step 2: From (3), taking the time derivation of ${\displaystyle \frac{1}{2}}{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{vi}$ denotes

$$\begin{array}{c}\hfill {\mathit{e}}_{vi}^{\mathrm{T}}{\dot{\mathit{e}}}_{vi}={\mathit{e}}_{vi}^{\mathrm{T}}\left({\mathit{R}}_i{\tau }_i+\mathit{G}+{\alpha }_{i0}+\Delta {\alpha }_i+{\mathit{D}}_i-{\dot{\mathit{v}}}_{di}\right).\end{array}$$

(27)

Using radial basis function neural network [44] to approximate uncertain component $\Delta {\alpha }_i$, $\Delta {\alpha }_i={[\Delta {\alpha }_{i1},\Delta {\alpha }_{i2},\Delta {\alpha }_{i3}]}^{\mathrm{T}}$.

$${\Delta \alpha }_{ij}={{\mathit{W}}_{ij}^{*}}^{\mathrm{T}}{\mathit{h}}_{ij}+l_{ij},$$

(28)

where ${{\mathit{W}}_{ij}^{*}}^{\mathrm{T}}\in {\Re }^{M\times 1}$ is an ideal weight matrix, ${\mathit{h}}_{ij}\in {\Re }^M$ is a basis function vector, $l_{ij}$ is a bounded approximation error.

Then, we have

$${\mathit{e}}_{vi}^{\mathrm{T}}(\Delta {\alpha }_i+{\mathit{D}}_i)=\sum _{j=1}^3{e}_{vij}{{\mathit{W}}_{ij}^{*}}^{\mathrm{T}}{\mathit{h}}_{ij}+\sum _{j=1}^3{e}_{vij}(l_{ij}+d_{ij}).$$

(29)

Using Young’s inequality, we obtain from (29) that

$$\begin{array}{c}{\mathit{e}}_{vi}^{\mathrm{T}}\left(\Delta {\alpha }_i+{\mathit{D}}_i\right)={\displaystyle \frac{{\mathit{e}}_{vi}^{\mathrm{T}}{\lambda }_i{\mathit{H}}_i}{2}}+{\displaystyle \frac{{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{vi}}{2}}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\end{array}$$

(30)

where ${\lambda }_i=max\{{{\mathit{W}}_{i1}^{*}}^{\mathrm{T}}{\mathit{W}}_{i1}^{*},{{\mathit{W}}_{i2}^{*}}^{\mathrm{T}}{\mathit{W}}_{i2}^{*},{{\mathit{W}}_{i3}^{*}}^{\mathrm{T}}{\mathit{W}}_{i3}^{*}\}$, ${\mathit{H}}_i$ $={\left[e_{vi1}{\mathit{h}}_{i1}^T{\mathit{h}}_{i1},e_{vi2}{\mathit{h}}_{i2}^T{\mathit{h}}_{i2},e_{vi3}{\mathit{h}}_{i3}^T{\mathit{h}}_{i3}\right]}^T$, there exists a unknown constant $g_{ij}$ such that $\left|l_{ij}+d_{ij}\right|\le g_{ij}$.

Based on (19) and (21), one has

$$\begin{array}{cc}\hfill {\mathit{e}}_{vi}^{\mathrm{T}}{\dot{\mathit{e}}}_{vi}& ={\mathit{e}}_{vi}^T\left({\mathit{R}}_i{\tau }_i+\mathit{G}+{\alpha }_{i0}+\Delta {\alpha }_i+{\mathit{D}}_i-{\dot{\mathit{v}}}_{di}\right)\hfill \\ & ={\mathit{e}}_{vi}^T\left({\mathit{R}}_i{\mathbf{\Gamma }}_i{\tau }_i^{\prime }+{\mathit{R}}_i{\delta }_i+\mathit{G}+{\alpha }_{i0}+\Delta {\alpha }_i+{\mathit{D}}_i-{\dot{\mathit{v}}}_{di}-{\mathit{u}}_i+{\mathit{u}}_i\right)\hfill \\ & ={\mathit{e}}_{vi}^{\mathrm{T}}(-{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}+{\mathit{R}}_i{\mathbf{\Gamma }}_i{\tau }_i^{\prime }+{\mathit{R}}_i{\delta }_i\hfill \\ & +\Delta {\alpha }_i+{\mathit{D}}_i-{\xi }_i{\mathit{e}}_{pi}-{\displaystyle \frac{{\widehat{\lambda }}_i{\mathit{H}}_i}{2}}-{\displaystyle \frac{{\mathit{e}}_{vi}}{2}}-{\mathit{R}}_i{\delta }_{max}+{\mathit{u}}_i)\hfill \end{array}$$

(31)

Note that ${\displaystyle \frac{-m}{1-\varphi }}\le {\displaystyle \frac{-{\eta }_{i}m}{1+{\eta }_i\varphi sign\left({\tau }_{ij}\right)}}\le {\displaystyle \frac{m}{1-\varphi }}$, we have ${\mathit{R}}_i{\delta }_i\le {\mathit{R}}_i{\delta }_{max}$. Take (30) into (31), we can obtain

$$\begin{array}{cc}\hfill {\mathit{e}}_{vi}^{\mathrm{T}}{\dot{\mathit{e}}}_{vi}& \le -{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}+{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{R}}_i{\mathbf{\Gamma }}_i{\tau }_i^{\prime }\hfill \\ & -{\displaystyle \frac{{\mathit{e}}_{vi}^{\mathrm{T}}{\stackrel{\sim }{\lambda }}_i{\mathit{H}}_i}{2}}-{\xi }_i{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{pi}+{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{u}}_i+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(32)

Consider the following Lyapunov function candidate

$$L={\displaystyle \frac{1}{2}}{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{e}}_{pi}+{\displaystyle \frac{1}{2}}{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{vi}+{\displaystyle \frac{1}{2}}{\mathit{y}}_{vi}^{\mathrm{T}}{\mathit{y}}_{vi}+{\displaystyle \frac{1}{2{\gamma }_i}}{{\displaystyle \stackrel{\sim }{\lambda }}}_i^2$$

(33)

where ${\stackrel{\sim }{\lambda }}_i={\widehat{\lambda }}_i-{\lambda }_i$, ${\gamma }_i$, are positive design parameters.

Based on (26) and (32), the time derivative of (33) leads to

$$\begin{array}{cc}\hfill \dot{L}& \le -{\mathit{e}}_{pi}^{\mathrm{T}}\left({\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}+{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\right)\hfill \\ & -{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}+{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{R}}_i{\mathbf{\Gamma }}_i{\mathit{\tau }}_i^{\prime }-{\displaystyle \frac{{\mathit{e}}_{vi}^{\mathrm{T}}{\stackrel{\sim }{\lambda }}_i{\mathit{H}}_i}{2}}\hfill \\ & +{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{u}}_i+{\mathit{y}}_{vi}^{\mathrm{T}}\left({\dot{\mathit{y}}}_{vi}+{\xi }_i{\mathit{e}}_{pi}\right)+{\displaystyle \frac{1}{{\gamma }_i}}{\stackrel{\sim }{\lambda }}_i{\dot{\stackrel{\sim }{\lambda }}}_i+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(34)

Note that $x\le x^m+x^n$, $x\ge 0,0<m<1,n>1$, the following inequality holds

$$\begin{array}{c}\hfill {\mathit{y}}_{vi}^T\left({\dot{\mathit{y}}}_{vi}+{\xi }_i{\mathit{e}}_{pi}\right)\le -{\kappa }_i\left({∥{\mathit{y}}_{vi}∥}^{2\alpha }+{∥{\mathit{y}}_{vi}∥}^{2\beta }\right)+{\displaystyle \frac{{\varpi }_i^2}{2}}\end{array}$$

(35)

where ${\kappa }_i={\lambda }_{min}\left({\mathbf{\kappa }}_i\right)-{\displaystyle \frac{1}{2}}$, and there exists a positive constant ${\varpi }_i$ so that $∥{\xi }_i{\mathit{e}}_{pi}-{\dot{\mathit{v}}}_{ci}∥\le {\varpi }_i$.

Considering that ${\mathbf{\Gamma }}_i$ is bounded and satisfied ${\mathbf{\Gamma }}_i\le {\widehat{\mathbf{\Gamma }}}_i=\mathrm{diag}\{{\left(1-\varphi \right)}^{-1},{\left(1-\varphi \right)}^{-1},$ ${\left(1-\varphi \right)}^{-1}\}$. Invoking Lemma 2, it follows along (20) that

$$\begin{array}{cc}\hfill {\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{R}}_i\widehat{{\mathbf{\Gamma }}_i}{\mathit{\tau }}_i^{\prime }& =-{\displaystyle \frac{{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{vi}\left({{\mathit{u}}_i}^{\mathrm{T}}{\mathit{u}}_i\right)}{\sqrt{{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{e}}_{vi}{{\mathit{u}}_i}^{\mathrm{T}}{\mathit{u}}_i+{\epsilon }_i}}}\hfill \\ & \le \sqrt{{\epsilon }_i}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{u}}_i\hfill \end{array}$$

(36)

By substituting (22), (35), and (36) into (34), we have

$$\begin{array}{cc}\hfill \dot{L}& \le -{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}-{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\hfill \\ & -{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}\hfill \\ & -{\kappa }_i\left({∥{\mathit{y}}_{vi}∥}^{2\alpha }+{∥{\mathit{y}}_{vi}∥}^{2\beta }\right)-{\chi }_i{\stackrel{\sim }{\lambda }}_i{\widehat{\lambda }}_i+{\displaystyle \frac{{\varpi }_i^2}{2}}+\sqrt{{\epsilon }_i}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(37)

Adding and subtracing the terms of ${\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }$, ${\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }$, the (37) can be rewritten as

$$\begin{array}{cc}\hfill \dot{L}& \le -{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}-{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\hfill \\ & -{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}\hfill \\ & -{\kappa }_i\left({∥{\mathit{y}}_{vi}∥}^{2\alpha }+{∥{\mathit{y}}_{vi}∥}^{2\beta }\right)-{\chi }_i{\stackrel{\sim }{\lambda }}_i{\widehat{\lambda }}_i\hfill \\ & -{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }-{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }+{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }+{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }\hfill \\ & +{\displaystyle \frac{{\varpi }_i^2}{2}}+\sqrt{{\epsilon }_i}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(38)

Using Young’s inequality, we can obtain

$$\begin{array}{cc}\hfill -{\chi }_i{\stackrel{\sim }{\lambda }}_i{\widehat{\lambda }}_i& \le -{\displaystyle \frac{{\chi }_i}{{\gamma }_i}}{\stackrel{\sim }{\lambda }}_i^2+{\displaystyle \frac{{\xi }_1{\chi }_i}{2}}{\lambda }_i^2,\hfill \end{array}$$

(39)

where ${\gamma }_i={\displaystyle \frac{2\xi }{2\xi -1}}$, with $\xi >{\displaystyle \frac{1}{2}}$.

Using Lemma 3, we have

$$\begin{array}{cc}\hfill {\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }& \le {\displaystyle \frac{{\chi }_i{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}+{\chi }_i\left(1-\beta \right){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}.\hfill \end{array}$$

(40)

From (39) and (40), it follows from (38) that

$$\begin{array}{cc}\hfill \dot{L}& \le -{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}-{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\hfill \\ & -{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{\mathit{K}}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}\hfill \\ & -{\kappa }_i\left({∥{\mathit{y}}_{vi}∥}^{2\alpha }+{∥{\mathit{y}}_{vi}∥}^{2\beta }\right)-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}{\stackrel{\sim }{\lambda }}_i^2-{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }-{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }+{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }\hfill \\ & +{\displaystyle \frac{\xi {\chi }_i}{2}}{\lambda }_i^2+{\chi }_i\left(1-\beta \right){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}+{\displaystyle \frac{{\varpi }_i^2}{2}}+\sqrt{{\epsilon }_i}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(41)

Suppose that there exist unknown constants c such that $max\left\{{\stackrel{\sim }{\lambda }}_i^2,2{\gamma }_i\right\}\le c$. The following two cases are discussed.

Case 1: If ${\stackrel{\sim }{\lambda }}_i^2<2{\gamma }_i$, then

$$\begin{array}{c}\hfill {\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}{\stackrel{\sim }{\lambda }}_i^2<0.\end{array}$$

(42)

Case 2: If ${\stackrel{\sim }{\lambda }}_i^2\ge 2{\gamma }_i$, then

$$\begin{array}{c}\hfill {\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}{\stackrel{\sim }{\lambda }}_i^2={\chi }_i{\left({\displaystyle \frac{c}{2{\gamma }_i}}\right)}^{\alpha }-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}c\ge 0.\end{array}$$

(43)

Summarizing Case 1 and Case 2, we have

$$\begin{array}{cc}\hfill \dot{L}& \le -{\mathit{e}}_{pi}^{\mathrm{T}}{\mathit{K}}_{1i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\alpha -2}-{\mathit{e}}_{pi}^{\mathrm{T}}{K}_{2i}{\mathit{e}}_{pi}{∥{\mathit{e}}_{pi}∥}^{2\beta -2}\hfill \\ & -{\mathit{e}}_{vi}^{\mathrm{T}}{K}_{3i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\alpha -2}-{\mathit{e}}_{vi}^{\mathrm{T}}{K}_{4i}{\mathit{e}}_{vi}{∥{\mathit{e}}_{vi}∥}^{2\beta -2}\hfill \\ & -{\kappa }_i\left({∥{\mathit{y}}_{vi}∥}^{2\alpha }+{∥{\mathit{y}}_{vi}∥}^{2\beta }\right)-{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }-{\chi }_i{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }+{\chi }_i{\left({\displaystyle \frac{c}{2{\gamma }_i}}\right)}^{\alpha }-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}c\hfill \\ & +{\displaystyle \frac{\xi {\chi }_i}{2}}{\lambda }_i^2+{\chi }_i\left(1-\beta \right){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}+{\displaystyle \frac{{\varpi }_i^2}{2}}+\sqrt{{\epsilon }_i}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}\hfill \end{array}$$

(44)

Define $k_{1i}=\lambda min\left({\mathit{K}}_{1i}\right),k_{2i}=\lambda min\left({\mathit{K}}_{2i}\right),k_{3i}=\lambda min\left({\mathit{K}}_{3i}\right),k_{4i}=\lambda min\left({\mathit{K}}_{4i}\right)$, $\zeta ={\chi }_i{\left({\displaystyle \frac{c}{2{\gamma }_i}}\right)}^{\alpha }-{\displaystyle \frac{{\chi }_i}{2{\gamma }_i}}c+{\displaystyle \frac{\xi {\chi }_i}{2}}{\lambda }_i^2+{\chi }_{1i}\left(1-\beta \right){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}+{\displaystyle \frac{{\varpi }_i^2}{2}}+\sqrt{{\epsilon }_i}+{\displaystyle \frac{3}{2}}+\sum _{j=1}^3{\displaystyle \frac{g_{ij}^2}{2}}$.

It follows from (44) that

$$\begin{array}{cc}\hfill \dot{L}& \le -2^{\alpha }{k}_{1i}{\left({{\displaystyle \frac{∥{\mathit{e}}_{pi}∥}{2}}}^2\right)}^{\alpha }-2^{\alpha }{k}_{3i}{\left({{\displaystyle \frac{∥{\mathit{e}}_{vi}∥}{2}}}^2\right)}^{\alpha }\hfill \\ & -2^{\alpha }{\kappa }_i{\left({\displaystyle \frac{{∥{\mathit{y}}_{vi}∥}^2}{2}}\right)}^{\alpha }-{\chi }_{1i}{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\alpha }\hfill \\ & -2^{\beta }{k}_{2i}{\left({{\displaystyle \frac{∥{\mathit{e}}_{pi}∥}{2}}}^2\right)}^{\beta }-2^{\beta }{k}_{4i}{\left({{\displaystyle \frac{∥{\mathit{e}}_{vi}∥}{2}}}^2\right)}^{\beta }\hfill \\ & -2^{\beta }{\kappa }_i{\left({\displaystyle \frac{{∥{\mathit{y}}_{vi}∥}^2}{2}}\right)}^{\beta }-{\chi }_{1i}{\left({\displaystyle \frac{{\stackrel{\sim }{\lambda }}_i^2}{2{\gamma }_i}}\right)}^{\beta }+\zeta \hfill \end{array}$$

(45)

Define ${\sigma }_1=4^{1-\alpha }·min\left\{2^{\alpha }{k}_{1i},2^{\alpha }{k}_{3i},2^{\alpha }{\kappa }_i,{\chi }_{1i}\right\}$, ${\sigma }_2=min\left\{2^{\beta }{k}_{2i},2^{\beta }{k}_{4i},2^{\beta }{\kappa }_i,{\chi }_{1i}\right\}$. According to Lemma 4, we have

$$\begin{array}{c}\hfill \dot{L}\le -{\sigma }_1{L}^{\alpha }-{\sigma }_2{L}^{\beta }+\zeta \end{array}$$

(46)

Recalling Lemma 1, it can be conclued that the system is practically fixed-time stable, and we can derive

$$\begin{array}{c}\hfill L\left(x\right)\le min\left\{{\left({\displaystyle \frac{\zeta }{{\sigma }_1\left(1-o\right)}}\right)}^{{\displaystyle \frac{1}{\alpha }}},{\left({\displaystyle \frac{\zeta }{{\sigma }_2\left(1-o\right)}}\right)}^{{\displaystyle \frac{1}{\beta }}}\right\}\end{array}$$

(47)

The setting time is

$$\begin{array}{c}\hfill T\le T_{max}:={\displaystyle \frac{1}{{\sigma }_{1}o\left(\alpha -1\right)}}+{\displaystyle \frac{1}{{\sigma }_{2}o\left(1-\beta \right)}}\end{array}$$

(48)

• Remark 4.Note that $e_{pi}$ can be made arbitrarily small by increasing $K_{3i}$, $K_{4i}$, ${\gamma }_i$ and decreasing ${\chi }_i$. Therefore, the formation tracking error can be made arbitrarily small by appropriate choice of the design parameters. During the simulation, it is also important to choose suitable ϕ, $m_1$, $a_{i0}$, ${\lambda }_{i1}$, ${\kappa }_{i0}$ to balance triggering times and control perfermance.

Further, it is proved that Zeno behavior can be avoided. We define ${\mathit{e}}_{\tau i}\left(t\right)={\mathit{\tau }}_i^{\prime }\left(t\right)-{\mathit{\tau }}_i\left(t\right)$. From (20) and (46), ${\mathit{\tau }}_i^{\prime }$ is a function of the bounded variables. Then, we have ${\displaystyle \frac{d}{dt}}\left|{\mathit{e}}_{\tau i}\right|\le \left|{\dot{\mathit{\tau }}}_i^{\prime }\right|$. It can be concluded that $|{\dot{\mathit{\tau }}}_i^{\prime }|$ is bounded for the entire closed-loop system and satisfying $|{\dot{\mathit{\tau }}}_i^{\prime }|\le {\vartheta }_{\tau i}$, where ${\vartheta }_{\tau i}={[{\vartheta }_{1\tau i},{\vartheta }_{2\tau i},{\vartheta }_{3\tau i}]}^{\mathrm{T}}$, in which ${\vartheta }_{j\tau i}$ is positive constant, $j=1,2,3$. The (16) reveals that ${\mathit{e}}_{\tau i}\left(t_h\right)=0$ and ${lim}_{t\to t_{h+1}}{\mathit{e}}_{\tau i}\left(t\right)=\mathit{m}$, we obtain that the lower bound of time intervals $t^{*}$ satisfy $t^{*}\ge {\displaystyle \frac{\mathit{m}}{{\mathit{\tau }}_{\delta i}}}$. The proof of Theorem 1 is completed. □

4. Performance Evaluation

In this section, we present numerical simulations to verify the effectiveness of the proposed event-triggered fixed-time control strategy.

4.1. Simulation Setup

4.1.1. Simulation Metrics

The communication topology of MAV/UAVs is shown in Figure 3. The initial states are given in Table 1. The external disturbance ${\mathit{D}}_i={\left[0.2cos\left(t\right),0.2sin\left(t\right),0.3sin\left(t\right)\right]}^{\mathrm{T}}$. The desired trajectory for MAV is given as: $x_d\left(t\right)=140t$, $y_d\left(t\right)=0$, $z_d\left(t\right)=3000-150t\left(0<t\le 10\right),z_d\left(t\right)=1500\left(t>10\right)$. In addition, the desired relative position of each aircraft in the MAV/UAVs system is set as $\Delta {\mathit{p}}_{1r}={\left[0,0,0\right]}^{\mathrm{T}}$, $\Delta {\mathit{p}}_{21}={\left[-100,100,0\right]}^{\mathrm{T}}$, $\Delta {\mathit{p}}_{31}={\left[-100,-100,0\right]}^{\mathrm{T}}$.

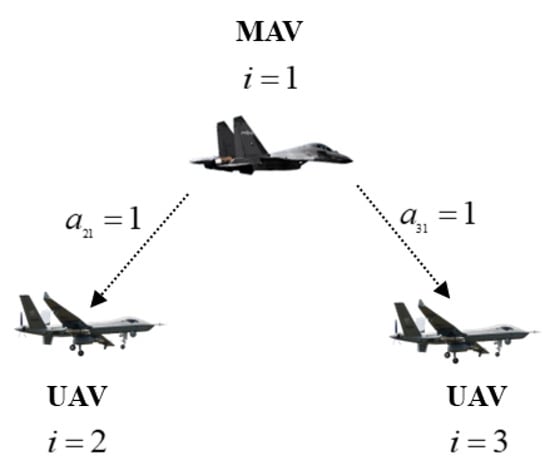
Figure 3. Communication topology.

Table 1. Initial States of MAV/UAVs.

	$\mathit{v}\left(0\right)$	$\mathit{x}\left(0\right)$	$\mathit{y}\left(0\right)$	$\mathit{z}\left(0\right)$
$MA{V}_1$	160 m/s	100 m	0 m	3000 m
$UA{V}_2$	140 m/s	−10 m	145 m	3000 m
$UA{V}_3$	150 m/s	−25 m	−170 m	3000 m

The desired trajectory for MAV is given as: $x_d\left(t\right)=140t$, $y_d\left(t\right)=0$, $z_d\left(t\right)=3000-150t\left(0<t\le 10\right),z_d\left(t\right)=1500\left(t>10\right)$. In addition, the desired relative position of each aircraft in the MAV/UAVs system is set as $\Delta {\mathit{p}}_{1r}={\left[0,0,0\right]}^{\mathrm{T}}$, $\Delta {\mathit{p}}_{21}={\left[-100,100,0\right]}^{\mathrm{T}}$, $\Delta {\mathit{p}}_{31}={\left[-100,-100,0\right]}^{\mathrm{T}}$. The nodes of RBF neural network are selected as 9, and the width is 5 [35]. Denote ${\mathbf{\Theta }}_i={\left[p_i^{\mathrm{T}},v_i^{\mathrm{T}},{\tau }_i^{\mathrm{T}}\right]}^{\mathrm{T}}\in {\Re }^9$. The basic function is $h_{ij}^l\left({\mathbf{\Theta }}_i\right)=exp\left[-{\left({\mathbf{\Theta }}_i-{\mathbf{{\rm Y}}}_i\right)}^{\mathrm{T}}\left({\mathbf{\Theta }}_i-{\mathbf{{\rm Y}}}_i\right)/{\zeta }^2\right],l=1,\dots ,9$.

The designed parameters specified in (19)–(21), (24), (25), (27), and (28) are set as follows: $m_1=2$, $a_{10}=a_{20}=a_{30}=1$, $\varphi =0.5$, ${\lambda }_{11}={\lambda }_{21}={\lambda }_{31}=1$, ${\lambda }_{12}={\lambda }_{22}={\lambda }_{32}=1$, $k_{10}=k_{20}=k_{30}=1$, $D=5$, $\epsilon =0.0001$, ${\mathit{K}}_{11}=\mathrm{diag}\{20,200,2\}$, ${\mathit{K}}_{12}=\mathrm{diag}\{20,20,40\}$, ${\mathit{K}}_{13}=\mathrm{diag}\{20,20,60\}$, ${\mathit{K}}_{21}=\mathrm{diag}\{10,120,1\}$, ${\mathit{K}}_{22}=\mathrm{diag}\{10,10,20\}$, ${\mathit{K}}_{23}=\mathrm{diag}\{10,10,30\}$, ${\mathit{K}}_{31}={\mathit{K}}_{32}={\mathit{K}}_{33}=\mathrm{diag}\{0.5,0.5,0.5\}$, ${\mathit{K}}_{41}={\mathit{K}}_{42}={\mathit{K}}_{43}=\mathrm{diag}\{0.3,0.3,0.3\}$, $\alpha =1.2$, $\beta =0.8$, ${\xi }_{11}={\xi }_{12}={\xi }_{13}=1$, ${\xi }_{21}={\xi }_{22}={\xi }_{23}=1$, $b_1=1$, $b_2=b_3=0$, ${\kappa }_1=\mathrm{diag}\{1000,20,1000\}$, ${\kappa }_2={\kappa }_3=\mathrm{diag}\{1900,1000,1000\}$, ${\gamma }_1={\gamma }_2={\gamma }_3=\mathrm{diag}\{0.25,0.25,0.25\}$,${\chi }_1={\chi }_2={\chi }_3=0.2$, $b_1=1$, $b_2=b_3=0$, $a_{12}=a_{13}=a_{23}=a_{32}=0$, $a_{21}=a_{31}=1$.

4.1.2. Simulation Scenarios

The task is set as a humanitarian mission, where the virtual leader provides the trajectory reference. Given the formation scenario involving a manned aerial vehicle (MAV) and two unmanned aerial vehicles (UAVs), the MAV is tasked with tracking the predetermined trajectory. During this process, the MAV issues specific operation tasks to the UAVs. Each UAV follows the MAV’s trajectory precisely, thereby forming a designated formation.

4.2. Experimental Results

Experimental results are presented in Figure 4, Figure 5, Figure 6 and Figure 7. Figure 4 illustrates the position of each aircraft in the MAV/UAV system. Successful formation synchronization tracking, as observed in Figure 4, confirms the effectiveness of the proposed control methods. Position errors for ${\mathit{e}}_{p1}$, ${\mathit{e}}_{p2}$ and ${\mathit{e}}_{p3}$ are shown in Figure 5a–c. Despite model uncertainties and external disturbances, the proposed fixed-time formation control method maintains high-precision tracking. Figure 6 displays the relative position curves between each UAV and the MAV, indicating that the three axes of relative position converge to the desired values within 4 s. According to (48), the maximum convergence time of the fixed-time control method is $T_{max}=35$ s. Obviously, the simulation result meets the requirement of the setting time.

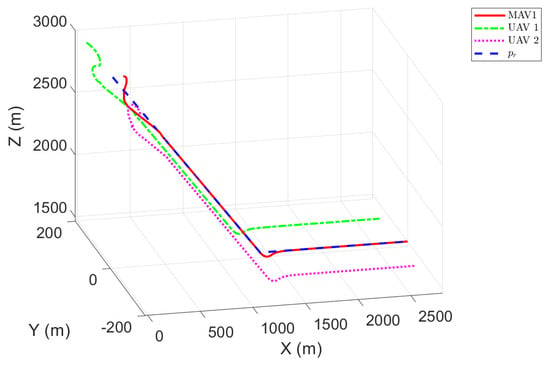
Figure 4. MAV/UAVs group formation.

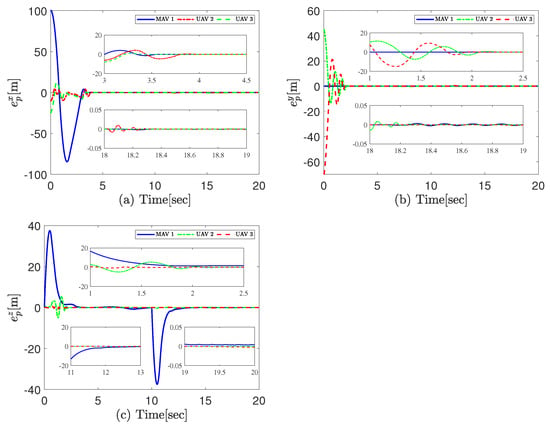
Figure 5. MAV/UAVs position tracking error curves. (a) x-direction variation curve. (b) y-direction variation curve. (c) z-direction variation curve.

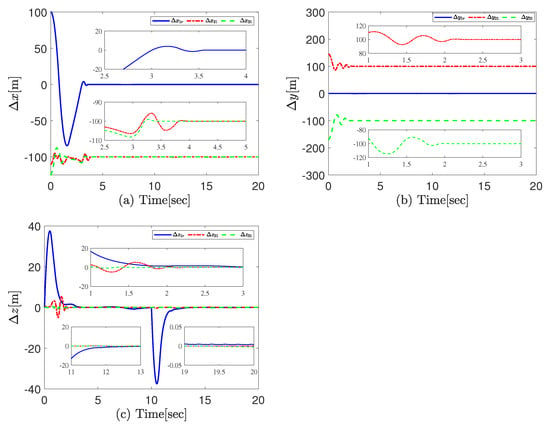
Figure 6. Response curves of relative positions for MAV/UAVs. (a) x-direction relative distances. (b) y-direction relative distances. (c) z-direction relative distances.

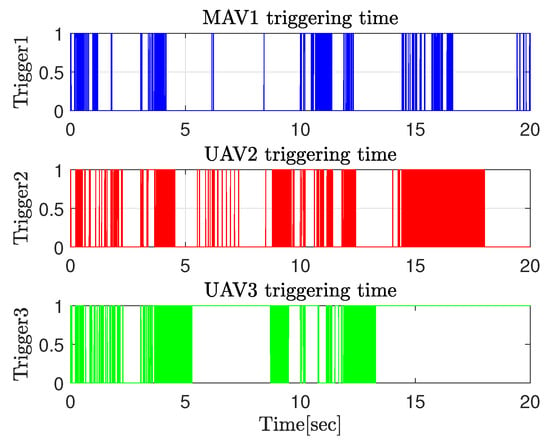
Figure 7. Event-triggering time.

The time interval and the number of triggering events are depicted in Figure 7. It is clear that throughout the simulation process, all triggering intervals have positive execution times, indicating that there is no Zeno behavior under the proposed event triggering mechanism. Additionally, to verify the superiority of the proposed model, comparisons were conducted with three control methods. The first is periodic sampling control, which removes the event-triggered strategy in the proposed model (Controller 1). Furthermore, we compared with fixed threshold event-triggering control (Controller 2) [22] and relative threshold event-triggering control (Controller 3) [24]. The result is shown in Table 2. It can be seen that compared with the three comparison methods, the proposed control method saves $86\%$, $34\%$, and $43\%$ of control transmission burden respectively, which significantly reduces the number of triggered events.

Table 2. The event-triggering times of the controller under different controllers.

Control Schemes	${\mathit{MAV}}_1$	${\mathit{UAV}}_2$	${\mathit{UAV}}_3$
Compared controller 1	20,000	20,000	20,000
Compared controller 2	3375	4410	4287
Compared controller 3	4542	4523	4953
Proposed controller	2150	4014	1807

5. Conclusions

This paper presents a novel switching threshold fixed-time event-triggered formation control mechanism for MAV/UAVs operating in environments with external disturbances and modeling uncertainties. A fixed-time filter is employed to estimate the desired velocity while eliminating the impact of speed oscillations on system stability, enhancing the robustness of the system. Additionally, a switching threshold event-triggered mechanism is developed to effectively reduce communication and computational burdens by adjusting the triggered moment according to system performance. As a result, the closed-loop system achieves practical fixed-time stability with all signals remaining bounded. Numerical simulations are provided to confirm the effectiveness of the proposed control mechanism. Demonstrating that the formation tracking errors converge to zero within a fix time, meanwhile, the desired formation configuration is successfully maintained even in the presence of disturbances and modeling uncertainties. Moreover, the event-triggering times is significantly reduced. In practical applications, as the number of event triggers is effectively reduced, the frequency of communication and the update frequency of actuators decrease. In actual flight control systems with limited computational and communication resources, this will effectively reduce the waste of resources and enhance system stability.

While this study has demonstrated the effectiveness of the proposed fixed-time control strategy for MAV/UAVs, several promising directions warrant further investigation. First, the dynamic model employed in this study is a 3-degree-of-freedom (3-DOF) point mass model, primarily focusing on the trajectory tracking of manned/unmanned aerial vehicle (MAV/UAV) formations. To achieve a more precise system description, future research will incorporate a nonlinear 6-degree-of-freedom (6-DOF) dynamic model with twelve state variables. This enhanced model will enable the decoupled analysis of rotational and translational dynamics while explicitly accounting for practical aircraft constraints, including pitch angle, roll angle, and heading angle limitations. Second, future work will focus on adopting a deep learning-based hierarchical active fault-tolerant control to estimate and compensate the actuator faults to enhance the fault tolerance of the system. Additionally, we plan to design a predefined-time stability control strategy for MAV/UAVs. Compared with fixed-time control method, the predefined-time control method allows the settling time to be determined by specific parameters, thereby further improving the convergence performance of the system.