Georeferenced UAV Localization in Mountainous Terrain Under GNSS-Denied Conditions
Abstract
1. Introduction
- A VBN architecture and SM technique efficient for high-altitude UAV localization in mountainous terrain.
- Orthorectification of aerial imagery using a projection model and DEM to mitigate geometric distortions, thereby improving matching accuracy with orthophoto maps.
- Validation in real flight experiments over mountainous regions.
2. Methods
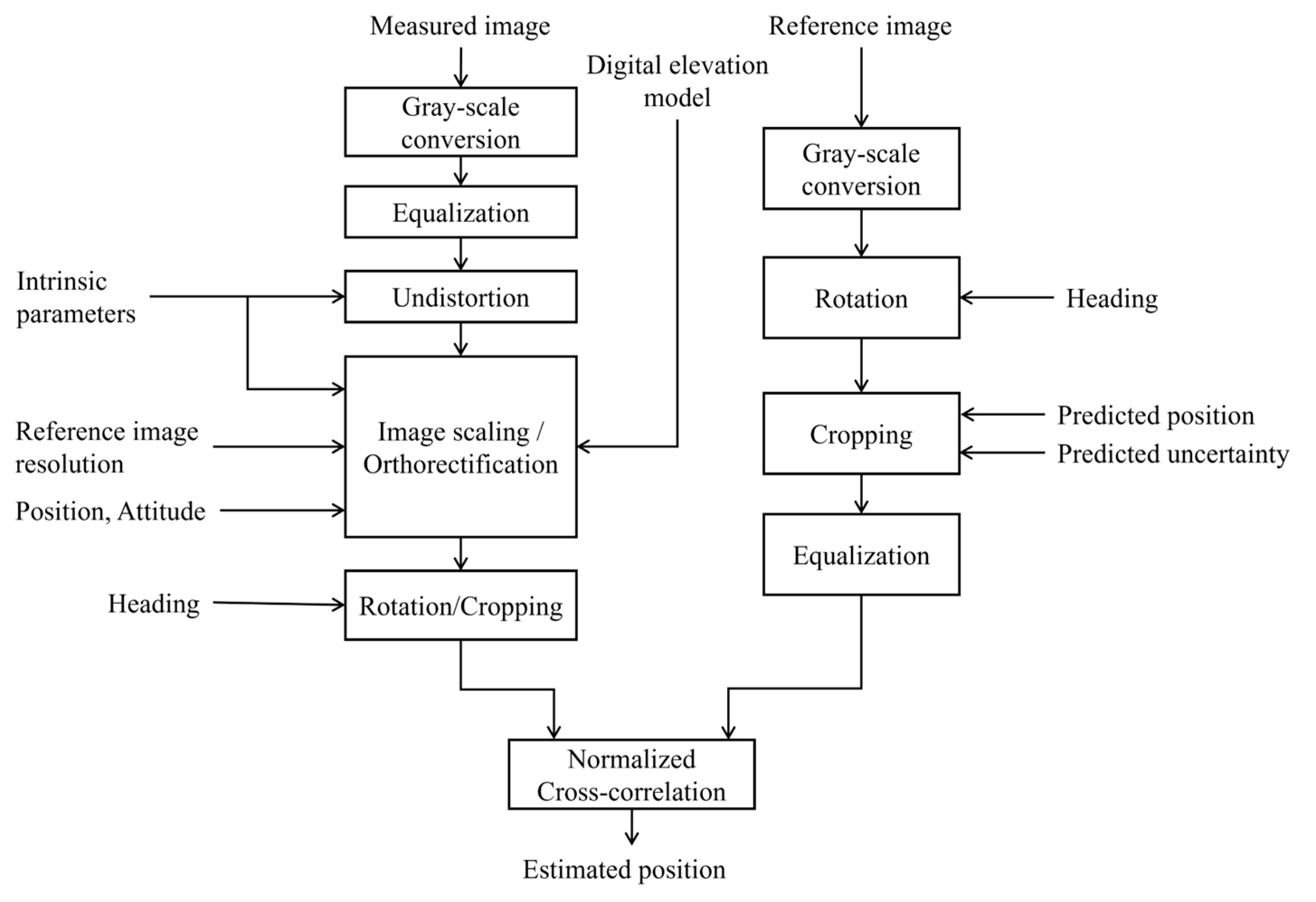
2.1. Overview
- Input Data: Measurements from the IMU, GNSS, barometric altimeter, and camera, along with reference data including orthophoto maps and DEMs. When GNSS is available, the GNSS navigation solution is used to correct INS errors; otherwise, the SM result is used.
- INS Mechanization: The IMU outputs are processed to compute the UAV’s position, velocity, and attitude using INS mechanization.
- Aerial Scene Matching: Aerial images are compared with the georeferenced orthophoto map to estimate the UAV’s position. Orthorectification is applied to compensate for terrain-induced geometric distortions using DEM data. Aerial images undergo image processing to achieve consistent resolution, rotation, and illumination with georeferenced images.
- Sensor Fusion: The proposed method employs three EKF-based sub-modules for sensor fusion: a 13-state EKF for horizontal navigation errors, attitude errors, and sensor biases; a 2-state EKF for vertical channel (altitude) stabilization; and a 2-state error estimator for the barometric altimeter. These sub-modules collectively produce a corrected navigation solution.
2.2. Aerial Scene Matching
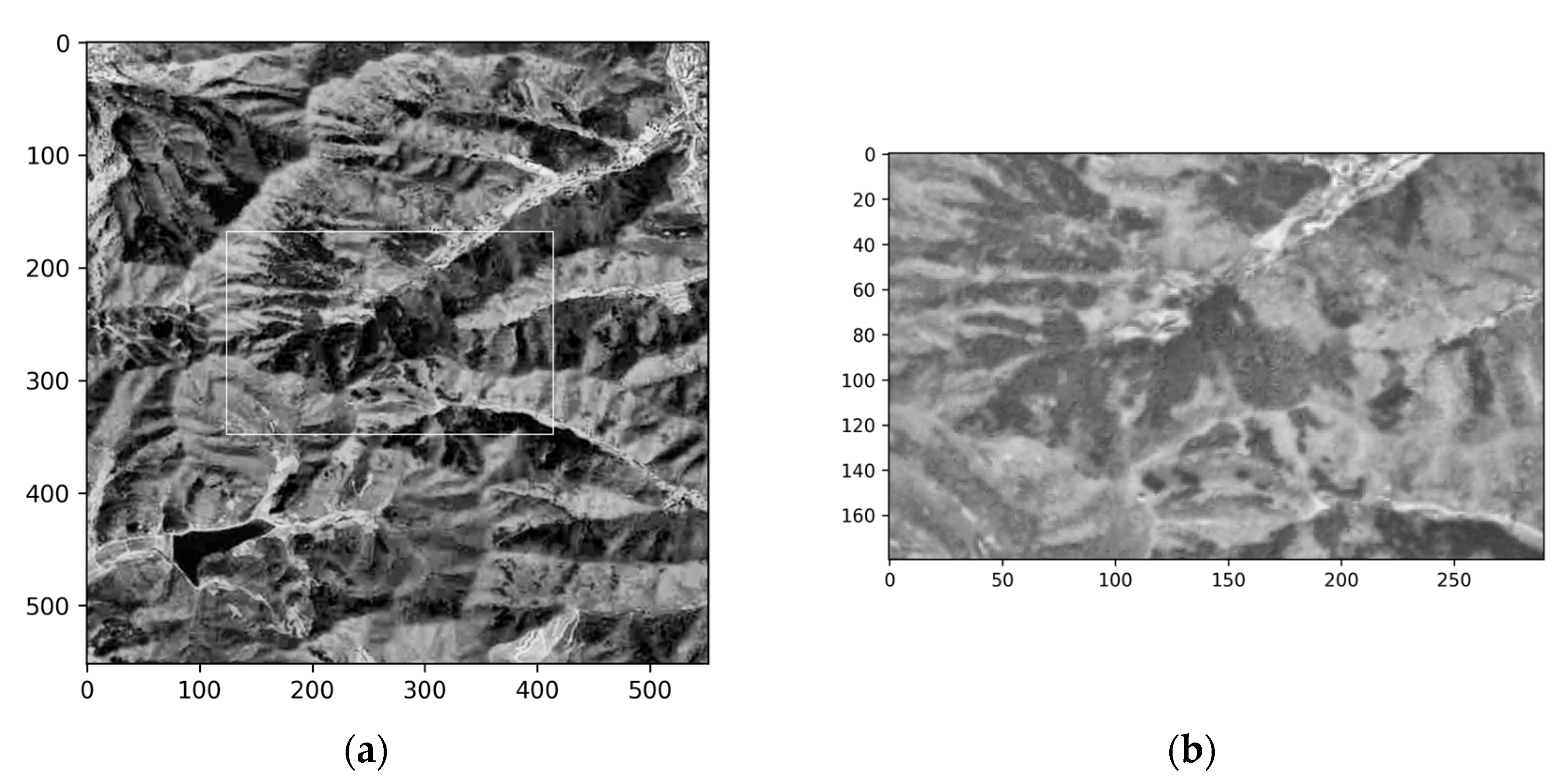
2.2.1. Georeferenced Image
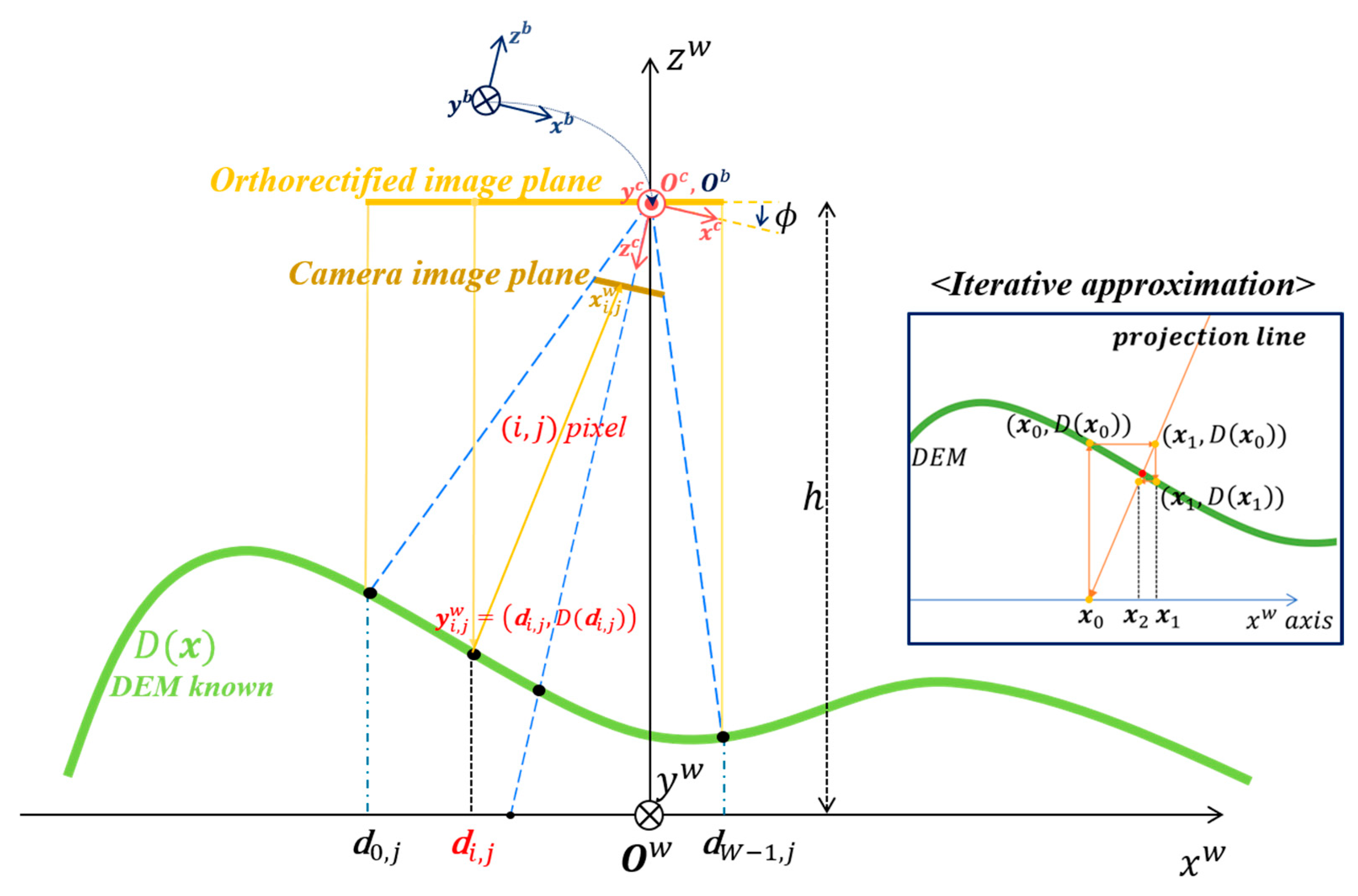
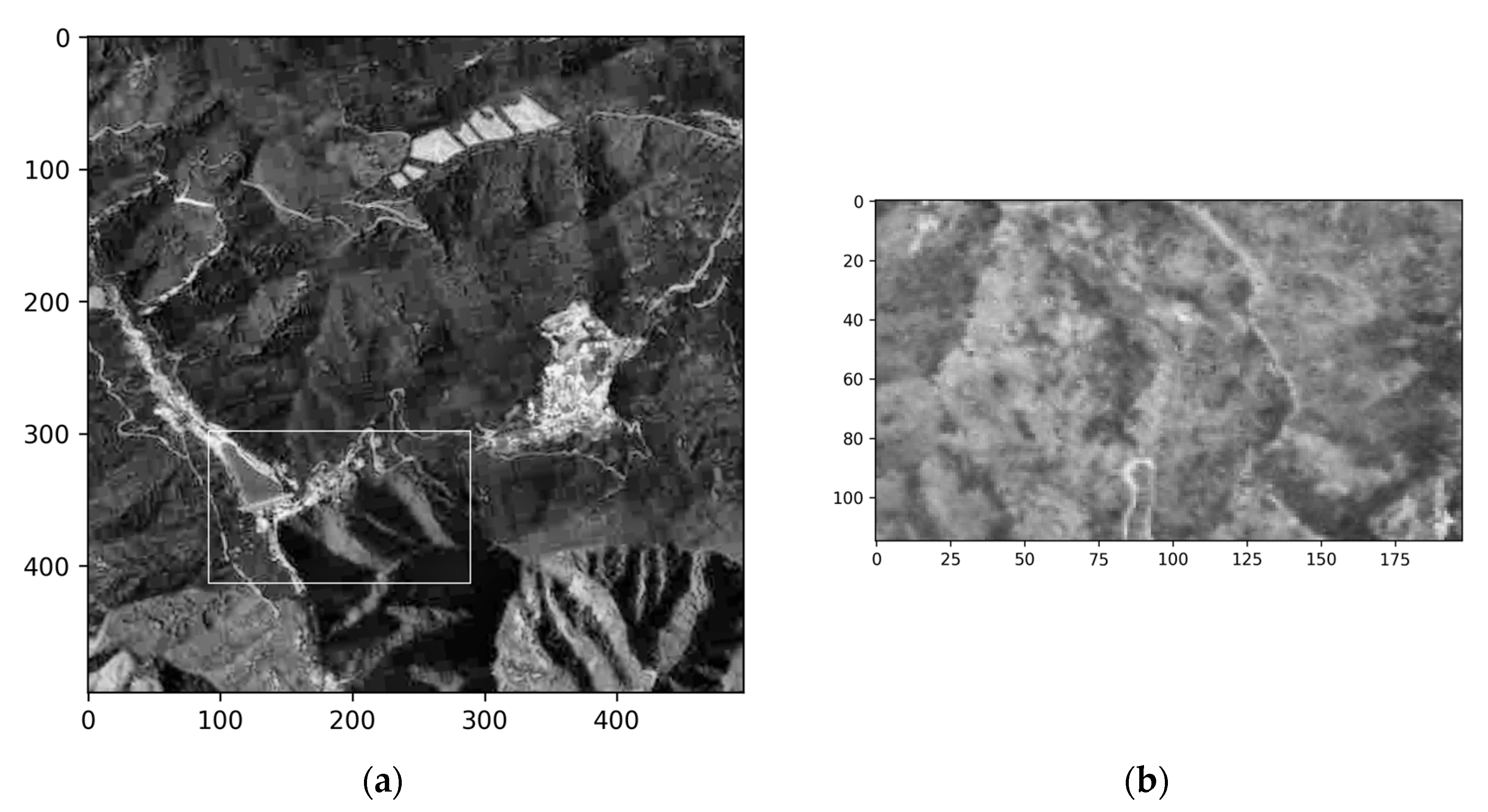
2.2.2. Orthorectification
- Projection Model Development: A projection model is created using the camera’s intrinsic (e.g., focal length) and extrinsic (e.g., position and attitude) parameters [27]. The camera position and attitude information determining the projection model uses aided navigation information estimated through the sensor fusion framework (Section 2.3).
- Pixel-to-Terrain Projection: The projection path for each pixel in the image sensor is computed based on the projection model.
- Pixel Georeferencing: Using the DEM, the intersection between each pixel’s projection line and the terrain is determined, yielding the actual geographic coordinates corresponding to each image pixel.
- Reprojection and Compensation: The image is reprojected to compensate for terrain relief displacements, aligning each pixel with its actual geographic location.
Orthorectification Using Camera Projection Model
| Algorithm 1. Fixed-Point Iteration for Finding Intersections of a 3D Line and a Discretized Data Surface. |
| Require: 3D line = *, discretized data , initial height , initial height offset , tolerance , maximum iterations |
| Ensure: Intersection point where and lies on the line |
| do |
| using 2D interpolation (e.g., bilinear) |
| then |
| 9: end if |
| 12: end while |
| 13: return Failure: Did not converge within N iterations |
| * The line is defined by the camera image pixel position and the reference point (0, 0, h) in the W-frame. |
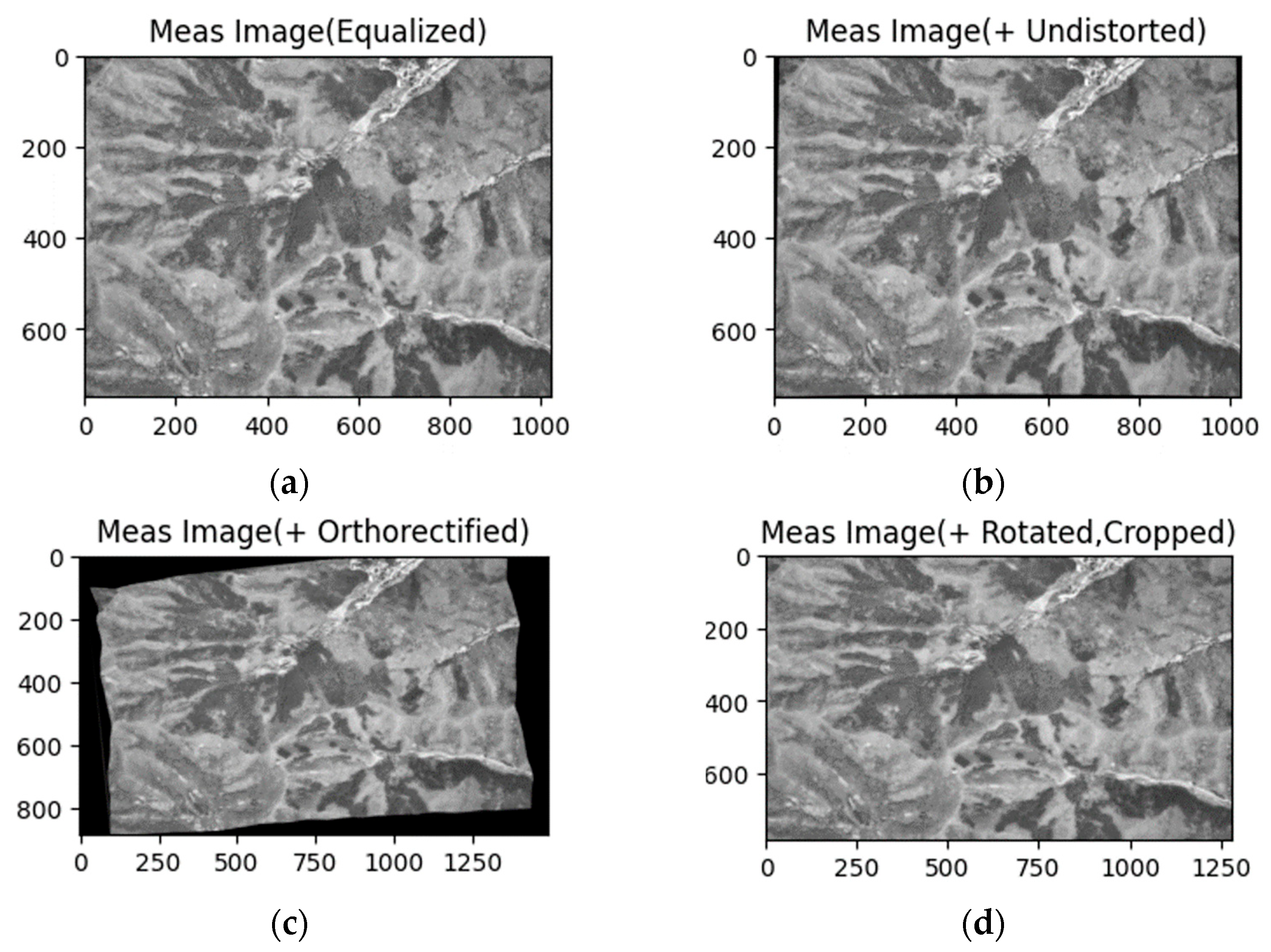
Orthorectification Results
2.2.3. Image Processing and Matching
- Illumination Normalization: Histogram equalization or Contrast-Limited Adaptive Histogram Equalization (CLAHE) [28] is applied to both UAV images and georeferenced images to mitigate variations in lighting and contrast, ensuring robustness across diverse environmental conditions.
- Lens Distortion Correction: UAV images are corrected for lens-induced distortions using pre-calibrated intrinsic camera parameters and distortion coefficients, ensuring accurate spatial geometry.
- Resolution Adjustment: To ensure spatial consistency between the UAV image and the georeferenced map, the UAV image is rescaled based on the aided altitude. The scaling factors in the and directions are computed as:
- Orthorectification: Orthorectification is performed to remove geometric distortions in aerial imagery caused by camera position, attitude, and terrain elevation variations, thereby ensuring consistency with the georeferenced orthophoto maps (Section 2.2.2).
- Rotational Alignment: Before template matching, the georeferenced image and the aerial image should be rotationally aligned using the UAV’s attitude data. The orthorectified aerial image shows a ground footprint rotated by the UAV’s heading. Since template matching is carried out by sliding a rectangular template over the georeferenced image, the orthorectified image would be excessively cropped without alignment. To minimize this effect, both the orthorectified image and the georeferenced image are rotated by the UAV’s heading angle, thus achieving rotational alignment. This rotation is implemented using a 2D affine transformation matrix defined as
- Template Matching: Following the preprocessing, template matching is employed to estimate the UAV’s position by correlating the UAV image (template) with a reference image. The similarity between the template and a region of the reference image is measured using NCC [29], which is known for robustness against linear illumination variations. NCC computes the normalized correlation coefficient between the template and a sliding window in the reference image.
2.3. Sensor Fusion
2.3.1. Horizontal Channel EKF
2.3.2. Vertical Channel EKF
2.3.3. Barometric Altimeter Error Estimator
3. Experimental Setups and Results
3.1. Experiment on Real Flight Aerial Image Dataset
3.1.1. Sensor Specification
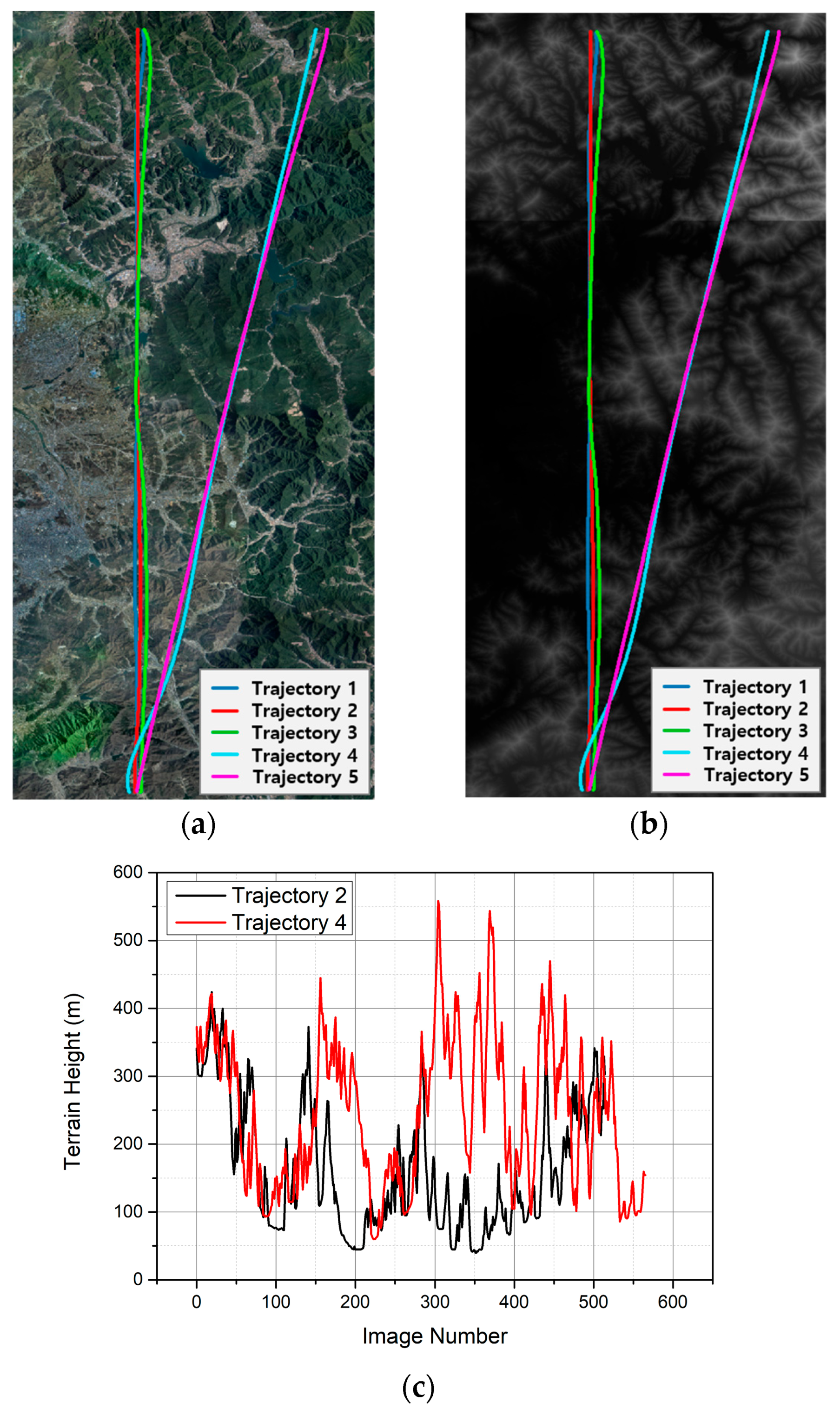
3.1.2. Flight Scenarios and Dataset Characteristics
3.1.3. Data Processing
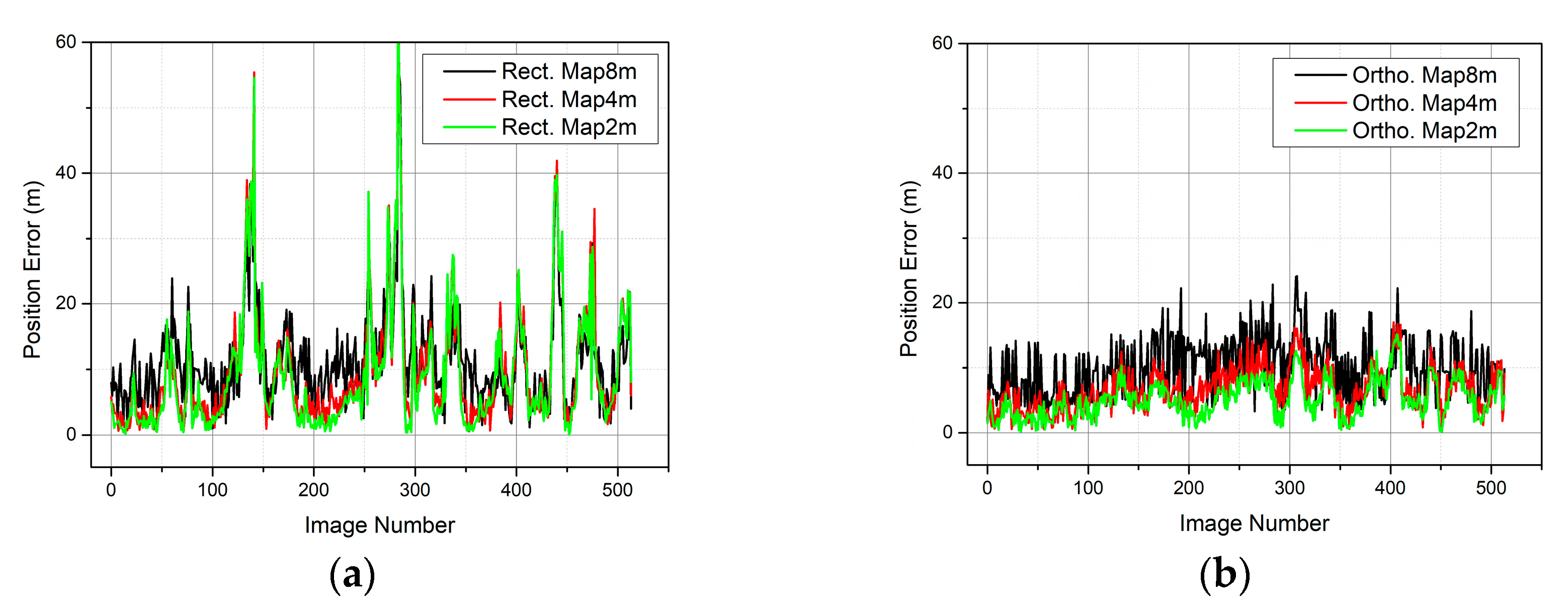
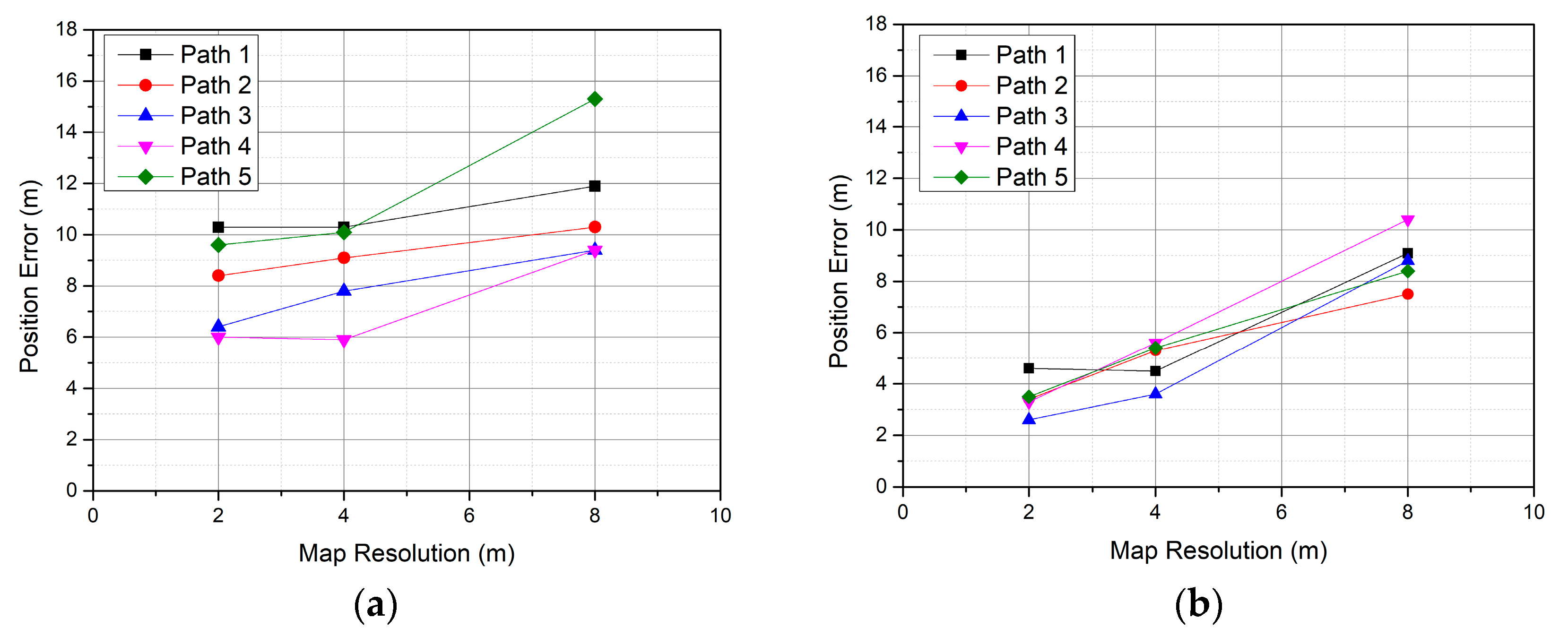
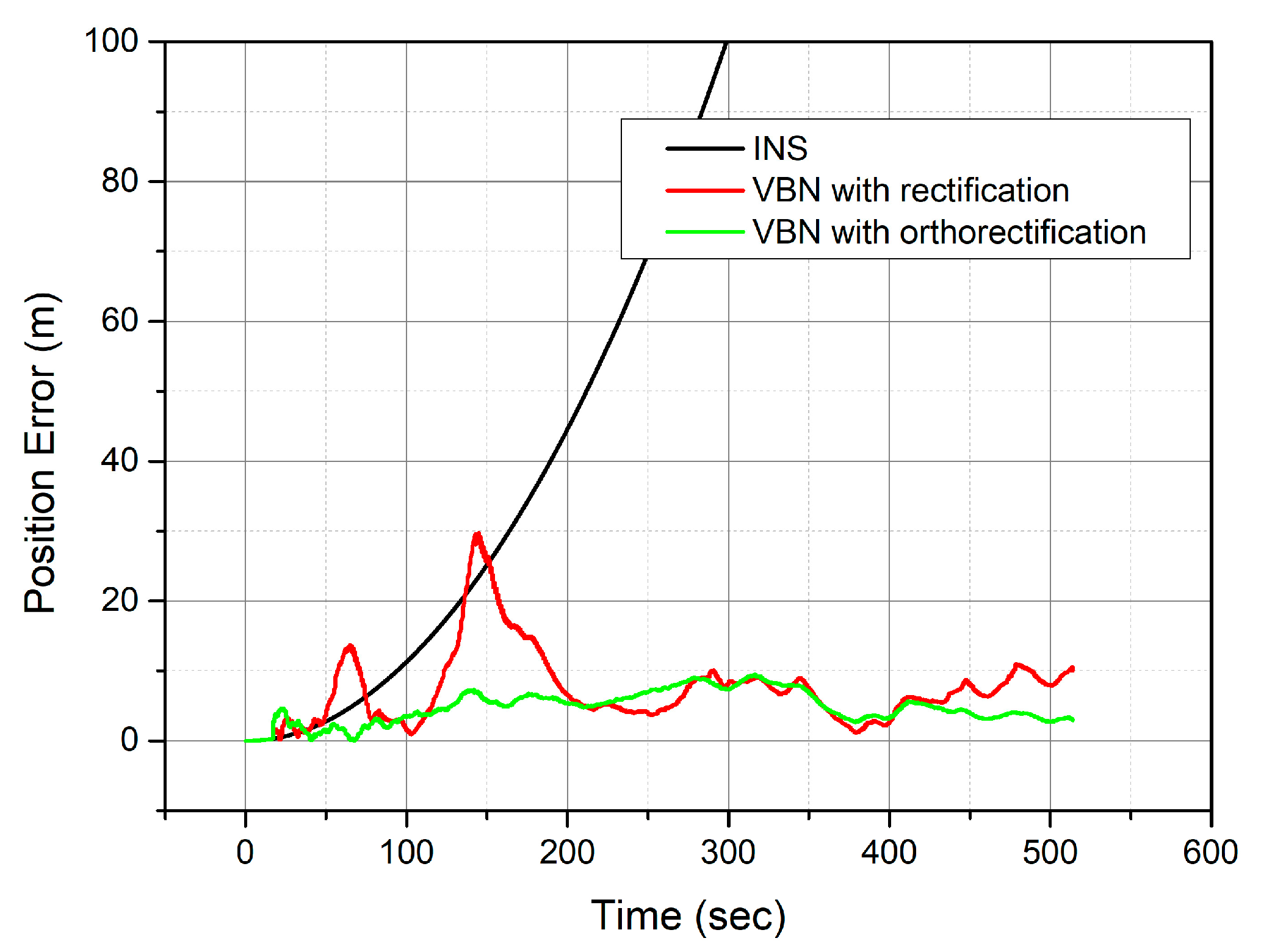
3.2. Localization Accuracy
4. Discussion
4.1. Effect of VBN Errors on SM
4.2. Effect of Flight Altitude and Shadows on SM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, Y.; Cheng, Y.; Manzoor, U.; Murray, J. A review of UAV autonomous navigation in GPS-denied environments. Robot. Auton. Syst. 2023, 170, 104533. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Liang, J.; Chen, Y.; Zhang, Y. Vision-aided inertial navigation for small unmanned aerial vehicles in GPS-denied environments. Int. J. Adv. Robot. Syst. 2013, 10, 276. [Google Scholar] [CrossRef]
- Chowdhary, G.; Johnson, E.N.; Magree, D.; Wu, A.; Shein, A. GPS-denied indoor and outdoor monocular vision aided navigation and control of unmanned aircraft. J. Field Robot. 2013, 30, 415–438. [Google Scholar] [CrossRef]
- Jurevičius, R.; Marcinkevičius, V.; Šeibokas, J. Robust GNSS-denied localization for UAV using particle filter and visual odometry. Mach. Vis. Appl. 2019, 30, 1181–1190. [Google Scholar] [CrossRef]
- Lu, Y.; Xue, Z.; Xia, G.S.; Zhang, L. A survey on vision-based UAV navigation. Geo-Spat. Inf. Sci. 2018, 21, 21–32. [Google Scholar] [CrossRef]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hongkong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Zhang, J.; Liu, W.; Wu, Y. Novel technique for vision-based UAV navigation. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2731–2741. [Google Scholar] [CrossRef]
- Aqel, M.O.; Marhaban, M.H.; Saripan, M.I.; Ismail, N.B. Review of visual odometry: Types, approaches, challenges, and applications. SpringerPlus 2016, 5, 1897. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Shan, M.; Wang, F.; Lin, F.; Gao, Z.; Tang, Y.Z.; Chen, B.M. Google map aided visual navigation for UAVs in GPS-denied environment. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 114–119. [Google Scholar]
- Conte, G.; Doherty, P. Vision-based unmanned aerial vehicle navigation using geo-referenced information. EURASIP J. Adv. Signal Process. 2009, 2009, 387308. [Google Scholar] [CrossRef]
- Yol, A.; Delabarre, B.; Dame, A.; Dartois, J.E.; Marchand, E. Vision-based absolute localization for unmanned aerial vehicles. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 3429–3434. [Google Scholar]
- Sim, D.G.; Park, R.H.; Kim, R.C.; Lee, S.U.; Kim, I.C. Integrated position estimation using aerial image sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1–18. [Google Scholar] [CrossRef]
- Wan, X.; Liu, J.; Yan, H.; Morgan, G.L. Illumination-invariant image matching for autonomous UAV localisation based on optical sensing. ISPRS J. Photogramm. Remote Sens. 2016, 119, 198–213. [Google Scholar] [CrossRef]
- Goforth, H.; Lucey, S. GPS-Denied UAV Localization using Pre-existing Satellite Imagery. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2974–2980. [Google Scholar]
- Gao, H.; Yu, Y.; Huang, X.; Song, L.; Li, L.; Li, L.; Zhang, L. Enhancing the localization accuracy of UAV images under GNSS denial conditions. Sensors 2023, 23, 9751. [Google Scholar] [CrossRef] [PubMed]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 2 November 2021; pp. 8922–8931. [Google Scholar]
- Hikosaka, S.; Tonooka, H. Image-to-Image Subpixel Registration Based on Template Matching of Road Network Extracted by Deep Learning. Remote Sens. 2022, 14, 2–26. [Google Scholar] [CrossRef]
- Woo, J.H.; Son, K.; Li, T.; Kim, G.; Kweon, I.S. Vision-based UAV Navigation in Mountain Area. In Proceedings of the IAPR Conference on Machine Vision Applications, Tokyo, Japan, 16–18 May 2007; pp. 236–239. [Google Scholar]
- Kinnari, J.; Verdoja, F.; Kyrki, V. GNSS-denied geolocalization of UAVs by visual matching of onboard camera images with orthophotos. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021; pp. 555–562. [Google Scholar]
- Chiu, H.P.; Das, A.; Miller, P.; Samarasekera, S.; Kumar, R. Precise vision-aided aerial navigation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 688–695. [Google Scholar]
- Ye, Q.; Luo, J.; Lin, Y. A coarse-to-fine visual geo-localization method for GNSS-denied UAV with oblique-view imagery. ISPRS J. Photogramm. Remote Sens. 2024, 212, 306–322. [Google Scholar] [CrossRef]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 152–236. [Google Scholar]
- Zuiderveld, K. Contrast Limited Adaptive Histogram Equalization. In Graphics Gems IV; Heckbert, P.S., Ed.; Academic Press: Cambridge, MA, USA, 1994; pp. 474–485. [Google Scholar]
- Briechle, K.; Hanebeck, U.D. Template Matching Using Fast Normalized Cross Correlation. In Proceedings of the SPIE, Orlando, FL, USA, 20 March 2001; pp. 95–102. [Google Scholar]
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology, 2nd ed.; Institution of Engineering and Technology: London, UK, 2004; Volume 17, pp. 319–438. [Google Scholar]
- Lee, J.; Sung, C.; Park, B.; Lee, H. Design of INS/GNSS/TRN Integrated Navigation Considering Compensation of Barometer Error. J. Korea Inst. Mil. Sci. Technol. 2019, 22, 197–206. [Google Scholar]






| Sensor | Output Rate | Resolution | FOV | Focal Length | Bias |
|---|---|---|---|---|---|
| Camera | 1 Hz | 4096 × 3000 pixels * | 37.84° (H), 29.19° (V) | 16 mm | — |
| Gyroscope | 300 Hz | — | — | — | 0.04°/h |
| Accelerometer | 300 Hz | — | — | — | 60 µg |
| Barometer | 5 Hz | — | — | — | — |
| Path ID | Heading (°) | Altitude (km) | Duration (min) | Length (km) | Speed (km/h) | GSD (m) |
|---|---|---|---|---|---|---|
| 1 | −172.9 | 3.5 | 8.7 | 44.5 | 304 | 2.3 |
| 2 | −8.4 | 3.5 | 8.5 | 44.6 | 311 | 2.3 |
| 3 | −176.9 | 2.5 | 8.9 | 44.6 | 300 | 1.5 |
| 4 | 6.6 | 2.5 | 9.4 | 45.4 | 289 | 1.5 |
| 5 | −165.4 | 2.5 | 9.8 | 45.4 | 278 | 1.5 |
| Path ID | Rect. 8 m | Rect. 4 m | Rect. 2 m | Ortho. 8 m | Ortho. 4 m | Ortho. 2 m |
|---|---|---|---|---|---|---|
| 1 | 11.9 | 10.3 | 10.3 | 9.1 | 4.5 | 4.6 |
| 2 | 10.3 | 9.1 | 8.4 | 7.5 | 5.3 | 3.4 |
| 3 | 9.4 | 7.8 | 6.4 | 8.8 | 3.6 | 2.6 |
| 4 | 9.4 | 5.9 | 6.0 | 10.4 | 5.6 | 3.4 |
| 5 | 15.3 | 10.1 | 9.6 | 8.4 | 5.4 | 3.5 |
| Case | Roll/Pitch Error (°) | Yaw Error (°) | Latitude/Longitude Error * (m) | Altitude Error (m) |
|---|---|---|---|---|
| 1 | 0.03 | 0.5 | 10 | 20 |
| 2 | 0.05 | 1 | 20 | 40 |
| 3 | 0.1 | 1.5 | 30 | 60 |
| Case | 2D RMSE (m) | |
|---|---|---|
| VBN with Orthorectification | VBN with Rectification | |
| Normal | 5.32 | 9.08 |
| 1 | 5.52 | 9.40 |
| 2 | 6.58 | 9.19 |
| 3 | 9.97 | 10.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, I.; Sung, C.-K.; Lee, H.; Nam, S.; Oh, J.; Lee, K.; Park, C. Georeferenced UAV Localization in Mountainous Terrain Under GNSS-Denied Conditions. Drones 2025, 9, 709. https://doi.org/10.3390/drones9100709
Lee I, Sung C-K, Lee H, Nam S, Oh J, Lee K, Park C. Georeferenced UAV Localization in Mountainous Terrain Under GNSS-Denied Conditions. Drones. 2025; 9(10):709. https://doi.org/10.3390/drones9100709
Chicago/Turabian StyleLee, Inseop, Chang-Ky Sung, Hyungsub Lee, Seongho Nam, Juhyun Oh, Keunuk Lee, and Chansik Park. 2025. "Georeferenced UAV Localization in Mountainous Terrain Under GNSS-Denied Conditions" Drones 9, no. 10: 709. https://doi.org/10.3390/drones9100709
APA StyleLee, I., Sung, C.-K., Lee, H., Nam, S., Oh, J., Lee, K., & Park, C. (2025). Georeferenced UAV Localization in Mountainous Terrain Under GNSS-Denied Conditions. Drones, 9(10), 709. https://doi.org/10.3390/drones9100709






