Abstract
The purpose of this study is to develop a design for maximum area drone coverage in a post-disaster flood situation. When it comes to covering a disaster-region for monitoring and detection of the extent of damage and losses, a suitable and technically balanced approach is vital to achieving the best solution while covering the maximum affected area. Therefore, a mathematical optimisation model is proposed to effectively capture maximum images of the impacted region. The particle swarm optimisation (PSO) algorithm is used to solve the optimisation problem. Modern relief missions heavily rely on drones, specifically in the case of flooding, to capture the damage due to the disaster and to create roadmaps to help impacted people. This system has convincing results for inertia, exploration, exploitation, velocity, and determining the height of the drones to enhance the response to a disaster. The proposed approach indicates that when maintaining the flight height of the drone above 120 m, the coverage can be enhanced by approximately 34% compared with a flight height of 100 m.
1. Introduction
Worldwide, approximately 2.6 billion people have been severely impacted by natural disasters [1] and a lack of a proper emergency response plans. In the post-disaster environment, the major goal of the disaster response and relief services is to quickly map the disaster-stricken areas to identify affected buildings or infrastructure. This allows rescuers to provide relief services to regions that need help. Once such sites are identified, the rescue operations can commence, and people can be evacuated to safety. The nature of the response undertaken determines the number of fatalities that can be prevented and can limit the extent of damage to infrastructure and lands. Time is very limited when a disaster strikes, and due to the severity of the disaster, it may not be possible or sufficiently safe for humans to reach impacted areas for post-disaster inspections. Drones have emerged as useful tools to conduct post-disaster relief activities [2] due to their agility and ease of operation. Given that they do not require the presence of human resources, such vehicles can be readily made available to use in case of emergencies. One main issue that disaster managers face when establishing their disaster response plans is the limited number of drones that are available to cover an impacted region [3]. Traditionally, to cover an impacted region, satellite imagery are extensively used for mapping land cover, weather forecasting, and obtaining global coverage of earth’s landmasses. Satellite images have some noise in the data as they are taken far from the earth [4], and also contain irrelevant data due to various barriers existing between the earth and the satellite, such as clouds and birds. This makes it hard to identify and analyse the target. In addition, accessing the satellite images is slow which is not effective in case of emergencies caused by disasters. However, with the availability of battery-operated drones, the reliance on satellite imagery has been significantly reduced. Drones can capture close-up, high-quality, noise-free images, and they can reach target sites with ease. High-resolution images captured by drones of the region are sent to the main station of disaster management authorities for further analysis [5]. These pictures can be used to analyse the state of the land, identify stranded people, estimate damage, and determine the rescue routes [6]. Images captured by drones during disasters are crucial for initiating rescue activities, analysing the extent of the damage, and planning an emergency response [7].
Research has been conducted to enhance the capabilities of drones for disaster management by acquiring photogrammetry-ready data which can be analysed for producing hazard maps, elevation models, and estimating the extent of the disaster and its characteristics. For instance, Ackerman [8] deployed the T-Hawk Micro Aerial Vehicle to collect images from the Fukushima Daiichi nuclear facility after a devastating earthquake hit Japan in March 2011. Due to its small size and single-rotor flight design, the aerial vehicle was able to capture images and hours of video at lower altitudes.
The drones need to be allocated appropriately to the required tasks to ensure maximum coverage of the disaster region [9]. Several constraints arise when allocating drones to disaster areas [10]. First, within a limited period, the drone must follow the shortest path to the target location and complete the allocated tasks. Each drone is battery operated, meaning that there is limited time (approximately 15–25 min) during which it can continuously operate on a mission [11]. This also requires minimizing the time taken by each drone to perform its task. Second, multiple drones are used by the disaster management authorities to be able to obtain full coverage of the affected area (Figure 1). Mismanagement of the drones by the operator results in the problem of deciding which drone to assign for the next task. For example, one drone may already have many tasks in its queue compared with another. Assigning too many tasks to one drone results in a condition known as drone attrition, which can be solved using optimisation [12]. Third, depending on the size of the affected area, multiple drones may be required to fully cover the region to capture images, deliver aid and locate victims. In this paper, we propose a mathematical optimisation model that integrates area coverage and minimum battery consumption, and at the same time, considers the limitations that occur while implementing drones during post-disaster management. An appropriate objective function applicable to drone allocation that accounts for the attrition of drones and the location of the target area is formulated.
Figure 1.
Objectives of the current study.
The most common algorithms utilised for solving maximum area coverage and minimum energy consumption of drones are [4], Glowworm swarm-based optimisation (GSO) [13], ant colony optimisation (ACO) [14], network flow optimization [15], and genetic algorithm (GA) [16]. Another new optimisation algorithm is the QUasi-Affine TRansformation Evolutionary algorithm (QUATRE) which solves complex multiple real-parameter optimisation problems. It is a simple and powerful stochastic optimisation problem, which, however, easily falls into local optimisation [17]. The PSO technique has been applied as a solution approach for tasks during environmental disasters. In a study conducted by Ravikumar [18], fuzzy logic using hybrid PSO was used for the forecasting of natural events and disaster management. Similarly, Sánchez-García et al. [19] proposed a novel distributed PSO algorithm for drone networking to explore disaster scenarios, which was compared with an optimal-trajectory planning algorithm for different scenarios (Table 1). Shi et al. [20] maximised the user coverage in the 5G network through optimum positioning of the drone. Furthermore, the application of the PSO algorithm has been tested for maximum area coverage while considering public safety and disaster management [21]. However, its application for the allocation of drones during rescue missions in the post-disaster period is limited and has not been attempted. The Table 1 presents the comparison of different existing algorithms:

Table 1.
Comparison of different existing algorithms.
There is great interest in drones and related innovations in fields, such as defence, search and rescue, farming, production, and natural environment observation [22,23]. Drones are capable of covering wide and extensive zones within a selected field, even without any modifications being made to the currently used frameworks of deployment [24]. However, the use of drones is not without costs. To effectively make use of these adaptable assets, it is fundamental to set up an association and observing framework for drones to identify their open-air course and formulate strategies in a way that is secure, time-efficient, and collision-free, and one that considers their working environment [25,26,27]. Taking into consideration the current progress in drone innovation, Federal Express [13], Amazon [14], DHL [15], and various other conglomerates that depend on package delivery have started exploring the possibility of using drones for delivering goods commercially. It is highly likely that in the near future, transportation systems will be operating through the integration of drones due to their cost-effectiveness and ease of use compared with conventional methods of transporting goods, such as lorries and trucks. Moreover, drones can reduce the overall costs of goods delivery by removing the cost of labour involved in transportation [28,29], and are quick and able to bypass traffic and congested paths. However, this leads to the important issue of drone steering. To maintain varied purposes of drone routing in practice, we present several contributions to drone energy consumption in this paper.
In the routing of drones, most of the published literature either assumes boundless fuel capacities [30] or does not fully consume or factor in the fuel for drones. The authors have identified few studies that consider the limitations of fuel when working with drone routing [31,32]. To attain a practical and effective routing, it is crucial to understand the components involved in determining the energy utilisation and the overall system for fuel consumption in drones.
In steering the drone, fuel utilisation is ordinarily correlated to the speed of the vehicle [33] which is a non-linear relation [34]. In the existing literature on drones, researchers have only utilised linear approximations for drone directing [35]. In any case, the data from industry suggest that this approach is not suitable for drones, as the combination of payload, speed and environmental conditions are quite basic. The point is to characterise which drone steering issues ought to be considered and how this varies from conventional steering issues. This paper contributes to the study of disaster area coverage using drones. The study covers the assessment of a flood disaster region which is mostly a residential area to provide a framework for evaluating flight height and area coverage using a fixed number of drones and area dimensions. Further, the battery consumption of the drones is analysed to derive the height and the battery usage during different phases of the flight. The assumptions made in this paper are that the study is conducted in a no-fly zone with no obstacles which can impact the drones or the flight trajectory. The focus of the paper is to consider the single objective of maximising area coverage.
The rest of the paper is organised as follows: Section 2 explains the device coverage methodology. The PSO algorithm is discussed in detail along with the mathematical formulation of the problem and application of PSO for its solution. Section 3 discusses the experimental arrangement and the implementation of the proposed solution. Section 3 presents the results. Section 4 discusses the results and the overall achievements of the research while Section 5 concludes the paper, summarising the research findings and identifying the future directions.
2. Problem Statement
This study aims to introduce an algorithm for the coverage of disaster regions using drones, solve the problem of maximum area coverage with a fixed number of drones and assess their energy consumption. Assuming the target is in the coverage, the device’s location set on the x- and y-axis is given as and , respectively. Similarly, the device’s path can be chosen from field of view (FoV). Assuming a set of devices is trying to cover stationary targets M in a hurdle free region, every device can place towards specific directions, .
The coverage matrix (based on the height of the drone, coverage radius, distance between the personnel and the drone) of each device is given as as:
The value of every is similar; the aim is to maximize the total targets covered. If an object is being covered by multiple cameras, it is still considered as a single target towards the whole aim.
is a binary variable whose value is 1 if it is covered by a single device at the least and the value will be 0 if it is not being covered at all.
The binary variable , takes the value as 1 if for direction d and angles x and y are chosen for the device i. The device location is two-dimensional while its direction and the target M are one-dimensional. The time complexity is O(N4). Hence, the optimum issue is non-deterministic and exponential. An NP-hard problem is one which cannot be solved by the model. These problems are at least as hard as the NP-complete problems and they do not have to be decision problems.
2.1. Device Coverage
The concept of the device’s field of view (FoV) is taken from Vikram and Nael in [10] (Figure 2). FoV is generally the area covered by the device, defined by the angle-of-view () and the depth-of-view (). The angle of view is further divided into a vertical angle of view () and a horizontal angle of view (). The depth of the field, on the other hand, denotes the visible area that is reasonably sharp.
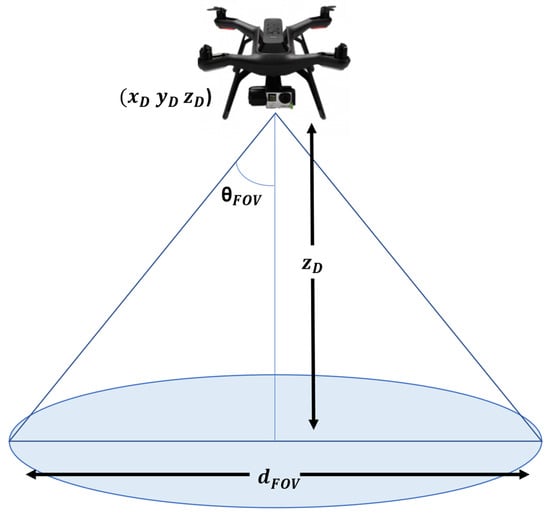
Figure 2.
Graphical concept of the device field of view.
In short, the FoV of a device can be described as a circular area that can be defined by its angle of view () and the depth of field ().
| depth of field | |
| and direction vector . |
The angle is given as:
is covered by if
2.2. Area Coverage
The drone’s trail is evaluated on the assumption that, from the start of the flight, the device is pointed downwards as depicted in Figure 3. The gap between two rows is selected as a function of the trail of the onboard device on the field [19]. The breadth L of the device’s trail can be calculated based on the breadth of the sensor , the camera’s lens focal distance , and the elevation of the device over a field (Figure 4) [9]:

Figure 3.
Sentera Multispectral Sensor Upgrade for the drone.
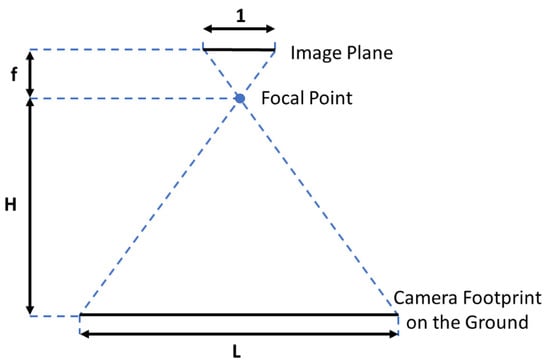
Figure 4.
Relationship between .
The area coverage by a drone on a three-phase disaster recovery mission is as follows [9]:
Here the three phases include the climb, cruise, and arrival of the drone. The rate of immediate area coverage by the drone is given by . The (changing area coverage) is given as follows:
The differential distance in the track is and device track width is given by . The area coverage is given as:
As mentioned earlier the area coverage rate is based on the horizontal component of the true airspeed () and the height of the camera over the ground (). Therefore, the equation is given as:
The path limitations are applied on the optimal control issues depending on the drone’s operational constraints. The path constraints are given below
2.3. Image Footprint Based on Ground Sample Distance (GSD)
Without considering topography, the GSD of a given image is given as:
where focal length is given by f, the size of the pixel is given by d, and distance from the centre of the camera projection to the ground is given by H. For a digital camera, the GSD is given as:
where,
where X and Y are image coordinates and the image coordinates of a pixel are given as m and n. A true operational challenge depends on the drone imagery, optimum flight and camera parameters. The operator can optimise the quality and efficiency of the drone by selecting flight parameters such as image overlap, flight speed and altitude. The influence of overlap may be a forward overlap or side overlap. The forward overlap can be managed by changing the number of images per second whereas side overlap is key component in planning a drone’s flight path.
3. Drone Optimisation
Different algorithms can be applied for drone optimisation. The most common methods are Generic Algorithm (GA) and Particle Swarm Optimization (PSO). PSO is a stochastic optimization technique that uses a swarm-based approach similar to the behaviour of animals such as insects, birds, and fishes to search a large region in the solution space of the optimised objective function. The movement of particles in a swarm is not limited and one can continuously search the possible solution space by updating their position and velocity. GAs iteratively update a population of individuals. On each iteration, the individuals are evaluated using a fitness function. A new generation of the population is obtained by probabilistically selecting fitter individuals from the one current generation. Some of these individuals are admitted to the next generation unchanged. Others are subjected to genetic operators such as crossover and mutation to create new offspring. A comparison of the features and applications of GA and PSO has been carried out [36] and is shown in Table 2 and Figure 5 below:

Table 2.
Comparison of GA and PSO.
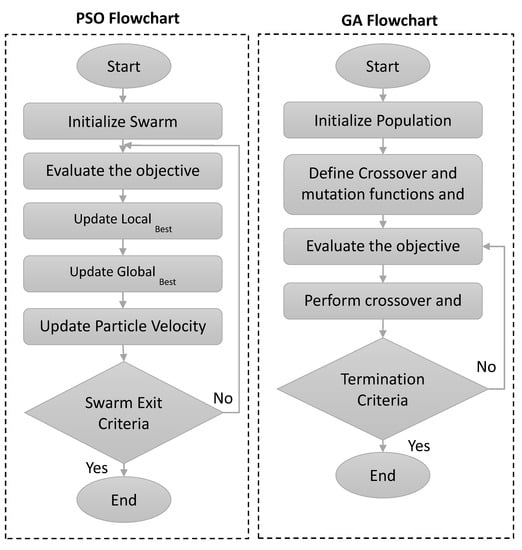
Figure 5.
Flowchart for PSO and GA.
The PSO algorithm uses a particle swarm to search for the best solution, while each particle keeps adjusting its best position and concerning other particles. The position, velocity, and particle best position define the particle position. The global best () position signifies the best fit value of the particle. Therefore, the particles keep a record of their personal best () and () and they modify their positions based on the current position and velocity, and the distance from the current position to the and , respectively [36]. The PSO algorithm optimises the height of the drones to render the maximum camera footprint. The best height of the drone was utilised for the simulation of maximum area coverage. The maximum and minimum velocity was used to calculate the area coverage and identify optimal battery utilisation. It was assumed that the personal and global best vectors are random variables (with arbitrary means and variances) so that there is no requirement for the stagnation assumption. Additionally, optimum weather conditions and an obstacle free zone were assumed.
PSO Pseudocode (Algorithm 1)
As per the given equation the position and velocity of the particle is adjusted:
: the velocity at given time
: position at given time
: Inertia weight
: learning/accelerating factor
, : number between 0 and 1(random and uniformly distributed)
| Algorithm 1 |
| 5: End for |
| 6: Repeat until stop criteria is satisfied |
| 7: For i = 1 to M (M = max iterations) |
| 8: For j = 1 to N |
| 14: then update velocity to be within (velocitymin, velocitymax) |
| 17: then update position to be within (upper bound, lower bound) |
| 18: End for |
| 19: End for |
GA Pseudocode (Algorithm 2)
| Algorithm 2: GA(n, χ, µ) |
| Initialise generation 0: |
| k:= 0; |
| Pk:= a population of n randomly-generated individuals; |
| Evaluate Pk: |
| Compute fitness(i) for each i ∈ Pk; |
| do { |
| Create generation |
| k + 1: |
| 1. Copy: |
| Select (1 − χ) × n members of Pk and insert into Pk+1; |
| 2. Crossover: |
| Select χ × n members of Pk; pair them up; produce offspring; insert the offspring into Pk+1; |
| 3. Mutate: |
| Select µ × n members of Pk+1; invert a randomly-selected bit in each; |
| Evaluate Pk+1: |
| Compute fitness(i) for each i ∈ Pk; |
| Increment: |
| k:= k + 1; |
| } |
| while the fitness of the fittest individual in Pk is not high enough; |
| return the fittest individual from Pk; |
Based on the above analysis, the PSO algorithm is used in the following section to solve the optimisation problem. The target of the current study is to examine the drone’s maximum area coverage and minimise its energy consumption to extend battery life. Figure 6 represents the altitude of the drone in the computation of the ground sampling distance and image footprint. The specifications of the drone and the camera impact the overall performance of area coverage and power consumption. The specifications of the drone models are maximum height, speed, and flight performance. The camera specifications are ground sampling distance (GSD), focal length, and FoV [37,38,39]. The definition of the scene in our experiment is the Hawkesbury flood region. The drones cover the disaster impacted area for gathering images and surveillance. As part of our experiment, we assumed all drones have the same performance, sensor, focal length, and flight behaviour at a given altitude, velocity and field of view. We also assume that the area is obstacle-free. Before designing the path of the drone to cover the disaster impacted region, we need to define the drone parameters.
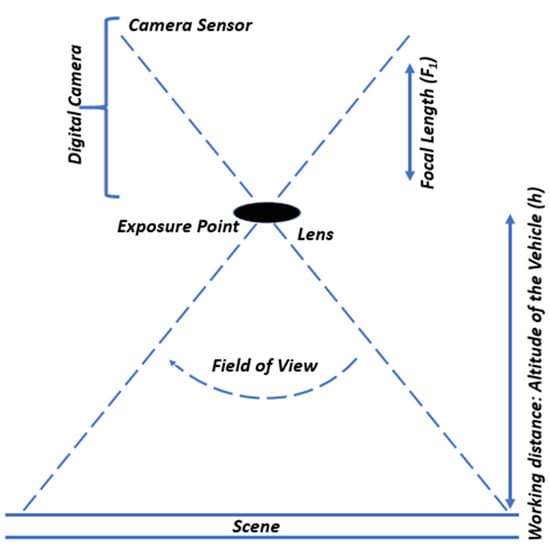
Figure 6.
The specifications of the drone and the camera.
3.1. Utilization of Resources for Optimal Outcome by Parameter Tuning
PSO objective function was formulated using the parameters mentioned in Table 3a to assess the height of the drones that renders the maximum area coverage of the disaster-impacted region. The simulation considers a maximum area of 200 km2. Initial results were computed to assess the number of drones required to generate the best area coverage. According to the initial analysis and the above results, optimal results are achieved when using 12 drones (Table 3b). The total number of drones used in the experiment was 12, each having the technology and ability to fly at the maximum altitude of 121.97 m, which is approximately 400 ft. and are the horizontal and vertical fields of view, respectively.
The number of iterations to reach a good solution is problem-dependent. Too few iterations may terminate the search prematurely, whereas a large number of iterations has the consequence of adding unnecessary computational complexity. The previous velocity, serves as a memory of the previous flight direction, i.e., movement in the immediate past. This memory term can be seen as a momentum, which prevents the particle from drastically changing direction, and to bias towards the current direction [40,41]. This component is also referred to as the inertia component. Inertia keeps the particle moving in the same direction with similar velocity. Inertia weight is a positive constant value that affects the convergence of the PSO. Cognitive weight influences the particle’s best position and local search. It is proportional to the distance of the particle from its own best position (referred to as the particle’s personal best position) found since the first-time step. Social weight influences the particle’s global best position and global search; it updates information obtained from all the particles in the swarm [42].
The PSO algorithm was used to derive the optimal flying altitude of the drones to maximize the area coverage of the disaster impacted region. Table 3a details the parameters used in the code and the corresponding values. The population size (num_of_particles) defined as 12 refers to the number of drones used. The upper bound and the lower bound are given as ub and lb, respectively, and represent the area to be covered in a 2D matrix. The particles in the PSO algorithm are within the specified boundaries of the upper and lower bounds. There were 20 rounds of trials performed on the solution before concluding on the outcome. is the maximum number of iterations during every round of the trial. Results from each trial were captured and the most near-optimal value of the objective function was documented. The experiments were performed with the social and cognitive constants, and based on the results, their values resulting in optimal behaviour were one and two, respectively.
The experiment involved tracking the area coverage while the drones were at different heights during a climb, phase, and descent. The height is measured in meters and the rendered area is measured in . We assume that the performance of every drone is the same at a given time, altitude, and velocity. The total area coverage was observed to be increasing with the increase in the flying height of the drones.
The research involved flying the drones in different altitudes across the climb, hover, and descent phases. As defined in Table 3a, the assumption is made that all the selected drones have maximum altitude support () up to 121.97 (). The maximum area coverage based on the maximum number of drones is given in Table 3b.
Considering the constants defined in Table 4, the velocity of the particles is calculated during each iteration according to Equation (20). If the calculated velocity exceeds the maximum velocity the velocity is updated to be within the defined range.

Table 4.
PSO parameters used in the simulation code.
The optimal drone height to provide the maximum area coverage in a multiphase trajectory of the drones is shown in Table 5. The experiment involved tracking the area coverage while the drones are at different heights during a climb, phase, and descent. The height is measured in meters and the rendered area is measured in square kilometres. Figure 7 displays the incremental area coverage as the flying altitude of the drones was gradually increased until the hover phase was reached. It was observed that the total area coverage increased with the increase in the flying height of the drones. There is a steep increase in the coverage as the drones move from climb to hover phase from 60 to 120 m altitude. The maximum area coverage was recorded as 182.62 at a flying altitude of 120 . The altitude recorded in the experiment is used as the altitude for the remaining research of this paper and is recorded as the Altitude of the drones in the solution () in Table 3a.

Table 5.
Drone height and the corresponding area coverage.
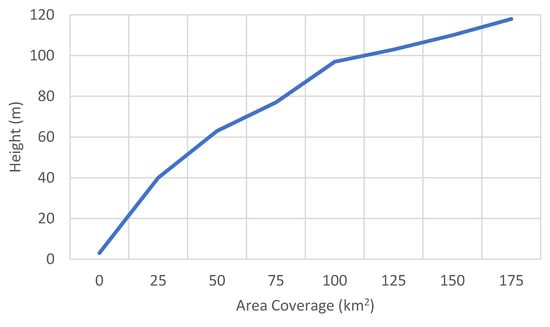
Figure 7.
Maximum area coverage is accomplished at 120 m height of the drone.
The next set of experiments were performed using the height of the drone that resulted in the maximum area coverage with 12 drones. Furthermore, the impact of the inertia weight on the area covered with the drone and PSO parameters defined in Table 1, Table 2 and Table 3 were explored while decreasing the inertia weight from 0.9 () to 0.4 () with each iteration. The equation for the inertia weight is:
where is the current iteration in the maximum iteration range. The value of the inertia weight () as calculated in Equation (3) is parameterized in Equation (2) to calculate the velocity in every iteration.
The inertia coefficient () is gradually reduced within the and to calculate the results of maximum coverage of the disaster-impacted region. The results of the simulation across a maximum of 20 iterations are displayed in the Appendix A (Table A1). It was observed that in every trial the best results were obtained within 20 iterations; hence in this study, we performed all simulations with the maximum iteration at 20. The value of the inertia decreased with every iteration and the results of the objective function value were recorded. The position () is the global best position of the particles during the iteration across the x- and y-axis. As the inertia decreased, the resulting value of the objective function was observed to be increasing. Although the optimal value was recorded as 98.25 during the first iteration at inertia = 0.9, the value showed a considerable rise to 173.65 (value rounded off to 2 decimal places) during the 20th iteration at inertia = 0.425. The area coverage was smaller during the early iterations but they started growing considerably as the inertia coefficient was minimised. There was no major change in the rate of optimal function value after the 15th iteration which is at inertia 0.55.
In the next simulation, the following parameters were used: the inertia coefficient (w) was kept constant at 0.55, exploration constant = 1, exploitation constant = 2, the height of drone (in meters) = 120, and FoV = 83.97. We then repeated the same steps. The inertia coefficient () was set to calculate the results for maximum coverage of the disaster-impacted region. The results of the simulation across a maximum of 20 iterations are displayed in Table 6. The results of the objective function value are recorded. Unlike the observations in Appendix A (Table A2), the constant inertia results in no major change in the objective function value across multiple iterations. The optimal value was recorded as 161.46 during the first iteration, with no considerable rise till the 20th iteration (161.48). There was no considerable change in the value of the target function after the eighth iteration. Considering the inertia coefficient as 0.55, it renders near-optimal outcomes in a reduced number of iterations. The solution which renders optimal results in fewer iterations is cost-effective as the computational cost of the solution is reduced.

Table 6.
Power Input Variables.
Figure 8 represents the contour plots for the objective function results. The right graph is a 3D representation of the changes of the value of the objective function from minima to maxima. The area is restricted within the upper and lower bounds as defined in Table 2. From the 3D plot, we assess the minimax model of the solution where the and -axis are restricted between −10 and 10. The -axis is represented as the optimal objective value. The yellow peaks represent the maxima, whereas the purple drops represent the minima. The 3D plot suggests that the maximum area coverage is close to 200 and is represented by the yellow section of the graph. When the same plot is visualised in a 2D contour, the contour lines represent a continuous distribution, and it can be observed that the maximum area coverage of the objective function is within 180–200 . The star marks represent the random positions of the particles in a swarm.
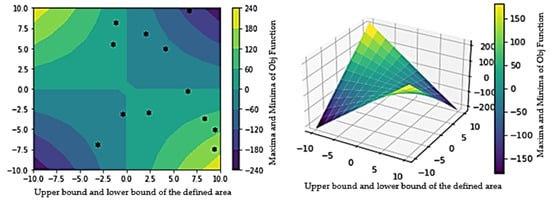
Figure 8.
Contour plot representation of the objective function value in a specified boundary within the defined upper and lower bounds.
The graph in Figure 9 represents the results of the objective function in calculating the maximum area coverage with the inertia coefficient set as constant at 0.55. The x-axis of the graph shows the number of iterations used during the simulation to arrive at the solution, and the y-axis shows the optimal value of the objective function and is represented as the fitness of the particle. The dotted red line running horizontally marks the final optimal value determined by the simulation. Multiple trials (from 10 to 100) were performed on the solution until the optimal value was reached.
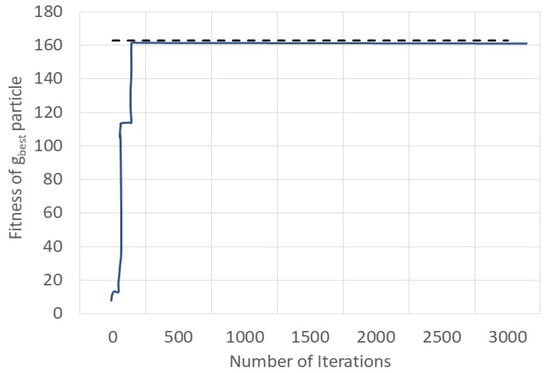
Figure 9.
Objective function value vs. iterations.
Comparison with GA Results
A study was performed to assess the performance of the objective function with a Genetic Algorithm. Figure 10 illustrates the performance of the fitness function.
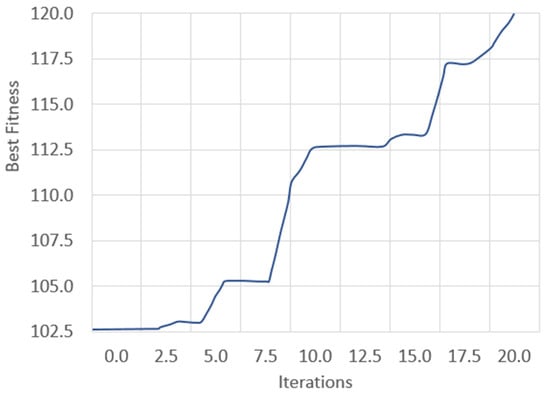
Figure 10.
Performance of the fitness function using a Genetic Algorithm.
The optimal value was recorded as 102.31 during the first iteration, and during the 20th iteration, the value was 120.53. Figure 10 represents the results of the objective function in calculating the maximum area coverage with 12 drones and 20 iterations. The x-axis of the graph shows the number of iterations used during the simulation to arrive at the solution, and the y-axis shows the optimal value of the objective function and is represented as the fitness of the chromosome. Multiple trials (from 10 to 100) were performed on the solution until the optimal value was reached.
The PSO solution suggests that the particles in the swarm would ultimately converge to the global best solution (Figure 10). In Figure 11, the green circles represent the particles’ best positions, and the red circle represents the global best position across the ,y-axes represented in a 3D plot. The particles move towards the position while calculating the optimal objective function value across the iterations. The convergence of the particles largely depends on the social and cognitive constants defined in Table 2.
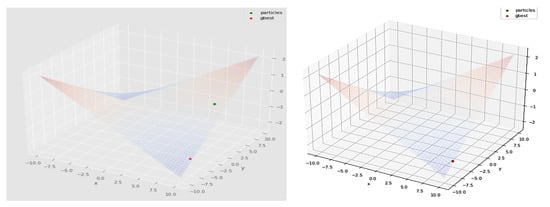
Figure 11.
Particles convergence at the position within the upper and lower bound in 3D representation.
3.2. Factors Affecting the Energy Consumption in Drones
3.2.1. The Weather Effect
In steering open-air drones, one must bargain with the stochastics of climate that impact the energy utilization of the drones [43,44,45,46]. These external factors can heavily impact the methodology for optimising the steering of drones. Two of the most fundamental components of weather that impact drones are wind and temperature.
3.2.2. Speed of Drones and Payload
The flying speed of a drone can be the basis for identifying the overall fuel utilisation. The flying speed is related to the speed and course of wind as these factors can influence the overall flying path and efficiency of the drone (Figure 12). The drone can have any of the following flying statuses:
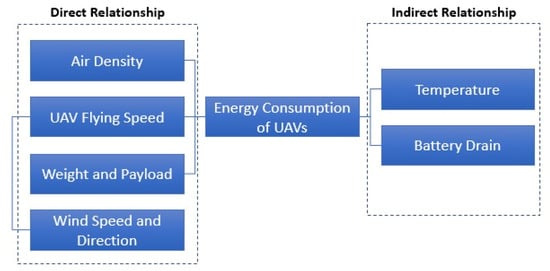
Figure 12.
Relationships of other factors on the energy consumption of drones.
- hovering,
- vertical flight: change of altitude by vehicle, landing or take-off
- horizontal flight: level flight or vehicle cruising
In this paper, we assume that the drone does not carry any additional payload weight. The drag coefficient () is used to quantify the resistance of the drone against the air density and is set to a constant value of 0.004.
Drones usually carry payloads such as camera gear or packages. The effect of diverse weights can be critical to the extent that they ought to be accounted for when determining the power utilization models [47,48].
4. Power Utilization Models for Drones
The distinctive power models are based on drone steering. The essential plan parameters for accomplishing the least lift for the takeoff of the drone include control, weight, width, thickness, drag coefficient, and surface area of the flying device (Figure 13). There are various other basic auxiliary plan issues concerning adjustment, control, and shape to attain flight [35].
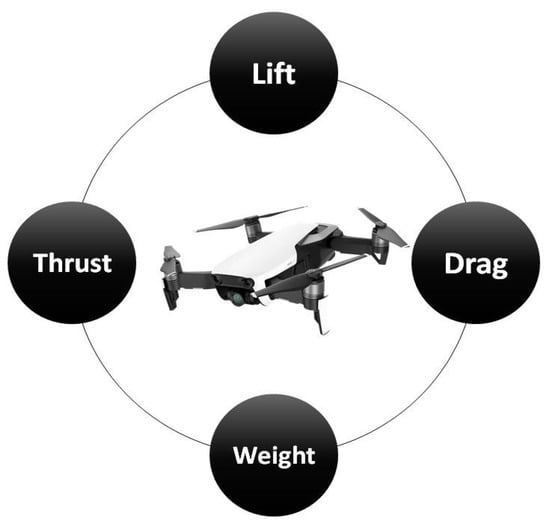
Figure 13.
Different forces acting on drone.
These parameters must be considered when evaluating a drone’s power utilisation under a specific set of situations as they influence the flight time and storage capacity of the drone [36]. A power utilization demonstration makes a difference by adjusting these parameters to achieve optimum energy utilisation by the drone. The following equation can be derived from Newton’s Second Law:
Since it’s in even motion, the weight of the drone is at the break-even point with and opposite to the lifting drive; this lifting drive is the response to redirecting the air downwards. Thus, the weight of the drone is given as:
W is the weight, is the air descending speed, and is the mass of the air being pushed . The width of the drone is given by . The mass of air per time unit is given as the thickness of the air multiplied by the speed of the drone increased by the region impacted by the drone [37,38,41].
Replacing this with our major lift, Equation (2) gives:
where is air thickness, is drone relative speed, and is the successful region influenced by the drone.
4.1. Power Consumption in Horizontal Movement
Lifting the drone in the air requires force, some of which is used to overcome the drag force which limits the forward movement through the air [38,39,42,43]. The drag force can be calculated as below [37]:
where is the parasitic drag, is the drag coefficient, is the front region, is the thickness of the air, and is drone speed. The force is given as [41]:
Therefore, the force required to overpower the parasitic drag is:
The drone needs force to overpower the parasitic drag and to lift itself [44]
The force required to overpower drag is the most prominent at high speeds, whereas the force required during a lift is the most prominent at slow speeds (Figure 14). The least force is required between these two extremes; that is, there is an ideal cruising speed.
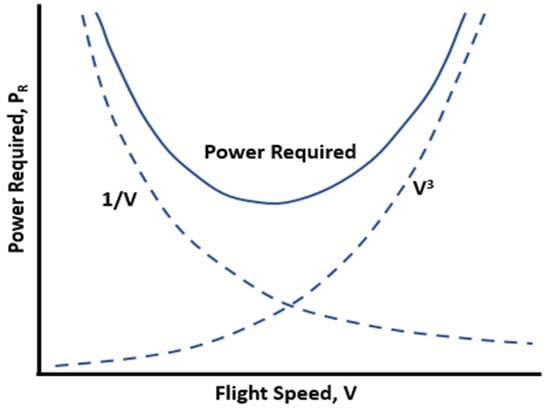
Figure 14.
Power vs. Flight Speed.
During the lift, there is an exchange of power from the drone to the air, which gives kinetic energy to the air while displacing it downwards and in return providing upward thrust to the drone [45,46]. The kinetic energy is often calculated as:
The force needed for the lift is the powerful energy given to the air per unit of time and substituting (8) we have:
From substituting (7) and (8) we obtain the energy required to lift as [41]:
where is the energy required for a lift, is the full weight of the drone, is the thickness of the air, is the width of the drone, and is the respective speed of the drone through the air. Reviewing our total energy Equation (28), the energy required for flight is:
is the energy required for the flight in watts, a is the aerodynamic drag coefficient, is the front-facing region in , W is the entire weight of the drone in , is the thickness of the air in , b is the width of drone in meters, and is the respective speed of the drone in considering the wind speed and course. By taking the subordinate of the full energy equation regarding the speed at that point, we can discover the speed for minimum energy [37,38,41,42,47].
The estimated minimum power speed can be substituted into the total energy equation to calculate the least energy required for flight [37,41,42,47].
The least energy speed is not the usual cruising speed of the drone, but it would be the absolute minimum speed that could be used.
4.2. Maximum Flying Speed
The ideal speed is the speed that gives the slightest sum of drag and is considered to have an ideal cruising speed (Figure 15) [38,43,47]. The full drag is the parasitic drag that was calculated above, in addition to the drag produced in throwing the air down.
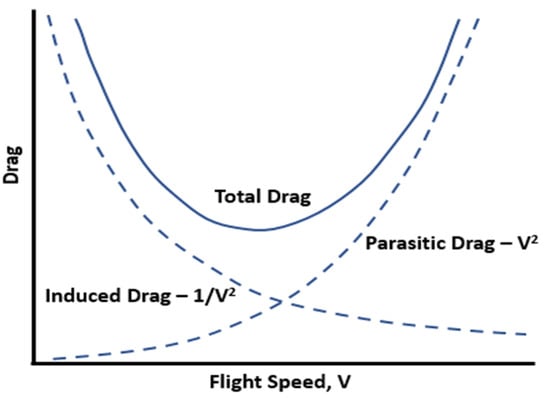
Figure 15.
Drag vs. Flight Speed.
The drag produced by the downward thrust of air translates to the power required for drones to move through the air [37,42,45]. Thus, the parasitic drag and the initiated drag is given as:
To find the speed with the least drag drive, the cruising speed is determined by taking the derivative of the whole energy condition for speed and setting the outcome equal to zero [36,43,47].
is the ideal cruising speed, is the weight of the flying machine, is the thickness of the air, is the front-facing region, is the drag coefficient, and is the width of the drone. Using this equation, we can input data about a drone and the density of the air to estimate the optimal flight speed.
4.3. Power Consumption during High Speeds
During inconsistent flight level, the thrust is equivalent to the drag of the drone, and the lift is equivalent to the overall weight of the drone; therefore, the propulsive thrust energy can be:
From Equation (30), it is given as:
and are the drag coefficient and the lift coefficient, respectively.
From (12), the overall energy in high speed is:
Power Utilisation in Vertical Take-off and Arrival
The power utilisation of drones is estimated by comparison with the energy consumption pattern of a helicopter which is found to be linearly correlated to the battery weight and payload under real-time [16,34].
Moreover, we expected that the energy consumed during take-off and landing is usually nearly identical to the energy consumed during hovers. Air thickness varies with temperature, so temperature variation will result in diverse air densities, and thereby will influence the energy utilisation of drones.
4.4. Factors Affecting Drone Energy Consumption
Several separate factors influence the power utilisation of drones. The wind direction and wind speed influence the speed of the drone (Figure 12). Previous research has shown that a drone flying into a headwind resulted in less energy utilisation [39,40], which was attributed to the expanding thrust caused by translational lift [27]. With the increase in the wind stream, the transitional lift grows so that less power is consumed in the flight [45]. After a certain limit is reached in wind speed, the advantage of transitional lift is lost due to the drag force [27].
Additionally, temperature and air thickness impact energy consumption and it is typically related to battery consumption. Air thickness impacts the lifting capacity of a flying machine and changes with temperature [49,50]. Research has found drone failures during lower temperatures even during short flight intervals [51]. The weight and payload individually play a part in the power utilization of drones.
4.5. Minimum Energy Consumption Model
The total weight of the drone () is equal to the sum of the actual weight of the device and the payload weight (Table 6). Payload weight can be considered as the weight of any relief or distribution material, or any additional equipment required to be carried by the drone for the mission.
The energy required to overpower the parasitic drag is:
The drone requires energy both to overpower the parasitic drag and for lifting itself:
Initial Power Constants
Overall Consumption
We performed the simulation to identify the optimal velocity between the and defined in Table 3 which would consume the minimum battery power.
The simulation was performed so that the velocity iteratively increases from −4 to 20 during the multiphase flight of the 12 drones. The drag power and the life power were noted for a single drone and the total power consumption was calculated for each velocity. Since in our paper we have assumed that all drones render similar performance at a given altitude, time, and velocity, the total power consumption of 12 drones is 12 times that of the calculated consumption.
Figure 16 depicts a spike in the power consumption during the climb phase of the drone which stabilises as it enters the hover phase. The highest energy consumption is observed as the drone moves from a negative velocity to a positive velocity at 1 m/s. As the velocity is gradually increased, the total power consumption continues to drop at a steep rate until it renders an almost straight line between 15 and 20 m/s where the total power is 1109.01 (Table 7). Hence, the power consumption is the highest during the climb phase of the drone and stabilizes as the drones enter the hover phase.
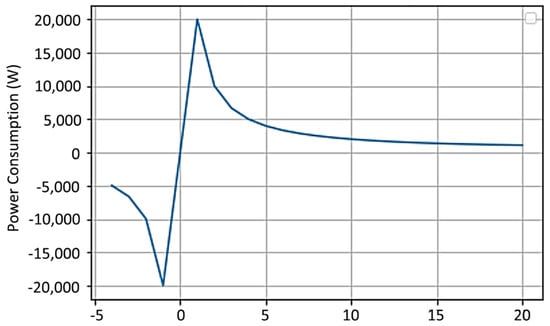
Figure 16.
Power Consumption of the drones during the flight.

Table 7.
Output of Power Consumption against Velocity (, ).
5. Conclusions
This study proposes a particle swarm optimisation model for solving the problem of maximum area coverage of drones with minimum energy consumption in the post-disaster period. Our main contributions can be summarised as follows:
- i
- Reaching the target with optimal battery consumption
- ii
- Assigning and maintaining the position of particles to cover the maximum area.
- iii
- Optimal usage of a minimum number of drones.
The proposed method can approximate how the drones can reach the target site by covering the minimum distance. The area coverage of drones is maximised via the horizontal component of the true airspeed () and the height of the camera over the ground.
The proposed approach indicates that when maintaining the flight height of the drone above 120 m, the coverage can be enhanced by approximately 34% compared with a flight height of 100 m. Extensive simulations were performed using characteristics of the drones such as inertia, exploration and exploitation constants, velocity, and height to enhance the response against disaster, minimise the losses and maximise the area coverage of the disaster impact region. The optimal area coverage was achieved during the hover phase of the drones. Based on the simulations, we conclude that the maximum area coverage is achieved at a flight altitude of 120 m and a velocity of 20 . A method for drone path allocation was established which will assist with improving risk response, and saving time when dealing with emergencies. Furthermore, the developed method can be utilised to allocate drones based on the impacted region. Currently, the number of drones has been taken as a constant value considering each drone always provides the same performance. Future research should investigate the impact of different performance levels of drones on the outcomes. Future research could include a multi-objective function to assess the resource allocation in terms of drones, battery, and energy utilization. The current study has been performed based on the assumption that the area is obstacle-free. In the future, the impacts of various types of disasters, such as floods, fire, storms, in a non-obstacle-free area could be assessed.
Author Contributions
Methodology, H.S.M. and A.W.A.H.; investigation, A.W.A.H. and S.T.W.; writing—original draft preparation, H.S.M. and A.W.A.H.; writing—review and editing, A.W.A.H. and S.T.W.; supervision A.W.A.H. and S.T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The codes/simulations are available with the corresponding author and can be shared on reasonable request.
Acknowledgments
We would like to thank CDRI for their support in conducting this research.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Dynamically updating the inertia coefficient from 0.4 to 0.9 per iteration.
Table A1.
Dynamically updating the inertia coefficient from 0.4 to 0.9 per iteration.
| Iteration | Inertia Coefficient | ||
|---|---|---|---|
| 1 | 0.9 | 98.25242778509373 | [−5.88992833 7.59274691] |
| 2 | 0.875 | 166.1080146338387 | [−7.56059946 10.] |
| 3 | 0.85 | 172.72538867068536 | [−7.86179693 10.] |
| 4 | 0.825 | 173.57247234463873 | [−7.90035293 10.] |
| 5 | 0.8 | 173.648669201639 | [−7.90382112 10.] |
| 6 | 0.775 | 173.65343241781065 | [−7.90403793 10.] |
| 7 | 0.75 | 173.65364285853295 | [−7.9040475 10.] |
| 8 | 0.725 | 173.65364297446501 | [−7.90404751 10.] |
| 9 | 0.7 | 173.65364297446501 | [−7.90404751 10.] |
| 10 | 0.675 | 173.65364297595357 | [−7.90404751 10.] |
| 11 | 0.65 | 173.65364297596602 | [−7.90404751 10.] |
| 12 | 0.625 | 173.65364297596608 | [−7.90404751 10.] |
| 13 | 0.6 | 173.65364297596608 | [−7.90404751 10.] |
| 14 | 0.575 | 173.65364297596608 | [−7.90404751 10.] |
| 15 | 0.55 | 173.65364297596608 | [−7.90404751 10.] |
| 16 | 0.525 | 173.65364297596608 | [−7.90404751 10.] |

Table A2.
Results of simulation with a constant inertia coefficient at 0.55.
Table A2.
Results of simulation with a constant inertia coefficient at 0.55.
| Iteration | Inertia Coefficient | ||
|---|---|---|---|
| 1 | 0.55 | 161.46087064166917 | [9.89232861 −7.42906912] |
| 2 | 0.55 | 161.4815220862256 | [9.89142012 −7.43070174] |
| 3 | 0.55 | 161.48153790723256 | [9.89141942 −7.43070299] |
| 4 | 0.55 | 161.48153791935488 | [9.89141942 −7.43070299] |
| 5 | 0.55 | 161.48153791936414 | [9.89141942 −7.43070299] |
| 6 | 0.55 | 161.48153791936414 | [9.89141942 −7.43070299] |
| 7 | 0.55 | 161.48153791936414 | [9.89141942 −7.43070299] |
| 8 | 0.55 | 161.48153791936414 | [9.89141942 −7.43070299] |
| 9 | 0.55 | 161.48153791936414 | [9.89141942 −7.43070299] |

Table A3.
Results of simulation with Genetic Algorithm.
Table A3.
Results of simulation with Genetic Algorithm.
| Iteration | |
|---|---|
| 1 | 102.31 |
| 2 | 102.31 |
| 3 | 102.31 |
| 4 | 102.31 |
| 5 | 102.72 |
| 6 | 102.72 |
| 7 | 105.09 |
| 8 | 105.09 |
| 9 | 105.09 |
| 10 | 110.69 |
| 11 | 112.86 |
| 12 | 112.86 |
| 13 | 112.86 |
| 14 | 112.86 |
| 15 | 113.55 |
| 16 | 113.55 |
| 17 | 117.61 |
| 18 | 117.61 |
| 19 | 118.73 |
| 20 | 120.53 |
References
- Sitek, P.; Wikarek, J. Capacitated vehicle routing problem with pick-up and alternative delivery (CVRPPAD): Model and implementation using hybrid approach. Ann. Oper. Res. 2019, 273, 257–277. [Google Scholar] [CrossRef] [Green Version]
- Sitek, P. A Hybrid Approach to the Two-Echelon Capacitated Vehicle Routing Problem (2E-CVRP). In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Turin, Italy, 2014; Volume 267, pp. 251–263. [Google Scholar]
- Nielsen, I.E.; Dang, Q.-V.; Bocewicz, G.; Banaszak, Z. A methodology for implementation of mobile robot in adaptive manufacturing environments. J. Intell. Manuf. 2015, 28, 1171–1188. [Google Scholar] [CrossRef]
- Yakıcı, E. Solving location and routing problem for UAVs. Comput. Ind. Eng. 2016, 102, 294–301. [Google Scholar] [CrossRef]
- Bolton, G.E.; Katok, E. Learning by doing in the newsvendor problem: A laboratory investigation of the role of experience and feedback. Manuf. Serv. Oper. Manag. 2008, 10, 519–538. [Google Scholar] [CrossRef] [Green Version]
- Avellar, G.S.C.; Pereira, G.A.S.; Pimenta, L.C.D.A.; Iscold, P. Multi-UAV routing for area coverage and remote sensing with minimum time. Sensors 2015, 15, 27783–27803. [Google Scholar] [CrossRef] [Green Version]
- Khosiawan, Y.; Nielsen, I. A system of UAV application in indoor environment. Prod. Manuf. Res. 2016, 4, 2–22. [Google Scholar] [CrossRef] [Green Version]
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The stanford entry in the urban challenge. In The DARPA Urban Challenge; Springer: Berlin/Heidelberg, Germany, 2009; Volume 56, pp. 91–123. [Google Scholar] [CrossRef] [Green Version]
- Khosiawan, Y.; Park, Y.; Moon, I.; Nilakantan, J.M.; Nielsen, I. Task scheduling system for UAV operations in indoor environment. Neural Comput. Appl. 2018, 31, 5431–5459. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Su, C.; Liu, Y.; Hu, M.; Zhu, Y. Unmanned aerial vehicle route planning in the presence of a threat environment based on a virtual globe platform. ISPRS Int. J. Geo Inf. 2016, 5, 184. [Google Scholar] [CrossRef] [Green Version]
- Xiang, J.; Liu, Y.; Luo, Z. Flight safety measurements of UAVs in congested airspace. Chin. J. Aeronaut. 2016, 29, 1355–1366. [Google Scholar] [CrossRef] [Green Version]
- Khosiawan, Y.; Khalfay, A.; Nielsen, I.E. Scheduling unmanned aerial vehicle and automated guided vehicle operations in an indoor manufacturing environment using differential evolution-fused particle swarm optimization. Int. J. Adv. Robot. Syst. 2018, 15, 172988141775414. [Google Scholar] [CrossRef]
- Krishnanand, K.; Ghose, D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications. Multiagent Grid Syst. 2006, 2, 209–222. [Google Scholar] [CrossRef] [Green Version]
- Kashef, S.; Nezamabadi-Pour, H. An advanced ACO algorithm for feature subset selection. Neurocomputing 2015, 147, 271–279. [Google Scholar] [CrossRef]
- Zargham, M.; Ribeiro, A.; Ozdaglar, A.; Jadbabaie, A. Accelerated dual descent for network flow optimization. IEEE Trans. Autom. Control 2013, 59, 905–920. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Meng, Z.; Pan, J.-S.; Xu, H. QUasi-Affine TRansformation Evolutionary (QUATRE) algorithm: A cooperative swarm based algorithm for global optimization. Knowl. Based Syst. 2016, 109, 104–121. [Google Scholar] [CrossRef]
- Frazzoli, E.; Bullo, F. Decentralized algorithms for vehicle routing in a stochastic time-varying environment. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No.04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3357–3363. [Google Scholar]
- Sundar, K.; Venkatachalam, S.; Rathinam, S. Analysis of mixed-integer linear programming formulations for a fuel-constrained multiple vehicle routing problem. Unmanned Syst. 2017, 5, 197–207. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Xu, W.; Zhou, H.; Zhang, N.; Zhang, S.; Shen, X. Multiple drone-cell deployment analyses and optimization in drone assisted radio access networks. IEEE Access 2018, 6, 12518–12529. [Google Scholar] [CrossRef]
- He, X.; Yu, W.; Xu, H.; Lin, J.; Yang, X.; Lu, C.; Fu, X. Towards 3D deployment of UAV base stations in uneven terrain. In Proceedings of the 2018 27th International Conference on Computer Communication and Networks (ICCCN), Hangzhou, China, 30 July–2 August 2018; pp. 1–9. [Google Scholar]
- Feng, Y.; Zhang, R.-Q.; Jia, G. Vehicle routing problems with fuel consumption and stochastic travel speeds. Math. Probl. Eng. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Kinney, G.W.; Hill, R.R.; Moore, J.T. Devising a quick-running heuristic for an unmanned aerial vehicle (UAV) routing system. J. Oper. Res. Soc. 2005, 56, 776–786. [Google Scholar] [CrossRef]
- Santos, R.M.; Orozco, J.; Ochoa, S.F.; Meseguer, R.; Mosse, D. Providing real-time message delivery on opportunistic networks. IEEE Access 2018, 6, 40696–40712. [Google Scholar] [CrossRef]
- Tang, B.; Fang, Q.; Zhu, Z.; Ma, W. Effective 2D route planning of UAV based on improved ant colony algorithm. Xibei Gongye Daxue Xuebao. J. Northwest. Polytech. Univ. 2013, 31, 683–688. [Google Scholar]
- Vickers, N.J. Animal Communication: When I’m Calling You, Will You Answer Too? Curr. Biol. 2017, 27, R713–R715. [Google Scholar] [CrossRef] [PubMed]
- Alyassi, R.; Khonji, M.; Chau, S.C.-K.; Elbassioni, K.; Tseng, C.-M.; Karapetyan, A. Autonomous recharging and flight mission planning for battery-operated autonomous drones. arXiv 2017, arXiv:1703.10049. [Google Scholar]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef] [Green Version]
- Guerriero, F.; Surace, R.; Loscrí, V.; Natalizio, E. A multi-objective approach for unmanned aerial vehicle routing problem with soft time windows constraints. Appl. Math. Model. 2014, 38, 839–852. [Google Scholar] [CrossRef]
- Habib, D.; Jamal, H.; Khan, S.A. Employing multiple unmanned aerial vehicles for Co-operative path planning. Int. J. Adv. Robot. Syst. 2013, 10, 235. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, D.; Pei, D. Autonomous route planning for UAV when threats are uncertain. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 19–22. [Google Scholar]
- Micheletto, M.; Petrucci, V.; Santos, R.; Orozco, J.; Mosse, D.; Ochoa, S.F.; Meseguer, R. Flying real-time network to coordinate disaster relief activities in urban areas. Sensors 2018, 18, 1662. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Jia, L.; Niu, S.; Zhang, F.; Tong, L.; Zhou, X. A space-time network-based modeling framework for dynamic unmanned aerial vehicle routing in traffic incident monitoring applications. Sensors 2015, 15, 13874–13898. [Google Scholar] [CrossRef] [Green Version]
- Abu-Mostafa, Y.S. Neural networks and learning. In Conference Series-Institute of Physics; IOP Publishing Ltd.: Bristol, England, 1992; Volume 127, p. 7. [Google Scholar]
- Joo, H.; Hwang, H.-Y. Surrogate aerodynamic model for initial sizing of solar high-altitude long-endurance UAV. J. Aerosp. Eng. 2017, 30, 04017064. [Google Scholar] [CrossRef]
- Hasanova, N. A Comparative study of particle swarm optimization and genetic algorithm. Qubahan Acad. J. 2020, 1, 33–45. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Energy Consumption in Unmanned Aerial Vehicles: A Review of Energy Consumption Models and Their Relation to the UAV Routing. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2018; Volume 853, pp. 173–184. [Google Scholar]
- Pedley, T.J. The simple science of flight: From insects to jumbo jets.henk tennekes. Q. Rev. Biol. 1998, 73, 343. [Google Scholar] [CrossRef]
- National Academies of Sciences and Medicine, E. Commercial Aircraft Propulsion and Energy Systems Research. In Commercial Aircraft Propulsion and Energy Systems Research: Reducing Global Carbon Emissions; National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Farokhi, S. Future Propulsion Systems and Energy Sources in Sustainable Aviation. In Future Propulsion Systems and Energy Sources in Sustainable Aviation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Greitzer, E.M. 16. Unified: Thermodynamics and Propulsion Prof. ZS Spakovszky (2008). 2017. Available online: https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/notes.html (accessed on 1 January 2022).
- Pagliaroli, T.; Camussi, R.; Candeloro, P.; Giannini, O.; Bella, G.; Panciroli, R. Aeroacoustic study of small scale rotors for mini drone propulsion: Serrated trailing edge effect. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Atlanta, GA, USA, 2018; p. 3449. [Google Scholar]
- Kroon, R. Mechanics and thermodynamics of propulsion. J. Frankl. Inst. 1965, 280, 454–455. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Nielsen, P.; Bocewicz, G.; Banaszak, Z. UAVs Fleet Mission planning subject to weather fore-cast and energy consumption constraints. In Conference on Automation; Springer: Cham, Switzerland, 2019; pp. 104–114. [Google Scholar]
- Nigam, N.; Bieniawski, S.; Kroo, I.; Vian, J. Control of Multiple UAVs for persistent surveillance: Algorithm and flight test results. IEEE Trans. Control Syst. Technol. 2011, 20, 1236–1251. [Google Scholar] [CrossRef]
- Kunz, P.J. Aerodynamics and Design for Ultra-Low Reynolds Number Flight (Issue June); Stanford University: Stanford, CA, USA, 2003. [Google Scholar]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Factors affecting energy consumption of unmanned aerial vehicles: An analysis of how energy consumption changes in relation to UAV routing. In Proceedings of the International Conference on Information Systems Architecture and Technology, Wrocław, Poland, 15–17 September 2018; Springer: Cham, Switzerland; pp. 228–238. [Google Scholar]
- Sugimoto, A. The effectiveness of feedback on Japanese language presentation. Int. J. Hum. Cult. Stud. 2019, 2019, 38–42. [Google Scholar] [CrossRef]
- Aloyce, O. Cost-Benefit Analysis of Wind Turbines Installation and Use in Dodoma Municipality; The University of Dodoma: Dodoma, Tanzania, 2016. [Google Scholar]
- Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Zbigniew, B. Planning deliveries with UAV routing under weather forecast and energy consumption constraints. IFAC-PapersOnLine 2019, 52, 820–825. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. UAV Mission planning subject to weather forecast constraints. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1004, pp. 65–76. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).