A Simple Method for Extracting Piezoelectric Coefficient d₃₁ by Fitting Experimental Data with an Analytical Model ^†

Abstract

This work presents a simple method to extract the piezoelectric coefficient $d_{31}$ based on analytical model fitting. A theoretical circuit model is developed for a piezoelectric circular membrane actuator based on PZT thin film. The circular diaphragm consists of a 12 µm silicon layer, an 800 nm thick PZT layer, and a 200 nm Ti/Pt layer, featuring a single 50% inner top electrode coverage. The proposed model is validated by the finite element method with a 2D axisymmetric model of a PZT piezoelectric membrane. Further, piezoelectric coefficient $d_{31}$ is extracted by fitting the Laser Doppler Vibrometer (LDV) experimental result with the analytical model.

1. Introduction

MEMS devices based on piezoelectric thin films have become ubiquitous in applications such as RF filters, acoustic devices, and energy harvesters [1]. The properties of the piezoelectric film play an important role in the performance of devices, especially the piezoelectric coefficient $d_{31}$. Several piezoelectric measurement techniques have been reported, including direct and indirect methods [2,3]. In this work, we propose a simple and easily accessible approach to measuring piezoelectric constants by fitting the Laser Doppler Vibrometer (LDV) experimental data with an analytical model.

2. Materials and Methods

Figure 1a shows a fabrication schematic consisting of a stack of Si/SiO2/Ti/Pt/PZT/Ti/Pt layers. Figure 1b shows the optical photograph of a fabricated PZT device. An equivalent circuit model is developed to predict the behavior of the piezoelectric actuator, including the influence of residual stress. The theoretical model is validated by a finite element simulation model, and the piezoelectric constant $d_{31}$ is then extracted by fitting LDV experimental data with the theoretical model.

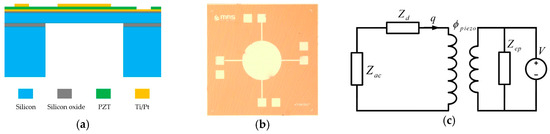
Figure 1. (a) Schematic of the piezoelectric actuator; (b) Optical photograph of the fabricated PZT device. (c) The equivalent circuit model of the piezoelectric membrane actuator.

3. Discussion

The equivalent circuit model is shown in Figure 1c, where $Z_{ac}$ is the acoustic impedance; $Z_d$ the diaphragm impedance; $q$ is the membrane volume velocity; and $Z_{ep}$ is the impedance collected from the piezoelectric film. ${\varnothing }_{piezo}$ is the transformer ratio related to volume velocity $q$ and actuation voltage $V$. By analyzing the model, the piezoelectric constant $d_{31}$ can be extracted by Equation (1) as follows:

$${\varphi }_{piezo}=\frac{j\omega 2\pi RE{d}_{31}{Z}_{p}F\left(k\right)}{D\left(1-v_{piezo}\right)}$$

(1)

where $\omega$ is the angular frequency; $R$ is the radius of the membrane; $E$ is the Young’s modulus; $Z_p$ is the distance from the mid-plane of the PZT layer to the neutral axis; $D$ is the flexural rigidity of the membrane; $v_{piezo}$ is the Poisson’s ratio of PZT; $F\left(k\right)$ is the vibration mode-related function; and $k$ is the radial mode shape number [4].

Figure 2a compares the theoretical and simulated results of the membrane displacement with a residual stress of 200 MPa, which match well. Figure 2b shows the displacement per voltage of a fabricated device measured by LDV and predicted by a theoretical model. The residual stress of the diaphragm is 200 MPa, as measured by a DektakXT stylus tool. To fit the experimental data, a measured quality factor value of 76 is substituted into the theoretical model. The theoretical and experimental results exhibit good agreement; the differences can be attributed to material parameters and fabrication tolerance. Subsequently, the piezoelectric constant $d_{31}$ is extracted as 18 pm/V. Figure 2c shows the polarization vs. electric field hysteresis loop of deposited PZT film at 1 kHz.

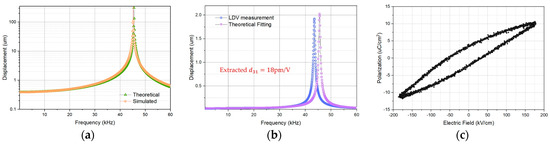
Figure 2. (a) Comparison of the theoretical and simulated results of the membrane displacement. (b) Results measured by LDV and predicted by the theoretical model. (c) P−E hysteresis loop of deposited PZT film at 1 kHz.