Nonlinear Evolution Equations of the Soliton Type: Old and New Results ^†

Abstract

An overview on the study of nonlinear evolution equations of soliton type is provided. In addition, 5th-order nonlinear evolution equations are shown to be connected to the Caudrey–Dodd–Gibbon–Sawada–Kotera (CDGSK) equation via Bäcklund transformations. The links are depicted in a wide net of links which we term a Bäcklund Chart. The links obtained previously by Rogers and Carillo and by Carillo and Fuchssteiner are revisited, and new results are obtained. A 5th-order nonlinear evolution equation, which does not seem to appear in any list of integrable equations, is provided. All the connected equations exhibit a very interesting symmetry structure enjoyed by the corresponding full hierarchies. Indeed, they all admit a hereditary recursion operator. Hence, each one of the mentioned equations represents the base member of a corresponding hierarchy of equations. These hierarchies are constructed via the recursive application of the respective recursion operators. The symmetry properties of such equations are recalled. Finally, we compare the net of links, derived via Bäcklund transformations, in the case of the fifth-order nonlinear evolution equations with an analog net of links connecting third-order Korteweg-de Vries (KdV) and modified Korteweg-de Vries (mKdV) equations. Analogies and discrepancies between the connections established in the case of fifth-order equations with respect to those established in the case of third-order equations are analyzed. This study aims to open the way for the construction of corresponding non-Abelian equations of the fifth order.

1. Introduction

The present investigation concerns nonlinear evolution equations, also known as soliton equations since they admit solutions which are rapidly decreasing functions as $x\to \pm \infty$ (it is generally assumed that M is the space of functions $u(x,t)$, which, for each fixed t, belongs to the Schwartz space S of rapidly decreasing functions on ${\mathrm{IR}}^n$, i.e., $S\left({\mathbf{R}}^n\right):=\{f\in C^{\infty }\left({\mathbf{R}}^n\right){:\left|\right|f\left|\right|}_{\alpha ,\beta }<\infty ,\forall \alpha ,\beta \in {\mathbf{N}}_0^n\}$, where ${\left|\right|f\left|\right|}_{\alpha ,\beta }:=su{p}_{x\in {\mathbf{R}}^n}\left|x^{\alpha }{D}^{\beta }f\left(x\right)\right|$, and $D^{\beta }:={\displaystyle \frac{{\partial }^{\beta }}{{\partial x}^{\beta }}}$; throughout this article, $n=1$.). Soliton solutions are of great interest in many applicative fields; see [1,2] for an introduction on the subject. Applications to nonlinear optics are given in [3,4,5,6]. Further results in different areas from theoretical physics [7,8] to biophysics [9] and also to the study of metamaterials [10] show the importance of investigations on soliton equations. An up-to-date panorama on integrable non linear evolution equations is given in [11].

A variety of different methods can be applied to study soliton equations such as symmetry methods [12,13,14,15], the Hirota method [16,17] and Darboux transformations methods [18,19]. In addition, Refs. [20,21,22,23,24,25,26,27,28] are devoted to classify linearizable nonlinear evolution equations. In a study by Levi [29], connections among different techniques are investigated. In addition, non linear equations are studied in [3,6,30,31,32] where nonlinear waves solutions are investigated.

2. Preliminary Notions and Bäcklund Transformations

The notion of Bäcklund transformation, firstly introduced by Bäcklund [33,34], is crucial to the results presented here. The subject has been studied in many books, such as [35,36,37,38,39,40,41,42], to consider those ones that which are related to soliton equations—the subject of the present study. Notably, via Bäcklund transformations, the Hamiltonian and bi-Hamiltonian structure admitted by a nonlinear linear differential equation [43,44,45,46,47,48] can be revealed.

Definition 1

(Bäcklund transformation). Given two evolution equations,

$$\begin{array}{cc}\hfill u_t& =K\left(u\right),K:M_1\to T{M}_1,u:(x,t)\in {\mathbb{R}}^n\times \mathbb{R}\to u(x,t)\in {\mathbb{R}}^m\subset M_1\\ \hfill v_t& =G\left(v\right),G:M_2\to T{M}_2,v:(x,t)\in {\mathbb{R}}^n\times \mathbb{R}\to v(x,t)\in {\mathbb{R}}^m\subset M_2\end{array}$$

where K and G are the $C^{\infty }$-vector field, a Bäcklund Transformation, according to [43,47], connects them whenever, denoted as $u(x,t)$ and $v(x,t)$ two solutions, respectively, of the two evolution equations, it follows that

$$if{B(u,v)|}_{t=0}=0\Rightarrow B(u,v)=0\forall t.$$

Then, $B(u,v)=0$ is termed Bäcklund Transformation.

Notably, most of the remarkable properties of soliton equations are preserved under Bäcklund Transformations [43,47], and, in particular, solutions are mapped into solutions.

Remark 1

([12,43]).

• If $u_t=K\left(u\right)$ admits a Recursion Operator  $\Phi \left(u\right)$, then we can write

  $$\begin{array}{|c|}\hline K\left(u\right)=\Phi \left(u\right)\left[u_x\right]\\ \hline\end{array}⟹\begin{array}{|c|}\hline u_t=\Phi \left(u\right)\left[u_x\right]\\ \hline\end{array}$$
• the  Recursion Operator  $K:M_1\to T{M}_1,\Phi \left(u\right):T{M}_1\to T{M}_1,\forall u\in M_1$ is such that

  1. 

  Φ maps symmetries into symmetries (A map $\sigma :M\to TM$ is said to be an infinitesimal symmetry generator (for short symmetry) if it leaves the evolution equation $u_t=K\left(u\right)$ invariant under the infinitesimal transformation $u\to u+ϵ\sigma$.

  2. 

  Thus, if u and σ are solutions, in turn, of $u_t=K\left(u\right)$ and ${\sigma }_t=K^{\prime }\left(u\right)\left[\sigma \right]$, then $\Phi \left(u\right)\sigma$ is also a solution of the latter. That is

  $$\begin{array}{|c|}\hline {(\Phi \left(u\right)\sigma )}_t=K^{\prime }(\Phi \left(u\right)\sigma )\\ \hline\end{array}⟺\begin{array}{|c|}\hline {\Phi }^{\prime }\left(u\right)u_t\sigma +\Phi \left(u\right){\sigma }_t=K^{\prime }\left(u\right)\Phi \left(u\right)\left[\sigma \right]\\ \hline\end{array}$$

  3. 

  Φ is  hereditary, i.e., satisfies the condition

  $$\begin{array}{|c|}\hline \Phi [K,A]=[K,\Phi A],\forall A\in TM\\ \hline\end{array}⟺\begin{array}{|c|}\hline [\Phi ,K]=0\\ \hline\end{array}$$

• Then, $\Phi \left(u\right)$ is a recursion operator for the hierarchy $\begin{array}{|c|}\hline u_t={(\Phi \left(u\right))}^n{u}_x\\ \hline\end{array}$.
• The property to admit a Recursion operator is preserved under Bäcklund Transformations.

Methods to construct recursion operators have been proposed by [49,50,51].

Definition 2

(Bäcklund Chart). A net of Bäcklund Transformations that connect evolution equations is termed the Bäcklund Chart.

The most well-known examples are represented by the Cole–Hopf transformation, which connects the Burgers equations to the linear heat equation.

Example 1

([52,53]).

$$\begin{array}{|c|}\hline u_t=u_{xx}+2u{u}_x\\ \hline\end{array}\stackrel{B}{--}\begin{array}{|c|}\hline v_t=v_{xx}\\ \hline\end{array}sothatB(u,v)=0reads\begin{array}{|c|}\hline v_x-uv=0\\ \hline\end{array}.$$

(1)

A second example is given by the transformation due to Gardner, Greene, Kruskal, and Miura, which connects the modified Korteweg-de Vries (mKdV) equation to the Korteweg-de Vries (KdV) equation.

Example 2

([54,55]).

$$\begin{array}{|c|}\hline u_t=u_{xxx}+6u{u}_x\\ \hline\end{array}\stackrel{B}{--}\begin{array}{|c|}\hline v_t=v_{xxx}-6v^2{v}_x\\ \hline\end{array}B(u,v)=0reads\begin{array}{|c|}\hline u+v_x+v^2=0\\ \hline\end{array}$$

(2)

3. Extension to Hierachies

In this Section, we answer the question of how to extend a Bäcklund Chart. To this end, we recall that if a given a nonlinear evolution equation, $u_t=K\left(u\right)$, admits a Recursion Operator $\Phi \left(u\right)$, $K\left(u\right)=\Phi \left(u\right)\left[u_x\right]$, then the properties listed in the previous Section allow us to construct a corresponding hierarchy of nonlinear evolution equations. Specifically, it reads as follows [56,57]:

$$\begin{array}{|c|}\hline u_t=\Phi {\left(u\right)}^n{u}_x,n\in N\\ \hline\end{array}$$

The properties of the recursion operator imply that the Bäcklund transformation that connects the two equations $u_t=K\left(u\right)$ and $v_t=G\left(v\right)$ also links the corresponding members of the hierarchies generated by the recursion operators they admit. As a consequence, the second equation $v_t=G\left(v\right)$ can also be proven to admit a recursion operator, here denoted as $\Psi \left(v\right)$, so that

$$\begin{array}{|c|}\hline u_t=\Phi {\left(u\right)}^n{u}_x\\ \hline\end{array}\stackrel{B}{--}\begin{array}{|c|}\hline v_t=\Psi {\left(v\right)}^n{v}_x\\ \hline\end{array}$$

where [43,47] the operator $\Psi \left(v\right)$ can be obtained by the Bäcklund transformation. The operator $\Pi$

$$\Pi :=B_v^{-1}{B}_u,\Pi :T{M}_1\to T{M}_2$$

(3)

where the subscripts denote Frechet derivatives, which transforms the field K(u) into G(s), gives the recursion operator $\Psi \left(v\right)$:

$$\begin{array}{|c|}\hline \Psi \left(v\right)=\Pi \Phi \left(u\right){\Pi }^{-1}.\\ \hline\end{array}$$

(4)

4. Operator Bäcklund Charts

A further generalization consists of considering nonlinear evolution equations in a non-Abelian setting. Specifically, here we consider the case when unknowns, denoted by capitalized letters, are operators on Banach spaces.

4.1. Heat–Burgers Operator Bäcklund Charts

According to [58], an Operator Bäcklund Chart can be constructed which relates the linear heat Operator equation to the Burgers Operator equation.

$$\begin{array}{|c|}\hline U_t=U_{xx}+2U{U}_x\\ \hline\end{array}\stackrel{BT}{--}\begin{array}{|c|}\hline V_t=V_{xx}\\ \hline\end{array}$$

(5)

where the Bäcklund transformation $B(U,V)=0$ reads $UV-V_x=0$ or $U=V^{-1}{V}_x$. Note that, to stress the non-commutative setting, it is convenient to write the Burgers operator equation in the following form:

$$U_t=U_{xx}+[U,U_x]+\{U,U_x\},$$

(6)

where, in turn, $[·,·]$ and $\{·,·\}$ denote the commutator and the anti-commutator.

The heat equation admits the recursion operator $\Phi \left(U\right)=D$; then the non-Abelian Burgers equation also admits a recursion operator, according to [58],

$$\begin{array}{|c|}\hline V_t={[\Psi \left(V\right)]}^n{V}_x\\ \hline\end{array}\stackrel{BT}{⟷}\begin{array}{|c|}\hline U_t={[\Phi \left(U\right)]}^n{U}_x\\ \hline\end{array}$$

(7)

where $\Phi \left(U\right)=D,\Psi \left(V\right)=\Pi \Phi \left(U\right){\Pi }^{-1}$ $B(U,V)=0⟹$$\Pi :=B_V^{-1}{B}_U^{\phantom{­}},\Pi :T{M}_1\to T{M}_2$

$${\displaystyle \begin{array}{|c|}\hline U_t=U_{xx}\\ \hline\end{array}⟷\begin{array}{|c|}\hline V_t=V_{xx}+[V,V_x]+\{V,V_x\}\\ \hline\end{array}}$$

where $[V,V_x]=V{V}_x-V_{x}V, \{V,V_x\}=V{V}_x+V_{x}V$, and the link $B(U,V)=0$ reads $\begin{array}{|c|}\hline V_x-VU=0\\ \hline\end{array}\mathrm{or}U=V^{-1}{V}_x$.

Also in the non-Abelian case, the Bäcklund Transformation relates each member of the Burgers operator hierarchy to the corresponding member of the Heat operator hierarchy [58]. Specifically,

$$V_{xx}+[V,V_x]+\{V,V_x\}=\Psi \left(V\right)V_x,\mathrm{where}$$

(8)

$$\Psi \left(V\right)\left(D+[V,·]\right)=\left(D+[V,·]\right)\left(D+V\right)$$

(9)

Then, the Burgers hierarchy reads $\begin{array}{|c|}\hline V_t={\Psi \left(V\right)}^n{V}_x,n\in \mathbb{N}\\ \hline\end{array}$, according to the detailed study in [59], where, in addition, a mirror Burgers hierarchy is constructed whose base member is

$$R_t=R_{xx}+[R_x,R]+\{R_x,R\}.$$

(10)

The latter also admits a recursion operator obtained in [59]. Remarkably, the hierarchies we obtained coincide with those by Levi, Ragnisco and Bruschi [60], who studied matrix equations. Non-Abelian Burgers equations were also studied by Gürses, Karasu and Turhan [61] and by Kupershmidt [62] and Hamanaka [63]. More generally, operator methods are devised in [64]. Non-Abelian nonlinear evolution equations are also studied in [21,26,65,66,67].

4.2. KdV–mKdV Operator Bäcklund Charts

Based on [68,69], the mKdV and KdV operator equations are related via

$$\begin{array}{|c|}\hline V_t=V_{xxx}-3\{V^2,V_x\}\\ \hline\end{array}\stackrel{M}{⟷}\begin{array}{|c|}\hline U_t=U_{xxx}+3\{U,U_x\}\\ \hline\end{array}$$

(11)

where the link M denotes the Miura transformation in the non-Abelian setting, i.e.,

$$M:U+V_x+V^2=0.$$

(12)

Again, the link relates the corresponding whole hierarchies and, hence, the previous can be extended to the hierarchies as follows:

$$\begin{array}{|c|}\hline V_t=[\Psi \left(V\right)]V_x\\ \hline\end{array}\stackrel{M}{⟷}\begin{array}{|c|}\hline U_t=[\Phi \left(U\right)]U_x\\ \hline\end{array}$$

(13)

where the KdV recursion operator is given by [68]

$$\Phi \left(U\right)=D^2+2\{U,·\}+\{U_x,·\}{D}^{-1}+[U,·]D^{-1}[U,·]D^{-1},$$

(14)

while the mKdV recursion operator [68] (to this end, methods to solve operator equations are crucial [70]) is

$$\Psi \left(V\right)=\left(D+[V,·]D^{-1}[V,·]\right)\left(D+\{V,·\}{D}^{-1}\{V,·\}\right).$$

(15)

The latter is obtained via the Miura transformation. Furthermore, in [68], the recursion operators are proved to enjoy all the properties in Section 1. Matrix equations and recursion operators were also studied in [71].

5. Third-Order Bäcklund Chart: An Extension

This Section is devoted to briefly recall the 3rd-Order Bäcklund Chart, extended in [72] to include the KdV eigenfunction equation [73], as depicked in the following Figure 1. The following net of Bäcklund transformations was obtained in [74]:

Figure 1. Extended Bäcklund chart which includes the KdV eigenfunction equation.

All the third-order nonlinear evolution equations are, respectively, listed in Figure 2. Figure 3, subsequently, shows, following the respective order in the Bäcklund chart, all the Bäcklund transformations linking the KdV-type equations in Figure 2.

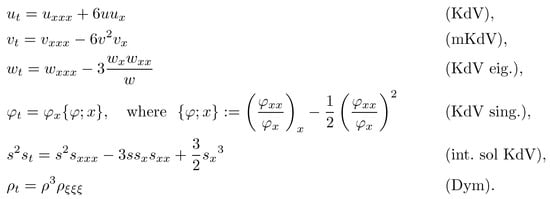
Figure 2. KdV-type equations linked via the Bäcklund chart in Figure 1.

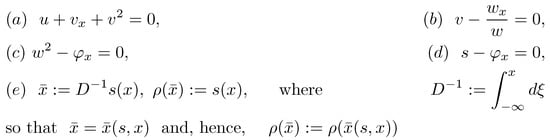
Figure 3. Bäcklund transformations depicted in the Bäcklund chart in Figure 1.

6. Fifth-Order Bäcklund Chart: An Extension

In this Section, we announce the new extension of a Bäcklund Chart obtained in [56,57]. Indeed, we started from the links therein and insert a further highly nonlinear nonlinear evolution equation. The proofs are in [75], where all the details are provided. The result in [75] is summarized by the following Bäcklund Chart, see Figure 4 and Figure 5, where, in turn, the links among the equations and the equations themselves, are listed. The Bäcklund Chart is obtained from the one in [56,57] with further insertion of the equation denoted as CGD eig., which stands for the Caudrey–Dodd–Gibbon–Sawada–Kotera eigenfunction equation, introduced below [75]:

Figure 4. Bäcklund transformations that link 5th-order equations listed in Figure 5.

Figure 5. Equations in the Bäcklund chart in Figure 4.

The Caudrey–Dodd–Gibbon–Sawada–Kotera eigenfunction equation (CGD eig.) (see Figure 5) that appears in the Bäcklund Chart is boxed to stress that this equation, to the best of our knowledge, does not appear in any list of integrable 5th-order nonlinear evolution equations. The other equations, in the 5th-order Bäcklund Chart (see [75] and references therein) are well-known ones [76,77,78].

In Figure 6, the list of transformations is given. Notably, the symmetry properties of the CGD eig. equation are studied in [75], where, on the basis of the Bäcklund Chart in Figure 4, such an equation is proved to admit a hereditary recursion operator. As a consequence, the Bäcklund Chart can be extended to the corresponding hierarchies, according to [56,57]. We only mention that the CGD eig. equation enjoys the same invariance enjoyed by the KdV eig. equation [72]; i.e., according to [75], it is invariant under the following transformation:

$$\mathrm{I}:{\widehat{w}}^2={\displaystyle \frac{ad-bc}{{(c{D}^{-1}\left(w^2\right)+d)}^2}}{w}^2,a,b,c,d\in \mathbb{C}s.t.ad-bc\ne 0,D^{-1}:={\int }_{-\infty }^{x}d\xi .$$

(16)

This variance follows as a consequence of the invariance under the Möbius group of transformations exhibited by the CDG Sing. equation in Figure 5.

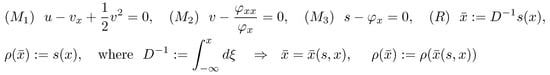
Figure 6. Bäcklund transformations that link 5th-order equations in Figure 4.

7. Remarks, Perspectives, and Open Problems

To close this short overview on old and new results, note that some important aspects were not included, for the sake of brevity, but are very important under the applicative viewpoint. In addition, some current and perspective research directions are mentioned. One of the aims is the construction of solutions admitted by nonlinear evolution equations.

7.1. Remarks and Further Obtained Results

• New Solutions

  -

  Abelian case: One very important consequence of the constructed Bäcklund Charts is that new solutions of nonlinear evolution equations can be constructed from known solutions of other equations in the same Chart. This was the case in [79], where solutions admitted by the Harry Dym equation were obtained from solutions of the KdV equation.

  -

  Non-Abelian case: Even more interesting is the case of Bäcklund Chart operators, in which new solutions can be obtained from known ones. Solutions of non-commutative equations are of great interest [69,80], such as in the case of a solution formula for the non-Abelian mKdV equation: we constructed solutions of the non-Abelian mKdV equation from solutions admitted by the non-Abelian KdV equation, obtained by Goncharenko [81]. In particular, matrix solutions admitted by the non-Abelian mKdV equation were obtained in [82] and references therein; a different approach to the matrix mKdV solution was given in [83]. Other approaches to non-Abelian cases are also interesting [21,63,84].

• New Invariances and Auto Bäcklund Transformations
  (Abelian and non-Abelian cases)

  -

  In both cases, via the constructed Bäcklund Charts, new invariance exhibited by the involved equations can be obtained, or well-known ones can be recovered. Results in this line are in [56,57] in cases of 5th-order nonlinear evolution equations, while in [74,85,86], invariances exhibited by 3rd-order nonlinear evolution equations connected with the KdV equation, via the Bäcklund Chart in Figure 1, were obtained. Furthermore, auto Bäcklund transformations admitted by the Harry Dym equation were obtained [74,85]. Remarkably, also in the non-Abelian case, interesting properties of the nonlinear evolution equations which appear in the Bäcklund Chart [68,69,87,88], follow from the chart itself; such as, e.g., to admit a recursion operator. A comparison between the Abelian and non-Abelian Bäcklund Charts concerning 3rd-order nonlinear evolution equations is given in [89]. Indeed, as pointed out therein, a richer structure [88], based also on results in [90], was revealed in the non-commutative case. In addition, further equations appear to be connected in the Bäcklund Chart previously obtained.

7.2. Perspectives and Open Problems

Many open problems deserve to be investigated in cases of hierarchies of nonlinear evolution equations whose base member is a 5th-order evolution equation [91]. Here, a list of issues we are working on is presented.

• The construction of the Hamiltonian and bi-Hamiltonian structure [45,48,56,92], of the CGD eig. equation, again via the Bäcklund Chart in [75], in Figure 4, and relying on results in [56], is in progress.
• Extensions from Abelian to non-Abelian in the case of 5th-order nonlinear evolution equations, which appear in the Bäcklund Chart in [75], are under investigation.
• A better understanding of the algebraic structure in the case of non-commutative non-linear evolution equations aiming to extend results from the Abelian [93,94] to the non-Abelian case.
• Can new operator solutions be constructed from our new Bäcklund Chart? We already obtained some results as pertains to this, and these are in [58,68,69,88].