Abstract
We present a combinatorial analysis of any maximal set of gate compositions parameterized over a finite alphabet which revealed an underlying fractal structure. Results are presented as global maps in the form of large 2D arrays where each row stands for an unfolded list of matrix elements for any unitary matrix resulting from a succession of Kronecker products while columns stand for all possible words representing such sequences. These can be given either in lexicographic order or via a non-binary (n-ary) Gray code in which case any such map can be factorized.
1. Introduction
For the past three decades, standard gate-based quantum circuitry has been well established and certain small sets of universal gate sets have been proposed [,].
Recent advances in Parametric Quantum Circuits (PQC) [,] and its variant Variational Quantum Computing (VQC) [], and most recently Relativistic VQC (RVQC) [,], as well as possible applications of the above in Quantum Machine Learning (QML) algorithms [], have brought new perspectives.
While several universal gate sets are based on a relatively simple parametrization over a Bloch sphere, the free parameters required for variational methods make it necessary to introduce arbitrary unitary operators where corresponds to a set of triplets of spherical angles per gate sampled from a continuum.
On the other hand, an early theorem by Solovay and Kitaev, which formed the basis of modern Quantum Compilers [], allows expressing any n qubit circuit based on arbitrary unitaries into some small fundamental universal gate set [,]. More recently, an approach based on Birkhoff’s theorem expressing unitaries via permutations also appeared in [].
Recent developments have also highlighted the significance of random quantum circuits with regard to entanglement properties including various types of phase transitions [,,].
It becomes evident that any types of symmetries inherent in the global structure of the full combinatorial set of arbitrary circuits, if present, may be of great significance to the further study of other emergent properties that appear after a certain threshold scale value.
More recent studies based on graph representation of qubit interaction in the form of Directed Acyclic Graphs (DAGs) [,,,,] also predict certain thresholds as in the case of the Kahn–Kalai conjecture, recently proven by Park and Pham [].
In what follows, we always assume an algebraic representation of an arbitrary circuit as a product of unitary matrices each of which is itself formed by the sequential Kronecker product of a finite set of gate representations including a subset of entangling matrices.
Any such finite set corresponds to an alphabet and the words formed by the alphabet letters can be used as indices to represent different sequences of any non-commuting matrix product.
This allows us to form a hierarchy of Global Maps as arithmetic representations of possible large unitary matrices made from any finite alphabet. Moreover, the use of a natural lexicographic order reveals the presence of possible symmetries and scale invariances across a hierarchy of tree structures and their associated exponential intervals from path enumeration, for any given alphabet.
We should stress the fact that the presentation that follows is strictly ‘phenomenological’ in that the sets of gates used as well as the global maps obtained are used as ideal mathematical objects having an interest of their own in that they reveal an invisible underlying order independently of their physical counterparts in their actual material implementations. Nevertheless, the kind of order revealed may prove (as the authors believe) greatly beneficial for simplification after the mathematical origins of this have been fully studied, something that is work in progress at the moment.
In the next section, we provide some basic definitions and tools for dealing with the problem of extracting such global maps via an appropriate decomposition of arbitrary length sequential Kronecker products into a set of permutations for the final matrix element indices.
Moreover, a special implicate product of two trees is introduced, where the first tree structure and its paths stand for words representing a combination of individual gates in a sequence of Kronecker products and the second holds all possible products of individual gate matrix elements. This results in a special algorithm for the correct enumeration of the resulting products of complex factors for each matrix element in two possible orderings, lexicographic and Gray-coded. The latter presents an advantage, allowing us to further factorize any global map into a set of multiplier sequences.
In Section 3, a direct application of a restricted gate set from the Pauli group is given that results in arithmetic fractal sets for both types of ordering and a similar example with an extended 6-gate set including a Hadamard gate. Some advantages of such a representation as well as additional research questions of a more mathematical nature are discussed in Section 4, concluding the present report.
2. Materials and Methods
By definition, an arbitrary quantum circuit is a representation of a large unitary operator acting on a number of qubits that admits a representation in terms of certain smaller operators both in series and in parallel. Each set of parallel operations represents a single layer while the sequential product of many layers of depth D stands for the total operator. The most general form then is equivalent to an algebraic matrix product
where
stands for the parallel realization of a number of gates of different dimensions , , ⋯ where the first represent single qubit operations while the others are additional entangling (non-factorizable) matrices. Most practical applications rarely use more than 2-qubit entangling gates.
From the algebra of Kronecker products, this always results in matrices where , with n being the number of single qubit gates, m the number of entangling gates and so on. This has the obvious restriction that for any input vector of k qubits, all possible combinations of unequal dimensions of parallel gates must form an integer partition of k.
The fundamental observation for the extraction of global maps for such a construct has to do with the fact that when Kronecker products are defined over matrices that repeat a finite set of elements, they essentially contain the exact same number of final products as the one defined by the paths of a symmetric rooted tree in lexicographic or Gray order plus an appropriate permutation. This fact is further analyzed in the next section.
2.1. Vectorization of Sequential Kronecker Products
The term vectorization has been used in linear algebra and computational applications to mean the unfolding of an arbitrary matrix into an equivalent one-dimensional list of elements via the correspondence
The existing literature provides certain formulas on the complete vectorization of a single Kronecker pair (e.g., []). Recursive application of such formulas is cumbersome and does not offer any advantage in bringing to the fore the essential connections we are interested in.
To this aim, we have to apply a different set of tools from combinatorics. In particular, we are utilising the fact that in products of unitaries, we are always dealing with powers of 2. It is then sufficient to examine the case for concatenations of the bit patterns of the associated indices of matrix elements for each such unitary matrix in an arbitrary sequence.
Assume then an arbitrary alphabet representing a finite set of gate matrices as letters such that any word w is to be associated with a sequential product via the representation
Before reaching the problem of the complete vectorization of such a word, we should first start from a fundamental observation on a single pair . We notice, in particular, that by construction every element of is combined with every element of . This leads to the original Kronecker product sharing the exact same elements with , where denotes the dyadic vector product, apart from a permutation. Thus, we may write the abstract relation
where . The advantage of this representation is that vectorizing the dyadic gives a straightfoward lexicographic indexing of all product elements with respect to their indices. The permutation matrix then carries the essential information of the Kronecker algebra, including its non-commutative character.
To reveal the nature of this permutation, we think of an auxiliary pair of matrices composed solely of the associated indices. In the simplest case of a matrix, let this be
We deliberately use an indexing from zero such that the maximal element always coincides with an integer of the form .
The arithmetic equivalent of the concatenation of two bit patterns over a sequence of exponential intervals takes the non-commuting form , where are the arithmetic values of the corresponding bit patterns. Assume then the equivalent of the Kronecker product with concatenative addition instead of multiplication. This takes the form of a recursion as
where now . The coefficient is a result of all matrices having dimensions so that all indices cover a total arithmetic interval .
Examination of the matrix reveals a well known pattern as
Following the order of the indices shows the familiar pattern of the self-similar plane filling curve known as the Lebesgue Z-curve. This is a recurring theme in a variety of contexts ranging from combinatorics to computer graphics, where it is mentioned as the Z-order, also used in the Quadtree image compression scheme [,].
The natural scale invariance of the above recursion makes it possible to expand over an arbitrary sequence of Kronecker products so that the exact permutation can be obtained directly from after repeating the iteration in (4) up to the total length of any product sequence. While this highly symmetric scheme is valid for any product sequence containing solely gate matrices, its expansion for cases where one may have mixtures of with matrices is rather straightforward. Since different dimensions cover different arithmetic intervals, one may adjust the basic recursion map by taking into account the different binary logarithm used each time by writing the more general form .
Alternatively, one can first create a new alphabet of all possible combinations of the two bases of distinct matrices so that every final product sequence works with the highest dimension, thus being always symmetric. An example of such a permutation for matrices is shown in Figure 1.
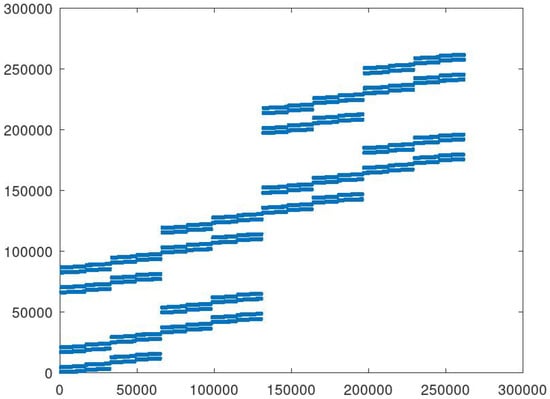
Figure 1.
Example of a symmetric permutation for a sequential Kronecker product.
Having established the exact way of forming the permutations for each sequence of Kronecker products, we can now proceed to the appropriate definitions for the global maps over any alphabet of possible gate matrices.
2.2. Global Maps
We choose the term Global Map here to mean an exaustive cataloguing of all possible sequential Kronecker products out of a finite set of gate elements, each represented in vectorized form with their products of complex factors in lexicographical order.
We always assume a finite set of gates of cardinality b taken as the basis of an associated alphabet. The words from such an alphabet shall be termed control words here. These words express the particular order of terms in a sequential product of given length .
A second set of words representing each of the final matrix elements is then associated with a ‘controlled’ alphabet defined by a secondary tree representing the fact that for each sequence of Kronecker products, all combinations of different sets of elements per individual matrix exist in the total Kronecker sequence.
The control words then serve to create a different permutation from each to be applied over all the b rows of an appropriate Look-Up Table (LUT), each row being made out of matrix elements of each separate gate element. The process is equivalent to a weighted symmetric rooted tree, the weight elements of which change dynamically at each node level to reflect the different composition of each sequence of Kronecker products.
To properly organize their presentation, it is necessary to introduce appropriate arrays depending on a single parameter, preferably the number of input qubits. Each global map will have to be built as an array where each row contains the unfolded form of the final matrix elements for all possible Kronecker sequences denoted by the controlled words.
We are particularly interested in cases where the inner symmetries of such a hierarchy indicate the existence of a special map
An immediate problem arises in the case of combined single qubit and higher entangling matrices due to the restriction mentioned in Section 2, where k must satisfy a specific number-theoretic condition in order for all combinations of gates in parallel to give rise to the same dimension, independently of the lengths of each sequential product.
Since we are interested in arbitrary, even random parametrizations over a Bloch sphere, we are forced to avoid some standard universal sets like rotations and phases plus CNOT or Clifford plus T gates [,].
Instead, it is much preferable to express everything in the much more symmetric language of universal Deutsch and Barenco gates always representable by matrices.
For all possible Kronecker product sequences of length l constructed from a finite set of b gate elements, this will naturally lead to a hierarchy of matrices , each of which contains all possible sequential Kronecker products of k elements in parallel with b denoting the base of an appropriate alphabet defined by the cardinality of some finite set of parametrizations of the same universal gate. We also assume the restriction with even cases being covered by taking an excess ‘inert’ qubit.
We may also adopt a generic parametrization by three angles given as
With the extraction of a common global phase factor, we arrive at the standard representation of a Barenco gate as
In order to complete a global map for any such set, we also recall the equivalence of the following three constructs: (a) the words formed by digits of the polynomial representation of all integers in an interval , (b) the set of paths of a symmetric rooted b-ary tree of depth k and (c) the words from the expansion of a non-commuting multinomial .
These correspondences are all ; hence, one can extract all necessary words by decoding all integers in an exponential interval and use an assignment map to construct all possible products via a scheme as
Then, we can readily reconstruct from a direct concatenation of rows given by .
In order to examine the possible symmetries of the lexicographic ordering, we can also utilize the associated permutations of Section 2.1 and concatenate a series of vectors .
2.3. Sequential Products and Sums of Roots-of-Unity
The use of a lexicographic ordering is important also because of its inherent connection with symbolic Fourier analysis often performed with the aid of Walls systems. Self-similarities observed there are often inherent in the primordial scale invariance underlying the unfolded lexicographic order of a system of strings also known as a Hamming Space [,].
These subjects will not be investigated further here but it is possible to provide a universal formula for the resulting values of the matrix elements in any . Given a triplet of arbitrary parameters , for any gate, all resulting products take the form
The various factors represent the accumulation of terms different than 0’s or 1’s in any product standing for a single matrix element of the final unitary. The superscripts in parentheses next to , are indices, not to confuse with raising to power. The set of all integer accumulator values in a global map follows a characteristic self-similar pattern which will be analyzed in the next section.
In (5), we use a convention where all terms are to be turned into cosines via a shift . We may also take all angle parameters on the unit circle via with three new real parameters in .
Then, from a known trigonometric formula for products of harmonics, it is possible to rewrite (5) as
where , and stands for a binary word from the set of all words in , with the sum running over all such words acting on the same vector of parameters for the third angle. For all practical purposes, we may take the case of rational values for the angles parametrization as assuming irreducible factors for the integers and . In such a case, one can always identify a maximal cyclic group such that the result in (6) would take the form
where we have used
The type of summands in (7) belong to a key concept of number theory including such cases like the Ramanujan and Kloosterman sums as well as the Gauss sums. Especially the latter have direct physical implications revealed in the work of Berry, where they have been associated with the self-imaging effect in the Talbot and Talbot–Lau interferometers as well as the celebrated Quantum Carpets [].
A fundamental identity, which is generic for such sums and can be used for simplifications, is given as
Then, the expression in (7) could be factorized as if arbitrary pairs of integers can be found to satisfy either of the two branches of (8).
While this is a cumbersome approach, there is one further step beyond the original lexicographic order which can reduce the complexity of these symbolic expressions in a unique manner, as explained in the next section.
2.4. Gray Codes and Multipliers
An additional permutation well known from coding theory and communications goes by the name of a Gray code [,]. Originally created for the binary system to minimize transmission errors, it has also been expanded to higher alphabets.
We shall here make use of non-binary or n-ary Gray codes which effectively represent an additional permutation of the original lexicographic ordering which is characterised by the fact that the Hamming distance of all consecutive words is minimal. In simpler terms, each product over a row of a global map differs by a single factor and each control word representing a sequential Kronecker product columnwise also differs by a single gate factor.
More formally, if we denote as the corresponding permutation induced by a Gray encoding in base b, then the original translation from any layer of gates in parallel can be made to correspond to a new global map now given as the concatenation of all rows , where stands for the vectorized sequential product in the same sense as in Section 2.1.
An immediate consequence of the basic property of any Gray code is that all products across any row of can be made to differ by a single factor. This is due to the correspondence between digits in the representation of all integer indices in interval per row and the complex factors of each algebraic product. In the new, Gray-coded sequence, traversing this interval of indices gives for every discrete step a transition between words and products as
where are word representations of two successive complex products standing for single matrix elements in the unfolded form of each unitary per control word. The exact position where a symbol changes is always given by a special map for each Gray code, known as the ruler function r such that [].
Consequently, one can reproduce the whole sequence of elements as the trajectory of a multiplicative dynamical system
where is the first product of any sequential Kronecker product corresponding to the word . Since most large Kronecker products result in sparse matrices, the recursion in (9) requires a replacement of zeros in the original gate definitions with an constant to avoid singular points. Conclusively, any large unitary matrix essentially contains a permuted sequence of partial products of the above prescribed multipliers.
Since Gray codes can be applied also columnwise, we may in fact consider a factorization of any global map as
where is the first element in the ordered set of all Kronecker products while the second term represents the set of multipliers for all initial conditions of any row sequence per control word in the b-ary alphabet.
3. Some Concrete Examples
3.1. Numerical Explorations
In any sequential Kronecker product, there may be a number of terms that are either zero or one, thus not contributing to the final products for each matrix element, as already commented in Section 2.3.
To obtain the exact number of terms, one may utilize a similar scheme as that of Section 2.1, leading to a natural arithmetic fractal structure as follows. Since we are interested in all non-zero factors greater than one, it is possible to use a ‘model’ matrix instead of the original Barenco gate like
with zero and all ones () blocks. The repeated Kronecker product of the above will provide all possible accumulators denoted by in Section 2.3 as logarithms of all final matrix elements greater than one. Results for a 4-fold product are shown in Figure 2.
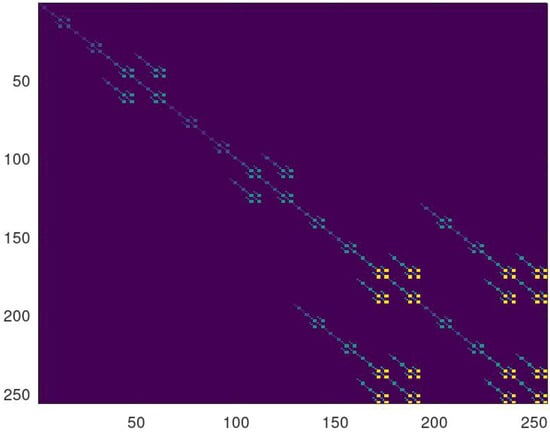
Figure 2.
Number of complex product terms for sequential Kronecker product. Standard color map is used, with blue to red (minimum to maximum) for integers.
Next, we provide a simple example of a global map for the case of the Pauli group , which leads to for all the control words and all 4-fold Kronecker products, leading to a matrix. Unique elements on the final array are restricted on the unit circle, which makes amplitudes a binary array. Magnitudes and phases are separately shown in Figure 3a and Figure 3b, respectively.
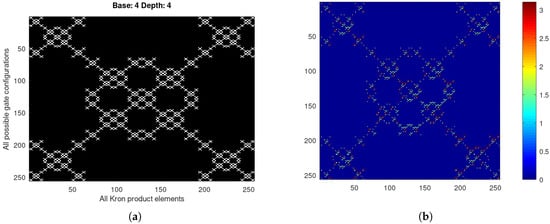
Figure 3.
(a) Magnitudes and (b) phases of the the resulting global map for the Pauli group.
In Figure 4, we also show the same result after applying a double Gray encoding as a permutation of both rows and columns over the same global map. It becomes evident that the Gray code effects a higher disorder.
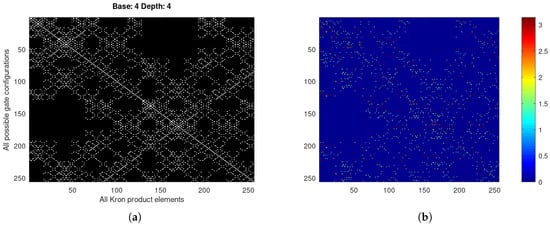
Figure 4.
(a) Magnitudes and (b) phases of the Gray-coded global map for the Pauli group.
To further our understanding of the underlying structure of these sets, we also try the extended gate set including also the Hadamard (H) and phase (S) gates. This now increases the alphabet with , leading to a array. Results are shown in Figure 5.
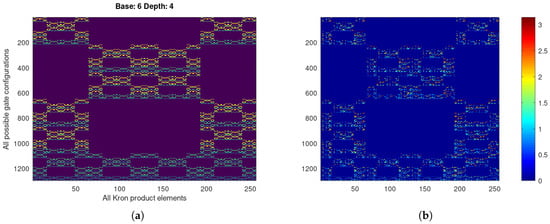
Figure 5.
(a) Magnitudes and (b) phases of the extended 6-gate set.
A complete gate set should, of course, include at least one controlled entangling gate like . The study of such sets is deferred for future work, the simple reason being that any such computation requires the introduction of a maximal fully symmetric tree of order for the row lengths in order to utilise the full symmetry of the lexicographic ordering in the output global map array. This results in huge combinatorial sets which cannot be properly examined by simple visual inspection. Instead, proper completion of this project demands the development of a special toolbox with additional methods for the study of large self-similar sets like wavelet analysis and other appropriate transforms. These issues are still under scrutiny, and some practical applications together with our main conjecture are discussed in more detail in the last paragraphs.
3.2. Applications
To elucidate the meaning of the above, we must clear out some more technical issues regarding the use of such objects as the arrays. In particular, the original computations represented by Equation (1) for any quantum circuit can be represented as a walk over the row index of such an array. Moreover, no need exists for reshaping the elements of any such row into the original unitary matrix. Instead, any of the original sequential matrix–vector products can be turned onto a dual vector–matrix product where the vector is given directly by one of the rows of and the matrix acting from the right can be constructed from the original input vector and the corresponding permutations of Section 2 as follows.
Let stand for any of the rows of the associated global map for a given finite set of gates and let be the associated permutation to its flattened, fully vectorized form. Given any input vector for which one wishes to obtain the associated product for some unitary , where , there is an exact correspondence with a product , where stands for the vector corresponding to , and the new matrix is a tiling of rows made of the original input vector . Each row of is constructed so as to reflect the correct indexing of products of the original. This is simply given as follows.
The first row is given by locating all indices from 1 to in the permutation vector of length . A row of the same length is constructed with the only non-zero elements from those of the original input vector at positions given by the alternative indices of the permutation vector. Then, the second row is constructed by the exact same elements of v, this time arranged according to the permuted indices in the interval , and so on. In this way, the contraction of any by the temporary auxiliary array will obtain the exact same result of any layer in the original Equations (1) and (2), using instead a set of direct actions on certain rows of the global map array.
While the role of the lexicographic indexing of any global map is to reveal a higher internal correlation, the use of Gray codes serves a rather different purpose. In particular, the theoretical result presented in the previous section allows using even a random initial sequence of multipliers in the case of variational circuits where there is no fixed parametrization. In such a case, the use of a dual representation via the auxiliary array transcription of input vectors turns the original circuit into a simpler recursive method based on signal mixing from a core parametric dynamical system. This paves the way for alternative analog implementations which may offer certain advantages in cases of Hamiltonian emulators. It can also be considered as an alternative for improvements over previous proposals [,,].
4. Discussion and Conclusions
The line of research presented in this work differs from existing ones since it targets the totality of possible circuits to the degree that such a presentation reveals higher correlations between the various components of any circuit. As a matter of fact, what the evidence of the previous sections reveal can be stated as the following conjecture:
Conjecture 1.
The set of automorphisms of global maps (results of all quantum computations) is highly correlated.
This poses a question for which no obvious answer appears in the existing literature. Specifically, if the set of all possible arrangements of any finite set of gates is highly correlated, possibly containing a fractal structure, then one should expect, with some probability to be estimated, that the set of all results obtained from the equivalent actions performed in copies of the same object should also appear to inherit these correlations. If this proves to be so, then one should expect the existence of classes of ’magic’ sequences allowing us to guess more difficult results from simpler ones via some recursive evaluation method that may be of lower complexity than each original isolated circuitry.
Moreover, certain scale invariances should affect such a method given that there is a natural hierarchy of exponential intervals for increasing depths and number of layers that allow for an inductive approach to the problem. Further numerical and analytical work is needed to specify the exact nature of possible recursive maps in various cases of base gate parametrization. Such a problem may be NP-hard for an arbitrary sequence of matrices but we currently have no proof of the associated complexity.
Moreover, new questions arise with respect to PQC and their VQC variants when it comes to study arbitrary variations of some original standard gate set. For instance, with reference to Figure 3 and Figure 5, one may ask whether a hierarchy of small variations over these original standard sets could lead to cascade phenomena akin to the previously known as Self-Organized Criticality ( per Back []) and its associated abelian and non-abelian Sandpile groups [,].
Last but not least, there is every reason to try extending the present technique to higher members of the general as, for instance, in the case of qutrits and qudits [,,] using Gell–Mann matrices and other higher order representations. Such extensions will hopefully follow in subsequent work.
Author Contributions
Conceptualization, T.R.; methodology, T.R.; software, T.R.; validation, T.R. and V.R.; formal analysis, T.R.; investigation, T.R.; resources, T.R. and V.R.; data curation, T.R.; writing—original draft preparation, T.R. and V.R.; writing—review and editing, T.R. and V.R.; visualization, T.R.; supervision, T.R. and V.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The in-house code and generated raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DAG | Directed Acyclic Graph |
| LUT | Look-Up Table |
| PQC | Parametric Quantum Circuits |
| QML | Quantum Machine Learning |
| RVQC | Relativistic Variational Quantum Computing |
| VQC | Variational Quantum Computing |
References
- Gruska, J. Quantum Computing; McGraw-Hill: London, UK, 1999. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef]
- Barthe, A.; Grossi, M.; Vallecorsa, S.; Tura, J.; Dunjko, V. Parameterized quantum circuits as universal generative models for continuous multivariate distributions. Quantum Inf. 2025, 11, 121. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nature Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Sabín, C.; Kok, P.; Johannson, G.; Delsing, P.; Fuentes, I. Towards universal quantum computation through relativistic motion. Sci. Rep. 2016, 6, 18349. [Google Scholar] [CrossRef] [PubMed]
- LeMaitre, P.A.; Perche, T.R.; Krumm, M.; Briegel, H.J. Universal Quantum Computer from Relativistic Motion. Phys. Rev. Lett. 2025, 134, 190601. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Marco, M.; Lorenzo, M.; Lorenzo, R.; Enrico, P. Quantum Compiling. arXiv 2021, arXiv:2112.00187. [Google Scholar]
- Daskin, A. Quantum compiler design method by using linear combinations of permutations. arXiv 2024, arXiv:2112.00187. [Google Scholar] [CrossRef]
- Agrawal, U.; Zabalo, A.; Chen, K.; Wilson, J.H.; Potter, A.C.; Pixley, J.H.; Gopalakrishnan, S.; Vasseur, R. Entanglement and Charge-Sharpening Transitions in U(1) Symmetric Monitored Quantum Circuits. Phys. Rev. A 2022, 12, 041002. [Google Scholar] [CrossRef]
- Zhuang, J.Z.; Wu, Y.K.; Duan, L.M. Dynamical phase transitions of information flow in random quantum circuits. Phys. Rev. Res. 2023, 5, L042043. [Google Scholar] [CrossRef]
- Niroula, P.; White, C.D.; Wang, Q.; Johri, S.; Zhu, D.; Monroe, C.; Noel, C.; Gullans, M.J. Phase transition in magic with random quantum circuits. Nat. Phys. 2024, 20, 1786–1792. [Google Scholar] [CrossRef]
- Clark, J.; Humble, T.; Thapliyal, H. TDAG: Tree-based Directed Acyclic Graph Partitioning for Quantum Circuits. In Proceedings of the Great Lakes Symposium on VLSI 2023 Conference, Knoxville, TN, USA, 5–7 June 2023; pp. 587–592. [Google Scholar]
- Beaudoin, C.; Phalak, K.; Ghosh, S. AltGraph: Redesigning Quantum Circuits Using Generative Graph Models for Efficient Optimization. In Proceedings of the Great Lakes Symposium on VLSI 2024, Clearwater, FL, USA, 12–14 June 2024; pp. 44–49. [Google Scholar]
- Clark, J.; Humble, T.; Thapliyal, H. A comparison of quantum compilers using a DAG-based or phase polynomial-based intermediate representation. J. Syst. Soft. 2025, 221, 112224. [Google Scholar]
- Arrighi, P.; Durbec, A.; Wilson, M. Quantum networks theory. Quantum 2024, 8, 1508. [Google Scholar] [CrossRef]
- DeCross, M.; Haghshenas, R.; Liu, M.; Rinaldi, E.; Gray, J.; Alexeev, Y.; Baldwin, C.H.; Bartolotta, J.P.; Bohn, M. Computational Power of Random Quantum Circuits in Arbitrary Geometries. Phys. Rev. X 2025, 15, 021052. [Google Scholar] [CrossRef]
- Park, J.; Pham, H.T. A proof of the Kahn–Kalai conjecture. J. Am. Math. Soc. 2023, 37, 235–243. [Google Scholar] [CrossRef]
- Magnus, J.R.; Neudecker, H. Matrix differential calculus with applications to simple, Hadamard, and Kronecker products. J. Math. Psych. 1985, 29, 474–492. [Google Scholar] [CrossRef]
- Tropf, H.; Herzog, H. Multidimensional Range Search in Dynamically Balanced Trees. Angew. Inform. 1981, 2, 71–77. [Google Scholar]
- Bern, M.; Eppstein, D.; Teng, S.H. Parallel construction of quadtrees and quality triangulations. Int. J. Comput. Geom. Appl. 1999, 2, 517–532. [Google Scholar] [CrossRef]
- Hendricus van Lindt, J. Introduction to Coding Theory, 1st ed.; Springer: Berlin, NY, USA, 1999. [Google Scholar]
- Astashkin, S.V. The Rademacher System in Function Spaces, 1st ed.; Birkhäuser: Cham, Switzerland, 2020. [Google Scholar]
- Berry, M.; Marzoli, I.; Schleich, W. Quantum carpets, carpets of light. Phys. World 2001, 14, 39. [Google Scholar] [CrossRef]
- Gilbert, E.N. Gray Codes and Paths on the n-Cube. Bell System Tech. J. 1958, 37, 815–826. [Google Scholar] [CrossRef]
- Herter, F.; Rote, G. Loopless Gray code enumeration and the Tower of Bucharest. Theor. Comput. Sci. 2018, 748, 40–54. [Google Scholar] [CrossRef]
- Mourya, S.; Cour, B.R.L.; Sahoo, B.D. Emulation of Quantum Algorithms Using CMOS Analog Circuits. IEEE Trans. Quant. Eng. 2023, 4, 1–16. [Google Scholar] [CrossRef]
- Pouse, W.; Peeters, L.; Hsueh, C.L.; Gennser, U.; Cavanna, A.; Kastner, M.A.; Mitchell, A.K.; Goldhaber-Gordon, D. Quantum simulation of an exotic quantum critical point in a two-site charge Kondo circuit. Nature Phys. 2023, 19, 492–499. [Google Scholar] [CrossRef]
- Meher, A.; Liu, Y.; Zhou, H. Error Mitigation of Hamiltonian Simulations from an Analog-Based Compiler (SimuQ). In Proceedings of the IEEE International Conference on Quantum Computing and Engineering (QCE), Montreal, QC, Canada, 15–20 September 2024; Volume 3. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organised Criticality; Copernicus Press: New York, NY, USA, 1996. [Google Scholar]
- Paoletti, G. Deterministic Abelian Sandpile Models and Patterns. Ph.D. Thesis, Universita de Pisa, Pisa, Italy, 2014. [Google Scholar]
- Perkinson, D.; Corry, S. Divisors and Sandpiles: An Introduction to Chip-Firing; American Mathematical Society: Providence, RI, USA, 2018. [Google Scholar]
- Li, B.; Yu, Z.H.; Fei, S.M. Geometry of Quantum Computation with Qutrits. Sci. Rep. 2013, 3, 2594. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.X.; Chen, X.B.; Yang, Y.X.; Wang, X. Geometry of Quantum Computation with Qudits. Sci. Rep. 2014, 4, 4044. [Google Scholar] [CrossRef] [PubMed]
- Wiersema, R.; Lewis, D.; Wierichs, D.; Carrasquilla, J.; Killoran, N. Here comes the SU(N): Multivariate quantum gates and gradients. Quantum 2024, 8, 1275. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).