Reciprocal Quantum Channels ^†

Abstract

We report the presence of an asymmetry that arises when considering the performances of quantum communication channels whose outputs are connected via a rigid, distance-preserving, yet not completely-positive, transformation. From a classical perspective these transmission lines should exhibit the same communication efficiency which is lost in the quantum setting.

1. Introduction

Quantum information theory often relies on harnessing effects which are counterintuitive with respect to the classical intuition to produce technological applications. One such effect arises when trying to communicate a chosen direction to a distant party. Indeed it turns out that, if we encode the directional information on the state of two quantum spin systems, such direction can be more efficiently estimated when using antiparallel spins rather than parallel ones [1]. The presence of similar asymmetries was recently reported in Ref. [2] in the broader context of classical communication on noisy quantum channels [3] by introducing the notion of reciprocal quantum maps. A reciprocal pair of quantum channels are two communication lines ${\Phi }_1$ and ${\Phi }_2$ acting on the same system which admit a rigid, distance-preserving, yet not completely-positive transformation $\Lambda$ that allows one to reproduce the outcome of the first from the corresponding outcome of the second, i.e.,

$$\begin{array}{c}\hfill {\Phi }_1=\Lambda \circ {\Phi }_2,\end{array}$$

(1)

the symbol “∘” representing super-operator composition. From a classical perspective these transmission lines should exhibit the same communication efficiency as the relative distance between different output states are exactly the same for the two mappings. This is no longer the case in the quantum setting where explicit asymmetric behaviours can be found. In the following we report a special instance of this effect that one can observe when analyzing the case of depolarizing channels [4].

2. Results

A depolarizing quantum channel ${\mathcal{D}}_{\lambda }^{\left(d\right)}$ is a completely-positive transformation which, acting on a quantum system S of dimension d, transforms its density matrices $\rho$ into the output states

$${\mathcal{D}}_{\lambda }^{\left(d\right)}\left[\rho \right]=\lambda \rho +\left(1-\lambda \right)\mathrm{T}\mathrm{r}\left[\rho \right]I/d,$$

(2)

with $\lambda$ a real parameter that characterizes the level of noise introduced by the map, and with I being the identity operator on the Hilbert space ${\mathcal{H}}_{\mathrm{S}}$ of S [4]. Complete-positivity forces $\lambda$ to only take values in the interval $[{\lambda }_m\left(d\right),1]$, the lower threshold being the negative quantity

$$\begin{array}{c}\hfill {\lambda }_m\left(d\right):=-1/(d^2-1).\end{array}$$

(3)

This set of maps have been extensively studied. In particular their associated classical and entanglement assisted capacities [3] have been explicitly computed, resulting in the following analytical expressions [4]:

$$\begin{array}{ccc}\hfill C\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)& =& {log}_{2}d-S_{min}\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill C_E\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)& =& C\left({\mathcal{D}}_{\lambda }^{\left(d^2\right)}\right),\hfill \end{array}$$

(5)

with $S_{min}\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right):={min}_{\rho }\left\{-Tr\left[{\mathcal{D}}_{\lambda }^{\left(d\right)}\left(\rho \right){log}_2\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\left(\rho \right)\right)\right]\right\}$ being the minimum von Neumann entropy attainable at the output of the channel, i.e., the quantity

$$S_{min}\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)=-\frac{1+(d-1)\lambda }{d}{log}_2\left(\frac{1+(d-1)\lambda }{d}\right)-(d-1)\frac{1-\lambda }{d}{log}_2\left(\frac{1-\lambda }{d}\right).$$

(6)

As also evident from Figure 1, the functions (4) and (5) exhibit a non-symmetric behaviour with respect to sign inversion of noise parameter in the domain where this is allowed, i.e., for $\lambda \in [{\lambda }_{min}\left(d\right),-{\lambda }_{min}\left(d\right)]$. In particular given $\lambda \in [0,-{\lambda }_{min}\left(d\right)]$ we have

$$\begin{array}{ccc}\hfill C\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)& <& C\left({\mathcal{D}}_{-\lambda }^{\left(d\right)}\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill C_E\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)& <& C_E\left({\mathcal{D}}_{-\lambda }^{\left(d\right)}\right),\hfill \end{array}$$

(8)

with the only exception of $d=2$ for which Equation (8) still holds but (7) is replaced with an identity (the function $C\left({\mathcal{D}}_{\lambda }^{(d=2)}\right)$ being even in the domain $[{\lambda }_{min}(d=2),-{\lambda }_{min}(d=2)]$).

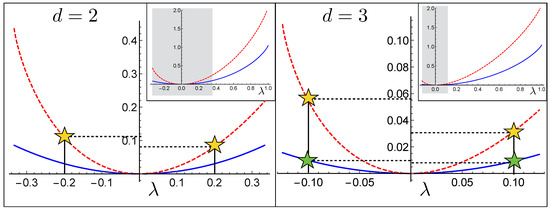
Figure 1. Plots of the classical capacity $C\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)$ of Equation (4) and entanglement assisted classical capacity $C_E\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)$ of Equation (5) as a function of the noise parameter $\lambda$ belonging to the interval of interest $[{\lambda }_{min}\left(d\right),-{\lambda }_{min}\left(d\right)]$, for $d=2$ (left panel) and $d=3$ (right panel). Notice the asymmetric behaviour of $C_E\left({\mathcal{D}}_{\lambda }^{\left(d\right)}\right)$ and $C\left({\mathcal{D}}_{\lambda }^{(d=3)}\right)$ (the classical capacity $C\left({\mathcal{D}}_{\lambda }^{(d=2)}\right)$ instead is symmetric). The insets show the capacity for the full range of $\lambda$. All the curves have being rescaled by ${log}_{2}d$.

It turns out that this is exactly the kind of example we are looking for. Indeed given $\lambda \in [0,-{\lambda }_{min}\left(d\right)]$, the channels ${\mathcal{D}}_{\lambda }^{\left(d\right)}$ and ${\mathcal{D}}_{-\lambda }^{\left(d\right)}$ represent an instance of reciprocal pairs, connected as in Equation (1) via the linear transformation

$$\begin{array}{c}\hfill \Lambda [\cdots ]:=-\mathrm{Id}[\cdots ]+2\mathrm{T}\mathrm{r}[\cdots ]I/d,\end{array}$$

(9)

with $\mathrm{Id}$ representing the identity channel, i.e., ${\mathcal{D}}_{-\lambda }^{\left(d\right)}=\Lambda \circ {\mathcal{D}}_{\lambda }^{\left(d\right)}$. Equation (9) is not completely positive, but as required by our definition, it acts as a rigid transformation which preserve the relative distance between states, i.e.,

$$\begin{array}{c}\hfill \parallel \Lambda \left[{\rho }_1\right]-\Lambda \left[{\rho }_2\right]\parallel =\parallel {\rho }_1-{\rho }_2\parallel ,\end{array}$$

(10)

for all ${\rho }_1$ and ${\rho }_2$, and for all suitable norm $\parallel \cdots \parallel$ (e.g., the trace-class norm).