A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal
Abstract
1. Introduction
2. Modeling
2.1. Fundamentals of Fractional Calculus
2.2. Weibull Distribution Damage
2.3. Establishment of FO Damage Creep Model
2.3.1. Basic Mechanical Components and Composition
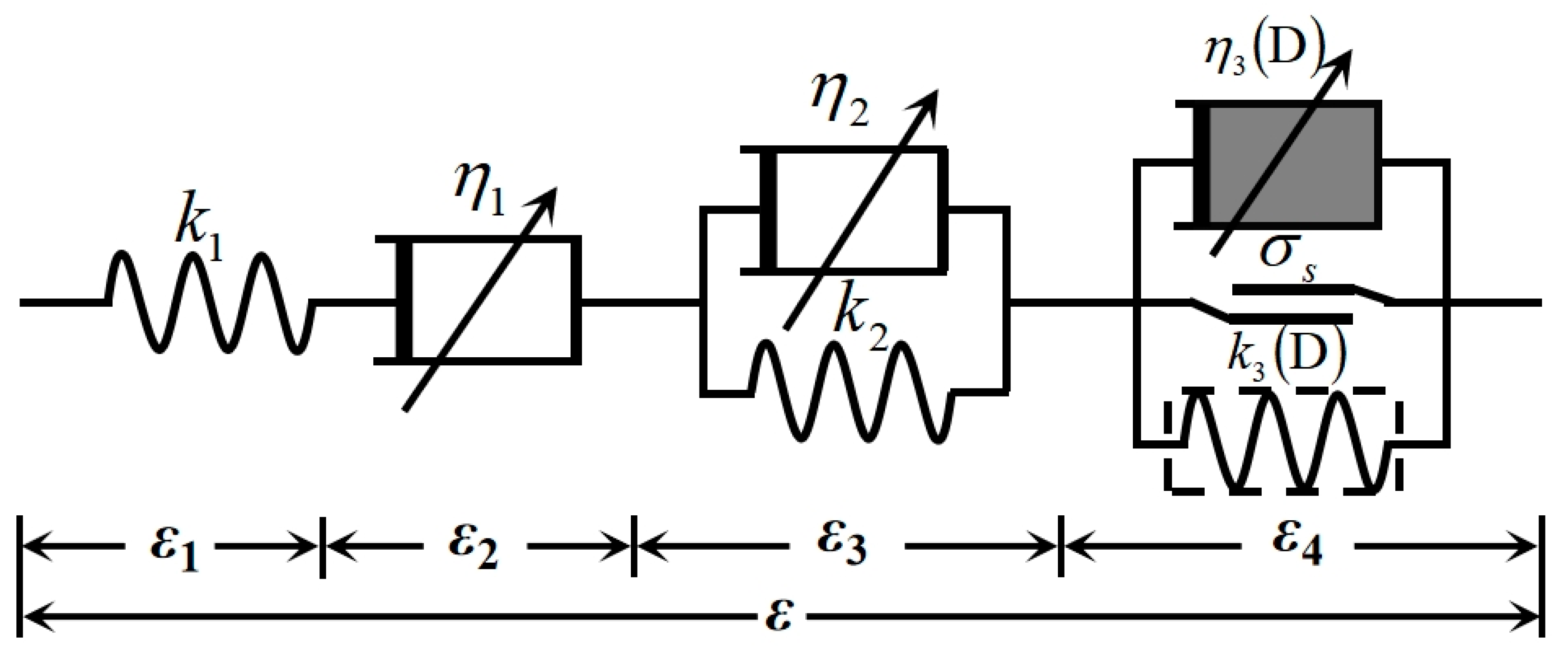
2.3.2. FO Damaged Creep Model
2.3.3. Triaxial Creep Constitutive Model
3. Results and Discussions
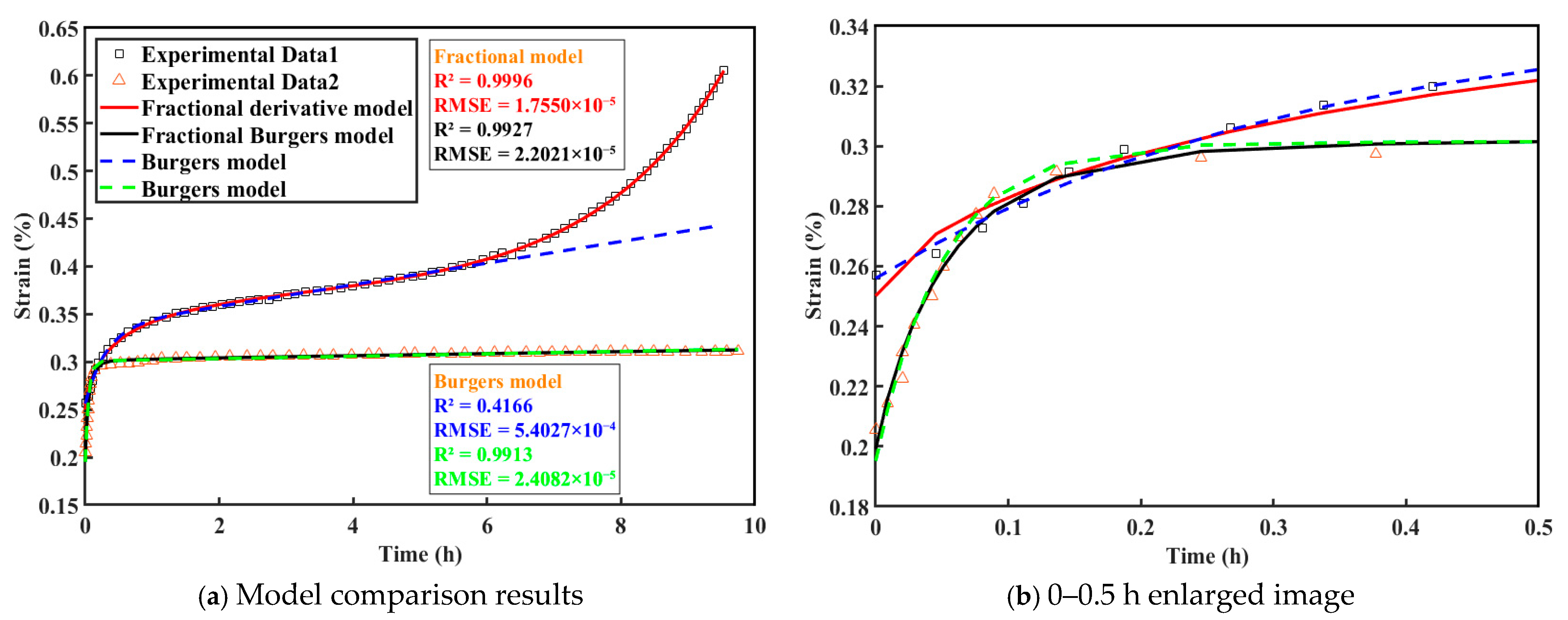
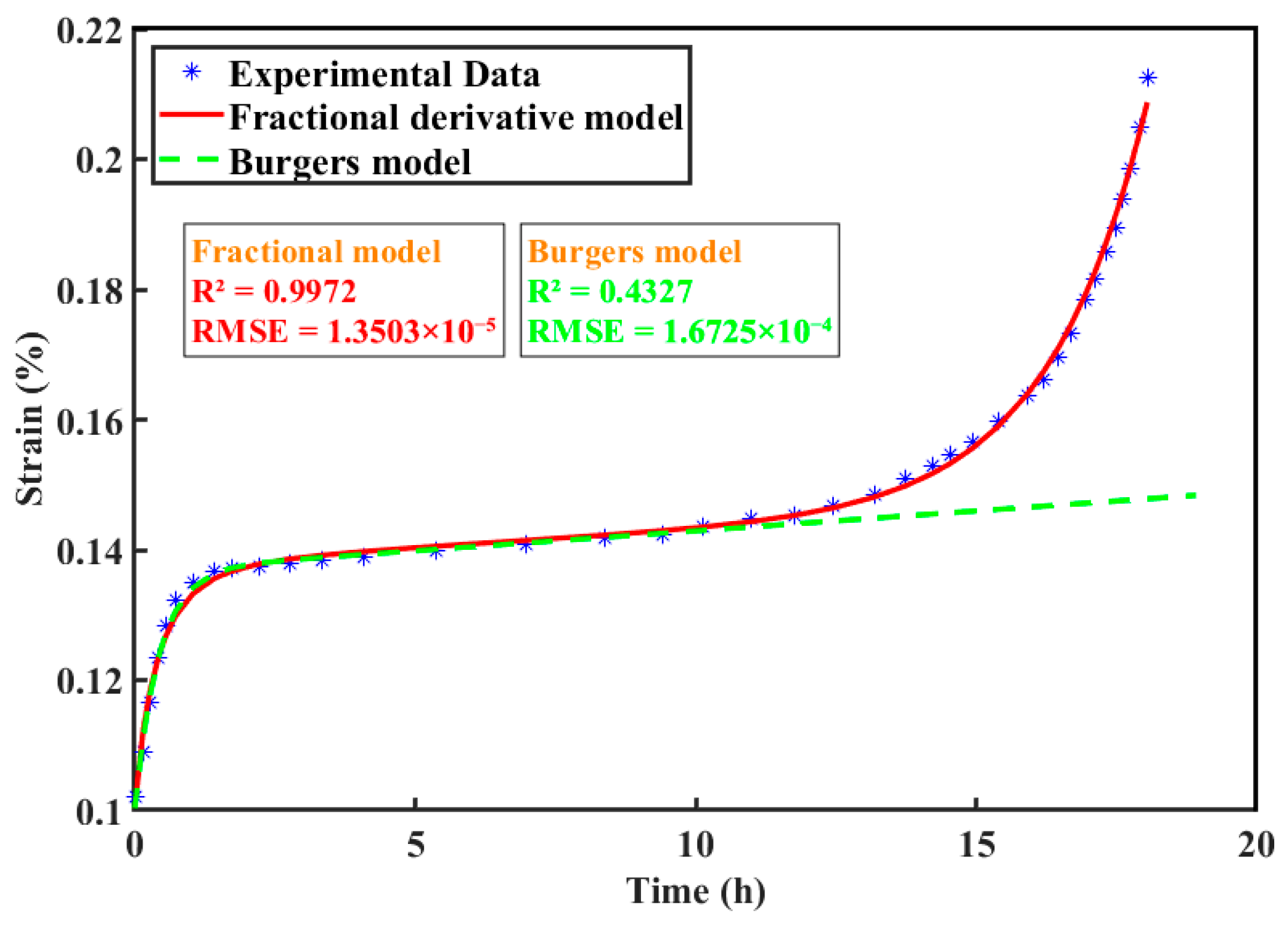
3.1. Parameter Identification
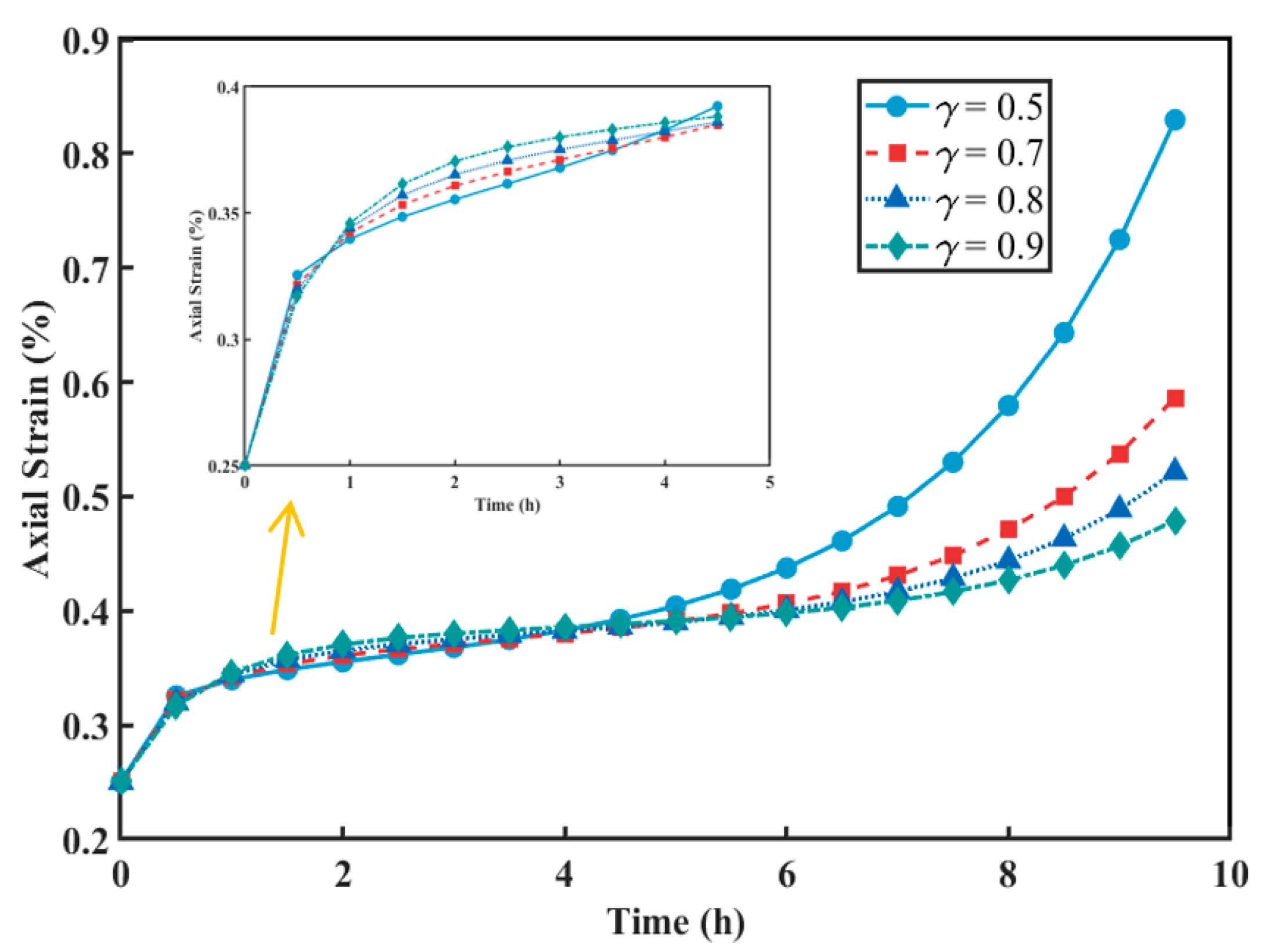
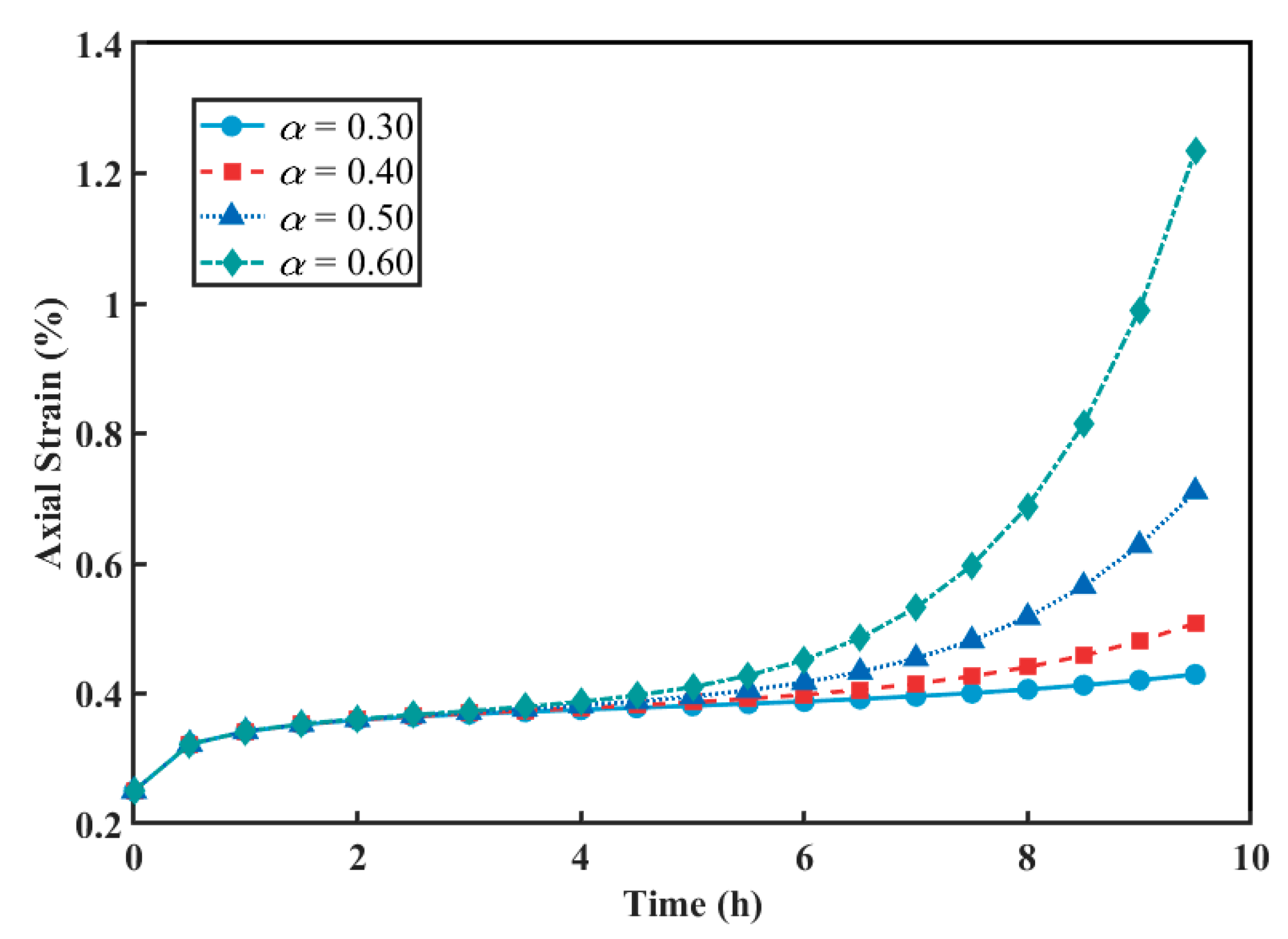
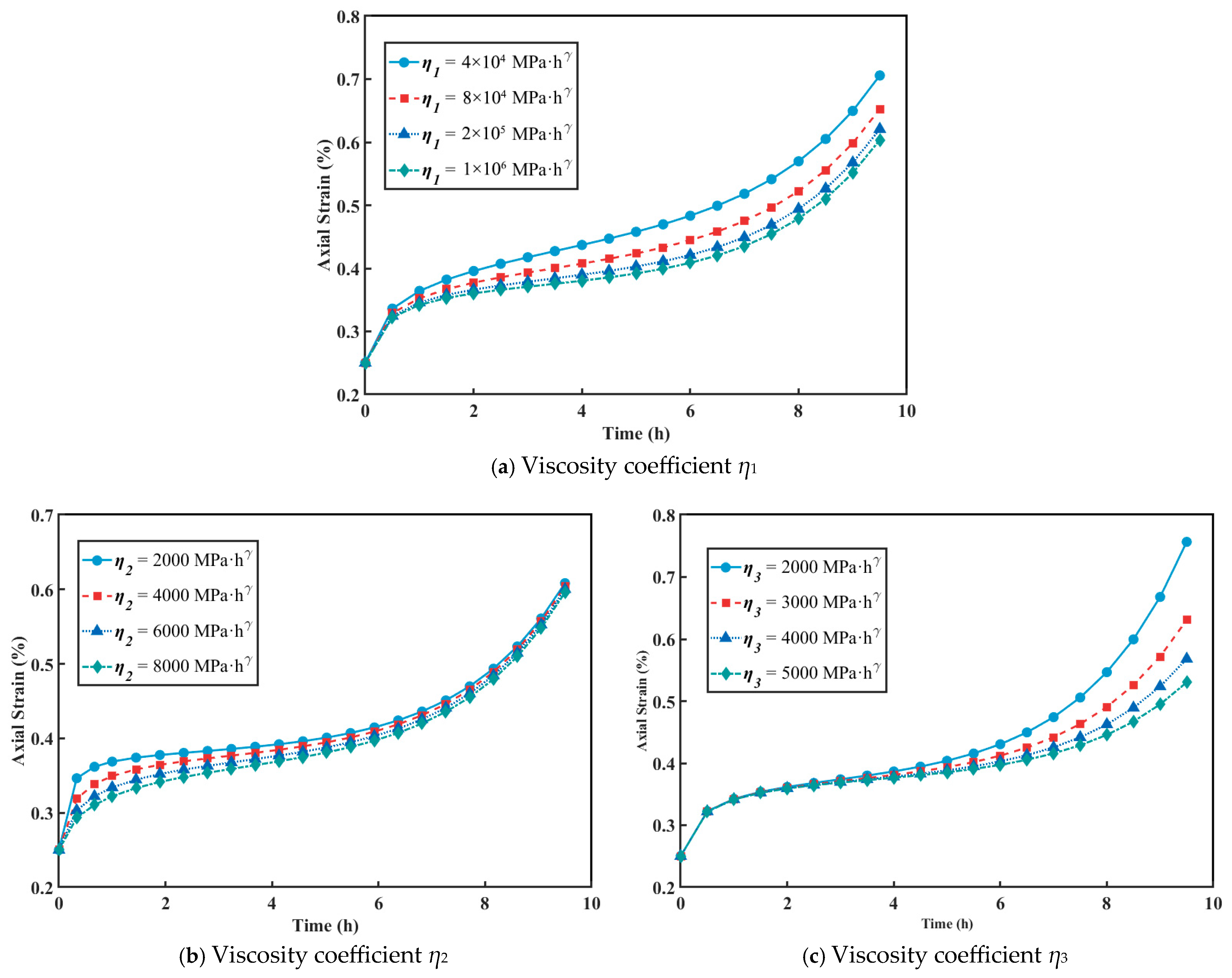
3.2. Parameter Sensitivity Analysis
4. Conclusions
- (1)
- A viscoelastic-plastic component considering damage has been constructed, which can simultaneously characterize the decline in viscosity coefficient and the degradation of the elastic modulus. This component was connected in series with elastic, viscous, and viscoelastic components. Then, Abel dashpots were introduced to replace Newton dashpots in the model, thus establishing a fractional damage creep model that can describe the ACS.
- (2)
- Nonlinear least squares fitting was performed on experimental data to determine model parameters and compare this model with the traditional Burgers model. The findings demonstrate that the established creep model can perfectly describe the full-stage mechanical behavior of deep coal during the creep process, which also shows that the proposed viscoelastic-plastic component can effectively capture the nonlinear growth phenomenon when stress exceeds long-term strength. In addition, rock freeze-thaw cycle triaxial compression experimental data were used for model validation, and the results showed a strong agreement between the model predictions and the experimental data, further confirming the reliability of the model.
- (3)
- Considering the availability of the model for other geological conditions, a detailed sensitivity analysis was performed to explore how each parameter affects the creep behavior, and the role of parameters in different creep stages was clarified, further supporting the credibility and broad applicability of the model. This study provides theoretical guidance for practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, J.; Yang, X.-G.; Li, H.-T.; Zhou, J.-W.; Fan, G.; Lu, G.-D. Effects of in-Situ Stresses on Dynamic Rock Responses under Blast Loading. Mech. Mater. 2020, 145, 103374. [Google Scholar] [CrossRef]
- Cao, N.; Jing, P.; Huo, Z.; Liang, Y.; Zhang, L. Simulation Study of Coal Seam Gas Extraction Characteristics Based on Coal Permeability Evolution Model under Thermal Effect. ACS Omega 2024, 9, 22871–22891. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Zhang, J.; Wang, J.; Li, F.; Zhou, Y. Research on Nonlinear Damage Hardening Creep Model of Soft Surrounding Rock under the Stress of Deep Coal Resources Mining. Energy Rep. 2022, 8, 1493–1507. [Google Scholar] [CrossRef]
- Li, M.; Zhu, F.; Mao, Y.; Fan, F.; Wu, B.; Deng, J. Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action. Fractal Fract. 2025, 9, 381. [Google Scholar] [CrossRef]
- Wu, F.; Gu, H.; Zhang, J.; Liu, C.; Chang, X.; Wei, M.; Jiang, Y.; Wang, P.; Yang, P.; Liu, H.; et al. Creep Instability Mechanism and Control Technology of Soft Coal Roadways Based on Fracture Evolution Law. Appl. Sci. 2023, 13, 9344. [Google Scholar] [CrossRef]
- Yang, C.; Daemen, J.J.K.; Yin, J.-H. Experimental Investigation of Creep Behavior of Salt Rock. Int. J. Rock Mech. Min. Sci. 1999, 36, 233–242. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L.; Duan, Z.Q.; Ding, J.Y. A Fractional Derivative Approach to Full Creep Regions in Salt Rock. Mech. Time-Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]
- Qi, Y.J.; Jiang, Q.H.; Wang, Z.J.; Zhou, C.B. A three-dimensional creep constitutive equation based on modified Nishihara model and its parameter identification. Chin. J. Rock Mech. Eng. 2012, 31, 347–355. (In Chinese) [Google Scholar]
- Yang, W.; Zhang, Q.; Li, S.; Wang, S. Time-Dependent Behavior of Diabase and a Nonlinear Creep Model. Rock Mech. Rock Eng. 2014, 47, 1211–1224. [Google Scholar] [CrossRef]
- Fahimifar, A.; Karami, M.; Fahimifar, A. Modifications to an Elasto-Visco-Plastic Constitutive Model for Prediction of Creep Deformation of Rock Samples. Soils Found. 2015, 55, 1364–1371. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A Creep Constitutive Model for Salt Rock Based on Fractional Derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.; Cai, Y.; Chen, L.; Wu, Z.; Liu, J. Effects of Damage and Fractional Derivative Operator on Creep Model of Fractured Rock. Rock Mech. Rock Eng. 2024, 57, 9323–9341. [Google Scholar] [CrossRef]
- Kruis, J.; Koudelka, T. Effect of Mechanical Damage on Moisture Transport in Concrete. Appl. Math. Comput. 2015, 267, 139–147. [Google Scholar] [CrossRef]
- Hou, R.; Zhang, K.; Tao, J.; Xue, X.; Chen, Y. A Nonlinear Creep Damage Coupled Model for Rock Considering the Effect of Initial Damage. Rock Mech. Rock Eng. 2019, 52, 1275–1285. [Google Scholar] [CrossRef]
- He, J.; Niu, F.; Jiang, H.; Jiao, C. Fractional Viscoelastic-Plastic Constitutive Model for Frozen Soil Based on Microcosmic Damage Mechanism. Mech. Mater. 2023, 177, 104545. [Google Scholar] [CrossRef]
- Liao, M.; Lai, Y.; Liu, E.; Wan, X. A Fractional Order Creep Constitutive Model of Warm Frozen Silt. Acta Geotech. 2017, 12, 377–389. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New Fractional Variable-Order Creep Model with Short Memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Liu, C.; Dong, T.; Qi, Y.; Guo, X. Variable-Order Time-Fractional Kelvin Peridynamics for Rock Steady Creep. Fractal Fract. 2025, 9, 197. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, L.; Bao, T.; Liu, Y. Fractional Order Creep Model for Dam Concrete Considering Degree of Hydration. Mech. Time-Depend. Mater. 2019, 23, 361–372. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, J.; Jean Damascene, N.; Dong, C.; Wang, Z. A Fractional Order Viscoelastic-Plastic Creep Model for Coal Sample Considering Initial Damage Accumulation. Alex. Eng. J. 2021, 60, 3921–3930. [Google Scholar] [CrossRef]
- Xiang, G.; Yin, D.; Cao, C.; Gao, Y. Creep Modelling of Soft Soil Based on the Fractional Flow Rule: Simulation and Parameter Study. Appl. Math. Comput. 2021, 403, 126190. [Google Scholar] [CrossRef]
- Kamdem, T.C.; Richard, K.G.; Béda, T. New Description of the Mechanical Creep Response of Rocks by Fractional Derivative Theory. Appl. Math. Model. 2023, 116, 624–635. [Google Scholar] [CrossRef]
- Wang, G.; He, W.; Lu, D.; Song, Z.; Du, X. A Peridynamic Method for Creep and Stress Relaxation Incorporating a Novel Fractional Viscoelastic Model. Eng. Anal. Bound. Elem. 2025, 171, 106104. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov Method for Fractional Differential Equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Nonnenmacher, T.F.; Metzler, R. On The Riemann-Liouville Fractional Calculus And Some Recent Applications. Fractals 1995, 03, 557–566. [Google Scholar] [CrossRef]
- Caputo, M. Linear Models of Dissipation Whose Q Is Almost Frequency Independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- AlBaidani, M.M. Analytical Insight into Some Fractional Nonlinear Dynamical Systems Involving the Caputo Fractional Derivative Operator. Fractal Fract. 2025, 9, 320. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. Remarks on Fractional Derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Almatarneh, M.; Zorlu, S.; Mahmudov, N.I. Existence of Solutions to Fractional Differential Equations with Mixed Caputo–Riemann Derivative. Fractal Fract. 2025, 9, 374. [Google Scholar] [CrossRef]
- Yang, X.; Wu, X.; Song, Q. Caputo−Wirtinger Integral Inequality and Its Application to Stability Analysis of Fractional-Order Systems with Mixed Time-Varying Delays. Appl. Math. Comput. 2024, 460, 128303. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Han, C.; Shao, Y. A Caputo Variable-Order Fractional Damage Creep Model for Sandstone Considering Effect of Relaxation Time. Acta Geotech. 2022, 17, 153–167. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Pu, S.; Zhu, Z.; Song, L.; Song, W.; Peng, Y. Fractional-Order Visco-Elastoplastic Constitutive Model for Rock under Cyclic Loading. Arab. J. Geosci. 2020, 13, 326. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Vatsala, A.S. Basic Theory of Fractional Differential Equations. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2677–2682. [Google Scholar] [CrossRef]
- Babets, D. Rock Mass Strength Estimation Using Structural Factor Based on Statistical Strength Theory. Solid State Phenom. 2018, 277, 111–122. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Yang, Z.; Li, H.; Zuo, H.; Wang, X.; Li, H. Stress-Electromagnetic Radiation (EMR) Numerical Model and EMR Evolution Law of Composite Coal-Rock under Load. ACS Omega 2022, 7, 40399–40418. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.Q. Damage mechanics analysis of rock strength. Chin. J. Rock Mech. Eng. 1999, 18, 23–27. (In Chinese) [Google Scholar]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Xu, W.Y.; Wei, L.D. Statistical damage constitutive model of rock. Chin. J. Rock Mech. Eng. 2002, 21, 787–791. (In Chinese) [Google Scholar]
- Xiang, S. Laplace Transforms for Approximation of Highly Oscillatory Volterra Integral Equations of the First Kind. Appl. Math. Comput. 2014, 232, 944–954. [Google Scholar] [CrossRef]
- Sobolev, V.; Gubenko, S.; Khomenko, O.; Kononenko, M.; Dychkovskyi, R.; Smolinski, A. Physical and Chemical Conditions for the Diamond Formation. Diam. Relat. Mater. 2025, 151, 111792. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Wang, X.; Wang, L.; Su, T.; Wei, Q.; Deng, T. A Triaxial Creep Model for Deep Coal Considering Temperature Effect Based on Fractional Derivative. Acta Geotech. 2022, 17, 1739–1751. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Li, G.; Wang, L.; Zhu, C.; Du, Y.; Zhou, Z. Three-Dimensional Nonlinear Model of Rock Creep under Freeze–Thaw Cycles. PLoS ONE 2023, 18, e0287605. [Google Scholar] [CrossRef] [PubMed]
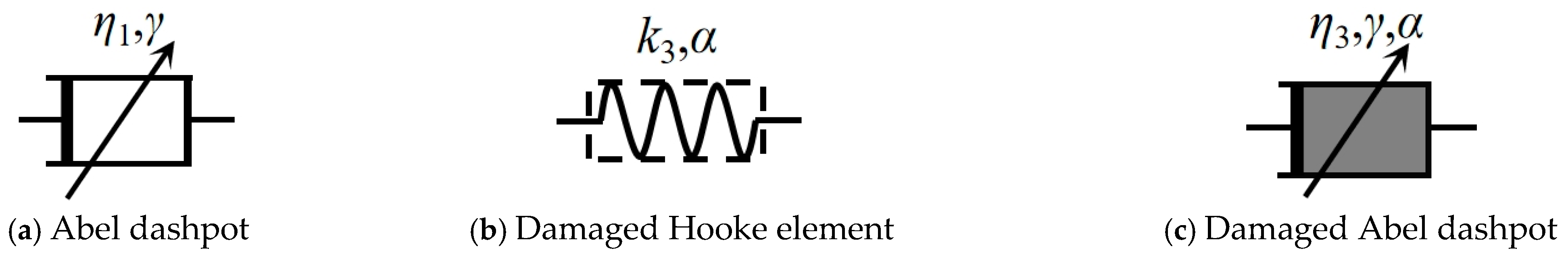



| Specimen ID | Diameter (mm) | Height (mm) | Mass (g) | Volume (cm3) | Density (g/cm3) | Uniaxial Compressive Strength (MPa) |
|---|---|---|---|---|---|---|
| UCT-1 | 49.64 | 100.48 | 258.49 | 194.34 | 1.33 | 15.60 |
| UCT-3 | 49.75 | 100.30 | 262.52 | 194.87 | 1.35 | 16.38 |
| Specimen ID | G1 (MPa) | G2 (MPa) | G3 (MPa) | η1 (MPa·hγ) | η2 (MPa·hγ) | η3 (MPa·hγ) | α | γ |
|---|---|---|---|---|---|---|---|---|
| UCT-1 | 4.19 × 103 | 8.09 × 103 | - | 6.89 × 105 | 551.91 | - | - | 0.9386 |
| UCT-3 | 3.33 × 103 | 6.14 × 103 | 2.93 × 106 | 1.30 × 106 | 4.91 × 103 | 3.38 × 103 | 0.4583 | 0.6820 |
| UCT-4 | 1.16 × 104 | 3.06 × 104 | 1.47 × 107 | 2.10 × 106 | 1.50 × 104 | 8.96 × 106 | 0.5645 | 0.9014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Song, H.; Zhou, H.; Xie, S.; Zhang, L.; Zhou, W. A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal. Fractal Fract. 2025, 9, 473. https://doi.org/10.3390/fractalfract9070473
Yang S, Song H, Zhou H, Xie S, Zhang L, Zhou W. A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal. Fractal and Fractional. 2025; 9(7):473. https://doi.org/10.3390/fractalfract9070473
Chicago/Turabian StyleYang, Shuai, Hongchen Song, Hongwei Zhou, Senlin Xie, Lei Zhang, and Wentao Zhou. 2025. "A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal" Fractal and Fractional 9, no. 7: 473. https://doi.org/10.3390/fractalfract9070473
APA StyleYang, S., Song, H., Zhou, H., Xie, S., Zhang, L., & Zhou, W. (2025). A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal. Fractal and Fractional, 9(7), 473. https://doi.org/10.3390/fractalfract9070473







