Some Fixed Point Results for Novel Contractions with Applications in Fractional Differential Equations for Market Equilibrium and Economic Growth

Abstract

In this study, we introduce two new classes of contractions, namely enriched $(\mathfrak{I},\rho ,\chi )$-contractions and generalized enriched $(\mathfrak{I},\rho ,\chi )$-contractions, within the context of normed spaces. These classes generalize several well-known contraction types, including $\chi$-contractions, Banach contractions, enriched contractions, Kannan contractions, Bianchini contractions, Zamfirescu contractions, non-expansive mappings, and $(\rho ,\chi )$-enriched contractions. We establish related fixed point results for the novel contractions in normed spaces endowed with the binary relations preserving key symmetric properties, ensuring consistency and applicability. The Krasnoselskij iteration method is refined to incorporate symmetric constraints, facilitating fixed point identification within these spaces. By appropriately selecting constants in the definition of enriched $(\mathfrak{I},\rho ,\chi )$-contractions, employing a suitable binary relation, or control function $\chi \in \Theta$, our framework generalizes and extends classical fixed point theorems. Illustrative examples highlight the significance of our findings in reinforcing fixed point conditions and demonstrating their broader applicability. Additionally, this paper explores how these ideas guarantee the stability of the production–consumption markets equilibrium and the economic growth model.

1. Introduction

The Banach contraction theorem, introduced in [1], is a fundamental result in metric fixed point theory with widespread implications across various mathematical and applied disciplines. It serves as a powerful tool in solving both linear and nonlinear ordinary and integral equations and has meaningful uses in fields such as image processing, fractal geometry, engineering, physics, and biology. The theorem asserts that if a self-mapping T on a complete metric space $(X,d)$ fulfills a contractive condition of the form $d(T\varsigma ,T\eta )\le \gamma d(\varsigma ,\eta )$ for all $\varsigma ,\eta \in X$, where $0\le \gamma <1)$, then T has a unique fixed point in X. Over time, extensive research has led to various generalizations and refinements of this theorem, including extensions to broader domains [2] and the introduction of more generalized contractive conditions [3,4], further expanding its applicability in both theoretical and practical contexts. Fixed point theory is very important in the study of economics, particularly in the analysis of models of economic growth and production–consumption equilibrium. It provides a mathematical framework within the production–consumption equilibrium framework to guarantee the existence of the equilibrium solutions or locations in markets where supply and demand are equal. Our findings allow economists to study how market forces adjust on their own to reach equilibrium without outside intervention. This technique, which is essential to the study of general equilibrium theory, examines producer–consumer interactions in multiple markets at the same time. Recent studies demonstrate that the Caputo fractional derivative provides a flexible framework for modeling dynamic systems with memory and hereditary properties, capturing long-term dependencies and delayed effects in economic growth more effectively than classical models. This approach has been successfully applied in various fields, such as fractional-order delayed zooplankton–phytoplankton dynamics [5], glycerol hydrogenolysis via heterogeneous catalysis [6], the (SEIrIsR) model with fractional infection stages [7], the seventh-order Caputo fractional KdV equation (including Sawada–Kotera–Ito and Lax applications) [8], the fractal fractional nonlinear coupled Burgers equation using a hybrid transform approach [9], and the dynamical analysis of a novel 4D hyperchaotic system with both integer and fractional-order methods [10].

Recently, Berinde and Pǎcurar [11] initiated an extended class of contractive operators, known as enriched contractions, which extend classical Banach contraction mappings and incorporate various non-expansive operators found in the literature.

A mapping $T:X\to X$ on a linear normed space $(X,\parallel ·\parallel )$ is called an enriched contraction if there exist $\rho \ge 0$ and $\gamma \in [0,\rho +1)$ such that, for all $\varsigma ,\eta \in X$, the contractive condition involving $\rho$ and $\gamma$ holds. Notice that non-expansive mappings do not always guarantee fixed point existence; in contrast, enriched contractions consistently ensure the presence of a unique fixed point. For further insights, we refer to Example 1(2) in [11]. Let K be a convex subset of the normed space X, and consider $\lambda \in (0, 1]$ with a mapping $T:K\to K$. The operator $T_{\lambda }:K\to K$, defined by $T_{\lambda }\left(\varsigma \right)=(1-\lambda )\varsigma +\lambda T\left(\varsigma \right)$, is the averaged mapping of T. Notably, the set of fixed points of $T_{\lambda }$ coincides with that of T. Extensive research has been conducted in this domain, with contributions from various scholars; see, for instance, [12,13,14] and the references therein.

Recently, Zhou et al. in [15] discussed the equivalence and convergence of several higher-order iteration schemes, including the Krasnoselskij iteration, under more general conditions. Their work extends classical fixed point results by considering generalized enriched contraction mappings in closed convex Banach spaces, which broadens the applicability of the Krasnoselskij and other iteration schemes. This contribution serves as a key reference for understanding the theoretical foundation of these iterative methods; additionally, see the related developments in [16,17,18].

Alam and Imdad [19] established fixed point results by introducing a weak contractive condition rather than the classical Banach contraction condition. This technique requires the contractive condition to be met only for elements belonging to a specific binary relation, rather than the whole space. Because of this study, fixed point theory has been extensively studied in the context of binary relations. Notably, Din, along with collaborators in [4,20,21], investigated Perov’s classical fixed point theorems under this setting. Their work included illustrative examples and applications within vector-valued spaces, highlighting the adaptability of this approach. Furthermore, Alam et al. [22] expanded the results of [19] by introducing even more instances of weaker conditions, thereby establishing the existence and uniqueness of fixed points for self-mappings governed by binary relations; see [23].

2. Preliminaries

We begin by revisiting some fundamentals of order-theoretic metric fixed point theory.

Definition 1 

([24]). Consider $X\ne \varnothing$, and let $\mathfrak{I}\subseteq X^2$. For all $\varsigma ,\eta \in X$, either $(\varsigma ,\eta )\in \mathfrak{I}$, that is, ς is related to η under $\mathfrak{I}$, commonly denoted as $\varsigma \mathfrak{I}\eta$ or $(\varsigma ,\eta )\notin \mathfrak{I}$, which means that ς is not related to η in $\mathfrak{I}$.

By definition, $X^2$, ∅, and ${\Delta }_X=\{(\varsigma ,\varsigma ):\varsigma \in X\}$ are well-known examples of binary relations on X, called, respectively, the universal relation, empty relation, and diagonal relation.

Throughout the study, $\mathfrak{I}$ denotes a non-empty binary relation. For simplicity, we will call it “binary relation” instead of explicitly stating “non-empty binary relation”. In the following sections, we introduce essential definitions and propositions that serve as the foundation for metric order-theoretic fixed point theorems. These fundamental notions form the necessary groundwork for further theoretical developments.

Definition 2 

([24]). Suppose $\mathfrak{I}\subseteq X^2$ and $\varsigma ,\eta \in X$; then, ς and η are said to be $\mathfrak{I}$-comparative if $(\varsigma ,\eta )\in \mathfrak{I}$ or $(\eta ,\varsigma )\in \mathfrak{I}$. We represent this relation as $[\varsigma ,\eta ]\in \mathfrak{I}$.

Proposition 1 

([19]). Consider a metric space $(X,d)$ with $\mathfrak{I}\subseteq X^2$, a self-mapping T on X, and $\gamma \in [0, 1)$. The following contractive conditions for all $\varsigma ,\eta \in X$ are equivalent:

(I) 

$(\varsigma ,\eta )\in \mathfrak{I}d(T\varsigma ,T\eta )\le \gamma d(\varsigma ,\eta )$;

(II) 

$[\varsigma ,\eta ]\in \mathfrak{I}d(T\varsigma ,T\eta )\le \gamma d(\varsigma ,\eta )$.

Definition 3 

([24]). Let $X\ne \varnothing$ and $\mathfrak{I}\subseteq X^2$. The inverse relation of $\mathfrak{I}$ is given by ${\mathfrak{I}}^{-1}=\{(\varsigma ,\eta )\in X^2:(\eta ,\varsigma )\in \mathfrak{I}\}$. The reflexive closure is denoted as ${\mathfrak{I}}^{\#}=\mathfrak{I}\cup {\Delta }_X$, and the symmetric closure is represented as ${\mathfrak{I}}^s=\mathfrak{I}\cup {\mathfrak{I}}^{-1}$.

Proposition 2 

([19,24,25]). If $\mathfrak{I}\subseteq X^2$ and $\varsigma ,\eta \in X$, then

$$[\varsigma ,\eta ]\in \mathfrak{I}\iff (\varsigma ,\eta )\in {\mathfrak{I}}^s.$$

Definition 4 

([19]). A sequence $\left\{{\varsigma }_j\right\}\subset X$ is called $\mathfrak{I}$-preserving if $({\varsigma }_j,{\varsigma }_{j+1})\in \mathfrak{I},\forall j\in {\mathbb{N}}_0.$

Definition 5 

([19]). Consider a metric space $(X,d)$ with $\mathfrak{I}\subseteq X^2$. The relation $\mathfrak{I}$ is said to be d-self-closed if for any $\mathfrak{I}$-preserving sequence $\left\{{\varsigma }_j\right\}$ with ${\varsigma }_j\stackrel{d}{\to }\varsigma$ under the metric d, there exists a subsequence $\left\{{\varsigma }_{j_k}\right\}$ such that $({\varsigma }_{j_k},\varsigma )\in \mathfrak{I}$ for all $k\in {\mathbb{N}}_0$.

Definition 6 

([19]). Let T be a self-mapping on X and $\mathfrak{I}\subseteq X^2$. The relation $\mathfrak{I}$ is said to be closed under T if, for all $\varsigma ,\eta \in X$, whenever $(\varsigma ,\eta )\in \mathfrak{I}$, then $(T\varsigma ,T\eta )\in \mathfrak{I}.$

Proposition 3 

([26]). If T is $\mathfrak{I}$-closed, then $T^j$ for all $j\in {\mathbb{N}}_0$ is also $\mathfrak{I}$-closed.

Proposition 4 

([19]). Let X, T, and $\mathfrak{I}$ be defined as per Definition 6. If $\mathfrak{I}$ is closed under T, then its symmetric closure ${\mathfrak{I}}^s$ also retains the property of T-closure.

Before proceeding, we discuss the concepts of $\parallel ·\parallel$-self-closedness and $\mathfrak{I}$-completeness in the context of normed spaces as follows:

Definition 7 

([12]). A normed space $(X,\parallel · \parallel )$ is said to be $\mathfrak{I}$-complete if every $\mathfrak{I}$-preserving Cauchy sequence converges in norm.

Definition 8 

([12]). A mapping T is termed $\mathfrak{I}$-continuous at ς if for any $\mathfrak{I}$-preserving sequence $\left\{{\varsigma }_j\right\}$ with $\parallel {\varsigma }_j-\varsigma \parallel \stackrel{\parallel ·\parallel }{\to }0$ implies $\parallel T\left({\varsigma }_j\right)-T\left(\varsigma \right)\parallel \stackrel{\parallel ·\parallel }{\to }0$. If this condition is met for all $\varsigma \in X$, then T is said to be $\mathfrak{I}$-continuous.

Every complete metric space is naturally $\mathfrak{I}$-complete, irrespective of the chosen binary relation $\mathfrak{I}$. In particular, when $\mathfrak{I}$ corresponds to the universal relation, $\mathfrak{I}$-completeness corresponds to the classical notion of completeness in metric spaces. Additionally, any continuous mapping is inherently $\mathfrak{I}$-continuous for all $\mathfrak{I}$, and if $\mathfrak{I}$ is universal, $\mathfrak{I}$-continuity is equivalent to standard continuity.

Definition 9 

([12]). In a normed space X with norm $\parallel · \parallel$, the relation $\mathfrak{I}$ is said to be $\parallel · \parallel$-self-closed if, for any $\mathfrak{I}$-preserving sequence $\left\{{\varsigma }_j\right\}$ converging to ς in norm, there exists a subsequence $\left\{{\varsigma }_{j_k}\right\}$ such that $[{\varsigma }_{j_k},\varsigma ]\in \mathfrak{I}$ for all $k\in {\mathbb{N}}_0$.

Definition 10 

([27]). Let $X\ne \varnothing$ with $\mathfrak{I}\subseteq X^2$. A subset $\mathcal{A}\subseteq X$ is known as $\mathfrak{I}$-directed if, for every $\varsigma ,\eta \in \mathcal{A}$, ∃$\omega \in X$, which implies $(\varsigma ,\omega )\in \mathfrak{I}$ and $(\eta ,\omega )\in \mathfrak{I}.$

Definition 11 

([28]). Let $X\ne \varnothing$ with $\mathfrak{I}\subseteq X^2$. For $\varsigma ,\eta \in X$, a path of length k (where k is a natural number) in $\mathfrak{I}$ from ς to η is a finite sequence $\{{\omega }_0,{\omega }_1,{\omega }_2,\dots ,{\omega }_k\}\subseteq X$ satisfying ${\omega }_0=\varsigma$, ${\omega }_k=\eta$, and $({\omega }_i,{\omega }_{i+1})\in \mathfrak{I}$ for each i with $0\le i\le k-1$.

Not long ago, Jleli and Samet [3] presented a well-known fixed point theorem in the complete metric space $(X,d)$. It uses the following generalized contraction condition:

$$\chi \left(d(T\varsigma ,T\eta )\right)\le \chi {\left(d(\varsigma ,\eta )\right)}^{\alpha },\forall \varsigma ,\eta \in X,$$

(1)

where $d(T\varsigma ,T\eta )>0$, and $\chi :(0,+\infty )\to (1,+\infty )$ is a mapping satisfying specific properties, which are given below, and $0<\alpha <1$. The contraction defined above is referred to as a $\chi$-contraction. The set of functions $\chi :(0,+\infty )\to (1,+\infty )$ satisfy the following conditions:

$\left({\chi }_1\right)$

$\chi$ is non-decreasing;

$\left({\chi }_2\right)$

For any sequence $\left\{c_n\right\}\subset {\mathbb{R}}^{+}$, ${lim}_{n\to +\infty }\chi \left(c_n\right)=1\iff {lim}_{n\to +\infty }{c}_n=0$;

$\left({\chi }_3\right)$

There exist $0<\beta <1$ and $0<\mu \le +\infty$ such that ${lim}_{c\to 0^{+}}{\displaystyle \frac{\chi \left(c\right)-1}{c^{\beta }}}=\mu$.

This is denoted by $\Theta$ in [3]. Examples of functions belonging to $\Theta$ include

(i)

${\chi }_1\left(\xi \right)=e^{\sqrt{\xi }}$, for all $\xi \in (0,+\infty )$;

(ii)

${\chi }_2\left(\xi \right)=2-{\displaystyle \frac{2}{\pi }}arctan{\displaystyle \frac{1}{{\xi }^{\kappa }}}$, for $\kappa \in (0,1)$ and $\xi \in (0,+\infty )$.

It was shown in [3] that any $\chi$-contraction over a Banach space possesses a unique fixed point. Afterwards, numerous generalizations and extensions of this result have been developed, as seen in [29,30,31].

Building upon the work of Rizwan et al. [14] and the contributions of Alam and Imdad with their collaborators [19,22], this study introduces enriched $(\mathfrak{I},\rho ,\chi )$-contractions and generalized enriched $(\mathfrak{I},\rho ,\chi )$-contractions, which extend the concepts of enriched contractions, $\chi$-contractions, enriched $(\rho ,\chi )$-contractions, Kannan contractions, and many more. To illustrate the applicability of our findings, we provide examples that validate the theoretical framework. The stability of the production–consumption equilibrium and the economic growth model are also examined in this study.

Finally, we revisit certain fundamentals and useful properties, which are necessary for our next discussions. Throughout this paper, we employ the following notations:

• $\mathrm{Fix}\left(T\right)$: The collection of all fixed points of T;
• ${\mathfrak{I}}_T:=\{\varsigma \in X:(\varsigma ,T\varsigma )\in \mathfrak{I}\}$;
• $\mathrm{Paths}(\varsigma ,\eta ;\mathfrak{I})$: The set of all paths in $\mathfrak{I}$ connecting $\varsigma$ and $\eta$;
• For $\rho \ge 0$, we define $\lambda ={\displaystyle \frac{1}{\rho +1}}\in (0, 1]$.

3. Main Results

In this section, we introduce the notions of enriched $(\mathfrak{I},\rho ,\chi )$-contractions and generalized enriched $(\mathfrak{I},\rho ,\chi )$-contractions and present fixed point results for these newly defined contractions, accompanied by illustrative examples.

Definition 12. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. A mapping $T:\mathcal{A}\to X$ is called an enriched $(\mathfrak{I},\rho ,\chi )$-contraction if there exist $\rho \in [0,+\infty )$, $\chi \in \Theta$, and $0<\alpha <1$ such that for all $\varsigma ,\eta \in X$ with $(\varsigma ,\eta )\in \mathfrak{I}$, and $T\varsigma -T\eta \ne \rho (\varsigma -\eta )$ such that

$$\chi \left({\displaystyle \frac{\parallel T\varsigma -T\eta +\rho (\varsigma -\eta )\parallel }{\rho +1}}\right)\le \chi (\parallel \varsigma -{\eta \parallel )}^{\alpha }.$$

(2)

To highlight the role of binary relation $\mathfrak{I}$, constant $\rho$, and control function $\chi$ in Definition 12, the mapping T is often referred to as an enriched $(\mathfrak{I},\rho ,\chi )$-contraction.

Definition 13. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. A mapping $T:\mathcal{A}\to X$ is called a generalized enriched $(\mathfrak{I},\rho ,\chi )$-contraction if there exist $\rho \in [0,+\infty )$, $\chi \in \Theta$, and $0<\alpha <1$ such that for all $\varsigma ,\eta \in X$ with $(\varsigma ,\eta )\in \mathfrak{I}$, and $T\varsigma -T\eta \ne \rho (\varsigma -\eta )$ such that

$$\chi \left({\displaystyle \frac{\parallel T\varsigma -T\eta +\rho (\varsigma -\eta )\parallel }{\rho +1}}\right)\le \chi {\left(max\left\{\parallel \varsigma -\eta \parallel ,{\displaystyle \frac{\parallel \varsigma -T\varsigma \parallel }{\rho +1}},{\displaystyle \frac{\parallel \eta -T\eta \parallel }{\rho +1}}\right\}\right)}^{\alpha }.$$

(3)

To highlight the role of binary relation $\mathfrak{I}$, constant $\rho$, and control function $\chi$ in Definition 13, the mapping T is often referred to as a generalized enriched $(\mathfrak{I},\rho ,\chi )$-contraction.

Remark 1. 

It is important to note that conditions (2) and (3) are not required to hold universally across the entire space X; rather, they apply only to points that are related under a specified binary relation $\mathfrak{I}$. Consequently, this formulation provides a weaker variant of the enriched $(\rho ,\chi )$-contractions introduced by Rizwan et al. [14], offering a more generalized framework for fixed point analysis within relational metric structures. However, if one considers $\mathfrak{I}=X\times X=\mathcal{A}\times \mathcal{A}$, then both definitions become equivalent, as the condition (2) would hold universally for all pairs of points in X.

By the symmetry property of the norm $\parallel ·\parallel$, the following result follows immediately. Consequently, we leave the details of the proof to the interested readers.

Proposition 5. 

A mapping T is an $(\mathfrak{I},\rho ,\chi )$-contraction if and only if T is also an $({\mathfrak{I}}^s,\rho ,\chi )$-contraction.

We now present the first main result involving the enriched $(\mathfrak{I},\rho ,\chi )$-contractions.

Theorem 1. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. Further suppose that

1. 

$(X,\parallel ·\parallel )$ is $\mathfrak{I}$-complete;

2. 

T is an enriched $(\mathfrak{I},\rho ,\chi )$-contraction;

3. 

$\mathfrak{I}$ is $T_{\lambda }$-closed, where $\lambda ={\displaystyle \frac{1}{\rho +1}}$;

4. 

$\mathfrak{I}$ is $\parallel · \parallel$-self-closed, or $T_{\lambda }$ is $\mathfrak{I}$-continuous;

5. 

${\mathfrak{I}}_{T_{\lambda }}\ne \varnothing$.

Then, T has a fixed point in $\mathcal{A}$, and the sequence $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j$ for all $j\ge 0$, converges to some fixed point of T, depending on the choice of initial point ${\varsigma }_0$.

Proof. 

It follows from (2) that for all $\varsigma ,\eta \in X$, with $(\varsigma ,\eta )\in \mathfrak{I}$ and $\parallel \rho (\varsigma -\eta )+T\varsigma -T\eta \parallel \ne 0$, we obtain

$$\chi \left(\parallel T_{\lambda }\varsigma -T_{\lambda }\eta \parallel \right)\le \chi {\left(\parallel \varsigma -\eta \parallel \right)}^{\alpha }.$$

(4)

This demonstrates that $T_{\lambda }$ is an enriched $(\mathfrak{I},0,\chi )$-contraction with $\lambda ={\displaystyle \frac{1}{1+\rho }}$.

In lieu of assumption (5), there exists an ${\varsigma }_0\in X$ such that $({\varsigma }_0,T_{\lambda }{\varsigma }_0)\in \mathfrak{I}$. Define a Krasnoselskij iterative scheme $\left\{{\varsigma }_j\right\}$ starting from the initial guess ${\varsigma }_0$ by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j,\forall j\in \mathbb{N}.$ As $\left({\varsigma }_0,T{\varsigma }_0\right)\in \mathfrak{I}$, using the $T_{\lambda }$-closedness of $\mathfrak{I}$ and Proposition 3; then, we obtain

$$\left(T_{\lambda }^j{\varsigma }_0,T_{\lambda }^{j+1}{\varsigma }_0\right)\in \mathfrak{I},\forall j\in \mathbb{N},$$

(5)

which further implies that

$$\left({\varsigma }_j,{\varsigma }_{j+1}\right)\in \mathfrak{I},\forall j\in \mathbb{N}.$$

(6)

This shows that $\left\{{\varsigma }_j\right\}$ is an $\mathfrak{I}$-preserving sequence. Next, we suppose that ${\varsigma }_j\ne {\varsigma }_{j+1}$ for all $j\in \mathbb{N}$. Otherwise, if ${\varsigma }_j={\varsigma }_{j+1}$ for some $j\in \mathbb{N}$, it follows that ${\varsigma }_j=T_{\lambda }{\varsigma }_j$, and the proof is complete. Therefore, for ${\varsigma }_j\ne {\varsigma }_{j+1}$ for all $j\in \mathbb{N}$, Equation (4) implies that

$$\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )=\chi (\parallel T_{\lambda }{\varsigma }_{j-1}-T_{\lambda }{\varsigma }_j\parallel )\le \chi (\parallel {\varsigma }_{j-1}-{\varsigma }_j{\parallel )}^{\alpha }.$$

(7)

Continuing this process, we obtain

$$\begin{array}{cc}\hfill 1<\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )& \le \chi (\parallel {\varsigma }_{j-1}-{\varsigma }_j{\parallel )}^{\alpha }\hfill \\ \hfill & \le \chi (\parallel {\varsigma }_{j-2}-{\varsigma }_{j-1}{\parallel )}^{{\alpha }^2}\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \chi (\parallel {\varsigma }_0-{\varsigma }_1{\parallel )}^{{\alpha }^j}.\hfill \end{array}$$

(8)

Thus, we have

$$\underset{j\to +\infty }{lim}\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )=1,$$

which, together with $\left({\chi }_2\right)$, implies

$$\underset{j\to +\infty }{lim}\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel =0.$$

(9)

Moreover, from $\left({\chi }_3\right)$, there exist $t\in (0,1)$ and $e\in (0,+\infty )$ for which

$$\underset{j\to +\infty }{lim}{\displaystyle \frac{\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1}{\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t}}=e.$$

(10)

Let $e<+\infty$, and define $\epsilon ={\displaystyle \frac{e}{2}}>0$. Then, according to the definition of the limit and (10), there exists $n_1\in \mathbb{N}$ such that for all $j>n_1$,

$$\left|{\displaystyle \frac{\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1}{\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t}}-e\right|<\epsilon .$$

so that we obtain

$${\displaystyle \frac{\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1}{\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t}}>e-\epsilon ={\displaystyle \frac{e}{2}}=\epsilon .$$

Equivalently, for all $j\ge n_1$, we have

$$\epsilon j\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t<j\left[\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1\right].$$

(11)

Next, assume $e=+\infty$, and let $\epsilon >0$. Therefore, there exists $n_1\in \mathbb{N}$ whereby for all $j\ge n_1$,

$${\displaystyle \frac{\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1}{\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t}}\ge \epsilon .$$

Then, for all $j>n_1$, we obtain

$$\epsilon j\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t\le j\left[\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1\right].$$

(12)

Using (8), (11), and (12), we derive

$$\epsilon j\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t\le j\left[\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )-1\right]\le \cdots \le j\left[\chi (\parallel {\varsigma }_0-{\varsigma }_1{\parallel )}^{{\alpha }^j}-1\right].$$

(13)

Taking the limit as $j\to +\infty$ in (13), we obtain

$$\underset{j\to +\infty }{lim}j{\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel }^t=0.$$

Thus, from (13), there exists $n_0\in \mathbb{N}$ such that for all $j\ge n_0$,

$$j\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel }^t\le 1.$$

Hence, for all $j\ge n_0$,

$$\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel \le {\displaystyle \frac{1}{j^{\frac{1}{t}}}}.$$

(14)

Next, to show $\left\{{\varsigma }_j\right\}$ is a Cauchy sequence, let $m\in \mathbb{N}$ and $\mathfrak{n}$ such that $m>\mathfrak{n}\ge n_0$. Then, from (14), we obtain

$$\parallel {\varsigma }_m-{\varsigma }_{\mathfrak{n}}\parallel \le \parallel {\varsigma }_m-{\varsigma }_{m-1}\parallel +\parallel {\varsigma }_{m-1}-{\varsigma }_{m-2}\parallel +\cdots +\parallel {\varsigma }_{\mathfrak{n}+1}-{\varsigma }_{\mathfrak{n}}\parallel .$$

Thus,

$$\parallel {\varsigma }_m-{\varsigma }_{\mathfrak{n}}\parallel \le \sum _{i=\mathfrak{n}}^m\parallel {\varsigma }_i-{\varsigma }_{i+1}\parallel \le \sum _{i=\mathfrak{n}}^m{\displaystyle \frac{1}{i^{\frac{1}{t}}}}\le \sum _{i=\mathfrak{n}}^{\infty }{\displaystyle \frac{1}{i^{\frac{1}{h}}}}.$$

Since the series ${\sum }_{i=\mathfrak{n}}^{\infty }{\displaystyle \frac{1}{i^{\frac{1}{t}}}}$ converges, it follows that $\left\{{\varsigma }_j\right\}$ is a Cauchy sequence. Therefore, according to the $\mathfrak{I}$-completeness of X, there exists ${\varsigma }^{*}\in X$ such that ${\varsigma }_j$ converges to ${\varsigma }^{*}$. Finally, from assumption (4), we will show that ${\varsigma }^{*}$ is a fixed point of T. Since $T_{\lambda }$ is $\mathfrak{I}$-continuous and $\left\{{\varsigma }_j\right\}$ is an $\mathfrak{I}$-preserving sequence with ${\varsigma }_j\to {\varsigma }^{*}$ in norm, it follows that ${\varsigma }_{j+1}=T_{\lambda }\left({\varsigma }_j\right)\to T_{\lambda }\left({\varsigma }^{*}\right)$ in norm. By the uniqueness of the limit, we conclude that $T_{\lambda }\left({\varsigma }^{*}\right)={\varsigma }^{*}$, meaning ${\varsigma }^{*}$ is a fixed point of $T_{\lambda }$, and thus, also a fixed point of T.

On the other hand, taking into account that $\mathfrak{I}$ is $\parallel · \parallel$-self-closed, and since $\left\{{\varsigma }_j\right\}$ is $\mathfrak{I}$-preserving with ${\varsigma }_j\to {\varsigma }^{*}$ in norm, there exists a subsequence $\left\{{\varsigma }_{j_k}\right\}$ such that $[{\varsigma }_{j_k},{\varsigma }^{*}]\in \mathfrak{I}\mathrm{for}\mathrm{all}k\in \mathbb{N}.$ Using assumption (2) with property $\left({\chi }_2\right)$ and Proposition 5, along with the convergence ${\varsigma }_{j_k}\to {\varsigma }^{*}$, we obtain that

$$\parallel {\varsigma }_{j_k+1}-T_{\lambda }{\varsigma }^{*}\parallel = \parallel T_{\lambda }{\varsigma }_{j_k}-T_{\lambda }{\varsigma }^{*}\parallel \le \parallel {\varsigma }_{j_k}-{\varsigma }^{*}\parallel \to 0\mathrm{as}k\to \infty .$$

Hence, ${lim}_{k\to \infty }{\varsigma }_{j_k+1}=T_{\lambda }{\varsigma }^{*}.$ Thus, $T_{\lambda }\left({\varsigma }^{*}\right)={lim}_{k\to \infty }{\varsigma }_{j_k+1}={lim}_{j\to \infty }{\varsigma }_j={\varsigma }^{*},$ which shows that ${\varsigma }^{*}$ is a fixed point of $T_{\lambda }$. Consequently, ${\varsigma }^{*}$ stands as a fixed point for both $T_{\lambda }$ and T. □

Next, we focus on the uniqueness of the fixed point for our enriched $(\mathfrak{I},\rho ,\chi )$-contractions. To achieve uniqueness, we impose additional conditions on the contraction mapping and the underlying relation. These extra constraints ensure that no two distinct fixed points can exist.

Theorem 2. 

Under all the assumptions of Theorem 1, and additionally supposing that

$$\mathrm{Paths}(\varsigma ,\eta ;\mathfrak{I})\ne ⌀\mathit{for}\mathit{every}\varsigma ,\eta \in \mathcal{A},$$

the self-mapping T admits a unique fixed point.

Proof. 

The existence part follows directly from Theorem 1. We now proceed to demonstrate the uniqueness part. In contrast, assume that T has two fixed points: ${\varsigma }^{*}$ and ${\eta }^{*}$. Then, there exists a path (denoted as $\{{\omega }_0,{\omega }_1,\dots ,{\omega }_m\}$) of some finite length m in $\mathfrak{I}$ from ${\varsigma }^{*}$ to ${\eta }^{*}$ such that

$${\omega }_0={\varsigma }^{*},{\omega }_m={\eta }^{*},[{\omega }_i,{\omega }_{i+1}]\in \mathfrak{I}\mathrm{for}\mathrm{each}i(0\le i\le m-1).$$

So, by letting $\parallel {\omega }_j-{\omega }_{j+1}\parallel ={\nabla }_j,\forall j\in \mathbb{N},$ and using the triangle inequality together with property $\left({\chi }_2\right)$ and (14), we obtain

$$\begin{array}{cc}\hfill \parallel {\varsigma }^{*}-{\eta }^{*}\parallel & = \parallel T_{\lambda }{\varsigma }^{*}-T_{\lambda }{\eta }^{*}\parallel = \parallel T_{\lambda }{\omega }_0-T_{\lambda }{\omega }_m\parallel \hfill \\ & \le \sum _{j=0}^{m-1}\parallel T_{\lambda }{\omega }_j-T_{\lambda }{\omega }_{j+1}\parallel \le \sum _{j=0}^{m-1}\parallel {\omega }_j-{\omega }_{j+1}\parallel \hfill \\ & =\sum _{j=0}^{m-1}{\nabla }_j\le \sum _{j=0}^{\infty }{\nabla }_j\hfill \\ & \le \sum _{j=0}^{\infty }{\displaystyle \frac{1}{j^{\frac{1}{h}}}}⟶\mathbf{0}.\hfill \end{array}$$

Thus, ${\varsigma }^{*}={\eta }^{*}$. □

If $\mathfrak{I}$ is complete or $\mathcal{A}$ is ${\mathfrak{I}}^s$-directed, the following result is noteworthy.

Corollary 1. 

If T fulfills the assumptions of Theorem 2, then T possesses a unique fixed point, provided that at least one of the following holds:

$$\left(I\right):\mathfrak{I}\mathit{is}\mathit{complete};$$

$$\left(II\right):X\mathit{is}{\mathfrak{I}}^s\text{-}\mathit{directed}.$$

Proof. 

Suppose condition $\left(I\right)$ holds. Then, for all $\varsigma ,\eta \in X$, the pair $[\varsigma ,\eta ]$ belongs to $\mathfrak{I}$ and, hence, forms a path of length 1 in ${\mathfrak{I}}^s$. This guarantees that

$$\mathrm{Paths}(\varsigma ,\eta ,{\mathfrak{I}}^s)\ne ⌀,$$

and the conclusion follows directly from Theorem 2.

Now, suppose that condition $\left(II\right)$ holds. Then, for any $\varsigma ,\eta \in X$, there exists $\omega \in X$ such that both $[\varsigma ,\omega ]$, and $[\eta ,\omega ]$ belong to $\mathfrak{I}$. These pairs form a path of length 2 in ${\mathfrak{I}}^s$, ensuring that

$$\mathrm{Paths}(\varsigma ,\eta ,{\mathfrak{I}}^s)\ne ⌀.$$

Consequently, Theorem 2 implies that T has a unique fixed point. □

By setting $\rho =0$ in Theorem 1, we obtain a fixed point result of theoretic order, which is the main result of Din et al. [21] in normed spaces.

Corollary 2. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. Further, suppose that

1. 

$(X,\parallel ·\parallel )$ is $\mathfrak{I}$-complete;

2. 

T is a theoretic-order χ-contraction;

3. 

$\mathfrak{I}$ is T-closed;

4. 

$\mathfrak{I}$ is $\parallel ·\parallel$-self-closed, or T is $\mathfrak{I}$-continuous;

5. 

${\mathfrak{I}}_T\ne \varnothing$.

Then, T has a fixed point in X, and the iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=T{\varsigma }_j$ for all $j\ge 0$, converges to some fixed point of T, depending on the choice of initial point ${\varsigma }_0$.

By setting the binary relation $\mathfrak{I}=X\times X$ in Theorem 1, our corollary recovers the main result of Rizwan et al. [14].

Corollary 3. 

Let $(X,\parallel · \parallel )$ be a normed space where

1. 

$(X,\parallel ·\parallel )$ is complete;

2. 

T is an enriched $(\rho ,\chi )$-contraction.

Then, T has a unique fixed point in X, and the scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j$ for all $j\ge 0$, converges to a unique fixed point of T for any choice of initial point ${\varsigma }_0$, where $\lambda ={\displaystyle \frac{1}{1+\rho }}$.

Setting $\mathfrak{I}=X\times X\mathrm{and}\rho =0$ in Theorem 1 yields fixed point results for JS-contractions (i.e., $\chi$-contractions), as introduced by Jleli and Samet in [3] in normed spaces.

Corollary 4. 

Let $(X,\parallel · \parallel )$ be a normed space. Suppose the following conditions hold:

1. 

$(X,\parallel ·\parallel )$ is complete;

2. 

T is a χ-contraction.

Then, T has a unique fixed point in X, and the Picard iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=T{\varsigma }_j$ for all $j\ge 0$, converges to a unique fixed point of T for any choice of ${\varsigma }_0$.

Similarly, by imposing different conditions on $\mathfrak{I}$, $\rho$, and a subset $\mathcal{A}$ of X or the control function $\chi$, many fixed point results available in the literature can be recovered as special cases of our framework. In what follows, we present an illustrative example that demonstrates our definition is a proper generalization of the existing contraction mappings.

Example 1. 

Let $X=\mathbb{R}$ be the usual normed space, and set $\mathcal{A}=[0,2]$. Consider the mapping $T:\mathcal{A}\to X$ defined by

$$T\left(\varsigma \right)=\left\{\begin{array}{cc}-\varsigma \hfill & \mathrm{if}\varsigma \in [0,1];\hfill \\ 2-3\varsigma \hfill & \mathrm{if}\varsigma \in \left[1,{\displaystyle \frac{3}{2}}\right];\hfill \\ 1-3\varsigma \hfill & \mathrm{if}\varsigma \in \left({\displaystyle \frac{3}{2}},2\right],\hfill \end{array}\right.$$

and the binary relation

$$\mathfrak{I}=\{(\varsigma ,\eta ):0\le \varsigma \le 1\mathrm{and}0\le \eta \le \frac{3}{2}\}.$$

If we set $\rho =3$, then the parameter λ becomes ${\displaystyle \frac{1}{4}}$, yielding the averaged operator

$$T_{{\displaystyle \frac{1}{4}}}\left(\varsigma \right)=\left\{\begin{array}{cc}{\displaystyle \frac{\varsigma }{2}}\hfill & \mathrm{if}\varsigma \in [0,1];\hfill \\ {\displaystyle \frac{1}{2}}\hfill & \mathrm{if}\varsigma \in \left[1,{\displaystyle \frac{3}{2}}\right];\hfill \\ {\displaystyle \frac{1}{4}}\hfill & \mathrm{if}\varsigma \in \left({\displaystyle \frac{3}{2}},2\right].\hfill \end{array}\right.$$

By routine calculation, we can verify that T is a non-self-enriched $(\mathfrak{I},\rho ,\chi )$-contraction, where $\rho =3$ and $\chi \left(t\right)=e^{t{e}^t}$ with $\alpha ={\displaystyle \frac{1}{2}}$. Moreover, note that $\mathcal{A}=[0,2]$, being a closed subset of X, is complete. Next, whenever $(\varsigma ,\eta )\in \mathfrak{I}$, we have $\varsigma \in [0,1]$ and $\eta \in \left[0,{\displaystyle \frac{3}{2}}\right]$. Then, for such ς and η, we obtain

• $T_{{\displaystyle \frac{1}{4}}}\varsigma ={\displaystyle \frac{\varsigma }{2}}\in [0,1]$;
• $T_{{\displaystyle \frac{1}{4}}}\eta ={\displaystyle \frac{\eta }{2}}\in \left[0,{\displaystyle \frac{3}{2}}\right]$ when $\eta \le 1$, and $T_{{\displaystyle \frac{1}{4}}}\eta ={\displaystyle \frac{1}{2}}\in \left[0,{\displaystyle \frac{3}{2}}\right]$ when $1\le \eta \le {\displaystyle \frac{3}{2}}$.

Thus, in all cases, $(T_{{\displaystyle \frac{1}{4}}}\varsigma ,T_{{\displaystyle \frac{1}{4}}}\eta )\in \mathfrak{I}$. Hence, $T_{{\displaystyle \frac{1}{4}}}$ is $\mathfrak{I}$-closed, and ${\mathfrak{I}}_{T_{{\displaystyle \frac{1}{4}}}}\ne \varnothing$ (since $(0,T_{{\displaystyle \frac{1}{4}}}\left(0\right))=(0,0)\in \mathfrak{I}$). Finally, it is evident that $T_{{\displaystyle \frac{1}{2}}}$ is not continuous. Let $\left\{{\varsigma }_j\right\}$ be a $\mathfrak{I}$-preserving sequence in X such that

$${\varsigma }_j\stackrel{\parallel · \parallel }{\to }\varsigma ,$$

with $({\varsigma }_j,{\varsigma }_{j+1})\in \mathfrak{I}$ for all $j\in \mathbb{N}$. Since $({\varsigma }_j,{\varsigma }_{j+1})\in \mathfrak{I}$, it follows that ${\varsigma }_j\in [0,1]$ for every j. As the interval $[0,1]$ is closed in X, we have $({\varsigma }_j,\varsigma )\in \mathfrak{I}$ for all j. Therefore, $\mathfrak{I}$ is $\parallel · \parallel$-self-closed. It is also easy to prove that $\mathrm{Paths}(\varsigma ,\eta ;\mathfrak{I})\ne ⌀\mathrm{for}\mathrm{every}\varsigma ,\eta \in \mathcal{A}.$ Consequently, all the assumptions of Theorem 2 are met; therefore, T has a unique fixed point, namely $x^{*}=0$.

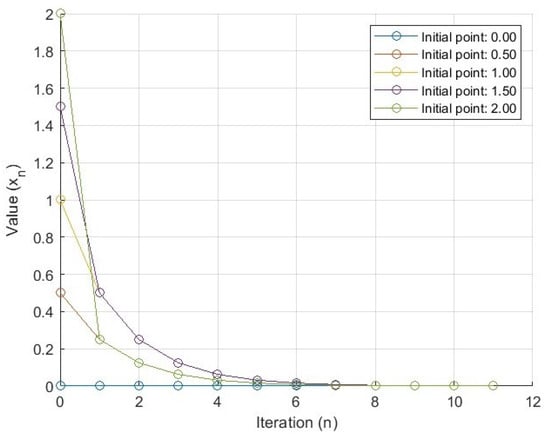
The convergence behavior of the Krasnoselskij iteration is clearly illustrated in

Table 1. Numerical analysis of Krasnoselskij iteration.

Iteration	Element 1	Element 2	Element 3	Element 4	Element 5
0	0.000000	0.500000	1.000000	1.500000	2.000000
1	0.000000	0.250000	0.500000	0.500000	0.250000
2	0.000000	0.125000	0.250000	0.250000	0.125000
3	0.000000	0.062500	0.125000	0.125000	0.062500
4	0.000000	0.031250	0.062500	0.062500	0.031250
5	0.000000	0.015625	0.031250	0.031250	0.015625
6	0.000000	0.007812	0.015625	0.015625	0.007812
7	0.000000	0.003906	0.007812	0.007812	0.003906
8	0.000000	0.001953	0.003906	0.003906	0.001953
9	0.000000	0.000977	0.001953	0.001953	0.000977
10	0.000000	0.000488	0.000977	0.000977	0.000488
11	0.000000	0.000244	0.000488	0.000488	0.000244

, showcasing the numerical results for selected initial points, and this is further visualized in Figure 1, demonstrating the iterations. These representations highlight the method’s efficiency and stability.

Remark 2. 

It should be noted that Example 1 plays a crucial role. In this example, the mapping T is neither a χ-contraction in the sense of Jleli and Samet, (since T is not continuous) nor an enriched contraction, as proposed by Berinde and Pecurar, as it is neither a self-mapping nor continuous. It is also clear that by taking $\varsigma ={\displaystyle \frac{3}{2}}$ and $\eta ={\displaystyle \frac{7}{4}}$ with $\rho =3$, we observe that

$$\parallel T_{{\displaystyle \frac{1}{4}}}\varsigma -T_{{\displaystyle \frac{1}{4}}}\eta \parallel =\parallel \varsigma -\eta \parallel ,$$

indicating the absence of any $\alpha \in (0,1)$, satisfying (1). Moreover, it does not satisfy the conditions of an enriched $(\rho ,\chi )$-contraction, as defined by Rizwan et al. [14]. However, within our framework, T qualifies as an enriched $(\mathfrak{I},\rho ,\chi )$-contraction. Hence, our results provide a proper generalization of the existing work.

Example 2. 

Let $X=\mathbb{R}$ and $\mathcal{A}=[0,1]$ with the usual norm $|\varsigma -\eta \parallel =|\varsigma -\eta |$. Let $T:\mathcal{A}\to \mathcal{A}$ be a mapping defined by

$$T\left(\varsigma \right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{5}},\hfill & \mathit{if}0\le \varsigma \le {\displaystyle \frac{1}{2}},\hfill \\ \varsigma -0.4,\hfill & \mathit{if}\varsigma \in \{0.6,0.8\},\hfill \\ {\displaystyle \frac{1}{5}}(1-\varsigma ),\hfill & \mathit{otherwise},\mathit{for}{\displaystyle \frac{1}{2}}<\varsigma \le 1\hfill \end{array}\right.$$

and construct a binary relation $\mathfrak{I}:=\{(\varsigma ,\eta )\in {\mathcal{X}}^2:\varsigma ,\eta \in [0,{\displaystyle \frac{1}{2}}]\}$. Since T is not continuous, it is not a Banach contraction, an enriched contraction, nor even a JS-contraction, as discussed in [1,3,11]. It can be also seen that for $\varsigma =0.6$ and $\eta =0.8$, we have $\parallel \varsigma -\eta \parallel =0.4=\parallel T\varsigma -T\eta \parallel \ne 0$ and so we cannot find any $\alpha >0$ for any $\chi \in \Theta$ such that it satisfies the following inequality with $\rho =0$:

$$\chi \left({\displaystyle \frac{\parallel T\varsigma -T\eta +\rho (\varsigma -\eta )\parallel }{\rho +1}}\right)\le \chi (\parallel \varsigma -{\eta \parallel )}^{\alpha }.$$

Therefore, it is not an enriched $(\rho ,\chi )$-contraction, introduced by Rizwan et al. in [14].

However, taking $\rho =0$ implies $\lambda =1$, and hence the operator T coincides with its averaged operator $T_{\lambda }$. Notice that there exists ${\displaystyle \frac{1}{2}}\in \mathcal{X}$ such that $({\displaystyle \frac{1}{2}},T{\displaystyle \frac{1}{2}})=({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}})\in \mathfrak{I}$; moreover, whenever $(\varsigma ,\eta )\in \mathfrak{I}$, then $(T\varsigma ,T\eta )=({\displaystyle \frac{1}{5}},{\displaystyle \frac{1}{5}})\in \mathfrak{I}$, showing that the binary relation $\mathfrak{I}$ is T-closed. Finally, for any $(\varsigma ,\eta )\in \mathfrak{I}$, we obtain

$$|T\varsigma -T\eta |=\left|{\displaystyle \frac{1}{5}}-{\displaystyle \frac{1}{5}}\right|=0,$$

and hence the inequality in Definition 12 holds for all $\chi \in \Theta$, that is, T is an enriched $(\mathfrak{I},\rho ,\chi )$-contraction. As all assumptions of Theorem 1 are satisfied, T has a fixed point.

Next, we present another fixed point result, which is the generalization of Theorem 1, and it is stated as follows:

Theorem 3. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. Suppose the following conditions hold:

1. 

$(X,\parallel ·\parallel )$ is $\mathfrak{I}$-complete;

2. 

T is a generalized enriched $(\mathfrak{I},\rho ,\chi )$-contraction;

3. 

$\mathfrak{I}$ is $T_{\lambda }$-closed, where $\lambda ={\displaystyle \frac{1}{\rho +1}}$;

4. 

$T_{\lambda }$ is $\mathfrak{I}$-continuous;

5. 

${\mathfrak{I}}_{T_{\lambda }}\ne \varnothing$.

Then, T has a fixed point in $\mathcal{A}$ and the Krasnoselskij iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j$ for all $j\ge 0$, converges to some fixed point of T, depending on the choice of initial point ${\varsigma }_0$.

Proof. 

According to the definition of the generalized enriched $(\mathfrak{I},\rho ,\chi )$-contraction, it follows that for all $\varsigma ,\eta \in X$, with $(\varsigma ,\eta )\in \mathfrak{I}$ and $\parallel \rho (\varsigma -\eta )+T\varsigma -T\eta \parallel \ne 0$ that

$$\chi \left(\parallel T_{\lambda }\varsigma -T_{\lambda }\eta \parallel \right)\le \chi {\left(max\{\parallel \varsigma -\eta \parallel ,\parallel \varsigma -T_{\lambda }\varsigma \parallel ,\parallel \eta -T_{\lambda }\eta \parallel \}\right)}^{\alpha }.$$

(15)

This demonstrates that $T_{\lambda }$ is a generalized enriched $(\mathfrak{I},0,\chi )$-contraction with $\lambda ={\displaystyle \frac{1}{1+\rho }}$.

In lieu of assumption (5), there exists an ${\varsigma }_0\in X$ such that $({\varsigma }_0,T_{\lambda }{\varsigma }_0)\in \mathfrak{I}$. Define a Krasnoselskij iterative scheme $\left\{{\varsigma }_j\right\}$ starting from the initial guess ${\varsigma }_0$ by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j,\forall j\in \mathbb{N}.$ As $\left({\varsigma }_0,T{\varsigma }_0\right)\in \mathfrak{I}$, by using the $T_{\lambda }$-closedness of $\mathfrak{I}$ and Proposition 3, we obtain

$$\left(T_{\lambda }^j{\varsigma }_0,T_{\lambda }^{j+1}{\varsigma }_0\right)\in \mathfrak{I},\forall j\in \mathbb{N},$$

(16)

which further implies that

$$\left({\varsigma }_j,{\varsigma }_{j+1}\right)\in \mathfrak{I},\forall j\in \mathbb{N}.$$

(17)

This shows that $\left\{{\varsigma }_j\right\}$ is a $\mathfrak{I}$-preserving sequence. Next, we suppose that ${\varsigma }_j\ne {\varsigma }_{j+1}$ for all $j\in \mathbb{N}$. Otherwise, if ${\varsigma }_j={\varsigma }_{j+1}$ for some $j\in \mathbb{N}$, it follows that ${\varsigma }_j=T_{\lambda }{\varsigma }_j$, and the proof is complete. Therefore, for ${\varsigma }_j\ne {\varsigma }_{j+1}$ for all $j\in \mathbb{N}$, Equation (15) implies that

$$\begin{array}{ccc}\hfill \chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )& =& \chi (\parallel T_{\lambda }{\varsigma }_{j-1}-T_{\lambda }{\varsigma }_j\parallel )\hfill \\ & \le & \chi (max\{\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_{j-1}-T_{\lambda }{\varsigma }_{j-1}\parallel ,\parallel {\varsigma }_j-T_{\lambda }{\varsigma }_j{\parallel \left\}\right)}^{\alpha }\hfill \\ & =& \chi (max\{\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel \left\}\right)}^{\alpha }\hfill \\ & =& \chi (max\{\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel \left\}\right)}^{\alpha }.\hfill \end{array}$$

(18)

If for some $j\in \mathbb{N}$, $max\{\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel \}=\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel$. Then, using (18), we obtain a contradiction. Indeed,

$$\begin{array}{c}\hfill \chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )\le \chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}{\parallel )}^{\alpha }<\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel ).\end{array}$$

Hence, for all $j\in \mathbb{N}$, we have $max\{\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel ,\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel \}=\parallel {\varsigma }_{j-1}-{\varsigma }_j\parallel .$ Therefore, (18) implies for all $j\in \mathbb{N}$ that

$$\begin{array}{c}\hfill \chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )\le \chi (\parallel {\varsigma }_{j-1}-{\varsigma }_j{\parallel )}^{\alpha }.\end{array}$$

Continuing this process, we obtain

$$\begin{array}{cc}\hfill 1<\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )& \le \chi (\parallel {\varsigma }_{j-1}-{\varsigma }_j{\parallel )}^{\alpha }\hfill \\ \hfill & \le \chi (\parallel {\varsigma }_{j-2}-{\varsigma }_{j-1}{\parallel )}^{{\alpha }^2}\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le \chi (\parallel {\varsigma }_0-{\varsigma }_1{\parallel )}^{{\alpha }^j}.\hfill \end{array}$$

(19)

Thus, we have

$$\underset{j\to +\infty }{lim}\chi (\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel )=1,$$

which, together with $\left({\chi }_2\right)$, implies

$$\underset{j\to +\infty }{lim}\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel =0.$$

(20)

Next, by using the same steps as in the proof of Theorem 1, finally, for all $j\ge n_0$, we obtain

$$\parallel {\varsigma }_j-{\varsigma }_{j+1}\parallel \le {\displaystyle \frac{1}{j^{\frac{1}{h}}}}.$$

(21)

To show $\left\{{\varsigma }_j\right\}$ is a Cauchy sequence, take two natural numbers: m and $\mathfrak{n}$ such that $m>\mathfrak{n}\ge n_0$. Then, from the triangular inequality and (21), we obtain

$$\parallel {\varsigma }_m-{\varsigma }_{\mathfrak{n}}\parallel \le \parallel {\varsigma }_m-{\varsigma }_{m-1}\parallel +\parallel {\varsigma }_{m-1}-{\varsigma }_{m-2}\parallel +\dots +\parallel {\varsigma }_{\mathfrak{n}+1}-{\varsigma }_{\mathfrak{n}}\parallel .$$

Thus,

$$\parallel {\varsigma }_m-{\varsigma }_{\mathfrak{n}}\parallel \le \sum _{i=\mathfrak{n}}^m\parallel {\varsigma }_i-{\varsigma }_{i+1}\parallel \le \sum _{i=\mathfrak{n}}^m{\displaystyle \frac{1}{i^{\frac{1}{h}}}}\le \sum _{i=\mathfrak{n}}^{\infty }{\displaystyle \frac{1}{i^{\frac{1}{h}}}}.$$

Since the series ${\sum }_{i=\mathfrak{n}}^{\infty }{\displaystyle \frac{1}{i^{\frac{1}{h}}}}$ converges, it follows that $\left\{{\varsigma }_j\right\}$ is a Cauchy sequence. Therefore, according to the $\mathfrak{I}$-completeness of X, there exists ${\varsigma }^{*}\in X$ such that ${\varsigma }_j$ converges to ${\varsigma }^{*}$. Using assumption (4), we show that ${\varsigma }^{*}$ is a fixed point of T. Since $T_{\lambda }$ is $\mathfrak{I}$-continuous and $\left\{{\varsigma }_j\right\}$ is an $\mathfrak{I}$-preserving sequence with ${\varsigma }_j\to {\varsigma }^{*}$ in norm, it follows that ${\varsigma }_{j+1}=T_{\lambda }\left({\varsigma }_j\right)\to T_{\lambda }\left({\varsigma }^{*}\right)$ in norm. According to the uniqueness of the limit, we conclude that $T_{\lambda }\left({\varsigma }^{*}\right)={\varsigma }^{*}$, meaning ${\varsigma }^{*}$ is a fixed point of $T_{\lambda }$, and thus, also a fixed point of T. □

By setting $\rho =0$ in Theorem 3, we obtain a generalized fixed point result of theoretic order, which is an extension of the main result of Din et al. [21] in normed spaces.

Corollary 5. 

Let $(X,\parallel · \parallel )$ be a normed space, and let $\mathfrak{I}$ be a binary relation on $\mathcal{A}$, where $\mathcal{A}\subseteq X$. Suppose the following conditions hold:

1. 

$(X,\parallel ·\parallel )$ is $\mathfrak{I}$-complete;

2. 

T is a generalized theoretic-order $(\mathfrak{I},\chi )$-contraction;

3. 

$\mathfrak{I}$ is T-closed;

4. 

T is $\mathfrak{I}$-continuous;

5. 

${\mathfrak{I}}_T\ne \varnothing$.

Then, T has a fixed point in X, and the iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=T{\varsigma }_j$ for all $j\ge 0$, converges to some fixed point of T, depending on the choice of initial point ${\varsigma }_0$.

By setting the binary relation $\mathfrak{I}=X\times X$ in Theorem 3, we obtain the following corollary:

Corollary 6. 

Let $(X,\parallel · \parallel )$ be a normed space, where $(X,\parallel · \parallel )$ is complete and T is a generalized enriched $(\rho ,\chi )$-contraction. Then, T has a unique fixed point in X, and the Krasnoselskii iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=(1-\lambda ){\varsigma }_j+\lambda T{\varsigma }_j$ for all $j\ge 0$, converges to a unique fixed point of T for any choice of initial point ${\varsigma }_0$, where $\lambda ={\displaystyle \frac{1}{1+\rho }}$.

Setting $\mathfrak{I}=X\times X\mathrm{and}\rho =0$ in Theorem 3 yields extended fixed point results for JS-contractions (i.e., generalized $\chi$-contractions) in normed spaces.

Corollary 7. 

Let $(X,\parallel · \parallel )$ be a Banach space, and let T be a generalized χ-contraction. Then, T has a unique fixed point in X, and the Picard iteration scheme $\left\{{\varsigma }_j\right\}$, given by ${\varsigma }_{j+1}=T{\varsigma }_j$ for all $j\ge 0$, converges to a unique fixed point of T for any choice of ${\varsigma }_0$.

Similarly, by imposing different conditions on $\mathfrak{I}$, $\rho$, and a subset $\mathcal{A}$ of X or the control function $\chi$, many generalized fixed point results can be recovered as special cases from our study.

4. Applications

The purpose of this section is to apply the findings from the preceding section to the analysis of economic issues. We refer to the following references [32,33,34,35] for the detailed study of equilibrium market models and economic growth models.

4.1. Application to the Market Equilibrium

In this part, we use the results from the previous section to build a model and verify the existence and uniqueness of an initial value problem that arises in the dynamic market equilibrium problem, which is a significant issue in the field of economics. Let ${\gamma }_{\mathrm{Prod}}$ represent production and ${\gamma }_{\mathrm{Con}}$ represent consumption. Examine daily pricing patterns, prices, and whether prices are rising or falling for ${\gamma }_{\mathrm{Prod}},$ and ${\gamma }_{\mathrm{Con}}$. These factors have a significant impact on markets. Economists, therefore, try to find out what $Q\left(t\right)$ is currently worth. Then, by assuming

$$\begin{array}{cc}& {\gamma }_{\mathrm{Prod}}={\Phi }_1+{\lambda }_{1}Q\left(h\right)+{\nabla }_1{\displaystyle \frac{dQ\left(h\right)}{dh}}+{\Psi }_1{\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}\hfill \\ & {\gamma }_{\mathrm{Con}}={\Phi }_2+{\lambda }_{2}Q\left(h\right)+{\nabla }_2{\displaystyle \frac{dQ\left(h\right)}{dh}}+{\Psi }_2{\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}\hfill \end{array}$$

initially, $Q\left(0\right)=0,{\displaystyle \frac{dPr}{dh}}\left(0\right)=0$, where ${\Phi }_1,{\Phi }_2,{\lambda }_1,{\lambda }_2,{\nabla }_1,{\nabla }_2,{\Psi }_1$, and ${\Psi }_2$ are constants. Dynamic economic equilibrium, or ${\gamma }_{\mathrm{Prod}}={\gamma }_{\mathrm{Con}}$, is the state in which market forces are balanced, or, to put it another way, the existing prices between production and consumption appear to be stable. Therefore, we obtain the following model:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\Phi }_1+{\lambda }_{1}Q\left(h\right)+{\nabla }_1{\displaystyle \frac{dQ\left(h\right)}{dh}}+{\Psi }_1{\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}={\Phi }_2+{\lambda }_{2}Q\left(h\right)+{\nabla }_2{\displaystyle \frac{dQ\left(h\right)}{dh}}+{\Psi }_2{\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}},\hfill \\ & \left({\Phi }_1-{\Phi }_2\right)+\left({\lambda }_1-{\lambda }_2\right)Q\left(h\right)+\left({\nabla }_1-{\nabla }_2\right){\displaystyle \frac{dQ\left(h\right)}{dh}}+\left({\Psi }_1-{\Psi }_2\right){\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}=0,\hfill \\ & \Psi {\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}+\nabla {\displaystyle \frac{dQ\left(h\right)}{dh}}+\lambda Q\left(h\right)=-\Phi ,\hfill \\ & {\displaystyle \frac{d^{2}Q\left(h\right)}{d{h}^2}}+{\displaystyle \frac{\nabla }{\Psi }}{\displaystyle \frac{dQ\left(h\right)}{dh}}+{\displaystyle \frac{\lambda }{\Psi }}Q\left(h\right)=-{\displaystyle \frac{\Phi }{\Psi }},\hfill \end{array}\right.\end{array}$$

where $\Phi ={\Phi }_1-{\Phi }_2,\lambda ={\lambda }_1-{\lambda }_2,\nabla ={\nabla }_1-{\nabla }_2$, and $\Psi ={\Psi }_1-{\Psi }_2$.

In addition, our initial value problem can be represented as follows:

$$Q^{″}\left(h\right)+{\displaystyle \frac{\nabla }{\Psi }}{Q}^{\prime }\left(h\right)+{\displaystyle \frac{\lambda }{\Psi }}Q\left(h\right)=-{\displaystyle \frac{\Phi }{\Psi }},\mathrm{with}Q\left(0\right)=0\mathrm{and}{Q}^{\prime }\left(0\right)=0$$

(22)

If production and consumption are studied for time $H_q$, problem (22) is clearly the same as

$$Q\left(h\right)={\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)\mathcal{J}\left(h^{*},h,Q\left(h\right)\right)dh$$

(23)

and the Green function $\mathcal{L}\left(h,h^{*}\right)$ is

$$\mathcal{L}\left(h,h^{*}\right)=\left\{\begin{array}{cc}h{e}^{{\displaystyle \frac{\lambda }{2\nabla }}\left(h^{*}-h\right)},\hfill & 0\le h\le s\le H_q\hfill \\ h^{*}{e}^{{\displaystyle \frac{\lambda }{2\nabla }}\left(h-h^{*}\right)},\hfill & 0\le h^{*}\le h\le H_q\hfill \end{array}\right.$$

where $\mathcal{J}:\left[0,H_q\right]\times {\Omega }^2\to \mathbb{R}$ denotes a continuous function.

Consider the function $T:\Omega \to \Omega$ to be defined as

$$TQ\left(h\right)={\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)\mathcal{J}\left(h^{*},h,Q\left(h\right)\right)dh$$

(24)

Moreover, the fixed point of T, as defined in (24), is clearly the solution to the dynamic market equilibrium issue (22). However, (22) actually controls the current price $Q\left(h\right)$.

Assume $C\left[0,H_q\right]$ indicates the collection of all continuous functions over the interval $\left[0,H_q\right]$, and subsequently, we denote $\Omega =C\left[0,H_q\right]$. Further, we take the usual norm on $\Omega$ as $\parallel \Psi \parallel ={max}_{h\in [0,H_q]}|\Psi \left(h\right)|,\forall \Psi \in \Omega$. Evidently, $\left(\Omega ,\parallel · \parallel \right)$ is a Banach space.

Theorem 4. 

Consider the operator $T:\Omega \to \Omega$, as defined in (24), such that

1. 

$\mathcal{L}:{\Omega }^2\to \mathbb{R}$ is a continuous function with

$$\underset{h^{*}\in \left[0,H_q\right]}{sup}{\int }_0^{H_q}w\left(h,h^{*}\right)dh\le {\displaystyle \frac{2\nabla }{\lambda }}{H}_q{e}^{{\displaystyle \frac{\lambda H_q}{2\nabla }}},$$

where $\nabla ,\lambda$ are constants;

2. 

There exists $Q_1\in \Omega$ such that $Q_1\left(h\right)+T{Q}_1\left(h\right)\ge 0$;

3. 

$\left|\mathcal{J}\left(h^{*},h,Q_1\left(t\right)\right)-\mathcal{J}\left(h^{*},h,Q_2\left(h\right)\right)\right|\le {\displaystyle \frac{\lambda }{2.h^{*}.\nabla H_q}}{e}^{-{\displaystyle \frac{\lambda H_q}{2\nabla }}-{\displaystyle \frac{{\tau }_q}{2}}}\left[\left|Q_1\left(h\right)-Q_2\left(h\right)\right|\right];{\tau }_q>0$ with $Q_1\left(h\right)+Q_2\left(h\right)\ge 0$.

Then, there is at least one solution in Ω for the problem (22).

Proof. 

We define the binary relation $\mathfrak{I}$ on $\Omega$ as

$$(Q_1,Q_2)\in \mathfrak{I}\iff Q_1\left(h\right)+Q_2\left(h\right)\ge 0,\forall h\in [0,H_q].$$

Then, for any $(Q_1,Q_2)\in \mathfrak{I}$, with the behavior of the kernel $\mathcal{J}$ and Green function $\mathcal{L}$, we simply obtain $T{Q}_1\left(h\right)+T{Q}_2\left(h\right)\ge 0.$ It implies that T is $\mathfrak{I}$-closed. Moreover, assumption (2) implies that there exists $Q_1\in \Omega$ such that $(Q_1,T{Q}_1)\in \mathfrak{I}$. Clearly, T is also continuous, as both $\mathcal{J}$ and $\mathcal{L}$ are continuous functions. Next, we show that T is an enriched $(\mathfrak{I},0,exp)$-contraction. From assumptions (1) and (2), we obtain

$$\begin{array}{cc}\hfill \left|T{Q}_1\left(h\right)-T{Q}_2\left(h\right)\right|& =\left|{\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)\mathcal{J}\left(h^{*},h,Q_1\left(h\right)\right)dh-{\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)\mathcal{J}\left(h^{*},h,Q_2\left(h\right)\right)dh\right|\hfill \\ & \le \left|{\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)\left\{\mathcal{J}\left(h^{*},h,Q_1\left(h\right)\right)-\mathcal{J}\left(h^{*},h,Q_2\left(h\right)\right)\right\}dh\right|\hfill \\ & \le \left|\mathcal{J}\left(h^{*},h,Q_1\left(h\right)\right)-\mathcal{J}\left(h^{*},h,Q_2\left(h\right)\right)\right|\left|{\int }_0^{H_q}\mathcal{L}\left(h,h^{*}\right)dh\right|\hfill \\ & \le {\displaystyle \frac{2\nabla }{\lambda }}{H}_q{e}^{{\displaystyle \frac{\lambda H_q}{2\nabla }}}·{\displaystyle \frac{\lambda }{2.h^{*}.\nabla H_q}}{e}^{-{\displaystyle \frac{\lambda H_q}{2\nabla }}-{\displaystyle \frac{{\tau }_q}{2}}}\left[\left|Q_1\left(h\right)-Q_2\left(h\right)\right|\right]\hfill \\ & \le e^{{\displaystyle \frac{-{\tau }_q}{2}}}∥Q_1\left(h\right)-Q_2\left(h\right)∥.\hfill \end{array}$$

Therefore, we simply imply

$$∥T{Q}_1\left(h\right)-T{Q}_2\left(h\right)∥\le e^{{\displaystyle \frac{-{\tau }_q}{2}}}∥Q_1\left(h\right)-Q_2\left(h\right)∥,\forall (Q_1,Q_2)\in \mathfrak{I}.$$

By considering

$$\chi \left(u\right)=exp\left(u\right),\forall u\in (0,\infty ),$$

we obtain

$$\chi \left[∥T{Q}_1\left(h\right)-T{Q}_2\left(h\right)∥\right]\le \chi {\left[∥Q_1\left(h\right)-Q_2\left(h\right)∥\right]}^{\alpha },\forall (Q_1,Q_2)\in \mathfrak{I},$$

where $\alpha =e^{{\displaystyle \frac{-{\tau }_q}{2}}}.$ This shows that T is an enriched $(\mathfrak{I},0,exp)$-contraction since all hypotheses of Theorem 1 are satisfied. This ultimately ensures a solution to problem (22). □

4.2. Application to the Economic Growth Model

Fractional differential equations are now widely used in many branches of science and engineering. The Caputo fractional in particular has a lot of potential for creating more accurate and perceptive models for economic growth. The Caputo fractional allows for more flexibility and a deeper understanding of economic processes, which helps with well-informed policymaking decisions by taking memory effects into consideration.

The fractional can be written as follows when used in economic growth modeling:

$${}^{C}D_t^c\left(y\left(h_q\right)\right)=\mathfrak{b}\left(h_q,y\left(h_q\right)\right),\left(0<h_q<1,1<c\le 2\right).$$

(25)

with the boundary conditions

$$y\left(0\right)=0,{}^{RL}I_t^{c}y\left(1\right)=y^{\prime }\left(0\right),$$

(26)

where ${}^{C}D_t^c\mathfrak{b}\left(h_q\right)$ represents the Caputo fractional derivative of order c, as defined by

$${}^{C}D_t^c\mathfrak{b}\left(h_q\right)={\displaystyle \frac{1}{\Gamma (j-c)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{j-c-1}{\mathfrak{b}}^j\left(w\right)\mathrm{d}w,$$

(27)

with $j-1<c<j,j=\left[c\right]+1$. Here, $\mathfrak{b}:[0,1]\times \mathbb{R}\to [0,+\infty )$ denotes a continuous function, C denotes the Caputo derivative, $h_q$ is an independent variable, and ${}^{RL}I_t^c\mathfrak{b}$ represents the Riemann–Liouville fractional integral of order c of a continuous function $f:{\mathbb{R}}^{+}\to \mathbb{R}$ described by

$${}^{RL}I_t^{c}f\left(h_q\right)={\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{c-1}f\left(w\right)\mathrm{d}w.$$

(28)

These equations may be used to illustrate various aspects of the economic dynamic and to model it. The gross domestic product (GDP) or another economic parameter that illustrates the economic status of a state or a particular region can be represented by the $y\left(h_q\right)$ variable. Additionally, the equation includes a nonlinear function $\mathfrak{b}\left(h_q,y\left(h_q\right)\right)$ that accounts for some of the variables that may influence economic growth. This could include government investment, innovation, investment levels, education, and other factors that affect the total amount of economic output. The economic system’s memory and non-local effects are indicated by the fractional order c. Recognizing that historical values may have an impact on how economic indicators evolve over time, it looks at how past economic conditions have affected the current situation. The initial stage of economic activity at the beginning of the review period can be represented as $y\left(0\right)=0$ or yield at the start of an under-review period; ${}^{RL}I_t^{c}y\left(1\right)=y^{\prime }\left(0\right)$ describe a relation among the aggregated values of economic variables within a duration (0 to 1), with an initial change in the economic variable with time at the start of the under-review period.

Suppose $\Omega =\{u:u\in C([0,1],\mathbb{R}\left)\right\}$ along the usual norm on $\Omega$ as $\parallel \Psi \parallel ={max}_{t\in [0,1]}|\Psi |,$ for all $\Psi \in \Omega$. Evidently, $\left(\Omega ,\parallel · \parallel \right)$ is a complete normed space. Further, consider the binary relation $\mathfrak{I}$ as $(\upsilon ,\omega )\in \mathfrak{I}$ if and only if $\upsilon \left(h_q\right)+\omega \left(h_q\right)>0$ for all $h_q\in [0,1].$

Theorem 5. 

Consider the nonlinear fractional differential equation

$${}^{C}D_t^c\left(y\left(h_q\right)\right)=\mathfrak{b}\left(h_q,y\left(h_q\right)\right),\left(0<h_q<1,1<c\le 2\right).$$

(29)

Suppose $\eta :{\mathbb{R}}^2\to \mathbb{R}$ is a given function. Assume that the following conditions are satisfied:

1. 

$\mathfrak{b}:[0,1]\times \mathbb{R}\to \mathbb{R}$ is continuous;

2. 

There exists $\tau >0$, for which $\mathfrak{b}:[0,1]\times \mathbb{R}\to \mathbb{R}$ satisfies the following inequality for every $\upsilon ,\omega \in C\left(\right[0,1],\mathbb{R})$ and $h_q\in [0,1]$,

$$\left|\mathfrak{b}\left(h_q,\upsilon \right)-\mathfrak{b}\left(h_q,\omega \right)\right|\le {\displaystyle \frac{\Gamma (c+1)}{8}}{e}^{{\displaystyle \frac{-\tau }{2}}}|\upsilon -\omega |$$

(30)

3. 

∃$k^{*}\in C([0,1],\mathbb{R})$, satisfying $k^{*}\left(h_q\right)+F{k}^{*}\left(h_q\right)>0$ for every $h_q\in [0,1]$, where $F:C\left(\right[0,1],\mathbb{R})\to C\left(\right[0,1],\mathbb{R})$ is defined as:

$$\begin{array}{c}\hfill F\upsilon \left(h_q\right)={\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{c-1}\mathfrak{b}(w,\upsilon \left(w\right))\mathrm{d}w+{\displaystyle \frac{2h_q}{\Gamma \left(\nu \right)}}{\int }_0^1\left({\int }_0^w{(w-m)}^{c-1}\mathfrak{b}(r,\upsilon \left(r\right))\mathrm{d}r\right)\mathrm{d}w,\end{array}$$

(31)

for each $h_q\in [0,1]$;

4. 

For sequence $\left\{{\upsilon }_n\right\}\subseteq C([0,1],\mathbb{R})$ such that ${\upsilon }_n\to \upsilon$ in $C\left(\right[0,1],\mathbb{R})$ with $({\upsilon }_n,{\upsilon }_{n+1})\in \mathfrak{I}$ for all $n\in \mathbb{N}$; therefore, $({\upsilon }_n,\upsilon )\in \mathfrak{I}$ for every $n\in \mathbb{N}$.

Then, (29) has a solution.

Proof. 

For each $t\in [0,1]$ with $(\upsilon ,\omega )\in \mathfrak{I}$ implies $F\upsilon \left(h_q\right)+F\omega \left(h_q\right)>0$. That is, $(F\upsilon ,F\omega )\in \mathfrak{I}$, and so F is $\mathfrak{I}$-closed. Notice that for $\upsilon \in \Omega$ is the solution of (29) if it satisfies the following for $h_q\in [0,1]$:

$$\begin{array}{cc}\hfill \upsilon \left(h_q\right)=& {\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{c-1}\mathfrak{b}(w,\upsilon \left(w\right))\mathrm{d}w\hfill \\ \hfill & +{\displaystyle \frac{2h_q}{\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{(w-r)}^{c-1}\mathfrak{b}(r,\upsilon \left(r\right))\mathrm{d}r\right)\mathrm{d}w.\hfill \end{array}$$

(32)

For each $(\upsilon ,\omega )\in \mathfrak{I}$ and for all $t\in [0,1]$, we obtain

$$\begin{array}{cc}& \left|F\upsilon \left(h_q\right)-F\omega \left(h_q\right)\right|\hfill \\ & =\left|{\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{c-1}\mathfrak{b}(w,\upsilon \left(w\right))\mathrm{d}w-{\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left(h_q-w\right)}^{c-1}\mathfrak{b}(w,\omega \left(w\right))\mathrm{d}w\right.\hfill \\ & +{\displaystyle \frac{2h_q}{\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{(w-r)}^{c-1}\mathfrak{b}(r,\upsilon \left(r\right))\mathrm{d}r\right)\mathrm{d}w\hfill \\ & \left.-{\displaystyle \frac{2h_q}{\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{(w-r)}^{c-1}\mathfrak{b}(r,\upsilon \left(r\right))\mathrm{d}r\right)\mathrm{d}w\right|\hfill \\ & \le {\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{\left|h_q-w\right|}^{c-1}|\mathfrak{b}(w,\upsilon \left(w\right))-\mathfrak{b}(w,\omega \left(w\right))|\mathrm{d}w\hfill \\ & +{\displaystyle \frac{2h_q}{\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{(w-r)}^{c-1}|\mathfrak{b}(r,\upsilon \left(r\right))-\mathfrak{b}(r,\upsilon \left(r\right))|\mathrm{d}r\right)\mathrm{d}w\hfill \end{array}$$

Using the inequality (30), we can further write

$$\begin{array}{cc}\hfill \left|F\upsilon \left(h_q\right)-F\omega \left(h_q\right)\right|\le & {\displaystyle \frac{1}{\Gamma \left(c\right)}}{\int }_0^{h_q}{|t-w|}^{c-1}{\displaystyle \frac{\Gamma (c+1)}{8}}{e}^{{\displaystyle \frac{-\tau }{2}}}|\upsilon \left(w\right)-\omega \left(w\right)|\mathrm{d}w\hfill \\ & +{\displaystyle \frac{2h_q}{\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{(w-r)}^{c-1}{\displaystyle \frac{\Gamma (c+1)}{8}}{e}^{{\displaystyle \frac{-\tau }{2}}}|\upsilon \left(r\right)-\omega \left(r\right)|\mathrm{d}r\right)\mathrm{d}w\hfill \\ \hfill =& {\displaystyle \frac{e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}{\int }_0^{h_q}{\left|h_q-w\right|}^{c-1}|\upsilon \left(w\right)-\omega \left(w\right)|\mathrm{d}w\hfill \\ & +{\displaystyle \frac{2e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}{\int }_0^1\left({\int }_0^w{|w-r|}^{c-1}|\upsilon \left(r\right)-\omega \left(r\right)|\mathrm{d}r\right)\mathrm{d}w\hfill \\ \hfill \le & {\displaystyle \frac{e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}\parallel \upsilon -\omega \parallel {\int }_0^{h_q}{\left|h_q-w\right|}^{c-1}\mathrm{d}w\hfill \\ & +{\displaystyle \frac{2e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}\parallel \upsilon -\omega \parallel {\int }_0^1\left({\int }_0^w{|w-r|}^{c-1}\mathrm{d}r\right)\mathrm{d}w\hfill \\ \hfill \le & {\displaystyle \frac{e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}\parallel \upsilon -\omega \parallel ·{\displaystyle \frac{\Gamma \left(c\right)}{\Gamma (c+1)}}\hfill \\ & +{\displaystyle \frac{2e^{\frac{-\tau }{2}}\Gamma (c+1)}{8\Gamma \left(c\right)}}\parallel \upsilon -\omega \parallel ·{\displaystyle \frac{\Gamma (c+1)}{\Gamma \left(c\right)\Gamma \left(1\right)}}\hfill \\ \hfill =& {\displaystyle \frac{e^{\frac{-\tau }{2}}}{8}}\parallel \upsilon -\omega \parallel +{\displaystyle \frac{e^{\frac{-\tau }{2}}}{4}}\parallel \upsilon -\omega \parallel \hfill \\ \hfill \le & e^{{\displaystyle \frac{-\tau }{2}}}\parallel \upsilon -\omega \parallel .\hfill \end{array}$$

This ultimately implies

$$\parallel F\upsilon \left(h_q\right)-F\omega \left(h_q\right)\parallel \le e^{{\displaystyle \frac{-\tau }{2}}}\parallel \upsilon -\omega \parallel .$$

(33)

By choosing

$$\chi \left(u\right)=exp\left(u\right),\forall u\in (0,\infty ),$$

we obtain

$$\chi \left[∥F\upsilon \left(h_q\right)-F\omega \left(h_q\right)∥\right]\le \chi [\parallel \upsilon -{\omega \parallel ]}^{\alpha },\forall (\upsilon ,\omega )\in \mathfrak{I},$$

where $\alpha =e^{{\displaystyle \frac{-\tau }{2}}}.$ This shows that T is an enriched $(\mathfrak{I},0,exp)$-contraction since all hypotheses of Theorem 1 are satisfied. This ultimately ensures a solution to problem (32) and, hence, the solution to the original fractional differential Equation (29). □

5. Conclusions and Future Directions

In conclusion, we have introduced two new classes: enriched $(\mathfrak{I},\rho ,\chi )$-contractions and generalized enriched $(\mathfrak{I},\rho ,\chi )$-contractions over normed spaces connected with a binary relation. Our results expand on prior ideas and offer a more comprehensive contractive structure, which advances the field of fixed point theory. These classes generalize several well-known contraction types, including $\chi$-contractions, Picard–Banach contractions, enriched contractions, Kannan contractions, Zamfirescu contractions, non-expansive mappings, and $(\rho ,\chi )$-enriched contractions. We establish fixed point results in normed spaces equipped with binary relations, preserving key symmetric properties, ensuring consistency, and applicability. The Krasnoselskij iteration method is refined to incorporate symmetric constraints, facilitating fixed point identification within these spaces. By appropriately selecting constants in the definition of enriched $(\mathfrak{I},\rho ,\chi )$-contractions, employing a suitable binary relation, or control function $\chi \in \Theta$, our framework generalizes and extends classical fixed point theorems. Illustrative examples highlight the significance of our findings in reinforcing fixed point conditions and demonstrating their broader applicability. Additionally, we apply our findings to guarantee the stability of the production-consumption market equilibrium and the economic growth model. This study provides a new direction in this field and expands the scope of applicable solutions.

It would be interesting in future work to explore numerical simulations, as they could help support and illustrate the theoretical results we’ve established in this study. We hope to include such simulations in future work to better understand how the proposed contraction types perform in practice. Moreover, it would be interesting to generalize these results further by combining enriched and generalized enriched contractions with other fixed point techniques, for example, by replacing the Krasnoselskij iteration with Mann or Ishikawa iterations, adopting Suzuki-type contractions, or introducing suitable control functions. These extensions could provide a broader framework and deeper insights into the behavior of iterative schemes in normed spaces.