Abstract
Water pollution is a significant threat for human health, particularly in developed countries. This study advances the mathematical understanding of WP transmission dynamics by developing a fractional–fractal derivative framework with non-singular kernels and the Mittage–Leffler function, which successfully preserves the non-local behavior of pollutants. The fractional–fractal derivatives in sense of the Atangana–Baleanu–Caputo formulation inherently captures the non-local and memory-dependent behavior of pollutant diffusion, addressing limitations of classical differential operators. A novel parameter, , is introduced to represent the recovery rate of water systems through treatment processes, explicitly modeling the bridge between natural purification mechanisms and engineered remediation efforts. Furthermore, this study establishes stability analysis, and the existence and uniqueness of the solution are established through fixed-point theory to ensure the mathematical stability of the system. Moreover, a numerical scheme based on the Newton polynomial is formulated, by obtaining significant simulations of pollution dynamics under various conditions. Graphical results show the effect of important parameters on pollutant evolution, providing useful information about the behavior of the system.
1. Introduction
Water pollution (WP) introduces vital challenges in the development of the world’s nations, due to its drastic impacts on the economy, human health, and the environment. Although water is an essential part of living organisms, the rapid growth in industrialization has badly affected freshwater contamination, and WP has thus become the most critical environmental issue in the current age. In particular, contaminated water serves as a carrier of waterborne diseases, which include cholera, diarrhea, typhoid, and hepatitis [1].
Mathematical modeling (MM) plays an important role in understanding and predicting the dynamics of complex systems across disciplines such as environmental pollution [2], epidemiology [3], fluid dynamics [4], and control theory [5]. MM acts as an interface between real-world phenomena and their mathematical representation, which allows us to analyze and investigate problems empirically. In 2024, Xu et al. [6] modeled a plankton–oxygen dynamical model and explored bifurcation along with its stability. Dorshan and Elisov [7] found chaotic attractors, while modeling a multi-rotor attitude system. Further application of MM can be observed in cubic equivalent systems [8,9,10], especially with the analysis of complex systems.
Apart from the above applications, MM has a great role in water power [11]. In 2023, Laskar et al. [12] studied the quality of spring water near Tuirial in a city in India. In the north-eastern state of India, two models, i.e., AHP-TOPSIS and AHP-VIKOR, were considered for the suitability of spring water [13]. Ren et al. [14] collected 168 water samples from seven different locations from the Laixi to the Yangtze Rivers and applied several statistical tools to check the quality of sub-watersheds. The control analysis of water in hilly areas, affecting the surface water, due to anthropogenic factors was studied by Wang et al. [15]. Recently, Cheng et al. [16] discussed the role of leaching in landfall and, indirectly, its impact on water pollution, by determining a strategy for leach reduction and pollution control. A new fractional model of WP based on the Levenberg–Marqurdt back-propagation method for control analysis was modeled for predictive water quality in various contexts [17].
Dynamical systems are further categorized into integer and fractional orders and are an important feature of Fractional Calculus (FC), which is the development of actual dynamical systems in terms of fractional differential equations [18,19]. There exist many studies about the usage of fractional derivatives in dynamical systems. In 2009, El-Sayed [20] considered a biological population system and transformed it into a fractional-order one to find its exact solution. The numerical modeling of a biological model along with a fractional derivative can be found in the work of Rihan [21]. A pine wilt disease-based model [22] with the Caputo–Febrizio derivative was studied to confirm the uniqueness of the solution and its stability. A system based on pantograph fractional-order differential equations [23] was studied to confirm the existence and uniqueness of the solution. In 2020, Ali et al. [24] performed mathematical analysis of dynamical systems along their boundary conditions. Marwan et al. [25] worked on the existence of a solution in a fractional-order attitude chaotic system. In 2024, a tumor–immune interaction dynamical model was investigated with the aid of a fractional derivative [26]. Recently, a non-local operator was considered in a fractional-order coronavirus disease 2019 model [27], which was modeled not only to study its existence and uniqueness but also to discuss its stability.
The new class of fractional operators has a variety of applications in chemical [28], financial [29], and biological systems [30] to develop new systems of differential equations (DEs). In accordance with applications of fractional differential equations (FDEs), a new method for fractal–fractional derivatives (FFDs) was introduced in FC [31] to enhance the analysis of fractional derivatives using different kernels and applications [32,33,34].
There have been several dynamical models designed so far including quadrotor unmanned aerial vehicles [35,36,37], cubic switching [38,39], energy supply and demand [40], switch–twist manifolds [41], and many more beyond these. Similarly, in addition to the above-mentioned dynamical systems, WP is an important issue for all living organisms, consisting of four dimensional systems of ordinary differential equations (ODEs) [42] representing the mathematical form of the systems as follows:
with the initial conditions ; ; ; and . The state variables , , , and in System (1) represent the number of polluted water sources (WSs), the WSs susceptible to pollution, the WSs infected due to WP, and the WSs recovered due to treatment for the insoluble class, respectively. Regarding the involved parameters in our considered dynamical system, is the rate of WP, is the rate of soluble CW, is the rate of insoluble contaminated water (CW), represents the rate at which insoluble water pollutants (WPs) turn into WP, shows the vanishing rate of WPs, is for the conversion rate of insoluble WPs into solute, and are the preserved rate of soluble and insoluble WPs, respectively, and is used for the re-susceptibility of filtered water.
Regardless of the progress made in these areas, there is still demand for further research on the intersection of FFDs and existence theory. This research work aims to explore this intersection and develop a numerical technique for solving nonlinear dynamical models via the results of existence theory and the Newton polynomial scheme.
This research secures significant importance by addressing the serious issue of WP through advanced MM and analysis. A novel parameter, , is introduced to represent the recovery rate of water pollution, which signifies the effectiveness of water treatment processes that not only reduce pollutant concentrations but also restore water quality. A higher value of indicates more efficiency in the control of water pollution. Furthermore, the intervention of explicitly bridges human intervention strategies with natural self-cleaning mechanisms, employing a comprehensive measure of water quality dynamics restoration. Further, utilizing FFDs in sense of the Atangana–Baleanu–Caputo (ABC) formulation [43,44,45], the model captures the memory effects and non-local dynamics inherent in pollution systems, providing a more accurate representation of real-world scenarios compared to traditional integer-order models. This study establishes the existence and stability of the solution using fixed-point theory (FPT), ensuring the mathematical robustness of the model.
Furthermore, the development of a Newton polynomial (NP) numerical scheme offers an efficient and accurate method for solving the system, enabling the simulation of pollution dynamics under various conditions. This research not only advances the field of environmental modeling but also provides practical insights for policymakers and stakeholders to design effective strategies for mitigating water pollution and promoting sustainable water resource management.
2. Preliminaries
In this section, we present some important lemmas and definitions about our research, in the context of fractal–fractional operators, defined as follows:
Definition 1
([45]). The Gamma function is defined as
where means the real part of p.
Definition 2
([46]). The authors define Euler’s first kind of integral as
for , ∈, such that , .
Definition 3
([45]). The relationship of the Gamma function and the Beta function is given by
Definition 4
([31]). The FFD in the sense of the ABC framework for the function , incorporating a generalized Mittag–Leffler function as a nonsingular kernel, is defined as
where , , where represents the fractal dimension of the measure and describes a Mittage–Leffler function and
Definition 5
([47]). The fractal derivative of the function , with the fractal measure (where q is a fractal scaling parameter), is defined as
Definition 6
([31]). The fractal–fractional integral (FFI) in sense of the ABC derivative for the function , incorporating a generalized Mittag–Leffler function as a nonsingular kernel, is defined as
satisfying that, also combine with,
Remark 1.
The FFD of the function , in the ABC sense, which incorporates a generalized Mittag–Leffler function as a nonsingular kernel, is defined as
Lemma 1.
Let the function ; then, the solution of
is given by
Definition 7.
The function is Lipschitz continuous (LC) on R with the Lipschitz constant if there exists a constant, , such that the inequality holds for all pairs:
for all .
Theorem 1.
Consider a closed convex subset, , within the Banach space . Let , where is a completely continuous operator in this space; then, is guaranteed to possess at least one fixed point.
Assumption 1.
The following norm properties are satisfied for any two functions.
- 1.
- 2.
3. Generalized FFWP Model
In this research work, the authors generalize the structure of the ordinary WP model (1), in the sense of the fractal–fractional differential operator, and introduce the new parameter , representing the re-susceptibility of filter water. The generalized WP model in the sense is
4. Existence of the Solutions
In this section, the focus is on the existence and uniqueness of the solution (EUS) of the proposed model (11), with particular emphasis on the boundedness and non-negativity.
4.1. Existence
To investigate existence of the system’s solution (11), the Picard–Lindolof method is adopted in this subsection.
Theorem 2.
The solutions of the model in (11) are uniformly bounded and non-negative.
Proof.
Then, the solutions remain confined to the hyperplane if . Since trajectories cannot escape into negative regions, is a positively invariant set; solutions starting within it remain non-negative for all future time, preserving biological or physical feasibility. □
Theorem 3.
The kernels , , , and satisfy the contraction and LC aspect.
Proof.
To make the kernels LC, let us take the difference of and ; we obtain
By deploying Assumption 1 and employing , the kernel thus satisfies the Lipschitz condition. Moreover,
using Assumption 1 and taking . Thus, the kernel satisfies the Lipschitz condition. Similarly,
where . Thus, the kernel satisfies the Lipschitz condition. Similarly,
for ; therefore, is LC. As a result, , , , and satisfy the LC condition. □
4.2. Uniqueness
Theorem 4.
The solution of the generalized WP model (11) is unique, if the following inequality,
is true, for first four non-negative integers.
Proof.
From the definition of the fractal–fractional integral in the ABC sense, we obtain
Picard’s operators , , and are generated using the FFI method. Therefore, Equation (16) becomes
If , , , and are Picard’s operators, then we can obtain
Hence, the boundedness can be formulated by employing the supremum norm to Picard’s operators as follows:
In view of Theorem 3, is LC, which means that is bounded. Thus, there exist the constants , , , and , such that
Thus,
by employing and letting there exist .
In Equation (21), we determined that is a bounded operator. Similarly, we can also determine the boundedness of the operators , , and , i.e.,
Let ∃ where .
Considering , for and , respectively to obtain
The operators , , , and are Picard bounded and, consequently are contraction mappings if the following conditions holds:, , , and are contraction mappings if the following conditions holds:
Moreover, if such that , then the operator satisfies the contraction principle. Also,
Suppose , then satisfies the contraction principle for . Moreover, from the third equation in System (11), we have
Now, let , then satisfies the contraction principle for . Similarly, for the last equation in System (11),
Further, suppose that , then the operator satisfies the contraction principle for
. Thus, the operators , , , and satisfy the contraction principle. Finally, we establish the uniqueness of the solution by assuming that both and satisfy the initial equation in System (11).
The difference of and in Equation (22) gives
Consequently,
Thus, the term
implies that Further, let and denote the two solutions of the second equation in the proposed model (11), such that
The difference of these two equations gives
Shifting the right side of Equation (23), we obtain that is negative. The term
and . Similarly, one can compute the conditions for and to obtain and , respectively. Consequently, the operators , , , and are well defined and adhere to contraction mapping principles. This ensures the uniqueness of the solution for the generalized WP model (11). □
4.3. Stability Analysis
This subsection analyzes the stability properties of the proposed model 11, specifically examining the criteria for Hyers–Ulam stability.
Definition 8.
The generalized WP model (11) is defined as Hyers–Ullam stable within the FFI framework if for every index , the positive constants satisfy all subsequent conditions:
For the generalized model (11), there exists an approximate solution (, , , ) so that the following equations are satisfied:
Thus, Equation (11) is said to be Hyers–Ullam stable if
5. Numerical Scheme Based on Proposed Model
The Newton polynomial numerical scheme for the considered FFDEs is . Applying FFI on both sides, we obtain
We replace “” with “” in Equation (27) to obtain
We apply a two-step Lagrange polynomial (LP) to obtain
where denotes the step size (the interval between two consecutive points in a set). Applying LP methods to Equation (28) results in
Solving the integrals in the aforementioned equation, we obtain
where =. Further, employing the NP scheme in the model in (11) gives
In all above cases, , with , and representing the corresponding kernels for each compartment.
6. Graphical Representations and Discussion
This section of this research work focuses on the graphical representation of the proposed model (11), using the assumed values of the compartment and parameters with the step size . MATLAB 2019b, a mathematical software tool, was employed to generate and analyze these graphs in detail. The following figures illustrate the analysis of different compartments for various values of fractal–fractional orders, i.e., and .
From the graphical analysis of the combined Figure 1a, it is observed that the number of polluted water sources decreased for different values of and . As a result, we can come to the conclusion that the fractional order and the fractal dimension had a significant impact on reducing the number of polluted water sources, . In Figure 1b, we observe that the number of susceptible water sources decreased for different values of and . Consequently, the fractional order and the fractal dimension had a significant impact on reducing the number of susceptible water sources, . In Figure 1c, it is observed that the number of infected water sources decreased for various values of and , which concludes that the fractional order and the fractal dimension reduced the number of infected water sources, . Similar was the case shown in Figure 1d, where the number of recovered water sources increased with the increase in and , and the fractional order along with the fractal dimension reduced the number of polluted water sources, .
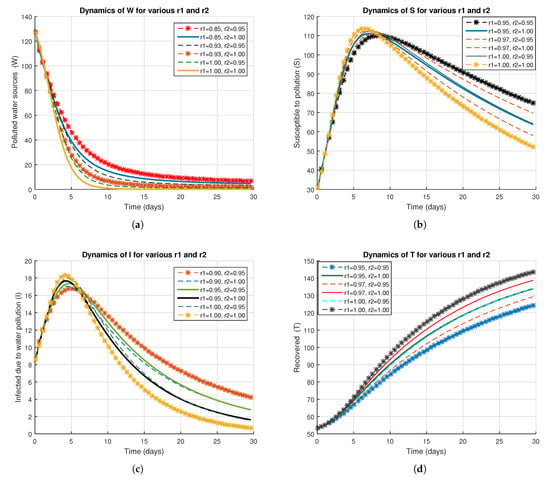
Figure 1.
Class of (a) , (b) , (c) , and (d) with different values of fractional operator () and fractal dimension ().
In Figure 2, we observe that the polluted, susceptible, and infected water sources decreased, while recovered water sources increased for various values of and , based on the inspection of graphical analysis; as the fractional order and the fractal dimension increased, the polluted, susceptible, and infected water sources decreased and recovered water increased. Thus, the fractal–fractional operator had a vital influence on the proposed model.
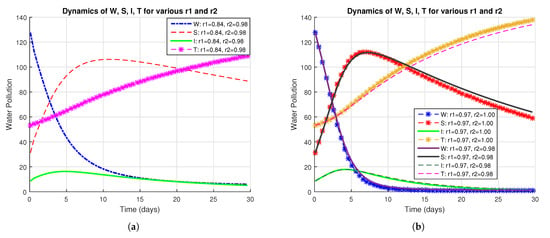
Figure 2.
(a,b) Class of , , , and with different values of fractional operator () and fractal dimension ().
Comparative Study
To check the effectiveness of the proposed numerical scheme with ordered classical numerical methods, such as the Runge–Kutta fourth-order (RK-4) method and modified Euler method (EM), by converting the considered model to a conventional integral-order model, e.g., . We performed the numerical simulations for the compartment of the proposed model with the step size using MATLAB-15 with Central Processing Unit (CPU) time comparison.
Thus, we compared the aforementioned numerical schemes for CPU time to see which method is cheaper regarding the consumption of time presented in Table 1. From Table 1, it is clear that our proposed method is more reliable than both the RK-4 method and Euler's methods. Furthermore, the NP scheme remains applicable and advantageous for fractional-order settings , where classical methods like RK-4 are not valid. This flexibility makes the NP approach particularly suited for modeling real-world processes with memory and non-locality, such as water pollution dynamics.

Table 1.
CPU time comparison for extended simulation intervals using NP, RK-4, and EM.
7. Conclusions
In this current study, a novel mathematical model for water pollution was examined using FFDs in the ABC sense, which effectively captured the memory and non-local dynamics of pollutant behavior. The inclusion of the parameter emphasized the critical role of improving efforts in relieving pollution. Moreover, the existence, uniqueness, and stability of solutions using fixed-point theory were mathematically analyzed. An NP numerical scheme was proposed to solve the system efficiently, by providing accurate simulations of pollution dynamics under changing conditions.
This research contributes to the field of environmental modeling by integrating advanced mathematical tools with practical applications, providing a framework for understanding and addressing WP. The analysis highlighted the importance of fractional-order modeling in capturing complex environmental processes and the results offer a platform for upcoming studies. Furthermore, the model serve as a valuable tool for policymakers and stakeholders to evaluate and design effective strategies for sustainable water resource management.
Author Contributions
Conceptualization, L.L., A.A., J.A., and J.Y.; methodology, L.L., A.A., J.A., and J.Y.; software, J.A. and J.Y.; validation, L.L., A.A., J.A., Y.W., L.G.A., and J.Y.; formal analysis, A.A., J.A., and L.G.A.; investigation, L.L.; resources, J.A.; writing—original draft preparation, J.A. and J.Y.; writing—review and editing, L.L., A.A., J.A., Y.W., L.G.A., and J.Y.; supervision, A.A. and J.Y.; funding acquisition, L.L., Y.W., L.G.A., and J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number NBU-FFR-2025-2618-02. This research is also funded by Natural Science Foundation of Shandong Province, China, OF Grant No. ZR2022QA057 (Y. Wei) and Zhejiang Normal University, Jinhua, China, OF Grant No. ZC034023928 (L. Loudahi).
Data Availability Statement
The original contributions presented in this study are included in the article material. Further inquiries can be directed to jk281723@gmail.com (J.A.) or wyl19910110@163.com (Y.W.).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABC | Atangana–Baleanu–Caputo |
| CW | Contaminated water |
| DEs | Differential equations |
| EUS | Existence and uniqueness of solution |
| FPT | Fixed-point theory |
| FC | Fractional Calculus |
| FDEs | Fractional differential equations |
| FFDs | Fractal–fractional derivatives |
| FFI | Fractal–fractional integral |
| LC | Lipschitz continuous |
| LP | Lagrange polynomial |
| MM | Mathematical modeling |
| NP | Newton polynomial |
| ODEs | Ordinary differential equations |
| RK4 | Runge–Kutta |
| WP | Water pollution |
| WSs | Water sources |
| WPs | Water pollutants |
References
- Schwarzenbach, R.P.; Egli, T.; Hofstetter, T.B.; Von Gunten, U.; Wehrli, B. Global water pollution and human health. Annu. Rev. Environ. Resour. 2010, 35, 109–136. [Google Scholar] [CrossRef]
- Mishra, A.K.; Dubey, R.S. Fractional-order modeling of groundwater contamination with non-local transport dynamics. J. Contam. Hydrol. 2023, 248, 104022. [Google Scholar]
- Podlubny, I. Fractional differential equations in disease modeling: New perspectives. Chaos Solit. Fractals 2020, 140, 110236. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. A fractional approach to turbulent flow with memory effects. Appl. Math. Model. 2021, 89, 1257–1272. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Chaotic Systems: Control and Synchronization; Springer: Berlin, Germany, 2019. [Google Scholar]
- Xu, C.; Zhao, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J.; Ahmad, S. Mathematical exploration on control of bifurcation for a plankton–oxygen dynamical model owning delay. J. Math. Chem. 2024, 62, 2709–2739. [Google Scholar] [CrossRef]
- Doroshin, A.V.; Elisov, N.A. Multi-rotor spacecraft attitude control by triggering chaotic modes on strange chaotic attractors. Nonlin. Dyn. 2024, 112, 4617–4649. [Google Scholar] [CrossRef]
- Chen, T.; Li, F.; Yu, P. Nilpotent center conditions in cubic switching polynomial Lienard systems by higher-order analysis. J. Differ. Equ. 2024, 379, 258–289. [Google Scholar] [CrossRef]
- Li, F.; Jin, Y.; Tian, Y.; Yu, P. Integrability and linearizability of cubic Z2 systems with non-resonant singular points. J. Differ. Equ. 2020, 269, 9026–9049. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y.; Yu, P.; Wang, J. Complex integrability and linearizability of cubic Z2-equivariant systems with two 1: q resonant singular points. J. Differ. Equ. 2021, 300, 786–813. [Google Scholar] [CrossRef]
- Gaimei, G.; Cheng, G. Mathematical modeling and application for simulation of water pollution accidents. Process Saf. Environ. Prot. 2019, 127, 189–196. [Google Scholar] [CrossRef]
- Laskar, N.; Singh, U.; Kumar, R.; Meena, S.K. Spring water quality and assessment of associated health risks around the urban Tuirial landfill site in Aizawl, Mizoram, India. Groundw. Sustain. Dev. 2022, 17, 100726. [Google Scholar] [CrossRef]
- Biswas, B.; Ghosh, A.; Sailo, B.L. Spring water suitable and vulnerable watershed demarcation using AHP-TOPSIS and AHP-VIKOR models: Study on Aizawl district of North-Eastern hilly state of Mizoram, India. Environ. Earth Sci. 2023, 82, 80. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, D.; Zhang, H.; Shi, H.; Chen, Q.; Li, M.; Chen, Q. Water quality assessment and pollution source apportionment using multivariate statistical techniques: A case study of the Laixi River Basin, China. Environ. Monit. Assess. 2023, 195, 287. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, F.; Cheng, Z.; Su, Q.; Cao, Y. Health risk cause of water around landfill in hilly area and prevention and control countermeasures. J. Environ. Manag. 2023, 346, 119019. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Wang, Y.; Ding, L.; Li, H.; Dong, W. Leachate reduction and pollution control strategies for landfills in hilly areas based on site condition analysis and numerical simulation. J. Environ. Manag. 2024, 367, 122033. [Google Scholar] [CrossRef]
- Sabir, Z.; Sadat, R.; Ali, M.R.; Said, S.B.; Azhar, M. A numerical performance of the novel fractional water pollution model through the Levenberg-Marquardt back propagation method. Arab. J. Chem. 2023, 16, 104493. [Google Scholar] [CrossRef]
- Ullah, M.S.; Higazy, M.; Kabir, K.A. Dynamic analysis of mean-field and fractional-order epidemic vaccination strategies by evolutionary game approach. Chaos Solit. Fractals 2022, 162, 112431. [Google Scholar] [CrossRef]
- Loudahi, L.; Yuan, J.; Dioubi, F. Stability Analysis of A Fractional Ordered Quadrotor Unmanned Aerial Vehicle Chaotic System. Fractals 2025, 33, 1–12. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Rida, S.Z.; Arafa, A.A.M. Exact solutions of fractional-order biological population model. Commun. Theor. Phys. 2009, 52, 992. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef]
- Shah, K.; Alqudah, M.A.; Jarad, F.; Abdeljawad, T. Semi-analytical study of Pine Wilt disease model with convex rate under Caputo-Febrizio fractional order derivative. Chaos Solit. Fractals 2020, 135, 109754. [Google Scholar] [CrossRef]
- Ahmad, I.; Nieto, J.J.; Shah, K. Existence and stability for fractional order pantograph equations with nonlocal conditions. Electron. J. Diff. Equ. 2020, 132, 1–6. [Google Scholar] [CrossRef]
- Ali, Z.; Shah, K.; Zada, A.; Kumam, P. Mathematical analysis of coupled systems with fractional order boundary conditions. Fractals 2020, 28, 2040012. [Google Scholar] [CrossRef]
- Marwan, M.; Ali, G.; Khan, R. Existence of solution and self-exciting attractor in the fractional-order gyrostat dynamical system. Complexity 2022, 2022, 3505634. [Google Scholar] [CrossRef]
- Ali, G.; Marwan, M.; Rahman, U.U.; Hleili, M. Investigation of fractional-ordered tumor-immune interaction model via fractional-order derivative. Fractals 2024, 32, 2450119. [Google Scholar] [CrossRef]
- Marwan, M.; Ali, G.; Li, F.; Abdallah, S.A.O.; Saidani, T. Semi-analytical analysis of a fractional-order pandemic dynamical model using non-local operator. Fractals, 2025; online first. [Google Scholar]
- Marwan, M.; Xiong, A.; Han, M.; Khan, R. Chaotic behavior of Lorenz-based chemical system under the influence of fractals. MATCH Commun. Math. Comput. Chem. 2024, 91, 307–336. [Google Scholar] [CrossRef]
- Alzaid, S.S.; Kumar, A.; Kumar, S.; Alkahtani, B.S.T. Chaotic behavior of financial dynamical system with generalized fractional operator. Fractals 2023, 31, 2340056. [Google Scholar] [CrossRef]
- Singh, J.; Agrawal, R.; Baleanu, D. Dynamical analysis of fractional order biological population model with carrying capacity under Caputo-Katugampola memory. Alex. Eng. J. 2024, 91, 394–402. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solit. Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solit. Fractals 2020, 136, 109860. [Google Scholar] [CrossRef] [PubMed]
- Farman, M.; Akgül, A.; Nisar, K.S.; Ahmad, D.; Ahmad, A.; Kamangar, S.; Saleel, C. A Epidemiological analysis of fractional order COVID-19 model with Mittag-Leffler kernel. AIMS Math. 2022, 7, 756–783. [Google Scholar] [CrossRef]
- Ullah, S.; Shah, K.; Sarwar, M.; Hleili, M.; Ali, A.; Abdeljawad, T. On analysis of a system of non-homogenous boundary value problems using hausdorff derivative with exponential kernel. J. App. Math. Comput. 2024, 70, 5805–5827. [Google Scholar] [CrossRef]
- Li, F.; Marwan, M.; Karawanich, K. On the bifurcations in a quadrotor unmanned aerial vehicle dynamical system using normal form theory. Nonlin. Dyn. 2025, 113, 6405–6425. [Google Scholar] [CrossRef]
- Marwan, M.; Li, F.; Ahmad, S.; Wang, N. Mixed obstacle avoidance in mobile chaotic robots with directional keypads and its non-identical generalized synchronization. Nonlin. Dyn. 2025, 113, 2377–2390. [Google Scholar] [CrossRef]
- Marwan, M.; Han, M.; Dai, Y.; Cai, M. The impact of global dynamics on the fractals of a quadrotor unmanned aerial vehicle (QUAV) chaotic system. Fractals 2024, 32, 2450043. [Google Scholar] [CrossRef]
- Li, F.; Yu, P.; Tian, Y.; Liu, Y. Center and isochronous center conditions for switching systems associated with elementary singular points. Commun. Nonlinear Sci. Numer. Simul. 2015, 28, 81–97. [Google Scholar] [CrossRef]
- Li, F.; Yu, P.; Liu, Y.; Liu, Y. Centers and isochronous centers of a class of quasi-analytic switching systems. Sci. China Math. 2018, 61, 1201–1218. [Google Scholar] [CrossRef]
- Chen, D.; Liu, W. Chaotic behavior and its control in a fractional-order energy demand-supply system. J. Comput. Nonlin. Dyn. 2016, 11, 061010. [Google Scholar] [CrossRef]
- Marwan, M.; Han, M.; Osman, M. Hidden covers (wings) in the fractals of chaotic systems using advanced Julia function. Fractals 2023, 31, 2350125. [Google Scholar] [CrossRef]
- Ebrahimzadeh, A.; Jajarmi, A.; Baleanu, D. Enhancing water pollution management through a comprehensive fractional modeling framework and optimal control techniques. J. Nonlin. Math. Phys. 2024, 31, 48. [Google Scholar] [CrossRef]
- Bushnaq, S.; Shah, K.; Alrabaiah, H. On modeling of coronavirus-19 disease under Mittag-Leffler power law. Adv. Differ. Equ. 2020, 2020, 487. [Google Scholar] [CrossRef] [PubMed]
- Din, A.; Abidin, M.Z. Analysis of fractional-order vaccinated Hepatitis-B epidemic model with Mittag-Leffler kernels. Math. Model. Numer. Simul. Appl. 2022, 2, 59–72. [Google Scholar] [CrossRef]
- Ali, Z.; Zada, A.; Shah, K. Ulam stability to a toppled system of nonlinear implicit fractional order boundary value problem. Bound. Value Probl. 2018, 1, 1–16. [Google Scholar] [CrossRef]
- France, J.; Thornley, J.H. Mathematical Models in Agriculture; Butterworths: London, UK, 1984. [Google Scholar]
- Deppman, A.; Megías, E.; Pasechnik, R. Fractal derivatives, fractional derivatives and q-deformed calculus. Entropy 2023, 25, 1008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).