Abstract
This work explores modern mathematical avenues as part of fractional calculus research. We apply fractional dispersion relations to the fractional wave equation to numerically examine various formulations of the generalized fractional wave equation. The research explores Drinfeld–Sokolov–Wilson and shallow water equations as fundamental differential equations forming the basis of wave theory studies. This work presents effective methods to obtain the numerical solution of the fractional-order FDSW and FSW coupled system equations. The analysis employs Caputo fractional derivatives during studies of fractional orders. This study develops the new iterative transform technique (NITM) and homotopy perturbation transform method (HPTM) using Elzaki transform (ET) with a new iteration method and a homotopy perturbation method. The proposed techniques generate approximation solutions that adopt an infinite fractional series with fractional order solutions converging towards analytic integer solutions. The proposed method demonstrates its precision through tabular simulations of computed approximations and their absolute error values while representing results with 2D and 3D graphics. The paper presents the physical analysis of solution dynamics across diverse ranges during a suitable time frame. The developed computational techniques yield numerical and graphical output, which are compared to analytic results to verify the solution convergence. The computational algorithms have proven their high accuracy, flexibility, effectiveness, and simplicity in evaluating fractional-order mathematical models.
1. Introduction
Researchers have pursued fractional calculus as a desirable field of research for many years, with ongoing growth in recent development [1,2]. In 1695, two mathematicians, Leibniz and L’Hospital, initially developed the concept [3]. Fractional calculus has managed the infinitesimal calculus as a discipline that explores the capability to differentiate some arbitrary functions with fractional orders, such as order differentiation [4]. Fractional calculus and its applications have appeared across multiple scientific fields, including physics, mathematical biology, viscoelasticity, signal processing, electrochemistry, finance, social science, and many more [5,6]. This specific field has emphasized the importance of fractional-order derivatives alongside their integrals [7]. Several researchers have demonstrated that fractional models derived from integer models serve as powerful tools for describing natural phenomena effectively [8,9,10,11,12]. The non-integer order differential-integral operators demonstrate greater flexibility than conventional operators because of their increased freedom. Two distinct approaches exist to define fractional derivatives, with Riemann–Liouville and Caputo establishing the first definitions. The analysis of Reimann–Liouville and Caputo models reveals significant gaps requiring deeper investigation in this field. Classical derivatives exhibit local behavior, whereas Caputo fractional derivatives have non-local characteristics that enable us to inspect interval-based changes instead of point-based changes. The property of the Caputo fractional derivative allows researchers to simulate physical phenomena, including ocean climate, atmospheric physics, dynamical systems, earthquakes, vibrations, and polymers, etc. (see the research papers [13,14,15,16,17,18]).
The recent advancement of real-world developments depends heavily on fractional differential equations (FDEs). Many analytical systems benefit from using fractional differential equations when establishing models for better management. These equations emerge in various fields, including electronic circuits and physics, as well as engineering, along with bioscience [19,20] and other scientific domains [21,22]. Mathematical handling of clients through fractional-order differential equations provides the finance industry with affordable solutions for managing financial crises [23,24]. DE applications can also be found in image and signal processing domains [25,26]. The mathematical models take two possible forms: linear and nonlinear, based on problem geometry requirements. Simple problems require ordinary differential equations (ODEs) for demonstration, whereas complex problems can be shown with partial differential equations (PDEs). The NPFDEs have established advanced modeling techniques to depict some real-life processes through their ability to incorporate multiple non-local effects, memory dynamics, and complex interactive systems [27]. The mathematical framework of the NPFDEs has united two concepts: the partial differential equations, which handle problems with multiple independent variables, and fractional calculus, which deals with non-integer order derivatives [28]. The NPFDEs have developed some practical applications across different domains because they have allowed us to model the complex systems that display the combined features of non-local connectivity, differential memory effects, and nonlinearity [29,30]. The NPFDEs contain fractional derivatives and nonlinear terms, leading to complex challenges during some analysis and solution processes. Approximate solution techniques have become essential for addressing the NPFDEs because most equations do not possess analytic solutions [31,32,33]. Numerous methods exist for obtaining approximate solutions, such as the optimal homotopy asymptotic method [34], the Exp-function method [35], the q-homotopy analysis method [36], the variational iteration method [37], the Yang transform decomposition method [38], the Homotopy analysis transform method [39], the reduced differential transform method [40,41], and the fractional sub-equation method [42], etc.
This research aims to derive solutions for the Fractional Drinfeld–Sokolov–Wilson (FDSW) coupled system and the fractional shallow water (FSW) coupled system. This fractional-order DSW equation incorporates memory effects and genetic consequences that help us understand the complex physical properties of systems. This system appears in the literature as [43].
where indicates the fractional derivative operator in the Caputo manner.
Shallow-water equations, which are crucial to applied mathematics and physics, first appeared in the latter half of the 18th century. When examined physically, shallow-water waves are defined as the noticeable displacements of bodies of water, such as the sea or ocean [44,45,46]. At the same time, many physical phenomena that resemble the motions of shallow-water waves are seen in a variety of scientific domains, such as fluid dynamics, nuclear physics, plasma physics, and other related subjects. This paper’s second coupled system is the fractional-order shallow-water (FSW) equation, which characterizes a thin fluid layer with a constant density in hydrostatic equilibrium. The coupled SW equation represents the associated wave motion. This system appears in the literature as [47]
where and denote the free surface and the horizontal velocity component.
In this paper, we combine the Elzaki transform with a new iterative method (NIM) and the Homotopy perturbation method (HPM) to evaluate the approximate results of nonlinear fractional DSW and SW equations. The main benefits of these methods are their simplicity and the minimal effort required for calculations. Additionally, the analytic solutions found in the literature and the solutions obtained through these methods agree perfectly. Numerical outcomes from these methods are more precise and accurate than those from other methods. To determine the accuracy of each approach, the numerical results are compared to the other methods. We will show that the results of the proposed approaches are predominantly consistent, proving their effectiveness and dependability. Nonetheless, the novel methods surpass the other literature approaches, increasing their value and effectiveness. To obtain precise and approximate results in a few simple steps, researchers may use this investigation as a core reference to explore these techniques and apply them in numerous applications. The presentation of two novel strategies for fractional nonlinear dynamical systems with minimal and progressive phases makes this work interesting. The structure of this article is divided into seven sections: Section 2 covers the fundamental concepts of fractional calculus needed in our research. Section 3 introduces the basic concepts of the NITM. Section 4 introduces the basic concepts of the ETDM. Section 5 of this work demonstrates the convergence results of the proposed approaches. In Section 6, the proposed approaches serve to solve both fractional DSW and fractional SW coupled systems. The conclusion segment appears as the last section.
2. Basic Definitions
In this portion, we expressed the basic results of FC associated with the current work.
Definition 1.
The non-integer derivative in Abel-Riemann manner is as [48,49,50]
with , and
Definition 2.
The non-integer Abel-Riemann integration operator is as [48,49,50]
with below properties:
Definition 3.
The non-integer derivative in Caputo manner is as [51]
with below properties
and
Definition 4.
The ET of a function is as [52]
Definition 5.
The ET of Caputo operator is given as [52]
3. Analysis of NITM
In this part, we construct the general solution of the FDE as below.
with
with indicates the linear and nonlinear terms. By implementing the ET to Equation (8), we get
After differentiation property
On implementing the inverse ET to Equation (11),
By iterative approach, we obtain
the nonlinear term is decomposed as
By using Equations (13)–(15) into Equation (12), we obtain
In terms of an iterative formula, we obtain
Thus, the solution in series form to Equation (8) illustrates
4. Analysis of ETDM
In this portion, we build the general solution of the FDE as below.
By implementing the ET to Equation (21), we get
On implementing the inverse ET, we get
where
Assume the series form as
The decomposition of nonlinear terms is as
with
By using Equations (25) and (26) into Equation (23), we get
On comparison of both sides, we may have
5. Convergence Analysis
The convergence analysis of the implemented approaches are discussed below.
Theorem 1.
Assuming ϱ is analytic in a neighborhood of and for every number m as well as for few real number and || thus the series is convergent and also
Also to describe boundedness of ||||, for every k the conditions on are given and is sufficient to guarantee series convergence.
Theorem 2.
If ϱ is and || for all m thus the series is convergent.
These are the conditions for series to be convergent.
The proofs can be checked in [53].
Theorem 3.
The outcome of (21) is unique at
Proof.
Suppose with the norm is Banach space, ∀ continuous function on Let is a non-linear mapping, thus
Suppose that and , where and are are two separate function values and , are Lipschitz constants.
I is contraction as . The outcome of (21) is unique in terms of Banach fixed point theorem. □
Theorem 4.
The outcome of (21) is convergent.
Proof.
Assume . To show that is a Cauchy sequence in H. Consider,
Let , then
where . Similarly, we have
As , we get . Hence,
Since when . Hence, is a Cauchy sequence in H, demonstrating the series is convergent. □
6. Applications
6.1. Example
Consider the nonlinear fractional DSW equation
with
- CaseI: Application of NITM
By implementing the ET to Equation (35), we obtain
On implementing the inverse ET, we obtain
By NITM, we have
At the end, the solution in series form is taken as
- Case II: Application of ETDM
By implementing the ET to Equation (35), we obtain
On implementing the inverse ET, we obtain
Assume the series form solution as
The nonlinear terms decomposes as So, we have
Similarly,
On
On
On
Thus, the solution in series form illustrates as
Inserting , we obtain
Figure 1 depicts the NITM approximate outcome (39) of for different values of . Figure 2 depicts the correspondence between NITM solution (39) and accurate solution (45) for at . Figure 3 displays the ETDM approximate solution (44) at different values while Figure 4 shows the comparison of ETDM solution (44) against accurate solution (45) for at . Figure 5 depicts the NITM approximate outcome (39) of for different values of . The Figure 6 depicts the correspondence between NITM solution (39) and accurate solution (45) for at . Figure 7 displays the ETDM approximate solution (44) at different values while Figure 8 shows the comparison of ETDM solution (44) against accurate solution (45) for at . All figures show that when fractional order approaches 1, the approximate solution predicts analytic solution behavior while matching the analytic solution identically for the case of , thus confirming the reliability of our proposed approaches. The NITM approximation (39) and ETDM approximation (44) get compared to the analytic solution (45) for through Table 1 and Table 2. Additionally, the NITM approximation (39) and ETDM approximation (44) get compared to the analytic solution (45) for through Table 3 and Table 4. The obtained approximations are shown in Table 1, Table 2, Table 3 and Table 4 for a range of values, which are 1, 0.95, 0.90, and 0.85, respectively, with and temporal variable . Table 5 and Table 6 shows a comparison among our methods solution with analytic and HPTM solution. The tables visualize the close match between our computational results and actual solutions at . Also, the solutions obtained by NITM are more suitable and efficient than those obtained by HPTM. Overall, the tabular and graphical data support the finding that both approaches work well, while NITM provides better accuracy in particular fractional contexts.
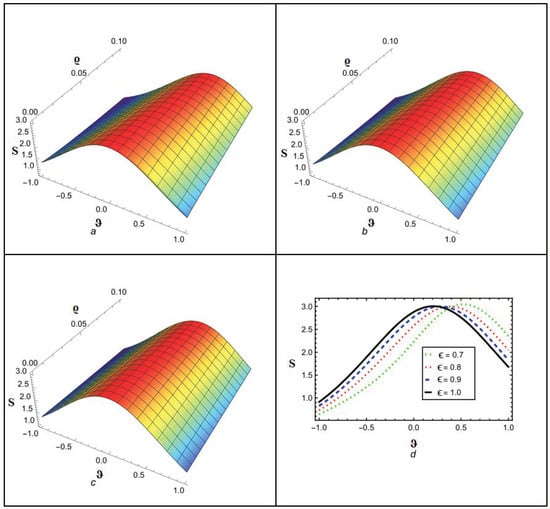
Figure 1.
Analytical solution behavior of NITM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
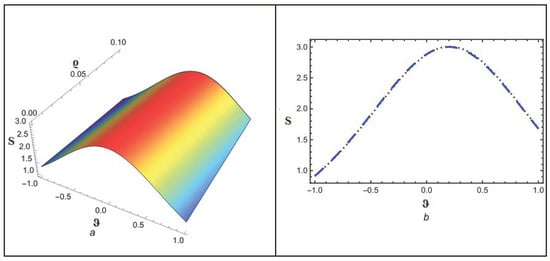
Figure 2.
(a,b) Accurate as well as analytical solution by NITM for .
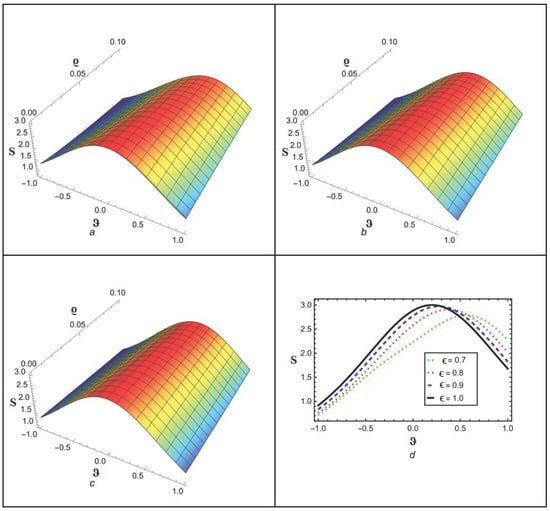
Figure 3.
Analytical solution behavior of ETDM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
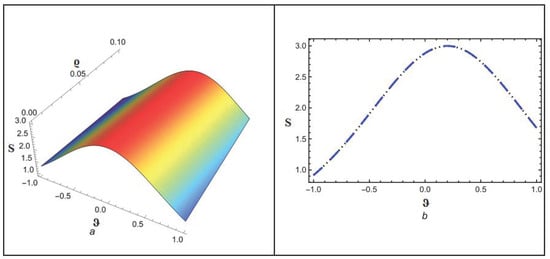
Figure 4.
(a,b) Accurate as well as analytical solution by ETDM for .
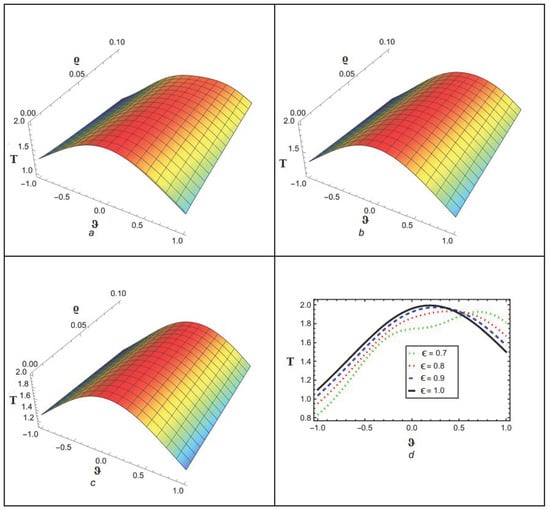
Figure 5.
Analytical solution behavior of NITM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
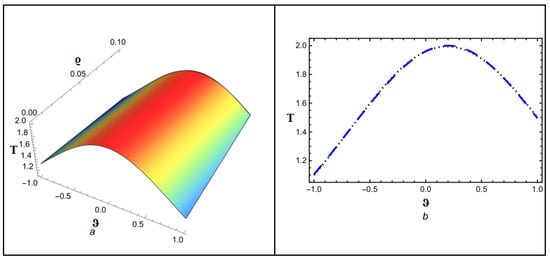
Figure 6.
(a,b) Accurate as well as analytical solution by NITM for .
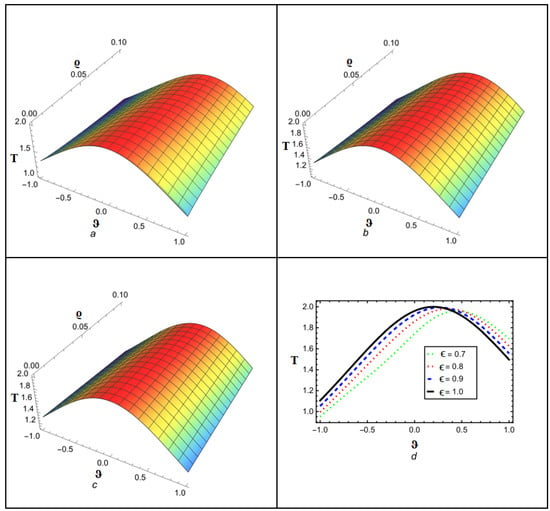
Figure 7.
Analytical solution behavior of ETDM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
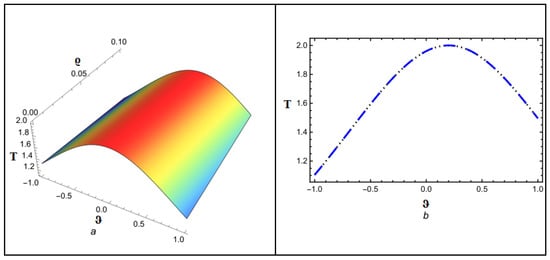
Figure 8.
(a,b) Accurate as well as analytical solution by ETDM for .

Table 1.
Accurate solution along with NITM solution at numerous orders of for .

Table 2.
Accurate solution along with ETDM solution at numerous orders of for .

Table 3.
Accurate solution along with NITM solution at numerous orders of for .

Table 4.
Accurate solution along with ETDM solution at numerous orders of for .

Table 5.
Comparative analysis of our methods solution with analytic and homotopy perturbation transform method (HPTM) solution for .

Table 6.
Comparative analysis of our methods solution with analytic and homotopy perturbation transform method (HPTM) solution for .
6.2. Example
Consider the nonlinear fractional DSW equation
with
- Case I: Application of NITM
By implementing the ET to Equation (46), we obtain
On implementing the inverse ET, we obtain
By NITM, we have
At the end, the solution in series form is taken as
- Case II: Application of ETDM
By implementing the ET to Equation (46), we obtain
On implementing the inverse ET, we obtain
Assume the series form solution as
The nonlinear terms decomposes as So, we have
Similarly,
On
On
Thus, the solution in series form illustrates as
Inserting , we obtain
Figure 9 depicts the NITM approximate outcome (50) of for different values of . The Figure 10 depicts the correspondence between the NITM solution (50) and the accurate solution (56) for at . Figure 11 displays the ETDM approximate solution (55) at different values, while Figure 12 shows the comparison of ETDM solution (55) against accurate solution (45) for at . Figure 13 depicts the NITM approximate outcome (50) of for different values of . The Figure 14 depicts the correspondence between NITM solution (50) and accurate solution (56) for at . Figure 15 displays the ETDM approximate solution (55) at different values while Figure 16 shows the comparison of the ETDM solution (55) against the accurate solution (56) for at . All figures show that when the fractional order approaches 1, the approximate solution predicts analytic solution behavior while matching the analytic solution identically for the case of , thus confirming the reliability of our proposed approaches. The NITM approximation (50) and the ETDM approximation (55) are compared to the analytic solution (56) for through Table 7 and Table 8. Additionally, the NITM approximation (50) and the ETDM approximation (55) are compared to the analytic solution (56) for through Table 9 and Table 10. The obtained approximations are shown in Table 7, Table 8, Table 9 and Table 10 for a range of values, which are 1, 0.95, 0.90, and 0.85, respectively, with temporal variable . The tables visualize the close match between our computational results and actual solutions at .
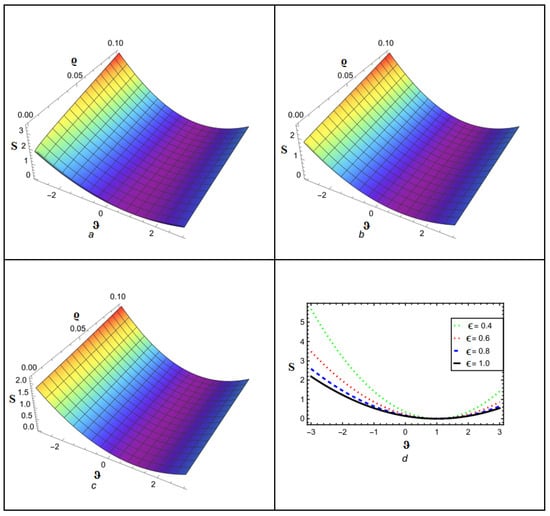
Figure 9.
Analytical solution behavior of NITM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
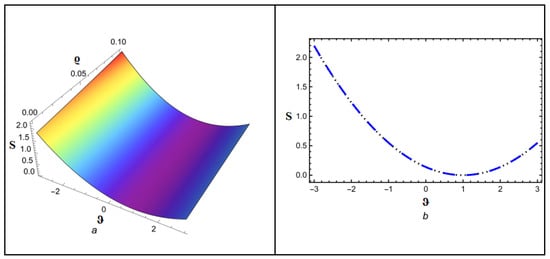
Figure 10.
(a,b) Accurate as well as analytical solution by NITM for .
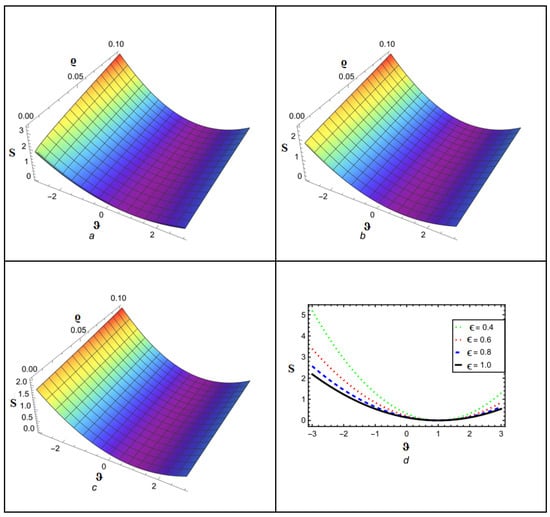
Figure 11.
Analytical solution behavior of ETDM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
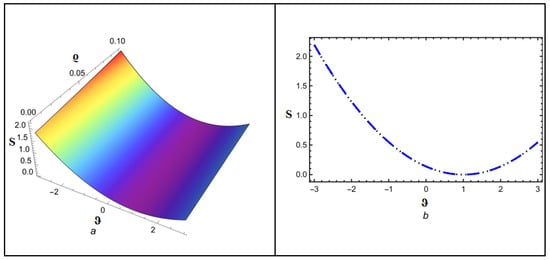
Figure 12.
(a,b) Accurate as well as analytical solution by ETDM for .
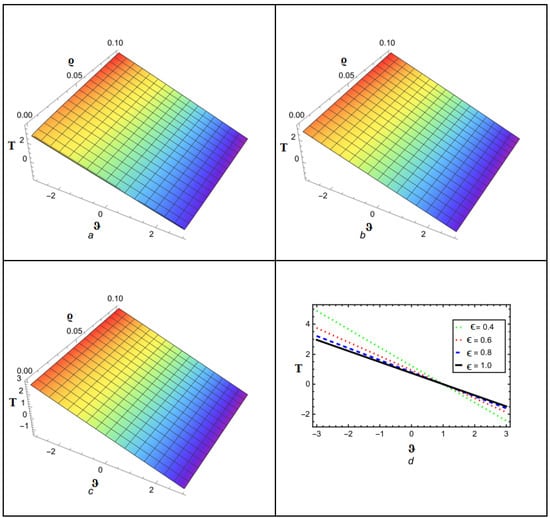
Figure 13.
Analytical solution behavior of NITM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
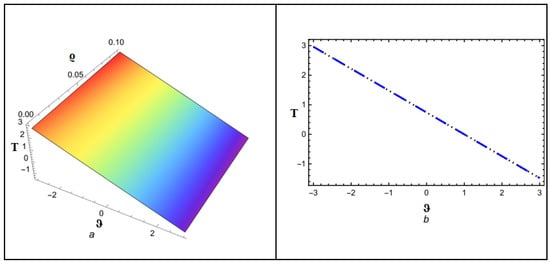
Figure 14.
(a,b) Accurate as well as analytical solution by NITM for .
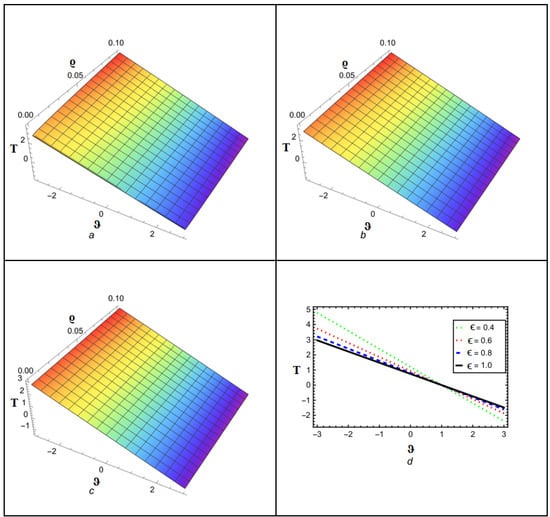
Figure 15.
Analytical solution behavior of ETDM for at (a) ϵ = 0.8 (b) ϵ = 0.9 (c) ϵ = 1 (d) various values of ϵ.
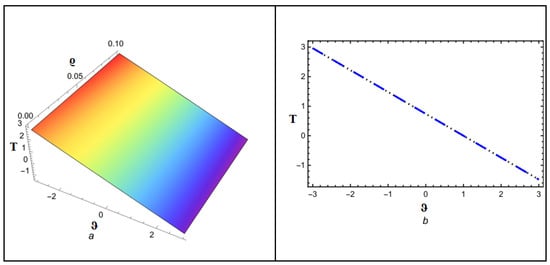
Figure 16.
(a,b) Accurate as well as analytical solution by ETDM for .

Table 7.
Accurate solution along with NITM solution at numerous orders of for .

Table 8.
Accurate solution along with ETDM solution at numerous orders of for .

Table 9.
Accurate solution along with NITM solution at numerous orders of for .

Table 10.
Accurate solution along with ETDM solution at numerous orders of for .
7. Conclusions
In this paper, we have successfully developed novel strategies for obtaining the approximate solution of fractional DSW and fractional SW equations with fractional derivatives. The implementation of the proposed methods for recurrence relations is straightforward, making it possible to achieve iterative results. The methods demonstrate excellent capability when handling nonlinear terms while producing series results through successive iterations. The technique requires an initial condition to generate simple iterative methods that produce approximate solutions near the analytic solution. The proposed methods need less computational effort while providing better efficiency in their operations. The displayed graphs and tables validate that the proposed schemes generate highly accurate results. The proposed schemes demonstrate high accuracy, making them suitable for exploring complex nonlinear differential equations of fractional order. The application of fractional derivatives establishes novel possibilities within mathematical modeling fields. Due to the beneficial results of using the suggested techniques, these techniques can be used to analyze different kinds of fractional wave equations that occur in different plasma models to understand the ambiguity surrounding specific behaviors that accompany certain nonlinear phenomena (such as solitary, shock, and cnoidal waves, etc.) that occur in different plasma models.
Funding
Prince Sattam bin Abdulaziz University funds this study under project number PSAU/2025/R/1446.
Data Availability Statement
The numerical data used to support the findings of this study are included within the article.
Acknowledgments
The author extends her appreciation to Prince Sattam bin Abdulaziz University for funding this research work through project number PSAU/2025/R/1446.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, A.P.; Bingi, K. Applications of fractional-order calculus in robotics. Fractal Fract. 2024, 8, 403. [Google Scholar] [CrossRef]
- Huang, G.; Qin, H.Y.; Chen, Q.; Shi, Z.; Jiang, S.; Huang, C. Research on application of fractional calculus operator in image underlying processing. Fractal Fract. 2024, 8, 37. [Google Scholar] [CrossRef]
- Pratap, H.; Kumar, S.; Singh, G. Brief history of fractional calculus: A survey. Migr. Lett. 2024, 21, 238–243. [Google Scholar]
- Das, S.; Das, S. Introduction to fractional calculus. In Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–18. [Google Scholar]
- Agarwal, P.; El-Sayed, A.A. Non-standard finite difference and Chebyshev collocation methods for solving fractional diffusion equation. Phys. A Stat. Mech. Its Appl. 2018, 500, 40–49. [Google Scholar] [CrossRef]
- Kulish, V.V.; Lage, J.L. Application of fractional calculus to fluid mechanics. J. Fluids Eng. 2002, 124, 803–806. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Caputo, M. Elasticita e Dissipazione; Zani-Chelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Baleanu, D.; Guvenc, Z.B.; Tenreiro Machado, J.A. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany; London, UK; New York, NY, USA, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Singh, J.; Kumar, D.; Nieto, J.J. A reliable algorithm for local fractional Tricomi equation arising in fractal transonic flow. Entropy 2016, 18, 206. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A hybrid computational approach for Klein-Gordan equations on Cantos sets. Nonlinear Dyn. 2017, 87, 511–517. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Mekkaoui, T.; Hammouch, Z.; Bulut, H. Active control of a chaotic fractional order economic system. Entropy 2015, 17, 5771–5783. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A.; Baleanu, D. New numerical approximations for space-time fractional Burgers equations via a Legendre spectral-collocation method. Rom. Rep. Phys. 2015, 67, 340–349. [Google Scholar]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Argyros, I.K. A new analysis for the Keller-Segel model of fractional order. Numer. Algorithms 2016, 75, 213–228. [Google Scholar] [CrossRef]
- Khan, A.; Zarin, R.; Humphries, U.W.; Akgül, A.; Saeed, A.; Gul, T. Fractional optimal control of COVID-19 pandemic model with generalized Mittag-Leffler function. Adv. Differ. Equ. 2021, 2021, 387. [Google Scholar] [CrossRef] [PubMed]
- Saeed, A.; Bilal, M.; Gul, T.; Kumam, P.; Khan, A.; Sohail, M. Fractional order stagnation point flow of the hybrid nanofluid towards a stretching sheet. Sci. Rep. 2021, 11, 20429. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-H.; Ali, A.; Khan, M.A.; Alshahrani, M.Y.; Muhammad, T.; Islam, S. Mathematical analysis of the TB model with treatment via Caputo-type fractional derivative. Discret. Dyn. Nat. Soc. 2021, 2021, 9512371. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Ali, A.; Khan, M.A.; Islam, S.; Ullah, S. Dynamics of fractional order COVID-19 model with a case study of Saudi Arabia. Results Phys. 2021, 21, 103787. [Google Scholar] [CrossRef]
- Ali, A.; Islam, S.; Khan, M.R.; Rasheed, S.; Allehiany, F.M.; Baili, J.; Khan, M.A.; Ahmad, H. Dynamics of a fractional order Zika virus model with mutant. Alex. Eng. J. 2021, 61, 4821–4836. [Google Scholar] [CrossRef]
- Ma, W.; Jin, M.; Liu, Y.; Xu, X. Empirical analysis of fractional differential equations model for relationship between enterprise management and financial performance. Chaos Solitons Fractals 2019, 125, 17–23. [Google Scholar] [CrossRef]
- Tien, D.N. Fractional stochastic differential equations with applications to finance. J. Math. Anal. Appl. 2013, 397, 334–348. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Singapore, 2015; Volume 4. [Google Scholar]
- Rao, A.; Vats, R.K.; Yadav, S. Analytical solution for time-fractional cold plasma equations via novel computational method. Int. J. Appl. Comput. Math. 2024, 10, 2. [Google Scholar] [CrossRef]
- Salehi, Y.; Schiesser, W.E. Introduction to Fractional Partial Differential Equations. In Numerical Integration of Space Fractional Partial Differential Equations: Vol 1-Introduction to Algorithms and Computer Coding in R; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–33. [Google Scholar]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Ravichandran, C. A review of fractional order epidemic models for life sciences problems: Past, present and future. Alex. Eng. J. 2024, 95, 283–305. [Google Scholar] [CrossRef]
- Pavani, K.; Raghavendar, K. A novel technique to study the solutions of time fractional nonlinear smoking epidemic model. Sci. Rep. 2024, 14, 4159. [Google Scholar] [CrossRef] [PubMed]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Momani, S. Non-perturbative analytical solutions of the space-and time-fractional Burgers equations. Chaos Solitons Fractals 2006, 28, 930–937. [Google Scholar] [CrossRef]
- Momani, S.; Abuasad, S. Application of He’s variational iteration method to Helmholtz equation. Chaos Solitons Fractals 2006, 27, 1119–1123. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Ouannas, A.; Bahia, G.; Batiha, I.M.; Grassi, G. The optimal homotopy asymptotic method for solving two strongly fractional-order nonlinear benchmark oscillatory problems. Mathematics 2021, 9, 2218. [Google Scholar] [CrossRef]
- Guner, O. Exp-function method and fractional complex transform for space-time fractional KP-BBM equation. Commun. Theor. Phys. 2017, 68, 149. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Shareef, E.H.; Mohamed, M.S.; Yang, X.J. Optimal q-homotopy analysis method for time-space fractional gas dynamics equation. Eur. Phys. J. Plus 2017, 132, 1–11. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Momani, S. Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 27–34. [Google Scholar] [CrossRef]
- AlBaidani, M.M.; Ganie, A.H.; Khan, A.; Aljuaydi, F. An Approximate Analytical View of Fractional Physical Models in the Frame of the Caputo Operator. Fractal Fract. 2025, 9, 199. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. New homotopy analysis transform method for solving multidimensional fractional diffusion equations. Arab. J. Basic Appl. Sci. 2020, 27, 27–44. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Awasthi, M.K.; Kumar, S. Analytical approximations of two and three dimensional time-fractional telegraphic equation by reduced differential transform method. Egypt. J. Basic Appl. Sci. 2014, 1, 60–66. [Google Scholar] [CrossRef]
- Ramani, P.; Khan, A.M.; Suthar, D.L.; Kumar, D. Approximate analytical solution for non-linear Fitzhugh-Nagumo equation of time fractional order through fractional reduced differential transform method. Int. J. Appl. Comput. Math. 2022, 8, 61. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Nawaz, T.; Azhar, E.; Akbar, M.A. Fractional sub-equation method to space-time fractional Calogero-Degasperis and potential Kadomtsev-Petviashvili equations. J. Taibah Univ. Sci. 2017, 11, 258–263. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Prakasha, D.G.; Baskonus, H.M.; Yel, G. A powerful approach for fractional Drin feld-Sokolov-Wilson equation with Mittag-Leffler law. Alex. Eng. J. 2019, 58, 1301–1311. [Google Scholar] [CrossRef]
- Gao, X.Y. Hetero-Bäcklund transformation, bilinear forms and multi-solitons for a (2+1)-dimensional generalized modified dispersive water-wave system for the shallow water. Chin. J. Phys. 2024, 92, 1233–1239. [Google Scholar] [CrossRef]
- Gao, X.Y. Open-ocean shallow-water dynamics via a (2+1)-dimensional generalized variable-coefficient Hirota-Satsuma-Ito system: Oceanic auto-Bäcklund transformation and oceanic solitons. China Ocean. Eng. 2025, in press. [CrossRef]
- Gao, X.Y. In an ocean or a river: Bilinear auto-Bäcklund transformations and similarity reductions on an extended time-dependent (3+1)-dimensional shallow water wave equation. China Ocean. Eng. 2025, 39, 160–165. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Odibat, Z.; Aldhaifallah, M.; Nisar, K.S. A comparison study of two modified analytical approach for the solution of nonlinear fractional shallow water equations in fluid flow. AIMS Math. 2020, 5, 3035–3055. [Google Scholar] [CrossRef]
- Neamaty, A.; Agheli, B.; Darzi, R. Applications of homotopy perturbation method and Elzaki transform for solving nonlinear partial differential equations of fractional order. J. Nonlin. Evolut. Equat. Appl. 2016, 2015, 91–104. [Google Scholar]
- Ali, L.; Zou, G.; Li, N.; Mehmood, K.; Fang, P.; Khan, A. Analytical treatments of time-fractional seventh-order nonlinear equations via Elzaki transform. J. Eng. Math. 2024, 145, 1. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Sedeeg, A.K.H. A coupling Elzaki transform and homotopy perturbation method for solving nonlinear fractional heat-like equations. Am. J. Math. Comput. Model 2016, 1, 15–20. [Google Scholar]
- Bhalekar, S.; Daftardar-Gejji, V. Convergence of the new iterative method. Int. J. Differ. Equ. 2011, 2011, 989065. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).