Pythagorean Fuzzy Overlap Functions and Corresponding Fuzzy Rough Sets for Multi-Attribute Decision Making

Abstract

As a non-associative connective in fuzzy logic, the analysis and research of overlap functions have been extended to many generalized cases, such as interval-valued and intuitionistic fuzzy overlap functions (IFOFs). However, overlap functions face challenges in the Pythagorean fuzzy (PF) environment. This paper first extends overlap functions to the PF domain by proposing PF overlap functions (PFOFs), discussing their representable forms, and providing a general construction method. It then introduces a new PF similarity measure which addresses issues in existing measures (e.g., the inability to measure the similarity of certain PF numbers) and demonstrates its effectiveness through comparisons with other methods, using several examples in fractional form. Based on the proposed PFOFs and their induced residual implication, new generalized PF rough sets (PFRSs) are constructed, which extend the PFRS models. The relevant properties of their approximation operators are explored, and they are generalized to the dual-domain case. Due to the introduction of hesitation in IF and PF sets, the approximate accuracy of classical rough sets is no longer applicable. Therefore, a new PFRS approximate accuracy is developed which generalizes the approximate accuracy of classical rough sets and remains applicable to the classical case. Finally, three multi-criteria decision-making (MCDM) algorithms based on PF information are proposed, and their effectiveness and rationality are validated through examples, making them more flexible for solving MCDM problems in the PF environment.

1. Introduction

Fuzzy set theory and rough set theory are two effective tools for dealing with fuzzy and uncertain information. In 1965, L.A. Zadeh proposed the fuzzy set theory [1], marking the birth of fuzzy mathematics. The core of fuzzy mathematics is the fuzzy sets, which aims to imitate the fuzzy thinking of the human brain and provide effective ideas and methods for solving various practical problems, especially the processing problems of complex systems with human intervention. It has found extensive applications in fields such as healthcare diagnosis [2], system evaluation [3], decision making [4], and other domains. In 1982, Pawlak first gave the concept of rough set theory [5], where the objective is to classify known knowledge through the equivalence relations, construct upper and lower approximate operators, and use known knowledge to describe unknown knowledge. It has been effectively utilized in fields such as machine learning [6], pattern analysis [7], knowledge discovery [8], and various other domains. In 1990, based on fuzzy sets and rough sets, the scholars Dubois et al. proposed fuzzy rough sets (FRSs) [9], where they introduced fuzzy relations into rough sets, enriched the rough set models, and expanded the scope of application of rough sets. Currently, there are many research results on fuzzy rough sets [10,11,12,13,14].

In many practical fuzzy problems, the membership and non-membership of classical fuzzy sets are often insufficient to explain the relationship between objects and sets. For example, in simulated voting problems, in addition to approval and disapproval, there is also the operation of abstention to remain neutral. Obviously, it is inaccurate to use classical fuzzy sets to deal with such problems. Therefore, in 1986, Atanassov introduced the hesitation degree to solve such problems and proposed IF sets [15]. IF sets are characterized by three parameters: membership, non-membership, and hesitation degree. Various generalized IFRS models have been studied thus far [16,17,18,19,20,21]. With the continuous in-depth study of many problems, researchers have found that the condition in which the sum of membership and non-membership degrees is less than or equal to one has become increasingly restrictive in solving certain problems. In 2013, Yager et al. proposed PF sets [22], which relaxed the constraint from the sum of membership and non-membership being less than one to the sum of their squares being less than or equal to one, greatly expanding the applicability of fuzzy set theory. Subsequently, the PF numbers [23] and the PF relations [24] were proposed. Naturally, PF sets have been introduced into rough set theory. Zhang et al. [25] first gave the definition of PFRSs. Since then, various generalized PFRS models have been proposed [26,27,28,29]. However, generalized PFRS models based on overlapping functions remain unexplored.

The process of combining a large amount of data from many different sources into a representative value is called information aggregation, and the mathematical models used to perform information aggregation are called aggregation functions. Bustince et al. proposed overlap functions in 2010 [30]. As a binary continuous aggregation function, this function emerged from addressing problems in image processing and classification tasks. Compared with the classical aggregation operators, namely t-norms and t-conorms, the overlap function is free from the constraints of “one as the unit element” and “associativity”. It has made rapid progress in both theory and applications since its proposal. There are many generalized overlap functions, such as interval-valued overlap functions [31] and IFOFs. However, existing research results have limited applicability in the PF domain.

This paper is mainly driven by two research motivations. First, since overlap functions are difficult to work with in the PF environment, they are extended to the PF domain, and a special lattice-valued overlap function, the PFOF, is proposed. Second, generalized PFRS models based on overlap functions have not been studied; thus, PFOFs are combined with rough set theory, and PF rough approximation operators are constructed using PFOFs and their induced fuzzy implications, leading to the proposal of a generalized PFRS model. The relationship between the research content of this paper and existing models is shown in Figure 1 (The blue part in the Figure 1 is the research content of this paper). Compared with classical PFRSs, PFRSs based on PFOFs offer greater flexibility by allowing different PFOFs to be used. (This flexibility is specifically demonstrated in Section 6.2.4 through a comparison between generalized PFRSs and the classical case).

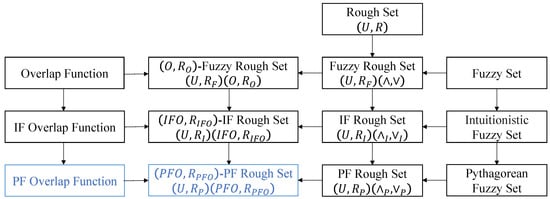
Figure 1. Relationships among related fuzzy rough sets.

The rest of this paper is organized as follows. Section 2 introduces some fundamental definitions which have been studied. Section 3 proposes the concept of PFOFs, discusses their representable forms, and presents a general construction method for PFOFs. Section 4 introduces a similarity measure for PF sets based on fuzzy scoring functions and verifies its effectiveness and rationality through examples. Section 5 proposes a novel PFRS based on PFOFs and the associated fuzzy residual implications, discusses its relevant properties, generalizes it to the dual-domain case, and constructs an approximation accuracy measure for PFRSs. Section 6 presents three MCDM methods based on PF information and verifies the effectiveness and rationality of the algorithm through examples. Finally, Section 7 summarizes the entire paper.

2. Fundamental Definitions

In this section, we go over several fundamental definitions related to fuzzy sets, overlap functions, and rough sets.

2.1. Fuzzy Sets

To address the ambiguity in concept extension and the uncertainty regarding whether a concept belongs to one category or another, American cybernetics expert L. A. Zadeh proposed the theory of fuzzy sets. Unlike classical set theory, which classifies elements as either belonging or not belonging to a set, fuzzy set theory innovatively introduces the concept of partial membership between elements and sets.

Definition 1

([1]). Let U be a domain and $\mu :U\to \left[0,1\right]$ denote the mapping of elements of domain U to $\left[0,1\right]$. Then, we define a fuzzy set M on domain U as follows:

$$\begin{array}{c}\hfill M=\left\{(m,{\mu }_F\left(m\right))\right|m\in U\},\end{array}$$

where ${\mu }_F\left(m\right)$ denotes the the degree to which m belongs to M and satisfies $0\le {\mu }_F\left(m\right)\le 1$.

Atanassov introduced the hesitation degree on the basis of the traditional fuzzy sets and described uncertain information in terms of three aspects: membership, non-membership, and hesitation.

Definition 2

([15]). Let U be a domain and ${\mu }_I,v_I:U\to [0,1]$ denote the mappings of the elements of domain U to $[0,1]$. Then, we define an IF set Z on domain U as follows:

$$\begin{array}{c}\hfill Z=\left\{(z,{\mu }_I\left(z\right),v_I\left(z\right),{\pi }_I\left(z\right))\right|z\in U\},\end{array}$$

where ${\mu }_I\left(z\right)$ denotes the degree to which z belongs to Z, $v_I\left(z\right)$ denotes the the degree to which z does not belong to Z which satisfies $0\le {\mu }_I\left(z\right)+v_I\left(z\right)\le 1$, ${\pi }_I\left(z\right)=1-{\mu }_I\left(z\right)-v_I\left(z\right)$, which denotes the hesitation of z concerning Z.

Yager proposed PF sets based on IF sets, relaxing the restrictions on membership and non-membership and allowing evaluators to assign values within a wider range, thereby more accurately describing the uncertainty of things and better reflecting reality.

Definition 3

([22]). Let U be a domain and ${\mu }_P,v_P:U\to [0,1]$ denote the mappings of the elements of domain U to $[0,1]$. Then, we define a PF set B on domain U as follows:

$$\begin{array}{c}\hfill B=\left\{(b,{\mu }_P\left(b\right),v_P\left(b\right),{\pi }_P\left(b\right))\right|b\in U\},\end{array}$$

where ${\mu }_P\left(b\right)$ denotes the degree to which b belongs to B, $v_P\left(b\right)$ denotes the degree to which b does not belong to B which satisfies $0\le {\mu }_P^2\left(b\right)+v_P^2\left(b\right)\le 1,{\pi }_P\left(b\right)=\sqrt{1-{{\mu }_P}^2\left(b\right)-{{\nu }_P}^2\left(b\right)}$, which denotes the hesitation of b concerning B.

Remark 1.

(1) The difference between classical sets and fuzzy sets

The boundaries of classical sets are clear. There is no element that belongs to a set and does not belong to it. For example, for a domain $u=\{a,b,c\}$, where a and b are even numbers and c is an odd number, the even-number set on the domain u is $\{a,b\}$, and the odd-number set is $\left\{c\right\}$. There is no element which is both even and odd.

The boundary of a fuzzy set is fuzzy and uncertain. An element can partially belong to a set, with the degree of membership indicating how much an element belongs to the set. This degree typically ranges between $[0,1]$. For example, the concept of height is fuzzy. If 60% of people think that a height of 180 cm is tall, then we can use 0.6 to represent the degree to which 180 cm belongs to the set of tall people. If, for a fuzzy set on the domain U, the degree of membership of each element is either zero or one, then it degenerates into a classical set. Therefore, classical sets are a special case of fuzzy sets.

(2) The difference between classical fuzzy sets, IF sets, and PF sets

For some practical problems, it is difficult to handle them solely with classical fuzzy sets. For example, in a voting problem, if 10 people vote for an activity, with 4 in favor, 3 against, and 3 unable to participate for some reason, then using a classical fuzzy set to represent support for the activity may not work well. If the membership function μ represents support for the activity, then $\mu =0.4$, and since the sum of membership and non-membership in the classical fuzzy set is one, only the non-membership degree v can represent the degree of non-voting and opposition (i.e., $v=0.6$), which leads to information loss. Therefore, the IF set introduces the hesitation degree π to solve this problem. IF sets satisfy $\mu +v+\pi =1$, where μ is the degree of membership, v is the degree of non-membership, and π is the hesitation, representing the uncertainty in the membership relationship. PF sets, based on IF sets, extend the condition $\mu +v+\pi =1$ to ${\mu }^2+v^2+\pi =1$, expanding the range which IF sets can represent and enhancing their applicability.

2.2. Overlap Functions

Definition 4

([30]). A binary function $O:{[0,1]}^2\to [0,1]$ is called an overlap function; if $\forall a,b,c\in [0,1]$, then it satisfies the following conditions:

a. 

Commutative: $O(a,b)=O(b,a)$;

b. 

Boundary condition: $O(a,b)=0\iff ab=0$;

c. 

Boundary condition: $O(a,b)=1\iff ab=1$;

d. 

Monotonicity: If $b\le c$, then $O(a,b)\le O(a,c)$;

e. 

Continuity.

If O satisfies $O(a,1)\le a$ for all $a\in [0,1]$, then O is called one-section deflation; if O satisfies $O(a,1)\ge a$ for all $a\in [0,1]$, then O is called one-section inflation.

Definition 5

([32]). We define the function $R_O:{[0,1]}^2\to [0,1]$ as follows:

$$\begin{array}{c}\hfill R_O(a,b)=max\{c\in [0,1]|O(a,c)\le b\},\end{array}$$

where O is an overlap function. Then, we call the function $R_O$ a residual implication induced by O.

2.3. Rough Sets

Definition 6

([5]). Let U be a domain. Any subset of $U\times U=\left\{(c_1,c_2)\right|c_1,c_2\in U\}$ is called a binary relation on the domain U.

Let R be a binary relation on U. R is called reflexive if R satisfies $\forall c\in U,(c,c)\in R$. R is called symmetric if R satisfies $\forall c_1,c_2\in U$, if $(c_1,c_2)\in R$, then $(c_2,c_1)\in R$. R is called transitive if R satisfies $\forall c_1,c_2,c_3\in U$, if $(c_1,c_2)\in R$ and $(c_2,c_3)\in R$, then $(c_1,c_3)\in R$.

R on the domain U which satisfies the reflexive, symmetric, and transitive relations is called an equivalence relation on U. $(U,R)$ is called a Pawlak approximate space.

Definition 7

([5]). Let $(U,R)$ be a Pawlak approximation space, where U is a domain and R is an equivalence relation on U. C is a subset of the domain U. Then, the rough approximation operators of C are defined as follows:

$$\begin{array}{c}\hfill R\downarrow C={\cup }_{c\in U}\left\{{\left[c\right]}_R\right|{\left[c\right]}_R\subseteq C\},\\ \hfill R\uparrow C={\cup }_{c\in U}\left\{{\left[c\right]}_R\right|{\left[c\right]}_R\cap C\ne \varnothing \},\end{array}$$

where ${\left[c\right]}_R$ denotes the equivalence class of c under the equivalence relation R.

Remark 2.

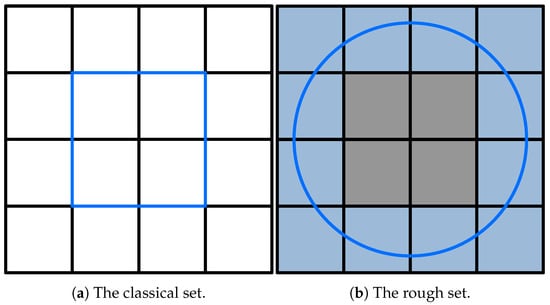
We use Figure 2 to illustrate the difference between rough sets and classical sets.

Figure 2. Difference between rough sets and classical sets.

We regard each square in Figure 2a as an element, and all the squares together form a domain. The blue box represents a set. As shown in the figure, the blue box contains the four elements in the center of the domain. Therefore, the set is described by the elements in the domain, making it a classical set.

From Figure 2b, we can see that the blue box not only completely contains the four elements in the center of the domain but also partially contains other elements. This scenario extends beyond the scope of classical sets. We use rough sets to represent this situation. The gray area in the figure represents the four elements which are completely contained, corresponding to the lower approximation of the set. The entire domain represents the upper approximation of the set, which includes both the gray and blue areas. Through the upper and lower approximations, we can represent undefined or uncertain sets.

Definition 8

([5]). Let $(U,R)$ be an approximation space $\varnothing \ne C\subseteq U$:

(1) 

The approximation accuracy of set C is defined as follows:

$$\begin{array}{c}\hfill {\alpha }_R\left(C\right)={\displaystyle \frac{|R\downarrow C|}{|R\uparrow C|}},\end{array}$$

where $\left|C\right|$ denotes the cardinality of the set C. It is stipulated that ${\alpha }_R(\varnothing )=1$.

(2) 

The roughness of set X is defined as follows:

$$\begin{array}{c}\hfill {\rho }_R\left(C\right)=1-{\alpha }_R\left(C\right).\end{array}$$

Definition 9

([9]). Let $R_F$ be a fuzzy relation on U. $R_F$ is called reflexive if $R_F$ satisfies $\forall m\in U,$$R_F(m,m)=1$. $R_F$ is called symmetric if $R_F$ satisfies $\forall m_1,m_2\in U,R_F(m_1,m_2)=R_F(m_2,m_1)$. $R_F$ is called transitive if $R_F$ satisfies $\forall m_1,m_2,m_3\in U$, $R_F(m_1,m_2)\wedge R_F(m_2,m_3)\le R_F(m_1,m_3)$.

$R_F$ on the domain U which satisfies the reflexive, symmetric, and transitive relations is called a fuzzy equivalence relation on U.

Definition 10

([9]). Let $(U,R_F)$ be a fuzzy approximation space, where U is a domain and $R_F$ is a fuzzy binary relation on U. M is a fuzzy set on U. Then, the fuzzy rough approximation operators of M are defined as follows:

$$\begin{array}{c}\hfill R_F\downarrow M\left(m_1\right)={\wedge }_{m_2\in U}(M\left(m_2\right)\vee (1-R_F(m_1,m_2))),\\ \hfill R_F\uparrow M\left(m_1\right)={\vee }_{m_2\in U}(M\left(m_2\right)\wedge R_F(m_1,m_2)),\end{array}$$

If the fuzzy set M satisfies $R_F\downarrow M\ne R_F\uparrow M$, then M is called undefinable, and the pair $(R_F\downarrow M,R_F\uparrow M)$ is called an FRS.

Remark 3.

If certain factors in classical rough sets are fuzzified, such as replacing the equivalence relation with a fuzzy one or replacing classical sets with fuzzy sets (both can be performed simultaneously), then classical rough sets become fuzzy rough sets. Therefore, fuzzy rough sets generalize classical rough sets.

3. PF Overlap Functions

In this section, we first give the definition of PFOFs, introduce the concept of representable PFOFs, and finally present a general method for generating PFOFs.

Definition 11.

Let $L_P$ be the set of all pairs $a=(a_1,a_2)$, where $a,b\in [0,1]$ and $a_1^2+a_2^2\le 1$. We define a partial order ${\le }_P$ on $L_P$ as follows. For any $a=(a_1,a_2),b=(b_1,b_2)\in L_P$, $a{\le }_{P}b$ if and only if $a_1\le b_1$ and $a_2\ge b_2$.

Theorem 1.

The partially ordered set $L_P$ is a complete lattice, that is, for any subset $S\subseteq L_P$, the supremum $sup\left(S\right)$ and infimum $inf\left(S\right)$ exist in $L_P$.

Proof. 

Let $S\subseteq L_P$ be an arbitrary subset. We define

$$\begin{array}{c}\hfill A=\{a\in [0,1]\mid \exists b\in [0,1]s.t.(a,b)\in S\},\\ \hfill B=\{b\in [0,1]\mid \exists a\in [0,1]s.t.(a,b)\in S\}.\end{array}$$

Since $A,B\subseteq [0,1]$, let $a^{*}=sup\left(A\right),b^{*}=inf\left(B\right)$. We claim that $(a^{*},b^{*})\in L_P$ and that it serves as the lowest upper bound of S in the order $L_P$.

Claim 1.

${\left(a^{*}\right)}^2+{\left(b^{*}\right)}^2\le 1.$

Take any $x\in A$. By the definition of A, there exists $y\in B$ such that $(x,y)\in S$. Since $S\subseteq L_P$, we know $x^2+y^2\le 1$, and hence $y\le \sqrt{1-x^2}$. But $b^{*}$ is the infimum of all such $y\in B$, and thus for every $x\in A$, we have $b^{*}\le y\le \sqrt{1-x^2}$. In particular, since x can be arbitrarily chosen to be close to $a^{*}$, letting $x\to a^{*}$ yields $b^{*}\le \sqrt{1-{\left(a^{*}\right)}^2}$. When squaring both sides, ${\left(a^{*}\right)}^2+{\left(b^{*}\right)}^2\le 1$, and thus $(a^{*},b^{*})\in L_P$.

Claim 2.

$(a^{*},b^{*})$ is an upper bound of S.

Take any $(x,y)\in S$. With the construction of A and B, we have $x\in A,y\in B$, and thus $x\le a^{*},y\ge b^{*}$. Recall that ${\le }_P$ is defined by $(x_1,x_2){\le }_P(y_1,y_2)$ if and only if $x_1\le y_1$ and $x_2\ge y_2$, and hence $(x,y){\le }_P(a^{*},b^{*})$. Thus, $(a^{*},b^{*})$ is an upper bound of S under ${\le }_P$.

Claim 3.

$(a^{*},b^{*})$ is the lowest upper bound of S under ${\le }_P$.

Suppose $(u,v)$ is any other upper bound of S. Then, for every $(x,y)\in S$, we have $(x,y){\le }_P(u,v),$ which means $x\le u$ and $y\ge v$. In particular, $a^{*}=sup\left(A\right)\le u,b^{*}=inf\left(B\right)\ge v$. Thus, we have $(a^{*},b^{*}){\le }_P(u,v)$, showing that $(a^{*},b^{*})$ is the lowest upper bound of S in ${\le }_P$.

Under Claims 1–3, the element $(a^{*},b^{*})$ is precisely $sup\left(S\right)$ in $(L_P,{\le }_P)$.

A completely analogous argument (reversing the roles of ≤ and ≥ or with a “dual” proof) shows that S also has an infimum in $L_P$. Consequently, $(L_P,{\le }_P)$ is a complete lattice. □

Definition 12.

A binary function $PO:L_P^2\to L_P$ is called a PFOF if for any $a,b,c\in L_P$, it satisfies the following:

a. 

Commutativity: $PO(a,b)=PO(b,a)$;

b. 

Boundary condition: $PO(a,b)=(0,1)\iff a$ or $b=(0,1)$;

c. 

Boundary condition: $PO(a,b)=(1,0)\iff a=b=(1,0)$;

d. 

Monotonicity: $PO(a,b){\le }_{P}PO(a,c)ifb{\le }_{P}c$;

e. 

Continuity: $\forall i\in I,b_i\in L_P,PO(a,{\vee }_P^{i\in I}{b}_i)={\vee }_P^{i\in I}PO(a,b_i),PO(a,{\wedge }_P^{i\in I}{b}_i)={\wedge }_P^{i\in I}PO(a,b_i),$ where ${\vee }_P,{\wedge }_P$ are the supremum and infimum operators of $(L_p,{\le }_p)$, respectively.

If $PO$ satisfies $PO(a,(1,0)){\le }_{P}a$ for all $a\in L_P$, then $PO$ is called one-section deflation, and if $PO$ satisfies $PO(a,(1,0)){\ge }_{P}a$ for all $a\in L_P$, then $PO$ is called one-section inflation.

Proposition 1.

For any $a=(a_1,a_2),b=(b_1,b_2)\in L_P$, we define the function $PO$ as follows:

$$\begin{array}{c}\hfill PO(a,b)=(\sqrt{O(a_1^2,b_1^2)},\sqrt{1-O(1-a_2^2,1-b_2^2)}),\end{array}$$

where O is an overlap function. Then, we call $PO$ a PFOF, $PO$ satisfies one-section deflation if O satisfies one-section deflation, and $PO$ satisfies one-section inflation if O satisfies one-section inflation.

Proof. 

(a)

Because of the commutativity of O, for all $a=(a_1,a_2),b=(b_1,b_2)\in L_P$, we have

$$\begin{array}{cc}\hfill PO(a,b)& =(\sqrt{O(a_1^2,b_1^2)},\sqrt{1-O(1-a_2^2,1-b_2^2)})\hfill \\ \hfill & =(\sqrt{O(b_1^2,a_1^2)},\sqrt{1-O(1-b_2^2,1-a_2^2)})\hfill \\ \hfill & =PO(b,a);\hfill \end{array}$$

(b)

According to Definition 11 and the boundary condition of O, we can obtain $PO(a,b)=(0,1)\iff \sqrt{O(a_1^2,b_1^2)}=0,\sqrt{1-O(1-a_2^2,1-b_2^2)}=1\iff O(a_1^2,b_1^2)=0,O(1-a_2^2,1-b_2^2)=0\iff a_1^2\wedge b_1^2=0,a_2^2\vee b_2^2=1\iff a=(0,1)$ or $b=(0,1);$

(c)

According to the boundary condition of O, we have $PO(a,b)=(1,0)\iff \sqrt{O(a_1^2,b_1^2)}=1,\sqrt{1-O(1-a_2^2,1-b_2^2)}=0\iff O(a_1^2,b_1^2)=1,O(1-a_2^2,1-b_2^2)=1\iff a_1^2\wedge b_1^2=1,a_2^2\vee b_2^2=0\iff a=b=(1,0);$

(d)

If $b{\le }_{P}c$, then according to Definition 11, we can obtain $b_1\le c_1,b_2\ge c_2$, and thus we have $b_1^2\le c_1^2,1-b_2^2\le 1-c_2^2$. By letting $PO(a,b)=(u_1,u_2),PO(a,c)=(v_1,v_2)$, we have $u_1=\sqrt{O(a_1^2,b_1^2)},u_2=\sqrt{1-O(1-a_2^2,1-b_2^2)}$ and $v_1=\sqrt{O(a_1^2,c_1^2)},v_2=\sqrt{1-O(1-a_2^2,1-c_2^2)}$. From the monotonicity of the overlap function, we know that $O(a_1^2,b_1^2)\le O(a_1^2,c_1^2),O(1-a_2^2,1-b_2^2)\le O(1-a_2^2,1-c_2^2)$, and thus there is $u_1\le v_1,u_2\ge v_2$; that is, $PO(a,b){\le }_{P}PO(a,c)$;

(e)

Firstly, we prove $\forall i\in I,b_i\in L_P,PO(a,{\vee }_P^{i\in I}{b}_i)={\vee }_P^{i\in I}PO(a,b_i)$. Because of the continuity of the overlap function, we have

$$\begin{array}{cc}\hfill O(a_1^2,{\vee }_{i\in I}{b}_{i1}^2)& ={\vee }_{i\in I}O(a_1^2,b_{i1}^2),\hfill \\ \hfill O(1-a_2^2,1-{\wedge }_{i\in I}{b}_{i2}^2)& =O(1-a_2^2,{\vee }_{i\in I}(1-b_{i2}^2))={\vee }_{i\in I}O(1-a_2^2,1-b_{i2}^2),\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill PO(a,{\vee }_P^{i\in I}{b}_i)& =(\sqrt{O(a_1^2,{\vee }_{i\in I}{b}_{i1}^2)},\sqrt{1-O(1-a_2^2,1-{\wedge }_{i\in I}{b}_{i2}^2)})\hfill \\ & =(\sqrt{O(a_1^2,{\vee }_{i\in I}{b}_{i1}^2)},\sqrt{1-O(1-a_2^2,{\vee }_{i\in I}(1-b_{i2}^2))})\hfill \\ & =({\vee }_{i\in I}\sqrt{O(a_1^2,b_{i1}^2)},\sqrt{1-{\vee }_{i\in I}O(1-a_2^2,1-b_{i2}^2)})\hfill \\ & =({\vee }_{i\in I}\sqrt{O(a_1^2,b_{i1}^2)},{\wedge }_{i\in I}\sqrt{1-O(1-a_2^2,1-b_{i2}^2)})\hfill \\ & ={\vee }_P^{i\in I}(\sqrt{O(a_1^2,b_{i1}^2)},\sqrt{1-O(1-a_2^2,1-b_{i2}^2)})\hfill \\ & ={\vee }_P^{i\in I}PO(a,b_i).\hfill \end{array}$$

Similarly, we can obtain $\forall i\in I,b_i\in L_P,PO(a,{\wedge }_P^{i\in I}{b}_i)={\wedge }_P^{i\in I}PO(a,b_i)$. Therefore, $PO(a,b)$ is continuous.

(f)

For $PO((1,0),a)=(\sqrt{O(1,a_1^2)},\sqrt{1-O(1,1-a_2^2)})$, if O satisfies one-section deflation, then $\sqrt{O(1,a_1^2)}\le a_1,\sqrt{1-O(1,1-a_2^2)}\ge a_2$, and thus $PO((1,0),a){\le }_{P}a$, $PO$ satisfies one-section deflation. Similarly, if O satisfies one-section inflation, then $PO$ satisfies one-section inflation.

□

Example 1.

(1) 

Given $O(a,b)={\displaystyle \frac{ab(a+b)}{2}}$, then

$$\begin{array}{c}\hfill PO(a,b)=(\sqrt{{\displaystyle \frac{a_1^2{b}_1^2(a_1^2+b_1^2)}{2}}},\sqrt{1-{\displaystyle \frac{(1-a_2^2)(1-b_2^2)(2-a_2^2-b_2^2)}{2}}})\end{array}$$

is a PFOF;

(2) 

Given $O(a,b)=min(a,b)$, then

$$\begin{array}{c}\hfill PO(a,b)=(\sqrt{min(a_1^2,b_1^2)},\sqrt{1-min(1-a_2^2,1-b_2^2)})\end{array}$$

is a PFOF.

Definition 13.

PFOF is representable if $\forall a=(a_1,a_2),b=(b_1,b_2)\in L_P$, and it can be expressed as $PO(a,b)=(\sqrt{O(a_1^2,b_1^2)},\sqrt{1-O(1-a_2^2,1-b_2^2)})$, where O is an overlap function.

Remark 4.

We can break down the expressible form of the PFOF into two parts for clarity. The first part, $\sqrt{O(a_1^2,b_1^2)}$, represents the aggregation of the membership part of the PF fuzzy numbers, where O is the overlap function, and $a_1$ and $b_1$ represent the membership values of the two PF fuzzy numbers. The second part, $\sqrt{1-O(1-a_2^2,1-b_2^2)}$, is the dual of the first part, except that $a_2$ and $b_2$ represent the non-membership values of the two PF fuzzy numbers. This part aggregates the non-membership values of the two PF fuzzy numbers.

Example 2.

(1) 

The PFOFs in Example 1 are all representable PFOFs;

(2) 

$PO(a,b)=(\sqrt{min(1,a_1^2{b}_1^2,(1-a_2^2)(1-b_2^2)},\sqrt{1-min(1,a_1^2{b}_1^2,(1-a_2^2)(1-b_2^2)})$ is an unrepresentable PFOF.

We can easily find that $PO$ is a PFOF (it satisfies the conditions of Definition 12). Let $O(a_1,b_1)=min(1,a_1{b}_1,(1-a_2)(1-b_2))$. There are four variables in the function $O(a_1,b_1)$, namely $a_1$, $b_1$, $a_2$, and $b_2$, where if $a_1=b_1=1$, we have $O(1,1)=min(1,1,(1-a_2)(1-b_2))$. The value of the function $O(1,1)$ also depends on $a_2,b_2$. If $a_2\vee b_2\ne 0$, then we can find $O(1,1)\ne 1$, and $O(a_1,b_1)$ does not satisfy the condition of the overlap function. It is proven that $PO(a,b)$ is an unrepresentable PFOF.

Proposition 2.

A binary function $PO:L_P^2\to L_P$ is a PFOF if there are two functions $u(a,b)$ and $v(a,b):{[0,1]}^2\to [0,1]$ such that $\forall a=(a_1,a_2),b=(b_1,b_2)\in L_P$:

$$\begin{array}{c}\hfill PO(a,b)=(\sqrt{{\displaystyle \frac{u(a_1^2,b_1^2)}{u(a_1^2,b_1^2)+v(a_1^2,b_1^2)}}},\sqrt{1-{\displaystyle \frac{u(1-a_2^2,1-b_2^2)}{u(1-a_2^2,1-b_2^2)+v(1-a_2^2,1-b_2^2)}}}),\end{array}$$

where $u(a,b),v(a,b)$ satisfies the following:

a. 

$u(a,b)$ and $v(a,b)$ are symmetric;

b. 

u is non-decreasing and v is non-increasing;

c. 

$u(a,b)=0\iff ab=0$;

d. 

$v(a,b)=0\iff ab=1$;

e. 

u and v are continuous.

Example 3.

Let $\left\{\begin{array}{c}u(a,b)=a^2{b}^2\hfill \\ v(a,b)=1-a^2{b}^2\hfill \end{array}\right.$. Then, $PO(a,b)=(a_1^2{b}_1^2,\sqrt{1-{(1-a_2^2)}^2{(1-b_2^2)}^2})$ is a PFOF.

4. Similarity Measure of PF Sets Based on Fuzzy Score Functions

In this section, we propose a new similarity measure for PF sets based on fuzzy score functions and use several examples to compare it with existing methods, demonstrating its effectiveness and rationality.

4.1. A New Similarity Measure for PF Sets

Before introducing the similarity measure, we first give the concept of fuzzy score functions.

Definition 14.

A binary function $\mathcal{FS}:{[0,1]}^2\to [0,1]$ is called a fuzzy score function if $\forall a,b,c,d\in [0,1]$ and it satisfies the following:

a. 

Boundary condition: $\mathcal{FS}(a,b)=0\iff a=0$ and $b=1$;

b. 

Boundary condition: $\mathcal{FS}(a,b)=1\iff a=1$ and $b=0$;

c. 

Monotonicity: $\mathcal{FS}(a,b)\le \mathcal{FS}(c,d)\iff a\le c$ and $b\ge d$;

d. 

Continuity.

Example 4.

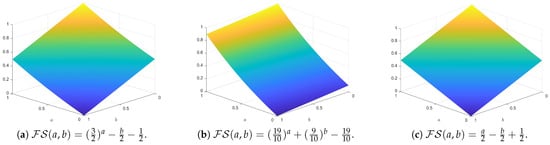
We define functions as follows:

(1) 

$\mathcal{FS}(a,b)={\left({\displaystyle \frac{3}{2}}\right)}^a-{\displaystyle \frac{b}{2}}-{\displaystyle \frac{1}{2}};$

(2) 

$\mathcal{FS}(a,b)={\left({\displaystyle \frac{19}{10}}\right)}^a+{\left({\displaystyle \frac{9}{10}}\right)}^b-{\displaystyle \frac{19}{10}};$

(3) 

$\mathcal{FS}(a,b)={\displaystyle \frac{a}{2}}-{\displaystyle \frac{b}{2}}+{\displaystyle \frac{1}{2}}.$

It is straightforward to confirm that the functions above are all fuzzy score functions. Figure 3 shows images with different $\mathcal{FS}$ values.

Figure 3. Images with different $\mathcal{FS}$ values.

Remark 5.

We apply the fuzzy score functions to calculate the score value of the PF numbers, where for any $a=(a_1,a_2),b=(b_1,b_2)\in L_P$, from the definition of the fuzzy score functions, we can clearly find the following:

a. 

$\mathcal{FS}(a_1,a_2)=0\iff a=(0,1)$;

b. 

$\mathcal{FS}(a_1,a_2)=1\iff a=(1,0)$;

c. 

$\mathcal{FS}(a_1,a_2)\le \mathcal{FS}(b_1,b_2)\iff a{\le }_{P}b$.

Then, we present a new PF set similarity measure based on fuzzy score functions. First, we introduce the definition of a generalized PF set similarity measure.

Definition 15

([33]). Let U be the domain. $PF\left(U\right)$ denotes all PF sets on the domain U, and the mapping $\mathcal{S}:PF{\left(U\right)}^2\to [0,1]$ is called a similarity measure of the PF set if $\forall B_1,B_2,B_3\in PF\left(U\right)$ and thus satisfies the following:

a. 

$0\le \mathcal{S}(B_1,B_2)\le 1$;

b. 

$\mathcal{S}(B_1,B_2)=\mathcal{S}(B_2,B_1)$;

c. 

$\mathcal{S}(B_1,B_2)=1\iff B_1=B_2$;

d. 

If $B_1{\subseteq }_P{B}_2{\subseteq }_P{B}_3$, then $\mathcal{S}(B_1,B_3)\le min(\mathcal{S}(B_1,B_2),\mathcal{S}(B_2,B_3))$, where ${\subseteq }_P$ is the inclusion operator of the PF sets.

Definition 16.

Let $U(b_1,b_2,\cdots ,b_n)$ be a domain and $\forall B_1,B_2\in PF\left(U\right),\mathcal{FS}:{[0,1]}^2\to [0,1]$ be the fuzzy score functions. Then, we define the following mapping $\mathcal{S}:PF{\left(U\right)}^2\to [0,1]$ as the PF sets similarity measure:

$$\begin{array}{c}\hfill \mathcal{S}(B_1,B_2)={\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}\end{array}$$

The following conditions are stipulated:

(1) 

$\mathcal{S}(\varnothing ,\varnothing )=1;$

(2) 

If $\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right))=\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))=0,$ then

$$\begin{array}{c}\hfill {\displaystyle \frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}=1.\end{array}$$

Remark 6.

We will analyze the PF set similarity measure in Definition 16 from the inside out. First, $\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right))$ and $\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))$ represent the results of the fuzzy scoring function on the ith element in PF sets $B_1$ and $B_2$, respectively, which can be understood as their fuzzy scoring values. Therefore, ${\displaystyle \frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}$ represents the ratio of the smaller number to the larger number in the fuzzy scoring values of the ith element in PF sets $B_1$ and $B_2$, which can reflect the similarity between the ith element in PF sets $B_1$ and $B_2$. ${\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}$ represents the average of all elements in PF sets $B_1$ and $B_2$ after the above operation, which is used to reflect the overall similarity between PF sets $B_1$ and $B_2$.

Theorem 2.

The PF set similarity measure proposed in Definition 16 satisfies all the conditions of the generalized PF set similarity measure in Definition 15.

Proof. 

(a) If $B_1=B_2=\varnothing$, $\mathcal{S}(\varnothing ,\varnothing )=1$, if $B_1$ and $B_2$ are not all ∅, then because $0\le \mathcal{FS}\le 1$, $\forall i\in I(1,2,\cdots ,n)$, we have

$$\begin{array}{cc}\hfill 0& \le min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))\hfill \\ & \le max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))\le 1,\hfill \end{array}$$

Then, we have

$$\begin{array}{c}\hfill 0\le {\displaystyle \frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}\le 1,\end{array}$$

We can obtain

$$\begin{array}{c}\hfill 0\le \sum _{i=1}^n{\displaystyle \frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}\le n,\end{array}$$

and therefore, there is

$$\begin{array}{c}\hfill 0\le {\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}=\mathcal{S}(B_1,B_2)\le 1;\end{array}$$

(b)

$$\begin{array}{cc}\hfill \mathcal{S}(B_1,B_2)& ={\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}\hfill \\ \hfill & ={\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right))}}{n}}\hfill \\ \hfill & =\mathcal{S}(B_2,B_1);\hfill \end{array}$$

(c) If $B_1=B_2\ne \varnothing$, $\forall i\in I$, we can obtain $min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),$$\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))=max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))$, and thus we have

$$\begin{array}{c}\hfill \mathcal{S}(B_1,B_2)={\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}={\displaystyle \frac{n}{n}}=1;\end{array}$$

By definition, if $B_1=B_2=\varnothing$, then $\mathcal{S}(B_1,B_2)=1$.

If $B_1\ne B_2$, according to the monotonicity of $\mathcal{FS}$, for some $i\in I_{sub}\subseteq I$, we can find that

$$\begin{array}{cc}\hfill 0& \le min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))\hfill \\ & <max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))\le 1,\hfill \end{array}$$

Then, for $i\in I$, there is

$$\begin{array}{c}\hfill 0\le \sum _{i=1}^n{\displaystyle \frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}<n,\end{array}$$

and furthermore

$$\begin{array}{c}\hfill 0\le {\displaystyle \frac{{\sum }_{i=1}^n\frac{min(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}{max(\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)),\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))}}{n}}=\mathcal{S}(B_1,B_2)<1,\end{array}$$

Thus, we find that if $B_1\ne B_2,\mathcal{S}(B_1,B_2)\ne 1$, hence $\mathcal{S}(B_1,B_2)=1\iff B_1=B_2$;

(d) If $B_1{\subseteq }_P{B}_2{\subseteq }_P{B}_3$, $\forall i\in I$, we obtain ${\mu }_P\left(B_1\left(b_i\right)\right)\le {\mu }_P\left(B_2\left(b_i\right)\right)\le {\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)\ge v_P\left(B_2\left(b_i\right)\right)\ge v_P\left(B_3\left(b_i\right)\right)$, and according to the monotonicity of $\mathcal{FS}$, we have $\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right))\le \mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right))\le \mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),$ $v_P\left(B_3\left(b_i\right)\right))$, and thus there is

$$\begin{array}{cc}\hfill \mathcal{S}(B_1,B_3)& ={\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_3\left(b_i\right)\right)}}{n}},\mathcal{S}(B_1,B_2)={\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)}}{n}},\hfill \\ \hfill \mathcal{S}(B_2,B_3)& ={\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_3\left(b_i\right)\right)}}{n}},\hfill \end{array}$$

We can obtain

$$\begin{array}{c}\hfill \mathcal{S}(B_1,B_3)={\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_3\left(b_i\right)\right)}}{n}}\le {\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)}}{n}}=\mathcal{S}(B_1,B_2),\\ \hfill \mathcal{S}(B_1,B_3)={\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_1\left(b_i\right)\right),v_P\left(B_1\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_3\left(b_i\right)\right)}}{n}}\le {\displaystyle \frac{{\sum }_{i=1}^n\frac{\mathcal{FS}({\mu }_P\left(B_2\left(b_i\right)\right),v_P\left(B_2\left(b_i\right)\right)}{\mathcal{FS}({\mu }_P\left(B_3\left(b_i\right)\right),v_P\left(B_3\left(b_i\right)\right)}}{n}}=\mathcal{S}(B_2,B_3),\end{array}$$

Therefore, $\mathcal{S}(B_1,B_3)\le min(\mathcal{S}(B_1,B_2),\mathcal{S}(B_2,B_3))$. □

4.2. Numerical Experiments

1. The numerical values in this section were derived from [34]. The $\mathcal{FS}$ in $\mathcal{S}$ is taken from Example 4(1). Table 1 presents the existing similarity measures, while Table 2 compares the numerical results obtained from the similarity measure in Definition 16 with those from existing methods.

Table 1. Existing similarity measures.

Author	Similarity Measure
Hung [35]	${\mathcal{S}}_{HY}(B_1,B_2)=1-{\displaystyle \frac{1}{n}}{\sum }_{i=1}^{n}max\left(\right|{\mu }_P\left(B_1\left(b_i\right)\right)-{\mu }_P\left(B_2\left(b_i\right)\right)|,|v_P\left(B_1\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right)\left|\right)$
Ye [36]	${\mathcal{S}}_Y(B_1,B_2)={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\displaystyle \frac{{\mu }_P\left(B_1\left(b_i\right)\right){\mu }_P\left(B_2\left(b_i\right)\right)+v_P\left(B_1\left(b_i\right)\right)v_P\left(B_2\left(b_i\right)\right)}{\sqrt{{\mu }_P{\left(B_1\left(b_i\right)\right)}^2+v_P{\left(B_1\left(b_i\right)\right)}^2}\sqrt{{\mu }_P{\left(B_2\left(b_i\right)\right)}^2+v_P{\left(B_2\left(b_i\right)\right)}^2}}}$
Chen [37]	${\mathcal{S}}_C(B_1,B_2)=1-{\displaystyle \frac{1}{2n}}{\sum }_{i=1}^n|{\mu }_P\left(B_1\left(b_i\right)\right)-v_P\left(B_1\left(b_i\right)\right)-({\mu }_P\left(B_2\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right))|$
Li [38]	${\mathcal{S}}_L(B_1,B_2)=1-\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n({({\mu }_P\left(B_1\left(b_i\right)\right)-{\mu }_P\left(B_2\left(b_i\right)\right))}^2+{(v_P\left(B_1\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right))}^2)}{2n}}}$
Hong [39]	${\mathcal{S}}_H(B_1,B_2)=1-{\displaystyle \frac{1}{2n}}{\sum }_{i=1}^n\left(\right|{\mu }_P\left(B_1\left(b_i\right)\right)-{\mu }_P\left(B_2\left(b_i\right)\right)|+|v_P\left(B_1\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right)\left|\right)$
Peng [40]	${\mathcal{S}}_P(B_1,B_2)=1-{\displaystyle \frac{1}{2n}}{\sum }_{i=1}^n|{\mu }_P\left(B_1\left(b_i\right)\right)-{\mu }_P\left(B_2\left(b_i\right)\right)-(v_P\left(B_1\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right))|$
Zhang [41]	${\mathcal{S}}_Z(B_1,B_2)={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left(2^{1-max\left(|{\mu }_P{\left(B_1\left(b_i\right)\right)}^2-{\mu }_P{\left(B_2\left(b_i\right)\right)}^2|,|v_P{\left(B_1\left(b_i\right)\right)}^2-v_P{\left(B_2\left(b_i\right)\right)}^2|,|{\pi }_P{\left(B_1\left(b_i\right)\right)}^2-{\pi }_P{\left(B_2\left(b_i\right)\right)}^2|\right)}-1\right)$
Qiao [34]	${\mathcal{S}}_Q(B_1,B_2)={\sum }_{i=1}^n{\omega }_i\sqrt[k]{O(N_a\left(\right|{\mu }_P\left(B_1\left(b_i\right)\right)-{\mu }_P\left(B_2\left(b_i\right)\right){|}^k),N_b\left(\right|v_P\left(B_1\left(b_i\right)\right)-v_P\left(B_2\left(b_i\right)\right){|}^k\left)\right)}$

Table 2. Calculation results of different similarity measures in numerical experiment 1.

Case	1	2	3	4
	${\mathit{b}}_{\mathbf{1}}=(\mathbf{0}.\mathbf{5},\mathbf{0}.\mathbf{5})$	${\mathit{b}}_{\mathbf{1}}=(\mathbf{0}.\mathbf{6},\mathbf{0}.\mathbf{4})$	${\mathit{b}}_{\mathbf{1}}=(\mathbf{0},\mathbf{0}.\mathbf{87})$	${\mathit{b}}_{\mathbf{1}}=(\mathbf{0}.\mathbf{6},\mathbf{0}.\mathbf{27})$
	${\mathit{b}}_{\mathbf{2}}=(\mathbf{0},\mathbf{0})$	${\mathit{b}}_{\mathbf{2}}=(\mathbf{0},\mathbf{0})$	${\mathit{b}}_{\mathbf{2}}=(\mathbf{0}.\mathbf{28},\mathbf{0}.\mathbf{55})$	${\mathit{b}}_{\mathbf{2}}=(\mathbf{0}.\mathbf{28},\mathbf{0}.\mathbf{55})$
${\mathcal{S}}_{HY}$	0.5000	0.4000	0.6800	0.6800
${\mathcal{S}}_Y$	$NAN$	$NAN$	0.8912	0.7794
${\mathcal{S}}_C$	1.0000	0.9000	0.7000	0.7000
${\mathcal{S}}_L$	0.5000	0.4901	0.6993	0.6993
${\mathcal{S}}_H$	0.5000	0.5000	0.7000	0.7000
${\mathcal{S}}_P$	1.0000	0.9000	0.7336	0.7444
${\mathcal{S}}_Z$	0.4142	0.3947	0.4596	0.6454
${\mathcal{S}}_Q$	0.5625	0.5376	0.8272	0.8272
Our method	0.9495	0.8689	0.1883	0.5391

From the numerical calculation results, we observe that certain similarity measures exhibit the following issues:

(1)

In Case 1, the calculated values of ${\mathcal{S}}_C$ and ${\mathcal{S}}_P$ are both one, yet $b_1\ne b_2$, which is unreasonable. Additionally, the similarity of ${\mathcal{S}}_Y$ with respect to the PF number $(0,0)$ cannot be calculated.

(2)

In both Case 1 and Case 2, while $b_2$ is the same, $b_1$ differs, yet the calculated result of ${\mathcal{S}}_H$ remains the same.

(3)

In both Case 3 and Case 4, $b_2$ is the same, but $b_1$ differs, and the calculated results for ${\mathcal{S}}_{HY}$, ${\mathcal{S}}_H$, ${\mathcal{S}}_C$, ${\mathcal{S}}_L$, and ${\mathcal{S}}_Q$ are identical.

These issues do not arise in the method we propose.

2. The following PF sets are given:

$$\begin{array}{cc}\hfill B_1& ={\displaystyle \frac{(0.3,0.3)}{b_1}}+{\displaystyle \frac{(0.4,0.4)}{b_2}}+{\displaystyle \frac{(0.4,0.4)}{b_3}}+{\displaystyle \frac{(0.4,0.4)}{b_4}};\hfill \\ \hfill B_2& ={\displaystyle \frac{(0.5,0.5)}{b_1}}+{\displaystyle \frac{(0.1,0.1)}{b_2}}+{\displaystyle \frac{(0.5,0.5)}{b_3}}+{\displaystyle \frac{(0.1,0.1)}{b_4}};\hfill \\ \hfill B_3& ={\displaystyle \frac{(0.5,0.4)}{b_1}}+{\displaystyle \frac{(0.4,0.5)}{b_2}}+{\displaystyle \frac{(0.3,0.3)}{b_3}}+{\displaystyle \frac{(0.2,0.2)}{b_4}};\hfill \\ \hfill B_4& ={\displaystyle \frac{(0.4,0.4)}{b_1}}+{\displaystyle \frac{(0.5,0.5)}{b_2}}+{\displaystyle \frac{(0.2,0.2)}{b_3}}+{\displaystyle \frac{(0.3,0.3)}{b_4}};\hfill \end{array}$$

Here, $\mathcal{FS}$ in $\mathcal{S}$ is taken from Example 4(2). Table 3 shows the similarity between B and other PF sets calculated by different similarity measures.

Table 3. Calculation results of different similarity measures in numerical experiment 2.

	$\mathcal{S}({\mathit{B}}_1,{\mathit{B}}_4)$	$\mathcal{S}({\mathit{B}}_2,{\mathit{B}}_4)$	$\mathcal{S}({\mathit{B}}_3,{\mathit{B}}_4)$	$\mathbf{Maximum}$
${\mathcal{S}}_{HY}$	0.8750	0.7500	0.9000	$\mathcal{S}(B_3,B_4)$
${\mathcal{S}}_Y$	1.0000	1.0000	0.9969	Unable to judge
${\mathcal{S}}_C$	1.0000	1.0000	0.9750	Unable to judge
${\mathcal{S}}_L$	0.8677	0.7261	0.9134	$\mathcal{S}(B_3,B_4)$
${\mathcal{S}}_H$	0.8750	0.7500	0.9250	$\mathcal{S}(B_3,B_4)$
${\mathcal{S}}_P$	1.0000	1.0000	0.9775	Unable to judge
${\mathcal{S}}_Z$	0.7722	0.6211	0.8726	$\mathcal{S}(B_3,B_4)$
${\mathcal{S}}_Q$	0.9825	0.9250	0.9925	$\mathcal{S}(B_3,B_4)$
Our method	0.7596	0.5619	0.7851	$\mathcal{S}(B_3,B_4)$

From Table 3, we can see that except for ${\mathcal{S}}_Y,{\mathcal{S}}_C$, and ${\mathcal{S}}_P$, the calculation results of other methods are all $\mathcal{S}(B_1,B_4)<\mathcal{S}(B_2,B_4)<\mathcal{S}(B_3,B_4)$.

Through the two experiments, it is shown that the PF similarity measure we proposed has certain effectiveness and rationality. Since the fuzzy scoring function is a family of functions, the similarity measure based on the fuzzy scoring function proposed in this paper is also a family of functions. Different fuzzy scoring functions can be selected for different problems, which has greater flexibility than existing methods.

5. PFRSs Based on PFOFs

In this section, we introduce a novel PFRS model derived from PFOFs, discuss its related properties, and extend it to the dual domain. Finally, we propose a new approximation accuracy measure for PFRSs.

Definition 17.

We define the function $R_{PO}:L_P^2\to L_P$ as

$$\begin{array}{c}\hfill R_{PO}(a,b)=sup\{c\in L_P:PO(a,c){\le }_{P}b\}\end{array}$$

where $PO$ is a PFOF. Then, we call the function $R_{PO}$ a residual implication induced by $PO$.

Example 5.

(1) 

Given $PO(a,b)=(a_1{b}_1,\sqrt{1-(1-a_2^2)(1-b_2^2)})$, we can find the induced residual implication as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}(1,0)& a_1\le b_{1}and{a}_2\ge b_2\\ (\sqrt{{\displaystyle \frac{1-b_2^2}{1-a_2^2}}},\sqrt{1-{\displaystyle \frac{1-b_2^2}{1-a_2^2}}})& a_1\le b_{1}and{a}_2<b_2\\ ({\displaystyle \frac{b_1}{a_1}},0)& a_1>b_{1}and{a}_2\ge b_2\\ ({\displaystyle \frac{b_1}{a_1}},\sqrt{1-{\displaystyle \frac{1-b_2^2}{1-a_2^2}}})& a_1>b_{1}and{a}_2<b_{2}and{\left({\displaystyle \frac{b_1}{a_1}}\right)}^2\le {\displaystyle \frac{1-b_2^2}{1-a_2^2}}\\ (\sqrt{{\displaystyle \frac{1-b_2^2}{1-a_2^2}}},\sqrt{1-{\displaystyle \frac{1-b_2^2}{1-a_2^2}}})& a_1>b_{1}and{a}_2<b_{2}and{\left({\displaystyle \frac{b_1}{a_1}}\right)}^2>{\displaystyle \frac{1-b_2^2}{1-a_2^2}}\end{array}\right.\end{array}$$

(2) 

Given $PO(a,b)=(\sqrt{min(a_1,b_1)},\sqrt{1-min(\sqrt{1-a_2^2},\sqrt{1-b_2^2})})$, we can find the induced residual implication as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}(1,0)& \sqrt{a_1}\le b_{1}and\sqrt{1-\sqrt{1-a_2^2}}\ge b_2\\ (1-b_2^2,\sqrt{1-{(1-b_2^2)}^2})& \sqrt{a_1}\le b_{1}and\sqrt{1-\sqrt{1-a_2^2}}<b_2\\ (b_1^2,0)& \sqrt{a_1}>b_{1}and\sqrt{1-\sqrt{1-a_2^2}}\ge b_2\\ (b_1^2,\sqrt{1-{(1-b_2^2)}^2})& \sqrt{a_1}>b_{1}and\sqrt{1-\sqrt{1-a_2^2}}<b_{2}and{b}_1^2\le 1-b_2^2\\ (1-b_2^2,\sqrt{1-{(1-b_2^2)}^2})& \sqrt{a_1}>b_{1}and\sqrt{1-\sqrt{1-a_2^2}}<b_{2}and{b}_1^2>1-b_2^2\end{array}\right.\end{array}$$

Definition 18

([42]). Let U and W be two domains. A PF set $R_P^d=\{(b_1,b_2),{\mu }_P(b_1,b_2),v_P(b_1,b_2)|(b_1,b_2)\in U\times W\}$ is called a PF relation on the dual domain $U\times W$. For every $(b_1,b_2)\in U\times W$, ${\mu }_P(b_1,b_2)$ represents the degree to which the elements $b_1\in U$ and $b_2\in W$ have the relation $R_P^d$, $v_P(b_1,b_2)$ represents the degree to which the elements $b_1\in U$ and $b_2\in W$ do not have the relation $R_P^d$, and the set of all PF relations on $U\times V$ is denoted by $PFR(U\times V)$. If $U=W$, then $R_P$ is called a PF relation on U.

The PF relation $R_P$ on the domain U is called reflexive if $\forall b\in U$, it satisfies $R_P(b,b)=(1,0)$; $R_P$ is called symmetric if $\forall b_1,b_2\in U$, it satisfies $R_P(b_1,b_2)=R_P(b_2,b_1)$; and $R_P$ is called transitive if $\forall b_1,b_2,b_3\in U$, it satisfies ${\mu }_P(b_1,b_3)\ge \sqrt{{\vee }_{b_2\in U}{({\mu }_P(b_1,b_2)\wedge {\mu }_P(b_2,b_3))}^2},v_P(b_1,b_3)\le \sqrt{{\wedge }_{b_2\in U}{(v_P(b_1,b_2)\vee v_P(b_2,b_3))}^2}$.

Definition 19.

Let $(U,R_P)$ be a PF approximation space, U be a domain, and $R_P$ be a PF relation on the domain U. $\forall B\in PF\left(U\right)$. We denote the PF rough approximation operators of B by $R_P{{\downarrow }_{R_{PO}}B,R_P\uparrow }_{PO}B$ as follows:

$$\begin{array}{c}\hfill R_P{\downarrow }_{R_{PO}}B\left(b_1\right)={\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),B\left(b_2\right)),\\ \hfill R_P{\uparrow }_{PO}B\left(b_1\right)={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B\left(b_2\right)),\end{array}$$

where $PO$ is a PFOF and $R_{PO}$ is the residual implication induced by $PO$. If $R_P{{\downarrow }_{R_{PO}}B\ne R_P\uparrow }_{PO}B$, then B is called undefinable, and the pair $(R_P{\downarrow }_{R_{PO}}B,R_P{\uparrow }_{PO}B)$ is called a PFRS.

Example 6.

Let $(U,R_P)$ be a PF approximation space and the domain $U=(b_1,b_2,b_3,b_4)$. Table 4 is the PF relation matrix, where $B={\displaystyle \frac{(0.80,0.50)}{b_1}}+{\displaystyle \frac{(0.70,0.60)}{b_2}}+{\displaystyle \frac{(0.60,0.20)}{b_3}}+{\displaystyle \frac{(0.90,0.40)}{b_4}}$.

Table 4. PF relation.

	${\mathit{b}}_1$	${\mathit{b}}_2$	${\mathit{b}}_3$	${\mathit{b}}_4$
$b_1$	(1, 0)	(0.8, 0.4)	(0.7, 0.2)	(0.5, 0.6)
$b_2$	(0.8, 0.4)	(1, 0)	(0.5, 0.5)	(0.8, 0)
$b_3$	(0.7, 0.2)	(0.5, 0.5)	(1, 0)	(0.2, 0.9)
$b_4$	(0.5, 0.6)	(0.8, 0)	(0.2, 0.9)	(1, 0)

When taking $R_{PO}$ and $PO$ in Example 5(2), according to Definition 19, we can obtain

$$\begin{array}{c}\hfill R_P{\downarrow }_{R_{PO}}B={\displaystyle \frac{(0.3600,0.7684)}{b_1}}+{\displaystyle \frac{(0.3600,0.7684)}{b_2}}+{\displaystyle \frac{(0.3600,0.7684)}{b_3}}+{\displaystyle \frac{(0.4900,0.7684)}{b_4}},\\ \hfill R_P{\uparrow }_{PO}B={\displaystyle \frac{(0.8944,0.1421)}{b_1}}+{\displaystyle \frac{(0.8944,0.2889)}{b_2}}+{\displaystyle \frac{(0.8367,0.1421)}{b_3}}+{\displaystyle \frac{(0.9487,0.2889)}{b_4}}.\end{array}$$

Theorem 3.

Let $(U,R_P)$ be the PF approximation space $\forall B_1,B_2\in PF\left(U\right)$. The PF rough approximation operators in Definition 19 satisfy the following:

(1) 

$R_P{\downarrow }_{R_{PO}}U=U$;

(2) 

$R_P{\uparrow }_{PO}\varnothing =\varnothing$;

(3) 

$B_1{\subseteq }_P{B}_2\Rightarrow R_P{\downarrow }_{R_{PO}}{B}_1{\subseteq }_P{R}_P{\downarrow }_{R_{PO}}{B}_2;R_P{{\uparrow }_{PO}{B}_1{\subseteq }_P{R}_P\uparrow }_{PO}{B}_2$;

(4) 

$R_P{\downarrow }_{R_{PO}}\left(B_1{\cap }_P{B}_2\right)=R_P{{\downarrow }_{R_{PO}}{B}_1{\cap }_P{R}_P\downarrow }_{R_{PO}}{B}_2$, where ${\cap }_P$ is the intersection operation of PF sets;

(5) 

$R_P{\uparrow }_{PO}\left(B_1{\cup }_P{B}_2\right)=R_P{{\uparrow }_{PO}{B}_1{\cup }_P{R}_P\uparrow }_{PO}{B}_2$, where ${\cup }_P$ is the union operation of PF sets;

(6) 

$R_P{\downarrow }_{R_{PO}}\left(B_1{\cup }_P{B}_2\right){\supseteq }_P{R}_P{{\downarrow }_{R_{PO}}{B}_1{\cup }_P{R}_P\downarrow }_{R_{PO}}{B}_2$;

(7) 

$R_P{\uparrow }_{PO}\left(B_1{\cap }_P{B}_2\right){\subseteq }_P{R}_P{{\uparrow }_{PO}{B}_1{\cap }_P{R}_P\uparrow }_{PO}{B}_2$.

Proof. 

(1)

$$\begin{array}{cc}\hfill R_P{\downarrow }_{R_{PO}}U& ={\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),U\left(b_2\right))\hfill \\ \hfill & ={\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),(1,0))\hfill \\ \hfill & =(1,0)\hfill \\ \hfill & =U;\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill R_P{\uparrow }_{PO}\varnothing & ={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),\varnothing \left(b_2\right))\hfill \\ \hfill & ={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),(0,1))\hfill \\ \hfill & =(0,1)\hfill \\ \hfill & =\varnothing ;\hfill \end{array}$$

(3) Since $B_1{\subseteq }_P{B}_2$, $\forall b_2\in U$, we have ${\mu }_P\left(B_1\left(b_2\right)\right)\le {\mu }_P\left(B_2\left(b_2\right)\right)$ and $v_P\left(B_1\left(b_2\right)\right)\ge v_P\left(B_2\left(b_2\right)\right)$, that is, $B_1\left(b_2\right){\le }_P{B}_2\left(b_2\right)$. Due to the monotonicity of $PO$, for any $b_1\in U$, we have

$$\begin{array}{cc}\hfill R_P{\uparrow }_{PO}{B}_1\left(b_1\right)& ={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B_1\left(b_2\right))\hfill \\ \hfill & {\le }_P{\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B_2\left(b_2\right))\hfill \\ \hfill & =R_P{\uparrow }_{PO}{B}_2\left(b_1\right),\hfill \end{array}$$

Therefore, we can obtain $R_P{{\uparrow }_{PO}{B}_1{\subseteq }_P{R}_P\uparrow }_{PO}{B}_2$. Similarly, we can prove that $R_P{{\downarrow }_{R_{PO}}{B}_1{\subseteq }_P{R}_P\downarrow }_{R_{PO}}{B}_2$;

(4)

$$\begin{array}{cc}\hfill R_P{\downarrow }_{R_{PO}}\left(B_1{\cap }_P{B}_2\right)\left(b_1\right)& ={\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),\left(B_1{\cap }_P{B}_2\right)\left(b_2\right))\hfill \\ \hfill & ={\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),B_1\left(b_2\right){\wedge }_P{B}_2\left(b_2\right))\hfill \\ \hfill & =\left({\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),B_1\left(b_2\right))\right){\wedge }_P\left({\wedge }_P^{b_2\in U}{R}_{PO}(R_P(b_1,b_2),B_2\left(b_2\right))\right)\hfill \\ \hfill & =R_P{{\downarrow }_{R_{PO}}{B}_1\left(b_1\right){\cap }_P{R}_P\downarrow }_{R_{PO}}{B}_2\left(b_1\right);\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill R_P{\uparrow }_{PO}\left(B_1{\cup }_P{B}_2\right)\left(b_1\right)& ={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),\left(B{\cup }_P{B}_2\right)\left(b_2\right))\hfill \\ \hfill & ={\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B_1\left(b_2\right){\vee }_P{B}_2\left(b_2\right))\hfill \\ \hfill & =\left({\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B_1\left(b_2\right))\right){\vee }_P\left({\vee }_P^{b_2\in U}PO(R_P(b_1,b_2),B_2\left(b_2\right))\right)\hfill \\ \hfill & =R_P{{\uparrow }_{PO}{B}_1\left(b_1\right){\cup }_P{R}_P\uparrow }_{PO}{B}_2\left(b_1\right);\hfill \end{array}$$

(6, 7) These are direct consequences of (3). □

Theorem 4.

Let U be a domain $R_{P1},R_{P2}\in PFR\left(U\right)$. If $R_{P1}{\subseteq }_P{R}_{P2}$, then for any $B\in PF\left(U\right)$, we have the following:

(1) 

$R_{P1}{{\uparrow }_{PO}B{\subseteq }_P{R}_{P2}\uparrow }_{PO}B$;

(2) 

$R_{P1}{{\downarrow }_{R_{PO}}B{\supseteq }_P{R}_{P2}\downarrow }_{R_{PO}}B$.

Proof. 

(1)

Since $R_{P1}{\subseteq }_P{R}_{P2}$, $\forall b_1,b_2\in U$, we have $R_{P1}(b_1,b_2){\le }_P{R}_{P2}(b_1,b_2)$, and because of the monotonicity of $PO$, we have

$$\begin{array}{cc}\hfill R_{P1}{\uparrow }_{PO}B\left(b_1\right)& ={\vee }_P^{b_2\in U}PO(R_{P1}(b_1,b_2),B\left(b_2\right))\hfill \\ \hfill & {\le }_P{\vee }_P^{b_2\in U}PO(R_{P2}(b_1,b_2),B\left(b_2\right))\hfill \\ \hfill & =R_{P2}{\uparrow }_{PO}B\left(b_1\right),\hfill \end{array}$$

Therefore, we can find $R_{P1}{{\uparrow }_{PO}B{\subseteq }_P{R}_{P2}\uparrow }_{PO}B$;

(2)

The proof method is similar to that in (1). We can easily obtain $R_{P1}{{\downarrow }_{R_{PO}}B{\supseteq }_P{R}_{P2}\downarrow }_{R_{PO}}B$.

□

We can also prove that the idempotence law of this model does not hold; that is, $R_P{\uparrow }_{PO}\left(R_P{\uparrow }_{PO}B\right)\ne R_P{\uparrow }_{PO}B,R_P{{\downarrow }_{R_{PO}}\left(R_P{\downarrow }_{R_{PO}}B\right)\ne R_P\downarrow }_{R_{PO}}B$.

Example 7.

Let B be the PF set in Example 6, and let it be known that $R_P{\uparrow }_{PO}B={\displaystyle \frac{(0.8944,0.1421)}{b_1}}+{\displaystyle \frac{(0.8944,0.2889)}{b_2}}+{\displaystyle \frac{(0.8367,0.1421)}{b_3}}+{\displaystyle \frac{(0.9487,0.2889)}{b_4}}$. Then, we can obtain $R_P{{\uparrow }_{PO}\left(R_P{\uparrow }_{PO}B\right)={\displaystyle \frac{(0.9457,0.1008)}{b_1}}+{\displaystyle \frac{(0.9457,0.2065)}{b_2}}+{\displaystyle \frac{(0.9147,0.1008)}{b_3}}+{\displaystyle \frac{(0.9740,0.2065)}{b_4}}\ne R_P\uparrow }_{PO}B$. We can also obtain $R_P{{\downarrow }_{R_{PO}}\left(R_P{\downarrow }_{R_{PO}}B\right)\ne R_P\downarrow }_{R_{PO}}B$.

Definition 20.

Let $(U,V,R_P^d)$ be a dual-domain PF approximation space, U and V be two domains, and $R_P^d$ be a PF relation on $U\times V$. Then, $\forall B\in PF\left(V\right)$, denote the PF rough approximation operators of B in $(U,V,R_P^d)$ by $R_P^d{{\downarrow }_{R_{PO}}B,R_P^d\uparrow }_{PO}B$ as follows:

$$\begin{array}{c}\hfill R_P^d{\downarrow }_{R_{PO}}B\left(b_1\right)={\wedge }_P^{b_2\in V}{R}_{PO}(R_P^d(b_1,b_2),B\left(b_2\right)),b_1\in U,\\ \hfill R_P^d{\uparrow }_{PO}B\left(b_1\right)={\vee }_P^{b_2\in V}PO(R_P^d(b_1,b_2),B\left(b_2\right)),b_1\in U,\end{array}$$

where $PO$ is a PFOF, $R_{PO}$ is the residual implication induced by $PO$, and the pair $(R_P^d{\downarrow }_{R_{PO}}B,R_P^d{\uparrow }_{PO}B)$ is called a dual-domain PFRS of B in $(U,V,R_P^d)$.

Theorem 5.

Let $(U,V,R_P^d)$ be the PF approximation space. Then, $\forall B_1,B_2\in PF\left(V\right)$, the PF rough approximation operators in Definition 20 satisfies the following:

(1) 

$B_1{\subseteq }_P{B}_2\Rightarrow R_P^d{\downarrow }_{R_{PO}}{B}_1{\subseteq }_P{R}_P^d{\downarrow }_{R_{PO}}{B}_2;R_P^d{{\uparrow }_{PO}{B}_1{\subseteq }_P{R}_P^d\uparrow }_{PO}{B}_2$;

(2) 

$R_P^d{\downarrow }_{R_{PO}}\left(B_1{\cap }_P{B}_2\right)=R_P^d{{\downarrow }_{R_{PO}}{B}_1{\cap }_P{R}_P^d\downarrow }_{R_{PO}}{B}_2$;

(3) 

$R_P^d{\uparrow }_{PO}\left(B_1{\cup }_P{B}_2\right)=R_P^d{{\uparrow }_{PO}{B}_1{\cup }_P{R}_P^d\uparrow }_{PO}{B}_2$;

(4) 

$R_P^d{\downarrow }_{R_{PO}}\left(B_1{\cup }_P{B}_2\right){\supseteq }_P{R}_P^d{{\downarrow }_{R_{PO}}{B}_1{\cup }_P{R}_P^d\downarrow }_{R_{PO}}{B}_2$;

(5) 

$R_P^d{\uparrow }_{PO}\left(B_1{\cap }_P{B}_2\right){\subseteq }_P{R}_P^d{{\uparrow }_{PO}{B}_1{\cap }_P{R}_P^d\uparrow }_{PO}{B}_2$.

Proof. 

The proof method is consistent with Theorem 3 and is omitted. □

Theorem 6.

Let U and V be two domains $R_{P1}^d,R_{P2}^d\in PFR(U\times V)$. If $R_{P1}^d{\subseteq }_P{R}_{P2}^d$, then for any $B\in PF\left(V\right)$, we have the following:

(1) 

$R_{P1}^d{{\uparrow }_{PO}B{\subseteq }_P{R}_{P2}^d\uparrow }_{PO}B$;

(2) 

$R_{P1}^d{{\downarrow }_{R_{PO}}B{\supseteq }_P{R}_{P2}^d\downarrow }_{R_{PO}}B$.

Proof. 

The proof method is consistent with Theorem 4 and is omitted. □

Next, the approximate accuracy and roughness of classical rough sets are extended to PFRSs.

Definition 21.

Let $(U,R_F)$ be a fuzzy approximation space, $R_F$ be a fuzzy relation on U, $\varnothing \ne M\subseteq U$, and the two fuzzy sets $R_F\uparrow M$ and $R_F\downarrow M$ be the fuzzy rough approximation operators of M:

(1) 

The approximate accuracy of the fuzzy set M is defined as follows:

$$\begin{array}{c}\hfill {\alpha }_{R_F}\left(M\right)={\displaystyle \frac{{\sum }_{m\in R_F\downarrow M}{\mu }_F\left(m\right)}{{\sum }_{m\in R_F\uparrow M}{\mu }_F\left(m\right)}},\end{array}$$

It is stipulated that ${\alpha }_{R_F}(\varnothing )=1$;

(2) 

The roughness of the fuzzy set M is defined as follows:

$$\begin{array}{c}\hfill {\rho }_{R_F}\left(M\right)=1-{\alpha }_{R_F}\left(M\right).\end{array}$$

From Definition 8, we observe that the approximation accuracy of classical rough sets is given by ${\alpha }_R\left(C\right)={\displaystyle \frac{|R\downarrow C|}{|R\uparrow C|}}$, where $|R\downarrow C|$ and $|R\uparrow C|$ denote the cardinalities of the sets $R\downarrow C$ and $R\uparrow C$, respectively; that is, they represent the number of elements belonging to $R\downarrow C$ and $R\uparrow C$. Since the membership degree of elements in classical sets is either zero or one, the cardinality of a set can also be interpreted as the sum of the membership degrees of its elements. Therefore, the approximation accuracy of fuzzy rough sets (FRSs) extends that of classical rough sets and remains applicable in the classical case.

For ${\sum }_{m\in R_F\downarrow M}{\mu }_F\left(m\right)$, a higher membership degree of elements in $R_F\downarrow M$ leads to a greater value of ${\sum }_{m\in R_F\downarrow M}{\mu }_F\left(m\right)$. Since, in classical fuzzy sets, the sum of the membership and non-membership degrees of each element equals one, an increase in the non-membership degree $v_F\left(m\right)$ results in a decrease in ${\mu }_F\left(m\right)$, thereby reducing the value of ${\sum }_{m\in R_F\downarrow M}{\mu }_F\left(m\right)$. The same principle applies to ${\sum }_{m\in R_F\uparrow M}{\mu }_F\left(m\right)$.

However, as intuitionistic fuzzy (IF) sets and Pythagorean fuzzy (PF) sets introduce hesitation, these rules no longer hold.

Example 8.

Two PF sets are given as follows:

$$\begin{array}{cc}\hfill R_P\downarrow B_1& ={\displaystyle \frac{(0.2,0.5)}{b_1}}+{\displaystyle \frac{(0.7,0.6)}{b_2}}+{\displaystyle \frac{(0.5,0.4)}{b_3}}+{\displaystyle \frac{(0.6,0.4)}{b_4}}\hfill \\ \hfill & \ne {\displaystyle \frac{(0.2,0.6)}{b_1}}+{\displaystyle \frac{(0.7,0.7)}{b_2}}+{\displaystyle \frac{(0.5,0.5)}{b_3}}+{\displaystyle \frac{(0.6,0.5)}{b_4}}\hfill \\ \hfill & =R_P\downarrow B_2,\hfill \end{array}$$

However, ${\sum }_{b\in R_P\downarrow B_1}{\mu }_P\left(b\right)={\sum }_{b\in R_P\downarrow B_2}{\mu }_P\left(b\right)$, and the approximate accuracy of classical FRSs is no longer applicable to PFRSs.

Definition 22.

Let $(U,R_P)$ be a PF approximation space, $R_P$ be a PF relation on U, $\varnothing \ne B{\subseteq }_{P}U$, and the two PF sets $R_P\downarrow B$ and $R_P\uparrow B$ be the PF rough approximation operators of B.

(1) 

The approximate accuracy of the PF set B is defined as follows:

$$\begin{array}{c}\hfill {\alpha }_{R_P}\left(B\right)={\displaystyle \frac{{\sum }_{b\in R_P\downarrow B}\mathcal{FS}({\mu }_P\left(b\right),v_P\left(b\right))}{{\sum }_{b\in R_P\uparrow B}\mathcal{FS}({\mu }_P\left(b\right),v_P\left(b\right))}},\end{array}$$

where $\mathcal{FS}$ is the fuzzy score functions in Definition 14. It is stipulated that ${\alpha }_{R_P}(\varnothing )=1$;

(2) 

The roughness of the PF set B is defined as follows:

$$\begin{array}{c}\hfill {\rho }_{R_P}\left(B\right)=1-{\alpha }_{R_P}\left(B\right).\end{array}$$

Example 9.

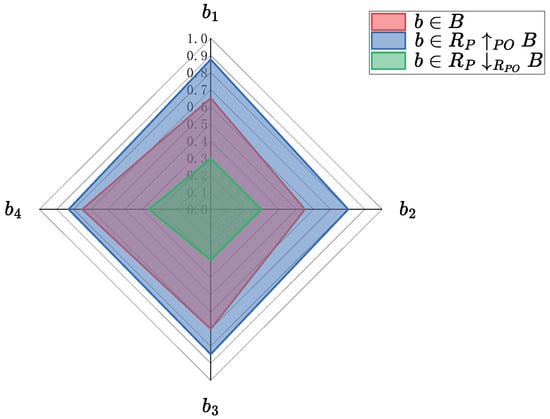
$\mathcal{FS}$ is taken from Example 4(3), and the approximate accuracy of the PFRS B in Example 6 is calculated to be 0.3719. Figure 4 shows the $\mathcal{FS}$ values of different elements in B and its upper and lower approximations, which more intuitively reflects the approximate accuracy of B.

Figure 4. $\mathcal{FS}$ values of elements in different sets.

Since ${\mu }_F\left(m\right)$ is a special case of $\mathcal{FS}({\mu }_F\left(m\right),v_F\left(m\right))$, the approximate accuracy of PFRSs is an extension of FRS and rough sets, and it is also applicable to the classical cases.

6. MCDM Methods Based on PF Information

In this section, we propose different MCDM algorithms based on the PF similarity measure and the PFRSs, give specific algorithm steps, and verify them with examples.

6.1. Typical Case I

6.1.1. Problem Analysis

Given a domain $C=\{c_1,c_2,\cdots ,c_m\}$ as the object domain and a domain $A=\{a_1,a_2,\cdots ,a_n\}$ as the attribute value domain, $a_n\left(c_m\right)=({\mu }_n\left(c_m\right),v_n\left(c_m\right))$, where ${\mu }_n\left(c_m\right)$ indicates the degree to which object $c_m$ satisfies attribute $a_n$, and $v_n\left(c_m\right)$ indicates the degree to which object $c_m$ does not satisfy attribute $a_n$, while ${\left({\mu }_n\left(c_m\right)\right)}^2+{\left(v_n\left(c_m\right)\right)}^2\le 1$. We need to sort the elements in the object domain and select the best one.

6.1.2. Decision Algorithm I

Step 1: First, we evaluate the attribute values of different elements in the object domain, obtain the PF relationship matrix $R_P^d$. (In response to specific problems, experts in related fields evaluate the attributes of the elements in the object field and complete the transformation of their attribute values from various numerical values to PF fuzzy information).

Step 2: According to the obtained PF relationship, we find the optimal solution $c_b$ and the worst solution $c_w$ of this problem, which are the PF sets in the domain A:

$$\begin{array}{c}\hfill a_n\left(c_b\right)=({\mu }_n\left(c_b\right),v_n\left(c_b\right)),{\mu }_n\left(c_b\right)=max{\left({\mu }_n\left(c\right)\right)}_{c\in C},v_n\left(c_b\right)=min{\left(v_n\left(c\right)\right)}_{c\in C};\\ \hfill a_n\left(c_w\right)=({\mu }_n\left(c_w\right),v_n\left(c_w\right)),{\mu }_n\left(c_w\right)=min{\left({\mu }_n\left(c\right)\right)}_{c\in C},v_n\left(c_w\right)=max{\left(v_n\left(c\right)\right)}_{c\in C}.\end{array}$$

Step 3: Using the similarity measure proposed in Definition 16, we calculate the similarity between the PF sets composed of the attributes of the elements in the object domain and the optimal solution $\mathcal{S}{(c,c_b)}_{c\in C}$ and the worst solution $\mathcal{S}{(c,c_w)}_{c\in C}$.

Step 4: We use the sorting score function ${\mathcal{R}}_1$ to evaluate the elements in the object domain and rank them based on their scores. The sorting score function is defined as follows:

$$\begin{array}{c}\hfill {\mathcal{R}}_1\left(c\right)={\displaystyle \frac{\mathcal{S}(c,c_b)}{\mathcal{S}(c,c_b)+\mathcal{S}(c,c_w)}},c\in C.\end{array}$$

6.1.3. Example Analysis I

We selected the best comprehensive service from four airlines $(c_1$, $c_2$, $c_3$, and $c_4)$, with attribute values $(a_1$, $a_2$, $a_3$, and $a_4)$ representing the reservation service, check-in procedure, cabin service, and responsiveness, respectively [43,44,45]. This problem involves a comprehensive evaluation of multiple airlines (decision-making schemes) based on attributes such as reservation services, check-in procedures, cabin services, and responsiveness. It requires weighting and ranking these attributes, making it a typical MCDM problem. The MCDM method quantifies the impact of various attributes, evaluates the pros and cons of each scheme, and helps decision makers objectively and systematically select the airline with the best overall service, thus enhancing the scientific and rational basis of the decision. To address this, we used Decision Algorithm I. Table 5 presents the expert evaluation matrix for the attributes of each airline.

Table 5. Attribute evaluation value matrix.

	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$
$c_1$	$(0.9,0.3)$	$(0.7,0.6)$	$(0.5,0.8)$	$(0.6,0.3)$
$c_2$	$(0.4,0.7)$	$(0.9,0.2)$	$(0.8,0.1)$	$(0.5,0.3)$
$c_3$	$(0.8,0.4)$	$(0.7,0.5)$	$(0.6,0.2)$	$(0.7,0.4)$
$c_4$	$(0.7,0.2)$	$(0.8,0.2)$	$(0.8,0.4)$	$(0.6,0.6)$

According to the attribute value evaluation matrix, the optimal solution $c_b$ and the worst solution $c_w$ are as follows:

$$\begin{array}{c}\hfill c_b={\displaystyle \frac{(0.9,0.2)}{a_1}}+{\displaystyle \frac{(0.9,0.2)}{a_2}}+{\displaystyle \frac{(0.8,0.1)}{a_3}}+{\displaystyle \frac{(0.7,0.3)}{a_4}};\\ \hfill c_w={\displaystyle \frac{(0.4,0.7)}{a_1}}+{\displaystyle \frac{(0.7,0.6)}{a_2}}+{\displaystyle \frac{(0.5,0.8)}{a_3}}+{\displaystyle \frac{(0.5,0.6)}{a_4}};\end{array}$$

When taking Example 4(1) as $\mathcal{FS}$ in the similarity measure, the similarities between different objects and the optimal solution and worst solution are calculated as follows (Table 6):

Table 6. Similarity calculation results.

	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$c_b$	0.7202	0.8089	0.8095	0.8298
$c_w$	0.7729	0.6893	0.6369	0.6227

We used the sorting score function ${\mathcal{R}}_1$ to score the elements in the object domain, and the results are as follows:

$$\begin{array}{c}\hfill {\mathcal{R}}_1\left(C\right)={\displaystyle \frac{0.4824}{c_1}}+{\displaystyle \frac{0.5399}{c_2}}+{\displaystyle \frac{0.5596}{c_3}}+{\displaystyle \frac{0.5713}{c_4}}.\end{array}$$

Therefore, the final result was $c_4>c_3>c_2>c_1$.

6.1.4. Decision Algorithm II

Step 1: First, we evaluate the attribute values of different elements in the object domain and obtain the PF relationship matrix $R_P^d$.

Step 2: According to the obtained PF relationship, we find the optimal solution $c_b$ and the worst solution $c_w$ of this problem, which are the PF sets in the domain A:

$$\begin{array}{c}\hfill a_n\left(c_b\right)=({\mu }_n\left(c_b\right),v_n\left(c_b\right)),{\mu }_n\left(c_b\right)=max{\left({\mu }_n\left(c\right)\right)}_{c\in C},v_n\left(c_b\right)=min{\left(v_n\left(c\right)\right)}_{c\in C};\\ \hfill a_n\left(c_w\right)=({\mu }_n\left(c_w\right),v_n\left(c_w\right)),{\mu }_n\left(c_w\right)=min{\left({\mu }_n\left(c\right)\right)}_{c\in C},v_n\left(c_w\right)=max{\left(v_n\left(c\right)\right)}_{c\in C}.\end{array}$$

Step 3: We calculate the PF rough approximation operators of the PF sets $c_b,c_w$ in the PF approximation space $(C,A,R_P^d):R_P^d{\uparrow }_{PO}{c}_b,R_P^d{\downarrow }_{R_{PO}}{c}_b,R_P^d{{\uparrow }_{PO}{c}_w,R_P^d\downarrow }_{R_{PO}}{c}_w$.

Step 4: We use the PFOFs to aggregate the PF rough approximation operators obtained; that is, we have

$$\begin{array}{c}\hfill \mathcal{OPT}=PO(R_P^d{\uparrow }_{PO}{c}_b,R_P^d{\downarrow }_{R_{PO}}{c}_b);\\ \hfill \mathcal{WO}=PO(R_P^d{\uparrow }_{PO}{c}_w,R_P^d{\downarrow }_{R_{PO}}{c}_w).\end{array}$$

Step 5: We use the sorting score function ${\mathcal{R}}_2$ to score the elements in $\mathcal{OPT}$ and $\mathcal{WO}$ and finally sort them according to the scores. The sorting score function is as follows:

$$\begin{array}{c}\hfill {\mathcal{R}}_2\left(x\right)={\displaystyle \frac{\mathcal{FS}\left(\mathcal{OPT}\right(c\left)\right)}{\mathcal{FS}\left(\mathcal{OPT}\right(c\left)\right)+\mathcal{FS}\left(\mathcal{WO}\right(c\left)\right)}},c\in C.\end{array}$$

where $\mathcal{FS}$ is the fuzzy score functions in Definition 14.

Remark 7.

Since the fuzzy scoring function is a family of functions, not all fuzzy scoring functions are suitable for solving specific problems. It is crucial to select an appropriate fuzzy scoring function. Therefore, different fuzzy scoring functions should be applied and compared with results from other methods to choose the correct parameters.

6.1.5. Example Analysis II

We apply Decision Algorithm II to the example in Section 6.1.3.

From Section 6.1.3, we can know that the optimal solution $c_b$ and the worst solution $c_w$ are as follows:

$$\begin{array}{c}\hfill c_b={\displaystyle \frac{(0.9,0.2)}{a_1}}+{\displaystyle \frac{(0.9,0.2)}{a_2}}+{\displaystyle \frac{(0.8,0.1)}{a_3}}+{\displaystyle \frac{(0.7,0.3)}{a_4}};\\ \hfill c_w={\displaystyle \frac{(0.4,0.7)}{a_1}}+{\displaystyle \frac{(0.7,0.6)}{a_2}}+{\displaystyle \frac{(0.5,0.8)}{a_3}}+{\displaystyle \frac{(0.5,0.6)}{a_4}}.\end{array}$$

We take the $PO$ and $R_{PO}$ of Example 5(2) and calculate the PF rough approximation operators of $c_b$ and $c_w$ for $R_P^d{\uparrow }_{PO}{c}_b$, $R_P^d{\downarrow }_{R_{PO}}{c}_b$, $R_P^d{\uparrow }_{PO}{c}_w$, and $R_P^d{\downarrow }_{R_{PO}}{c}_w$ as follows:

$$\begin{array}{c}\hfill R_P^d{\uparrow }_{PO}{c}_b={\displaystyle \frac{(0.9487,0.2146)}{c_1}}+{\displaystyle \frac{(0.9487,0.0708)}{c_2}}+{\displaystyle \frac{(0.8944,0.1421)}{c_3}}+{\displaystyle \frac{(0.8944,0.1421)}{c_4}};\\ \hfill R_P^d{\downarrow }_{R_{PO}}{c}_b={\displaystyle \frac{(0.4900,0.4146)}{c_1}}+{\displaystyle \frac{(0.4900,0.4146)}{c_2}}+{\displaystyle \frac{(0.4900,0.4146)}{c_3}}+{\displaystyle \frac{(0.4900,0.2800)}{c_4}};\\ \hfill R_P^d{\uparrow }_{PO}{c}_w={\displaystyle \frac{(0.8367,0.4472)}{c_1}}+{\displaystyle \frac{(0.8367,0.4472)}{c_2}}+{\displaystyle \frac{(0.8367,0.4472)}{c_3}}+{\displaystyle \frac{(0.8367,0.4472)}{c_4}};\\ \hfill R_P^d{\downarrow }_{R_{PO}}{c}_w={\displaystyle \frac{(0.1600,0.9330)}{c_1}}+{\displaystyle \frac{(0.1600,0.9330)}{c_2}}+{\displaystyle \frac{(0.1600,0.9330)}{c_3}}+{\displaystyle \frac{(0.1600,0.9330)}{c_4}}.\end{array}$$

For $PO$ in Example 5(1), we aggregated the obtained PF rough approximation operators, obtaining $\mathcal{OPT}$ and $\mathcal{WO}$ as follows:

$$\begin{array}{c}\hfill \mathcal{OPT}={\displaystyle \frac{(0.4696,0.4583)}{c_1}}+{\displaystyle \frac{(0.4696,0.4196)}{c_2}}+{\displaystyle \frac{(0.4383,0.4343)}{c_3}}+{\displaystyle \frac{(0.4383,0.3115)}{c_4}};\\ \hfill \mathcal{WO}={\displaystyle \frac{(0.1339,0.9467)}{c_1}}+{\displaystyle \frac{(0.1339,0.9647)}{c_2}}+{\displaystyle \frac{(0.1339,0.9647)}{c_3}}+{\displaystyle \frac{(0.1339,0.9647)}{c_4}}.\end{array}$$

We took $\mathcal{FS}$ in Example 4(1) and used the ranking score function ${\mathcal{R}}_2$ to score the elements in the object domain. The results are as follows:

$$\begin{array}{c}\hfill {\mathcal{R}}_2\left(C\right)={\displaystyle \frac{0.8013}{c_1}}+{\displaystyle \frac{0.8076}{c_2}}+{\displaystyle \frac{0.8015}{c_3}}+{\displaystyle \frac{0.8200}{c_4}}.\end{array}$$

Therefore, the final result was $c_4>c_2>c_3>c_1$.

6.1.6. Comparative Analysis

Figure 5 and Table 7 show the ranking results of the proposed method and existing methods.

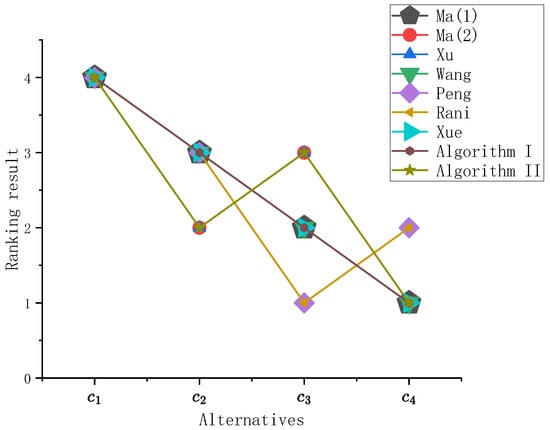
Figure 5. Ranking results between different methods.

Table 7. Ranking results between different methods.

	Ranking Result
Ma(1) [43]	$c_4>c_3>c_2>c_1$
Ma(2) [43]	$c_4>c_2>c_3>c_1$
Xu ([44])	$c_4>c_2>c_3>c_1$
Wang [45]	$c_4>c_3>c_2>c_1$
Peng [40]	$c_3>c_4>c_2>c_1$
Rani [46]	$c_3>c_4>c_2>c_1$
Xue [47]	$c_4>c_3>c_2>c_1$
Algorithm I	$c_4>c_3>c_2>c_1$
Algorithm II	$c_4>c_2>c_3>c_1$

As shown in Figure 5 and Table 7, the worst choice identified by all existing methods was $c_1$, while the best choice was either $c_4$ or $c_3$, with $c_4$ being the predominant selection. The results obtained by Algorithms I and II were consistent with this pattern. Specifically, the results of Algorithm I aligned with those of the methods proposed by Ma(1), Wang, and Xue, whereas the results of Algorithm II matched those of Ma(2) and Xu. This comparison demonstrates the efficiency and rationality of the approach presented in this section.

6.2. Typical Case II

6.2.1. Problem Analysis

Given the domain $C=\{c_1,c_2,\cdots ,c_m\}$ as the pattern domain and the domain $A=\{a_1,a_2,\cdots ,a_n\}$ as the attribute value domain, $a_n\left(c_m\right)=({\mu }_n\left(c_m\right),v_n\left(c_m\right))$, where ${\mu }_n\left(c_m\right)$ indicates the degree to which elements in the pattern $c_m$ need to have the attribute $a_n$, $v_n\left(c_m\right)$ indicates the degree to which elements in the pattern $c_m$ do not need to have the attribute $a_n$, and ${\left({\mu }_n\left(c_m\right)\right)}^2+{\left(v_n\left(c_m\right)\right)}^2\le 1$. The existing individual $c_s\notin C$ is a PF set in the domain A, and its pattern affiliation needs to be determined based on its attribute value.

6.2.2. Decision Algorithm III

Step 1: First, we evaluate the attribute values of different elements in the pattern domain and obtain the PF relationship matrix $R_P^d$.

Step 2: Based on the obtained PF relationship, we calculate the PF rough approximation operators $R_P^d{{\uparrow }_{PO}{c}_s,R_P^d\downarrow }_{R_{PO}}{c}_s$ of individual $c_s$ in the PF approximation space $(C,A,R_P^d)$.

Step 3: We use the PFOFs to aggregate the PF rough approximation operators obtained:

$$\begin{array}{c}\hfill \mathcal{RESULT}=PO(R_P^d{\uparrow }_{PO}{c}_s,R_P^d{\downarrow }_{R_{PO}}{c}_s).\end{array}$$

Step 4: We use the fuzzy score functions $\mathcal{FS}$ to score the elements in the $\mathcal{RESULT}$ and finally sort them according to the scores.

6.2.3. Example Analysis III

Decision Algorithm III was applied to solve the typical problem raised in the literature [24]. Let $C=\{c_1,c_2,c_3,c_4,c_5\}$ represent the five departments of a company for recruitment, which are the administrative department, human resources department, R&D department, finance department, and sales department. Another domain $A=\{a_1,a_2,a_3,a_4,a_5,a_6\}$ represents the six abilities which the company requires job seekers to have, which are mathematical ability, computer level, English speaking, interpersonal relationship handling, adaptability, and organizational management ability. Table 8 is the PF relationship between C and A, which is the scoring standard for the company to recruit new employees. Through evaluation, an employed person obtains the following six abilities: $c_s={\displaystyle \frac{(0.7,0.4)}{a_1}}+{\displaystyle \frac{(0.9,0.2)}{a_2}}+{\displaystyle \frac{(0.7,0.4)}{a_3}}+{\displaystyle \frac{(0.6,0.2)}{a_4}}+{\displaystyle \frac{(0.6,0.5)}{a_5}}+{\displaystyle \frac{(0.8,0.5)}{a_6}}$.

Table 8. Scoring criteria for recruitment of new employees.

	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$	${\mathit{a}}_6$
$c_1$	(0.3, 0.9)	(0.2, 0.8)	(0.7, 0.3)	(0.7, 0.4)	(0.8, 0.3)	(0.8, 0.2)
$c_2$	(0.1, 0.9)	(0.4, 0.7)	(0.6, 0.5)	(0.3, 0.8)	(0.8, 0.4)	(0.7, 0.5)
$c_3$	(0.8, 0.2)	(1, 0)	(0.7, 0.3)	(0.4, 0.7)	(0.5, 0.6)	(0.6, 0.5)
$c_4$	(0.7, 0.3)	(0.5, 0.4)	(0.8, 0.4)	(0.6, 0.5)	(0.7, 0.4)	(0.6, 0.6)
$c_5$	(0.2, 0.6)	(0.1, 0.7)	(0.7, 0.2)	(0.6, 0.5)	(0.9, 0.1)	(0.7, 0.6)

When taking the $PO$ and $R_{PO}$ from Example 5(2), we calculated the PF rough approximation operators of $c_s$ as follows:

$$\begin{array}{c}\hfill R_P^d{\uparrow }_{PO}{c}_s={\displaystyle \frac{(0.8944,0.2889)}{c_1}}+{\displaystyle \frac{(0.8367,0.3660)}{c_2}}+{\displaystyle \frac{(0.9487,0.1421)}{c_3}}+{\displaystyle \frac{(0.8367,0.2889)}{c_4}}+{\displaystyle \frac{(0.8367,0.2889)}{c_5}};\\ \hfill R_P^d{\downarrow }_{R_{PO}}{c}_s={\displaystyle \frac{(0.3600,0.6641)}{c_1}}+{\displaystyle \frac{(0.3600,0.6641)}{c_2}}+{\displaystyle \frac{(0.3600,0.6641)}{c_3}}+{\displaystyle \frac{(0.3600,0.6641)}{c_4}}+{\displaystyle \frac{(0.3600,0.6641)}{c_5}}.\end{array}$$

When taking the $PO$ in Example 5(1) and aggregating the PF rough approximation operators, we had

$$\begin{array}{c}\hfill \mathcal{RESULT}={\displaystyle \frac{(0.3320,0.6960)}{c_1}}+{\displaystyle \frac{(0.3012,0.7161)}{c_2}}+{\displaystyle \frac{(0.3415,0.6700)}{c_3}}+{\displaystyle \frac{(0.3012,0.6960)}{c_4}}+{\displaystyle \frac{(0.3012,0.6960)}{c_5}};\end{array}$$

We took $\mathcal{FS}$ in Example 4(1) and scored the elements in result:

$$\begin{array}{c}\hfill \mathcal{FS}\left(\mathcal{RESULT}\right)={\displaystyle \frac{0.2914}{c_1}}+{\displaystyle \frac{0.2718}{c_2}}+{\displaystyle \frac{0.3135}{c_3}}+{\displaystyle \frac{0.2819}{c_4}}+{\displaystyle \frac{0.2819}{c_5}}.\end{array}$$

Therefore, the final result was $c_3>c_1>c_4=c_5>c_2$.

6.2.4. Comparative Analysis

By changing the PFOFs and fuzzy score functions in Algorithm III, Figure 6 and Table 9 display the ranking results for various parameter settings. Case 1 was the result obtained in Section 6.2.3; Case 2 changed the aggregation operator of Step 3 in Section 6.2.3 from the PFOFs to $b_1⨁b_2=(\sqrt{{\mu }_P{\left(b_1\right)}^2+{\mu }_P{\left(b_2\right)}^2-{\mu }_P{\left(b_1\right)}^2{\mu }_P{\left(b_2\right)}^2},v_P{\left(b_1\right)}^2{v}_P{\left(b_2\right)}^2)$ in the literature [23]; Case 3 changed the fuzzy score function of Step 4 in Section 6.2.3 to Example 4(2); Case 4 changed the fuzzy score function of Step 4 in Section 6.2.3 to Example 4(3); Case 5 changed the fuzzy score function of Step 4 in Section 6.2.3 to $S\left(b\right)={\mu }_P{\left(b\right)}^2-v_P{\left(b\right)}^2$ in the literature [23]; and Case 6 changed the PFOF of Step 2 in Section 6.2.3 to Example 5(1) and changed the PFOF of Step 3 in Section 6.2.3 to Example 5(2).

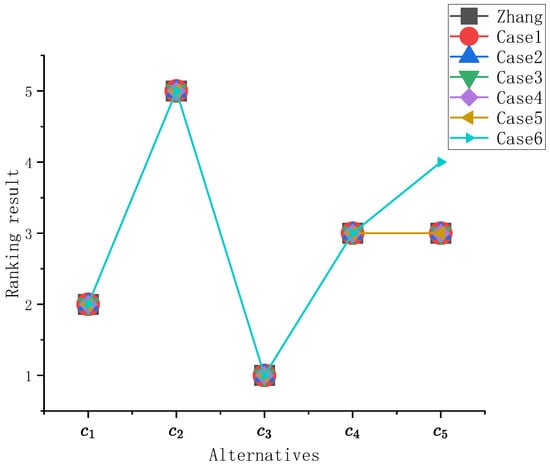
Figure 6. Ranking results in different situations.

Table 9. Ranking results in different situations.

	Ranking Result
Zhang	$c_3>c_1>c_4=c_5>c_2$
Case 1	$c_3>c_1>c_4=c_5>c_2$
Case 2	$c_3>c_1>c_4=c_5>c_2$
Case 3	$c_3>c_1>c_4=c_5>c_2$
Case 4	$c_3>c_1>c_4=c_5>c_2$
Case 5	$c_3>c_1>c_4=c_5>c_2$
Case 6	$c_3>c_1>c_4>c_5>c_2$

It can be seen from the images and tables that the results obtained from Cases 1–5 were all $c_3>c_1>c_4=c_5>c_2$, which is consistent with the results obtained in the literature, indicating the effectiveness of the method. However, the order of $c_4$ and $c_5$ in the literature could not be distinguished, which is a defect. By changing the parameters in the algorithm as shown in Case 6, the above defect can be overcome, which shows that the PFRSs based on the PFOFs had greater flexibility and superiority than the classical PFRSs.

As shown in the images and tables, the results obtained from Cases 1–5 followed the order $c_3>c_1>c_4=c_5>c_2$, which is consistent with the results reported in the literature, indicating the effectiveness of the method. However, in the literature, the order of $c_4$ and $c_5$ could not be distinguished, which is a limitation. By adjusting the parameters in the algorithm, as demonstrated in Case 6, this limitation can be overcome, demonstrating that PFRSs based on PFOFs offer greater flexibility and superiority over classical PFRSs.

The algorithm proposed in this paper has certain limitations. Specifically, since the algorithm does not include a mechanism for handling unequal attribute weights, it cannot be directly applied to problems involving attribute weights. However, this issue can be addressed. For example, when constructing the PF relationship matrix, one can first apply the aggregation operator $\lambda b=(\sqrt{1-{(1-{\mu }_P{\left(b\right)}^2)}^{\lambda }},{\left(v_P\left(b\right)\right)}^{\lambda })$ to integrate the attribute weights with their corresponding PF information and then proceed with the proposed algorithm.

7. Conclusions

In summary, this paper introduces and explores several developments in the PF fuzzy domain. First, we proposed the concept of PFOFs, analyzed their properties, and established a general construction approach. Next, a novel similarity measure for PF sets was presented, with its effectiveness and rationality demonstrated through examples. Furthermore, a generalized PFRSs model was formulated using PFOFs and fuzzy implications, extending it to the dual domain and providing a method for assessing the approximation accuracy of PFRSs. Finally, three MCDM algorithms based on PF information were developed, with examples illustrating their effectiveness and practicality. In the future, PFRSs models can be further extended to investigate covering-PFRSs based on PFOFs [48].