Family of Fuzzy Mandelblog Sets

Abstract

In this paper, we consider the family of parameterized Mandelbrot-like sets generated as any point $c\in \mathbb{C}\setminus \left\{0\right\}$ of the complex plane belongs to any member of this family for a real parameter $t\ge 1$, provided that its corresponding orbit of 0 does not escape to infinity under iteration $f_c^n\left(0\right)={\left[f_c^{n-1}\left(0\right)\right]}^2+log{c}^t$; otherwise, it is not a member of this set. This classically means there is only a binary membership possibility for all points. Here, we call this type of fractal set a Mandelblog set, and then we introduce a membership function that assigns a degree to each c to be an element of a fuzzy Mandelblog set under the iterations, even if the orbits of the points are not limited. Moreover, we provide numerical examples and gray-scale graphics that illustrate the membership degrees of the points of the fuzzy Mandelblog sets under the effects of iteration parameters. This approach enables the formation of graphs for these fuzzy fractal sets by representing points that belong to the set as white pixels, points that do not belong as black pixels, and other points, based on their membership degrees, as gray-toned pixels. Furthermore, the membership function facilitates the direct proofs of the symmetry criteria for these fractal sets.

1. Introduction

The concept of fuzziness was initially established by Lotfi A. Zadeh in 1965 through his pioneering research on the fuzzy set theory [1]. The fuzzy set theory is based upon the concept of membership of any point to a continuous range $\left[0,1\right]$, facilitating the mathematical depiction of vagueness and graded uncertainty by extending the classical set theory, which utilizes binary membership functions with values in $\left\{0,1\right\}$ [2]. This development offered a robust framework for examining phenomena with insufficient and sharp boundaries, interrelating quantitative mathematical formulations with the qualitative human mind. Introducing fuzzy sets has immediately drawn attention from a broad spectrum of researchers. The pioneering studies constructing the framework of this theory were presented by Dijkman, Van Haeringen, and de Lange [3], Dubois and Prade [4], Goetschel and Voxman [5], Kaufmann and Gupta [6], and Vachnadze and Markozashvilli [7], who investigated their algebraic structures, topological properties, and potential for generalizing classical concepts such as measures, relations, and functions. The primary factor for efficiently adopting fuzzy set theory is simulating real-world scenarios with prevalent ambiguity and partial truth. This versatility has enabled its incorporation into various fields, such as decision theory, control engineering, pattern recognition, and artificial intelligence. It also inspires extensions into fuzzy topology, fuzzy measure theory, and fuzzy differential equations.

The second half of the 20th century was a period marked by significant discoveries in the mathematical sciences. During this time, while fuzzy set theory was being developed, introducing a new perspective to set theory, logic, and decision-making, the Mandelbrot set, renowned for its visual esthetic and complexity, revolutionized the field of fractal geometry.

The Mandelbrot set has a crisp membership criterion, i.e., for any given point, there exists a definitive answer to the question of whether that point belongs to the set or not in accordance with the logic of classical set theory. On the other hand, the fuzzy set theory allows each point to have a degree of membership, rather than a binary state, providing a more nuanced and descriptive representation of border behavior. To integrate the advantage of this theory with this fractal set, a novel approach was proposed to bridge the fuzzy set theory and the classical Mandelbrot set by assigning a membership degree to each point, which quantifies the extent to which it belongs to the set [8]. This concept offered a new perspective on complex dynamical systems, facilitating a gradual rather than binary characterization of set membership. This development prompted interest in the concept of fuzziness within Mandelbrot-like structures. Extending the framework to higher-order polynomial mappings, the generalized fuzzy Mandelbrot and Mandelbar sets were subsequently examined in [9]. In parallel, the combination of fuzzy set theory with noise-perturbed nonlinear dynamics emerged, and the effects of dynamical noise perturbations on the fuzzy Mandelbric set were explored, revealing how additive and multiplicative noises modify its geometric and topological features [10].

In addition to numerous generalizations of the Mandelbrot set, a fractional Mandelbrot set [11] was introduced by Wang et al., who also conducted an initial analysis of its dynamics, examining features such as dimension, symmetry, and connectedness [12]. Danca et al. subsequently carried out a comparable study, confirming and extending the results [13]. Additionally, fractional Mandelbrot sets with impulse presented a new perspective to fractional Mandelbrot maps in [14]. The impact of impulse and parameters on the novel fractal sets was examined through dimensional analysis. Moreover, by the fact that an intuitionistic fuzzy set is a direct generalization of a fuzzy set, the intuitionistic fuzzy Mandelbrot set was introduced by [15].

In retrospect, the introduction of the Mandelbrot set (even if it was not yet known by this name) into the literature dates back to the independent pioneering of the studies of Gaston Julia and Pierre Fatou around 1910 in the field now known as complex dynamics [16,17,18]. The most well-known example they studied was the iteration of $z\to z^2+c$, where z starts at 0 and c is a fixed complex number. Benoît Mandelbrot generated the first visual representation of the sets that Julia and Fatou had considered in the late 19th century by monitoring the behavior of these parameters on the complex plane [19]. Then, the general monic univariate polynomial family of iterations $z\to {\left(z\right)}^p+c$ has become a current study subject for positive, negative integers, or fractional p. During this period, the visual and theoretical investigations of the generalizations and modifications of the Mandelbrot set have been active topics. For instance, Panwar et al. proposed an approach by modifying the constant term $log\left({\displaystyle \frac{1}{c^t}}\right)$ instead of c, where t is a real number that is greater than or equal to 1, while changing the Picard iteration with the Ishikawa iteration [20]. In addition, Tanveer et al. introduced a new modification by replacing the fixed term c with $log{c}^t$. In the meantime, they proved the escape criterion under the Mann and the Picard-Mann iterations [21,22]. Recently, using an iteration scheme extended with s-convexity, the Julia and Mandelbrot sets were visualized for ${\left(z\right)}^p+log{c}^t$ in [23] and $z^p-q{z}^2+rz+sin{c}^w$ [24]. In addition, a novel fast-convergent iterative technique was developed and improved upon earlier approaches in [25].

This paper focuses on the modified Mandelbrot sets, studied by [21,22,23], which we refer to as Mandelblog sets for $p=2$. The novelty lies in combining fuzziness with fractal sets of logarithmic deformations, resulting in a parameterized family of fuzzy fractals for positive real values of the parameters. This is achieved through a gradual assessment of situations where points escape with different velocities from each family member. For this purpose, after outlining the basic concepts of fuzzy sets used throughout the article in Section 2, fuzzy Mandelblog sets are introduced in Section 3. In this section, various examples are described in detail, both visually and computationally, utilizing the presented methodology, which draws on fuzzy set theory. Algorithm A1 is also provided to report the pseudo-codes used for generating a diverse array of captivating fractal patterns. Moreover, we prove the symmetry properties of the fuzzy Mandelblog sets by the novel membership function.

2. Preliminaries

This section provides an introduction to the basic concepts of fuzzy sets used throughout the article.

A fuzzy set $\tilde{A}$ is defined by a membership function ${\mu }_{\tilde{A}}\left(x\right)$ that assigns a real number value in the interval $\left[0,1\right]$ to each point in X and denoted by

$$\tilde{A}=\left\{\left(x,{\mu }_{\tilde{A}}\left(x\right)\right)\left|x\in X\right.\right\}.$$

The reference set X is called the universe of discourse, and the set of all fuzzy sets defined on X is denoted by $\mathcal{F}\left(X\right)$ [1].

The complement of a fuzzy set $\tilde{A}=\left\{\left(x,{\mu }_{\tilde{A}}\left(x\right)\right)\left|x\in X\right.\right\}$ is defined by

$${\tilde{A}}^{\prime }=\left\{\left(x,{\mu }_{{\tilde{A}}^{\prime }}\left(x\right)\right)\left|x\in X\right.\right\}$$

where ${\mu }_{{\tilde{A}}^{\prime }}\left(x\right)=1-{\mu }_{\tilde{A}}\left(x\right)$ [1].

A fuzzy set $\tilde{A}\in \mathcal{F}\left(X\right)$ is empty if and only if ${\mu }_{\tilde{A}}\left(x\right)=0$, and it is the universe of discourse X if and only if ${\mu }_{\tilde{A}}\left(x\right)=1$ for all $x\in X$ [1].

The support of a fuzzy set $\tilde{A}$ is the crisp set of all $x\in X$ such that ${\mu }_{\tilde{A}}\left(x\right)>0$ and denoted by $\mathrm{supp}\left(A\right):=\left\{x\in X\left|{\mu }_A\left(x\right)>0\right.\right\}$. Here, a crisp set means a classical set where an element is either fully a member or not a member at all [1,2].

3. Fuzzy Mandelblog Sets

The Mandelbrot set is defined by the quadratic function $f_c\left(z\right)=z^2+c$. It consists of those complex numbers c for which the sequence ${\left\{f_c^n\left(0\right)\right\}}_{n\in \mathbb{N}}$, obtained by iterating from $z=0$, which does not diverge, and it is denoted by $\mathbb{M}=\left\{c\in \mathbb{C}|{\left\{f_c^n\left(0\right)\right\}}_{n\in \mathbb{N}}\mathrm{is}\mathrm{bounded}\right\},$ where $f_c^n$ denotes the n-fold composition of $f_c$ with itself [26]. Numerous variations in the traditional Mandelbrot set, with their intriguing visualizations, have recently become a hot topic of research. A recent modification is the set of complex numbers c for which the complex-valued function $f_c\left(z\right)=z^p+log{c}^t$ does not diverge when iterated from $z=0$, where $c\in \mathbb{C}\setminus \left\{0\right\}$, $p\in \mathbb{N}$, $p\ge 2$, $t\in \mathbb{R}$, and $t\ge 1$ [21,22,23]. Also, Tanveer et al. proved the escape criteria for complex numbers c by using the Mann and the Picard-Mann iterations instead of the Picard iteration [21].

In this section, we deal with the aforementioned fractals for $p=2$ and various parameters t, which we call Mandelblog sets. Before examining the results of fuzzifying these fractal structures, we first directly establish, in the following lemma, the escape criterion for the Mandelblog sets under the classical (Picard) iteration, which corresponds to the special case $\alpha =1$ of the generalized iteration incorporating the control parameter $\alpha \in (0,1]$ and the degree $p\ge 2$ that is given in [21].

Lemma 1.

Let $f_c\left(z\right)=z^2+log{c}^t$ where $c\in \mathbb{C}\setminus \left\{0\right\}$, $\lambda ={\displaystyle \frac{log{c}^t}{c}}$, and $t\in \left[1,\infty \right)$. The forward orbit ${\left\{f_c^n\left(0\right)\right\}}_{n\ge 0}$ diverges to infinity (i.e., $\left|f_c^n\left(0\right)\right|\to \infty$ as $n\to \infty$) provided that the following apply:

(i) 

$\left|log{c}^t\right|>\left|\lambda \right|+2$,

(ii) 

$\left|log{c}^t\right|\le \left|\lambda \right|+2$ and $\left|f_c^k\left(0\right)\right|>\left|\lambda \right|+2$ for some $k\in \mathbb{N}$.

Proof. 

Here, the proof is found by mathematical induction.

(i)

Let $z_k$ denote the k-th term in the sequence obtained by repeatedly applying the function $f_c$ starting from 0. First, it is obvious that $\left|z_1\right|=\left|log{c}^t\right|>\left|z_0\right|$. Since $\left|log{c}^t\right|>\left|\lambda \right|+2$, there exists $a>0$ such that $\left|log{c}^t\right|=\left|\lambda \right|+2+a$, namely $a=\left|log{c}^t\right|-(\left|\lambda \right|+2)$. Thus, in the second step we find $\left|z_2\right|>\left|z_1\right|$ from

$$\begin{array}{cc}\hfill \left|z_2\right|& =\left|{\left(log{c}^t\right)}^2+log{c}^t\right|\hfill \\ \hfill & \ge {\left|log{c}^t\right|}^2-\left|log{c}^t\right|\hfill \\ \hfill & =\left|log{c}^t\right|\left(\left|log{c}^t\right|-1\right)\hfill \\ \hfill & =\left|z_1\right|\left(\left|\lambda \right|+2+a-1\right)\hfill \\ \hfill & =\left|z_1\right|\left(\left|\lambda \right|+a+1\right)\hfill \end{array}$$

by the fact that $\left|\lambda \right|+a+1>1$. In the next iteration step $z_3={z_2}^2+log{c}^t$, it is found that $\left|z_3\right|>\left|z_2\right|$ as a result of the following operations:

$$\begin{array}{cc}\hfill \left|z_3\right|& =\left|{z_2}^2+log{c}^t\right|\hfill \\ \hfill & \ge {\left|z_2\right|}^2-\left|log{c}^t\right|\hfill \\ \hfill & ={\left|z_2\right|}^2-\left|z_1\right|\hfill \\ \hfill & >{\left|z_2\right|}^2-\left|z_2\right|\hfill \\ \hfill & =\left|z_2\right|\left(\left|z_2\right|-1\right)\hfill \\ \hfill & =\left|z_2\right|\left(\left|{\left(log{c}^t\right)}^2+log{c}^t\right|-1\right)\hfill \\ \hfill & \ge \left|z_2\right|\left({\left|log{c}^t\right|}^2-\left|log{c}^t\right|-1\right)\hfill \\ \hfill & =\left|z_2\right|\left({\left(\left|\lambda \right|+2+a\right)}^2-\left(\left|\lambda \right|+2+a\right)-1\right)\hfill \\ \hfill & =\left|z_2\right|\underset{>1}{\underbrace{\left({\left|\lambda \right|}^2+\left(3+2a\right)\left|\lambda \right|+a^2+3a+1\right)}}.\hfill \end{array}$$

Now, assume that $\left|z_k\right|>\left|z_{k-1}\right|$ is true for $n=k$. Then, for $n=k+1$ it is proved that  

$$\begin{array}{cc}\hfill \left|z_{k+1}\right|& =\left|{z_k}^2+log{c}^t\right|\hfill \\ \hfill & \ge {\left|z_k\right|}^2-\left|log{c}^t\right|\hfill \\ \hfill & ={\left|z_k\right|}^2-\left|z_1\right|,\left\{\left|z_k\right|>\left|z_{k-1}\right|>\left|z_1\right|\right\}\hfill \\ \hfill & >{\left|z_k\right|}^2-\left|z_k\right|\hfill \\ \hfill & =\left|z_k\right|\left(\left|z_k\right|-1\right)\hfill \\ \hfill & =\left|z_k\right|\left(\left|{z_{k-1}}^2+log{c}^t\right|-1\right)\hfill \\ \hfill & \ge \left|z_k\right|\left({\left|z_{k-1}\right|}^2-\left|log{c}^t\right|-1\right),\left\{\left|z_{k-1}\right|>\left|z_{k-2}\right|>\dots >\left|z_1\right|=\left|log{c}^t\right|\right\}\hfill \\ \hfill & >\left|z_k\right|\left({\left|log{c}^t\right|}^2-\left|log{c}^t\right|-1\right)\hfill \\ \hfill & =\left|z_k\right|\left({\left(\left|\lambda \right|+2+a\right)}^2-\left(\left|\lambda \right|+2+a\right)-1\right)\hfill \\ \hfill & =\left|z_k\right|\underset{>1}{\underbrace{\left({\left|\lambda \right|}^2+\left(3+2a\right)\left|\lambda \right|+a^2+3a+1\right)}}.\hfill \end{array}$$

Consequently, if $\left|log{c}^t\right|>\left|\lambda \right|+2$ is satisfied, then the orbit of $\left\{f_c^n\left(0\right)\right\}$ goes to infinity.

(ii)

For $k\in \mathbb{N}$, denote ${\omega }_k:=f_c^k\left(0\right)$. By the hypotheses of the lemma, there exists $k\in \mathbb{N}$ such that $\left|log{c}^t\right|\le \left|\lambda \right|+2<\left|{\omega }_k\right|$. By the reverse triangle inequality, we obtain

$$\begin{array}{cc}\hfill \left|{\omega }_{k+1}\right|=& \left|{\omega }_k^2+log{c}^t\right|\hfill \\ \hfill \ge & {\left|{\omega }_k\right|}^2-\left|log{c}^t\right|\hfill \\ \hfill >& {\left|{\omega }_k\right|}^2-\left|{\omega }_k\right|,\left\{\left|log{c}^t\right|<\left|{\omega }_k\right|\right\}\hfill \\ \hfill =& \left|{\omega }_k\right|\left(\left|{\omega }_k\right|-1\right)\hfill \\ \hfill >& \left|{\omega }_k\right|\left(\left|\lambda \right|+1\right),\left\{\left|\lambda \right|+2<\left|{\omega }_k\right|\right\}\hfill \\ \hfill >& \left|{\omega }_k\right|.\hfill \end{array}$$

Thus, by virtue of $\left|{\omega }_{k+1}\right|>\left|{\omega }_k\right|$ and mathematical induction

$$\left|{\omega }_{k+n}\right|>\left|{\omega }_k\right|$$

for all $n\in \mathbb{N}$. Therefore, the sequence $s_n:=\left|{\omega }_{k+n}\right|$ is strictly increasing and satisfies

$$s_n>s_0=\left|{\omega }_k\right|>\left|\lambda \right|+2\ge 2.$$

Moreover, for all $n\ge 0$ we have

$$s_{n+1}=\left|{\omega }_{k+n+1}\right|\ge s_n^2-\left|log{c}^t\right|>s_n^2-s_n=s_n\left(s_n-1\right).$$

Consequently,

$$s_{n+1}-s_n>s_n\left(s_n-2\right)\ge s_0\left(s_0-2\right)=:\epsilon >0,$$

which implies $s_n\ge s_0+n\epsilon \to \infty$ as $n\to \infty$. Hence, $\left|f_c^n\left(0\right)\right|\to \infty$, i.e., the forward orbit ${\left\{f_c^n\left(0\right)\right\}}_{n\ge 0}$ diverges to infinity.

□

Therefore, the following definition based on this lemma is given:

Definition 1.

Let $\tilde{M}=\left\{\left(c,\mu \left(c\right)\right)\left|c\in \mathbb{C}\setminus \left\{0\right\}\right.\right\}$ be a fuzzy set given by the membership function $\mu :\mathbb{C}\to \left[0,1\right]$ defined by

$$\mu \left(c\right)=\left\{\begin{array}{c}1,\mathrm{if}\left|f_c^n\left(0\right)\right|\le \left|\lambda \right|+2\mathrm{for}\mathrm{all}n\in \mathbb{N},\hfill \\ {\displaystyle \frac{\left|f_c^{k-1}\left(0\right)\right|}{\left|f_c^k\left(0\right)\right|}},\mathrm{if}\left|f_c^k\left(0\right)\right|>\left|\lambda \right|+2\mathrm{and}\left|f_c^{k-1}\left(0\right)\right|\le \left|\lambda \right|+2\mathrm{for}\mathrm{a}k\in \mathbb{N},\hfill \end{array}\right.$$

(1)

under the iteration $f_c^n\left(0\right)={\left[f_c^{n-1}\left(0\right)\right]}^2+log{c}^t$ where $\lambda ={\displaystyle \frac{log{c}^t}{c}}$ for any  $t\ge 1$ such that $t\in \mathbb{R}$. Then $\tilde{M}$ is called a fuzzy Mandelblog set for each t.

This definition provides a more informative characterization compared to a binary membership of points to a Mandelblog set. The complete algorithmic procedure used to evaluate $\mu \left(c\right)$ on a discrete grid is provided in Algorithm A1. Based on this algorithm, gray-scale graphs of some fuzzy Mandelblog sets for integer and non-integer values of t are generated in Figure 1 and Figure 2, respectively.

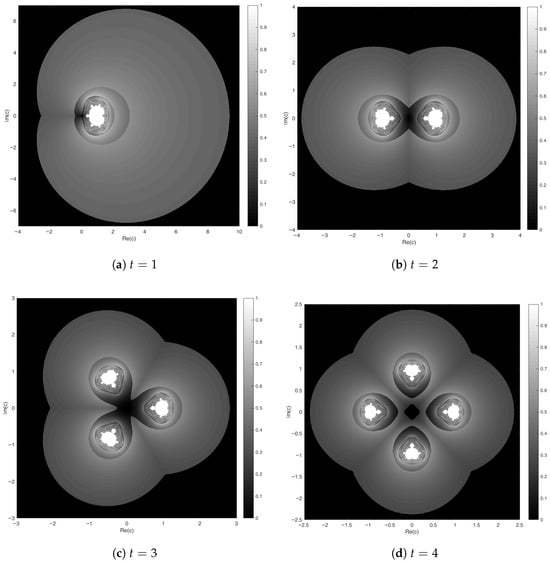
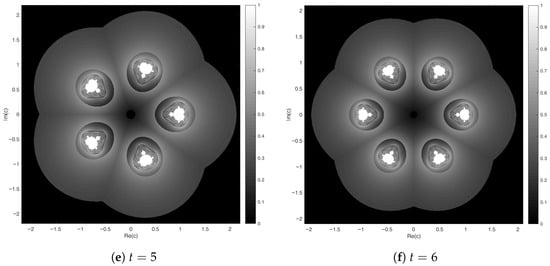
Figure 1. The fuzzy Mandelblog sets for some integer parameters t.

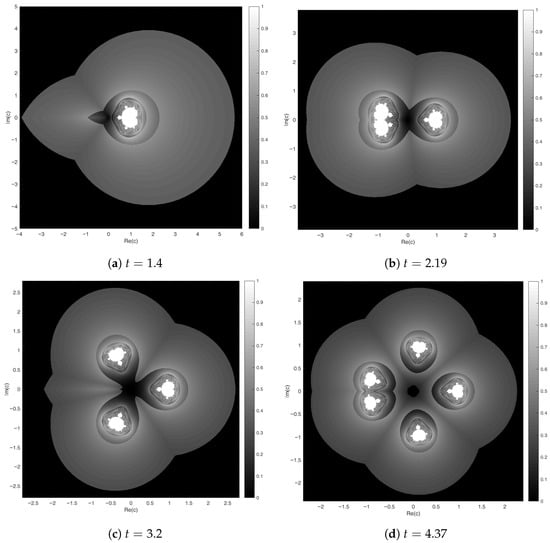
Figure 2. The fuzzy Mandelblog sets for some non-integer parameter t.

These fuzzy Mandelblog sets are generated by a finite maximum number of iterations due to the limited computational resources of real machines. Obviously, increasing the maximum number of iterations concretizes the figures, as it enables the accurate determination of the membership degrees of a larger number of complex numbers. The following figures show that complex numbers with membership degrees of 1 and 0 are found in the regions of white and black pixels, respectively. These points are either full members or non-members of Mandelblog sets, and they constitute crisp subsets. In addition to them, the other pixels have gray tones from black to white based on a recently established fuzzy membership function, and the darker pixels have fewer membership degrees. Moreover, the symmetries seen in the Figure 1 and Figure 2 caused by the changing values of the parameter t can be clarified by the same membership degrees of elements.

The visualizations were performed on an Intel(R) Core(TM) i3-1005G1 processor (1.20 GHz) with 16 GB of RAM using MATLAB 2016a. The computation times of Algorithm A1 for a grid of $2048\times 2048$ points and a maximum of 250 iterations are about 19.5 s.

Additionally, the approximate dimensions of the fuzzy Mandelblog sets can be determined. The concept of fractal dimension is used to describe the complexity of crisp sets. In particular, the box-counting dimension estimates the scaling of the number of boxes needed to cover a set across different resolutions [27]. However, in the presence of graded membership (gray-scale data), the classical box-counting procedure is not directly applicable because it is intended for binary images, that is, images with a black object on a white background. To overcome this problem, the concept of fuzzy fractal dimension has emerged, combining classical fractal analysis with the theory of fuzzy sets in various ways [28,29,30].

From this perspective, we refer to Algorithm 3 presented in [30] for determining the fuzzy box dimension based on gray-scale levels. To apply this fuzzy fractal dimension based on the escape time algorithm, we take our membership function $\mu :X\to [0,1]$ defined on a given grid $X\subset \mathbb{C}$. To work with 256 discrete gray levels, the quantified membership value of any non-zero c is given by $\widehat{\mu }\left(c\right)={\displaystyle \frac{J_{256}\left(c\right)}{256}}\in [0,1]$ where $J_{256}\left(c\right)=⌈256\mu \left(c\right)⌉$ such that $⌈r⌉=min\{n\in \mathbb{N}:n\ge r\}$. By partitioning X into $m\times m$ boxes B with $m=2^k$, we define

$$N_k\left(j\right)=\mathrm{Card}\{B:L_k\left(B\right)=j\}$$

where $L_k\left(B\right)={\displaystyle \underset{c\in B}{max}}\left\{J_{256}\left(c\right)\right\}$. The fuzzy fractal dimension is calculated by

$$\widehat{\delta }=max\{{\widehat{\delta }}_1,{\widehat{\delta }}_2,\dots ,{\widehat{\delta }}_{256}\}$$

where ${\widehat{\delta }}_j={\displaystyle \frac{ln{N}_k\left(j\right)}{ln{2}^k}}$. Consequently, $\widehat{\delta }$ gives us the approximate box dimension of a fuzzy Mandelblog set $\tilde{M}=\left\{\left(c,\mu \left(c\right)\right)\left|c\in X\setminus \left\{0\right\}\right.\right\}$.

Then the implementation of this procedure to the fuzzy Mandelblog set with parameter $t=1$ defined on the rectangular domain $[-4,10]\times [-7,7]$ with grid resolution $N=2048$ yields its approximate fuzzy box dimension $\widehat{\delta }\approx 1.857$; see Figure 3.

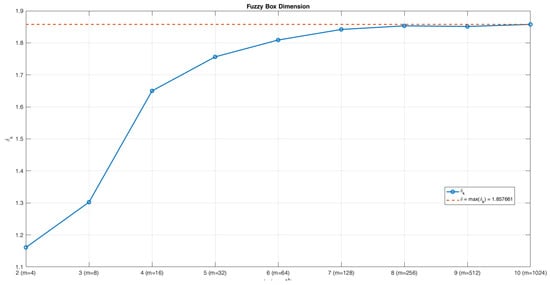
Figure 3. The fuzzy box dimension of the fuzzy Mandelblog set of $t=1$.

Furthermore, the smaller copies of the fuzzy Mandelblog set of $t=1$ can be directly observed within any fuzzy Mandelblog set of $t\ge 1$, and zooming in also reveals that the baby fuzzy Mandelblog set of $t=1$ is included within itself; see Figure 1 and Figure 2. By zooming in on the regions $\left[0.5,1.5\right]\times \left[-1,1\right]$, $\left[0,6\right]\times \left[-0.3,0.3\right]$, $\left[0.15,0.25\right]\times \left[-0.05,0.05\right]$, and $\left[0.195,0.205\right]\times \left[-0.005,0.005\right]$, respectively, some close-up views displaying the fuzzy Mandelblog set of $t=1$ are presented in Figure 4 to illustrate the approximate self-similarity and scaling behavior inherent to the fuzzy extension of the Mandelblog sets. This zooming behavior mirrors the fuzzy Mandelblog set’s quasi-self-similarity property: similar geometric patterns repeat at different sizes with consecutive magnifications, however, not in exactly the same form.

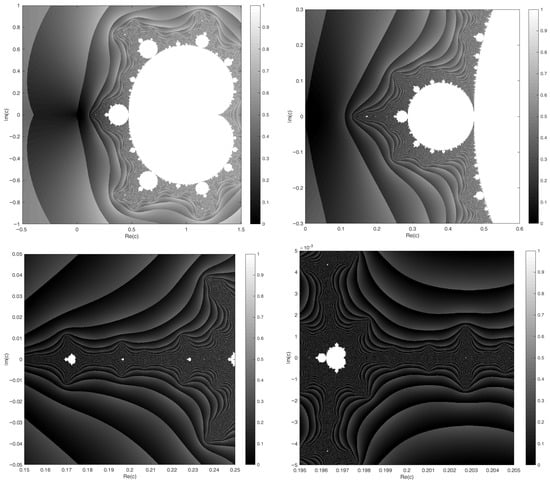
Figure 4. Progressive zooms into a fuzzy Mandelblog set of $t=1$.

Now, let us give a numerical example of a point satisfying $\left|log{c}^t\right|>\left|\lambda \right|+2$ to see that its membership degree is zero.

Example 1.

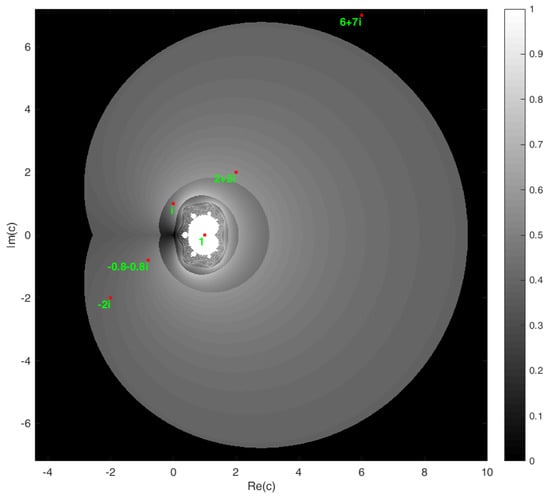
Let $t=1$ and $c=6+7i$, then the trajectory of the initial point 0 is determined by iterating the function $f_c^n\left(0\right)={\left[f_c^{n-1}\left(0\right)\right]}^2+logc$ as follows: $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log\left(6+7i\right)\cong 2.222+0.862\mathrm{i}$. Their norms are calculated norms as $\left|z_0\right|=0, \left|z_1\right|\cong 2.384$. Consequently, it is seen that $\left|z_1\right|>\left|\lambda \right|+2$ in the first iteration step since $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(6+8i\right)\right|}{\left|6+8i\right|}}+2\cong {\displaystyle \frac{2.384}{9.2195}}+2\cong 2.2586$. Because of $\mu \left(6+7i\right)={\displaystyle \frac{\left|z_0\right|}{\left|z_1\right|}}\cong {\displaystyle \frac{0}{2.384}}=0$ then $\left(6+7i,0\right)\in \tilde{M}$. Since the membership degree of $c=6+7i$ is 0, it is in the black region as can be seen in Figure 5.

Figure 5. The points 1, i, $-0.8-0.8i$, $-2i$, $2+2i$, $6+7i$ on the fuzzy Mandelblog set for $t=1$.

To prove the situation seen in Example 1 in general, the following lemma is given.

Lemma 2.

The fuzzy subset ${\tilde{M}}_0=\left\{\left(c,\mu \left(c\right)\right)\left|\left|log{c}^t\right|>\left|\lambda \right|+2,c\in \mathbb{C}\setminus \left\{0\right\}\right.\right\}$ is an empty fuzzy set.

Proof. 

Let us prove that $\mu \left(c\right)=0$ if and only if $\left|log{c}^t\right|>\left|\lambda \right|+2$. Firstly, it is assumed that $\mu \left(c\right)=0$, which means that $\left|{\displaystyle \frac{f_c^{k-1}\left(0\right)}{f_c^k\left(0\right)}}\right|=0$ for a $k\in \mathbb{N}$ under the iteration $f_c^n\left(0\right)={\left[f_c^{n-1}\left(0\right)\right]}^2+log{c}^t$. So $\left|f_c^{k-1}\left(0\right)\right|=0$ and $f_c^k\left(0\right)=log{c}^t$. Therefore, this is satisfied only for $k=1$. Thus, we find $\mu \left(c\right)=0$ implies that $\left|f_c^0\left(0\right)\right|=0\le \left|\lambda \right|+2$ and $\left|f_c^1\left(0\right)\right|=\left|log{c}^t\right|>\left|\lambda \right|+2$. Conversely, assume that $\left|log{c}^t\right|>\left|\lambda \right|+2$. If we apply the iteration with the initial point $f_c^0\left(0\right)=0$, we obtain $f_c^1\left(0\right)=0^2+log{c}^t=log{c}^t$. So $\left|f_c^1\left(0\right)\right|>\left|\lambda \right|+2$ is satisfied in the first iteration step. This proves that $\mu \left(c\right)=\left|{\displaystyle \frac{f_c^0\left(0\right)}{f_c^1\left(0\right)}}\right|={\displaystyle \frac{0}{\left|log{c}^t\right|}}=0$.    □

The following numerical examples are given for some points escaping from the Mandelblog set of $t=1$ with different velocities, that is, having different membership values in this fuzzy Mandelblog set.

Example 2.

We determine membership value of the following c points to fuzzy Mandelblog set of $t=1$. Thus, the trajectory of the initial point 0 is found iterating the function $f_c^n\left(0\right)={\left[f_c^{n-1}\left(0\right)\right]}^2+logc$ for these points.

• Let $c=1$. Then $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log1=0$, $z_2={z_1}^2+log1={\left(0+0i\right)}^2+log1=0$, and goes on. As seen from all the steps, it is found $\mu \left(c\right)=1$ since $\left|z_n\right|=0\le \left|\lambda \right|+2$ for all $n\in \mathbb{N}$. It is a white pixel as seen in Figure 5.
• Let $c=-0.8-0.8i$, then $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log\left(-0.8-0.8i\right)\cong 0.123+3.927i$, $z_2={z_1}^2+log\left(-0.8-0.8i\right)\cong -15.283+4.892i.$ The norms of these terms are found as $\left|z_0\right|=0$, $\left|z_1\right|\cong 3.928$, $\left|z_2\right|\cong 16.045$. Thus, it is achieved that $\left|z_2\right|>\left|\lambda \right|+2$ in the second iteration step from $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(-0.8-0.8i\right)\right|}{\left|-0.8-0.8i\right|}}+2\cong 5.47$. As a result, the membership degree of c is obtained as $\mu \left(-0.8-0.8i\right)={\displaystyle \frac{\left|z_1\right|}{\left|z_2\right|}}\cong {\displaystyle \frac{3.928}{16.045}}\cong 0.245$. c corresponds to a gray pixel as seen in Figure 5.
• Let $c=-2i$. Then under the iterations we get $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log\left(-2i\right)\cong 0.6931-1.5708\mathrm{i}$, $z_2={z_1}^2+log\left(-2i\right)\cong -1.2939-3.7474\mathrm{i}.$ Also, their norms are calculated for these iteration steps as $\left|z_0\right|=0$, $\left|z_1\right|\cong 1.716$, $\left|z_2\right|\cong 3.9659$. In the second iteration step, we attain $\left|z_2\right|>\left|\lambda \right|+2$ by the fact that $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(-2i\right)\right|}{\left|-2i\right|}}+2\cong 2.8582$. The membership degree of $-2i$ is found as $\mu \left(-2i\right)={\displaystyle \frac{\left|z_1\right|}{\left|z_2\right|}}\cong {\displaystyle \frac{1.7164}{3.9659}}\cong 0.4328$ and its location can be seen on the gray region in Figure 5.
• Let $c=i$, then the first three terms of the sequence are $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log\left(i\right)\cong 1.571\mathrm{i}$, $z_2={z_1}^2+log\left(i\right)\cong -2.468+1.571\mathrm{i}$, $z_3={z_2}^2+log\left(i\right)\cong 3.622-6.186\mathrm{i}.$ Up to the third iteration step, the norms are calculated as $\left|z_0\right|=0$, $\left|z_1\right|\cong 1.571$, $\left|z_2\right|\cong 2.926$, $\left|z_3\right|\cong 7.168$. Consequently, it is seen that $\left|z_3\right|>\left|\lambda \right|+2$ in the third iteration step since $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(i\right)\right|}{\left|i\right|}}+2\cong 3.571$. Furthermore, it is obtained that $\mu \left(i\right)={\displaystyle \frac{\left|z_2\right|}{\left|z_3\right|}}\cong {\displaystyle \frac{2.926}{7.168}}\cong 0.408$. So the membership degree of $c=i$ is approximately $0.408$, and its location is shown in Figure 5.
• Let $c=2+2i$, then $z_0=0+0i$, $z_1={\left(0+0i\right)}^2+log\left(2+2i\right)\cong 1.0397+0.7854\mathrm{i}$, $z_2={z_1}^2+log\left(2+2i\right)\cong 1.5039+2.4164\mathrm{i}.$ The norms of the terms of the sequence formed by these iteration steps are found as $\left|z_0\right|=0$, $\left|z_1\right|\cong 1.303$, $\left|z_2\right|\cong 2.85$. Thus, $\left|z_2\right|>\left|\lambda \right|+2$ in the second iteration step from the fact that $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(2+2i\right)\right|}{\left|2+2i\right|}}+2\cong 2.46$. Consequently, $\mu \left(2+2i\right)={\displaystyle \frac{\left|z_1\right|}{\left|z_2\right|}}\cong {\displaystyle \frac{1.303}{2.85}}\cong 0.457$ is found, i.e., the membership degree of $2+2i$ is approximately $0.457$. Evidently, this point is in the gray region as marked in Figure 5.

 

Additionally, the effects of varying parameter t on the fuzzy Mandelblog sets, where the membership degrees of the same points can be seen in Figure 6 and Figure 7, respectively.

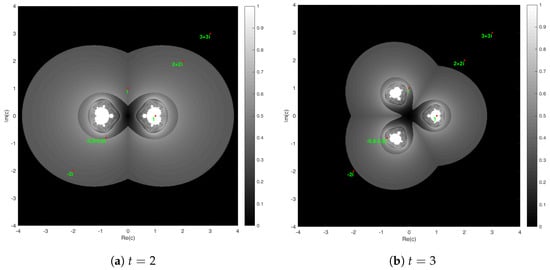
Figure 6. The points 1, i, $-0.8-0.8i$, $-2i$, $3+3i$ on the fuzzy Mandelblog sets of $t=2$ and $t=3$, respectively.

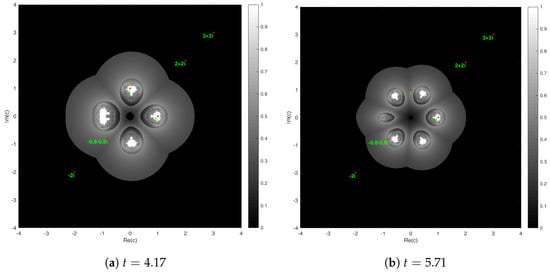
Figure 7. The points 1, i, $-0.8-0.8i$, $-2i$, $3+3i$ on the fuzzy Mandelblog sets of $t=4.17$ and $t=5.71$, respectively.

The next numerical example demonstrates that the membership degrees of a complex number and its symmetries with respect to the real, imaginary axes, and origin may have identical values, which can be intuited from the graphics.

Example 3.

Let $t=1$ and $c=1+i$. Additionally, its symmetries around the real axis $\overline{c}$, the imaginary axis $-\overline{c}$, and the origin $-c$ are considered. The first six terms of the sequences formed by the iterations $z_n=z_{n-1}^2+log\left(c\right)$, $z_n=z_{n-1}^2+log\left(\overline{c}\right)$, $z_n=z_{n-1}^2+log\left(-\overline{c}\right)$, and $z_n=z_{n-1}^2+log\left(-c\right)$, respectively, where $z_0=0+0i$ are given in Table 1.

In addition, the norms of these first six terms are given in Table 2.

Firstly, it is determined that the escape criteria is the same for c and $\overline{c}$, by the fact that $\left|z_5\right|>\left|\lambda \right|+2$ in the fifth iteration step, such that $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(1+i\right)\right|}{\left|1+i\right|}}+2\cong 2.607$. Thus, it is obtained that $\mu \left(1+i\right)=\mu \left(1-i\right)={\displaystyle \frac{\left|z_4\right|}{\left|z_5\right|}}\cong {\displaystyle \frac{2.1761}{4.9312}}\cong 0.4413$. The points $c=1+i$ and $\overline{c}=1-i$ are drawn on the fuzzy Mandelblog set of $t=1$ with the same color of pixel.

Secondly, it is found that the escape criteria is equal for $-\overline{c}$ and $-c$ because of $\left|z_2\right|>\left|\lambda \right|+2$ in the second iteration step where $\left|\lambda \right|+2={\displaystyle \frac{\left|log\left(-1+i\right)\right|}{\left|-1+i\right|}}+2\cong 3.684$. Consequently, $\mu \left(-1+i\right)=\mu \left(-1-i\right)={\displaystyle \frac{\left|z_1\right|}{\left|z_2\right|}}\cong {\displaystyle \frac{2.3822}{6.4667}}\cong 0.3684$. This means that the membership degree of $-\overline{c}=-1+i$ and $-c=-1-i$ is identical and approximately $0.3684$. These points on the fuzzy Mandelblog set of $t=1$ are the pixels with the same color.

Table 1. The six terms of the sequences formed by the iterations with the fixed terms $1+i$, $1-i$, $-1+i$, and $-1-i$, respectively.

	$\mathit{c}=1+\mathit{i}$	$\overline{\mathit{c}}=1-\mathit{i}$	$-\overline{\mathit{c}}=-1+\mathit{i}$	$-\mathit{c}=-1-\mathit{i}$
$z_0$	$0+0i$	$0+0i$	$0+0i$	$0+0i$
$z_1$	$0.34657+0.7854i$	$0.34657-0.7854i$	$0.34657+2.3562i$	$0.34657-2.3562i$
$z_2$	$-0.15013+1.3298i$	$-0.15013-1.3298i$	$-5.08602+3.9888i$	$-5.08602-3.9888i$
$z_3$	$-1.39933+0.3858i$	$-1.39933-0.3858i$	$10.3047-38.205i$	$10.3047+38.205i$
$z_4$	$2.15587-0.2944i$	$2.15587+0.2944i$	$-1354.08-785.35i$	$-1354.08+785.35i$
$z_5$	$4.90767-0.4841i$	$4.90767+0.4841i$	. . .	. . .

Table 1. The six terms of the sequences formed by the iterations with the fixed terms $1+i$, $1-i$, $-1+i$, and $-1-i$, respectively.

	$\mathit{c}=1+\mathit{i}$	$\overline{\mathit{c}}=1-\mathit{i}$	$-\overline{\mathit{c}}=-1+\mathit{i}$	$-\mathit{c}=-1-\mathit{i}$
$z_0$	$0+0i$	$0+0i$	$0+0i$	$0+0i$
$z_1$	$0.34657+0.7854i$	$0.34657-0.7854i$	$0.34657+2.3562i$	$0.34657-2.3562i$
$z_2$	$-0.15013+1.3298i$	$-0.15013-1.3298i$	$-5.08602+3.9888i$	$-5.08602-3.9888i$
$z_3$	$-1.39933+0.3858i$	$-1.39933-0.3858i$	$10.3047-38.205i$	$10.3047+38.205i$
$z_4$	$2.15587-0.2944i$	$2.15587+0.2944i$	$-1354.08-785.35i$	$-1354.08+785.35i$
$z_5$	$4.90767-0.4841i$	$4.90767+0.4841i$	. . .	. . .

Table 2. The norms of six terms of the sequences formed by the iterations with the fixed terms $1+i$, $1-i$, $-1+i$, and $-1-i$, respectively.

	$\mathit{c}=1+\mathit{i}$	$\overline{\mathit{c}}=1-\mathit{i}$	$-\overline{\mathit{c}}=-1+\mathit{i}$	$-\mathit{c}=-1-\mathit{i}$
$\left|z_0\right|$	0	0	0	0
$\left|z_1\right|$	$0.8589$	$0.8589$	$2.3822$	$2.3822$
$\left|z_2\right|$	$1.3066$	$1.3066$	$6.4667$	$6.4667$
$\left|z_3\right|$	$1.4515$	$1.4515$	$39.5829$	$39.5829$
$\left|z_4\right|$	$2.1761$	$2.1761$	$1565.36$	$1565.36$
$\left|z_5\right|$	$4.9312$	$4.9312$	. . .	. . .

Table 2. The norms of six terms of the sequences formed by the iterations with the fixed terms $1+i$, $1-i$, $-1+i$, and $-1-i$, respectively.

	$\mathit{c}=1+\mathit{i}$	$\overline{\mathit{c}}=1-\mathit{i}$	$-\overline{\mathit{c}}=-1+\mathit{i}$	$-\mathit{c}=-1-\mathit{i}$
$\left|z_0\right|$	0	0	0	0
$\left|z_1\right|$	$0.8589$	$0.8589$	$2.3822$	$2.3822$
$\left|z_2\right|$	$1.3066$	$1.3066$	$6.4667$	$6.4667$
$\left|z_3\right|$	$1.4515$	$1.4515$	$39.5829$	$39.5829$
$\left|z_4\right|$	$2.1761$	$2.1761$	$1565.36$	$1565.36$
$\left|z_5\right|$	$4.9312$	$4.9312$	. . .	. . .

The case $t=1$ assumed in the aforementioned example can be investigated for different real values of t in a similar manner. For instance, the membership values of $1+i$ and its symmetries in the fuzzy Mandelblog sets of integers are seen in Table 3.

Table 3. The membership degrees of $c=1+i$ and its symmetries about the real and imaginary axes and the origin for the integer parameters $1\le t\le 8$.

	$\mathit{\mu }\left(\mathit{c}\right)$	$\mathit{\mu }\left(\overline{\mathit{c}}\right)$	$\mathit{\mu }\left(-\overline{\mathit{c}}\right)$	$\mathit{\mu }\left(-\mathit{c}\right)$
$t=1$	0.4413	0.4413	0.3684	0.3684
$t=2$	0.4330	0.4330	0.4330	0.4330
$t=3$	0.3209	0.3209	0.3369	0.3369
$t=4$	0.2535	0.2535	0.2535	0.2535
$t=5$	0.2771	0.2771	0.3517	0.3517
$t=6$	0.2893	0.2893	0.2893	0.2893
$t=7$	0.2845	0.2845	0.2405	0.2405
$t=8$	0.2651	0.2651	0.2651	0.2651

The identical values of the membership degrees given in Table 3 for a fixed complex number present geometrical interpretations if all complex numbers are considered. For this purpose, we give the following theorems. First, we clarify the symmetry of each fuzzy Mandelblog set for each real number $t\ge 1$ with respect to the real axis.

Theorem 1.

Each member of the family of fuzzy Mandelblog sets for each real number $t\ge 1$ is symmetric about the real axis.

Proof. 

$\left|f_{\overline{c}}^n\left(0\right)\right|=\left|f_c^n\left(0\right)\right|$ is proved with respect to mathematical induction.

• For the first iteration step $n=1$, we get

  $$\left|f_{\overline{c}}^1\left(0\right)\right|=\left|{\left(f_{\overline{c}}^0\left(0\right)\right)}^2+log{\left(\overline{c}\right)}^t\right|=\left|{\left(0+0i\right)}^2+log{\left(\overline{c}\right)}^t\right|=\left|log{\left(\overline{c}\right)}^t\right|,$$

  $$\left|f_c^1\left(0\right)\right|=\left|{\left(f_c^0\left(0\right)\right)}^2+log{\left(c\right)}^t\right|=\left|{\left(0+0i\right)}^2+log{\left(c\right)}^t\right|=\left|log{\left(c\right)}^t\right|.$$
  This proves $\left|f_{\overline{c}}^1\left(0\right)\right|=\left|f_c^1\left(0\right)\right|$ from the fact that $\left|log\left({\overline{c}}^t\right)\right|=\left|\overline{log{c}^t}\right|=\left|log{c}^t\right|$ is satisfied for any real number $t\ge 1$ and each $c\in \mathbb{C}\setminus \left\{0\right\}$.
• For the second iteration step $n=2$, the equality $\left|f_{\overline{c}}^2\left(0\right)\right|=\left|f_c^2\left(0\right)\right|$ is proved from the calculations

  $$\begin{array}{cc}\hfill \left|f_{\overline{c}}^2\left(0\right)\right|& =\left|{\left(f_{\overline{c}}^1\left(0\right)\right)}^2+log{\left(\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|{\left(log{\left(\overline{c}\right)}^t\right)}^2+log{\left(\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|\overline{{\left(log{\left(c\right)}^t\right)}^2+log{c}^t}\right|\hfill \\ \hfill & =\left|\overline{f_c^2\left(0\right)}\right|\hfill \\ \hfill & =\left|f_c^2\left(0\right)\right|.\hfill \end{array}$$
• Assume that $\left|f_{\overline{c}}^k\left(0\right)\right|=\left|f_c^k\left(0\right)\right|$ is true for $n=k$. For $n=k+1$, it is easy to prove that

  $$\left|f_{\overline{c}}^{k+1}\left(0\right)\right|=\left|{\left(f_{\overline{c}}^k\left(0\right)\right)}^2+log{\overline{c}}^t\right|=\left|{\left(\overline{f_c^k\left(0\right)}\right)}^2+\overline{log{c}^t}\right|=\left|\overline{{\left(f_c^k\left(0\right)\right)}^2+log{c}^t}\right|=\left|\overline{f_c^{k+1}\left(0\right)}\right|.$$
  Therefore, $\left|f_{\overline{c}}^{k+1}\left(0\right)\right|=\left|f_c^{k+1}\left(0\right)\right|$.

First, let $\mu \left(c\right)=1$ which means that $\left|f_c^n\left(0\right)\right|\le \left|\lambda \right|+2\mathrm{for}\mathrm{all}n\in \mathbb{N}$. Thus, $\left|f_{\overline{c}}^n\left(0\right)\right|=\left|f_c^n\left(0\right)\right|$ requires that $\mu \left(\overline{c}\right)=1$, i.e., $\mu \left(c\right)=\mu \left(\overline{c}\right)$. Secondly, let $\mu \left(c\right)\ne 1$, then we achieve the desired result from

$$\mu \left(\overline{c}\right)={\displaystyle \frac{\left|f_{\overline{c}}^k\left(0\right)\right|}{\left|f_{\overline{c}}^{k+1}\left(0\right)\right|}}={\displaystyle \frac{\left|\overline{f_c^k\left(0\right)}\right|}{\left|\overline{f_c^{k+1}\left(0\right)}\right|}}={\displaystyle \frac{\left|f_c^k\left(0\right)\right|}{\left|f_c^{k+1}\left(0\right)\right|}}=\mu \left(c\right).$$

This completes the proof.     □

The same values in the first and third columns of Table 3 provide only a point that inspires the idea of the symmetries of certain fuzzy Mandelblog sets with respect to the imaginary axis. Note that such symmetry occurs for the fuzzy Mandelblog sets of positive even integer parameters $t\ge 1$.

Theorem 2.

Each member with the parameter $t=2\omega$, $\omega \in {\mathbb{Z}}^{+}$ of the family of fuzzy Mandelblog sets is symmetric about the imaginary axis.

Proof. 

The mathematical induction is applied as follows:

• For $n=1$;

  $$\begin{array}{c}\left|f_{-\overline{c}}^1\left(0\right)\right|=\left|{\left(f_{-\overline{c}}^0\left(0\right)\right)}^2+log{\left(-\overline{c}\right)}^t\right|=\left|log{\left(-\overline{c}\right)}^{2\omega }\right|,\hfill \\ \left|f_c^1\left(0\right)\right|=\left|\overline{f_c^1\left(0\right)}\right|=\left|\overline{{\left(f_c^0\left(0\right)\right)}^2+log{\left(c\right)}^t}\right|=\left|\overline{log{c}^{2\omega }}\right|=\left|log{\left(\overline{c}\right)}^{2\omega }\right|.\hfill \end{array}$$
  Here, recall ${(-\overline{c})}^{2\omega }={(-1)}^{2\omega }{\left(\overline{c}\right)}^{2\omega }={\left(\overline{c}\right)}^{2\omega }$ for any positive integer $\omega$. Therefore, $\left|log{\left(-\overline{c}\right)}^{2\omega }\right|=\left|log{\left(\overline{c}\right)}^{2\omega }\right|$ shows that $\left|f_{-\overline{c}}^1\left(0\right)\right|=\left|f_c^1\left(0\right)\right|$.
• For $n=2$;

  $$\begin{array}{cc}\hfill \left|f_{-\overline{c}}^2\left(0\right)\right|& =\left|{\left(f_{-\overline{c}}^1\left(0\right)\right)}^2+log{\left(-\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|{\left(log{\left(-\overline{c}\right)}^t\right)}^2+log{\left(-\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|{\left(log{\left(-\overline{c}\right)}^{2\omega }\right)}^2+log{\left(-\overline{c}\right)}^{2\omega }\right|\hfill \\ \hfill & =\left|{\left(log{\left(\overline{c}\right)}^{2\omega }\right)}^2+log{\left(\overline{c}\right)}^{2\omega }\right|\hfill \\ \hfill & =\left|{\left(log{\left(\overline{c}\right)}^t\right)}^2+log{\left(\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|{\left(\overline{log{c}^t}\right)}^2+\overline{log{c}^t}\right|\hfill \\ \hfill & =\left|\overline{{\left(log{c}^t\right)}^2+log{c}^t}\right|\hfill \\ \hfill & =\left|\overline{f_c^2\left(0\right)}\right|=\left|f_c^2\left(0\right)\right|.\hfill \end{array}$$
• For $n=k$, let $\left|f_{-\overline{c}}^k\left(0\right)\right|=\left|\overline{f_c^k\left(0\right)}\right|$ be true. For $n=k+1$;

  $$\begin{array}{cc}\hfill \left|f_{-\overline{c}}^{k+1}\left(0\right)\right|& =\left|{\left(f_{-\overline{c}}^k\left(0\right)\right)}^2+log{\left(-\overline{c}\right)}^t\right|\hfill \\ \hfill & =\left|{\left(\overline{f_c^k\left(0\right)}\right)}^2+\overline{log{c}^t}\right|\hfill \\ \hfill & =\left|\overline{{\left(f_c^k\left(0\right)\right)}^2+log{c}^t}\right|\hfill \\ \hfill & =\left|\overline{f_c^{k+1}\left(0\right)}\right|=\left|f_c^{k+1}\left(0\right)\right|.\hfill \end{array}$$

First, let $\mu \left(c\right)=1$ which means that $\left|f_c^n\left(0\right)\right|\le \left|\lambda \right|+2\mathrm{for}\mathrm{all}n\in \mathbb{N}$. By the fact that $\left|f_c^n\left(0\right)\right|=\left|f_{-\overline{c}}^n\left(0\right)\right|$ for all positive even integer t, it is clear that $\mu \left(-\overline{c}\right)=1$, i.e., $\mu \left(c\right)=\mu \left(-\overline{c}\right)$. Secondly, let $\mu \left(c\right)\ne 1$, then it is obtained that

$$\mu \left(-\overline{c}\right)={\displaystyle \frac{\left|f_{-\overline{c}}^n\left(0\right)\right|}{\left|f_{-\overline{c}}^{n+1}\left(0\right)\right|}}={\displaystyle \frac{\left|\overline{f_c^n\left(0\right)}\right|}{\left|\overline{f_c^{n+1}\left(0\right)}\right|}}={\displaystyle \frac{\left|f_c^n\left(0\right)\right|}{\left|f_c^{n+1}\left(0\right)\right|}}=\mu \left(c\right).$$

Therefore, the proof is completed.     □

Since each member with the parameter $t=2\omega$ for $\omega \in {\mathbb{Z}}^{+}$ of the family of fuzzy Mandelblog sets is symmetric with respect to both the real axis and the imaginary axis, the following corollary is obvious.

Corollary 1.

Each member with the parameter $t=2\omega$, $\omega \in {\mathbb{Z}}^{+}$ of the family of fuzzy Mandelblog sets is symmetric about the origin.

Remark 1.

The values in Table 3 for $t=2\omega +1$ such that $\omega \in {\mathbb{Z}}^{+}$ are the counterexamples which prove that the preservation of symmetry properties is lost for the odd parameters, thus contradicting the symmetries satisfied for the even parameters in Theorem 2 and Corollary 1.

Theorem 3.

A fuzzy Mandelblog set $\tilde{M}$ of parameter t has t-fold rotational symmetries where $t\in {\mathbb{Z}}^{+}$.

Proof. 

The proof can be found via proving that the degree of membership remains invariant by the rotation of any point $c\in \mathbb{C}\setminus \left\{0\right\}$ through the angle ${\displaystyle \frac{2\pi j}{t}}$ where $j=0,1,\dots t-1$ and $t\in {\mathbb{Z}}^{+}$. So, let us prove $\mu \left(\lambda ·c\right)=\mu \left(c\right)$ for any complex number $\lambda =e^{2\pi ij/t}$. Recall that $e^{2\pi ij}=1$, that is, $log{\lambda }^t=log\left(e^{2\pi ij}\right)=0$ for any integer j.

• In the first iteration step of $n=1$, it is found that $f_{\lambda ·c}^1\left(0\right)=log{\left(\lambda ·c\right)}^t=log{\lambda }^t+log{c}^t={f_c}^1\left(0\right)$.
• In the second iteration step of $n=2$, it is found that $f_{\lambda ·c}^2\left(0\right)={\left(log{\left(\lambda ·c\right)}^t\right)}^2+log{\left(\lambda ·c\right)}^t={\left(log{\lambda }^t+log{c}^t\right)}^2+log{\lambda }^t+log{c}^t={\left(log{c}^t\right)}^2+log{c}^t=f_c^2\left(0\right).$
• In the ${\left(k-1\right)}^{\mathrm{th}}$ iteration step of $n=k-1$, assume that $f_{\lambda ·c}^{k-1}\left(0\right)=f_c^{k-1}\left(0\right)$ is true. Then in the $k^{\mathrm{th}}$ iteration step of $n=k$, it is obtained that $f_{\lambda ·c}^k\left(0\right)={\left(f_{\lambda ·c}^{k-1}\left(0\right)\right)}^2+log{\left(\lambda ·c\right)}^t={\left(f_c^{k-1}\left(0\right)\right)}^2+log{\lambda }^t+log{c}^t={\left(f_c^{k-1}\left(0\right)\right)}^2+log{c}^t=f_c^k\left(0\right)$.

Thus, the statement $f_{\lambda ·c}^n\left(0\right)=f_c^n\left(0\right)$ iteration step also holds true for all $n\in \mathbb{N}$, which completes the induction steps.

Therefore, $\mu \left(\lambda ·c\right)={\displaystyle \frac{\left|f_{\lambda ·c}^{n-1}\left(0\right)\right|}{\left|f_{\lambda ·c}^n\left(0\right)\right|}}={\displaystyle \frac{\left|f_c^{n-1}\left(0\right)\right|}{\left|f_c^n\left(0\right)\right|}}=\mu \left(c\right)$ is a natural result.    □

4. Conclusions

In this study, we considered a new family of fractal sets generated by replacing the fixed complex point c with $log{c}^t$, where each new real value of $t\ge 1$ generates a distinct fractal set. To construct this dynamical system family, which we called the family of fuzzy Mandelblog sets, we defined a membership function by assigning a degree to each point in the complex plane to be a member of any fuzzy Mandelblog set. The visual representations of the members of this family were produced in gray-scale, ranging from black to white, reflecting the increasing membership degrees of complex numbers from 0 to 1. On these images, the positions of certain points, whose membership degrees had been calculated in advance in our paper, were identified, and while their locations remained fixed as the real parameter t varied, the changes in their membership degrees were computed mathematically and illustrated visually.

The main contributions and novelties of this work can be summarized as follows:

• A membership function $\mu$ is introduced to construct each fuzzy Mandelblog set $\tilde{M}$.    
• The empty fuzzy subset ${\tilde{M}}_0$ is expressed.    
• Each fuzzy Mandelblog set $\tilde{M}$ is proven to be symmetric with respect to the real axis in the complex plane, both visually and theoretically.
• Each fuzzy Mandelblog set $\tilde{M}$ with even positive integer parameters is proven to be symmetric with respect to the imaginary axis in the complex plane, both visually and theoretically.
• Each fuzzy Mandelblog set $\tilde{M}$ with even positive integer parameters is proven to be symmetric with respect to the origin in the complex plane, both visually and theoretically.
• Each fuzzy Mandelblog set $\tilde{M}$ with positive integer parameters possesses t-fold rotational symmetries.

Future research may investigate the family of fuzzy Mandelblog sets $\tilde{M}$ in greater depth. The complex relationships between different topological and geometrical properties of these sets can also be revealed using this discovery as a starting point. Moreover, further directions for this research include exploring various iteration schemes for fuzzy Mandelblog sets. Additionally, the presented fuzzification approach may be extended to the intuitionistic approach.