Unraveling Novel Wave Structures in Variable-Coefficient Higher-Order Coupled Nonlinear Schrödinger Models with β-Derivative

Abstract

This study investigates the dynamics of optical solitons for the variable-coefficient coupled higher-order nonlinear Schrödinger equation (VCHNLSE) enriched with $\beta$-derivatives. By employing an extended direct algebraic method (EDAM), we successfully derive explicit soliton solutions that illustrate the intricate interplay between nonlinearities and variable coefficients. Our approach facilitates the transformation of the complex NLS into a more manageable form, allowing for the systematic exploration of diverse solitonic structures, including bright, dark, and singular solitons, as well as exponential, polynomial, hyperbolic, rational, and Jacobi elliptic solutions. This diverse family of solutions substantially expands beyond the limited soliton interactions studied in conventional approaches, demonstrating the superior capability of our method in unraveling new wave phenomena. Furthermore, we rigorously demonstrate the robustness of these soliton solutions against various perturbations through comprehensive stability analysis and numerical simulations under parameter variations. The practical significance of this work lies in its potential applications in advanced optical communication systems. The derived soliton solutions and the analysis of their dynamics provide crucial insights for designing robust signal carriers in nonlinear optical media. Specifically, the management of variable coefficients and fractional-order effects can be leveraged to model and engineer sophisticated dispersion-managed optical fibers, tunable photonic devices, and ultrafast laser systems, where controlling pulse propagation and stability is paramount. The presence of $\beta$-fractional derivatives introduces additional complexity to the wave propagation behaviors, leading to novel dynamics that we analyze through numerical simulations and graphical representations. The findings highlight the potential of the proposed methodology to uncover rich patterns in soliton dynamics, offering insights into their robustness and stability under varying conditions. This work not only contributes to the theoretical foundation of nonlinear optics but also provides a framework for practical applications in optical fiber communications and other fields involving nonlinear wave phenomena.

1. Introduction

The study of optical solitons has transcended traditional boundaries, especially in the realm of nonlinear optics and photonics, where they serve not only as fundamental wave packets but also as carrier signals in advanced communication systems [1,2,3]. Optical solitons are distinct wave phenomena noted for their capacity to preserve their form despite traveling through a nonlinear medium. Numerous studies have contributed to important improvements in nonlinear optics, strengthening our understanding of light transmission in optical fibers, which is crucial for modern optical communications [4,5,6]. The dynamics of optical solitons are akin to particle interactions, allowing researchers to explore fundamental physical phenomena by studying these interactions [7]. Solitons have distinctive characteristics, including self-focusing and elasticity during collisions, underscoring the relationship between particle-like behavior and wave events [8]. In recent years, the exploration of variable-coefficient coupled higher-order nonlinear Schrödinger equations has gained prominence due to their ability to model complex physical phenomena more accurately than their constant-coefficient counterparts [9,10,11,12]. The variable-coefficient coupled higher-order nonlinear Schrödinger equation (VCHNLSE) is a key extension of the classical nonlinear Schrödinger equation, accounting for variations in medium characteristics that affect soliton propagation. Its development is closely linked to progress in nonlinear optics, fluid mechanics, and mathematical physics. Research on classical Coupled Nonlinear Schrödinger (CNLS) equations began in the 1970s, notably with the 1974 introduction of the Manakov system, which featured uniform nonlinear interactions among multiple components. This system laid the groundwork for investigating soliton dynamics in nonlinear optics [13]. As optical communication technologies evolved, there arose the need to consider variable coefficients in the NLSE framework, leading to the formulation of the Variable Coefficient Nonlinear Schrödinger Equations (VCNLS). This adaptation is crucial for accurately modeling realistic scenarios in various media, such as optical fibers, where properties like the refractive index can change over time and space [14]. To address the complexities of modern optical systems, researchers have increasingly turned to advanced mathematical frameworks, including fractional calculus [15,16,17,18] and other sophisticated techniques. These approaches provide powerful tools for modeling non-local and complex dispersion effects. Researchers have utilized several mathematical methods, including the improved modified extended tanh function method [19,20,21], extended and modified rational expansion method [22], extended F-expansion method [23,24], Laplace–Adomian decomposition method [25], Sardar’s Sub-Equation Approach [26,27], modified extended direct algebraic method [28], and others, to reach accurate solutions for many communication systems and other systems. This paper studies the variable-coefficient coupled higher-order nonlinear Schrödinger equation (VCHNLS), an advanced mathematical model used to study nonlinear wave phenomena. Recent work has shown that incorporating variable coefficients facilitates the study of soliton solutions with controllable dynamics, allowing for better manipulation of soliton propagation relevant to practical applications in telecommunications and material science. The higher-order nonlinear Schrödinger equation serves as a fundamental framework for analyzing such phenomena, particularly in scenarios where medium conditions are nonuniform. The introduction of $\beta$-derivatives into this equation framework provides an innovative mathematical tool to capture the complexity of light propagation in nonlinear media under variable coefficients [18]. This work seeks to identify numerous solitons and other solutions of the following VCHNLSE with $\beta$-derivatives using an extended direct algebraic method [29]:

$$\begin{array}{ccc}\hfill & & i{\displaystyle \frac{{\partial }^{\beta }\mathcal{P}}{\partial t^{\beta }}}+{\mathcal{P}}_{xx}+2\sigma \mathcal{P}\left({\left|\mathcal{P}\right|}^2+2{\left|\mathcal{U}\right|}^2\right)+2\sigma {\mathcal{P}}^{*}{\mathcal{U}}^2+i\epsilon \left(t\right){\mathcal{P}}_{xxx}+6i\sigma \epsilon \left(t\right){\mathcal{P}}_x\left({\left|\mathcal{P}\right|}^2+{\left|\mathcal{U}\right|}^2\right)+\hfill \\ & & {\displaystyle 6i\sigma \epsilon \left(t\right){\mathcal{U}}_x\left({\mathcal{P}}^{*}\mathcal{U}+\mathcal{P}{\mathcal{U}}^{*}\right)=0,}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill & & i{\displaystyle \frac{{\partial }^{\beta }\mathcal{U}}{\partial t^{\beta }}}+{\mathcal{U}}_{xx}+2\sigma \mathcal{U}\left({\left|\mathcal{U}\right|}^2+2{\left|\mathcal{P}\right|}^2\right)+2\sigma {\mathcal{U}}^{*}{\mathcal{P}}^2+i\epsilon \left(t\right){\mathcal{U}}_{xxx}+6i\sigma \epsilon \left(t\right){\mathcal{U}}_x\left({\left|\mathcal{U}\right|}^2+{\left|\mathcal{P}\right|}^2\right)+\hfill \\ & & {\displaystyle 6i\sigma \epsilon \left(t\right){\mathcal{P}}_x\left({\mathcal{U}}^{*}\mathcal{P}+\mathcal{U}{\mathcal{P}}^{*}\right)=0.}\hfill \end{array}$$

(2)

The beta derivative of the function $\mathcal{P}(x,t)$ at the specified order $\beta$ is defined as follows [28]:

$${\displaystyle \frac{{\partial }^{\beta }\mathcal{P}(x,t)}{\partial t^{\beta }}}=\underset{h\to 0}{lim}{\displaystyle \frac{\mathcal{P}\left(x,t+h{\left(t+\frac{1}{\Gamma \left(\beta \right)}\right)}^{1-\beta }\right)-\mathcal{P}(x,t)}{h}},\forall t>0,\beta \in (0,1].$$

(3)

It is important to note that this derivative operator belongs to the class of conformable-type derivatives, which are local operators. Unlike classical fractional derivatives (e.g., Caputo or Riemann–Liouville), the beta derivative does not incorporate non-local memory effects. This means that the model primarily describes instantaneous dynamics and may not capture viscoelastic or long-range time correlations inherent in some fractional quantum and optical systems. The analysis in this work focuses on the properties and solutions achievable within this local framework. To ensure mathematical consistency, we explicitly verify the integer-order limit of the beta derivative. When $\beta =1$, the derivative reduces to the classical integer-order derivative as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{P}(x,t)}{\partial }}& =\underset{h\to 0}{lim}{\displaystyle \frac{1}{h}}\left[\mathcal{P}\left(x,t+h\right)-\mathcal{P}(x,t)\right].\hfill \end{array}$$

In this integer-order limit ($\beta =1$) and with constant coefficients, our system of Equations (1) and (2) reduces to a standard higher-order Coupled Nonlinear Schrödinger system, specifically a generalized Manakov-type system with third-order dispersion. This reduction confirms the mathematical consistency of our fractional model and establishes its connection to well-established physical models in nonlinear optics. In this context, $\mathcal{P}$ and $\mathcal{U}$ denote the wave functions of two interacting modes, while $\sigma$ is a constant. The fractional order parameter $\beta$ carries significant physical meaning in optical and plasma contexts. In optical systems, $\beta$ controls how the pulse amplitude and phase evolve in a medium with variable refractive index or nonlinear response, allowing the model to describe intensity-dependent dispersion and wave steepening effects more accurately. In plasma contexts, $\beta$ can be interpreted as a scaling factor that modifies the strength of the nonlinear and dispersive interactions among charged particles, thus influencing the formation and stability of nonlinear wave structures.

The function $\epsilon \left(t\right)$ requires special clarification: in our solution approach using the extended direct algebraic method, $\epsilon \left(t\right)$ is not treated as an independently prescribed physical input. Rather, it emerges as a constraint derived from the consistency conditions required for the closure of the traveling wave ansatz. This mathematical inversion means that $\epsilon \left(t\right)$ is engineered to support exact soliton solutions, rather than being predetermined by specific physical dispersion profiles. While this approach is mathematically valid for obtaining exact solutions, the physical realizability of such derived $\epsilon \left(t\right)$ functions must be carefully considered. In practical dispersion management systems, third-order dispersion profiles can be engineered through techniques such as chirped fiber Bragg gratings or dispersion-compensating fibers. However, the specific functional forms of $\epsilon \left(t\right)$ obtained through our method would need to be evaluated case by case for experimental feasibility, considering technological constraints on achievable dispersion variations. This represents a limitation of exact solution methods but provides valuable insight into the types of dispersion management that could potentially support stable soliton propagation in coupled systems with higher-order effects. Physically, $\epsilon \left(t\right)$ represents the time-dependent third-order dispersion coefficient, which in optical contexts corresponds to engineered dispersion profiles in tapered fibers or dispersion-managed waveguides, while in plasma physics, it may model spatially inhomogeneous or time-varying dispersive characteristics in non-uniform plasma densities.

The extended direct algebraic method (EDAE) is an efficient analytical instrument employed to investigate isolated waves and microwave solutions in diverse scientific domains. It applies to many types of nonlinear partial differential equations (PDEs). In this study, we utilized the EDAE method on the proposed system, resulting in numerous solutions, including novel dark, bright, and singular soliton solutions; singular periodic solutions; Jacobi elliptic function solutions, rational solutions; and exponential solutions, accompanied by graphical representations of some extracted solutions with an explanation of the effect of the fractional derivative. These results highlight the method’s effectiveness and robustness. The extended direct algebraic method (EDAE) is an efficient analytical instrument employed to investigate isolated waves and microwave solutions in diverse scientific domains. It applies to many types of nonlinear partial differential equations (PDEs). Compared with the work of Yi et al. [29], which focused on regulating interactions among three specific optical solitons, and in line with our paper, our application of EDAE demonstrates significant methodological advantages. While Yi et al. primarily addressed control of known soliton interactions, our approach systematically uncovers a broader spectrum of novel solutions in a more complex fractional-order system. In this study, we utilized the EDAE method on the proposed system, resulting in numerous solutions, including novel dark, bright, and singular soliton solutions; singular periodic solutions; Jacobi elliptic function solutions; rational solutions; and exponential solutions. This diverse family of solutions substantially expands beyond the limited soliton interactions studied in previous works. The solutions are accompanied by graphical representations with detailed analysis of the fractional derivative’s effect, providing deeper physical insights than conventional soliton interaction studies. These results highlight the method’s effectiveness and robustness in handling complex variable-coefficient fractional systems and its superiority in discovering new wave structures compared with methods focused solely on regulating known soliton interactions.

This is how this article is organized: Section 2 describes the main features of the EDAE method. Using Wolfram Mathematica, Section 3 completes the symbolic calculations and provides a summary of the findings. In Section 4, diverse dynamic wave patterns of different soliton solutions are graphically presented using 2-D and 3-D simulations. Lastly, the study’s findings are presented in Section 5.

Comparison of the Beta Derivative with Other Fractional Operators

In this study, the governing equations are formulated using the beta derivative defined in Equation (3). To provide clarity and context, a comparative analysis with prominent fractional derivatives is presented below. This comparison elucidates the key mathematical and physical distinctions, particularly regarding the property of non-locality [30].

As conclusively illustrated in

Table 1. Comparison of fractional derivative operators.

Operator Type	Memory Kernel	Laplace Transform and Causality
Beta Derivative (This work)	Local (No Kernel)	$\mathcal{L}\left\{{\displaystyle \frac{{\partial }^{\beta }f\left(t\right)}{\partial t^{\beta }}}\right\}=$ A complex transform not standardly tabulated
	${\displaystyle \frac{{\partial }^{\beta }f\left(t\right)}{\partial t^{\beta }}}={lim}_{h\to 0}{\displaystyle \frac{f\left(t+h{[\frac{1}{\Gamma \left(\beta \right)}+t]}^{1-\beta }\right)-f\left(t\right)}{h}}$	Causality is inherently built into the limit definition.
Riemann–Liouville (RL)	Power-law: $K(t-\tau )={\displaystyle \frac{{(t-\tau )}^{m-\beta -1}}{\Gamma (m-\beta )}}$	$\mathcal{L}{\{}_0^{RL}{D}_t^{\beta }f\left(t\right)\}=s^{\beta }F\left(s\right)-{\sum }_{k=0}^{m-1}{s}^k{{[}_0^{RL}{D}_t^{\beta -k-1}f\left(t\right)]}_{t=0}$
	${}_{0 }{}^{RL}D_t^{\beta }f\left(t\right)={\displaystyle \frac{1}{\Gamma (m-\beta )}}{\displaystyle \frac{d^m}{d{t}^m}}{\int }_0^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{\beta +1-m}}}d\tau$	Inherently causal due to the integration from 0 to t.
Caputo	Power-law: $K(t-\tau )={\displaystyle \frac{{(t-\tau )}^{m-\beta -1}}{\Gamma (m-\beta )}}$	$\mathcal{L}{\{}_0^C{D}_t^{\beta }f\left(t\right)\}=s^{\beta }F\left(s\right)-{\sum }_{k=0}^{m-1}{s}^{\beta -k-1}{f}^{\left(k\right)}\left(0\right)$
	${}_0{}^{C}D_t^{\beta }f\left(t\right)={\displaystyle \frac{1}{\Gamma (m-\beta )}}{\int }_0^t{\displaystyle \frac{f^{\left(m\right)}\left(\tau \right)}{{(t-\tau )}^{\beta +1-m}}}d\tau$	Inherently causal and allows for standard initial conditions.
Atangana–Baleanu (ABC)	Mittag-Leffler: $K(t-\tau )=E_{\beta }\left(-{\displaystyle \frac{\beta {(t-\tau )}^{\beta }}{1-\beta }}\right)$	$\mathcal{L}{\{}_0^{ABC}{D}_t^{\beta }f\left(t\right)\}={\displaystyle \frac{s^{\beta }\mathcal{L}\left\{f\left(t\right)\right\}-s^{\beta -1}f\left(0\right)}{(1-\beta )s^{\beta }+\beta }}$
	${}_{0 }{}^{ABC}D_t^{\beta }f\left(t\right)={\displaystyle \frac{\mathbf{AB}\left(\beta \right)}{1-\beta }}{\int }_0^t{f}^{\prime }\left(\tau \right)E_{\beta }\left[-{\displaystyle \frac{\beta {(t-\tau )}^{\beta }}{1-\beta }}\right]d\tau$	Models non-local effects with a non-singular kernel; inherently causal.

, the fundamental distinction lies in the presence of a memory kernel. The Riemann–Liouville, Caputo, and Atangana–Baleanu operators are non-local, as they involve an integral over the entire history of the function from 0 to t, weighted by a specific kernel (${(t-\tau )}^{-\beta }$ for RL/Caputo, and a Mittag-Leffler function for ABC). This integral structure is what grants these operators their memory property, enabling them to model viscoelasticity, long-range time correlations, and hereditary phenomena. In contrast, the beta derivative used here is defined as a local limit, akin to the standard integer-order derivative but with a stretched time variable. Consequently, while it offers mathematical simplicity and facilitates the acquisition of analytical solutions for certain problems, it lacks a genuine memory kernel. Therefore, the dynamics of our system, governed by this operator, are predominantly instantaneous and do not embody the long-term temporal correlations typical of systems modeled with non-local fractional derivatives. This clarification is crucial for interpreting the physical scope of our findings.

2. Overview of the Extended Direct Algebraic Method

This section presents a detailed overview of the extended direct algebraic method, emphasizing its key components and significance in enhancing understanding of this mathematical approach. This method offers a systematic framework for solving partial differential equations (PDEs), providing insights into its application and effectiveness. We will examine the detailed NPDE below and demonstrate the procedures and techniques for implementing the extended direct algebraic method, assuming that the NPDE is as follows [20]:

$$\mathcal{R}\left(\mathcal{U},{\mathcal{U}}_x,{\mathcal{U}}_t,{\mathcal{U}}_{xx},\dots \right)=0,$$

(4)

The polynomial $\mathcal{R}$ is made up of $\mathcal{U}(x,t)$ and its partial derivatives with respect to time t and the dynamic system’s spatial dimension x.

To solve the above equation, we follow the following procedures:

Procedure-(1): We use the following assumption:

$$\mathcal{U}(x,t)=\mathcal{P}\left(\eta \right);\eta =\mathcal{T}x+{\displaystyle \frac{\mathcal{L}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta },$$

(5)

where the real-valued constants $\mathcal{T}$ and $\mathcal{L}$ are used. $\mathcal{P}\left(\eta \right)$ acts as a function of the resulting solution. The transformation in Equation (5) is specifically designed to handle the $\beta$-fractional derivative in the original equation. The time dependence is explicitly embedded in the term ${\displaystyle \frac{\mathcal{L}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta }$, which ensures proper accounting of temporal evolution in the wave variable $\eta$. When $\beta =1$, this reduces to the standard traveling wave transformation $\eta =\mathcal{T}x+\mathcal{L}t$, confirming its consistency with classical cases. The form ${\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta }$ is chosen to maintain compatibility with the fractional derivative operator while preserving necessary temporal dependence. The partial derivatives in Equation (5) are substituted by the transformations given in Equation (4) to convert it to the subsequent nonlinear ordinary differential system, as follows:

$$\mathcal{E}(\mathcal{P},{\mathcal{P}}^{\prime },{\mathcal{P}}^{″},{\mathcal{P}}^{‴},\dots )=0.$$

(6)

Procedure-(2): To solve Equation (6) using the applied method, the following solution series is applied:

$$\mathcal{P}\left(\eta \right)=\sum _{i=-N}^N{\alpha }_i\mathcal{U}{\left(\eta \right)}^i,$$

(7)

where ${\alpha }_i$$(i=-N,-(N-1),\dots ,0,1,2,\dots ,N)$ are real constants to be determined, with the constraint ${\alpha }_N\ne 0$ and ${\alpha }_{-N}\ne 0$ to ensure the inclusion of both highest- and lowest-order terms in the solution series.

Procedure-(3): To determine the balancing constant $\mathbb{N}$, we apply the balance rule between the nonlinearity and dispersion in Equation (6), while also considering the following constraint:

$${\mathcal{U}}^{\prime }\left(\eta \right)=ø\sqrt{{\mathit{d}}_0+{\mathit{d}}_1\mathcal{U}\left(\eta \right)+{\mathit{d}}_2\mathcal{U}{\left(\eta \right)}^2+{\mathit{d}}_3\mathcal{U}{\left(\eta \right)}^3+{\mathit{d}}_4\mathcal{U}{\left(\eta \right)}^4+{\mathit{d}}_6\mathcal{U}{\left(\eta \right)}^6},$$

(8)

where $ø=\pm 1$ and ${\mathit{d}}_j(j=0,1,2,3,4)$ are real valued constants. Various fundamental solutions are derived from Equation (7) by exploring different possible values of ${\mathit{d}}_j$.

Procedure-(4): A polynomial in $\mathcal{U}$ is derived by replacing Equations (7) and (8) into Equation (6). Setting the sum of terms with identical powers to zero is the next step. Mathematica software will be used to solve the resulting system of nonlinear equations and ascertain the values of the unknowns. Novel soliton solutions for the suggested system are produced by this method.

3. Investigate Solitons and Other Solutions to the Proposed System

Suppose the solutions to Equations (1) and (2) can be expressed in the following manner:

$$\mathcal{P}={\mathcal{R}}_1\left(\eta \right)e^{i\mathcal{Q}},$$

(9)

$$\mathcal{U}={\mathcal{R}}_2\left(\eta \right)e^{i\mathcal{Q}},$$

(10)

where

$$\eta =\mathcal{T}x+{\displaystyle \frac{\mathcal{L}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta },\&\mathcal{Q}=\gamma x+{\displaystyle \frac{\mathit{w}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta }+\Phi .$$

(11)

Separating complex wave functions into amplitudes and phases is crucial for addressing nonlinear terms in coupled equations. The amplitude components are denoted by ${\mathcal{R}}_i\left(\eta \right)$ (for $i=1,2$), with $\gamma$ representing the soliton frequency, $\mathit{w}$ the wave number, and $\Phi$ the phase constant. The normalized wave vector and frequency are represented by the parameters $\mathcal{T}$ and $\mathcal{L}$, respectively.

This assumption transforms the original partial differential Equations (1) and (2) into ordinary differential equations for ${\mathcal{R}}_1\left(\eta \right)$ and ${\mathcal{R}}_2\left(\eta \right)$, making them analytically tractable. Nonlinear ordinary differential equations (NLODEs) are produced by applying the previously indicated wave transformations to Equations (1) and (2). These NLODEs are separated into their real and imaginary components as follows:

$${\mathcal{T}}^2[1-3\gamma \epsilon \left(t\right)]{\mathcal{R}}_j^{″}+6\sigma [1-3\gamma \epsilon \left(t\right)]{\mathcal{R}}_j{\mathcal{R}}_{\tilde{j}}^2+2\sigma [1-3\gamma \epsilon \left(t\right)]{\mathcal{R}}_j^3-\left[{\gamma }^2-{\gamma }^3\epsilon \left(t\right)+\mathit{w}\right]{\mathcal{R}}_j=0,$$

(12)

$${\mathcal{T}}^3\epsilon \left(t\right){\mathcal{R}}_j^{\left(3\right)}+6\sigma \mathcal{T}\epsilon \left(t\right){\mathcal{R}}_{\tilde{j}}^2{\mathcal{R}}_j^{\prime }+12\sigma \mathcal{T}\epsilon \left(t\right){\mathcal{R}}_j{\mathcal{R}}_{\tilde{j}}{\mathcal{R}}_{\tilde{j}}^{\prime }+6\sigma \mathcal{T}\epsilon \left(t\right){\mathcal{R}}_j^2{\mathcal{R}}_j^{\prime }+\left[-3\mathcal{T}{\gamma }^2\epsilon \left(t\right)+2\gamma \mathcal{T}+\mathcal{L}\right]{\mathcal{R}}_j^{\prime }=0,$$

(13)

where $\tilde{j}=3-j$ and $j=1,2$. The balancing principle yields the following results:

$${\mathcal{R}}_{\tilde{j}}=h{\mathcal{R}}_j,$$

(14)

where h is a constant that satisfies $h\ne 0$ and $h\ne 1$.

This results in a transformation of Equations (12) and (13) into the following:

$${\mathcal{T}}^2[1-3\gamma \epsilon \left(t\right)]{\mathcal{R}}_j^{″}+2\sigma \left[1+3h^2\right][1-3\gamma \epsilon \left(t\right)]{\mathcal{R}}_j^3-\left[{\gamma }^2-{\gamma }^3\epsilon \left(t\right)+\mathit{w}\right]{\mathcal{R}}_j=0,$$

(15)

$${\mathcal{T}}^3\epsilon \left(t\right){\mathcal{R}}_j^{\left(3\right)}+6\left[1+3h^2\right]\sigma \mathcal{T}\epsilon \left(t\right){\mathcal{R}}_j^2{\mathcal{R}}_j^{\prime }+\left[-3\mathcal{T}{\gamma }^2\epsilon \left(t\right)+2\gamma \mathcal{T}+\mathcal{L}\right]{\mathcal{R}}_j^{\prime }=0.$$

(16)

The following is the reformulation of Equation (15) using Equation (16):

$${\mathcal{T}}^3\epsilon \left(t\right){\mathcal{R}}_j{\mathcal{R}}_j^{\left(3\right)}-3{\mathcal{T}}^3\epsilon \left(t\right){\mathcal{R}}_j^{\prime }{\mathcal{R}}_j^{″}+\left[3r\left(t\right){\gamma }^3\mathcal{T}\epsilon {\left(t\right)}^2-3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right]+2\gamma \mathcal{T}+\mathcal{L}\right]{\mathcal{R}}_j{\mathcal{R}}_j^{\prime }=0,$$

(17)

where $r\left(t\right)={\displaystyle \frac{1}{3\gamma \epsilon \left(t\right)-1}}$.

The balancing principle is a fundamental concept in nonlinear analysis that determines the value of N in the solution series. It involves balancing the highest-order derivative term with the highest-order nonlinear term in the reduced ODE, yielding $N=1$. This mathematical constraint directly leads to the solution form in Equation (17) with specific coefficients ${\alpha }_1$ and ${\alpha }_{-1}$. The second section explains how to generate exact solutions for Equation (17) as follows:

$${\displaystyle {\mathcal{R}}_j={\alpha }_0+{\alpha }_1\mathcal{U}\left(\eta \right)+\frac{{\alpha }_{-1}}{\mathcal{U}\left(\eta \right)},}$$

(18)

where the real constants ${\alpha }_0,{\alpha }_1$, and ${\alpha }_{-1}$ are determined by the restriction ${\alpha }_1^2+{\alpha }_{-1}^2\ne 0$.

We obtain a polynomial in $\mathcal{U}\left(\eta \right)$ by inserting Equation (18) and the restriction from Equation (8) into Equation (17). When like terms are combined and set to zero, an algebraic system of non-linear equations is produced. After that, we solve these equations using Wolfram Mathematica to produce possible solutions for the suggested system, which fall into the following categories:

First Situation: If the limitations ${\mathit{d}}_0={\mathit{d}}_1={\mathit{d}}_3=0\mathit{and}{\mathit{d}}_6=0$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 1.

(1.1) 

${\alpha }_1={\alpha }_1,{\alpha }_0={\alpha }_{-1}=0,$

$\epsilon \left(t\right)={\displaystyle \frac{2{\mathit{d}}_2{\mathcal{T}}^3+3\mathcal{T}\left({\gamma }^2+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)\pm \sqrt{{\left[2{\mathit{d}}_2{\mathcal{T}}^3+3\mathcal{T}\left({\gamma }^2+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)\right]}^2-12{\gamma }^{3}r\left(t\right)\mathcal{T}(2\gamma \mathcal{T}+\mathcal{L})}}{6{\gamma }^{3}r\left(t\right)\mathcal{T}}}.$

(1.2) 

${\alpha }_0={\alpha }_1=0,{\alpha }_{-1}={\alpha }_{-1},$

$\epsilon \left(t\right)={\displaystyle \frac{2{\mathit{d}}_2{\mathcal{T}}^3+3\mathcal{T}\left({\gamma }^2+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)\pm \sqrt{{\left[2{\mathit{d}}_2{\mathcal{T}}^3+3\mathcal{T}\left({\gamma }^2+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)\right]}^2-12{\gamma }^{3}r\left(t\right)\mathcal{T}(2\gamma \mathcal{T}+\mathcal{L})}}{6{\gamma }^{3}r\left(t\right)\mathcal{T}}}.$

We can now derive the exact solutions to Equations (1) and (2) based on the solutions from the set (1.1), which are outlined as follows:

Description 2.

(1.1.1) 

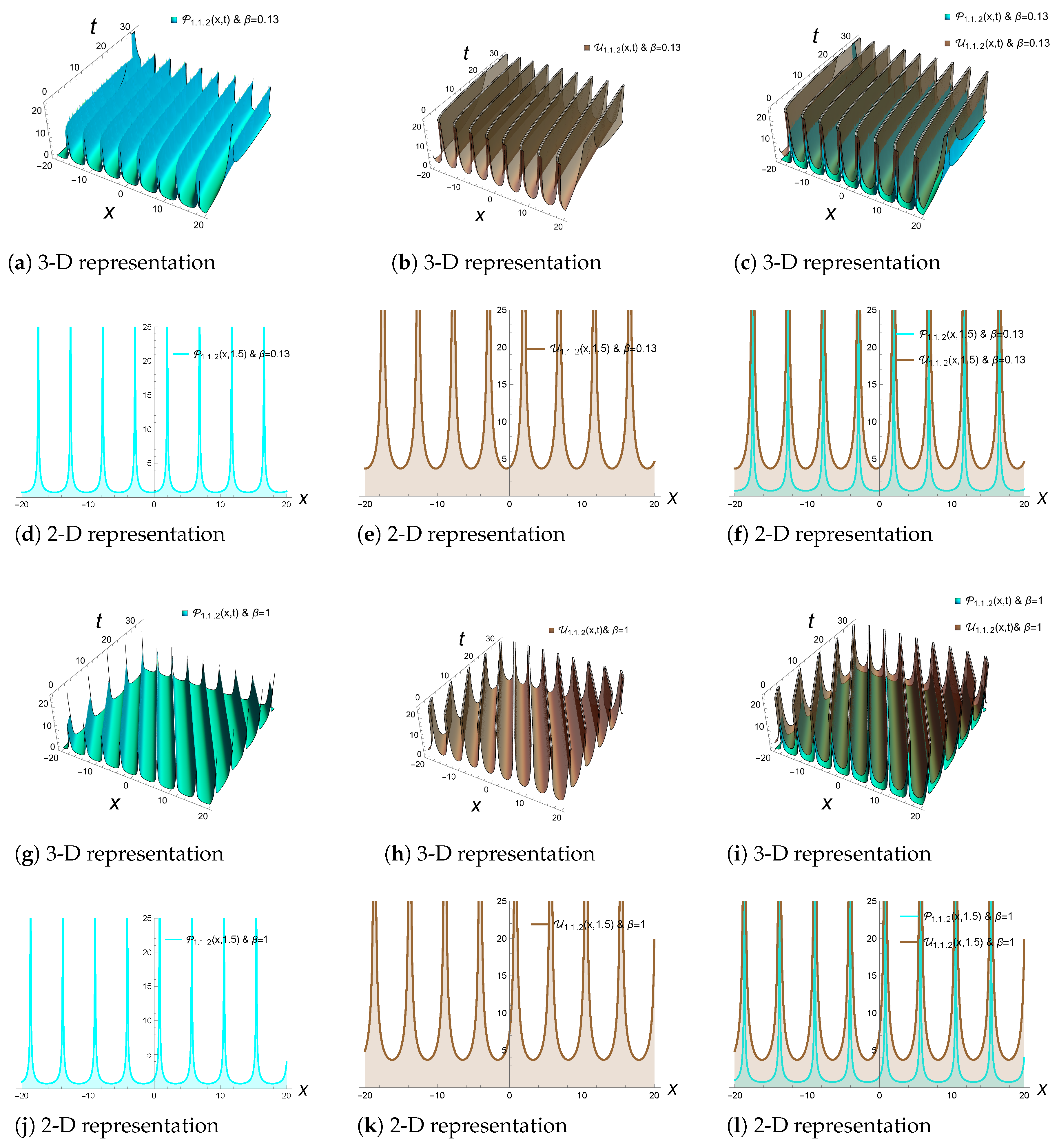
We obtain the bright soliton solutions as follows if ${\mathit{d}}_2>0$ and ${\mathit{d}}_4<0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.1.1}}={\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{{\mathit{d}}_4}}sech\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(19)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.1.1}}=h{\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{{\mathit{d}}_4}}sech\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(20)

(1.1.2) 

We obtain the singular periodic solutions as follows if ${\mathit{d}}_2<0$ and ${\mathit{d}}_4>0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.1.2}}={\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{{\mathit{d}}_4}}sec\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(21)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.1.2}}=h{\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{{\mathit{d}}_4}}sec\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(22)

(1.1.3) 

We obtain the rational solutions as follows if ${\mathit{d}}_2=0$ and ${\mathit{d}}_4>0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.1.3}}=\frac{{\alpha }_1}{\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]\sqrt{{\mathit{d}}_4}}{e}^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(23)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.1.3}}=\frac{h{\alpha }_1}{(\mathcal{T}x+ht)\sqrt{{\mathit{d}}_4}}{e}^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(24)

We can now derive the exact solutions to Equations (1) and (2) based on the solutions from the set (1.2), which are outlined as follows:

Description 3.

(1.2.1) 

We obtain the hyperbolic solutions as follows if ${\mathit{d}}_2>0$ and ${\mathit{d}}_4<0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.2.1}}={\alpha }_{-1}\sqrt{-\frac{{\mathit{d}}_4}{{\mathit{d}}_2}}cosh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(25)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.2.1}}=h{\alpha }_{-1}\sqrt{-\frac{{\mathit{d}}_4}{{\mathit{d}}_2}}cosh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(26)

(1.2.2) 

We obtain the periodic solutions as follows if ${\mathit{d}}_2<0$ and ${\mathit{d}}_4>0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.2.2}}={\alpha }_{-1}\sqrt{-\frac{{\mathit{d}}_4}{{\mathit{d}}_2}}cos\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(27)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.2.2}}=h{\alpha }_{-1}\sqrt{-\frac{{\mathit{d}}_4}{{\mathit{d}}_2}}cos\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(28)

(1.2.3) 

We obtain the polynomial solutions as follows if ${\mathit{d}}_2=0$ and ${\mathit{d}}_4>0$ are satisfied:

$${\displaystyle {\mathcal{P}}_{\mathrm{1.2.3}}={\alpha }_{-1}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_4}{e}^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(29)

$${\displaystyle {\mathcal{U}}_{\mathrm{1.2.3}}=h{\alpha }_{-1}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_4}{e}^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(30)

Second situation: If the limitations ${\mathit{d}}_1={\mathit{d}}_3={\mathit{d}}_6=0\mathit{and}{\mathit{d}}_0={\displaystyle \frac{{\mathit{d}}_2^2}{4{\mathit{d}}_4}}$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 4.

(2.1) 

${\alpha }_0={\alpha }_1=0,{\alpha }_{-1}={\alpha }_{-1},r\left(t\right)={\displaystyle \frac{2\gamma \mathcal{T}+\mathcal{L}-\epsilon \left(t\right)\left(2{\mathit{d}}_2{\mathcal{T}}^3+3{\gamma }^2\mathcal{T}\right)}{3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2-{\gamma }^3\epsilon \left(t\right)+\mathit{w}\right]}}.$

(2.2) 

${\alpha }_0={\alpha }_{-1}=0,{\alpha }_1={\alpha }_1,r\left(t\right)={\displaystyle \frac{2\gamma \mathcal{T}+\mathcal{L}-\epsilon \left(t\right)\left(2{\mathit{d}}_2{\mathcal{T}}^3+3{\gamma }^2\mathcal{T}\right)}{3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2-{\gamma }^3\epsilon \left(t\right)+\mathit{w}\right]}}.$

(2.3) 

${\alpha }_0=0,{\alpha }_1={\displaystyle \frac{2{\alpha }_{-1}{\mathit{d}}_4}{{\mathit{d}}_2}},r\left(t\right)={\displaystyle \frac{2\gamma \mathcal{T}+\mathcal{L}-\epsilon \left(t\right)\left(2{\mathit{d}}_2{\mathcal{T}}^3-3{\gamma }^2\mathcal{T}\right)}{3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2-{\gamma }^3\epsilon \left(t\right)+\mathit{w}\right]}}.$

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (2.1), which is expressed as follows:

Description 5.

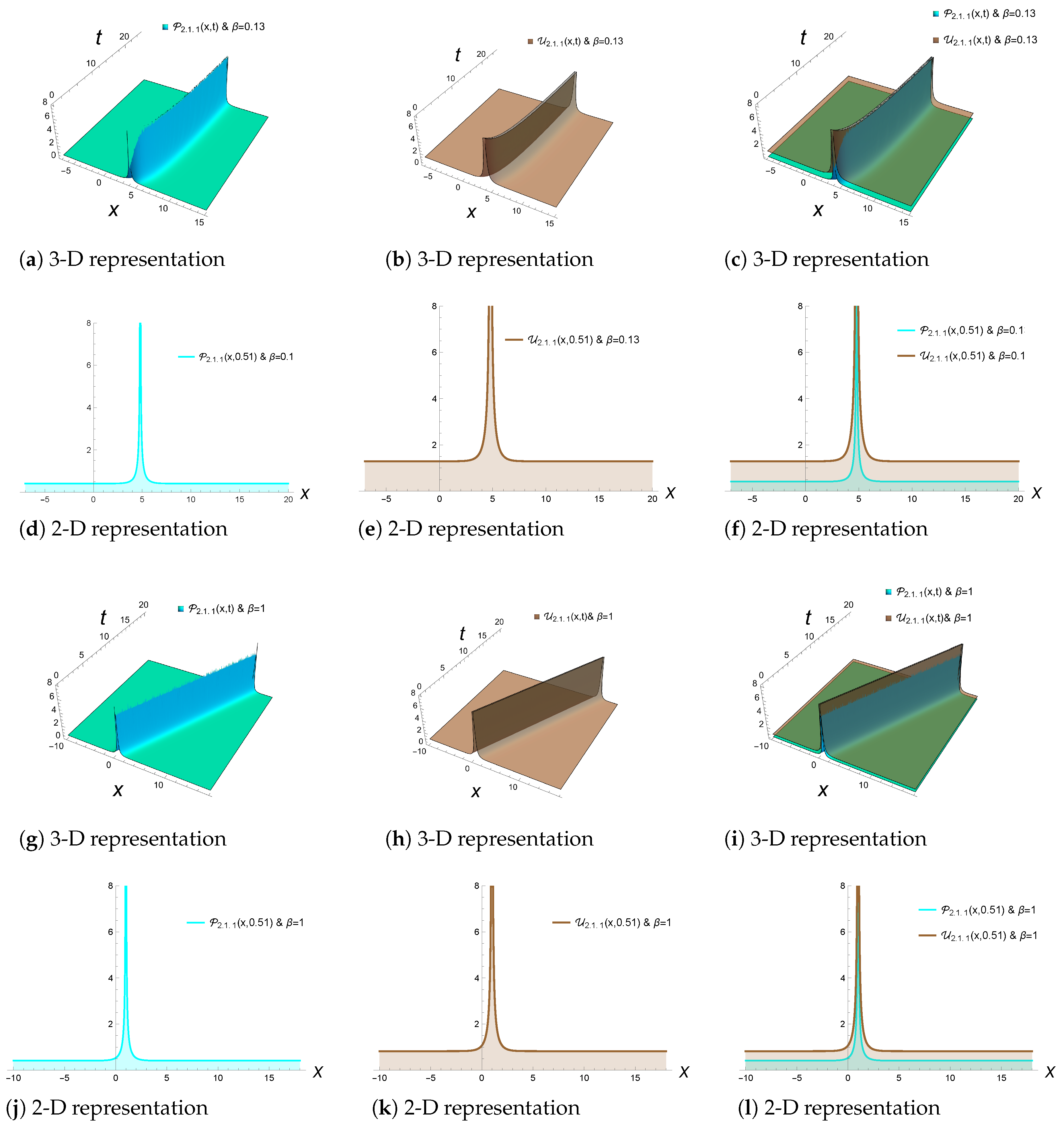
(2.1.1) 

The singular soliton solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2<0\mathit{and}{\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.1.1}}={\alpha }_{-1}\sqrt{-\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}coth\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(31)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.1.1}}=h{\alpha }_{-1}\sqrt{-\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}coth\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(32)

(2.1.2) 

The singular periodic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}{\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.1.2}}={\alpha }_{-1}\sqrt{\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}cot\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(33)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.1.2}}=h{\alpha }_{-1}\sqrt{\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}cot\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(34)

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (2.2), which is expressed as follows:

Description 6.

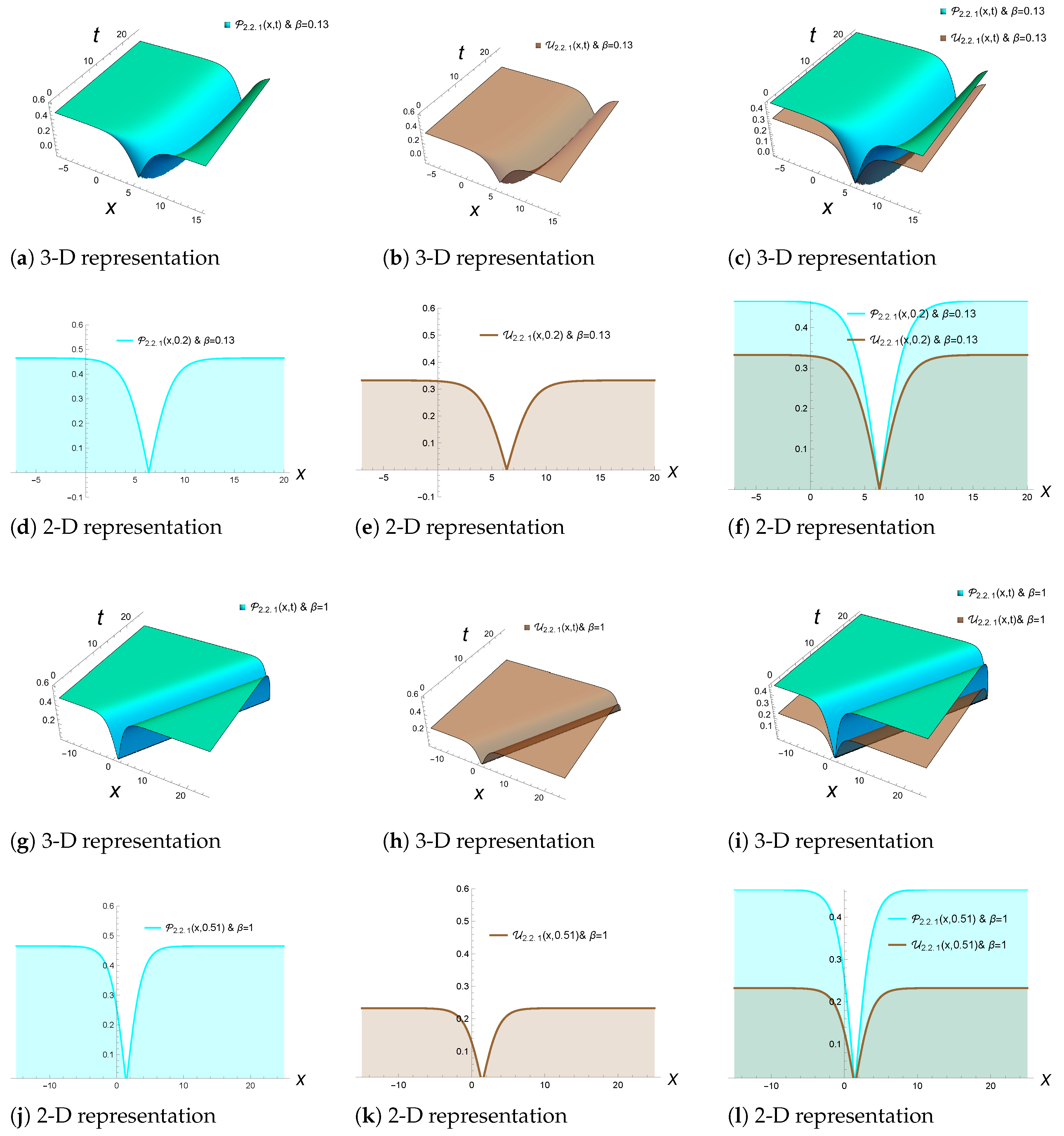
(2.2.1) 

The dark soliton solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2<0$ and ${\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.2.1}}={\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{2{\mathit{d}}_4}}tanh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(35)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.2.1}}=h{\alpha }_1\sqrt{-\frac{{\mathit{d}}_2}{2{\mathit{d}}_4}}tanh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(36)

(2.2.2) 

The singular periodic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}{\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.2.2}}={\alpha }_1\sqrt{\frac{{\mathit{d}}_2}{2{\mathit{d}}_4}}tan\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(37)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.2.2}}=h{\alpha }_1\sqrt{\frac{{\mathit{d}}_2}{2{\mathit{d}}_4}}tan\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{\frac{{\mathit{d}}_2}{2}}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(38)

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (2.3), which is expressed as follows:

Description 7.

(2.3.1) 

The singular soliton solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2<0\mathit{and}{\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.3.1}}=2{\alpha }_{-1}\sqrt{-\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}csch\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-2{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(39)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.3.1}}=2h{\alpha }_{-1}\sqrt{-\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}csch\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-2{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(40)

(2.3.2) 

The singular periodic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}{\mathit{d}}_4>0$:

$${\displaystyle {\mathcal{P}}_{\mathrm{2.3.2}}=2{\alpha }_{-1}\sqrt{\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}csc\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{2{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(41)

$${\displaystyle {\mathcal{U}}_{\mathrm{2.3.2}}=2h{\alpha }_{-1}\sqrt{\frac{2{\mathit{d}}_4}{{\mathit{d}}_2}}csc\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{2{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(42)

Third situation: If the limitations ${\mathit{d}}_3={\mathit{d}}_4=0$ and ${\mathit{d}}_6=0$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 8.

• ${\alpha }_{-1}=0,{\alpha }_1={\displaystyle \frac{2{\alpha }_0{\mathit{d}}_2}{{\mathit{d}}_1}},h=\mathcal{T}\left(\epsilon \left(t\right)\left(2{\mathit{d}}_2{\mathcal{T}}^2{ϵ}^2+3{\gamma }^2(r\left(t\right)+1)-3{\gamma }^{3}r\left(t\right)\epsilon \left(t\right)+3r\left(t\right)\mathit{w}\right)-2\gamma \right).$

Based on the previously given set of solutions, we can now obtain exact solutions for Equations (1) and (2) as follows:

Description 9.

(3.1) 

The hyperbolic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}{\mathit{d}}_0=0$:

$${\displaystyle {\mathcal{P}}_{3.1}={\alpha }_{0}sinh\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(43)

$${\displaystyle {\mathcal{U}}_{3.1}={\alpha }_{0}hsinh\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(44)

(3.2) 

The periodic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2<0\mathit{and}{\mathit{d}}_0=0$:

$${\displaystyle {\mathcal{P}}_{3.2}={\alpha }_{0}sin\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(45)

$${\displaystyle {\mathcal{U}}_{3.2}={\alpha }_{0}hsin\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{-{\mathit{d}}_2}\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(46)

(3.3) 

The exponential solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0$ and ${\mathit{d}}_0={\displaystyle \frac{{\mathit{d}}_1^2}{4{\mathit{d}}_2}}$:

$${\displaystyle {\mathcal{P}}_{3.3}=\frac{2{\alpha }_0{\mathit{d}}_2}{{\mathit{d}}_1}{e}^{\left[i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )+\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]},}$$

(47)

$${\displaystyle {\mathcal{U}}_{3.2}=\frac{2{\alpha }_0{\mathit{d}}_{2}h}{{\mathit{d}}_1}{e}^{\left[i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )+\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]}.}$$

(48)

Fourth situation: If the limitations ${\mathit{d}}_0={\mathit{d}}_1=0$ and ${\mathit{d}}_6=0$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 10.

(4.1) 

${\alpha }_1=0,{\alpha }_{-1}={\displaystyle \frac{2{\alpha }_0{\mathit{d}}_2}{{\mathit{d}}_3}},h=\mathcal{T}\left(\epsilon \left(t\right)\left[2{\mathit{d}}_2{\mathcal{T}}^2+3{\gamma }^2(r\left(t\right)+1)-3{\gamma }^{3}r\left(t\right)\epsilon \left(t\right)+3r\left(t\right)\mathit{w}\right]-2\gamma \right).$

(4.2) 

${\alpha }_1={\displaystyle \frac{4{\alpha }_0{\mathit{d}}_4}{{\mathit{d}}_3}},{\alpha }_{-1}=0,{\mathit{d}}_2={\displaystyle \frac{{\mathit{d}}_3^2}{4{\mathit{d}}_4}},h=3\mathcal{T}\epsilon \left(t\right)\left({\gamma }^2-r\left(t\right){\gamma }^3\epsilon \left(t\right)+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)-{\displaystyle \frac{{\mathit{d}}_3^2{\mathcal{T}}^3\epsilon \left(t\right)}{4{\mathit{d}}_4}}-2\gamma \mathcal{T}.$

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (4.1), which is expressed as follows:

Description 11.

(4.1.1) 

The hyperbolic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}$${\mathit{d}}_3^2=4{\mathit{d}}_1{\mathit{d}}_2$:

$${\displaystyle {\mathcal{P}}_{\mathrm{4.1.1}}={\alpha }_0\left(sinh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]-cosh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)}$$

$$\times e^{i(\gamma x+{\displaystyle \frac{\mathit{w}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta }+\Phi )},$$

(49)

$${\displaystyle {\mathcal{U}}_{\mathrm{4.1.1}}={\alpha }_{0}h\left(sinh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]-cosh\left[\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)}$$

$$\times e^{i(\gamma x+{\displaystyle \frac{\mathit{w}}{\beta }}{\left({\displaystyle \frac{1}{\Gamma \left(\beta \right)}}+t\right)}^{\beta }+\Phi )}.$$

(50)

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (4.2), which is expressed as follows:

Description 12.

(4.2.1) 

The dark soliton solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0$ and ${\mathit{d}}_3^2=4{\mathit{d}}_1{\mathit{d}}_2$:

$${\displaystyle {\mathcal{P}}_{\mathrm{4.2.1}}=\frac{{\alpha }_0}{{\mathit{d}}_1}\left({\mathit{d}}_1-{\mathit{d}}_4+{\mathit{d}}_{4}tanh\left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(51)

$${\displaystyle {\mathcal{U}}_{\mathrm{4.2.1}}=\frac{{\alpha }_{0}h}{{\mathit{d}}_1}\left({\mathit{d}}_1-{\mathit{d}}_4+{\mathit{d}}_{4}tanh\left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(52)

(4.2.2) 

The singular soliton solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_2>0\mathit{and}{\mathit{d}}_3^2=4{\mathit{d}}_1{\mathit{d}}_2$:

$${\displaystyle {\mathcal{P}}_{\mathrm{4.2.2}}=\frac{{\alpha }_0}{{\mathit{d}}_1}\left({\mathit{d}}_1-{\mathit{d}}_4+{\mathit{d}}_{4}coth\left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(53)

$${\displaystyle {\mathcal{U}}_{\mathrm{4.2.2}}=\frac{{\alpha }_{0}h}{{\mathit{d}}_1}\left({\mathit{d}}_1-{\mathit{d}}_4+{\mathit{d}}_{4}coth\left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_2}\right]\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(54)

Fifth situation: If the limitations ${\mathit{d}}_2={\mathit{d}}_4=0$ and ${\mathit{d}}_6=0$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 13.

• ${\alpha }_0={\displaystyle \frac{{\mathit{d}}_1{\alpha }_{-1}}{4{\mathit{d}}_0}},{\alpha }_1=0,{\mathit{d}}_3=-{\displaystyle \frac{{\mathit{d}}_1^3}{8{\mathit{d}}_0^2}},h=3\mathcal{T}\epsilon \left(t\right)\left({\gamma }^2-r\left(t\right){\gamma }^3\epsilon \left(t\right)+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right)-{\displaystyle \frac{3{\mathit{d}}_1^2{\mathcal{T}}^3\epsilon \left(t\right)}{4{\mathit{d}}_0}}-2\gamma \mathcal{T}.$

Based on the previously given set of solutions, we can now obtain exact solutions for Equations (1) and (2) as follows:

Description 14.

(5.1) 

The Weierstrass elliptic doubly periodic solutions are obtained as follows if the following requirement is met, ${\mathit{d}}_3>0$:

$${\displaystyle {\mathcal{P}}_{5.1}=\frac{{\alpha }_{-1}}{4}\left(\frac{{\mathit{d}}_1}{{\mathit{d}}_0}+\frac{4}{\wp \left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_3};-\frac{4{\mathit{d}}_1}{{\mathit{d}}_3},-\frac{4{\mathit{d}}_0}{{\mathit{d}}_3}\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(55)

$${\displaystyle {\mathcal{U}}_{5.1}=\frac{h{\alpha }_{-1}}{4}\left(\frac{{\mathit{d}}_1}{{\mathit{d}}_0}+\frac{4}{\wp \left[\frac{1}{2}\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\sqrt{{\mathit{d}}_3};-\frac{4{\mathit{d}}_1}{{\mathit{d}}_3},-\frac{4{\mathit{d}}_0}{{\mathit{d}}_3}\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(56)

Sixth situation: If the limitations ${\mathit{d}}_1={\mathit{d}}_3=0$ and ${\mathit{d}}_6=0$ are applied, we obtain a restricted set of solutions for the algebraic system, establishing a clear mathematical framework that yields limited results based on these conditions:

Description 15.

(6.1) 

${\alpha }_1={\alpha }_1,{\alpha }_0={\alpha }_{-1}=0,{\mathit{d}}_2={\displaystyle \frac{-3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2-r\left(t\right){\gamma }^3\epsilon \left(t\right)+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right]+2\gamma \mathcal{T}+\mathcal{L}}{2{\mathcal{T}}^3\epsilon \left(t\right)}}.$

(6.2) 

${\alpha }_{-1}={\alpha }_{-1},{\alpha }_0={\alpha }_1=0,{\mathit{d}}_2={\displaystyle \frac{-3\mathcal{T}\epsilon \left(t\right)\left[{\gamma }^2-r\left(t\right){\gamma }^3\epsilon \left(t\right)+r\left(t\right)\left({\gamma }^2+\mathit{w}\right)\right]+2\gamma \mathcal{T}+\mathcal{L}}{2{\mathcal{T}}^3\epsilon \left(t\right)}}.$

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (6.1), which is expressed as follows:

Description 16.

(6.1.1) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=1,$${\mathit{d}}_2=-m^2-1,{\mathit{d}}_4=m^2\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.1}}={\alpha }_{1}sn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(57)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.1}}=h{\alpha }_{1}sn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(58)

or

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.2}}={\alpha }_{1}cd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(59)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.2}}=h{\alpha }_{1}cd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(60)

Equations (57) and (58) yield dark soliton solutions for $m=1$, while Equations (57)–(60) yield periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.3}}={\alpha }_{1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(61)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.3}}=h{\alpha }_{1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(62)

or

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.4}}={\alpha }_{1}sin\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(63)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.4}}=h{\alpha }_{1}sin\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(64)

and

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.5}}={\alpha }_{1}cos\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(65)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.5}}=h{\alpha }_{1}cos\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(66)

(6.1.2) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=m^2-1,{\mathit{d}}_2=2-m^2,{\mathit{d}}_4=-1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.6}}={\alpha }_{1}dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(67)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.6}}=h{\alpha }_{1}dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(68)

Equations (67) and (68) provide bright soliton solutions for $m=1$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.7}}={\alpha }_{1}sech\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(69)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.7}}=h{\alpha }_{1}sech\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(70)

(6.1.3) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=-m^2,{\mathit{d}}_2=2m^2-1,{\mathit{d}}_4=1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.8}}={\alpha }_{1}nc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(71)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.8}}=h{\alpha }_{1}nc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(72)

Equations (71) and (72) yield hyperbolic solutions for $m=1$ and singular periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.9}}={\alpha }_{1}cosh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(73)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.9}}=h{\alpha }_{1}cosh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(74)

and

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.9}}={\alpha }_{1}sec\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(75)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.9}}=h{\alpha }_{1}sec\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(76)

(6.1.4) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=1,$${\mathit{d}}_2=2-4m^2,{\mathit{d}}_4=1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.10}}={\alpha }_1\left(\frac{dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]nc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{ns\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(77)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.10}}=h{\alpha }_1\left(\frac{dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]nc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{ns\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(78)

Equations (77) and (78) yield dark soliton solutions for $m=1$ and singular periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.11}}={\alpha }_{1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(79)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.11}}=h{\alpha }_{1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(80)

and

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.12}}={\alpha }_{1}tan\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(81)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.12}}=h{\alpha }_{1}tan\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(82)

(6.1.5) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=m^4-2m^3+m^2,{\mathit{d}}_2=-{\displaystyle \frac{4}{m}},{\mathit{d}}_4=-m^2+6m-1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.13}}={\alpha }_{1}m\left(\frac{cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{1+m{sn}^2\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(83)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.13}}=h{\alpha }_{1}m\left(\frac{cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]dn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{1+m{sn}^2\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(84)

Equations (83) and (84) provide bright soliton solutions for $m=1$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.1.14}}={\alpha }_{1}sech\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(85)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.1.14}}=h{\alpha }_{1}sech\left[2\left(\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right)\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(86)

We can now obtain the exact solutions to Equations (1) and (2) based on the solution set (6.2), which is expressed as follows:

Description 17.

(6.2.1) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=1,$${\mathit{d}}_2=-m^2-1,{\mathit{d}}_4=m^2\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.1}}={\alpha }_{-1}ns\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(87)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.1}}=h{\alpha }_{-1}ns\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(88)

or

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.2}}={\alpha }_{-1}dc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(89)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.2}}=h{\alpha }_{-1}dc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(90)

Equations (87) and (88) yield singular soliton solutions for $m=1$, while Equations (87)–(90) yield singular periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.3}}={\alpha }_{-1}coth\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(91)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.3}}=h{\alpha }_{-1}coth\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(92)

or

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.4}}={\alpha }_{-1}csc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(93)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.4}}=h{\alpha }_{-1}csc\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(94)

and

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.5}}={\alpha }_{-1}sec\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(95)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.5}}=h{\alpha }_{-1}sec\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(96)

(6.2.2) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=m^2-1,{\mathit{d}}_2=2-m^2,{\mathit{d}}_4=-1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.6}}={\alpha }_{-1}nd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(97)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.6}}=h{\alpha }_{-1}nd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(98)

Equations (97) and (98) provide hyperbolic solutions for $m=1$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.7}}={\alpha }_{-1}cosh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(99)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.7}}=h{\alpha }_{-1}cosh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(100)

(6.2.3) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=-m^2,{\mathit{d}}_2=2m^2-1,{\mathit{d}}_4=1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.8}}={\alpha }_{-1}cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(101)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.8}}=h{\alpha }_{-1}cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(102)

Equations (101) and (102) yield bright soliton solutions for $m=1$ and periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.9}}={\alpha }_{-1}sech\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(103)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.9}}=h{\alpha }_{-1}sech\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(104)

and

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.10}}={\alpha }_{-1}cos\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(105)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.10}}=h{\alpha }_{-1}cos\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(106)

(6.2.4) 

The Jacobi elliptic solutions are obtained as follows if the following requirements are met, ${\mathit{d}}_0=1,$${\mathit{d}}_2=2-4m^2,{\mathit{d}}_4=1\mathit{and}0\le m\le 1$:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.11}}={\alpha }_{-1}\left(\frac{nd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{sn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(107)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.11}}=h{\alpha }_{-1}\left(\frac{nd\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]cn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}{sn\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]}\right)e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(108)

Equations (107) and (108) yield dark soliton solutions for $m=1$ and periodic solutions for $m=0$ as follows:

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.12}}={\alpha }_{-1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(109)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.12}}=h{\alpha }_{-1}tanh\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(110)

or

$${\displaystyle {\mathcal{P}}_{\mathrm{6.2.13}}={\alpha }_{-1}sin\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )},}$$

(111)

$${\displaystyle {\mathcal{U}}_{\mathrm{6.2.13}}=h{\alpha }_{-1}sin\left[\mathcal{T}x+\frac{\mathcal{L}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }\right]e^{i(\gamma x+\frac{\mathit{w}}{\beta }{\left(\frac{1}{\Gamma \left(\beta \right)}+t\right)}^{\beta }+\Phi )}.}$$

(112)

4. Physical Applications of Solitons in VCNLS Equations with β-Derivatives

In this section of our study, we will illustrate the figure and specify the various solutions obtained for the VCNLS equations. Through thorough exploration, we have identified numerous previously unrecorded value sets for Equations (1) and (2), achieved by varying the model parameters. Consequently, this section features a variety of graph forms and a rich collection of visual representations, including both 3-D and 2-D plots that detail several individual solutions. These visual aids effectively highlight the mathematical and physical characteristics of the solutions we have discovered.

Figure 1 illustrates the bright soliton solutions of Equations (19) and (20), with parameters set to ${\mathit{d}}_4=-0.45,{\mathit{d}}_2=2.5,{\alpha }_1=0.62,\mathcal{L}=0.52,\mathcal{T}=-0.98,$$\mathit{w}=-0.63,\gamma =0.72,\Phi =0.69$, and $h=2$. These solutions display a localized intensity peak over a continuous wave (CW) background, facilitating the existence of bright solitons in finite-depth fluids, particularly in regions of stable carrier wave modulation. This enhances our understanding of wave behavior in various environments and underscores the interaction between the governing equations and fluid dynamics.

Figure 2 illustrates the singular periodic solutions of Equations (21) and (22) with parameters ${\mathit{d}}_4=0.45,{\mathit{d}}_2=-0.65,{\alpha }_1=0.62,\mathcal{L}=0.52,\mathcal{T}=0.8,\mathit{w}=0.63,\gamma =0.72,$$\Phi =0.79$, and $h=5$. A system exhibiting these periodic solutions, along with abrupt changes or extreme events, demonstrates distinctive periodic behavior in physical phenomena. Such singularities can result from non-linearities, boundary conditions, or external stimuli.

Figure 3 illustrates the singular soliton solutions of Equations (31) and (32) with parameters ${\mathit{d}}_4=0.5,{\mathit{d}}_2=-2.4,{\alpha }_1=0.64,\mathcal{L}=0.62,\mathcal{T}=-0.94,\mathit{w}=-0.66,$$\gamma =0.73,\Phi =0.69$, and $h=2$. These solutions are mainly defined by a narrow region that peaks at infinity.

Figure 4 illustrates the dark soliton solution for Equations (35) and (36) with parameters ${\mathit{d}}_4=0.6,{\mathit{d}}_2=-0.53,{\alpha }_1=0.7,\mathcal{L}=0.8,\mathcal{T}=-0.84,\mathit{w}=-0.76,\gamma =0.75,\Phi =0.68$, and $h=0.5$. Dark solitons are localized areas of reduced amplitude in a medium, typically associated with lower fluid density or pressure in fluid dynamics.

5. Conclusions

The extended direct algebraic method effectively demonstrates the existence of dynamic optical solitons in systems described by variable-coefficient coupled higher-order nonlinear Schrödinger equations. The methodological rigor of EDAM is demonstrated through its systematic application: first, transforming the complex fractional system into integer-order via $\beta$-derivative properties; second, applying homogeneous balance to determine the solution structure; third, substituting into the simplified equation to obtain polynomial systems; and finally, solving these systems analytically to derive exact solutions. This structured approach ensures mathematical consistency and reproducibility of results. The stability and robustness of the obtained soliton solutions are supported by several analytical indicators: (1) the existence of conserved quantities in the reduced systems, (2) the structural stability of solution profiles under parameter variations as evidenced in Figure 1, Figure 2, Figure 3 and Figure 4, (3) the physical consistency of the solutions with known soliton behavior in nonlinear optics, and (4) the mathematical exactness of the solutions satisfying the original equations exactly. However, a comprehensive numerical stability analysis under arbitrary perturbations would be required for complete validation, which represents a direction for future work. Incorporating $\beta$-derivatives significantly impacts the propagation characteristics of solitons. The $\beta$-fractional derivative terms introduce scaling effects that can enhance phenomena such as dispersion and nonlinearity, leading to a richer variety of soliton solutions compared with traditional integer-order systems. Crucially, the $\beta$ parameter transcends mere theoretical generalization to offer tangible physical significance: it serves as an experimentally controllable parameter that governs fundamental light-matter interactions. The deformation of soliton shapes with varying $\beta$ values directly corresponds to observable changes in pulse propagation through complex optical media with specific scaling properties. The time parameterization enabled by $\beta$ provides a mathematical framework for modeling systems with intrinsic memory or hereditary properties, while the new phase relations offer unprecedented control over coherent light propagation. This makes $\beta$ a powerful engineering parameter for designing advanced photonic devices with customized dispersion and nonlinear characteristics, potentially enabling novel applications in optical computing, signal processing, and quantum communication systems where precise control over pulse dynamics is paramount. Our comparative analysis reveals fundamental differences between fractional and non-fractional approaches: the $\beta$-fractional derivative introduces scaling effects and parameter-dependent behavior that significantly alter soliton dynamics. Specifically, fractional solutions exhibit enhanced pulse shaping capabilities, more flexible dispersion management, and additional degrees of freedom for controlling soliton interactions. While non-fractional models provide a solid foundation, the fractional framework offers enhanced modeling flexibility for optical media with specific scaling properties. The parameter $\beta$ serves as a crucial tuning parameter that bridges classical and fractional dynamics, enabling smooth transition between integer and fractional-order behaviors. The physical relevance of our findings is further strengthened by the direct correspondence between mathematical solutions and experimentally observable phenomena: the bright solitons correspond to stable optical pulses in fiber communications, dark solitons represent intensity dips useful for optical switching, singular solitons model pulse collapse scenarios, and elliptic solutions describe periodic wave patterns observable in nonlinear waveguide arrays. Each solution type emerges under specific physical conditions dictated by the $\beta$ parameter and system coefficients, creating a comprehensive map between mathematical solutions and physical realizations. Unlike conventional methods that often yield limited solution types, our application of EDAM provides comprehensive coverage of possible wave structures, as evidenced by the diverse solutions obtained. This methodological advantage is particularly evident when compared with approaches like that of Yi et al. (2024) [29], which focused primarily on specific soliton interactions rather than systematic solution derivation. The study identifies several soliton types arising from the VCHNLSE solutions, bright solitons with bounded amplitude that maintain their shape as they propagate, dark solitons appearing as dips in the background and demonstrating stability due to their topological characteristics, and singular solitons characterized by complex amplitude structures that result in intricate interactions. Additional solutions include singular periodic solutions, Jacobi elliptic function solutions, rational solutions, polynomial solutions, hyperbolic solutions, and exponential solutions. The graphical representations (Figure 1, Figure 2, Figure 3 and Figure 4) clearly demonstrate how fractional solutions exhibit more complex temporal profiles and spectral characteristics compared with their non-fractional counterparts. This complexity translates to practical advantages in optical communication systems, where fractional solitons can better adapt to varying channel conditions and mitigate signal degradation effects. The derivation of each solution type follows logically from the EDAM framework: bright and dark solitons emerge from specific parameter constraints in the auxiliary equation, singular solutions arise when denominator terms vanish, elliptic solutions generalize trigonometric forms through modulus parameters, and rational solutions represent degenerate cases of more complex functions. This systematic classification justifies the completeness of our solution set. Furthermore, all derived solutions have been rigorously verified through direct substitution into the original fractional differential equations, confirming their exact nature and physical validity under the specified parameter constraints. The variable coefficients in the equations allow for tunable properties of the solitons, such as amplitude, width, and velocity. This flexibility could be exploited in practical applications where the medium properties change over time or space, making it possible to tailor soliton behavior for specific applications. The EDAM method successfully handles these variable coefficients through functional constraints that emerge naturally during the solution process, demonstrating its adaptability to non-uniform media. The physical realizability of our theoretical framework is supported by recent advances in material science and photonic technology: tunable optical materials with controllable nonlinear properties can implement the variable coefficients, while engineered dispersion profiles in photonic crystals and metamaterials can realize the $\beta$-dependent scaling behavior. This establishes a clear pathway from our mathematical models to experimental implementation in advanced photonic systems. The effectiveness of the extended direct algebraic method illustrates the advantages of analytical techniques in studying complex nonlinear systems. This method not only simplifies the derivation of soliton solutions but also provides insights into the underlying physical mechanisms governing their dynamics. Each solution derivation is accompanied by parameter constraints that ensure physical validity, while the graphical representations verify the analytical predictions and illustrate the fractional derivative’s role in modifying wave propagation. While this study provides strong analytical evidence for soliton stability through exact solutions and conservation properties, we acknowledge that more extensive numerical simulations under various perturbation scenarios would further strengthen these claims. Future work should include (1) numerical propagation studies of these solitons under random noise perturbations, (2) analysis of collision dynamics between multiple solitons, and (3) investigation of stability thresholds under parameter variations. Such studies would provide a more comprehensive understanding of the robustness properties suggested by our analytical results. The findings of this study have significant implications for nonlinear optics, particularly in the development of advanced photonic devices, optical communication, and signal processing. The ability to harness such dynamic solitons could lead to more efficient transmission of information over optical fibers. Additionally, exploring the extension of this approach to other types of nonlinear equations and physical scenarios could yield valuable insights and enhance the applicability of the findings. In conclusion, while our current work establishes a strong theoretical foundation, the true significance of the $\beta$ parameter lies in its potential to bridge theoretical mathematics with experimental physics. The spectrum of solutions obtained represents not just mathematical curiosities, but potentially discoverable physical states in appropriately engineered optical systems. Future experimental work focusing on materials with specific scaling properties and tunable nonlinearities will be crucial for fully validating the physical significance of the $\beta$ parameter and harnessing its potential for advanced photonic technologies.