Influence of Truncated M-Fractional Derivative on Soliton Dynamics and Stability Analysis of Fifth-Order KdV Equation Using Improved Modified Extended Tanh Function Method

Abstract

In this study, we explore the soliton solutions of the truncated M-fractional fifth-order Korteweg–de Vries (KdV) equation by applying the improved modified extended tanh function method (IMETM). Novel analytical solutions are obtained for the proposed system, such as brigh soliton, dark soliton, hyperbolic, exponential, Weierstrass, singular periodic, and Jacobi elliptic periodic solutions. To validate these results, we present detailed graphical representations of selected solutions, demonstrating both their mathematical structure and physical behavior. Furthermore, we conduct a comprehensive linear stability analysis to investigate the stability of these solutions. Our findings reveal that the fractional derivative significantly affects the amplitude, width, and velocity of the solitons, offering new insights into the control and manipulation of soliton dynamics in fractional systems. The novelty of this work lies in extending the IMETM approach to the truncated M-fractional fifth-order KdV equation for the first time, yielding a wide spectrum of exact analytical soliton solutions together with a rigorous stability analysis. This research contributes to the broader understanding of fractional differential equations and their applications in various scientific fields.

1. Introduction

Nonlinear partial differential equations (NLPDEs) play a fundamental role in modeling a wide variety of nonlinear phenomena in physics, engineering, and applied sciences. They arise naturally in optical fibers, plasma physics, fluid mechanics, and mathematical physics, where soliton and wave structures often govern the underlying dynamics. In recent years, numerous analytical and numerical techniques have been developed to construct exact and approximate solutions to NLPDEs, reflecting the continuous interest in exploring their complex behaviors. For instance, Lü and Chen [1] employed the Hirota bilinear approach to derive novel interaction solutions such as lump–stripe and lump–soliton configurations, which demonstrated the richness of nonlinear wave interactions. In a complementary direction, Zaman et al. [2] investigated fractional-type nonlinear evolution equations and reported diverse traveling wave phenomena, extending the applicability of fractional calculus in wave propagation problems. These results highlight the ability of fractional operators and bilinear techniques to reveal intricate nonlinear structures. Considerable attention has also been given to nonlinear Schrödinger (NLS)-type models due to their significance in optical fiber communication. Ali et al. [3] examined soliton solutions in a generalized perturbed NLS equation with dual-power law nonlinearity, while Abbas et al. [4] employed a complete discrimination system approach to establish optical dromion structures in fractional Kuralay equations. Similarly, Soliman and co-workers [5,6] studied gap solitons and fractional wave structures in higher-order NLS equations, emphasizing the influence of dispersive reflectivity and $\beta$-fractional dispersion effects. On the numerical side, Faheem et al. [7] proposed a Gegenbauer wavelet-based scheme to approximate solutions of space–time fractional Klein–Gordon equations, confirming the value of hybrid computational approaches in studying fractional PDEs. In parallel, Hussain et al. [8] constructed optical soliton solutions for generalized NLS models incorporating cubic, quintic, septic, and nonic nonlinearities, further extending the scope of nonlinear wave models in higher-order nonlinear regimes. Classic contributions by Wazwaz and collaborators [9,10] explored bright and dark soliton propagation in $(2+1)$-dimensional cubic NLS systems, including effects of higher-order dispersion and nonlinearities. These works have inspired further research into higher-dimensional soliton models and their stability properties.

Nonlinear evolution equations, particularly of the Korteweg–de Vries (KdV) and nonlinear Schrödinger (NLS) types, have played a central role in describing nonlinear wave propagation in diverse physical settings, ranging from plasma physics to nonlinear optics and fluid mechanics. The concept of solitons—localized waves that preserve their shape during propagation and interaction—remains at the heart of these investigations due to their stability and practical applications in information transmission and energy transport. Recent advances have increasingly focused on the integration of fractional calculus into nonlinear wave models. Fractional operators provide a powerful framework to incorporate memory and hereditary effects, thereby capturing physical phenomena that classical integer-order models often fail to describe. In this regard, Ablowitz et al. [11] introduced a new class of fractional integrable nonlinear soliton equations, establishing a rigorous connection between fractional operators and integrable systems. Their findings highlight how fractionalization extends the landscape of soliton theory, offering a richer set of mathematical structures and solution behaviors. Complementary developments have also targeted higher-order KdV-type equations, which model a wider range of dispersive and nonlinear effects. Choudhury et al. [12] investigated the stability and dynamics of solitons in a perturbed fifth-order KdV equation, emphasizing the intricate balance between nonlinear terms and higher-order dispersion. Their work demonstrated not only the existence of regular and embedded solitons, but also provided insight into their long-term stability, which is crucial for understanding nonlinear wave evolution in realistic environments. The Korteweg–de Vries (KdV) equation stands as a cornerstone in mathematical physics, illustrating a myriad of phenomena associated with wave propagation in shallow water and other dispersive media. This third-order nonlinear partial differential equation models the evolution of solitary waves, known as solitons, which maintain their shape over time and interact with one another in remarkably complex ways. Moreover, advancements in soliton theory have led to the exploration of higher-dimensional extensions, such as the Kadomtsev–Petviashvili equation discussed in [13], revealing rich structures and interactions that enrich the theoretical landscape of mathematical physics. Consequently, the KdV equation not only impacts practical applications, but also propels mathematical inquiry into the nature of nonlinear dynamics.

In this research study, we focus on truncated M-Fractional Derivative fifth-order Korteweg–de Vries (KdV). The truncated M-Fractional KdV equation represents a significant extension of traditional models, incorporating fractional time derivatives that reflect more complex wave dynamics. This equation is formulated within the framework of nonlocal nonlinear evolution equations, providing a rich interaction between soliton solutions and fractional calculus. The emergence of multiple soliton solutions is facilitated by the properties of this equation, which demonstrate a complex interplay between nonlinearity and dispersion. For instance, by employing the inverse scattering transform (IST), one can derive exact solutions expressed in terms of Jacobian elliptic functions, paralleling results seen in other integrable systems like the classical KdV equation [14]. Moreover, the integrability characteristics of the M-Fractional KdV equation, similar to the historical significance of the KdV equation itself, underscore the potential for discovering further analytical methods that could enhance our understanding of soliton interactions in more generalized settings, including varying coefficients [15,16]. The interplay between fractional derivatives and soliton theory thus poses intriguing questions for further research. This model reads as [17]:

$$\begin{array}{c}\hfill D_{M,t}^{\alpha ,\beta }q+a_{1}q{D}_{M,x}^{\alpha ,\beta }q+b{D}_{M,x}^{3\alpha ,\beta }q+a_2{q}^2{D}_{M,x}^{\alpha ,\beta }q+a_{3}q{D}_{M,x}^{3\alpha ,\beta }q+a_4{D}_{M,x}^{\alpha ,\beta }q{D}_{M,x}^{2\alpha ,\beta }q+a_5{D}_{M,x}^{5\alpha ,\beta }q=0,\end{array}$$

(1)

Here, $q=q(x,t)$ is a function with complex values that represent the wave profile. $D_{M,t}^{\alpha ,\beta }q$ depicts the changing optical field over time. The coefficient $a_1$ governs the strength of the nonlinear term in the equation, indicating the speed and direction of wave propagation. It influences the convection effects on the solution profile. The coefficient $a_2$ is associated with the quadratic nonlinear term coupled with spatial derivatives, affecting the interactions between different components of the solution and contributing to the overall nonlinearity of the system. The coefficient $a_3$ influences the cubic nonlinear term involving the product of the function and its spatial derivatives, impacting the system’s nonlinearity and the formation of complex structures in the solution. The coefficient $a_4$ is linked to the mixed derivative terms in the equation, indicating the coupling between spatial derivatives and nonlinear terms. It affects the interplay between different orders of derivatives in the system. The coefficient $a_5$ governs the fifth-order spatial derivative term, influencing the spatial complexity and higher-order curvature effects in the system. It determines the strength of the quintic nonlinear term in the equation. These parameters collectively shape the behavior, nonlinear interactions, and stability properties of the KdV equation, offering insights into the intricate dynamics of the system [18,19]. The M fractional derivative expands the scope of differentiation beyond integer orders, providing a powerful mathematical tool to describe and analyze systems with fractional dynamics, offering insights into a wide range of physical, biological, and engineering phenomena. It is defined as [20]:

$$\begin{array}{c}{D}_M^{\alpha ,\beta }f\left(t\right)=\underset{\delta \to 0}{lim}{\displaystyle \frac{f\left(t{E}_{\beta }\left(\delta t^{1-\alpha }\right)\right)-f\left(t\right)}{\delta }},t>0,0<\alpha \le 1,\beta >0,\hfill \end{array}$$

Here, $E_{\beta }(·)$ denotes the one-parameter truncated Mittag–Leffler function, defined by the series

$$E_{\beta }\left(z\right)=\sum _{k=0}^J{\displaystyle \frac{z^k}{\mathrm{\Gamma }(\beta k+1)}},\beta >0,$$

where J is a truncation index depending on the level of approximation considered. For $\beta =1$, this reduces to the truncated exponential function, $E_1\left(z\right)={\sum }_{k=0}^J{z}^k/k!$.

The soliton solutions of this generalized equation present not only a fascinating mathematical curiosity but also serve as tools for understanding wave propagation in complex media where traditional integer-order derivations fail to capture underlying dynamics effectively. By investigating the characteristics and behaviors of these solitons, the research aims to provide insights that bridge the gap between mathematical theory and real-world applications [21,22,23,24].

IMETM serves as a powerful analytical technique for deriving exact wave solutions to nonlinear fractional partial differential equations (PDEs), particularly in studying solitary waves and soliton dynamics.

In this work, we successfully apply this method to obtain novel analytical solutions for the proposed system, such as bright solion, dark soliton, hyperbolic, exponential, Weierstrass, singular periodic, and Jacobi elliptic periodic solutions. To validate these results, we present detailed graphical representations of selected solutions, demonstrating both their mathematical structure and physical behavior. Furthermore, we conduct a comprehensive linear stability analysis to investigate the stability of these solutions. Our findings confirm the robustness and versatility of IMETM in handling complex nonlinear wave phenomena.

This study is organized in the following form: Section 2 presents the fundamental methodology of the IMETM. Section 3 develops the analytical solutions through symbolic computations. Section 4 examines the linear stability characteristics of the system. Section 5 illustrates the dynamic wave patterns of various soliton solutions using 2D and 3D graphical representations. Finally, Section 6 summarizes the principal findings and conclusions.

2. The IMETM Approach

The IMETM procedure has been outlined in [25].

Consider the general nonlinear fractional differential model (NLFDM) of the form:

$$\mathcal{M}\left(u,D_{M,t}^{\alpha ,\beta }u,D_{M,x}^{\alpha ,\beta }u,D_{M,x}^{2\alpha ,\beta }u,D_{M,t}^{2\alpha ,\beta }u,\dots \right)=0.$$

(2)

To apply the proposed scheme on Equation (2), the following sequence of steps is carried out:

Step (A): Introduce a traveling wave transformation to reduce Equation (2) to an ODE:

$$u(x,t)=\mathrm{\Phi }\left(\zeta \right),\zeta ={\displaystyle \frac{k\mathrm{\Gamma }(\beta +1)}{\alpha }}\left(x^{\alpha }-c{t}^{\alpha }\right),$$

(3)

where k stands for the wave number and c is the phase velocity. Substitution into Equation (2) yields a nonlinear ODE of the form

$$\mathcal{R}\left(\mathrm{\Phi },{\mathrm{\Phi }}^{\prime },{\mathrm{\Phi }}^{\prime \prime },{\mathrm{\Phi }}^{\left(3\right)},{\mathrm{\Phi }}^{\left(4\right)},\dots \right)=0.$$

(4)

Step (B): Assume the solution of Equation (4) can be expressed as a finite series expansion:

$$\mathrm{\Phi }\left(\zeta \right)=\sum _{m=-M}^M{d}_m{\psi }^m\left(\zeta \right),$$

(5)

where $\psi \left(\zeta \right)$ satisfies an auxiliary equation of the form

$${\psi }^{\prime }\left(\zeta \right)=\sqrt{q_0+q_1\psi \left(\zeta \right)+q_2{\psi }^2\left(\zeta \right)+q_3{\psi }^3\left(\zeta \right)+q_4{\psi }^4\left(\zeta \right)}.$$

(6)

Within the IMETM framework, the qualitative nature of the solutions strongly depends on the coefficients $q_i$ in Equation (6). Specifically:

• $q_2>0$, $q_4<0$$\Rightarrow$ hyperbolic-type soliton solutions (such as: ${\mathrm{sech}}^2$).
• $q_2<0$, $q_4>0$$\Rightarrow$ trigonometric-type solutions (such as: ${\sec }^2$).
• $q_2=0$, $q_4>0$$\Rightarrow$ polynomial or rational structures.
• Mixed signs $\Rightarrow$ elliptic or Weierstrass-type periodic solutions.

Hence, each parameter regime leads to a distinct functional family, corresponding to the classification in Section 3.

Step (C): The order M in Equation (5) is determined using the balancing principle applied to Equation (4).

Step (D): Substitution of Equations (5) and (6) into Equation (4), followed by coefficient comparison of ${\psi }^n\left(\zeta \right)$, produces a system of nonlinear algebraic relations.

Step (E): These algebraic systems can be solved with symbolic computation packages such as Mathematica, leading to explicit expressions for $d_m$ and wave parameters such as k and c.

Step (F): By choosing different parameter sets $(q_0,q_1,q_2,q_3,q_4)$, a variety of closed-form solutions can be constructed. A few representative cases are:

Case 1:  $q_0=q_1=q_3=0$

$$\psi \left(\zeta \right)=\sqrt{-\frac{q_2}{q_4}}\mathrm{sech}\left(\sqrt{q_2}\zeta \right),q_2>0,q_4<0,$$

$$\psi \left(\zeta \right)=\sqrt{-\frac{q_2}{q_4}}\sec \left(\sqrt{-q_2}\zeta \right),q_2<0,q_4>0,$$

$$\psi \left(\zeta \right)=\sqrt{-\frac{q_2}{q_4}}\csc \left(\sqrt{-q_2}\zeta \right),q_2<0,q_4>0.$$

Case 2:  $q_1=q_3=0$, $q_0=\frac{q_2^2}{4q_4}$

$$\psi \left(\zeta \right)=\sqrt{\frac{-q_2}{2q_4}}tanh\left(\sqrt{-\frac{q_2}{2}}\zeta \right),q_2<0,q_4>0.$$

Case 3:   $q_3=q_4=0$

$$\psi \left(\zeta \right)={\displaystyle \frac{q_{1}sinh\left(2\sqrt{q_2}\zeta \right)}{2q_2}}-{\displaystyle \frac{q_1}{2q_2}},q_2>0,q_0=0,$$

$$\psi \left(\zeta \right)=exp\left(\sqrt{q_2}\zeta \right)-{\displaystyle \frac{q_1}{2q_2}},q_2>0,q_0={\displaystyle \frac{q_1^2}{4q_2}}.$$

Case 4:   $q_0=q_1=0$

$$\psi \left(\zeta \right)=-{\displaystyle \frac{q_2}{q_3}}\left[tanh\left(\frac{\sqrt{q_2}\zeta }{2}\right)+1\right],q_2>0,q_4={\displaystyle \frac{q_3^2}{4q_2}}.$$

Case 5:   $q_2=q_4=0$

$$\psi \left(\zeta \right)=\wp \left(\frac{\sqrt{q_3}\zeta }{2};-\frac{4q_1}{q_3},-\frac{4q_0}{q_3}\right),q_3>0.$$

Case 6:   $q_1=q_3=0$

$$\psi \left(\zeta \right)=\mathrm{dn}\left(\zeta \right|m),q_0=m^2-1,q_2=2-m^2,q_4=-1.$$

Step (G): Finally, the explicit forms of $\mathrm{\Phi }\left(\zeta \right)$ are obtained by substituting the solutions of Equation (6) into the expansion in Equation (5), yielding different exact solutions of the original fractional model Equation (2).

3. Application to the Considered Model

In this part, we aim to construct solutions for Equation (1) under the following assumption:

$$\begin{array}{c}\hfill q(x,t)=Q\left(z\right),z={\displaystyle \frac{h\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\nu t^{\alpha }\right)}{\alpha }}.\end{array}$$

(7)

Here, $\nu$ denotes the wave velocity, h corresponds to the wave number, while $(\alpha ,\beta )$ represent the orders of the fractional derivatives.

Upon substituting Equation (7) into Equation (1), the fractional NLPDE is reduced to a standard ordinary differential equation, which takes the following form:

$$\begin{array}{c}\hfill h^3{Q}^{\left(3\right)}\left(z\right)\left(a_{3}Q\left(z\right)+b\right)+a_5{h}^5{Q}^{\left(5\right)}\left(z\right)+h{Q}^{\prime }\left(z\right)\left(a_4{h}^2{Q}^{\prime \prime }\left(z\right)+a_{1}Q\left(z\right)+a_{2}Q{\left(z\right)}^2-\nu \right)=0.\end{array}$$

(8)

To apply the adopted approach, it is necessary to identify the integer N. By applying the balancing principle to Equation (8), we find that $N=2$.

Accordingly, the solution of the resulting ODE can be written as:

$$Q\left(z\right)=s_0+s_1\lambda \left(z\right)+{\displaystyle \frac{s_2}{\lambda \left(z\right)}}+s_3{\lambda }^2\left(z\right)+{\displaystyle \frac{s_4}{{\lambda }^2\left(z\right)}}.$$

(9)

Substituting Equation (9) together with Equation (6) into Equation (8), and then equating the coefficients of $\lambda \left(z\right)$ to zero, we derive a system of nonlinear algebraic equations. These equations are solved using Mathematica software packages V.13.3, and the results are summarized as follows:

Case (1):  $p_0=p_1=p_3=0$

$$\begin{array}{cc}& s_1=s_2=s_4=0,\\ & a_1=-{\displaystyle \frac{4h^2\left(-180a_5{h}^2{p}_4^2{s}_0+60a_5{h}^2{p}_2{p}_4{s}_3+a_3{p}_2{s}_3^2+a_4{p}_2{s}_3^2-3a_3{p}_4{s}_0{s}_3-3a_4{p}_4{s}_0{s}_3+3b{p}_4{s}_3\right)}{s_3^2}},\\ & a_2=-{\displaystyle \frac{6h^2{p}_4\left(60a_5{h}^2{p}_4+2a_3{s}_3+a_4{s}_3\right)}{s_3^2}},\\ & \nu ={\displaystyle \frac{2h^2\left(180a_5{h}^2{p}_4^2{s}_0^2+8a_5{h}^2{p}_2^2{s}_3^2-120a_5{h}^2{p}_2{p}_4{s}_0{s}_3-2a_4{p}_2{s}_0{s}_3^2+3a_4{p}_4{s}_0^2{s}_3+2b{p}_2{s}_3^2-6b{p}_4{s}_0{s}_3\right)}{s_3^2}}.\end{array}$$

From this configuration, both a bright solitary wave and singular periodic solutions for Equation (1) can be obtained as:

$$\begin{array}{c}\hfill q_1(x,t)=s_0-{\displaystyle \frac{p_2{s}_3}{p_4}}{\sec \mathrm{h}}^2\left({\displaystyle \frac{h\sqrt{p_2}\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\nu t^{\alpha }\right)}{\alpha }}\right).\mathrm{for}{p}_2>0,p_4<0.\end{array}$$

(10)

$$\begin{array}{c}\hfill q_2(x,t)=s_0-{\displaystyle \frac{p_2{s}_3}{p_4}}{\sec }^2\left({\displaystyle \frac{h\sqrt{-p_2}\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\nu t^{\alpha }\right)}{\alpha }}\right).\mathrm{for}{p}_2<0,p_4>0.\end{array}$$

(11)

$$\begin{array}{c}\hfill q_3(x,t)=s_0-{\displaystyle \frac{p_2{s}_3}{p_4}}{\csc }^2\left({\displaystyle \frac{h\sqrt{-p_2}\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\nu t^{\alpha }\right)}{\alpha }}\right)..\mathrm{for}{p}_2<0,p_4>0.\end{array}$$

(12)

Case (2):   $p_1=p_3=0,p_0={\displaystyle \frac{p_2^2}{4p_4}}$

$$\begin{array}{ccc}& & s_0={\displaystyle \frac{3\left(2a_5{h}^2{p}_2+b\right)}{a_4}},\hfill \\ & & s_1=-{\displaystyle \frac{168\sqrt{2}{a}_5{h}^2\sqrt{-p_2}\sqrt{p_4}}{a_4}},\hfill \\ & & s_2=s_4=0,\hfill \\ & & p_4=-{\displaystyle \frac{a_4{s}_3}{168a_5{h}^2}},\hfill \\ & & p_2={\displaystyle \frac{3\left(a_{4}b-196a_1{a}_5\right)}{470a_4{a}_5{h}^2}},\hfill \\ & & a_2=-{\displaystyle \frac{a_4^2}{1176a_5}},\hfill \\ & & a_3=-{\displaystyle \frac{a_4}{3}},\hfill \\ & & \nu ={\displaystyle \frac{-940a_{5}b{h}^2{p}_2-34036a_5^2{h}^4{p}_2^2+3b^2}{392a_5}}.\hfill \end{array}$$

In this case, the obtained solution corresponds to a dark soliton:

$$\begin{array}{cc}\hfill & q_4(x,t)={\displaystyle \frac{42}{1175a_4^2}}(a_4\left(253b-336a_4{s}_0\right)+3a_4\left(789b-1568a_4{s}_0\right)\\ & {tanh}^2\left({\displaystyle \frac{\sqrt{\frac{3}{235}}\sqrt{\frac{196a_1}{a_4}-\frac{b}{a_5}}\mathrm{\Gamma }(\beta +1)\left(a_4^2\left(55225a_5{x}^{\alpha }+618b^2{t}^{\alpha }\right)-242256a_1{a}_4{a}_{5}b{t}^{\alpha }+7504938a_1^2{a}_5^2{t}^{\alpha }\right)}{110450\alpha a_4^2{a}_5}}\right)-\\ & 6\left(784a_4\left(b-2a_4{s}_0\right)+5b{a}_4\right)\times \\ & tanh\left({\displaystyle \frac{\sqrt{\frac{3}{235}}\sqrt{\frac{196a_1}{a_4}-\frac{b}{a_5}}\mathrm{\Gamma }(\beta +1)\left(a_4^2\left(55225a_5{x}^{\alpha }+618b^2{t}^{\alpha }\right)-242256a_1{a}_4{a}_{5}b{t}^{\alpha }+7504938a_1^2{a}_5^2{t}^{\alpha }\right)}{110450\alpha a_4^2{a}_5}}\right)\\ & \mathrm{for}{\displaystyle \frac{196a_1}{a_4}}-{\displaystyle \frac{b}{a_5}}>0.\end{array}$$

(13)

Case (3):  $p_4=p_3=0$

For the first scenario, when $p_0=0,p_2>0$, the following relations are obtained:

$$\begin{array}{ccc}& & s_3={\displaystyle \frac{p_2{s}_1}{p_1}},\hfill \\ & & p_2=-{\displaystyle \frac{a_1}{\left(a_3+a_4\right)h^2}},\hfill \\ & & a_2=0,\hfill \\ & & \nu ={\displaystyle \frac{1}{2}}{h}^2\left(32a_5{h}^2{p}_2^2-8a_4{p}_2{s}_0+a_4{p}_1{s}_1+8b{p}_2\right),\hfill \\ & & s_2=s_4=0.\hfill \end{array}$$

This leads to a hyperbolic-type solution:

$$\begin{array}{cc}\hfill & q_6(x,t)=s_0-{\displaystyle \frac{\left(a_3+a_4\right)h^2{p}_1{s}_1}{8a_1}}\times \\ & (cosh\left({\displaystyle \frac{2\sqrt{-\frac{a_1}{a_3+a_4}}\mathrm{\Gamma }(\beta +1)\left(8a_1\left(a_3+a_4\right)t^{\alpha }\left(a_4{s}_0-b\right)+{\left(a_3+a_4\right)}^2\left(a_4{h}^2{p}_1{s}_1{t}^{\alpha }-2x^{\alpha }\right)+32a_1^2{a}_5{t}^{\alpha }\right)}{\alpha {\left(a_3+a_4\right)}^2}}\right)-3).\end{array}$$

(14)

For the second scenario, $p_0={\displaystyle \frac{p_1^2}{4p_2}},p_2>0$, we obtain:

$$\begin{array}{ccc}& & s_2=s_3=s_4=0,\hfill \end{array}$$

In this setting, an exponential-type solution emerges:

$$\begin{array}{cc}\hfill & q_7(x,t)=s_0+\\ & {\displaystyle \frac{1}{2}}{s}_1(2exp\left(-{\displaystyle \frac{\sqrt{-\frac{a_1}{a_3+a_4}}\mathrm{\Gamma }(\beta +1)\left(2a_1\left(a_3+a_4\right)t^{\alpha }\left(a_4{s}_0-b\right)+{\left(a_3+a_4\right)}^2\left(a_4{h}^2{p}_1{s}_1{t}^{\alpha }-2x^{\alpha }\right)+2a_1^2{a}_5{t}^{\alpha }\right)}{2\alpha {\left(a_3+a_4\right)}^2}}\right)+\\ & {\displaystyle \frac{\left(a_3+a_4\right)h^2{p}_1}{a_1}}).\end{array}$$

(15)

Case (4):  $p_0=p_1=0,p_2={\displaystyle \frac{p_3^2}{4p_4}},p_2>0$

$$\begin{array}{ccc}& & s_1=s_2=s_4=0,\hfill \\ & & s_3={\displaystyle \frac{84b{p}_4}{13a_4{p}_2}},\hfill \\ & & a_1={\displaystyle \frac{2a_4{h}^2{p}_2\left(13a_4{s}_0+49b\right)}{49b}},\hfill \\ & & a_2=-{\displaystyle \frac{13a_4^2{h}^2{p}_2}{49b}},\hfill \\ & & a_3=0,\hfill \\ & & a_5=-{\displaystyle \frac{b}{13h^2{p}_2}},\hfill \\ & & \nu ={\displaystyle \frac{h^2{p}_2\left(1274a_{4}b{s}_0+169a_4^2{s}_0^2+1764b^2\right)}{637b}}.\hfill \end{array}$$

This case provides a dark-soliton solution of the form:

$$\begin{array}{ccc}\hfill & & q_8(x,t)={\displaystyle \frac{21b{\left(tanh\left(\frac{h\sqrt{p_2}\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\frac{h^2{p}_2{t}^{\alpha }\left(1274a_{4}b{s}_0+169a_4^2{s}_0^2+1764b^2\right)}{637b}\right)}{2\alpha }\right)+1\right)}^2}{13a_4}}+s_0.\hfill \end{array}$$

(16)

Case (5):  $p_2=p_4=0,p_3>0$

$$\begin{array}{ccc}& & s_2=s_3=s_4=0,\hfill \\ & & a_1={\displaystyle \frac{3h^2{p}_3\left(15a_5{h}^2{p}_3{s}_0+a_3{s}_0{s}_1+a_4{s}_0{s}_1-b{s}_1\right)}{s_1^2}};a_2=-{\displaystyle \frac{3h^2{p}_3\left(15a_5{h}^2{p}_3+2a_3{s}_1+a_4{s}_1\right)}{2s_1^2}},\hfill \\ & & \nu ={\displaystyle \frac{h^2\left(9a_5{h}^2{p}_1{p}_3{s}_1^2+45a_5{h}^2{p}_3^2{s}_0^2+a_4{p}_1{s}_1^3+3a_4{p}_3{s}_0^2{s}_1-6b{p}_3{s}_0{s}_1\right)}{2s_1^2}}.\hfill \end{array}$$

This configuration yields a solution in terms of the Weierstrass elliptic function:

$$\begin{array}{cc}\hfill q(x,t)=s_1\wp & \left({\displaystyle \frac{h\mathrm{\Gamma }(\beta +1)\sqrt{p_3}\left(x^{\alpha }-\frac{h^2{t}^{\alpha }\left(a_4{p}_1{s}_1^3+9h^2{a}_5{p}_1{p}_3{s}_1^2+3a_4{p}_3{s}_0^2{s}_1-6b{p}_3{s}_0{s}_1+45h^2{a}_5{p}_3^2{s}_0^2\right)}{2s_1^2}\right)}{2\alpha }};\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{4p_1}{p_3}},-{\displaystyle \frac{4p_0}{p_3}}\right)+s_0.\hfill \end{array}$$

(17)

Case (6):  $p_1=p_3=0$

$$\begin{array}{cc}& a_1=-{\displaystyle \frac{4h^2\left(-180a_5{h}^2{p}_4^2{s}_0+60a_5{h}^2{p}_2{p}_4{s}_3+a_3{p}_2{s}_3^2+a_4{p}_2{s}_3^2-3a_3{p}_4{s}_0{s}_3-3a_4{p}_4{s}_0{s}_3+3b{p}_4{s}_3\right)}{s_3^2}},\\ & a_2=-{\displaystyle \frac{6h^2{p}_4\left(60a_5{h}^2{p}_4+2a_3{s}_3+a_4{s}_3\right)}{s_3^2}},\\ & \nu ={\displaystyle \frac{2h^2{s}_3\left(3p_4{s}_0\left(a_4{s}_0-2b\right)+s_3\left(2p_2\left(b-a_4{s}_0\right)+a_4{p}_0{s}_3\right)\right)+8a_5{h}^4\left(45p_4^2{s}_0^2+2p_2^2{s}_3^2+p_4\left(9p_0{s}_3^2-30p_2{s}_0{s}_3\right)\right)}{s_3^2}}.\end{array}$$

The corresponding solution is expressed using Jacobi elliptic functions as:

$$\begin{array}{ccc}\hfill & & q(x,t)=s_3\mathrm{dn}{\left(\left.{\displaystyle \frac{h\mathrm{\Gamma }(\beta +1)\left(x^{\alpha }-\nu t^{\alpha }\right)}{\alpha }}\right|m\right)}^2+s_0,\mathrm{for}{p}_0=m^2-1,p_2=2-m^2,p_4=-1.\hfill \end{array}$$

(18)

4. Graphical Representation of Selected Solutions

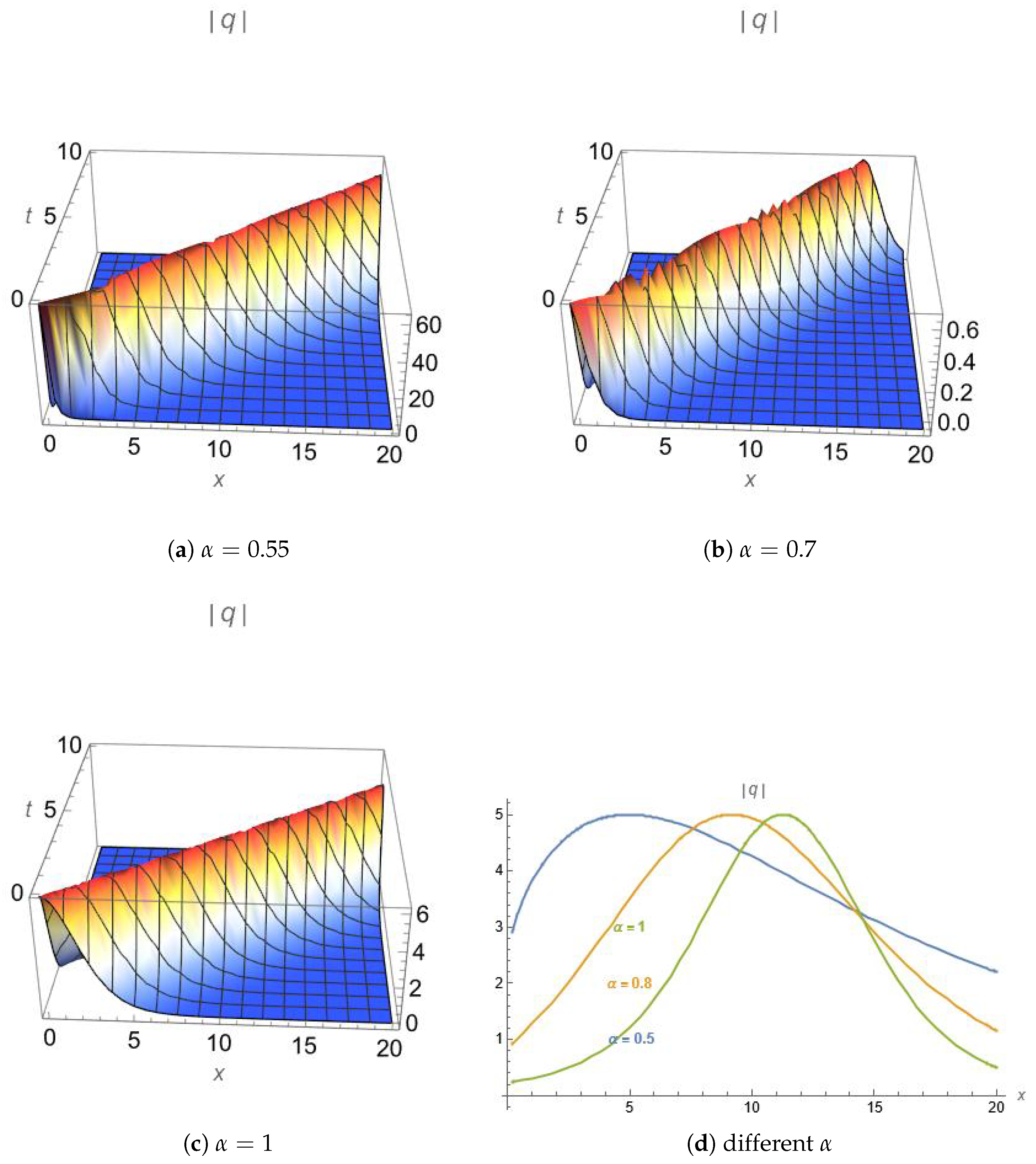
Figure 1 illustrates a numerical simulation corresponding to one of the obtained solutions, particularly the bright soliton described by Equation (10). The chosen parameters for this case are $h=0.1$, $p_2=1.2$, $p_4=-1$, $\nu =0.44$, $s_3=3.66$, $s_0=0.09$, $\beta =2$, and $t=25.6$ s. These parameter values are selected to guarantee bounded and stable soliton structures, while effectively highlighting the role of the fractional order $\alpha$ in shaping the amplitude and width.

Figure 2 corresponds to another solution of Equation (16), exhibiting a dark solitary wave. Here, the parameters are assigned as $h=-0.1,a_4=1.33,p_2=1.2,s_0=1.33,$ $b=2.5,t=30$ s, and $\beta =2$. The chosen values ensure the solution remains stable and are particularly effective in visualizing the impact of fractional parameters on the depth and spatial spread of the soliton.

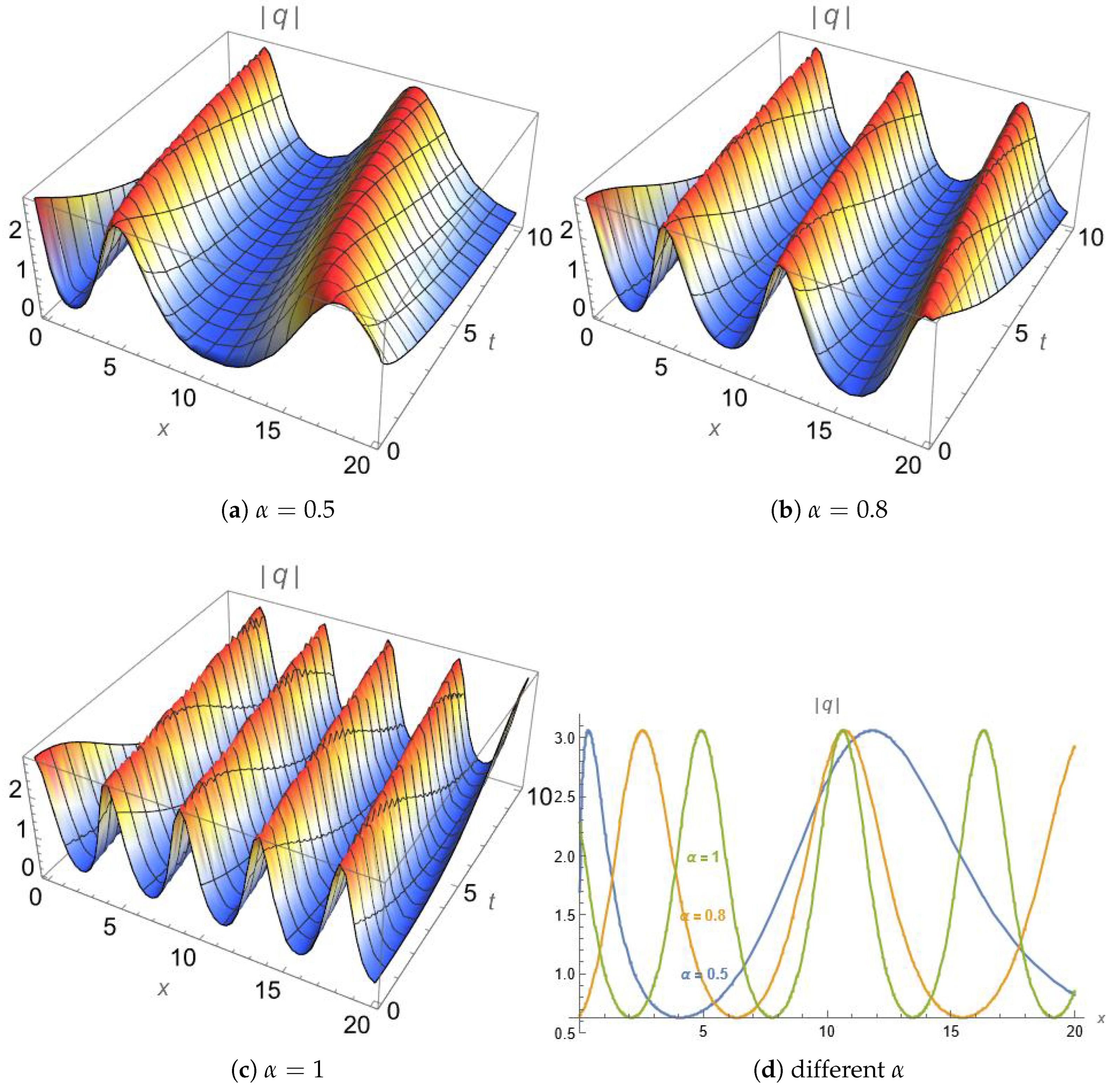
Figure 3 portrays a periodic solution expressed in terms of Jacobi elliptic functions, based on Equation (18). The input parameters are $h=0.45,\nu =0.6,p_4=0.53,s_3=2.81,$ $s_0=0.48,\beta =2,m=0.86$, and $t=10.5$. These settings were carefully chosen to clearly exhibit the periodic wave structure while avoiding excessively sharp oscillatory patterns.

The obtained waveforms illustrate the inherent property of solitons to retain both their form and velocity over long propagation distances. This phenomenon arises from the interplay between dispersion and nonlinearity. Dispersion naturally tends to broaden the pulse over time, whereas nonlinearity induces self-focusing, effectively counteracting this spreading. When these two mechanisms are precisely balanced, the result is a stable soliton that propagates without distortion or notable decay in its waveform.

5. Discussion

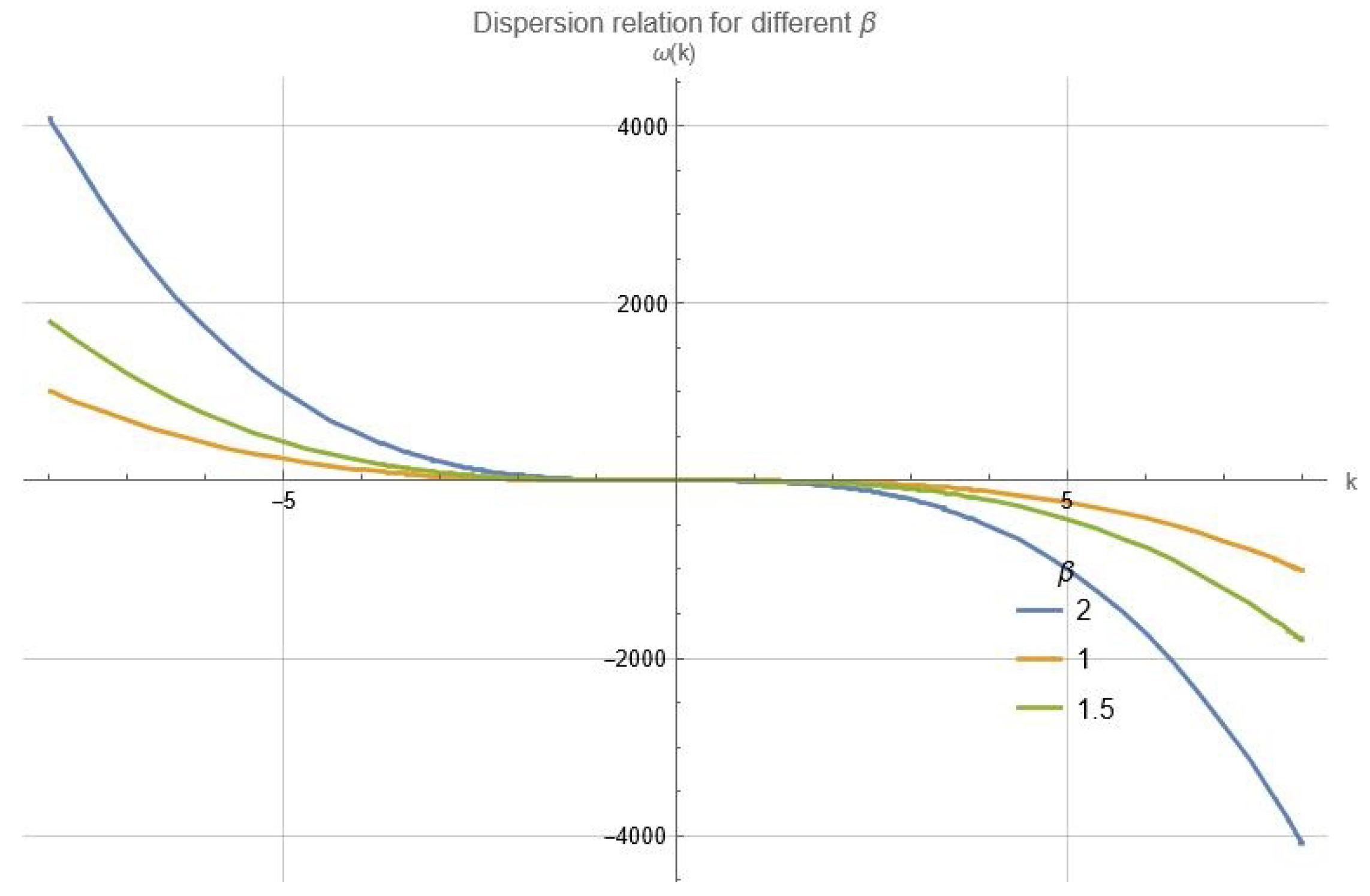
Due to their complex, nonlinear order dynamics, it is essential to include fractional calculus in the modeling of nonlocal systems. Optical systems showcase propagation that depends on frequency whereas nonlocal systems have interactions extending beyond immediate spatial or temporal neighborhoods. Incorporating fractional calculus facilitates graphical representations of soliton solutions which hold vital information about these system’s behavior that is essential for developing advanced photonic technologies and applications.

It is essential to highlight the physical interpretation of the derived solutions. The bright soliton solutions represent localized wave packets with enhanced intensity, whereas the dark soliton solutions characterize localized reductions in intensity superimposed on a continuous background field. Both are of central importance in optical fibers, plasma waves, and fluid models. In the present truncated M-fractional framework, the fractional parameters $\alpha$ and $\beta$ provide additional control mechanisms: decreasing $\alpha$ broadens the soliton width due to enhanced memory effects, whereas increasing $\alpha$ leads to narrower, sharper localization. Meanwhile, the parameter $\beta$ influences the effective dispersive and dissipative contributions, thereby tuning the propagation velocity and stability of the wave. For periodic solutions expressed in Jacobi elliptic functions, the fractional orders modify the modulation depth and wavelength, offering tunability not available in classical integer-order models. The obtained soliton solutions are not only of mathematical interest but also possess practical significance in real-world systems. For example, bright and dark solitons are widely used in optical fiber communication systems to enable long-distance, high-speed data transmission with minimal distortion. Similarly, higher-order KdV-type solitons arise in plasma physics, where they describe ion-acoustic and magnetosonic waves, and in fluid dynamics, where they model shallow water wave propagation and coastal engineering phenomena. Moreover, periodic and elliptic solutions are relevant in nonlinear optics and photonics, corresponding to wave trains in birefringent fibers and photonic crystals. These diverse applications highlight the physical relevance of the present analytical results.

6. Linear and Spectral Stability Analysis

We consider the truncated M-fractional fifth-order KdV-type model used in this work,

$$D_{M,t}^{\alpha ,\beta }q+a_{1}q{D}_{M,x}^{\alpha ,\beta }q+b{D}_{M,x}^{3\alpha ,\beta }q+a_2{q}^2{D}_{M,x}^{\alpha ,\beta }q+a_{3}q{D}_{M,x}^{3\alpha ,\beta }q+a_4\left(D_{M,x}^{\alpha ,\beta }q\right)\left(D_{M,x}^{2\alpha ,\beta }q\right)+a_5{D}_{M,x}^{5\alpha ,\beta }q=0,$$

(19)

where $0<\alpha \le 1$, $\beta >0$, and $D_{M,\xi }^{\gamma ,\beta }$ denotes the truncated M-fractional derivative of order $\gamma$ with parameter $\beta$ with respect to $\xi \in \{x,t\}$.

Linearization About a Uniform State

Let $q_0$ be a constant background and write a small perturbation

$$q(x,t)=q_0+\epsilon u(x,t),0<\epsilon \ll 1.$$

Since spatial derivatives of $q_0$ vanish, discarding $O\left({\epsilon }^2\right)$ terms yields the linearized equation

$$D_{M,t}^{\alpha ,\beta }u+(a_1{q}_0+a_2{q}_0^2)D_{M,x}^{\alpha ,\beta }u+(a_3{q}_0+b)D_{M,x}^{3\alpha ,\beta }u+a_5{D}_{M,x}^{5\alpha ,\beta }u=0.$$

(20)

We seek normal modes of the form

$$u(x,t)=\widehat{u}exp\left\{i\left(k{x}^{\alpha }-\omega t^{\alpha }\right)\right\},k\in \mathbb{R}.$$

(21)

Consistent with the wave variable used in Section 3 (viz. $z=\frac{h\mathrm{\Gamma }(\beta +1)}{\alpha }(x^{\alpha }-\nu t^{\alpha })$), each M-fractional derivative contributes a factor $\mathrm{\Gamma }(\beta +1)$ per order:

$$D_{M,t}^{\alpha ,\beta }{e}^{i(k{x}^{\alpha }-\omega t^{\alpha })}=-i\mathrm{\Gamma }(\beta +1)\omega e^{i(·)},D_{M,x}^{\alpha ,\beta }{e}^{i(·)}=i\mathrm{\Gamma }(\beta +1)k{e}^{i(·)},$$

and in general $D_{M,x}^{m\alpha ,\beta }{e}^{i(·)}={\left(i\mathrm{\Gamma }(\beta +1)k\right)}^m{e}^{i(·)}$. Substituting (21) into (20) gives the dispersion relation

$$-\mathrm{\Gamma }(\beta +1)\omega +\mathrm{\Gamma }(\beta +1)(a_1{q}_0+a_2{q}_0^2)k-\mathrm{\Gamma }{(\beta +1)}^3(a_3{q}_0+b)k^3+\mathrm{\Gamma }{(\beta +1)}^5{a}_5{k}^5=0,$$

(22)

hence

$$\omega \left(k\right)=\left(a_1{q}_0+a_2{q}_0^2\right)k-\mathrm{\Gamma }{(\beta +1)}^2(a_3{q}_0+b)k^3+\mathrm{\Gamma }{(\beta +1)}^4{a}_5{k}^5.$$

(23)

For real k, the right-hand side of (23) is real, so $Im\omega \left(k\right)=0$ and the uniform state $q\equiv q_0$ is spectrally (neutrally) stable to small harmonic perturbations. The fractional parameter $\beta$ enters through $\mathrm{\Gamma }(\beta +1)$ and rescales dispersion, strengthening the $k^3$ and $k^5$ contributions as $\beta$ increases. Figure 4 represents the dispersion relation $\omega \left(k\right)$ from (23) for several values of $\beta$ .

7. Conclusions

In summary, this study presents a comprehensive exploration of soliton solutions for the truncated M-fractional derivative fifth-order Korteweg–de Vries (KdV) equation through IMETM. Our investigation marks a significant advancement in understanding the effects of fractional derivatives on both spatial and temporal dynamics. By employing IMETM, we successfully derived a diverse array of solutions, including bright and dark solitons, singular periodic solutions, and hyperbolic, exponential, Weierstrass, and Jacobi periodic solutions.

The versatility demonstrated by IMETM in producing multiple solution types highlights its effectiveness in tackling complex nonlinear fractional differential equations. Our graphical simulations further elucidate the intricate wave dynamics, revealing the critical role of the fractional order parameter, $\alpha$. Notably, we observed that variations in $\alpha$ can modulate wave propagation by shifting the wave without affecting its magnitude or shape, underscoring the nuanced interplay between fractional derivatives and wave characteristics.

These findings not only validate the efficacy of IMETM for the fifth-order KdV equation, but also suggest its broader applicability across a wide spectrum of fractional derivative partial differential equations. The originality of our work is manifested in (i) the derivation of several new analytical solution families for the truncated M-fractional fifth-order KdV equation, and (ii) the demonstration of how the fractional order parameters modulate soliton dynamics and stability. Consequently, IMETM emerges as a valuable and robust tool for researchers in the field of nonlinear fractional systems, paving the way for future studies to explore deeper insights into the rich dynamics of such equations. We anticipate that our work will inspire further investigation into the applications of fractional calculus in various physical contexts, thereby enhancing our understanding of complex wave phenomena.

8. Future Work

The present study has established the effectiveness of the Improved Modified Extended Tanh Function Method (IMETM) in deriving exact analytical solutions of the truncated M-fractional fifth-order KdV equation. Building on these results, several directions for future research can be pursued:

• Higher-dimensional models: Extending the truncated M-fractional derivative framework to multidimensional generalizations such as the Kadomtsev–Petviashvili (KP) and Davey–Stewartson equations.
• Numerical validation: Developing robust numerical schemes (finite difference, spectral methods) to compare with the analytical soliton profiles obtained in this work.
• Experimental relevance: Investigating the applicability of the derived solutions in optical fiber systems, plasmas, and shallow water environments through experimental or simulation-based studies.
• Nonlinear interactions: Studying soliton collisions, bound states, and chaotic behavior under the influence of fractional operators and higher-order dispersive effects.
• Other fractional operators: Comparing the truncated M-fractional derivative with other nonlocal operators (e.g., Atangana–Baleanu and Caputo–Fabrizio) to evaluate the universality and physical implications of the obtained solutions.

These directions can broaden the scope of fractional soliton theory and deepen the connection between mathematical models and real-world applications.