Optical Multi-Peakon Dynamics in the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model Using a Novel Integral Approach
Abstract
1. Introduction
1.1. Formulation of Model
1.2. Literature Review
1.3. Research Aim and Objectives
1.4. Contribution and Originality
1.5. Advantages of MGERIF Method
1.6. Limitations of MGERIF Method
1.7. Summarization
2. Fractional-Order Calculus
3. Mathematical Investigation
4. Multivariate Generalized Exponential Rational Integral Function Method
- Step 01: The solution of Equation (16) is derived through the MGERIF as follows:Here, , , (with i = 1, 2, …, N) are arbitrary constants, and the function satisfies the following relation:Here, (for i = 1, 2, 3, 4) are parameters. Setting their values allows Equation (18) to be rewritten in familiar representations in Table 1.
- Step 02: The homogeneous balance principle yields the positive integer N by equating the highest-order derivative and nonlinear terms in Equation (16).
- Step 03: Substituting Equations (17) and (18) in Equation (16) yields the polynomial in term of for . Equating the coefficients of identical powers equal to zero results in a system of nonlinear algebraic equations. Solving this system, in conjunction with Equation (18), provides the solutions to Equation (4).
4.1. Solutions by MGERIF Method
4.2. The Familiar Sin Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
4.3. The Familiar Cosine Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
4.4. The Familiar Exponential Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
4.5. The Familiar Cosine Hyperbolic Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
4.6. The Familiar Sin Hyperbolic Description
- Case 1.1:
- Case 1.2:
- Case 1.3:
- Case 1.4:
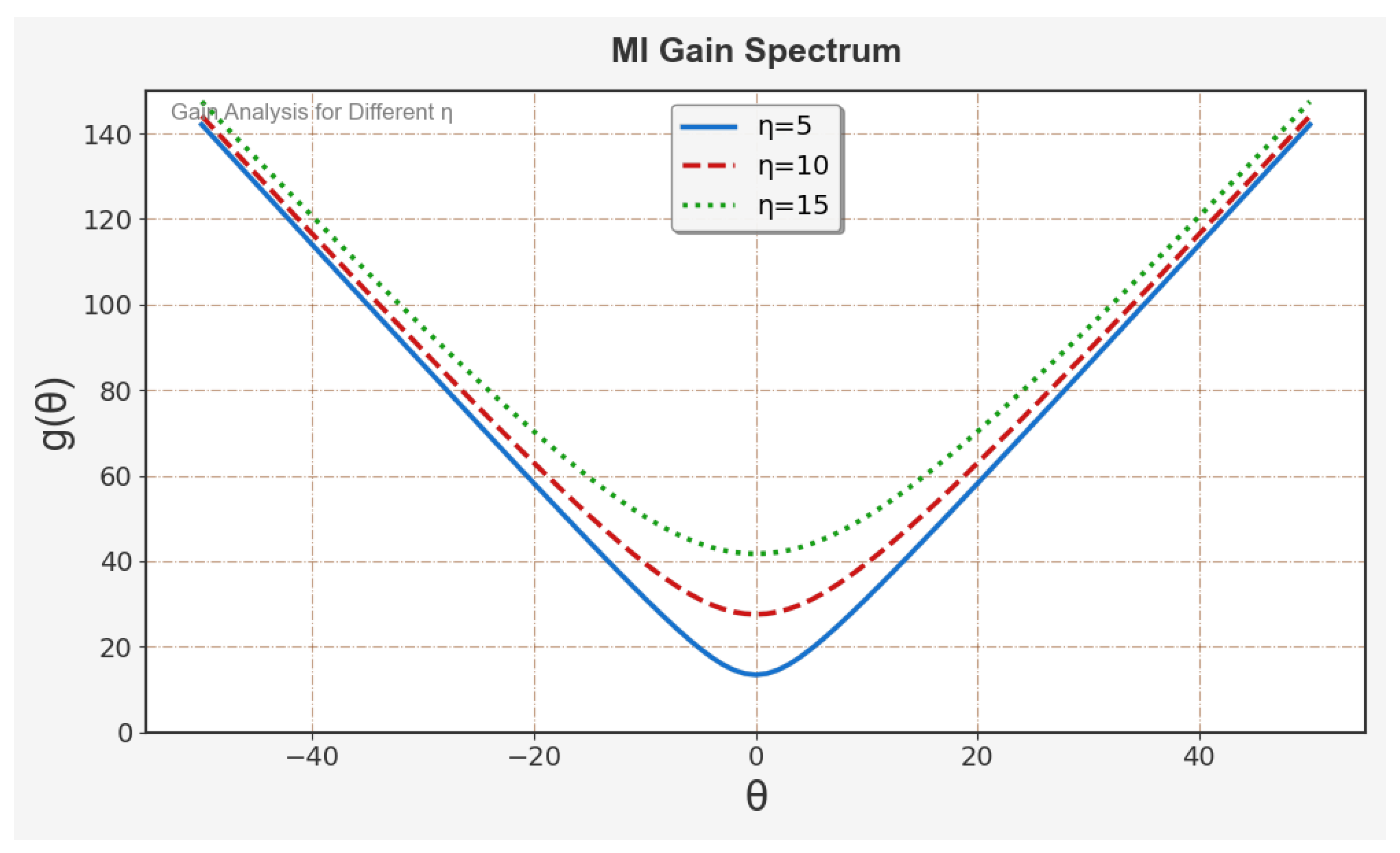
5. Modulation Instability Analysis
Stability of the Equation (24) Solution
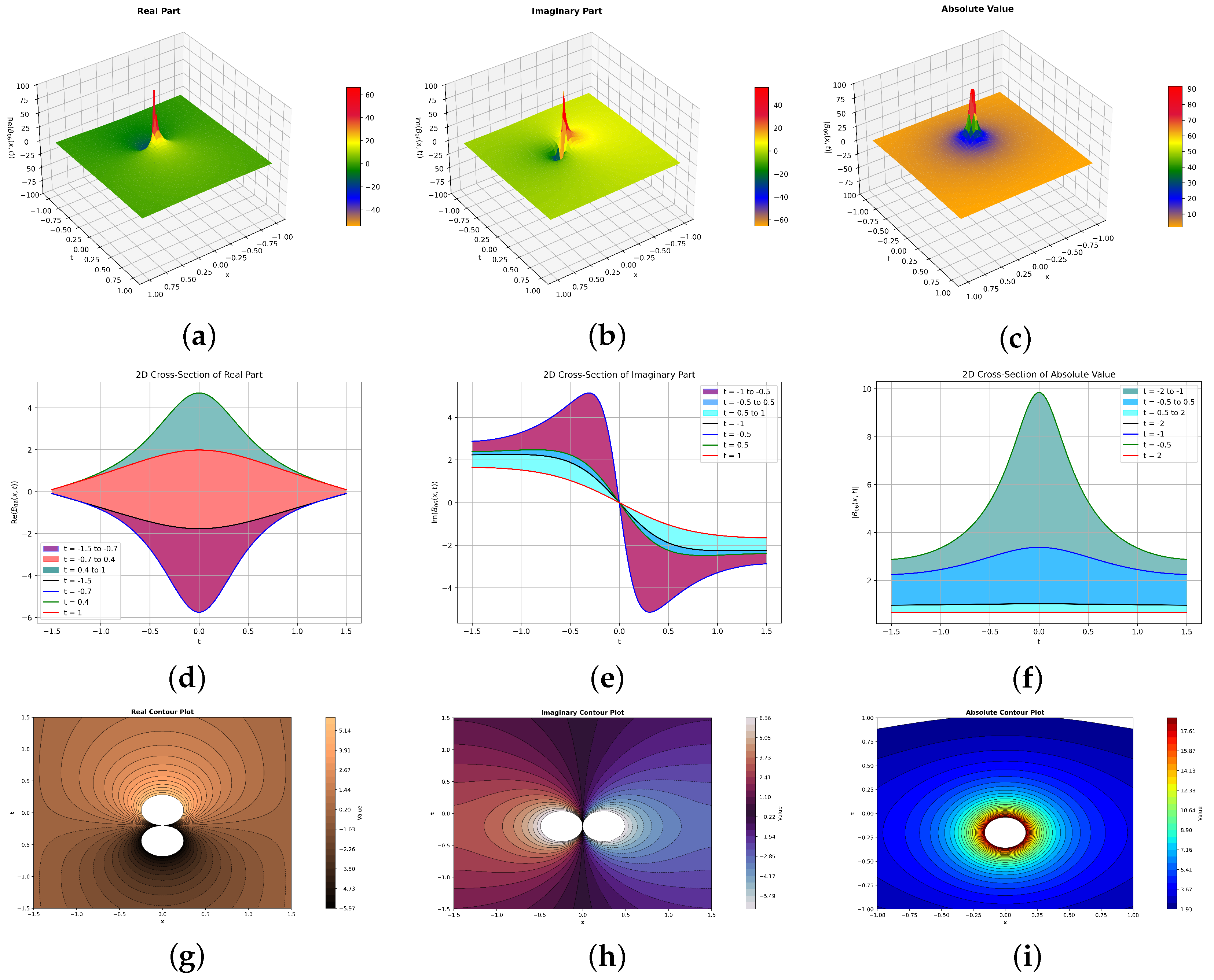
6. Graphical Description
7. Comparison with Previous Literature
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| x | Spatial coordinate/propagation distance |
| t | Temporal coordinate (retarded time) |
| Complex optical field envelope | |
| a | Coefficient of transverse diffraction |
| b | Group velocity dispersion (GVD) parameter |
| c | Cubic nonlinear coefficient (Kerr-type nonlinearity) |
| Quintic nonlinear coefficient | |
| Order of conformable fractional derivative () | |
| Conformable fractional derivative operator | |
| Scaling parameter in the conformable -derivative definition (Equation (5)); | |
| adjusts the normalization term | |
| Traveling wave transformation variable | |
| Frequency/wave number parameter | |
| Soliton velocity parameter | |
| d | Velocity parameter in transformation/integration constant |
| Phase function |
| Amplitude function | |
| Transformed amplitude function | |
| Constant term in the MGERIF ansatz; sets the baseline level of the solution | |
| Free constant controlling localization and oscillation; affects soliton width and position | |
| Coefficients for positive powers in the MGERIF ansatz; regulate growth, | |
| oscillatory features, and multi-soliton structures | |
| Phase-related integration constant; shifts the solution phase and influences | |
| propagation direction | |
| Coefficients for negative powers in the MGERIF ansatz; control decay, tail behavior, | |
| and localization strength | |
| N | Degree from homogeneous balance principle, fixes truncation index of ansatz |
| Generalized exponential rational function (core of MGERIF ansatz) | |
| Parameters defining numerator/denominator polynomials of | |
| Exponent parameters governing growth/decay in | |
| Normalized optical power in MI analysis | |
| Perturbation function in MI | |
| ∗ | Complex conjugate |
| Amplitudes of perturbation modes | |
| Normalized wave number of perturbation | |
| Frequency of perturbation | |
| MI gain spectrum |
References
- Farooq, K.; Hussain, E.; Younas, U.; Mukalazi, H.; Khalaf, T.M.; Mutlib, A.; Shah, S.A.A. Exploring the wave’s structures to the nonlinear coupled system arising in surface geometry. Sci. Rep. 2025, 15, 11624. [Google Scholar] [CrossRef]
- Yokus, A.; Isah, M.A. Unveiling novel insights: Nonlinear dispersion dynamics of optical solitons through new ϕ6-Model expansion in the Klein–Gordon equation. Chin. J. Phys. 2025, 95, 476–492. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Ali, K.; Akram, U.; Abbas, S.O.; Bekir, A.; Seadawy, A.R. Stability analysis and solitary wave solutions for Yu–Toda–Sasa–Fukuyama equation. Nonlinear Dyn. 2025, 113, 2611–2623. [Google Scholar] [CrossRef]
- Manivel, M.; Venkatesh, A.; Kumar, K.A.; Raj, M.P.; Fadugba, S.E.; Kekana, M. Quantitative modeling of monkeypox viral transmission using Caputo fractional variational iteration method. Partial. Differ. Equ. Appl. Math. 2025, 13, 101026. [Google Scholar] [CrossRef]
- Mandal, S.; Sil, S.; Ghosh, S. On the Lie symmetry analysis of three-dimensional perturbed shear flows. Chaos Solitons Fractals 2025, 191, 115875. [Google Scholar] [CrossRef]
- Alquran, M. Investigating fluctuation varieties in the propagation of the perturbed KdV equation with time-dependent perturbation coefficient. Partial. Differ. Equ. Appl. Math. 2025, 14, 101206. [Google Scholar] [CrossRef]
- Farooq, K.; Hussain, E.; Abujabal, H.A.; Alshammari, F.S. Propagation of nonlinear dispersive waves in shallow water and acoustic media in the framework of integrable Schwarz–Korteweg–de Vries equation. AIMS Math. 2025, 10, 17543–17566. [Google Scholar] [CrossRef]
- Mehdi, B.K.; Mousa, A.A.A.; Baloch, S.A.; Demirbilek, U.; Ghallab, A.; Siddique, I.; Zulqarnain, R.M. Exploration of soliton dynamics and chaos in the Landau–Ginzburg–Higgs equation through extended analytical approaches. J. Nonlinear Math. Phys. 2025, 32, 22. [Google Scholar] [CrossRef]
- Li, Z. Optical solutions of the nonlinear Kodama equation with the M-truncated derivative via the extended (G′/G)-expansion method. Fractal Fract. 2025, 9, 300. [Google Scholar] [CrossRef]
- Abdalla, M.; Roshid, M.M.; Ullah, M.S.; Hossain, I. Dynamical analysis, and the effect of fractional parameters on optical soliton solution for Yajima–Oikawa model in short-wave and long-wave. Chaos Solitons Fractals 2025, 199, 116697. [Google Scholar] [CrossRef]
- Farooq, K.; Alshammari, F.S.; Li, Z.; Hussain, E. Soliton dynamics and stability in the Boussinesq equation for shallow water applications. Front. Phys. 2025, 13, 1637491. [Google Scholar] [CrossRef]
- Jlali, L.; Rizvi, S.T.R.; Shabbir, S.; Seadawy, A.R. Study of Optical Solitons and Quasi-Periodic Behaviour for the Fractional Cubic Quintic Nonlinear Pulse Propagation Model. Mathematics 2025, 13, 2117. [Google Scholar] [CrossRef]
- Tariq, K.U.; Khater, M.M.A.; Inc, M. On Some Novel Bright, Dark and Optical Solitons to the Cubic-Quintic Nonlinear Non-Paraxial Pulse Propagation Model. Opt. Quant. Electron. 2021, 53, 726. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Raza, U. Detailed Analysis for Chirped Pulses to Cubic-Quintic Nonlinear Non-Paraxial Pulse Propagation Model Using the Extended Trial Function Method. J. Geom. Phys. 2022, 178, 104561. [Google Scholar] [CrossRef]
- Khater, M.M.A. Nonparaxial Pulse Propagation in a Planar Waveguide with Kerr–Like and Quintic Nonlinearities; Computational Simulations. Chaos Solitons Fractals 2022, 157, 111970. [Google Scholar] [CrossRef]
- Khater, M.M.A. Computational Simulations of the Cubic-Quintic Nonlinear Helmholtz Model. J. Ocean Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Zhong, X.; Du, X.; Cheng, K. Evolution of Finite Energy Airy Pulses and Soliton Generation in Optical Fibers with Cubic-Quintic Nonlinearity. Opt. Express 2015, 23, 29467–29475. [Google Scholar] [CrossRef]
- Akbar, M.A.; Abdullah, F.A.; Khatun, M.M. An Investigation of Optical Solitons of the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model: An Analytic Approach and the Impact of Fractional Derivative. Opt. Quantum Electron. 2023, 56, 58. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Hashem, A.F.; Ul Hassan, A.; Shabbir, S.; Al-Moisheer, A.S.; Seadawy, A.R. Exploring Novel Optical Soliton Molecule for the Time Fractional Cubic–Quintic Nonlinear Pulse Propagation Model. Fractal Fract. 2025, 9, 497. [Google Scholar] [CrossRef]
- Kaya Sağlam, F.N. Exploring soliton solutions of the nonlinear time-fractional Schrödinger model via M-truncated and Atangana–Baleanu fractional operators. J. New Theory 2025, 2025, 53–67. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Seadawy, A.R.; Mirzazadeh, M.; Yildirim, A. Extracting the ultimate new soliton solutions of some nonlinear time-fractional PDEs via the conformable fractional derivative. Fractal Fract. 2024, 8, 210. [Google Scholar] [CrossRef]
- Yasmin, H.; Zubair, M.; Mahmood, A.; Ali, A. Analytical soliton-like solutions to the (2+1)-dimensional fractional asymmetric Nizhnik–Novikov–Veselov system. Front. Phys. 2024, 12, 1443986. [Google Scholar] [CrossRef]
- Iqbal, M.; Din, A.; Ahmed, N.; Khan, T.U. Exploring the peakon soliton molecules and solitary wave structure to the nonlinear damped Korteweg–de Vries equation. Open Phys. 2025, 23, 20250198. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A. Motion dynamics of two-dimensional fundamental and vortex solitons in the fractional medium with the cubic–quintic nonlinearity. arXiv 2024, arXiv:2402.16809. [Google Scholar] [CrossRef]
- Murad, M.A.S.; Alshammari, F.S.; Salih, M.S.; Farooq, K. Optical soliton structures in the nonlinear conformable Schrödinger equation with quadratic–cubic nonlinearity. Nonlinear Dyn. 2025, 113. [Google Scholar] [CrossRef]
- Sanchez-Ortiz, J.; Lopez-Cresencio, O.U.; Arciga-Alejandre, M.P.; Ariza-Hernandez, F.J. A Random Riemann–Liouville Integral Operator. Mathematics 2025, 13, 2524. [Google Scholar] [CrossRef]
- Bouchenak, A.; Batiha, I.M.; Hatamleh, R.; Aljazzazi, M.; Jebril, I.H.; Al-Horani, M. Study and Analysis of the Second Order Constant Coefficients and Cauchy-Euler Equations via Modified Conformable Operator. Int. J. Robot. Control Syst. 2025, 5, 794–812. [Google Scholar] [CrossRef]
- AlBaidani, M.M.; Ganie, A.H.; Khan, A.; Aljuaydi, F. An Approximate Analytical View of Fractional Physical Models in the Frame of the Caputo Operator. Fractal Fract. 2025, 9, 199. [Google Scholar] [CrossRef]
- Farooq, K.; Tedjani, A.H.; Li, Z.; Hussain, E. Soliton Dynamics of the Nonlinear Kodama Equation with M-Truncated Derivative via Two Innovative Schemes: The Generalized Arnous Method and the Kudryashov Method. Fractal Fract. 2025, 9, 436. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; Fotoula, G.R.T.; Jäntschi, L.; Fendzi, M.W.; Tala-Tebue, E.; Nguenang, J.P.; Pradeep, J.; Ghanshyam, T.G.; Kenfack-Jiotsa, A.; Smerat, A.; et al. Nuclei discovered new practical insights via optimized soliton-like pulse analysis in a space fractional-time beta-derivatives equations. Sci. Rep. 2025, 15, 8440. [Google Scholar] [CrossRef]
- Hussain, E.; Tedjani, A.H.; Farooq, K.; Beenish. Modeling and Exploration of Localized Wave Phenomena in Optical Fibers Using the Generalized Kundu–Eckhaus Equation for Femtosecond Pulse Transmission. Axioms 2025, 14, 513. [Google Scholar] [CrossRef]
- Kumar, D.; Saharan, A.; Kumar, A. Exploring soliton patterns and dynamical analysis of the solitary wave form solutions of the (3+1)-dimensional Wazwaz–Benjamin–Bona–Mahony equation. Mod. Phys. Lett. B 2025, 39, 2550102. [Google Scholar] [CrossRef]
- Algolam, M.S.; Roshid, M.M.; Alsharafi, M.; Younis, B.; Aldwoah, K.; Osman, O. Bifurcation analysis, modulation instability and dynamical analysis of soliton solutions for generalized (3+1)-dimensional nonlinear wave equation with m-fractional operator. Sci. Rep. 2025, 15, 12929. [Google Scholar] [CrossRef] [PubMed]



| Reference | Year | Method/Model Used | Solution Type | Limitations | Advancement in Present Work |
|---|---|---|---|---|---|
| Zhong et al. [17] | 2015 | Analytical & numerical study of Airy pulses | Soliton generation and finite-energy Airy beams | Focused on Airy-type beams only | Captures lump, kink, and peakon solutions |
| Tariq et al. [13] | 2021 | Extended trial function method on cubic–quintic NPPP | Bright, dark, and optical solitons | Focused on integer-order PDE, limited wave classes | Includes fractional-order effects and multi-peakon solutions |
| Khater [15] | 2021 | Khater II and generalized exponential methods | Optical pulse propagation in planar waveguides | Relies on computational simulations only | Analytical multi-peakon solutions derived in fractional domain |
| Khater [16] | 2022 | Numerical simulation of CQ-HE | Optical pulse dynamics | Purely numerical, lacks analytical insight | Provides exact analytical solutions validated graphically |
| Rizi et al. [14] | 2022 | Jacobian elliptic function method | Chirped solitary waves | Restricted to periodic/elliptic forms | Extends to rational, trigonometric, and exponential solutions |
| Akbar et al. [18] | 2024 | -expansion method | Fractional solitary wave solutions | Limited to basic trigonometric/hyperbolic forms | Integrates rational, exponential, and hybrid solutions |
| Rizvi et al. [19] | 2025 | Sub-ODE method | Wide range of soliton solutions | Cannot unify different solution structures | Unifies polynomial, exponential, trigonometric, and rational solutions |
| Jlali et al. [12] | 2025 | Complete discrimination system of polynomial method (CDSPM) | Analytical soliton & quasi-periodic solutions; chaos analysis | Restricted to algebraic polynomial balance | MGERIF generates mixed rational–integral structures beyond polynomial scope |
| Present Study | 2025 | Conformable cubic–quintic nonlinear Schrödinger-type model using MGERIF | Multi-peakon, lump, kink, and bright/dark solitons | Some redundant/irrelevant solutions need filtering; complex algebraic systems in higher dimensions | Introduces unified framework with fractional derivatives, provides physical interpretation for optical pulse propagation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, E.; Abdullah, A.R.; Farooq, K.; Younas, U. Optical Multi-Peakon Dynamics in the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model Using a Novel Integral Approach. Fractal Fract. 2025, 9, 631. https://doi.org/10.3390/fractalfract9100631
Hussain E, Abdullah AR, Farooq K, Younas U. Optical Multi-Peakon Dynamics in the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model Using a Novel Integral Approach. Fractal and Fractional. 2025; 9(10):631. https://doi.org/10.3390/fractalfract9100631
Chicago/Turabian StyleHussain, Ejaz, Aljethi Reem Abdullah, Khizar Farooq, and Usman Younas. 2025. "Optical Multi-Peakon Dynamics in the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model Using a Novel Integral Approach" Fractal and Fractional 9, no. 10: 631. https://doi.org/10.3390/fractalfract9100631
APA StyleHussain, E., Abdullah, A. R., Farooq, K., & Younas, U. (2025). Optical Multi-Peakon Dynamics in the Fractional Cubic–Quintic Nonlinear Pulse Propagation Model Using a Novel Integral Approach. Fractal and Fractional, 9(10), 631. https://doi.org/10.3390/fractalfract9100631







