Impressive Exact Solitons to the Space-Time Fractional Mathematical Physics Model via an Effective Method

Abstract

A new class of truncated M-fractional exact soliton solutions for a mathematical physics model known as a truncated M-fractional (1+1)-dimensional nonlinear modified mixed-KdV model are achieved. We obtain these solutions by using a modified extended direct algebraic method. The obtained results consist of trigonometric, hyperbolic trigonometric and mixed functions. We also discuss the effect of fractional order derivative. To validate our results, we utilized the Mathematica software. Additionally, we depict some of the obtained kink, periodic, singular, and kink-singular wave solitons, using two and three dimensional graphs. The obtained results are useful in the fields of fluid dynamics, nonlinear optics, ocean engineering and others. Furthermore, these employed techniques are not only straightforward, but also highly effective when used to solve non-linear fractional partial differential equations (FPDEs).

1. Introduction

Fractional calculus have much importance in many fields of science and engineering like; fluid dynamics, plasma physics, optical fibers, chemistry, biology, economics etc. Naturally occurring phenomenon are represented in the form of fractional partial differential equations (FPDEs). Distinct techniques have been developed to the numerical and exact solutions of the FPDEs. For example, generalized exponential rational function method [1], extended trial equation technique [2], improved Fan sub-equation technique [3], modified extended tanh function technique [4], multi exp-function scheme [5], generalized double auxiliary equation technique [6], Bäcklund transformations [7], transformed rational function method [8], Darboux transformation [9] etc.

In our study, we utilize a straightforward and powerful method: modified extended direct algebraic method. This method has various applications. For example, optical soliton solutions to the nonlinear Schrödinger equation are obtained [10], kink wave and lump wave solutions for the fractional coupled Higgs system are achieved [11], bright and dark-singular combo soliton solutions for the Lakshmanan-Porseizian-Daniel model are gained [12], singular, dark and bright wave solutions for the Gerdjikov-Ivanov equation are gained [13], singular-periodic, rational, exponential and other solutions for the highly dispersive perturbed nonlinear Schrödinger equation are obtained [14], dark, bright, singular and other kinds of soliton solutions for the extended (2+1)-dimensional perturbed nonlinear Schrödinger equation are gained [15].

One of the mathematical physics model; (1+1)-dimensional modified mixed Korteweg-de Vries (mmKdV) equation. This model have much importance in nonlinear optics, fluid dynamics and other fields. This model is solved by different techniques earlier. For example; distinct kinds of topological and non-topological soliton solutions are gained by applying the extended rational sinh-cosh technique, extended rational sine-cosine technique and polynomial function technique [16], dark, bright and periodic wave solutions are obtained by utilizing the Homogenous balance technique [17] etc.

The objective of our study is to investigate some new types of M-fractional exact soliton solutions for the (1+1)-dimensional non-linear modified mixed-KdV model by employing the modified extended direct algebraic method and show the effect of truncated M-fractional derivative on the solutions.

This paper contains the various sections; Modified extended direct algebraic method is explained in Section 2, concerning model and it’s mathematical analysis are explained in Section 3, exact soliton solutions are gained in Section 4, some gained results are shown graphically in Section 5, conclusion in Section 6.

2. Modified Extended Direct Algebraic Method

The fundamental steps of this technique are given as [11]:

• Step 1: Considering a NLPDE:

  $$G(f,f^2,f^2{f}_x,f_{xx},f_{xt},\dots )=0,$$

  (1)

here $f=f(x,t)$ represents a wave profile. Consider a wave transformations:

$$f(x,t)=F(\mathit{\xi }),\mathit{\xi }=x+\mathit{\lambda }t.$$

(2)

Using Equation (2) into Equation (1), a NLODE is gained

$$Z(F,F^{2}F\prime ,F″,\dots )=0.$$

(3)

Step 2: Consider Equation (3) has solution given as:

$$F(\mathit{\xi })=\sum _{s=-n}^n{\mathit{\alpha }}_s{\mathit{\psi }}^s(\mathit{\xi })$$

(4)

here ${\mathit{\alpha }}_s(s=-n,\dots ,0,1,2,3,\dots ,n)$ are the unknowns and ${\mathit{\alpha }}_n\ne 0$. A new profile $\mathit{\psi }(\mathit{\xi })$ satisfies the ODE:

$$\mathit{\psi }\prime (\mathit{\xi })=\log (d)\left(p+q\mathit{\psi }(\mathit{\xi })+r\mathit{\psi }{(\mathit{\xi })}^2\right)$$

(5)

where p, q and r are the constants and $d\ne 0,1$. Notice that Equation (5) has solutions for the following different cases:

• Case 1: if $q^2-4pr<0$ and $r\ne 0$, we have

  $${\mathit{\psi }}_1(\mathit{\xi })=-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}.$$

  (6)

$${\mathit{\psi }}_2(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}.$$

(7)

$${\mathit{\psi }}_3(\mathit{\xi })=-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(8)

$${\mathit{\psi }}_4(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(9)

$${\mathit{\psi }}_5(\mathit{\xi })=-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(10)

Case 2:

$${\mathit{\psi }}_6(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}.$$

(11)

$${\mathit{\psi }}_7(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}.$$

(12)

$${\mathit{\psi }}_8(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(13)

$${\mathit{\psi }}_9(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(14)

$${\mathit{\psi }}_{10}(\mathit{\xi })=-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}.$$

(15)

Case 3: if $pr>0$ and $q=0$, we have

$${\mathit{\psi }}_{11}(\mathit{\xi })=\sqrt{\frac{p}{r}}{\tan }_B(\sqrt{pr}\mathit{\xi }).$$

(16)

$${\mathit{\psi }}_{12}(\mathit{\xi })=-\sqrt{\frac{p}{r}}{\cot }_B(\sqrt{pr}\mathit{\xi }).$$

(17)

$${\mathit{\psi }}_{13}(\mathit{\xi })=\sqrt{\frac{p}{r}}({\tan }_B(2\sqrt{pr}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(2\sqrt{pr}\mathit{\xi }))).$$

(18)

$${\mathit{\psi }}_{14}(\mathit{\xi })=-\sqrt{\frac{p}{r}}({\cot }_B(2\sqrt{pr}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(2\sqrt{pr}\mathit{\xi }))).$$

(19)

$${\mathit{\psi }}_{15}(\mathit{\xi })=\frac{1}{2}\sqrt{\frac{p}{r}}({\tan }_B(\frac{1}{2}\sqrt{pr}\mathit{\xi })-{\cot }_B(\frac{1}{2}\sqrt{pr}\mathit{\xi })).$$

(20)

Case 4: if $pr<0$ and $q=0$, we have

$${\mathit{\psi }}_{16}(\mathit{\xi })=-\sqrt{-\frac{p}{r}}{\tanh }_B(\sqrt{-pr}\mathit{\xi }).$$

(21)

$${\mathit{\psi }}_{17}(\mathit{\xi })=-\sqrt{-\frac{p}{r}}{\coth }_B(\sqrt{-pr}\mathit{\xi }).$$

(22)

$${\mathit{\psi }}_{18}(\mathit{\xi })=-\sqrt{-\frac{p}{r}}({\tanh }_B(2\sqrt{-pr}\mathit{\xi })\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2\sqrt{-pr}\mathit{\xi }))).$$

(23)

$${\mathit{\psi }}_{19}(\mathit{\xi })=-\sqrt{-\frac{p}{r}}({\coth }_B(2\sqrt{-pr}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(2\sqrt{-pr}\mathit{\xi }))).$$

(24)

$${\mathit{\psi }}_{20}(\mathit{\xi })=-\frac{1}{2}\sqrt{-\frac{p}{r}}({\tanh }_B(\frac{1}{2}\sqrt{-pr}\mathit{\xi })+{\coth }_B(\frac{1}{2}\sqrt{-pr}\mathit{\xi })).$$

(25)

Case 5: if $r=p$ and $q=0$, we have

$${\mathit{\psi }}_{21}(\mathit{\xi })={\tan }_B(p\mathit{\xi }).$$

(26)

$${\mathit{\psi }}_{22}(\mathit{\xi })=-{\cot }_B(p\mathit{\xi }).$$

(27)

$${\mathit{\psi }}_{23}(\mathit{\xi })={\tan }_B(2p\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(2p\mathit{\xi }).$$

(28)

$${\mathit{\psi }}_{24}(\mathit{\xi })=-{\cot }_B(2p\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(2p\mathit{\xi }).$$

(29)

$${\mathit{\psi }}_{25}(\mathit{\xi })=\frac{1}{2}{\tan }_B(\frac{1}{2}p\mathit{\xi })-\frac{1}{2}{\cot }_B(\frac{1}{2}p\mathit{\xi }).$$

(30)

Case 6: if $r=-p$ and $q=0$, we have

$${\mathit{\psi }}_{26}(\mathit{\xi })=-{\tanh }_B(p\mathit{\xi }).$$

(31)

$${\mathit{\psi }}_{27}(\mathit{\xi })=-{\coth }_B(p\mathit{\xi }).$$

(32)

$${\mathit{\psi }}_{28}(\mathit{\xi })=-{\tanh }_B(2p\mathit{\xi })\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2p\mathit{\xi }).$$

(33)

$${\mathit{\psi }}_{29}(\mathit{\xi })=-{\coth }_B(2p\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(2p\mathit{\xi }).$$

(34)

$${\mathit{\psi }}_{30}(\mathit{\xi })=-\frac{1}{2}{\tanh }_B(\frac{1}{2}p\mathit{\xi })-\frac{1}{2}{\coth }_B(\frac{1}{2}p\mathit{\xi }).$$

(35)

Case 7: if $q^2-4pr=0$, we have

$${\mathit{\psi }}_{31}(\mathit{\xi })=-2\frac{p(q\mathit{\xi }\log (d)+2)}{q^2\mathit{\xi }\log (d)}.$$

(36)

Case 8: if $q=\mathit{\rho }$ $p=m\mathit{\rho }$$(m\ne 0)$ and $r=0$, we have

$${\mathit{\psi }}_{32}(\mathit{\xi })=d^{\mathit{\rho }\mathit{\xi }}-m.$$

(37)

Case 9: if $q=r=0$, we have

$${\mathit{\psi }}_{33}(\mathit{\xi })=p\mathit{\xi }\log (d).$$

(38)

Case 10: if $p=q=0$, we have

$${\mathit{\psi }}_{34}(\mathit{\xi })=-\frac{1}{r\mathit{\xi }\log (d)}.$$

(39)

Case 11: if $p=0$, $q\ne 0$ and $r\ne 0$, we have

$${\mathit{\psi }}_{35}(\mathit{\xi })=-\frac{cq}{r({\cosh }_B(q\mathit{\xi })-{\sinh }_B(q\mathit{\xi })+c)}.$$

(40)

$${\mathit{\psi }}_{36}(\mathit{\xi })=-\frac{q({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\xi }))}{r({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\xi })+f)}.$$

(41)

Case 12: if $q=\mathit{\rho }$$r=m\mathit{\rho }$$(m\ne 0)$ and $p=0$, we have

$${\mathit{\psi }}_{37}(\mathit{\xi })=\frac{c{d}^{\mathit{\rho }\mathit{\xi }}}{c-mf{d}^{\mathit{\rho }\mathit{\xi }}}.$$

(42)

where $c,f>0$ and represent the deformation parameters.

Step 3: Begin this step by putting Equation (4) along Equation (5) into Equation (3). Next sum coefficients of each ${\mathit{\psi }}^s$ term, then set the coefficients of same order equal to zero to gain a set of equations in ${\mathit{\alpha }}_s$ and $\mathit{\lambda }$. By manipulating this set of equations, results for the unknowns are found. Step 4: Inserting Equation (4), where the values of ${\mathit{\alpha }}_s$ and $\mathit{\lambda }$ are now known into Equation (3) will yield solutions to Equation (1).

3. Model Description and Mathematical Analysis

Let us assume a truncated M-fractional (1+1)-dimensional nonlinear modified mixed-KdV model given as:

$$D_{M,t}^{\mathit{\alpha },{\rm Y}}u+(a\sqrt{u}+bu)D_{M,x}^{\mathit{\alpha },{\rm Y}}u+\mathit{\tau }{D}_{M,3x}^{3\mathit{\alpha },{\rm Y}}u=0,$$

(43)

where

$$D_{M,x}^{\mathit{\alpha },{\rm Y}}u=\underset{\mathit{\tau }\to 0}{\lim }\frac{u(x{E}_{{\rm Y}}(\mathit{\tau }{x}^{1-\mathit{\alpha }}))-u(x)}{\mathit{\tau }},0<\mathit{\alpha }\le 1,{\rm Y}\in (0,\infty )$$

(44)

where $E_{{\rm Y}}(.)$ is a truncated Mittag-Leffler (TML) function mention in [18,19].

Here $u=u(x,t)$ is a wave function. Equation (1) represents a modified mixed Korteweg-de Vries (mmKdV) model which explains the flat-topped electron distribution having a stronger non-linearity that corresponds to the small-width and high-velocity of the wave [20,21,22]. To find the solutions of Equation (1), we suppose the following:

$$u=g^2;g=g(x,t).$$

(45)

By putting Equation (45) into Equation (43), yields

$$g{D}_{M,t}^{\mathit{\alpha },{\rm Y}}g+(a{g}^2+b{g}^3)D_{M,x}^{\mathit{\alpha },{\rm Y}}g+\mathit{\tau }(g{D}_{M,3x}^{3\mathit{\alpha },{\rm Y}}g+3D_{M,x}^{\mathit{\alpha },{\rm Y}}g{D}_{M,2x}^{2\mathit{\alpha },{\rm Y}}g)=0.$$

(46)

Consider a wave transformation given as:

$$g=G(\mathit{\xi });\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}-\mathit{\lambda }{t}^{\mathit{\alpha }}).$$

(47)

here $\mathit{\theta }$ represents the wave-amplitude and $\mathit{\lambda }$ denotes the wave velocity.

By using Equation (47) into Equation (46), we get

$$-6\mathit{\lambda }{G}^2+4a{G}^3+3b{G}^4+12\mathit{\tau }{\mathit{\theta }}^2(G{G}^{\prime \prime }+{(G^{\prime })}^2)=0.$$

(48)

By applying the Homogenous balance approach into Equation (48), we gain the natural number $m=1$. Now we will solve the Equation (48) with the help of two different techniques.

4. Exact Soliton Solutions

For $m=1$, Equation (4) changes into

$$G(\mathit{\xi })={\mathit{\alpha }}_{-1}{(\mathit{\psi }(\mathit{\xi }))}^{-1}+{\mathit{\alpha }}_0+{\mathit{\alpha }}_1\mathit{\psi }(\mathit{\xi }).$$

(49)

Putting Equation (49) along Equation (5) into Equation (48), we obtain the following sets for discussion.

• Set 1:

  $$\left\{{\mathit{\alpha }}_{-1}=-\frac{4ap}{5bq},{\mathit{\alpha }}_0=-\frac{4a}{5b},{\mathit{\alpha }}_1=-\frac{4ar}{5bq},\mathit{\lambda }=-\frac{16a^2\left(q^2-4pr\right)}{75b{q}^2},\mathit{\tau }=-\frac{4a^2}{75b{\mathit{\theta }}^2{q}^2{\log }^2(d)}\right\}$$

  (50)

Case 1: if $q^2-4pr<0$ and $r\ne 0$, we have

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(51)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(52)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(53)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(54)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}+\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(55)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2\left(q^2-4pr\right)}{75b{q}^2}{t}^{\mathit{\alpha }})$.

• Case 2:

  $$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

  (56)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(57)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(58)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(59)

$$\begin{array}{c}u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi }))}{2r})\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{4ap}{5bq}(-\frac{q}{2r}-\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(60)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2\left(q^2-4pr\right)}{75b{q}^2}{t}^{\mathit{\alpha }})$.

• Case 8:

  $$u(x,t)=(-\frac{4a}{5b}-\frac{4am}{5b}(d^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}-m{)}^{-1}{)}^2.$$

  (61)

Case 11:

$$u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{cq}{r({\cosh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+c)}){)}^2.$$

(62)

$$u(x,t)=(-\frac{4a}{5b}-\frac{4ar}{5bq}(-\frac{q({\cosh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})))}{r({\cosh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+f)}){)}^2.$$

(63)

Case 12:

$$u(x,t)=(-\frac{4a}{5b}-\frac{4am}{5b}(\frac{c{d}^{\mathit{\rho }\mathit{\xi }}}{c-mf{d}^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}}){)}^2.$$

(64)

Set 2:

$$\begin{array}{c}\{{\mathit{\alpha }}_{-1}=\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)},{\mathit{\alpha }}_0=\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)},{\mathit{\alpha }}_1=0,\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathit{\lambda }=-\frac{16a^2}{75b},\mathit{\tau }=-\frac{4a^2}{75b{\mathit{\theta }}^2{\log }^2(d)(q^2-4pr)}\}\end{array}$$

(65)

Case 1:

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(66)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(67)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(68)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(69)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(70)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 2:

  $$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

  (71)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(72)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(73)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(74)

$$\begin{array}{c}u(x,t)=(\frac{2\sqrt{a^2{q}^2(q^2-4pr)}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(75)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 3:

  $$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(\sqrt{\frac{p}{r}}{\tan }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

  (76)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{\frac{p}{r}}{\cot }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(77)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(\sqrt{\frac{p}{r}}({\tan }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\sec }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(78)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{\frac{p}{r}}({\cot }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\csc }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(79)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(\frac{1}{2}\sqrt{\frac{p}{r}}({\tan }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\cot }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^{-1}{)}^2.\end{array}$$

(80)

Case 4:

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}{\tanh }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(81)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}{\coth }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(82)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}({\tanh }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\mathit{\iota }\sqrt{cf}sec{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(83)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}({\coth }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\sqrt{cf}csc{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(84)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-4pr}}{5br}(-\frac{1}{2}\sqrt{-\frac{p}{r}}({\tanh }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+\hfill \\ \hfill {\coth }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^{-1}{)}^2.\end{array}$$

(85)

Case 5:

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a\mathit{\iota }}{5b}({\tan }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(86)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a\mathit{\iota }}{5b}(-{\cot }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(87)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a\mathit{\iota }}{5b}({\tan }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\sec }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(88)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a\mathit{\iota }}{5b}(-{\cot }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\csc }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(89)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a\mathit{\iota }}{5b}(\frac{1}{2}{\tan }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\cot }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(90)

Case 6:

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a}{5b}(-{\tanh }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(91)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a}{5b}(-{\coth }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(92)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a}{5b}(-{\tanh }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(93)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a}{5b}(-{\coth }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}csc{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(94)

$$u(x,t)=(\frac{-2a}{5b}-\frac{4a}{5b}(-\frac{1}{2}{\tanh }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\coth }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(95)

Case 8:

$$u(x,t)=(\frac{4am}{5b}(d^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}-m{)}^{-1}{)}^2.$$

(96)

Set 3:

$$\begin{array}{c}\{{\mathit{\alpha }}_{-1}=0,{\mathit{\alpha }}_0=\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)},{\mathit{\alpha }}_1=\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)},\mathit{\lambda }=-\frac{16a^2}{75b},\hfill \\ \hfill \mathit{\tau }=-\frac{4a^2}{75b{\mathit{\theta }}^2{\log }^2(d)(q^2-4pr)}\}\end{array}$$

(97)

Case 1:

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(98)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(99)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(100)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(101)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(102)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 2:

  $$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

  (103)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(104)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(105)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(106)

$$\begin{array}{c}u(x,t)=(\frac{2aq\sqrt{q^2-4pr}-2a(q^2-4pr)}{5b(q^2-4pr)}+\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(107)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 3:

  $$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(\sqrt{\frac{p}{r}}{\tan }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

  (108)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{\frac{p}{r}}{\cot }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(109)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(\sqrt{\frac{p}{r}}({\tan }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\sec }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(110)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{\frac{p}{r}}({\cot }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\csc }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(111)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(\frac{1}{2}\sqrt{\frac{p}{r}}({\tan }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\cot }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)))}^2.\end{array}$$

(112)

Case 4:

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}{\tanh }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(113)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}{\coth }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(114)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}({\tanh }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\mathit{\iota }\sqrt{cf}sec{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(115)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}({\coth }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\sqrt{cf}csc{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(116)

$$\begin{array}{c}u(x,t)=(\frac{-2a}{5b}-\frac{2a\sqrt{-pr}}{5pb}-\frac{1}{2}\sqrt{-\frac{p}{r}}({\tanh }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+\hfill \\ \hfill {\coth }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^2.\end{array}$$

(117)

Case 5:

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\mathit{\iota }}{5b}({\tan }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(118)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\mathit{\iota }}{5b}(-{\cot }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(119)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\mathit{\iota }}{5b}({\tan }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\sec }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(120)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\mathit{\iota }}{5b}(-{\cot }_B(2p\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(121)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a\mathit{\iota }}{5b}(\frac{1}{2}{\tan }_B(\frac{1}{2}p\mathit{\xi })-\frac{1}{2}{\cot }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(122)

Case 6:

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a}{5b}(-{\tanh }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(123)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a}{5b}(-{\coth }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(124)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a}{5b}(-{\tanh }_B(2p\mathit{\xi })\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(125)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a}{5b}(-{\coth }_B(2p\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(126)

$$u(x,t)=(\frac{-2a}{5b}-\frac{2a}{5b}(-\frac{1}{2}{\tanh }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\coth }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(127)

Case 11:

$$u(x,t)=(\frac{4ar}{5bq}(-\frac{cq}{r({\cosh }_B(q\mathit{\xi })-{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+c)}){)}^2.$$

(128)

$$u(x,t)=(\frac{4ar}{5bq}(-\frac{q({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})))}{r({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+f)}){)}^2.$$

(129)

Case 12:

$$u(x,t)=(\frac{4am}{5b}(\frac{c{d}^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}}{c-mf{d}^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}}){)}^2.$$

(130)

Set 4:

$$\begin{array}{c}\{{\mathit{\alpha }}_{-1}=-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)},{\mathit{\alpha }}_0=-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)},{\mathit{\alpha }}_1=0,\hfill \\ \hfill \mathit{\lambda }=-\frac{16a^2}{75b},\mathit{\tau }=-\frac{4a^2}{75b{\mathit{\theta }}^2{\log }^2(d)(q^2-4pr)}\}\end{array}$$

(131)

Case 1:

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(132)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(133)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(134)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(135)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(136)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 2:

  $$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

  (137)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{)}^{-1}{)}^2.\end{array}$$

(138)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(139)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(140)

$$\begin{array}{c}u(x,t)=(-\frac{2\sqrt{a^2{q}^2(q^2-4pr)}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4p\sqrt{a^2(q^2-4pr)}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{)}^{-1}{)}^2.\end{array}$$

(141)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 3:

  $$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(\sqrt{\frac{p}{r}}{\tan }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

  (142)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{\frac{p}{r}}{\cot }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(143)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(\sqrt{\frac{p}{r}}({\tan }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\sec }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(144)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{\frac{p}{r}}({\cot }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\csc }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(145)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(\frac{1}{2}\sqrt{\frac{p}{r}}({\tan }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\cot }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^{-1}{)}^2.\end{array}$$

(146)

Case 4:

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}{\tanh }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(147)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}{\coth }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(148)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}({\tanh }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\mathit{\iota }\sqrt{cf}sec{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(149)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\sqrt{-\frac{p}{r}}({\coth }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill (\sqrt{cf}csc{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){))}^{-1}{)}^2.\end{array}$$

(150)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-4pr}}{5br}(-\frac{1}{2}\sqrt{-\frac{p}{r}}({\tanh }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+\hfill \\ \hfill {\coth }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^{-1}{)}^2.\end{array}$$

(151)

Case 5:

$$u(x,t)=(\frac{2a}{5b}+\frac{4a\mathit{\iota }}{5b}({\tan }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(152)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a\mathit{\iota }}{5b}(-{\cot }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(153)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a\mathit{\iota }}{5b}({\tan }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\sec }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(154)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a\mathit{\iota }}{5b}(-{\cot }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\csc }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(155)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a\mathit{\iota }}{5b}(\frac{1}{2}{\tan }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\cot }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(156)

Case 6:

$$u(x,t)=(\frac{2a}{5b}+\frac{4a}{5b}(-{\tanh }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(157)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a}{5b}(-{\coth }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(158)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a}{5b}(-{\tanh }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(159)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a}{5b}(-{\coth }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}csc{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(160)

$$u(x,t)=(\frac{2a}{5b}+\frac{4a}{5b}(-\frac{1}{2}{\tanh }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\coth }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)}^{-1}{)}^2.$$

(161)

Case 8:

$$u(x,t)=(-\frac{4am}{5b}(d^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}-m{)}^{-1}{)}^2.$$

(162)

Set 5:

$$\begin{array}{c}\{{\mathit{\alpha }}_{-1}=0,{\mathit{\alpha }}_0=-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)},{\mathit{\alpha }}_1=-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)},\mathit{\lambda }=-\frac{16a^2}{75b},\hfill \\ \hfill \mathit{\tau }=-\frac{4a^2}{75b{\mathit{\theta }}^2{\log }^2(d)(q^2-4pr)}\}\end{array}$$

(163)

Case 1:

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\tan }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(164)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}{\cot }_B(\frac{1}{2}\sqrt{-(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(165)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\sec }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(166)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\cot }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(167)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}+\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{-(q^2-4pr)}({\tan }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })-({\cot }_B(\frac{1}{4}\sqrt{-(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(168)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 2:

  $$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\tanh }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

  (169)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}{\coth }_B(\frac{1}{2}\sqrt{(q^2-4pr)}\mathit{\xi })}{2r}{))}^2.\end{array}$$

(170)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\sqrt{-(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}sec{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(171)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\coth }_B(\sqrt{(q^2-4pr)}\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(172)

$$\begin{array}{c}u(x,t)=(-\frac{2aq\sqrt{q^2-4pr}+2a(q^2-4pr)}{5b(q^2-4pr)}-\frac{4ar\sqrt{q^2-4pr}}{5b(q^2-4pr)}(-\frac{q}{2r}-\hfill \\ \hfill \hspace{1em}\hspace{1em}\frac{\sqrt{(q^2-4pr)}({\tanh }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })-({\coth }_B(\frac{1}{4}\sqrt{(q^2-4pr)}\mathit{\xi })))}{2r}{))}^2.\end{array}$$

(173)

where $\mathit{\xi }=\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})$.

• Case 3:

  $$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(\sqrt{\frac{p}{r}}{\tan }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

  (174)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{\frac{p}{r}}{\cot }_B(\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(175)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(\sqrt{\frac{p}{r}}({\tan }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\sec }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(176)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{\frac{p}{r}}({\cot }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}{\csc }_B(2\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(177)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(\frac{1}{2}\sqrt{\frac{p}{r}}({\tan }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\cot }_B(\frac{1}{2}\sqrt{pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){)))}^2.\end{array}$$

(178)

Case 4:

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}{\tanh }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(179)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}{\coth }_B(\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(180)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}({\tanh }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\mathit{\iota }\sqrt{cf}sec{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(181)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}(-\sqrt{-\frac{p}{r}}({\coth }_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm \hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\sqrt{cf}csc{h}_B(2\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)))}^2.\end{array}$$

(182)

$$\begin{array}{c}u(x,t)=(\frac{2a}{5b}+\frac{2a\sqrt{-pr}}{5pb}-\frac{1}{2}\sqrt{-\frac{p}{r}}({\tanh }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\coth }_B(\frac{1}{2}\sqrt{-pr}\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})){))}^2.\end{array}$$

(183)

Case 5:

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\mathit{\iota }}{5b}({\tan }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(184)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\mathit{\iota }}{5b}(-{\cot }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(185)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\mathit{\iota }}{5b}({\tan }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))\pm (\sqrt{cf}{\sec }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(186)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\mathit{\iota }}{5b}(-{\cot }_B(2p\mathit{\xi })\pm (\sqrt{cf}{\csc }_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(187)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a\mathit{\iota }}{5b}(\frac{1}{2}{\tan }_B(\frac{1}{2}p\mathit{\xi })-\frac{1}{2}{\cot }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(188)

Case 6:

$$u(x,t)=(\frac{2a}{5b}+\frac{2a}{5b}(-{\tanh }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(189)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a}{5b}(-{\coth }_B(p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(190)

$$u(x,t)=(\frac{2a}{5b}+\frac{2a}{5b}(-{\tanh }_B(2p\mathit{\xi })\pm (\mathit{\iota }\sqrt{cf}sec{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(191)

$$u(x,t)=(\frac{+2a}{5b}+\frac{2a}{5b}(-{\coth }_B(2p\mathit{\xi })\pm (\sqrt{cf}csc{h}_B(2p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(192)

$$u(x,t)=(\frac{+2a}{5b}+\frac{2a}{5b}(-\frac{1}{2}{\tanh }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))-\frac{1}{2}{\coth }_B(\frac{1}{2}p\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))){)}^2.$$

(193)

Case 11:

$$u(x,t)=(-\frac{4ar}{5bq}(-\frac{cq}{r({\cosh }_B(q\mathit{\xi })-{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+c)}){)}^2.$$

(194)

$$u(x,t)=(-\frac{4ar}{5bq}(-\frac{q({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})))}{r({\cosh }_B(q\mathit{\xi })+{\sinh }_B(q\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }}))+f)}){)}^2.$$

(195)

Case 12:

$$u(x,t)=(-\frac{4am}{5b}(\frac{c{d}^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}}{c-mf{d}^{\mathit{\rho }\mathit{\theta }\frac{\Gamma (1+{\rm Y})}{\mathit{\alpha }}(x^{\mathit{\alpha }}+\frac{16a^2}{75b}{t}^{\mathit{\alpha }})}}){)}^2.$$

(196)

5. Physical Behavior of Solutions

In this portion, we presenta the behavior of our gained kink, periodic, singular, and kink-singular solitons solutions are shown in the following Figures. Figure 1 illustrations a kink-singular shape of $u(x,t)$ occur in Equation (51) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=2.5;b=0.4;\mathit{{\rm Y}}=1;r=0.5;\mathit{\theta }=0.9;p=1;q=1;\mathit{\alpha }=0.8$. Figure 2 illustrations a kink-singular shape of $u(x,t)$ occur in Equation (52) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=2.5;b=0.4;\mathit{{\rm Y}}=1;r=0.5;\mathit{\theta }=0.3;p=1;q=1;\mathit{\alpha }=0.8$. Figure 3 illustrations a kink shape of $u(x,t)$ occur in Equation (53) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=2.5;b=0.4;c=1.3;\mathit{{\rm Y}}=1;r=0.5;\mathit{\theta }=0.3;p=1;q=1;f=1.5;\mathit{\alpha }=0.8$. (Figure 4) illustrations a kink shape of $u(x,t)$ occur in Equation (56) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=2.5;b=0.4;\mathit{{\rm Y}}=1;r=0.5;\mathit{\theta }=0.3;p=1;q=1;\mathit{\alpha }=0.8$. Figure 5 illustrations a kink-singular shape of $u(x,t)$ occur in Equation (57) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=0.5;b=1.4;\mathit{{\rm Y}}=1;r=0.5;\mathit{\theta }=1;p=1;q=1;\mathit{\alpha }=0.8$. Figure 6 illustrations a periodic shape of $u(x,t)$ occur in Equation (60) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=5.1;b=2.4;\mathit{{\rm Y}}=2;r=0.5;\mathit{\theta }=2.3;p=1;q=1;\mathit{\alpha }=0.5$. Figure 7 illustrations a singular shapeof $u(x,t)$ occur in Equation (61) in (a) 3-dim and (b) 2-dim graphs with $d=3;a=2;b=0.4;\mathit{{\rm Y}}=1;m=1;\mathit{\theta }=0.3;\mathit{\alpha }=0.6$.

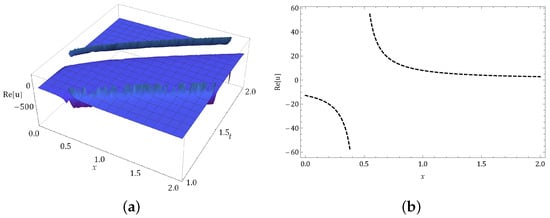
Figure 1. Graph of $u(x,t)$ occur in Equation (51) in (a) 3-dim and (b) 2-dim graphs.

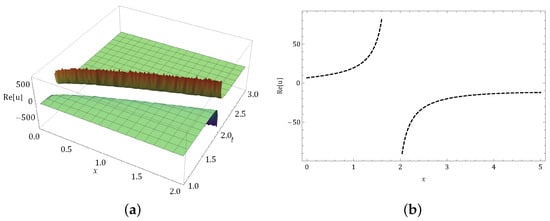
Figure 2. Graph of $u(x,t)$ occur in Equation (52) in (a) 3-dim and (b) 2-dim graphs.

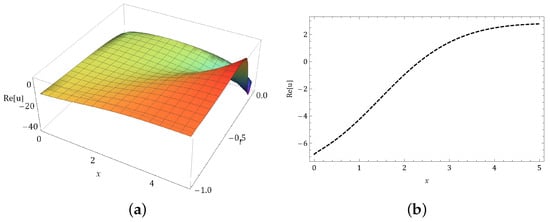
Figure 3. Graph of $u(x,t)$ occur in Equation (53) in (a) 3-dim and (b) 2-dim graphs.

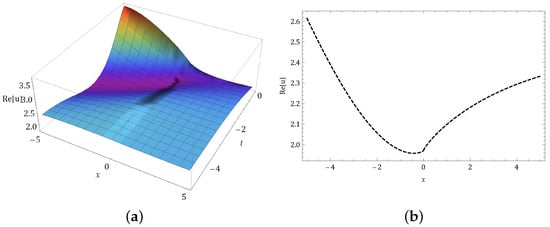
Figure 4. Graph of $u(x,t)$ occur in Equation (56) in (a) 3-dim and (b) 2-dim graphs.

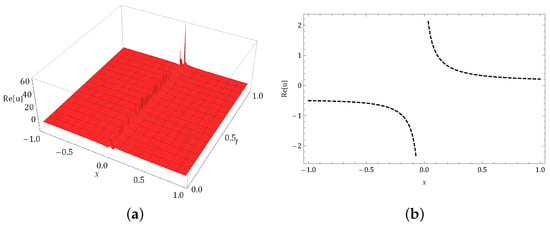
Figure 5. Graph of $u(x,t)$ occur in Equation (57) in (a) 3-dim and (b) 2-dim graphs.

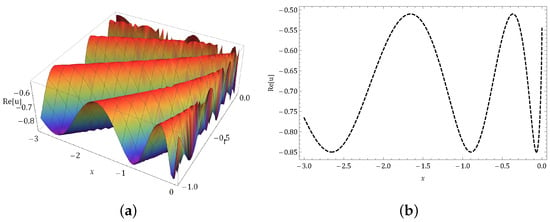
Figure 6. Graph of $u(x,t)$ occur in Equation (60) in (a) 3-dim and (b) 2-dim graphs.

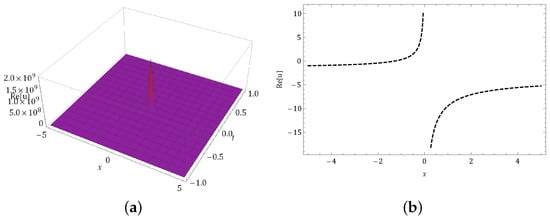
Figure 7. Graph of $u(x,t)$ occur in Equation (61) in (a) 3-dim and (b) 2-dim graphs.

6. Conclusions

A new class of truncated M-fractional exact soliton solutions for a truncated M-fractional (1+1)-dimensional nonlinear modified mixed-KdV model are obtained successfully. For this aim; modified extended direct algebraic method is used. The obtained results including the kink, periodic, singular, and kink-singular soliton solutions. We also discuss the effect of fractional order derivative. To validate as well as to obtain our results, we utilized the Mathematica software. Additionally, we depict some of the obtained wave solitons, using two and three dimensional graphs. The obtained results are useful in the fields of fluid dynamics, nonlinear optics, ocean engineering and others. Furthermore, these employed techniques are not only straightforward, but also highly effective when used to solve non-linear fractional partial differential equations (FPDEs).