Abstract
This article focuses the event-triggered adaptive finite-time control scheme for the states constrained fractional-order nonlinear systems (FONSs) under uncertain parameters and external disturbances. The backstepping scheme is employed to construct the finite-time controller via a series of barrier Lyapunov function (BLF) to solve that all the state constraints are not violated. Different from the trigger condition with fixed value, the event-triggered strategy is applied to overcome the communication burden of controller caused by the limited communication resources. By utilizing fractional-order Lyapunov analysis, all variables in the resulted system are proven to be bounded, and the tracking error converges to the small neighborhood around origin in finite time and without the Zeno behavior. Finally, the effectiveness of the proposed control scheme is verified by the simulation analysis of a bus power system.
1. Introduction
Fractional-order nonlinear systems (FONSs) established by fractional calculus can present the physical systems accurately for lots of different areas such as infectious diseases [1,2], image processing [3,4], secret communication [5,6], circuit [7,8], vehicle engineering [9,10], etc. Furthermore, many controller design problem for FONSs have been researched, in which the adaptive technique as a very powerful tool have been investigated by combining with backstepping mechanism to deal with the uncertainties in FONSs [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].
All above mentioned achievements ignore the state constraints. In plentiful physical systems, it is generally widespread that the system states can change within a specified range, and the control system may become unstable when the system states violate these constraints. Therefore, it is practical significance to control FONSs with state constraints. To tackle the state constraints issue for FONSs, the barrier Lyapunov function (BLF) as the predominant approach by applying error constraint is used to limit the state [26,27,28,29]. The authors in [28] design the adaptive controller for the FONSs under tate constraints, and the states remain in the bounds by introducing the BLF. In [29], an adaptive dynamic surface control scheme by using asymmetric BLF is proposed for FONSs with states constraints and input nonlinearity to achieve the tracking performance.
In fact, the above literature can theoretically guarantee the infinite-time stability of the control system, namely, the control system obtain the desired performance only when the time tends to infinity. In order to complete faster transient performance and better disturbance rejection ability by using the finite-time control, many contributions in this field have been reported for both integer-order nonlinear systems [30,31,32] and FONSs [22,33,34,35,36,37,38]. In [22], a finite-time adaptive neural controller is developed for a class of the FONSs, and the errors converge to zero in finite time. The author in [33] develops fractional order finite-time output feedback controllers for nonlinear interconnected systems to ensure the finite time stability. A sliding mode controller is developed for FONSs to ensure all variables arrive at a domain within the fixed time in [34]. The author in [35] presentes the fractional-order fuzzy controller with finite-time performance for tumor systems with finite-time stability. In [36], an adaptive neural finite-time controller for the FONSs under unknown dynamics is proposed to obtain finite-time convergence. The authors in [37] develop the finite-time adaptive controller for uncertain FONSs by using the command filter. For a class of FONSs with faults, the authors in [38] present a fuzzy adaptive dynamic sliding mode controller. However, the communication with time-trigger method may lead to the waste of resource coming from the huge data transmission.
Event-triggered control (ETC) can reduce the limited computation resources and communication, which is only triggered when the condition is met. In [39], the ETC strategy for the FONSs is designED to ensure the stability and reduce computational burden. In [40], the distributed ETC for multiagent fractional-order systems is designed to sSolve the problem of limited communication resources. For the FONS with unmodeled dynamic in [41], the neural adaptive ETC is presented to reduce computational burden. For the integrator FONS under disturbances and unknown dynamic in [42], an adaptive ETC method is proposed to reduce the amount of computation required for transmission. In [43], an adaptive fuzzy ETC scheme is developed for FONS under uncertainty to reduce the transmission of the control signal. In [44], an adaptive fuzzy hybrid ETC for the uncertain time-delay FONS under actuator fault is proposed to improve the efficiency of computing resource. To our best knowledge, there is a lack of research on the finite-time adaptive event-triggered controller of the FONSs with full-state constraints and uncertain parameters bringing forward the challenge.
Based on above discussion, this article will design a finite-time event-triggered adaptive controller for full-states constrained FONSs with uncertain parameters and external disturbances by combining backstepping technique and event-triggered scheme. The significance and contributions are as follows:
- (1)
- Compared with full-state constraints results in [28,29] without finite time performance, the finite-time event-triggered adaptive controller is exploited by combing BLFs and backstepping technology, and the finite-time convergence of the close-loop signals can be guaranteed. Compared with the finite-time controller in [36,37,38], it is further resolved that the state constraints are not violated.
- (2)
- Different from the conventional periodic controllers in [28,29,36,37,38], an event triggered adaptive controller is proposed and the stability is proved by using finite-time fractional-order Lyapunov criterion, in which the control signals are updated only via the event-triggering mechanism largely reducing the consumption of network resources and communication burden.
2. Problem Descriptions
Consider the following strict-feedback FONS with uncertain parameters and external disturbances:
where and denote the state vectors, denotes the output, u denoted controller input, is the external disturbance, and and denote known smooth functions. is the system fractional order. the Caputo fractional derivative of is denoted as [45,46]:
where , . is defined as , when .
Control objective: (1) output y can track the signal in finite time; (2) all the states are within the bounds of the constraints; and (3) Zeno behavior is avoided to occur.
Assumption 1.
For , there are positive , , and , s.t. , , and .
The desired signal is the known bounded signal in real application. Then, according to the maximum value of , and , the bounds , and can be obtained.
Assumption 2.
There are unknown constants and , s.t. . Without loss of generality, .
Assumption 3.
is bounded, and with
Lemma 1.
In [47,48]. Let , , then holds for .
Lemma 2.
In [49]. Let . Assume that is convex (i.e., ), then, holds for .
Lemma 3.
In [50]: For and , it is hold that:
Lemma 4.
In [51,52]. When satisfy for , we obtain
Lemma 5.
In [53]: Suppose , , and , then
3. Finite-Time Adaptive Controller with State Constraints
In this section, a finite-time ETC adaptive method will be developed for the systems (1) combined with the backstepping technology. The event-triggered actual controller, virtual controller and adaptive parameter estimation will be structured by the choice of BLF, for which the detailed design process is presented as follows.
Step 1: Define , from system (1) the Caputo fractional derivative of is
Denote , where is the estimate parameter of . Consider the BLF candidate function as
where and is a design parameter. and its definition will be given later.
According to Lemmas 1 and 2, the derivative of is
The Young’s inequality can be applied to obtain
where .
The virtual control signal and parameter estimation are designed as follows
where , and .
Step 2: The Caputo fractional derivative of yields
The Lyapunov candidate function is selected as
where and .
Using the Young’s inequality, yields
where is a design parameter.
The virtual controller and the parameter estimation are designed as
where and are the design parameters.
Step : Define , and we can obtain
Consider the Lyapunov candidate function as
where , , and .
Using the Young’s inequality, yields
where .
Construct the virtual control and the parameter estimation as
where and .
Then, the can be rewritten as
Step n: The Caputo fractional derivative of is given as
Consider the Lyapunov candidate function as
where , , and .
The derivative of is
From the Young’s inequality it is true that
where .
The controller u with event-triggered mechanism and the parameter estimation are constructed as follows
where
and , and . is the update time. is the sampling error, and are known parameters.
From and (35), we have , where and . Then
Theorem 1.
Considering the FONSs (1) under Assumptions 1–3, suppose that initial constraint is satisfied, by designing the event-triggered actual controller (34), with virtual controllers (11), (19), (27), the parameter estimation (12), (20), (28) and (37), it confirms that: (1) all the signals are bounded and Zeno behavior is avoided; (2) the tracking signal can be well tracked and the state variables keep within the set in finite-time T; and (3) for , error satisfies , where
Proof.
Due to , , we obtain
According to parameter estimation error , it holds
Then, one can obtain
According to Lemma 3, choose and , then one can obtain
According to Lemma 4, one can obtain
For , (50) is rewritten as . If , we obtain
Let , then . From Lemma 5, we obtain
Then
According to and Caputo fractional integral, we obtain
Then, we obtain . Using the definition of , it holds
This implies that
It can be found that tracking error converges to in finite time T.
From , the boundedness of as well as can be obtained, which means that satisfies . Due to with the boundedness of and , it holds that state is bounded. From (11), the virtual controller is a function of and . Then, is also bounded with the supremum of . Based on the definition of , it holds that and are bounded. In the same way, the boundedness of , and controller u can be obtained.
In order to avoid Zeno behavior, it requires to prove that there is a constant such that for , . Based on the sampling error , it holds . From the definition of in (36), it holds that such that . According to and , one gets , which means that the Zeno behavior is avoided to occur.
Due to with from Assumption 1, we get . Define , one can obtain . From , it holds . Define , one can have . Similarly, one can get , . Thus, all do not transgress the set in finite-time T. □
4. Simulation
In this section, the validity of the devised finite time constraint ETC strategy will be illustrated by a single-machine-infinite bus power system presented as [54]:
where and are the system states, y is the output of systems, u is the controller input, , , , , , , and . and are the external disturbances. The virtual control laws are constructed as
The adaptive laws are given as
Design the following event-triggered strategy
The design parameters in (59)–(61) are chosen as and . The initial conditions are selected as and . The desired signal is , and the constraints are presented as and .
Figure 1 and Figure 2 show the trajectories of the reference signal, system output and system state. It is obvious that all system states maintain the given constraints by using the proposed finite-time ETC scheme. The event-triggered actuator control input u is described in Figure 3. Figure 4 presents the trajectories of parameters estimation. It can be found that the parameter estimation is not smooth causing the compensation of nonlinear uncertainty to fluctuate, which is the main reason that the state trajectory of is not smooth in Figure 2. The sequence of steps of event-triggered sampling and the number of accumulated events are shown in Figure 5 and Figure 6, respectively. One can obtain that the stability and good tracking performance can be both guaranteed with the reduced communication burden.
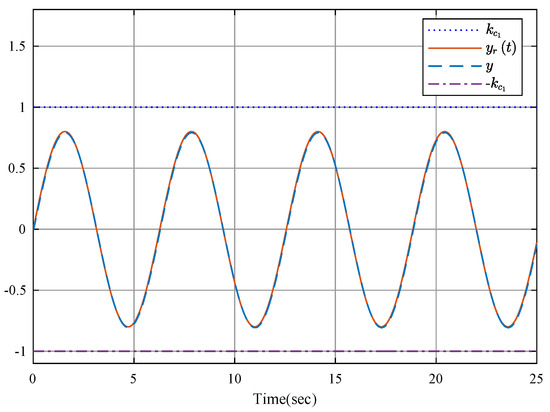
Figure 1.
System output y and tracking signal .
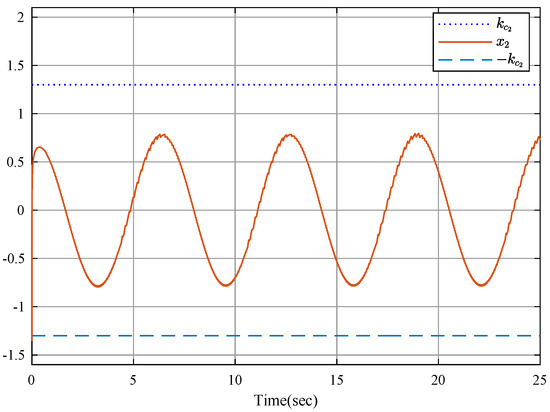
Figure 2.
State trajectory .
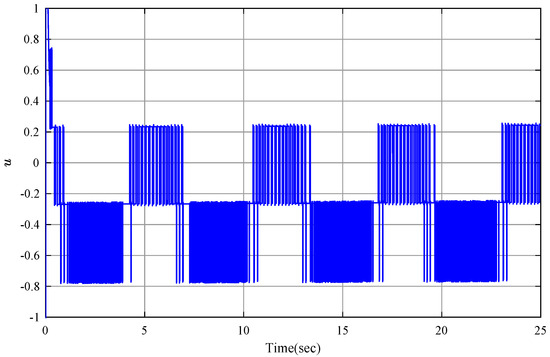
Figure 3.
Control input u.
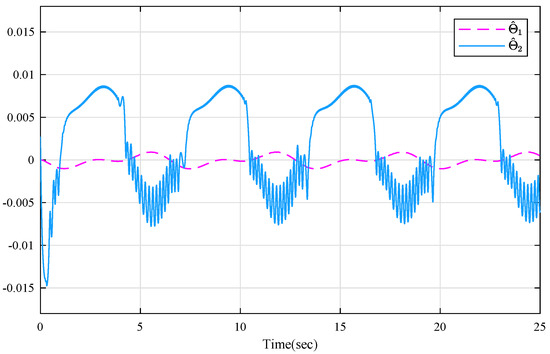
Figure 4.
Parameters estimation and .
Figure 5.
The interval of the triggered transmission.
Figure 6.
The number of the accumulated events.
5. Conclusions
An finite-time adaptive ETC scheme for FONSs with full-state constraints, uncertain parameters and external disturbances has been presented. By using the backstepping technology and a series of BLFs, the finite-time adaptive controller and parameter estimator are constructed. The dynamic event-triggered strategy is employed to overcome the limited communication resources. On the basis of the fractional-order Lyapunov analysis, all variables are bounded without the Zeno behavior and the tracking error converges to a small neighborhood around zero in finite time. The provided simulation results have further demonstrated the validity of the proposed control strategy. In the future, the controller design and stability analysis for nonlinear switching fractional order system controllers will be researched.
Author Contributions
Methodology, C.W.; Software, W.L.; Formal analysis, W.L.; Investigation, C.W. and W.L.; Resources, M.L.; Data curation, M.L.; Writing—original draft, C.W.; Writing—review and editing, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported in part by National Natural Science Foundation of China (62205280).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Debbouche, N.; Ouannas, A.; Batiha, I.M.; Grassi, G. Chaotic dynamics in a novel COVID-19 pandemic model described by commensurate and incommensurate fractional-order derivatives. Nonlinear Dyn. 2021, 109, 33–45. [Google Scholar] [CrossRef]
- Biala, T.A.; Khaliq, A. A fractional-order compartmental model for the spread of the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105764. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Shi, X.; Chen, X. Image Analysis by Fractional-Order Gaussian-Hermite Moments. IEEE Trans. Image Process. 2022, 31, 2488–2502. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Mou, J.; Xiong, L.; Wang, Z.; Xu, J. Fractional-order double-ring erbium-doped fiber laser chaotic system and its application on image encryption. Opt. Laser Technol. 2021, 140, 107074. [Google Scholar] [CrossRef]
- Soleimanizadeh, A.; Nekoui, M.A. Optimal type-2 fuzzy synchronization of two different fractional-order chaotic systems with variable orders with an application to secure communication. Soft Comput. 2021, 25, 6415–6426. [Google Scholar] [CrossRef]
- Li, R.G.; Wu, H.N. Adaptive synchronization control with optimization policy for fractional-order chaotic systems between 0 and 1 and its application in secret communication. ISA Trans. 2019, 92, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Jin, T.; Xia, H.; Deng, W.; Li, Y.; Chen, H. Uncertain fractional-order multi-objective optimization based on reliability analysis and application to fractional-order circuit with caputo type. Circuits Syst. Signal Process. 2021, 40, 5955–5982. [Google Scholar] [CrossRef]
- Wang, M.; Liao, X.; Deng, Y.; Li, Z.; Su, Y.; Zeng, Y. Dynamics, synchronization and circuit implementation of a simple fractional-order chaotic system with hidden attractors. Chaos Solitons Fractals 2020, 130, 109406. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Lam, B.D.; Choi, S.B. Smart dampers-based vibration control—Part 2: Fractional-order sliding control for vehicle suspension system. Mech. Syst. Signal Process. 2021, 148, 107145. [Google Scholar] [CrossRef]
- Chen, E.; Xing, W.; Wang, M.; Ma, W.; Chang, Y. Study on chaos of nonlinear suspension system with fractional-order derivative under random excitation. Chaos Solitons Fractals 2021, 152, 111300. [Google Scholar] [CrossRef]
- Fei, J.; Wang, H.; Fang, Y. Novel neural network fractional-order sliding-mode control with application to active power filter. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3508–3518. [Google Scholar] [CrossRef]
- Liu, H.; Li, S.; Wang, H.; Sun, Y. Adaptive fuzzy control for a class of unknown fractional-order neural networks subject to input nonlinearities and dead-zones. Inf. Sci. 2018, 454–455, 30–45. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X.; Zhang, Z. Adaptive Command Filtered Neuro-Fuzzy Control Design for Fractional-Order Nonlinear Systems with Unknown Control Directions and Input Quantization. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7238–7249. [Google Scholar] [CrossRef]
- Hu, T.; He, Z.; Zhang, X.; Zhong, S. Event-triggered consensus strategy for uncertain topological fractional-order multiagent systems based on Takagi–Sugeno fuzzy models. Inf. Sci. 2021, 551, 304–323. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Cao, J.; Wang, H.; Zhou, Y. Adaptive neural network backstepping control of fractional-order nonlinear systems with actuator faults. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5166–5177. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Tong, S. Adaptive fuzzy output-feedback decentralized control for fractional-order nonlinear large-scale systems. IEEE Trans. Cybern. 2021, 52, 12795–12804. [Google Scholar] [CrossRef]
- Mohammadi, S.; Hejazi, S.R. Using particle swarm optimization and genetic algorithms for optimal control of non-linear fractional-order chaotic system of cancer cells. Math. Comput. Simul. 2023, 206, 538–560. [Google Scholar] [CrossRef]
- Kiruthika, R.; Krishnasamy, R.; Lakshmanan, S.; Prakash, M.; Manivannan, A. Non-fragile sampled-data control for synchronization of chaotic fractional-order delayed neural networks via LMI approach. Chaos Solitons Fractals 2023, 169, 113252. [Google Scholar] [CrossRef]
- Sattar, D.; Braik, M.S. Metaheuristic methods to identify parameters and orders of fractional-order chaotic systems. Expert Syst. Appl. 2023, 228, 120426. [Google Scholar] [CrossRef]
- Biamou, A.L.M.; Tamba, V.K.; Tagne, F.K.; Takougang, A.C.N. Fractional-order-induced symmetric multi-scroll chaotic attractors and double bubble bifurcations in a memristive coupled Hopfield neural networks. Chaos Solitons Fractals 2024, 178, 114267. [Google Scholar] [CrossRef]
- Qi, J.; Cui, Q.; Bai, L.; Sun, Y. Investigating exact solutions, sensitivity, and chaotic behavior of multi-fractional order stochastic Davey–Sewartson equations for hydrodynamics research applications. Chaos Solitons Fractals 2024, 180, 114491. [Google Scholar] [CrossRef]
- Li, Y.X.; Wei, M.; Tong, S. Event-Triggered Adaptive Neural Control for Fractional-Order Nonlinear Systems Based on Finite-Time Scheme. IEEE Trans. Cybern. 2021, 52, 9481–9489. [Google Scholar] [CrossRef] [PubMed]
- Wang, C. Adaptive Terminal Sliding-Mode Synchronization Control with Chattering Elimination for a Fractional-Order Chaotic System. Fractal Fract. 2024, 8, 188. [Google Scholar] [CrossRef]
- Mseddi, A.; Abid, A.; Naifar, O.; Rhaima, M.; Ben Makhlouf, A.; Mchiri, L. Investigation of the Robust Fractional Order Control Approach Associated with the Online Analytic Unity Magnitude Shaper: The Case of Wind Energy Systems. Fractal Fract. 2024, 8, 187. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Gallegos, J.A. Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems. Fractal Fract. 2024, 8, 109. [Google Scholar] [CrossRef]
- Shahvali, M.; Azarbahram, A.; Naghibi-Sistani, M.B.; Askari, J. Bipartite consensus control for fractional-order nonlinear multi-agent systems: An output constraint approach. Neurocomputing 2020, 397, 212–223. [Google Scholar] [CrossRef]
- Zouari, F.; Ibeas, A.; Boulkroune, A.; Cao, J.; Arefi, M.M. Adaptive neural output-feedback control for nonstrict-feedback time-delay fractional-order systems with output constraints and actuator nonlinearities. Neural Netw. 2018, 105, 256–276. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Cui, L.; Liang, M.; Li, J.; Wang, Y. Adaptive Neural Network Control for a Class of Fractional-Order Nonstrict-Feedback Nonlinear Systems with Full-State Constraints and Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6677–6689. [Google Scholar] [CrossRef]
- Zouari, F.; Ibeas, A.; Boulkroune, A.; Jinde, C.; Arefi, M.M. Neural network controller design for fractional-order systems with input nonlinearities and asymmetric time-varying Pseudo-state constraints. Chaos Solitons Fractals 2021, 144, 110742. [Google Scholar] [CrossRef]
- Wang, H.; Bai, W.; Zhao, X.; Liu, P.X. Finite-Time-Prescribed Performance-Based Adaptive Fuzzy Control for Strict-Feedback Nonlinear Systems with Dynamic Uncertainty and Actuator Faults. IEEE Trans. Cybern. 2021, 52, 6959–6971. [Google Scholar] [CrossRef]
- Qi, W.; Hou, Y.; Zong, G.; Ahn, C.K. Finite-time event-triggered control for semi-Markovian switching cyber-physical systems with FDI attacks and applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2665–2674. [Google Scholar] [CrossRef]
- Li, Y.X.; Hou, Z.; Che, W.W.; Wu, Z.G. Event-based design of finite-time adaptive control of uncertain nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3804–3813. [Google Scholar] [CrossRef]
- Huong, D.C.; Thong, L.B.; Yen, D.T.H. Output feedback control and output feedback finite-time control for nonlinear fractional-order interconnected systems. Comput. Appl. Math. 2021, 40, 185. [Google Scholar] [CrossRef]
- Kavikumar, R.; Kwon, O.M.; Lee, S.H.; Sakthivel, R. Input-output finite-time IT2 fuzzy dynamic sliding mode control for fractional-order nonlinear systems. Nonlinear Dyn. 2022, 108, 3745–3760. [Google Scholar] [CrossRef]
- Dhanalakshmi, P.; Senpagam, S.; Mohanapriya, R. Finite-time fuzzy reliable controller design for fractional-order tumor system under chemotherapy. Fuzzy Sets Syst. 2022, 432, 168–181. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Shi, Z.; Gao, Z. Neural-Network-Based Finite-Time Bipartite Containment Control for Fractional-Order Multi-Agent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3804–3813. [Google Scholar] [CrossRef] [PubMed]
- You, X.; Dian, S.; Liu, K.; Guo, B.; Xiang, G.; Zhu, Y. Command Filter-Based Adaptive Fuzzy Finite-Time Tracking Control for Uncertain Fractional-Order Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2022, 31, 226–240. [Google Scholar] [CrossRef]
- Xue, G.; Lin, F.; Li, S.; Liu, H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf. Sci. 2022, 600, 189–208. [Google Scholar] [CrossRef]
- Wei, M.; Li, Y.X.; Tong, S. Event-triggered adaptive neural control of fractional-order nonlinear systems with full-state constraints. Neurocomputing 2020, 412, 320–326. [Google Scholar] [CrossRef]
- Zhao, D.; Li, Y.; Li, S.; Cao, Z.; Zhang, C. Distributed Event-Triggered Impulsive Tracking Control for Fractional-Order Multiagent Networks. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4544–4556. [Google Scholar] [CrossRef]
- Cao, B.; Nie, X. Event-triggered adaptive neural networks control for fractional-order nonstrict-feedback nonlinear systems with unmodeled dynamics and input saturation. Neural Netw. 2021, 142, 288–302. [Google Scholar] [CrossRef] [PubMed]
- Shahvali, M.; Naghibi-Sistani, M.B.; Askari, J. Dynamic Event-Triggered Control for a Class of Nonlinear Fractional-Order Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2131–2135. [Google Scholar] [CrossRef]
- You, X.; Shi, M.; Guo, B.; Zhu, Y.; Lai, W.; Dian, S.; Liu, K. Event-triggered adaptive fuzzy tracking control for a class of fractional-order uncertain nonlinear systems with external disturbance. Chaos Solitons Fractals 2022, 161, 112393. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, W.X.; Yu, W. Observer-Based Event-Triggered Adaptive Fuzzy Control for Fractional-Order Time-Varying Delayed MIMO Systems Against Actuator Faults. IEEE Trans. Fuzzy Syst. 2022, 30, 5445–5459. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999; p. 2. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Aguila Camacho, N.; Duarte Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Chen, W.; Dai, H.; Song, Y.; Zhang, Z. Convex Lyapunov functions for stability analysis of fractional order systems. IET Control Theory Appl. 2017, 11, 1070–1074. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive Neural Control for Output Feedback Nonlinear Systems Using a Barrier Lyapunov Function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov Functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Peng, X.; Wu, H.; Cao, J. Global Nonfragile Synchronization in Finite Time for Fractional-Order Discontinuous Neural Networks with Nonlinear Growth Activations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2123–2137. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).