The Four-Dimensional Natural Transform Adomian Decomposition Method and (3+1)-Dimensional Fractional Coupled Burgers’ Equation

Abstract

This research article introduces the four-dimensional natural transform Adomian decomposition method (FNADM) for solving the (3+1)-dimensional time-singular fractional coupled Burgers’ equation, along with its associated initial conditions. The FNADM approach represents a fusion of four-dimensional natural transform techniques and Adomian decomposition methodologies. In order to observe the influence of time-Caputo fractional derivatives on the outcomes of the aforementioned models, two examples are illustrated along with their three-dimensional figures. The effectiveness and reliability of this approach are validated through the analysis of these examples related to the (3+1)-dimensional time-singular fractional coupled Burgers’ equations. This study underscores the method’s applicability and effectiveness in addressing the complex mathematical models encountered in various scientific and engineering domains.

1. Introduction

The significance of fractional calculus in the realm of applied mathematics has become increasingly apparent, with fractional differential equations serving as indispensable tools in the modeling of real-world phenomena. These equations find application across diverse disciplines, including mathematical biology, various engineering fields, chemical processes, and applied sciences models. Furthermore, they have been extensively employed in various branches of physical science, notably in the realms of viscoelasticity control, diffusion, heat conduction, dynamical systems, and related areas [1,2,3,4,5,6,7].

Given its importance across multiple domains, a plethora of techniques have been devised to investigate both the computational and exact solutions associated with fractional differential equations. Over the past centuries, a multitude of definitions for fractional derivatives have been introduced. The following represents a select few of these definitions: Riemann–Liouville definition [8,9], Caputo [10], Caputo–Fabrizio [11], Riesz [12], Hilfer [13], Erdélyi–Kober [14], Atangana–Baleanu [15], and Grunwald–Letnikov [16]. Accordingly, to address these issues, numerous effective numerical and analytical approaches have been proposed, such as the homotopy analysis [17], residual power series [18], Lie symmetry groups [19], iterative reproducing kernels [20], approximate analytics [21], differential transform [22,23], variational iteration [24], homotopy perturbation transform [25], q-homotopy [26], operational matrices [27], meshless RBF [28], natural decomposition transform [29], and Adam–Bashforth–Moulton [30].

The construction of the natural transform decomposition method involved integrating two potent techniques: the natural transform and the Adomian decomposition methods. The natural transform decomposition method represents a novel and efficient approach to solving differential equations, which has been extensively studied in various papers [31,32,33,34]. This method is utilized to address the various physical phenomena modeled by fractional PDEs, as demonstrated in several research works. For instance, it has been applied to solve a coupled system of nonlinear PDEs [35], analyze the fractional unsteady flow of a polytropic gas model [36], investigate the solution of fractional telegraph equations [37], solve the fractional coupled KdV equation [38], find the solution of fractional-order heat and wave equations [39], and solve the fractional Klein-Gordon equation [40], and the double natural transform method with the Adomian decomposition method was used to solve a singular one-dimensional Boussinesq equation in [41].

The Burgers’ equation, introduced by Harry Bateman in 1915 [42], serves as a fundamental partial differential equation that is widely employed across various domains of applied mathematics to describe numerous physical phenomena. Initially proposed as the one-dimensional nonlinear Burgers’ equation of integral order, it was further investigated by Burger J.M., who explored its application as a coupled system of equations to model turbulent flow [43]. Subsequently, mathematicians and researchers have conducted numerous, significant, and intriguing studies on the Burgers’ equation. Over time, it has been recognized that this equation can effectively model phenomena, including shock waves, turbulence, aerodynamics, heat conduction, acoustic waves, and more [44,45,46].

In the literature, numerous techniques have been employed to study various forms of the Burgers’ equation for both integer order and time-fractional approaches. Additionally, various methods have been developed to derive both exact and approximate solutions for these equations. For example, numerical solutions for the one-dimensional Burgers’ equation have been investigated by Benton and Platzman [47]. In [48], the authors proposed a modified and expanded tanh-function method to obtain its exact solution. The homotopy perturbation method was suggested by researchers in [49] to achieve the exact solution of the nonlinear Burgers’ equation. Majeed et al. [50] numerically addressed the solution of one-dimensional time-fractional Burgers and Fishers equations using the cubic B-spline approximation method. In [51], Singh et al. analyzed a one-dimensional time-fractional model for the damped Burgers’ equation involving the Caputo-Fabrizio fractional derivative. Two different difference schemes were applied by Peng X. and Qiu W. et al. [52,53] to solve the mixed-type time-fractional Burger’s equation and the one-dimensional time-fractional Burger’s equation. The Laplace homotopy perturbation method was employed by the authors of [54] to solve the time-fractional Burgers’ equation. In [55], an explicit solution for the coupled viscous Burgers’ equation was provided using the Adomian decomposition method, while in [56], a combination of Laplace transform and new homotopy perturbation methods was utilized to derive closed-form solutions for the coupled Burgers’ equation. The solution of the time-fractional two-mode coupled Burgers’ equation was discussed in [57], and in [58], a multiple fractional power series approach was employed to analyze the solution of a system of nonlinear fractional Burgers’ equations.

For higher dimensions, in [59], a numerical solution for the two-dimensional Burgers’ equation is presented using the Adomian decomposition method. The Laplace decomposition method is employed by the authors in [60] to solve the two-dimensional nonlinear Burgers’ equations, while in [61], they explore the solution of the singular two-dimensional fractional coupled Burgers’ equation using the triple Laplace Adomian decomposition method. Additionally, in [62], the solution of the singular two-dimensional Burgers’ equation is introduced using the conformable triple Sumudu transform. On the other hand, the exact solutions for the cases of (3+1)-dimensional, two-dimensional-coupled, (2+1)-dimensional, and (1+1)-dimensional Burgers’ equations are presented in [63], and the numerical solution of the three-dimensional fractional coupled Burgers’ equation is discussed using various numerical methods in [64].

The goal of this study is to employ four-dimensional natural transform Adomian decomposition methods to solve the (3+1)-dimensional time-fractional coupled Burgers’ equation and evaluate the approximation solution. Our methodology integrates the four-dimensional natural transform and Adomian decomposition approaches, avoiding the linearization or discretization of variables, thus providing both approximate and accurate solutions. The structure of the paper is outlined as follows. Section 2 provides a concise overview of the basic definitions of natural transforms and the Caputo fractional derivative. In Section 3, we introduce the four-dimensional natural Adomian decomposition method (FNADM) for solving three-dimensional fractional coupled Burgers’ equations, accompanied by an illustrative example. Section 4 delves into the discussion of the four-dimensional natural Adomian decomposition method and the singular (3+1)-dimensional fractional coupled Burgers’ equation. Finally, Section 5 presents the succinct conclusions drawn from this study.

2. Basic Definitions of the Natural Transform Method

In this section, we address some of the definitions of fractional calculus using the natural transform method.

Definition 1

([31]). The natural transform of a function, $f\left(t\right)$, is defined by the integral

$$N^{+}\left[f\left(t\right)\right]=R\left(s;u\right)={\int }_0^{\infty }{e}^{-st}f\left(tu\right)dt,s>0,u>0,$$

(1)

where s and u are transform variables. Over the set of functions

$$A=\left\{\begin{array}{c}f\left(t\right):\exists M,{\tau }_1,{\tau }_2>0,\mathit{such}\mathit{that}\\ \left|f\left(t\right)\right|<M{e}^{\frac{\left|t\right|}{{\tau }_j}},\mathit{if}t\in {(-1)}^j\times [0,\infty ),j=1,2.\end{array}\right\}$$

the natural transform is defined by

$$N^{+}\left[f\left(t\right)\right]=R\left(s;u\right)=\frac{1}{u}{\int }_0^{\infty }{e}^{-\frac{s}{u}t}f\left(t\right)dt,Re\left(s\right),Re\left(u\right)>0,$$

(2)

where $Re\left(·\right)$ is the Reynolds number (see [65]).

Definition 2.

The inverse natural transform of $R\left(s;u\right)$ is defined by

$$N^{-1}\left[R\left(s;u\right)\right]=f\left(t\right)=\frac{1}{2\pi i}{\int }_{ϵ-i\infty }^{ϵ+i\infty }R\left(s;u\right)e^{\frac{st}{u}}ds,u>0s>0.$$

(3)

Definition 3

([18]). The Caputo time-fractional derivative operator of order $\gamma >0$ is given by

$$D_t^{\gamma }f(\zeta ,t)=\frac{{\partial }^{\gamma }f(\zeta ,t)}{\partial t^{\gamma }}=\left\{\begin{array}{cc}\frac{1}{\Gamma (n-\gamma )}{\int }_0^t{(t-x)}^{n-\gamma -1}\frac{{\partial }^{n}f(\zeta ,x)}{\partial x^n}dx& n-1<\gamma <n\\ \frac{{\partial }^{n}f(\zeta ,t)}{\partial t^n}& \gamma =n\in N\end{array}\right.$$

(4)

Definition 4

([37]). If $n\in N$, where $n-1<\gamma ⩽n$ and $R\left(s;u\right)$ is the natural transform of a function, $f\left(t\right)$, then the natural transform of the Caputo fractional derivative of $\frac{{\partial }^{\gamma }f(\zeta ,t)}{\partial t^{\gamma }}$ is given by

$$N^{+}\left[\frac{{\partial }^{\gamma }f(\zeta ,t)}{\partial t^{\gamma }}\right]=\frac{s^{\gamma }}{v^{\gamma }}R\left(s;u\right)-\sum _{k=0}^{n-1}\frac{s^{\gamma -(k+1)}}{v^{\gamma -k}}{\left[\frac{{\partial }^{k}f(\zeta ,t)}{\partial t^k}\right]}_{t=0}.$$

(5)

The four-dimensional natural transform, $N_4^{+}$, of a function, $f(x,y,z,t)$, and its inverse, $N_4^{-}$, are defined by the following:

Definition 5.

Let $f(x,y,z,t)$ be a continuous function of four variables, $x,y,z,t$. The four-dimensional natural transform of the function f is defined by

$$\begin{array}{ccc}\hfill N_4^{+}\left[f\left(x,y,z,t\right)\right]& =& \frac{1}{u_1{u}_2{u}_{3}v}{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\frac{p_1}{u_1}x-\frac{p_2}{u_2}y-\frac{p_3}{u_3}z-\frac{s}{v}t}f(x,y,z,t)dtdxdydz,\hfill \end{array}$$

where $Re\left(s\right),Re\left(p_i\right),Re\left(u_j\right),$ and $Re\left(v\right)>0,i,j=0,1,2.$ The four-dimensional inverse natural transform, $N_4^{-1}$, is given by

$$N_4^{-1}\left(N_4^{+}\left[f\right]\right)=\frac{1}{{\left(2\pi i\right)}^4}{\int }_{\alpha -i\infty }^{\alpha -i\infty }{\int }_{\beta -i\infty }^{\beta -i\infty }{\int }_{\gamma -i\infty }^{\gamma -i\infty }{\int }_{\delta -i\infty }^{\delta -i\infty }{e}^{\frac{p_1}{u_1}x+\frac{p_2}{u_2}y+\frac{p_3}{u_3}z+\frac{s}{v}t}{N}_4^{+}\left[f\right]dsd{p}_{1}d{p}_{2}d{p}_3,$$

where $N_4^{-1}\left(N_4^{+}\left[f\left(x,y,z,t\right)\right]\right)=f\left(x,y,z,t\right)$.

If the four-dimensional natural transform of the function $f(x,y,z,t)$ is given by

$$N_4^{+}\left[f\left(x,y,z,t\right)\right]=R\left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right),$$

then the four-dimensional natural transforms of $\frac{\partial f}{\partial x},$$\frac{\partial f}{\partial y},\frac{\partial f}{\partial z},$$\frac{\partial f}{\partial t}$ and $\frac{{\partial }^{2}f}{\partial t^2}$ are given by

$$\begin{array}{ccc}\hfill N_4^{+}\left[\frac{\partial f}{\partial x}\right]& =& \frac{p_1}{u_1}R\left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{1}{u_1}f\left(0,p_2,p_3,s;0,u_2,u_3,v\right),\hfill \\ \hfill N_4^{+}\left[\frac{\partial f}{\partial y}\right]& =& \frac{p_2}{u_2}R\left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{1}{u_2}f\left(p_1,0,p_3,s;u_1,0,u_3,v\right),\hfill \\ \hfill N_4^{+}\left[\frac{\partial f}{\partial z}\right]& =& \frac{p_3}{u_3}R\left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{1}{u_3}f\left(p_1,p_2,0,s;u_1,u_2,0,v\right),\hfill \end{array}$$

(6)

and

$$\begin{array}{ccc}\hfill N_4^{+}\left[\frac{\partial f}{\partial t}\right]& =& \frac{s}{v}R\left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{1}{v}f\left(p_1,p_2,p_3,0;u_1,u_2,u_3,0\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill N_4^{+}\left[\frac{{\partial }^{2}f}{\partial t^2}\right]& =& \frac{s^2}{v^2}R-\frac{s}{v^2}f\left(p_1,p_2,p_3,0;u_1,u_2,u_3,0\right)-\frac{1}{v}\frac{\partial f\left(p_1,p_2,p_3,0;u_1,u_2,u_3,0\right)}{\partial t},\hfill \end{array}$$

(8)

3. Analysis of the Four-Dimensional Natural Adomian Decomposition Method

In this work, we consider the following system of (3+1)-dimensional time-fractional coupled Burger’s equations to illustrate our method; we called this the four-dimensional natural Adomian decomposition method (FNADM):

$$\begin{array}{ccc}\hfill D_t^{\alpha }\Psi +\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z& =& \frac{1}{Re}\left({\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}\right)+\Psi ,x,y,z,t>0,\hfill \\ \hfill D_t^{\alpha }\varphi +\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z& =& \frac{1}{Re}\left({\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}\right)+\varphi ,x,y,z,t>0,\hfill \\ \hfill D_t^{\alpha }\chi +\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z& =& \frac{1}{Re}\left({\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}\right)+\chi ,x,y,z,t>0,\hfill \\ \hfill m-1& <& \alpha <m;\hfill \end{array}$$

(9)

with the initial conditions

$$\Psi (x,y,z,0)=f(x,y,z),\varphi (x,y,z,0)=g(x,y,z),\chi (x,y,z,0)=h(x,y,z),$$

where $D_t^{\alpha }=\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}$ is the fractional Caputo derivative, $\Psi (x,y,z,t),$ $\varphi (x,y,z,t)$ and $\chi (x,y,z,t)$ are the velocity components to be specified; $f,g$, and h are known functions, and $Re$ is the Reynolds number. It can be shown that the four-dimensional natural transform of the fractional Caputo derivative $D_t^{\alpha }=\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}$ is given by

$$\begin{array}{c}\hfill N_4^{+}\left[D_t^{\alpha }\omega (x,y,z,t)\right]=\frac{s^{\alpha }}{v^{\alpha }}\left(N_4^{+}\left[\omega (x,y,z,t))\right]-N_4^{+}\left[\omega (x,y,z,0))\right]\right)\end{array}$$

(10)

In order to achieve the goal of determining the solution to Equation (9), we apply the four-dimensional natural Adomian decomposition methods as follows:

• Step 1: By implementing the four-dimensional natural transform to Equation (9), we obtain

$$\begin{array}{ccc}\hfill \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\Psi (x,y,z,t)\right]& =& \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\Psi (x,y,z,0)\right]-N_4^{+}\left(\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z-\Psi \right)\hfill \\ & & +N_4^{+}\left(\frac{1}{Re}\left({\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}\right)\right),\hfill \\ \hfill \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\varphi (x,y,z,t)\right]& =& \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\varphi (x,y,z,0)\right]-N_4^{+}\left(\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z-\varphi \right)\hfill \\ & & +N_4^{+}\left(\frac{1}{Re}\left({\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}\right)\right),\hfill \\ \hfill \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\chi (x,y,z,t)\right]& =& \frac{s^{\alpha }}{v^{\alpha }}{N}_4^{+}\left[\chi (x,y,z,0)\right]-N_4^{+}\left(\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z-\chi \right)\hfill \\ & & +N_4^{+}\left(\frac{1}{Re}\left({\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}\right)\right).\hfill \end{array}$$

(11)

• Step 2: Now, by using the differentiation property of the natural transform, we have

$$\begin{array}{ccc}\hfill N_4^{+}\left[\Psi (x,y,z,t)\right]& =& N_4^{+}\left[\Psi (x,y,z,0)\right]-\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z-\Psi \right)\hfill \\ & & +\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}\right)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill N_4^{+}\left[\varphi (x,y,z,t)\right]& =& N_4^{+}\left[\varphi (x,y,z,0)\right]-\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z-\varphi \right)\hfill \\ & & +\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}\right)\right),\hfill \\ \hfill N_4^{+}\left[\chi (x,y,z,t)\right]& =& N_4^{+}\left[\chi (x,y,z,0)\right]-\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z-\chi \right)\hfill \\ & & +\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}\right)\right).\hfill \end{array}$$

(12)

• Step 3: By employing the inverse four-dimensional natural transform for Equation (12), we obtain

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& f(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z\right)-\Psi \right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}\right)\right)\right],\hfill \\ \hfill \varphi (x,y,z,t)& =& g(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z\right)-\varphi \right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}\right)\right)\right],\hfill \\ \hfill \chi (x,y,z,t)& =& h(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z-\chi \right)\right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}\right)\right)\right].\hfill \end{array}$$

(13)

• Step 4: The four-dimensional natural Adomian decomposition method assumes series solutions of the functions $\Psi (x,y,z,t)$, $\varphi (x,y,z,t)$, and $\chi (x,y,z,t)$, which are determined by

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& \sum _{n=0}^{\infty }{\Psi }_n(x,y,z,t),\varphi (x,y,z,t)=\sum _{n=0}^{\infty }{\varphi }_n(x,y,z,t),\hfill \\ \hfill \chi (x,y,z,t)& =& \sum _{n=0}^{\infty }{\chi }_n(x,y,z,t).\hfill \end{array}$$

(14)

Moreover, we supposed that the nonlinear terms $\Psi {\Psi }_x,$$\varphi {\Psi }_y,$$\chi {\Psi }_z$:$\Psi {\varphi }_x,$$\varphi {\varphi }_y,$$\chi {\varphi }_z$, $\Psi {\chi }_x,$$\varphi {\chi }_y,$ and $\chi {\chi }_z$ are defined by

$$\begin{array}{ccc}\hfill \Psi {\Psi }_x& =& \sum _{n=0}^{\infty }{A}_n,\varphi {\Psi }_y=\sum _{n=0}^{\infty }{B}_n,\chi {\Psi }_z=\sum _{n=0}^{\infty }{C}_n,\Psi {\varphi }_x=\sum _{n=0}^{\infty }{D}_n,\hfill \\ \hfill \varphi {\varphi }_y& =& \sum _{n=0}^{\infty }{E}_n,\chi {\varphi }_z=\sum _{n=0}^{\infty }{F}_n,\Psi {\chi }_x=\sum _{n=0}^{\infty }{G}_n,\varphi {\chi }_y=\sum _{n=0}^{\infty }{H}_n,\hfill \\ \hfill \chi {\chi }_z& =& \sum _{n=0}^{\infty }{K}_n,\hfill \end{array}$$

(15)

by substituting Equations (14) and (15) into Equation (13), we have

$$\begin{array}{ccc}\Psi (x,y,z,t)& =\hfill & f(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\displaystyle \sum _{n=0}^{\infty }}\left(A_n+B_n+C_n\right)-{\displaystyle \sum _{n=0}^{\infty }}{\Psi }_n\right)\right]\hfill \\ & +\hfill & N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\displaystyle \sum _{n=0}^{\infty }}\left({\Psi }_{nxx}+{\Psi }_{nyy}+{\Psi }_{nzz}\right)\right)\right)\right)={\displaystyle \sum _{n=0}^{\infty }}{\Psi }_n(x,y,z,t),\hfill \\ & \hfill & \hfill \end{array}$$

(16)

$$\begin{array}{ccc}\varphi (x,y,z,t)& =\hfill & g(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\displaystyle \sum _{n=0}^{\infty }}\left(D_n+E_n+F_n\right)-{\displaystyle \sum _{n=0}^{\infty }}{\varphi }_n\right)\right]\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\displaystyle \sum _{n=0}^{\infty }}\left({\varphi }_{nxx}+{\varphi }_{nyy}+{\varphi }_{nzz}\right)\right)\right)\right)={\displaystyle \sum _{n=0}^{\infty }}{\varphi }_n(x,y,z,t),\hfill \\ & \hfill & \hfill \end{array}$$

(17)

and

$$\begin{array}{ccc}\chi (x,y,z,t)& =\hfill & h(x,y,z)-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\displaystyle \sum _{n=0}^{\infty }}\left(G_n+H_n+K_n\right)-{\displaystyle \sum _{n=0}^{\infty }}{\chi }_n\right)\right]\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\displaystyle \sum _{n=0}^{\infty }}\left({\chi }_{nxx}+{\chi }_{nyy}+{\chi }_{nzz}\right)\right)\right)\right)={\displaystyle \sum _{n=0}^{\infty }}{\chi }_n(x,y,z,t).\hfill \\ & \hfill & \hfill \end{array}$$

(18)

• Step 5: After applying the four-dimensional natural Adomian decomposition method, we introduce the recursive relations as follows:

$$\begin{array}{ccc}\hfill {\Psi }_0(x,y,z,t)& =& f(x,y,z),{\varphi }_0(x,y,t)=g(x,y,z),\hfill \\ \hfill {\chi }_0(x,y,t)& =& h\left(x,y,z\right),\hfill \end{array}$$

(19)

and the remaining components ${\Psi }_{n+1},$${\varphi }_{n+1}$, and ${\chi }_{n+1},n\ge 0$ are given by

$$\begin{array}{ccc}\hfill {\Psi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(A_n+B_n+C_n-{\Psi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\Psi }_{nxx}+{\Psi }_{nyy}+{\Psi }_{nzz}\right)\right)\right),\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\varphi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(D_n+E_n+F_n-{\varphi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\varphi }_{nxx}+{\varphi }_{nyy}+{\varphi }_{nzz}\right)\right)\right),\hfill \end{array}$$

(21)

and

$$\begin{array}{ccc}\hfill {\chi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(G_n+H_n+K_n-{\chi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\frac{1}{Re}\left({\chi }_{nxx}+{\chi }_{nyy}+{\chi }_{nzz}\right)\right)\right).\hfill \end{array}$$

(22)

where the first few terms of the Adomian polynomials $A_n$, $B_n$, $C_n$, $D_n,E_n,F_n,G_n,H_n$, and $K_n$ are given by

$$\begin{array}{ccc}\hfill A_0& =& {\Psi }_0{\Psi }_{0x},A_1={\Psi }_0{\Psi }_{1x}+{\Psi }_1{\Psi }_{0x},\hfill \\ \hfill A_2& =& {\Psi }_0{\Psi }_{2x}+{\Psi }_1{\Psi }_{1x}+{\Psi }_2{\Psi }_{0x},\hfill \\ \hfill A_3& =& {\Psi }_0{\Psi }_{3x}+{\Psi }_1{\Psi }_{2x}+{\Psi }_2{\Psi }_{1x}+{\Psi }_3{\Psi }_{0x},\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill B_0& =& {\varphi }_0{\Psi }_{0y},B_1={\varphi }_0{\Psi }_{1y}+{\varphi }_1{\Psi }_{0y},\hfill \\ \hfill B_2& =& {\varphi }_0{\Psi }_{2y}+{\varphi }_1{\Psi }_{1y}+{\varphi }_2{\Psi }_{0y},\hfill \\ \hfill B_3& =& {\varphi }_0{\Psi }_{3y}+{\varphi }_1{\Psi }_{2y}+{\varphi }_2{\Psi }_{1y}+{\varphi }_3{\Psi }_{0y},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill C_0& =& {\chi }_0{\Psi }_{0z},C_1={\chi }_0{\Psi }_{1z}+{\chi }_1{\Psi }_{0z},\hfill \\ \hfill C_2& =& {\chi }_0{\Psi }_{2z}+{\chi }_1{\Psi }_{1z}+{\chi }_2{\Psi }_{0z},\hfill \\ \hfill C_3& =& {\chi }_0{\Psi }_{3z}+{\chi }_1{\Psi }_{2z}+{\chi }_2{\Psi }_{1z}+{\chi }_3{\Psi }_{0z}.\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill D_0& =& {\Psi }_0{\varphi }_{0x},D_1={\Psi }_0{\varphi }_{1x}+{\Psi }_1{\varphi }_{0x},\hfill \\ \hfill D_2& =& {\Psi }_0{\varphi }_{2x}+{\Psi }_1{\varphi }_{1x}+{\Psi }_2{\varphi }_{0x},\hfill \\ \hfill D_3& =& {\Psi }_0{\varphi }_{3x}+{\Psi }_1{\varphi }_{2x}+{\Psi }_2{\varphi }_{1x}+{\Psi }_3{\varphi }_{0x}.\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill E_0& =& {\varphi }_0{\varphi }_{0y},E_1={\varphi }_0{\varphi }_{1y}+{\varphi }_1{\varphi }_{0y},\hfill \\ \hfill E_2& =& {\varphi }_0{\varphi }_{2y}+{\varphi }_1{\varphi }_{1y}+{\varphi }_2{\varphi }_{0y},\hfill \\ \hfill E_3& =& {\varphi }_0{\varphi }_{3y}+{\varphi }_1{\varphi }_{2y}+{\varphi }_2{\varphi }_{1y}+{\varphi }_3{\varphi }_{0y}.\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill F_0& =& {\chi }_0{\varphi }_z,F_1={\chi }_0{\varphi }_{1z}+{\chi }_1{\varphi }_{0z},\hfill \\ \hfill F_2& =& {\chi }_0{\varphi }_{2z}+{\chi }_1{\varphi }_{1z}+{\chi }_2{\varphi }_{0z},\hfill \\ \hfill F_3& =& {\chi }_0{\varphi }_{3z}+{\chi }_1{\varphi }_{2z}+{\chi }_2{\varphi }_{1z}+{\chi }_3{\varphi }_{0z}.\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill G_0& =& {\Psi }_0{\chi }_{0x},G_1={\Psi }_0{\chi }_{1x}+{\Psi }_1{\chi }_{0x},\hfill \\ \hfill G_2& =& {\Psi }_0{\chi }_{2x}+{\Psi }_1{\chi }_{1x}+{\Psi }_2{\chi }_{0x},\hfill \\ \hfill G_3& =& {\Psi }_0{\chi }_{3x}+{\Psi }_1{\chi }_{2x}+{\Psi }_2{\chi }_{1x}+{\Psi }_3{\chi }_{0x}.\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill H_0& =& {\varphi }_0{\chi }_{0y},H_1={\varphi }_0{\chi }_{1y}+{\varphi }_1{\chi }_{0y},\hfill \\ \hfill H_2& =& {\varphi }_0{\chi }_{2y}+{\varphi }_1{\chi }_{1y}+{\varphi }_2{\chi }_{0y},\hfill \\ \hfill H_3& =& {\varphi }_0{\chi }_{3y}+{\varphi }_1{\chi }_{2y}+{\varphi }_2{\chi }_{1y}+{\varphi }_3{\chi }_{0y},\hfill \end{array}$$

(30)

and

$$\begin{array}{ccc}\hfill K_0& =& {\chi }_0{\chi }_z,K_1={\chi }_0{\chi }_{1z}+{\chi }_1{\chi }_{0z},\hfill \\ \hfill K_2& =& {\chi }_0{\chi }_{2z}+{\chi }_1{\chi }_{1z}+{\chi }_2{\chi }_{0z},\hfill \\ \hfill K_3& =& {\chi }_0{\chi }_{3z}+{\chi }_1{\chi }_{2z}+{\chi }_2{\chi }_{1z}+{\chi }_3{\chi }_{0z}.\hfill \end{array}$$

(31)

We show that the inverse four-dimensional natural transform with respect to $p_i,u_j,s,$ and $v,i,j=0,1,2,3$ exists for Equations (20)–(22).

For the purpose of explaining the four-dimensional natural Adomian decomposition method for solving the (3+1)-dimensional time-fractional coupled Burgers’ equation, we will consider the following example at $Re=1$:

Example 1.

Consider the (3+1)-dimensional time-fractional coupled Burgers’ equation

$$\begin{array}{ccc}\hfill D_t^{\alpha }\Psi +\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z& =& {\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}+\Psi ,x,y,z,t>0,\hfill \\ \hfill D_t^{\alpha }\varphi +\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z& =& {\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}+\varphi ,x,y,z,t>0,\hfill \\ \hfill D_t^{\alpha }\chi +\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z& =& {\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}+\chi ,x,y,z,t>0,\hfill \\ \hfill n-1<& \alpha & <n.\hfill \end{array}$$

(32)

with the initial conditions

$$\Psi (x,y,z,0)=2x-y-z,\varphi (x,y,z,0)=2x-y-z,\chi (x,y,z,0)=2x-y-z.$$

As mentioned in the above steps, we obtain

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& 2x-y-z-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\Psi }_x+\varphi {\Psi }_y+\chi {\Psi }_z-\Psi \right)\right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_{xx}+{\Psi }_{yy}+{\Psi }_{zz}\right)\right],\hfill \\ \hfill \varphi (x,y,z,t)& =& 2x-y-z-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\varphi }_x+\varphi {\varphi }_y+\chi {\varphi }_z-\varphi \right)\right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\varphi }_{xx}+{\varphi }_{yy}+{\varphi }_{zz}\right)\right],\hfill \\ \hfill \chi (x,y,z,t)& =& 2x-y-z-N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\Psi {\chi }_x+\varphi {\chi }_y+\chi {\chi }_z-\chi \right)\right]\hfill \\ & & +N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_{xx}+{\chi }_{yy}+{\chi }_{zz}\right)\right].\hfill \end{array}$$

(33)

The zeroth components ${\Psi }_0,{\varphi }_0$, and ${\chi }_0$ are determined by the method to be the same as the initial conditions, so we have

$${\Psi }_0=2x-y-z,{\varphi }_0=2x-y-z,{\chi }_0=2x-y-z.$$

The remaining components ${\Psi }_{n+1}$, ${\varphi }_{n+1},{\chi }_{n+1},$$n\ge 0$ are given by

$$\begin{array}{ccc}\hfill {\Psi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(A_n+B_n+C_n-{\Psi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_{nxx}+{\Psi }_{nyy}+{\Psi }_{nzz}\right)\right),\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\varphi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(D_n+E_n+F_n-{\varphi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\varphi }_{nxx}+{\varphi }_{nyy}+{\varphi }_{nzz}\right)\right),\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\chi }_{n+1}(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(G_n+H_n+K_n-{\chi }_n\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_{nxx}+{\chi }_{nyy}+{\chi }_{nzz}\right)\right),\hfill \end{array}$$

(36)

by substituting $n=0$ into Equations (34)–(36), we obtain

$$\begin{array}{ccc}\hfill {\Psi }_1(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(A_0+B_0+C_0-{\Psi }_0\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_{0xx}+{\Psi }_{0yy}+{\Psi }_{0zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(2x-y-z\right)\right]=\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill {\varphi }_1(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(D_0+E_0+F_0-{\varphi }_0\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\varphi }_{0xx}+{\varphi }_{0yy}+{\varphi }_{0zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(2x-y-z\right)\right]=\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)},\hfill \end{array}$$

(38)

and

$$\begin{array}{ccc}\hfill {\chi }_1(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(G_0+H_0+K_0-{\chi }_0\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_{0xx}+{\chi }_{0yy}+{\chi }_{0zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(2x-y-z\right)\right]=\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}.\hfill \end{array}$$

(39)

Similarly, when $n=1,$ we have

$$\begin{array}{ccc}\hfill {\Psi }_2(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_0{\Psi }_{1x}+{\Psi }_1{\Psi }_{0x}+{\varphi }_0{\Psi }_{1y}+{\varphi }_1{\Psi }_{0y}\right)\right]\hfill \\ & & -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_0{\Psi }_{1z}+{\chi }_1{\Psi }_{0z}-{\Psi }_1\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_{1xx}+{\Psi }_{1yy}+{\Psi }_{1zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\right)\right]\hfill \\ & =& \left(2x-y-z\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\varphi }_2(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_0{\varphi }_{1x}+{\Psi }_1{\varphi }_{0x}+{\varphi }_0{\varphi }_{1y}+{\varphi }_1{\varphi }_{0y}\right)\right]\hfill \\ & & -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_0{\varphi }_{1z}+{\chi }_1{\varphi }_{0z}-{\varphi }_1\right)\right]\hfill \\ & & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\varphi }_{1xx}+{\varphi }_{1yy}+{\varphi }_{1zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\right)\right]\hfill \\ & =& \left(2x-y-z\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\chi }_2(x,y,z,t)& =& -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\Psi }_0{\chi }_{1x}+{\Psi }_1{\chi }_{0x}+{\varphi }_0{\chi }_{1y}+{\varphi }_1{\chi }_{0y}\right)\right]\hfill \\ & & -N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_0{\chi }_{1z}+{\chi }_1{\chi }_{0z}-{\chi }_1\right)\right]\hfill \\ & +& N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left({\chi }_{1xx}+{\chi }_{1yy}+{\chi }_{1zz}\right)\right)\hfill \\ & =& N_4^{-1}\left[\frac{v^{\alpha }}{s^{\alpha }}{N}_4^{+}\left(\left(2x-y-z\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\right)\right]\hfill \\ & =& \left(2x-y-z\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}.\hfill \end{array}$$

At $n=2,$ we obtain

$${\Psi }_3=\left(2x-y-z\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)},$$

$${\varphi }_3=\left(2x-y-z\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)},$$

$${\chi }_3=\left(2x-y-z\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}.$$

Therefore, the solution to Equation (32) is defined as

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& \sum _{n=0}^{\infty }{\Psi }_n={\Psi }_0+{\Psi }_1+{\Psi }_2+{\Psi }_3+\dots \dots \hfill \\ \hfill \Psi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots ,\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill \varphi (x,y,z,t)& =& \sum _{n=0}^{\infty }{\varphi }_n={\varphi }_0+{\varphi }_1+{\varphi }_2+{\varphi }_3+\dots \dots \hfill \\ \hfill \varphi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots ,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \chi (x,y,z,t)& =& \sum _{n=0}^{\infty }{\chi }_n={\chi }_0+{\chi }_1+{\chi }_2+{\chi }_3+\dots \dots \hfill \\ \hfill \chi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{\left(2x-y-z\right)t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots ,\hfill \end{array}$$

at $\alpha =1$, the solution of the above equation becomes

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t}{1!}+\frac{\left(2x-y-z\right)t^2}{2!}+\frac{\left(2x-y-z\right)t^3}{3!}+\dots ,\hfill \\ & =& \left(2x-y-z\right)e^t\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \varphi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t}{1!}+\frac{\left(2x-y-z\right)t^2}{2!}+\frac{\left(2x-y-z\right)t^3}{3!}+\dots \hfill \\ & =& \left(2x-y-z\right)e^t\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \chi (x,y,z,t)& =& \left(2x-y-z\right)+\frac{\left(2x-y-z\right)t}{1!}+\frac{\left(2x-y-z\right)t^2}{2!}+\frac{\left(2x-y-z\right)t^3}{3!}+\dots \hfill \\ & =& \left(2x-y-z\right)e^t.\hfill \end{array}$$

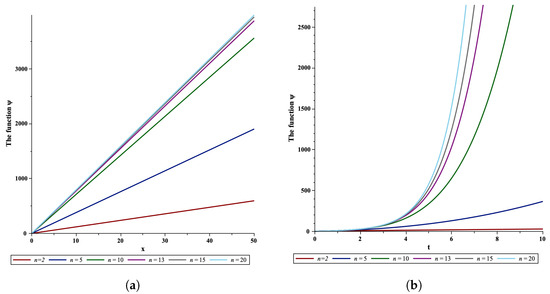
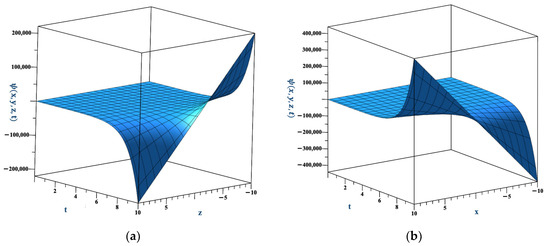
For $0<\alpha <1$, by using the ratio test and Gautschi’s inequality, it can be proven that the series is absolutely convergent. In order to illustrate the convergence, let us consider, for example, $z=y=0$ and $\alpha =0.5$. Figure 1a,b depict the convergence of the series representing the function $\Psi (x,y,z,t)$ with respect to x at $t=3$ and with respect to t at $x=1$, respectively, showing rapid convergence to the exact solution after a few terms. In order to display the three-dimensional demonstration for the results of Example 1, we take different values of the variables to show the exact solution of $\Psi (x,y,z,t)$. Figure 2a,b show $\Psi (x,y,z,t)$ at $\alpha =1$ with $y=0$ and $x=0,z=0$, respectively. The illustrations were generated using the Maple software 2023.0.

Figure 1. (a) The convergence of the series representing $\Psi$ with respect to x at $\alpha =0.5$. (b) The convergence of the series representing $\Psi$ with respect to t at $\alpha =0.5$.

Figure 2. (a) The function $\Psi (x,y,z,t)$ at $x=0,y=0$. (b) The function $\Psi (x,y,z,t)$ at $z=0,y=0$.

4. Four-Dimensional Natural Adomian Decomposition Method and Singular (3+1)-Dimensional Fractional Coupled Burgers’ Equation

In order to explain the basic idea of the four-dimensional natural Adomian decomposition method, we consider a general singular (3+1)-dimensional time-fractional coupled Burgers’ equation of the form

$$\begin{array}{ccc}\hfill D_t^{\alpha }\Psi & =& \frac{1}{x}{\left(x{\Psi }_x\right)}_x+\frac{1}{y}{\left(y{\Psi }_y\right)}_y+\frac{1}{z}{\left(z{\Psi }_z\right)}_z-\frac{1}{x}\Psi {\Psi }_x-\frac{1}{y}\varphi {\Psi }_y-\frac{1}{z}\chi {\Psi }_z+\Psi \hfill \\ \hfill D_t^{\alpha }\varphi & =& \frac{1}{x}{\left(x{\varphi }_x\right)}_x+\frac{1}{y}{\left(y{\varphi }_y\right)}_y+\frac{1}{z}{\left(z{\varphi }_z\right)}_z-\frac{1}{x}\Psi {\varphi }_x-\frac{1}{y}\varphi {\varphi }_y-\frac{1}{z}\chi {\varphi }_z+\varphi \hfill \\ \hfill D_t^{\alpha }\chi & =& \frac{1}{x}{\left(x{\chi }_x\right)}_x+\frac{1}{y}{\left(y{\chi }_y\right)}_y+\frac{1}{z}{\left(z{\chi }_z\right)}_z-\frac{1}{x}\Psi {\chi }_x-\frac{1}{y}\varphi {\chi }_y-\frac{1}{z}\chi {\chi }_z+\chi \hfill \\ \hfill x,y,t& >& 0,\hfill \end{array}$$

(41)

with the initial conditions

$$\Psi (x,y,z,0)=f(x,y,z),\varphi (x,y,z,0)=g(x,y,z),\chi (x,y,z,0)=h(x,y,z),$$

where $D_t^{\alpha }=\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}$ is the fractional Caputo derivative. $\frac{1}{x}{\left(x{\Psi }_x\right)}_x$, $\frac{1}{y}{\left(y{\Psi }_y\right)}_y$, and $\frac{1}{z}{\left(z{\chi }_z\right)}_z$ are called Bessel operators, and $\Psi (x,y,z,t),\varphi (x,y,z,t)$, and $\chi \left(x,y,z,t\right)$ are the velocity components. $f(x,y,z),$$g(x,y,z)$, and $h(x,y,z)$ are known functions. Let $N_4^{+}\left[\Psi (x,y,z,t)\right]=\Psi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)$ and $N_4^{+}\left[\Psi (x,y,z,0)\right]=\Psi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)$, and similarly for the functions $\varphi$ and $\chi$. In order to obtain the solution of Equation (41), we will employ the following steps.

• Step 1: Multiply both sides of Equation (41) by $xyz$ to obtain

$$\begin{array}{ccc}xyz{D}_t^{\alpha }\Psi & =\hfill & yz{\left(x{\Psi }_x\right)}_x+xz{\left(y{\Psi }_y\right)}_y+xy{\left(z{\Psi }_z\right)}_z-yz\Psi {\Psi }_x-xz\varphi {\Psi }_y-xy\chi {\Psi }_z+xyz\Psi \hfill \\ xyz{D}_t^{\alpha }\varphi & =\hfill & yz{\left(x{\varphi }_x\right)}_x+xz{\left(y{\varphi }_y\right)}_y+xy{\left(z{\varphi }_z\right)}_z-yz\Psi {\varphi }_x-xz\varphi {\varphi }_y-xy\chi {\varphi }_z+xyz\varphi \hfill \\ xyz{D}_t^{\alpha }\chi & =\hfill & yz{\left(x{\chi }_x\right)}_x+xz{\left(y{\chi }_y\right)}_y+xy{\left(z{\chi }_z\right)}_z-yz\Psi {\chi }_x-xz\varphi {\chi }_y-xy\chi {\chi }_z+xyz\chi .\hfill \end{array}$$

(42)

• Step 2: Operating the four-dimensional natural transform for both sides of Equation (42) yields

$$\begin{array}{c}\frac{{\left(-1\right)}^3{u}_1{u}_2{u}_3{\partial }^3}{\partial p_1\partial p_2\partial p_3}\left(\frac{s^{\alpha }}{v^{\alpha }}\Psi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{s^{\alpha }}{v^{\alpha }}\Psi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\right)=N_4^{+}\left(\Delta \right)\end{array}$$

(43)

$$\begin{array}{c}\frac{{\left(-1\right)}^3{u}_1{u}_2{u}_3{\partial }^3}{\partial p_1\partial p_2\partial p_3}\left(\frac{s^{\alpha }}{v^{\alpha }}\Phi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{s^{\alpha }}{v^{\alpha }}\Phi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\right)=N_4^{+}\left(\Lambda \right)\end{array}$$

(44)

$$\begin{array}{c}\frac{{\left(-1\right)}^3{u}_1{u}_2{u}_3{\partial }^3}{\partial p_1\partial p_2\partial p_3}\left(\frac{s^{\alpha }}{v^{\alpha }}\Pi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)-\frac{s^{\alpha }}{v^{\alpha }}\Pi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\right)=N_4^{+}\left({\rm Y}\right),\end{array}$$

(45)

where

$$\begin{array}{ccc}\hfill \Delta & =& yz{\left(x{\Psi }_x\right)}_x+xz{\left(y{\Psi }_y\right)}_y+xy{\left(z{\Psi }_z\right)}_z-yz\Psi {\Psi }_x-xz\varphi {\Psi }_y-xy\chi {\Psi }_z+xyz\Psi \hfill \\ \hfill \Lambda & =& yz{\left(x{\varphi }_x\right)}_x+xz{\left(y{\varphi }_y\right)}_y+xy{\left(z{\varphi }_z\right)}_z-yz\Psi {\varphi }_x-xz\varphi {\varphi }_y-xy\chi {\varphi }_z+xyz\varphi \hfill \end{array}$$

and

$${\rm Y}=yz{\left(x{\chi }_x\right)}_x+xz{\left(y{\chi }_y\right)}_y+xy{\left(z{\chi }_z\right)}_z-yz\Psi {\chi }_x-xz\varphi {\chi }_y-xy\chi {\chi }_z+xyz\chi .$$

Hence, we have

$$\begin{array}{ccc}\hfill \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Psi & =& \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Psi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)-\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}{N}_4^{+}\left(\Delta \right)\hfill \\ \hfill \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Phi & =& \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Phi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)-\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}{N}_4^{+}\left(\Lambda \right)\hfill \\ \hfill \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Pi & =& \frac{{\partial }^3}{\partial p_1\partial p_2\partial p_3}\Pi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)-\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}{N}_4^{+}\left({\rm Y}\right).\hfill \end{array}$$

(46)

• Step 3: By integrating both sides of Equation (46) from 0 to $p_1,0$ to $p_2$ and 0 to $p_3$ with respect to $p_1,p_2$, and $p_3$, respectively, we have

$$\begin{array}{ccc}\hfill \Psi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)& =& \Psi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\hfill \\ & & -\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\Delta \right)d{p}_{1}d{p}_{2}d{p}_3\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill \Phi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)& =& \Phi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\hfill \\ & & -\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\Lambda \right)d{p}_{1}d{p}_{2}d{p}_3\hfill \end{array}$$

(48)

and

$$\begin{array}{ccc}\hfill \Pi \left(p_1,p_2,p_3,s;u_1,u_2,u_3,v\right)& =& \Pi \left(p_1,p_2,p_3;u_1,u_2,u_3\right)\hfill \\ & & -\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left({\rm Y}\right)d{p}_{1}d{p}_{2}d{p}_3.\hfill \end{array}$$

(49)

• Step 4: By applying the inverse four-dimensional natural transform to Equations (47)–(49), we obtain

$$\begin{array}{ccc}\hfill \Psi \left(x,y,z,t\right)& =& f(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\Delta \right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill \varphi \left(x,y,z,t\right)& =& g(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\Lambda \right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \end{array}$$

(51)

and

$$\begin{array}{ccc}\hfill \chi \left(x,y,z,t\right)& =& h(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left({\rm Y}\right)d{p}_{1}d{p}_{2}d{p}_3\right).\hfill \end{array}$$

(52)

• Step 5: By substituting Equations (14) and (15) into Equations (50) and (52), we obtain

$$\Psi (x,y,z,t)=\sum _{n=0}^{\infty }{\Psi }_n(x,y,z,t)=f(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\sum _{n=0}^{\infty }{\Delta }_n\right)d{p}_{1}d{p}_{2}d{p}_3\right)$$

(53)

$$\varphi (x,y,z,t)=\sum _{n=0}^{\infty }{\varphi }_n(x,y,z,t)=g(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\sum _{n=0}^{\infty }{\Lambda }_n\right)d{p}_{1}d{p}_{2}d{p}_3\right)$$

(54)

and

$$\chi (x,y,z,t)=\sum _{n=0}^{\infty }{\chi }_n(x,y,z,t)=h(x,y,z)-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(\sum _{n=0}^{\infty }{{\rm Y}}_n\right)d{p}_{1}d{p}_{2}d{p}_3\right).$$

(55)

• Step 6: After applying the four-dimensional natural Adomian decomposition method, we introduce the recursive relations as follows:

$$\begin{array}{ccc}\hfill {\Psi }_0(x,y,z,t)& =& f(x,y,z),{\varphi }_0(x,y,t)=g(x,y,z)\hfill \\ \hfill {\chi }_0(x,y,t)& =& h(x,y,z),\hfill \end{array}$$

(56)

The remaining components, ${\Psi }_{n+1},{\varphi }_{n+1}$, and ${\chi }_{n+1},n>0$, are given by

$$\begin{array}{ccc}{\Psi }_{n+1}(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\Psi }_{nx}\right)}_x+xz{\left(y{\Psi }_{ny}\right)}_y+xy{\left(z{\Psi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{A}_n+xz{B}_n+xy{C}_n-xyz{\Psi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right),\hfill \\ & \hfill & \hfill \end{array}$$

(57)

$$\begin{array}{ccc}{\varphi }_{n+1}(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\varphi }_{nx}\right)}_x+xz{\left(y{\varphi }_{ny}\right)}_y+xy{\left(z{\varphi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{D}_n+xz{E}_n+xy{F}_n-xyz{\varphi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right),\hfill \\ & \hfill & \hfill \end{array}$$

(58)

and

$$\begin{array}{ccc}{\chi }_{n+1}(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\chi }_{nx}\right)}_x+xz{\left(y{\chi }_{ny}\right)}_y+xy{\left(z{\chi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{G}_n+xz{H}_n+xy{K}_n-xyz{\chi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right).\hfill \\ & \hfill & \hfill \end{array}$$

(59)

We show that four inverse natural transforms with respect to $p_1,p_2,p_3,s;u_1,u_2,u_3,v$ exist for Equations (57)–(59). In the following example, we apply the four-dimensional natural Adomian decomposition method to solve the singular (3+1)-dimensional time-fractional coupled Burgers’ equation.

Example 2.

We consider the singular (3+1)-dimensional time-fractional coupled Burgers’ equations, given by

$$\begin{array}{ccc}\hfill D_t^{\alpha }\Psi & =& \frac{1}{x}{\left(x{\Psi }_x\right)}_x+\frac{1}{y}{\left(y{\Psi }_y\right)}_y+\frac{1}{z}{\left(z{\Psi }_z\right)}_z-\frac{1}{x}\Psi {\Psi }_x-\frac{1}{y}\varphi {\Psi }_y-\frac{1}{z}\chi {\Psi }_z+\Psi \hfill \\ \hfill D_t^{\alpha }\varphi & =& \frac{1}{x}{\left(x{\varphi }_x\right)}_x+\frac{1}{y}{\left(y{\varphi }_y\right)}_y+\frac{1}{z}{\left(z{\varphi }_z\right)}_z-\frac{1}{x}\Psi {\varphi }_x-\frac{1}{y}\varphi {\varphi }_y-\frac{1}{z}\chi {\varphi }_z+\varphi \hfill \\ \hfill D_t^{\alpha }\chi & =& \frac{1}{x}{\left(x{\chi }_x\right)}_x+\frac{1}{y}{\left(y{\chi }_y\right)}_y+\frac{1}{z}{\left(z{\chi }_z\right)}_z-\frac{1}{x}\Psi {\chi }_x-\frac{1}{y}\varphi {\chi }_y-\frac{1}{z}\chi {\chi }_z+\chi ,\hfill \\ \hfill x,y,t& >& 0,\hfill \end{array}$$

(60)

subject to the initial conditions

$$\begin{array}{ccc}\hfill \Psi (x,y,z,0)& =& 2x^2-y^2-z^2,\varphi (x,y,z,0)=2x^2-y^2-z^2,\hfill \\ \hfill \chi (x,y,z,0)& =& 2x^2-y^2-z^2.\hfill \end{array}$$

By following the steps outlined above, we have

$$\begin{array}{ccc}\Psi \left(x,y,t\right)& =\hfill & 2x^2-y^2-z^2-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\Psi }_x\right)}_x+xz{\left(y{\Psi }_y\right)}_y+xy{\left(z{\Psi }_z\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & +\hfill & N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz\Psi {\Psi }_x+xz\varphi {\Psi }_y+xy\chi {\Psi }_z-xyz\Psi \right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & \hfill \end{array}$$

(61)

and

$$\begin{array}{ccc}\varphi \left(x,y,z,t\right)& =\hfill & 2x^2-y^2-z^2-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\varphi }_x\right)}_x+xz{\left(y{\varphi }_y\right)}_y+xy{\left(z{\varphi }_z\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz\Psi {\varphi }_x-xz\varphi {\varphi }_y-xy\chi {\varphi }_z-xyz\varphi \right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & \hfill \end{array}$$

(62)

$$\begin{array}{ccc}\chi \left(x,y,t\right)& =\hfill & 2x^2-y^2-z^2-N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\chi }_x\right)}_x+xz{\left(y{\chi }_y\right)}_y+xy{\left(z{\chi }_z\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz\Psi {\chi }_x-xz\varphi {\chi }_y-xy\chi {\chi }_z-xyz\chi \right)\right)d{p}_{1}d{p}_{2}d{p}_3\right).\hfill \\ & \hfill & \hfill \end{array}$$

(63)

By applying Equations (56)–(59), we obtain

$$\begin{array}{ccc}\hfill {\Psi }_0(x,y,z,t)& =& 2x^2-y^2-z^2,{\varphi }_0(x,y,z,t)=2x^2-y^2-z^2,\hfill \\ \hfill {\chi }_0(x,y,z,t)& =& 2x^2-y^2-z^2,\hfill \end{array}$$

(64)

and the remaining components, ${\Psi }_{n+1},{\varphi }_{n+1}$, and ${\chi }_{n+1},n>0$, are given by

$$\begin{array}{ccc}{\Psi }_{n+1}(x,y,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\Psi }_{nx}\right)}_x+xz{\left(y{\Psi }_{ny}\right)}_y+xy{\left(z{\Psi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{A}_n+xz{B}_n+xy{C}_n-xyz{\Psi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right),\hfill \end{array}$$

(65)

$$\begin{array}{ccc}{\varphi }_{n+1}(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\varphi }_{nx}\right)}_x+xz{\left(y{\varphi }_{ny}\right)}_y+xy{\left(z{\varphi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{D}_n+xz{E}_n+xy{F}_n-xyz{\varphi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right),\hfill \\ & \hfill & \hfill \end{array}$$

(66)

and

$$\begin{array}{ccc}{\chi }_{n+1}(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\chi }_{nx}\right)}_x+xz{\left(y{\chi }_{ny}\right)}_y+xy{\left(z{\chi }_{nz}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{G}_n+xz{H}_n+xy{K}_n-xyz{\chi }_n\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right).\hfill \\ & \hfill & \hfill \end{array}$$

(67)

where the first few terms of the Adomian polynomials, $A_n$, $B_n,C_n,D_n,E_n,F_n,G_n,H_n$, and $K_n$, are given by Equations (23)–(31), respectively. By substituting $n=0$ into Equations (65)–(67), we obtain

$$\begin{array}{ccc}{\Psi }_1(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\Psi }_{0x}\right)}_x+xz{\left(y{\Psi }_{0y}\right)}_y+xy{\left(z{\Psi }_{0z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{A}_0+xz{B}_0+xy{C}_0-xyz{\Psi }_0\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\Psi }_1(x,y,z,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}.\hfill \end{array}$$

(68)

$$\begin{array}{ccc}{\varphi }_1(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\varphi }_{0x}\right)}_x+xz{\left(y{\varphi }_{0y}\right)}_y+xy{\left(z{\varphi }_{0z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{D}_0+xz{E}_0+xy{F}_0-xyz{\varphi }_0\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\varphi }_1(x,y,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}.\hfill \end{array}$$

(69)

and

$$\begin{array}{ccc}{\chi }_1(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\chi }_{0x}\right)}_x+xz{\left(y{\chi }_{0y}\right)}_y+xy{\left(z{\chi }_{0z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & +\hfill & N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{G}_0+xz{H}_0+xy{K}_0-xyz{\chi }_0\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\chi }_1(x,y,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}.\hfill \end{array}$$

(70)

Similarly, at $n=1$, we obtain

$$\begin{array}{ccc}{\Psi }_2(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\Psi }_{1x}\right)}_x+xz{\left(y{\Psi }_{1y}\right)}_y+xy{\left(z{\Psi }_{1z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & +\hfill & N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{A}_1+xz{B}_1+xy{C}_1-xyz{\Psi }_1\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\Psi }_2(x,y,z,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)},\hfill \end{array}$$

(71)

$$\begin{array}{ccc}{\varphi }_2(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\varphi }_{1x}\right)}_x+xz{\left(y{\varphi }_{1y}\right)}_y+xy{\left(z{\varphi }_{1z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{D}_1+xz{E}_1+xy{F}_1-xyz{\varphi }_1\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\varphi }_2(x,y,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)},\hfill \end{array}$$

(72)

and

$$\begin{array}{ccc}{\chi }_2(x,y,z,t)& =\hfill & -N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}{N}_4^{+}\left(yz{\left(x{\chi }_{1x}\right)}_x+xz{\left(y{\chi }_{1y}\right)}_y+xy{\left(z{\chi }_{1z}\right)}_z\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ & \hfill & +N_4^{-1}\left(\frac{v^{\alpha }}{s^{\alpha }{u}_1{u}_2{u}_3}\underset{0}{\overset{p_1}{\int }}\underset{0}{\overset{p_2}{\int }}\underset{0}{\overset{p_3}{\int }}\left(N_4^{+}\left(yz{G}_1+xz{H}_1+xy{K}_1-xyz{\chi }_1\right)\right)d{p}_{1}d{p}_{2}d{p}_3\right)\hfill \\ {\chi }_2(x,y,t)& =\hfill & \left(2x^2-y^2-z^2\right)\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}.\hfill \end{array}$$

(73)

At $n=2$

$${\Psi }_3(x,y,z,t)=\left(2x^2-y^2-z^2\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)},$$

$${\varphi }_3(x,y,t)=\left(2x^2-y^2-z^2\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)},$$

and

$${\chi }_3(x,y,t)=\left(2x^2-y^2-z^2\right)\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}.$$

At $n=3,$ we have

$${\Psi }_4(x,y,z,t)=\left(2x^2-y^2-z^2\right)\frac{t^{4\alpha }}{\Gamma \left(4\alpha +1\right)},$$

$${\varphi }_4(x,y,t)=\left(2x^2-y^2-z^2\right)\frac{t^{4\alpha }}{\Gamma \left(4\alpha +1\right)},$$

and

$${\chi }_4(x,y,t)=\left(2x^2-y^2-z^2\right)\frac{t^{4\alpha }}{\Gamma \left(4\alpha +1\right)}.$$

The solution to Equation (60) is given by

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& {\Psi }_0+{\Psi }_1+{\Psi }_2+\dots +{\Psi }_n+\dots ,\hfill \\ \hfill \varphi (x,y,z,t)& =& {\varphi }_0+{\varphi }_1+{\varphi }_2+\dots +{\varphi }_n+\dots ,\hfill \\ \hfill \chi (x,y,z,t)& =& {\chi }_0+{\chi }_1+{\chi }_2+\dots +{\chi }_n+\dots \dots \hfill \end{array}$$

Hence, the solution is given by

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& \left(2x^2-y^2-z^2\right)\left(1+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots \right),\hfill \\ \hfill \varphi (x,y,z,t)& =& \left(2x^2-y^2-z^2\right)\left(1+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots \right),\hfill \\ \hfill \chi (x,y,z,t)& =& \left(2x^2-y^2-z^2\right)\left(1+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}+\frac{t^{2\alpha }}{\Gamma \left(2\alpha +1\right)}+\frac{t^{3\alpha }}{\Gamma \left(3\alpha +1\right)}+\dots \right).\hfill \end{array}$$

(74)

When $\alpha =1$ is substituted into Equation (60), we obtain the solution to the singular (3+1)-dimensional time-fractional coupled Burgers’ equation

$$\begin{array}{ccc}\hfill {\Psi }_t& =& \frac{1}{x}{\left(x{\Psi }_x\right)}_x+\frac{1}{y}{\left(y{\Psi }_y\right)}_y+\frac{1}{z}{\left(z{\Psi }_z\right)}_z-\frac{1}{x}\Psi {\Psi }_x-\frac{1}{y}\varphi {\Psi }_y-\frac{1}{z}\chi {\Psi }_z+\Psi \hfill \\ \hfill {\varphi }_t& =& \frac{1}{x}{\left(x{\varphi }_x\right)}_x+\frac{1}{y}{\left(y{\varphi }_y\right)}_y+\frac{1}{z}{\left(z{\varphi }_z\right)}_z-\frac{1}{x}\Psi {\varphi }_x-\frac{1}{y}\varphi {\varphi }_y-\frac{1}{z}\chi {\varphi }_z+\varphi \hfill \\ \hfill {\chi }_t& =& \frac{1}{x}{\left(x{\chi }_x\right)}_x+\frac{1}{y}{\left(y{\chi }_y\right)}_y+\frac{1}{z}{\left(z{\chi }_z\right)}_z-\frac{1}{x}\Psi {\chi }_x-\frac{1}{y}\varphi {\chi }_y-\frac{1}{z}\chi {\chi }_z+\chi \hfill \\ \hfill x,y,t& >& 0,\hfill \end{array}$$

with the initial conditions

$$\begin{array}{ccc}\hfill \Psi (x,y,z,0)& =& 2x^2-y^2-z^2,\varphi (x,y,z,0)=2x^2-y^2-z^2,\hfill \\ \hfill \chi (x,y,z,0)& =& 2x^2-y^2-z^2\hfill \end{array}$$

which is given by

$$\begin{array}{ccc}\hfill \Psi (x,y,z,t)& =& \left(2x^2-y^2-z^2\right)e^t,\varphi (x,y,z,t)=\left(2x^2-y^2-z^2\right)e^t\hfill \\ \hfill \chi (x,y,z,t)& =& \left(2x^2-y^2-z^2\right)e^t.\hfill \end{array}$$

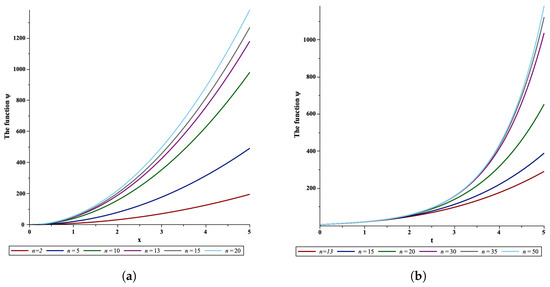
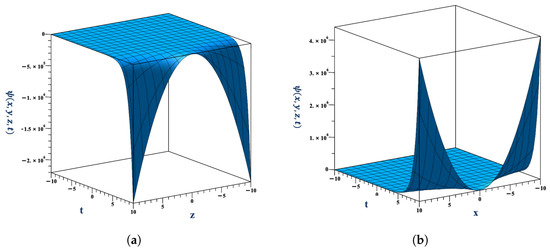
For $0<\alpha <1$, in a similar manner, it can be proved that the series is absolutely convergent. In order to illustrate the convergence, let us consider, for example, $z=y=0$ and $\alpha =0.25$. Figure 3a,b illustrate the convergence of the series representing the function ψ with respect to x at $t=2$ and with respect to t at $x=1$, respectively, which clearly converges rapidly to the exact solution after a few terms. In order to display the three-dimensional demonstration for the results of Example 2, we take different values of the variables. Figure 4a,b show the exact solution $\Psi (x,y,z,t)$ at $\alpha =1$, $y=0$ with $x=0,z=0$, respectively. The illustrations were generated using Maple software.

Figure 3. (a) The convergence of the series representing $\Psi$ with respect to x at $\alpha =0.25$. (b) The convergence of the series representing $\Psi$ with respect to t at $\alpha =0.25$.

Figure 4. (a) The function $\Psi (x,y,z,t)$ at $x=0,y=0$. (b) The function $\Psi (x,y,z,t)$ at $z=0,y=0$.

5. Conclusions

This study introduces a numerical method for solving the (3+1)-dimensional time-fractional coupled Burgers’ equation and its associated initial conditions. The method proposed herein integrates the four-dimensional natural transform techniques and Adomian decomposition methods to formulate the FNADM technique. By effectively leveraging the four-dimensional natural transform, the FNADM method addresses the Caputo fractional derivative of (3+1)-dimensional functions in coupled Burgers’ equations. Two illustrative examples accompanied by figures demonstrate the convergence of the series generated by the FNADM method. The computational findings and graphical representations underscore the method’s efficacy and suitability for solving high-dimensional fractional differential equations. This method introduces a numerical approach to handle multi-dimensional fractional differential equations and exhibits potential applicability across diverse real-world problems. Future research directions may involve investigating the stability and error analysis of FNADM and extending its applicability to more complex problems.