Abstract
The Zoomeron equation plays a significant role in many fields of physics, especially in soliton theory, such as helping to reveal new distinctive properties in different physical phenomena such as fluid dynamics, laser physics, and nonlinear optics. By using the Riccati–Bernoulli sub-ODE approach and the Backlund transformation, we search for soliton solutions of the fractional Zoomeron nonlinear equation. A number of solutions have been put forth, such as kink, anti-kink, cuspon kink, lump-type kink solitons, single solitons, and others defined in terms of pseudo almost periodic functions. The (2 + 1)-dimensional fractional Zoomeron equation given in a form undergoes precise dynamics. We use the computational software, Matlab 19, to express these solutions graphically by changing the value of various parameters involved. A detailed analysis of their dynamics allows us to obtain completely better insights necessarily with the elementary physical phenomena controlled by the fractional Zoomeron equation.
1. Introduction
Nonlinear partial differential equations (NLPDEs) play a crucial role in the fields of physics and mathematics, enabling the explanation of various physical systems across nonlinear optics, condensed matter physics, biological physics, fluid dynamics, and hydrodynamics. These equations are fundamental tools for representing the temporal and spatial changes of physical quantities, as demonstrated by their integration into significant principles of physics such as Newton’s classical mechanics, Schrodinger’s quantum mechanics, and Einstein’s general relativity equations. The identification of precise solutions for nonlinear partial differential equations (PDEs) holds immense importance in explaining the fundamental characteristics of various phenomena and physical processes in natural and engineering sciences. By providing accurate solutions, researchers acquire insights into the underlying mechanisms of intricate nonlinear phenomena. These solutions aid in creating visual representations, hence revealing phenomena like the spatial concentration of transition processes, the existence or non-existence of stable states in varying circumstances, and the emergence of maximum regimes. In this context, the steady work on the development and improvement of efficient techniques to solve nonlinear differential equations is of vital importance. The above approach is integral to both proposing accurate solutions and gaining a better understanding of related phenomena, which implies the successful development of diverse academic areas. The crucial concepts of the idea of a single wave are closely associated with the current global environment. To resolve such problems, a significant number of scientific methods are applied [1,2,3,4,5,6]. Nonlinear scientific problems are often addressed through the application of ansatz and sub-equation theories [7], tan() expansion scheme [8], Hirota scheme [9], MSE method [10], unified method [11], Riemann–Hilbert problem [12], and other techniques [13,14,15,16,17]. These approaches have been crucial in improving our understanding and analysis of nonlinear processes. As a consequence of its application, advances in soliton theory have led to the development of a variety of nonlinear models, including the Zoomeron model [18], the KP hierarchy model [19], the geophysical KdV structure [20], the KDV–Burger system [21], the Jimbo–Miwa nonlinear system [22], and more. Fractional partial differential equations are widely utilized in fields such as biological physics, signal processing, fluid mechanics, electromagnetism, and more. In the past few decades, numerous effective techniques have been proposed to accurately determine the solutions of the exact waves associated with (FPDEs), such as the ()-expansion method [23], ()-expansion method [24], exp()-function method [25], F-expansion method [26], sine and cosine methods [27], and so on [28,29,30,31,32].
Russell first proposed the idea of solitons, which are wave components with a steady form and speed, in 1834 [33]. This concept was further explored in 1976 by Calogero and Degasperis, who discovered solitons with variable velocities and connected them to polarization effects. This discovery resulted in the identification of two types of solitons: one type, called Boomeron, traveled from a distant point towards it, while the other type, called Trappon, showed repetitive oscillations around a fixed point as a result of changes in the spatial field [34]. This realization led to the development of the interconnected Boomeron equation as well as other integrable systems of linked wave equations [35,36,37,38]. The nonlinear Zoomeron equation, a scalar nonlinear evolution equation (NLEE), is one example of such a system. The solitons of the Zoomeron equation are similar to Boomerons and Trappons in that they are particles that are perpetually confined in a direction that may change [38]. A variety of analytical methods were used by researchers in recent studies to develop new exact solutions to the (2+1)-dimensional time fractional Zoomeron equation. Several techniques have been employed, including the extended exp()-expansion method [39], generalized -expansion method [40], and the improved Bernoulli sub-equation function method [41]. In this study, we utilize the intricate traveling wave transformation to simplify the (2 + 1)-dimensional fractional Zoomeron equation into an ordinary differential equation. We incorporate the Riccatti–Bornoulli sub-Ode approach along with Backlund transformation to investigate the precise solutions of the (2 + 1)-dimensional fractional Zoomeron equation. Here is how to formulate the nonlinear fractional Zoomeron equation:
Within this particular framework, the function is represented by the variable (F), where (F) is the wave pattern magnitude. Moreover, the operator defining -derivatives of powers is accurately consistent with the one given in reference [42] following modern scientific approaches.
Furthermore, the suggested methodology [43,44,45] is praised for its ability to manage intricate algebraic computations. Additionally, this approach can identify problems across multiple disciplines, including physics, fluid dynamics, biology, chemistry, and optical fibers. It has the potential to be deployed in biological processes and plants, industrial functions, and environmental fluid dynamics to provide better optimization algorithms and predictive tools while improving our understanding of fluidic phenomena. The Riccati–Bernoulli sub-ODE technique utilizing the Backlund transformation makes fractional Partial Differential Equations a set of algebraic systems. This transformation of the described algebraic systems allows us to extract critical information on the principal processes underlying complicated dynamism. The metamorphosis presents a harrowing increasing knowledgeability of the primary physical processes involved. The most remarkable characteristic of this method is that it shows a high degree of certainty in producing finite numerical solutions. It, hence, confirms the validated methodology of the derived solutions for the investigated equations. Another inherent attribute of the signal-wave technique is its ability to generate a broad spectrum of single-wave solutions, therefore, making it more realistic and applicable compared to other methods.
2. Methodology
This section explains the procedural framework guiding the methodology used to address the nonlinear fractional partial differential equations. The focus lies on offering a flexible scope that captures the complexities associated with the nonlinear fractional partial differential equations.
where f is an unspecified function, (Q) is a polynomial in (), and t denotes all its partial derivatives, including non-linear terms and the highest-order derivatives. This transformation is based on the complex wave paradigm.
where are constants.
Using the traveling wave transformation, Equation (3) can be changed into the following nonlinear ordinary differential equation:
Examining the presumptive solution for , subject to the restriction that and occur simultaneously,
Here, the function is obtained through the following Backlund transformation:
where (), (a), and (b) are constants, assuming that , and the function is defined as follows:
According to reference [46], the solution of Equation (8) is usually accepted:
- (i)
- ).
- (ii)
- ).
- (iii)
- .
The equilibrium state in Equation (5) is obtained as a result of a homogeneous balance composed of the linear polymer analysis and the rationalization of the nonlinear and the highest-order derivative components [47].
The degree of the function (f) is represented by the symbol (D) in this case, which is written as , where (N) is a positive integer. Furthermore, the three integers and J are positive. Equation (7) is substituted into Equation (6), and the terms are arranged according to the numbers of the same degree of . This polynomial, when equated to zero, gives an algebraic system of equations by coefficients. The system is solved, after which the unknown coefficients are determined by the computational tool Maple. Finally, the calculated values are substituted back into Equation (6), and, thus, the function is obtained.
3. Execution of the Problem
In this section, the fractional Zoomeron problem is handled, using the suggested method and applying the subsequent wave transformation. Later, we investigate the formal solution of the given fractional partial differential equation with the complex field envelope as the function of retarded time (t) on the axis of rotation and the propagation depth (x) and (y):
The nonlinear ordinary differential equation can be deduced by substituting Equation (10) into Equation (1).
Upon integrating Equation (11) twice, we obtain the following:
where the second integration constant is 0 and the prime represents the derivative with respect to . The balanced equilibrium state () is determined by balancing the highest-order derivative term with the highest-order nonlinear term . Now, substituting Equation (6) along with Equations (7) and (8) into Equation (12), and collecting the coefficients of , and then setting them to zero, we obtain a system of algebraic equations. Solving this system of algebraic equations with the assistance of Maple, we obtain the following results:
Case 1:
Case 2:
Case 3:
Solution Set 1: The singular traveling wave solutions for case 1, when (), are derived from Equation (1).
or
Solution Set 2: The singular traveling wave solutions for case 1, when (), are derived from Equation (1).
or
Solution Set. 3: The singular traveling wave solutions for case 1, when (), are derived from Equation (1).
Solution Set 4: The singular traveling wave solutions for case 2, when (), are derived from Equation (1).
or
Solution Set 5: The singular traveling wave solutions for case 2, when (), are derived from Equation (1).
or
Solution Set 6: The singular traveling wave solutions for case 2, when (), are derived from Equation (1).
The solution set for the following values of () that follow are obtained by assuming case 3.
Solution Set 7: The singular traveling wave solutions for case 3, when (), are derived from Equation (1).
or
Solution Set 8: The singular traveling wave solutions for case 3, when (), are derived from Equation (1).
or
Solution Set 9: The singular traveling wave solutions for case 3, when (), are derived from Equation (1).
4. Results and Discussion
The main goal of the present study is to apply a new scientific procedure integrated into a solid framework to decompose the fractional Zoomeron equation. The equation in terms of fractional derivatives is a difficult problem, requiring advanced methods. By using a common but debatable complicated transformation, recommended by the most recent research, fractional partial differential equations are transformed into ordinary differential equations, which can then be explored using additional methods. The utilization of the techniques in the form of series is a major breakthrough, allowing for a complete examination of the solutions of the equation.
In this work, we provide a new method for solving the unknown coefficients of the series solutions, revealing a very complex algebraic system. Additionally, we solve the system of equations and their series solutions based on which the unknown coefficients are calculated using the Maple 13 software. The solutions are then solved using the Riccati–Bernoulli sub-ODE algorithm, obtaining the solutions in three families: hyperbolic, rational, and trigonometric. Consequently, numerous analytical solutions originate, representing a variety of mathematical structures that underline the fractional Zoomeron equation. To sum up, from a conventional point of view, the method proposed is a powerful analysis tool. It allows one to obtain many periodic and single solitary traveling wave solutions that can be radically transformed according to the specific requirements. These findings would be beneficial for understanding the general laws of various physical problems and developing new approaches that could address some specific non-linear phenomena for the presented field. However, the discovery presented has implications for the actual solutions of the entire field. Additionally, the observations present an opportunity to strengthen numerical solvers by integrating supplementary series-based solutions. By plotting solutions using specific parameter values, a more in-depth analysis of their behavior can be determined. This approach offers valuable insights for refining numerical techniques. Our framework supports a variety of soliton solutions, such as kink, anti-kink, periodic, and breather solitons, which are widely used in many physical fields. For example, in particle theory, kink solitons serve as immediate manifestations of topologically stable line solitons and analogs of dislocations in solids. Anti-kink solitons are useful in condensed matter physics to simulate stone-like behavior, for example, tears in nanostructures or biological tissues. Periodic solitons are economically important in optical fiber communications because they preserve the shape of a pulse as it travels over long distances. Lastly, breather solitons are of great use in the field of nonlinear optics, where they can also emit short light pulses when they are absorbed, and in oceanography, where they can contribute to the emergence of rogue waves. Our innovative fractional-order solutions mark a significant departure from traditional-order methods, delivering accurate depictions of wave phenomena including kinks, anti-kinks, periodic oscillations, and breather solitons. These solutions showcase distinctive characteristics like powerful peaks and mysterious dark valley-shaped waves, serving as essential tools for replicating soliton dynamics in optical fibers, interpreting shock wave patterns in fluid mechanics, and unraveling the complex nature of solitons in plasma physics. The subsequent visuals in our research offer compelling illustrations that clarify the intricate properties embedded within these solutions, providing a concrete and insightful representation of their behavior. In order to clarify the unique characteristics of different periodic and single solutions, we use the Matlab program, customizing certain parameter values to the precise solutions. The following images offer graphical depictions that enable a thorough comprehension of the characteristics and actions of the solutions in a concrete and palpable way.
Figure 1 provides several levels of detail for both the real and imaginary parts of Solution . The plotted kink and anti-kink structures exemplify the progression and changes of along various spatial and temporal resolutions, demonstrating its complex behavior.
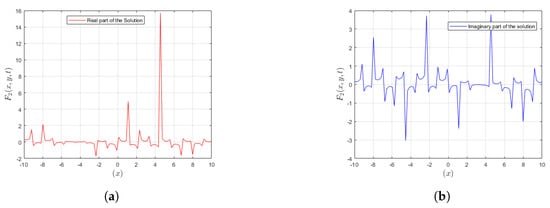
Figure 1.
In these graphical representations, variations are shown for the real and imaginary parts of the solution . (a) A plot representing the real part of is presented. (b) A plot representing the img part of is depicted.
Figure 1 presents real and imaginary parts of Solution at various detail levels similar to Figure 2. This figure depicts different detail levels of the real and imaginary parts of the given solution . The lump-type kink is observed to vary and develop considerable features and relationships across the detail levels.
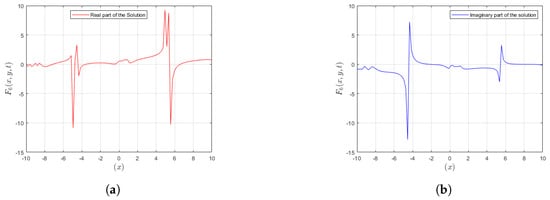
Figure 2.
In these graphical representations, variations are shown for the real and imaginary parts of the solution . (a) A plot depicting the real part of is presented. (b) A plot representing the Img part of is depicted.
Figure 3 shows how the real and imaginary parts of Solution interact at several levels of granularity. This render of breather data allows for a more comprehensive grasp of the underlying characteristics and temporal behavior at different phases and scales.
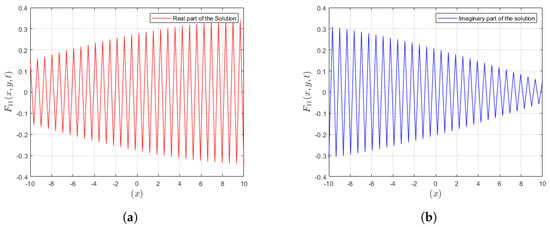
Figure 3.
In these graphical representations, variations are shown for the real and imaginary parts of the solution . (a) A plot representing the real part of is presented. (b) A plot representing the img part of is depicted.
In Figure 4, the twining periodic figure displays how in the real and imaginary parts of its solution differ in space and time and are contrasted across various resolutions. Therefore, this fully represents how evolves and changes with respect to () on different levels of resolutions in the two different dimensions.
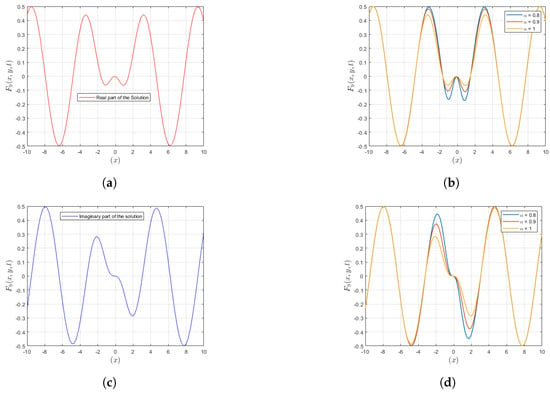
Figure 4.
In these graphical representations, variations are shown for the real and imaginary parts of the solution . (a) A plot representing the real part of is presented. (b) A plot representing the real part of is depicted for different values of . (c) A plot representing the img part of is presented. (d) A plot representing the img part of is depicted for different values of .
Figure 5 shows the evolution of a cuspon kink soliton solution with varying parameters of alpha. It displays the complex alterations in the profile of the solution as alpha takes on various values, highlighting the complex dynamics present in the system.
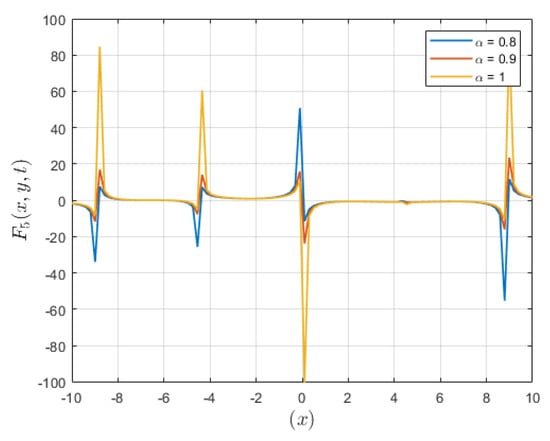
Figure 5.
A plot representing solution is depicted for different values of .
Figure 6 shows the evolution of a lump-type kink soliton solution with varying values of parameter alpha. It displays the complex alterations in the profile of the solution as alpha takes on various values, highlighting the complex dynamics present in the system.
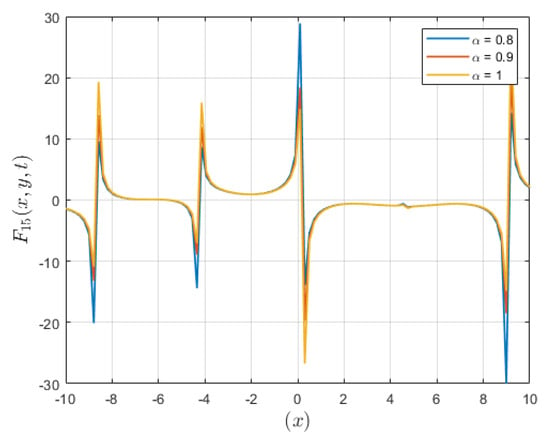
Figure 6.
A plot representing solution is depicted for different values of .
Figure 7 shows that the variations in parameter () have a stronger effect on the observed wave propagation than those in (). These () fluctuations cause noticeable changes in the wave properties, overpowering the effects of () fluctuations. This finding emphasizes how important () is for controlling the dynamics of wave movement in the system.
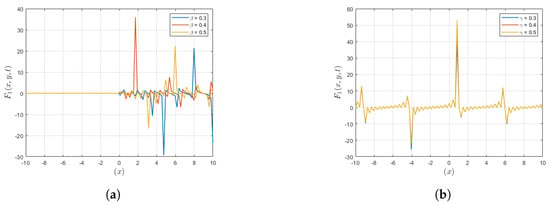
Figure 7.
In these graphical representations, and variations are shown for the solution . (a) A plot representing variation of with respect to . (b) A plot representing variation of with respect to .
In Figure 8, similar to Figure 7, parameter ()’s variations have a stronger effect on the observed multiple-kink wave propagation than the fluctuations of (). These () fluctuations produce observable changes in the wave properties, outweighing the impacts resulting from ()’s variations. This finding highlights the role that () plays in controlling the dynamics of wave propagation in the system.
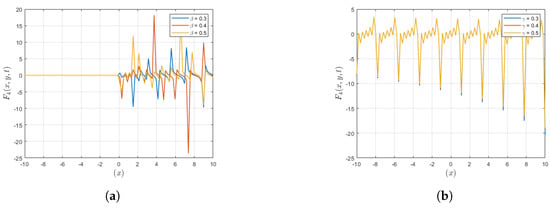
Figure 8.
In these graphical representations, and variations are shown for the solution . (a) A plot representing variation of with respect to . (b) A plot representing variation of with respect to .
In the case of Figure 9, the figure shows a single-lump soliton, and as the () values increase, the wave moves towards singularities due to variations in (). The wave tends to concentrate or localize more strongly as () grows, leading to singularities in the end. This picture emphasizes how important () is in determining how the soliton behaves, especially in terms of its propensity for concentration and the formation of singularities.
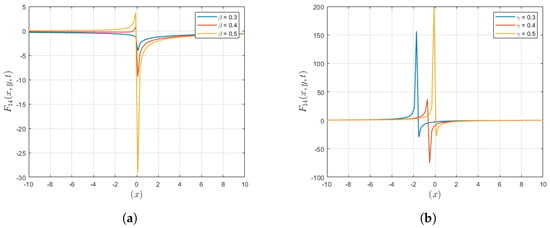
Figure 9.
In these graphical representations, and variations are shown for the solution . (a) A plot representing variation of with respect to . (b) A plot representing variation of with respect to .
In addition to the aforementioned plotted solutions, we also explore fascinating solitary solutions in the domain of nonlinear dynamics. There are a few lump-type kink solitary solutions that exhibit localized perturbations in the wave profile, specifically , , and . Similarly, indicates the presence of dromian solitons with distinct propagation characteristics. In addition, illustrates the intricate wave interactions associated with cusp kink solitons. To further deepen our knowledge, presents the idea of multiple kink solitons, in which the wave shows many localized kinks present at the same time, resulting in coherent propagation dynamics. All these different approaches provide insightful information on the intricate and intriguing behaviors seen in nonlinear systems. In Table 1, Comparison of the current approach with the alternative exp-function [37] and -expansion [40] methods.

Table 1.
Comparison of the current approach with the alternative exp-function [37] and -expansion [40] methods.
5. Conclusions
In the scope of the current investigation, we use this new methodology and are able to find exact solutions of the fractional Zoomeron equation. This method can find solitary solutions and can find three sorts of solutions in particular: trigonometric, hyperbolic, and rational. As such, this approach is regarded as highly novel, and its use to obtain completely new solutions for the fractional Zoomeron equation in three dimensions can potentially act as a starting point for further investigations. Furthermore, we prove the effectiveness of the new method as a way to explore alternative and even coordinate soliton solutions in mathematical physics. In conclusion, we can say that the current method can be considered as very powerful and capable of solving problems in various areas. Additionally, it can be distinguished by its credibility and multiple solutions. Thus, its potential in research is huge.
Author Contributions
Conceptualization, M.A.; Methodology, M.A.; Software, K.M.; Validation, K.M.; Formal analysis, M.N.; Investigation, M.N. and Z.A.; Resources, S.A. and M.M.A.-S.; Writing—review & editing, Z.A.; Visualization, S.A.; Supervision, M.M.A.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Scientific Research Deanship at University of Ha’il Saudi Arabia through project number <RG-23 098>.
Data Availability Statement
All data were contained in the main text.
Acknowledgments
This research was funded by Scientific Research Deanship at University of Ha’il Saudi Arabia through project number <RG-23 098>.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ullah, M.S.; Ali, M.Z.; Roshid, H.O.; Seadawy, A.R.; Baleanu, D. Collision phenomena among lump, periodic and soliton solutions to a (2+1)-dimensional Bogoyavlenskiis breaking soliton model. Phys. Lett. A 2021, 397, 127263. [Google Scholar] [CrossRef]
- Triki, H.; Pan, A.; Zhou, Q. Pure-quartic solitons in presence of weak nonlocality. Phys. Lett. A 2023, 459, 128608. [Google Scholar] [CrossRef]
- Yang, J.; Liang, S.; Zhang, Y. Travelling waves of a delayed SIR epidemic model with nonlinear incidence rate and spatial diffusion. PLoS ONE 2011, 6, e21128. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.Q.; Zhao, X.H. Resonant solitons of the B-type Kadomtsev-Petviashvili equation. Phys. Lett. A 2023, 458, 128592. [Google Scholar] [CrossRef]
- Zhong, W.P.; Yang, Z.; Belic, M.; Zhong, W.Y. Controllable optical rogue waves in inhomogeneous media. Phys. Lett. A 2022, 453, 128469. [Google Scholar] [CrossRef]
- Zarmi, Y. Sine-Gordon equation in (1+2) and (1+3) dimensions: Existence and classification of traveling-wave solutions. PLoS ONE 2015, 10, e0124306. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.F.; Wang, X.F.; Zang, T.T.; Qiu, W.H. Stability analysis, solitary wave and explicit power series solutions of a (2 + 1)-dimensional nonlinear Schrodinger equation in a multicomponent plasma. Int. J. Numer. Methods Heat Fluid Flow 2021, 3, 1732–1748. [Google Scholar] [CrossRef]
- Manafian, J. Optical soliton solutions for Schrodinger type nonlinear evolution equations by the tan(Θ/2)-expansion method. Optik 2016, 127, 4222–4245. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ahmed, O.; Mahbub, M.A. Collision phenomena between lump and kink wave solutions to a (3+1)-dimensional Jimbo-Miwa-like model. Partial. Differ. Equ. Appl. Math. 2022, 5, 100324. [Google Scholar] [CrossRef]
- Ullah, M.S.; Roshid, H.O.; Ali, M.Z.; Noor, N.F.M. Novel dynamics of wave solutions for Cahn-Allen and diffusive predator-prey models using MSE scheme. Partial. Differ. Equ. Appl. Math. 2021, 3, 100017. [Google Scholar] [CrossRef]
- Nandi, D.C.; Ullah, M.S.; Roshid, H.O.; Ali, M.Z. Application of the unified method to solve the ion sound and Langmuir waves model. Heliyon 2022, 8, e10924. [Google Scholar] [CrossRef]
- Yang, J.J.; Tian, S.F.; Li, Z.Q. Riemann-Hilbert problem for the focusing nonlinear Schrodinger equation with multiple high-order poles under nonzero boundary conditions. Phys. D Nonlinear Phenom. 2022, 432, 133162. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Probing families of optical soliton solutions in fractional perturbed Radhakrishnan Kundu Lakshmanan model with improved versions of extended direct algebraic method. Fractal Fract. 2023, 7, 512. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Saad Alshehry, A.; Imran, M.; Khan, A.; Weera, W. Fractional view analysis of Kuramoto Sivashinsky equations with non-singular kernel operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Khan, H.; Arif, M. Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions. Math. Methods Appl. Sci. 2020, 43, 199–212. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating symmetric soliton solutions for the fractional coupled konno onno system using improved versions of a novel analytical technique. Mathematics 2023, 11, 2686. [Google Scholar] [CrossRef]
- Irshad, A.; Mohyud-Din, S.T. The solitary wave solutions of Zoomeron equation. WJST 2013, 10, 201–208. [Google Scholar]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. New solitary wave solutions to the (2+1)-dimensional Calogero-Bogoyavlenskii-Schiff and the Kadomtsev-Petviashvili hierarchy equations. Indian J. Phys. 2017, 91, 1237–1243. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ashraf, F.; Younis, M.; Iqbal, H.; Baleanu, D. Lump and Interaction solutions of a geophysical Korteweg-de Vries equation. Results Phys. 2020, 19, 103661. [Google Scholar] [CrossRef]
- Fan, E.G.; Zhang, J.; Hon, B.Y. A new complex line soliton for the two-dimensional KdV-Burgers equation. Phys. Lett. A 2001, 291, 376–380. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, S.; Dong, H. Hybrid solutions of (3 + 1)-dimensional Jimbo-Miwa equation. Math. Probl. Eng. 2017, 2017, 5453941. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. New Travelling Wave and Anti-Kink Wave Solutions of Space-Time Fractional (3 + 1)-Dimensional Jimbo-Miwa Equation. Chin. J. Phys. 2020, 67, 79–85. [Google Scholar] [CrossRef]
- Yokus, A.; Durur, H.; Ahmad, H.; Thounthong, P.; Zhang, Y.-F. Construction of Exact Traveling Wave Solutions of the Bogoyavlenskii Equation by (G/G,1/G)-Expansion and (1/G)-Expansion Techniques. Results Phys. 2020, 19, 103409. [Google Scholar] [CrossRef]
- Arshed, S. New Soliton Solutions to the Perturbed Nonlinear Schrodinger Equation by exp(−ϕ)-Expansion method. Optik 2020, 220, 165123. [Google Scholar] [CrossRef]
- Yldrm, Y. Optical Solitons with Biswas-Arshed Equation by F-Expansion Method. Optik 2021, 227, 165788. [Google Scholar] [CrossRef]
- Akbar, M.A.; Akinyemi, L.; Yao, S.W.; Jhangeer, A.; Rezazadeh, H.; Khater, M.M.; Ahmad, H.; Inc, M. Soliton Solutions to the Boussinesq Equation through Sine-Gordon Method and Kudryashov Method. Results Phys. 2021, 25, 104228. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasilshchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Iqbal, N.; Aly, S.; Nonlaopon, K. Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series. Symmetry 2022, 14, 1944. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Sawalha, M.M.; Shah, R. Approximate analytical methods for a fractional-order nonlinear system of Jaulent Miodek equation with energy-dependent Schrdinger potential. Fractal Fract. 2023, 7, 140. [Google Scholar] [CrossRef]
- Shah, R.; Alkhezi, Y.; Alhamad, K. An analytical approach to solve the fractional Benney equation using the q-homotopy analysis transform method. Symmetry 2023, 15, 669. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Ababneh, O.Y.; Shah, N.A.; Nonlaopon, K. Combination of Laplace transform and residual power series techniques of special fractional-order non-linear partial differential equations. AIMS Math. 2023, 8, 5266–5280. [Google Scholar] [CrossRef]
- Miura, M.R. Backlund Transformation; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Younis, M.; Rizvi, S.T.R. Dispersive dark optical soliton in (2 + 1)-dimensions by (G′/G)-expansion with dual-power law nonlinearity. Optik 2015, 126, 5812–5814. [Google Scholar] [CrossRef]
- Degasperis, A.; Rogers, C.; Schief, W.K. Isothermic surfaces generated via Backlund and Moutard Transformations, Boomeron and Zoomeron connections. Stud. Appl. Math. 2002, 109, 39–65. [Google Scholar] [CrossRef]
- Abazari, R. The solitary wave solutions of Zoomeron equation. Appl. Math. Sci. 2011, 5, 2943–2949. [Google Scholar]
- Khan, K.; Akbar, A.M. Traveling wave solutions of the (2 + 1)-dimensional Zoomeron equation and the Burgers equations via the MSE method and the exp-function method. Ain Shams Eng. J. 2014, 5, 247–256. [Google Scholar] [CrossRef]
- Morris, M.R.; Leach, P.G.L. Symmetry reductions and solutions to the Zoomeron equation. Phys. Scr. 2014, 90, 15. [Google Scholar] [CrossRef]
- Kumar, D.; Kaplan, M. New analytical solutions of (2 + 1)-dimensional conformable time fractional Zoomeron equation via two distinct techniques. Chin. J. Phys. 2018, 56, 2173–2185. [Google Scholar] [CrossRef]
- Li, Z.; Han, T. Bifurcation and exact solutions for the (2 + 1)-dimensional conformable time-fractional Zoomeron equation. Adv. Differ. Equ. 2020, 2020, 656. [Google Scholar] [CrossRef]
- Demirbilek, U.; Ala, V.; Mamedov, K.R. Exact solutions of conformable time fractional Zoomeron equation via IBSEFM. Appl. Math. J. Chin. Univ. 2021, 36, 554–563. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H.; Usta, H. On generalized the conformable fractional calculus. TWMS J. Appl. Eng. Math. 2019, 9, 792799. [Google Scholar]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the modified Korteweg-de Vries equation in deterministic case and random case. J. Phys. Math. 2017, 8, 2090-0902. [Google Scholar]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the nonlinear Schrdinger problem with the probability distribution function in the stochastic input case. Eur. Phys. J. Plus. 2017, 132, 339. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equa. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Lu, D.; Shi, Q. New Jacobi elliptic functions solutions for the combined KdV-mKdV equation. Int. J. Nonlinear Sci. 2010, 10, 320–325. [Google Scholar]
- Zhang, Y. Solving STO and KD equations with modified Riemann–Liouville derivative using improved (G/G′)-expansion function method. Int. J. Appl. Math. 2015, 45, 16–22. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).