Complementary Metal Oxide Semiconductor Circuit Realization of Inverse Chebyshev Low-Pass Filter of Order (1 + α)

Abstract

This paper presents the CMOS circuit realization of a low-pass Inverse Chebyshev fractional-order filter (FOF) of order (1 + α) using the inverse-follow-the-leader feedback (IFLF) topology. A nonlinear least squares optimization routine is used to determine the coefficients of the fractional-order transfer function to approximate the stop-band characteristics. The Inverse Chebyshev FOF of orders 1.3, 1.6, and 1.9 using cross-coupled operational transconductance amplifier (OTA) was designed in united microelectronics corporation (UMC) 180 nm complementary metal–oxide–semiconductor process. The MATLAB and Cadence Spectre simulations are used to validate the implementation of the fractional-order filter of orders 1.3, 1.6 and 1.9. The dynamic range (DR) of the filter is found to be 83.04 dB, 86.13 dB, and 84.71 dB, respectively, for order of 1.3, 1.6, and 1.9. The simulation results such as magnitude response, transient plot, Monte Carlo, and PVT plots, have justified the design accuracy.

1. Introduction

The research on fractional order (FO) analog filters has gained greater significance due to their ability to provide additional control over the filter characteristics [1]. The FO filters offer various advantages, such as precise control of parameters such as stop-band attenuation [2], cut-off frequency [3], the shaping of the passband [4], the stop-band ripple [5], etc. The design of continuous-time (CT) filters based on operational transconductance amplifiers (OTAs) [6,7,8,9,10] for different applications is discussed in the literature. The transconductor-based realization of FO filters has been addressed in the literature [11,12,13,14]. The implementation of fractional step filters using field programmable analog array hardware [15] has been presented. The fractional order passive and active filter realizations of Kerwin–Huelsman–Newcomb (KHN) and Sallen–Key for the Butterworth response are presented in [16]. The circuit realization of FO Butterworth low-pass filter (LPF) using a differential voltage current conveyor (DVCC) and fractance devices have been investigated [17,18]. An FO transitional Butterworth–Butterworth filter using the current feedback operational amplifier (CFOA) was discussed [19]. The transconductance-capacitance (${\mathrm{G}}_{\mathrm{m}}$ − C) FO Bessel filter of (1 + α) was investigated [20]. The design of approximated fractional order Chebyshev lowpass filters using nonlinear least squares optimization was explored in [21]. The design of approximated fractional-order Inverse Chebyshev lowpass filters using the nonlinear least squares fitting routine and op-amp-based circuit realization was described in [5]. The design and circuit realization of a fractional order Inverse Chebyshev low-pass filter using particle swarm optimization was considered in [22]. The design of power law FOF [23,24,25] and companding FOF [26] were also explored. A simple procedure to realize Butterworth filter transfer function of order (1 + α) based on the curve fitting of the frequency response magnitude data by a minimum-phase state-space model using a Log-Chebyshev magnitude design is presented by Julia Nako et al. [27]. The design of higher-order fractional filters reported in [28] has also employed the same state-space model to fit its magnitude response data.

The CMOS circuit realization of the Inverse Chebyshev fractional-order filter was not discussed in the literature. In this work, the fractional order Inverse Chebyshev filter having an order of (1 + α), which is a generalized filter of second order [5], is considered. The fractional-order Inverse Chebyshev filter transfer function is implemented based on the inverse follow-the-leader feedback (IFLF) configuration using OTA.

The design methodology of Inverse Chebyshev fractional-order filter with numerical analysis, least square curve fitting, and transfer function approximations are presented in Section 2. The CMOS circuit realization of Inverse Chebyshev fractional-order filter using the cross-coupled OTA is discussed in Section 3. The simulation results performance parameters and concluding remarks are presented in Section 4, Section 5 and Section 6, respectively.

2. Design of Inverse Chebyshev Fractional-Order Filter

2.1. Inverse Chebyshev Fractional-Order Filter

Inverse Chebyshev filters find applications in biomedical signal processing, audio equalizers, and video or data transmission [4,22]. The electroencephalogram (EEG) [29] signal frequencies ranges from 0.1 Hz to more than 100 Hz. Typically, EEG signals are generally categorized as delta (δ) (0.1–4 Hz), theta (θ) (4–8 Hz), alpha (α) (8 to 13 Hz), and beta (β) (13 to 30 Hz) and gamma (γ) (30 to 100 Hz). The frequency band of an electrocardiogram (ECG) signal can vary depending on the application, but it typically ranges from 0.05 to 100 Hz. Many such bioelectric signals have a relatively low-frequency content, but the recording systems are susceptible to powerline interference and other noise signals. The Inverse Chebyshev low-pass notch (LPN) filter [30] can simultaneously perform the required low-pass filtering and removal of the narrow band interference.

The biomedical signal recordings such as electrocardiograph (ECG), magnetoencephalograph (MEG) and electroencephalograph (EEG) are often exposed to strong power line interference (PLI) (50/60 Hz), second harmonic PLI (100/120 Hz). The presence of EMG or muscle noise [31] (high frequency noise of above 100 Hz) represents a major problem in many ECG applications, especially in recordings acquired during exercise. The low-pass notch (LPN) filters are particularly effective for ECG signal analysis, especially for removing 100 Hz muscle noise. Other applications of LPN include exercise stress testing, seismic signal processing, sensor signal conditioning (e.g., temperature, pressure), data acquisition and industrial automation systems.

Inverse Chebyshev fractional-order filters were synthesized using some optimization functions called least square curve fitting (lscurvefit) [4] and particle swarm optimization [22]. The designed filters were realized using OPAMP and passive RC ladder networks. In both techniques, the multiple input biquad (MIB) technique was used in realizing the filter. In this work, CMOS OTA is used as an active element and the fractional-order Inverse Chebyshev filter is designed using cross-coupled differential pair architecture in the UMC 180 nm CMOS process. The integer order approximation of the fractional-order transfer function is considered.

2.1.1. Background

The Inverse Chebyshev FOF of order (1 + α) is designed for a cut-off frequency of 8 Hz and a notch frequency of 100 Hz. The ripple factor ‘ϵ’ of a Chebyshev filter is related to stopband attenuation by

$$\mathsf{ϵ}=1/\sqrt{{\left(10\right)}^{{\displaystyle \frac{{\mathrm{A}}_{\mathrm{S}}}{10}}}-1}$$

(1)

where $A_s$ is stopband attenuation in dB. From (1), for the stopband attenuation $A_s$ value of 50 dB, the minimum stopband ripple factor $ϵ$ will be 0.003162. For Inverse Chebyshev biquad [5,22] with passband gain $A_p$ as 0 dB and $A_s$ as 50 dB, the transfer function normalized to 1.414 rad/s is given by

$$H_{INE}\left(s\right)=0.003162\ast {\displaystyle \frac{\left(s^2+1.9999\right)}{s^2+0.1123s+0.0063}}$$

(2)

The transfer function of second order LPF, approximated for Inverse Chebyshev response, is typically that of a low-pass notch and is given as

$$H_{INT}^2\left(s\right)={\displaystyle \frac{\left[s^2+k^2{{\omega }_P}^2\right]}{s^2+s\frac{{\omega }_P}{Q_P}+{\omega }_P^2}}$$

(3)

where $k^2$ is the DC gain, ${\omega }_P$ is the pole frequency, $k{\omega }_P$ is the notch frequency and $Q_P$ is the quality factor.

2.1.2. Least Square Fitting Function

The transfer function (TF) of fractional Inverse Chebyshev low-pass filter of order $\left(1+\alpha \right)$ is given by

$$H_{FON}^{1+\alpha }\left(s\right)={\displaystyle \frac{k_4\left[k_1{s}^{1+\alpha }+1\right]}{k_2{s}^{1+\alpha }+k_3{s}^{\alpha }+1}}$$

(4)

The coefficients $k_1$, $k_2$, $k_3$, $k_4$ in (4) of the fractional Inverse Chebyshev LPF for an order of 0.1 to 0.9 are selected suitably using MATLAB optimization routine lscurvefit to approximate the ripple behavior in the stopband of the magnitude response, with different attenuation in the transition band, which depends on ‘α’. A nonlinear least squares fitting [5] is used to solve the optimization problem over the frequency range $\omega \in [{10}^{-3},{10}^3$] rad/s. The computed values of filter coefficients $k_1$, $k_2$, $k_3$, $k_4$ are given in Table 1.

Table 1. Coefficient values for (1 + $\alpha$) fractional-order transfer function.

Parameter	$\mathsf{\alpha }=0.3$	$\mathsf{\alpha }=0.6$	$\mathsf{\alpha }=0.9$
$k_1$	0.2406	0.4456	0.5648
$k_2$	45.7526	94.5257	143.9983
$k_3$	0.1100	0.1136	12.5186
$k_4$	0.9691	0.9617	1.0333
${\tau }_1$	0.3807	0.5706	0.8032
${\tau }_2$	5.7397	11.3584	10.8355
${\tau }_3$	20.0702	14.4206	13.2069
${\theta }_w$	${13.983}^{°}$	${11.32}^{°}$	${9.5}^{°}$
$G_0$	181.34	211.83	201.85
$G_1$	24.5	26.49	17.83
$G_2$	1.618	1.179	0.9403
$G_3$	1	1	1

2.1.3. Stability

The mapping from the $s^{\alpha }$-plane to W-plane [12,32] results in the characteristic equation

$$k_2({W)}^{m+k}+k_3{W}^k+1=0$$

(5)

where $W=s^{1/m}$ and m, k arepositive integers. The stability condition in this case is that all the pole angles have $⌈{\theta }_W⌉>(\pi /2m)=9^{°}.$ For α = 0.3, 0.6, 0.9, the pole angles are ${13.98}^{°}$, ${11.32}^{°}$ and ${9.5}^{°}$, respectively, which confirm the stability condition.

2.1.4. Transfer Function Approximation

The second-order approximation of Laplacian variable $s^{\alpha }$ using the continued fraction expansion (CFE) [1,15] used for implementing fractional-order filter is given by

$$s^{\alpha }={\displaystyle \frac{a_0{s}^2+a_{1}s+a_2}{a_2{s}^2+a_{1}s+a_0}}$$

(6)

The design equations for coefficients $a_0,a_1,a_2$[1] in (6) are given by

$$\begin{gathered} a_0={\alpha }^2+3\alpha +2 \\ {a}_1=8-2{\alpha }^2 \\ {a}_2={\alpha }^2-3\alpha +2 \end{gathered}$$

(7)

The approximated integer order transfer function of fractional-order inverse Chebyshev filter of order (1 + α) can be derived as

$$H_{FON}^{1+\alpha }\left(s\right)={\displaystyle \frac{k_4}{k_2\ast a_0}}\left[{\displaystyle \frac{A_3\ast s^3+A_2\ast s^2+A_1\ast s+A_0}{s^3+B_2\ast s^2+B_1\ast s+B_0}}\right]$$

(8)

where

$$\begin{gathered} A_3=k_1\ast a_0 \\ {A}_2=k_1\ast a_1+a_2 \\ {A}_1=k_1\ast a_2+a_1 \\ {A}_0=a_0 \end{gathered}$$

(9)

$$\begin{gathered} B_2={\displaystyle \frac{k_2{a}_1+k_3{a}_0+a_2}{k_2\ast a_0}} \\ {B}_1={\displaystyle \frac{k_2{a}_2+k_3{a}_1+a_1}{k_2\ast a_0}} \\ {B}_0={\displaystyle \frac{k_2{a}_2+a_0}{k_2\ast a_0}} \end{gathered}$$

(10)

2.1.5. Functional Block Diagram

The approximated integer order TF (8) can be implemented using IFLF, which is a multiple-loop feedback (MLF) structure. The corresponding functional block diagram (FBD) is shown in Figure 1.

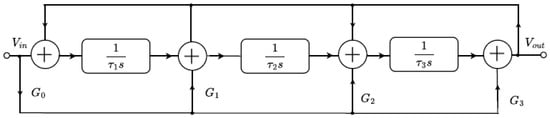
Figure 1. Functional block diagram of IFLF topology.

The transfer function for the filter structure in Figure 1 is given by

$${\displaystyle \frac{V_{out}}{V_{in}}}={\displaystyle \frac{G_3{s}^3+\frac{G_2}{{\tau }_1}{s}^2+\frac{G_1}{{\tau }_1{\tau }_2}s+\frac{G_0}{{\tau }_1{\tau }_2{\tau }_3}}{s^3+\frac{1}{{\tau }_1}{s}^2+\frac{1}{{\tau }_1{\tau }_2}s+\frac{1}{{\tau }_1{\tau }_2{\tau }_3}}}$$

(11)

3. CMOS Circuit Realization of Inverse Chebyshev Fractional-Order Filter

The circuit realization of fractional low-pass Inverse Chebyshev filter of order $(1+\alpha )$ using transconductance and capacitance ($G_m-C)$ approach is shown in Figure 2.

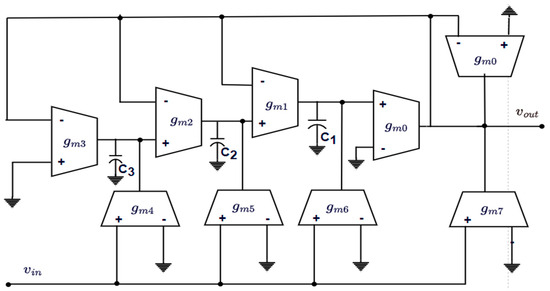
Figure 2. OTA-C realization of fractional-order Inverse Chebyshev LPF of order (1 + α).

The gain factors $G_0$, $G_1$, $G_2$, $G_3$ and time constants ${\tau }_i(i=0,1,2)$ in the functional block diagram of Figure 1 are related to transconductances and capacitances of $G_m-C$ circuit in Figure 2 and are given as

$$G_0={\displaystyle \raisebox{1ex}{$g_{m4}$}\!\left/ \!\raisebox{-1ex}{$g_{m3}$}\right.}; G_1={\displaystyle \raisebox{1ex}{$g_{m4}$}\!\left/ \!\raisebox{-1ex}{$g_{m3};$}\right.}{G}_2={\displaystyle \raisebox{1ex}{$g_{m4}$}\!\left/ \!\raisebox{-1ex}{$g_{m3}$}\right.}; G_3=1$$

(12a)

$${\tau }_1={\displaystyle \raisebox{1ex}{$C_1$}\!\left/ \!\raisebox{-1ex}{$g_{m1}$}\right.}; {\tau }_2={\displaystyle \raisebox{1ex}{$C_2$}\!\left/ \!\raisebox{-1ex}{$g_{m2}$}\right.}; {\tau }_3={\displaystyle \raisebox{1ex}{$C_3$}\!\left/ \!\raisebox{-1ex}{$g_{m3}$}\right.} ;$$

(12b)

3.1. CMOS OTA Architecture

The schematic circuit of cross-coupled CMOS OTA [9] with biasing used for realization of fractional-order Inverse Chebyshev LPF is shown in Figure 3.

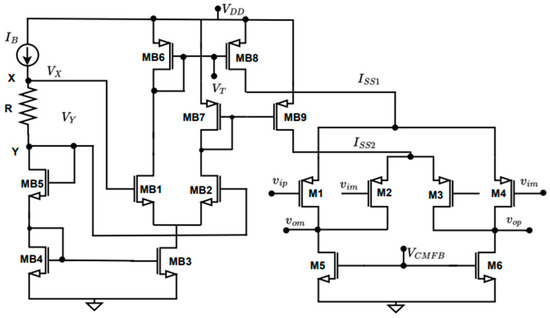
Figure 3. Schematic circuit of cross-coupled CMOS OTA with tail current generation [9].

The PMOS differential pairs M1-M4 and M2-M3 are operated in the sub-threshold region, and they receive tail currents $I_{ss1}$ and $I_{ss2}$, respectively. The effective transconductance of cross-coupled OTA is the difference between the transconductances of the two source-coupled PMOS differential pairs M1-M4 and M2-M3 and is given by

$$g_{m,eff}={\displaystyle \frac{I_{ss1}-I_{ss2}}{2\eta V_T}}={\displaystyle \frac{{△I}_{ss}}{2\eta V_T}}$$

(13)

The transconductance of cross-coupled OTA in Figure 3 can be tuned by varying the external resistor R connected between the nodes X and Y for a fixed value of current I. The value of R will set the voltage difference between nodes X and Y, which will be reflected as ${△I}_{ss}.$ The aspect ratio of transistors used in cross-coupled OTA and biasing circuit are summarized in Table 2.

Table 2. Transistor size of cross-coupled OTA.

Transistor	$[\mathbf{m}\mathbf{\ast }(\mathbf{W}/\mathbf{L}\left)\right]\mathbf{\mu }\mathbf{m}$
M1, M2, M3, M4	$4\ast (2/40)$
M5, M6	$(0.25/48)$
MB1, MB2	$2\ast (1/48)$
MB3, MB4, MB5	$2\ast (1/48)$
MB6, MB7, MB8, MB9	$2\ast (10/1)$

* denotes multiplication.

3.2. Common-Mode Feedback Circuit

The common-mode feedback signal ${\mathrm{V}}_{\mathrm{C}\mathrm{M}\mathrm{F}\mathrm{B}}$ in Figure 3 is fed by the error amplifier stage of the common-mode feedback (CMFB) scheme [33,34] illustrated in Figure 4a. The sizes of transistors used in CMFB circuit of Figure 4b are given in Table 3.

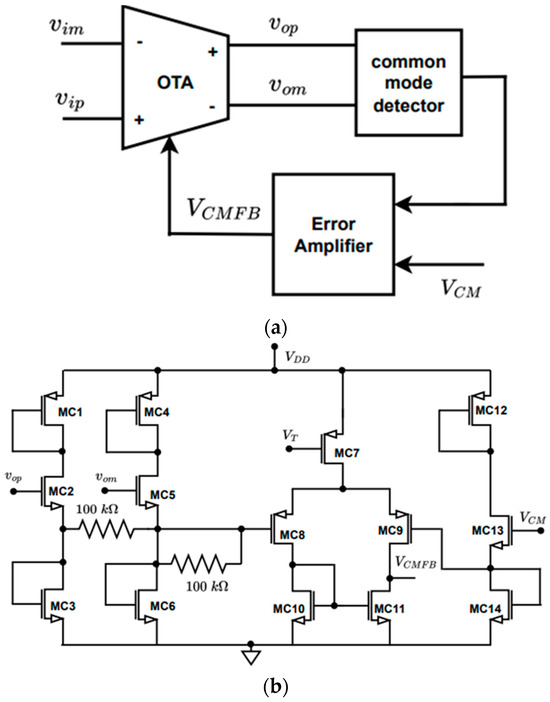
Figure 4. CMFB scheme: (a) conceptual block diagram; (b) circuit diagram.

Table 3. Sizes of transistors in CMFB circuit.

Transistor	$[\mathbf{m}\mathbf{\ast }(\mathbf{W}/\mathbf{L}\left)\right]\mathbf{\mu }\mathbf{m}$
MC1, MC4, MC12	$(1/1)$
MC2, MC3, MC5, MC6, MC13, MC14	$(0.5/10)$
MC7	$4\ast (10/1)$
MC8, MC9	$2\ast (2/20)$
MC10, MC11	$\left(0.25/48\right)$

* denotes multiplication.

4. Simulation Results

The design and simulation of FO Inverse Chebyshev filter circuits in Figure 2, of orders 1.3, 1.6, and 1.9 are performed using Cadence Virtuoso 6.1.6 and Spectre tool with UMC 180 nm CMOS technology and 1.8 V power supply. The schematic circuit of FO Inverse Chebyshev filter drawn in Cadence Virtuoso is shown in Figure 5. Here, $I_B$ and $V_{CM}$ are bias current and common-mode signal of OTA. The resistors $R_{\mathrm{0,1},\dots 7}$ are used to tune transconductance values of OTAs. The values of circuit elements used for simulation are given in Table 4.

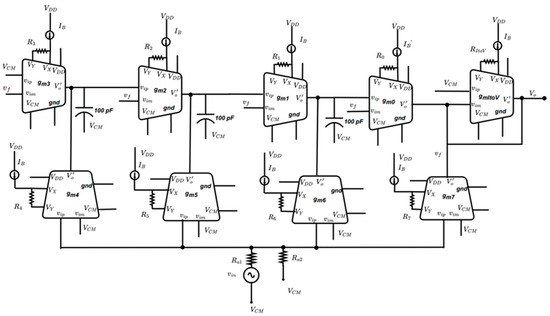
Figure 5. Schematic of OTA based Inverse Chebyshev FOF circuit of order (1 + α) drawn in Cadence Virtuoso.

Table 4. Summary of the circuit elements for inverse Chebyshev fractional filter of order 1.3, 1.6 and 1.9.

Parameter	$\mathsf{\alpha }=0.3$	$\mathsf{\alpha }=0.6$	$\mathsf{\alpha }=0.9$
$g_{m0}, g_{m7} \left(\mathrm{\mu }\mathrm{S}\right)$	$1$	$1$	$1$
${R }_{ItoV }$(MΩ)	1.606	1.606	1.606
$g_{m1 }\left(\mathrm{n}\mathrm{S}\right)$	122.16	81.51	$57.9$
$R_1$ (kΩ)	123.84	82.52	58.64
$g_{m2} \left(\mathrm{n}\mathrm{S}\right)$	8.103	4.09	4.29
$R_2$ (kΩ)	8.27	4.2	4.4
$g_{m3} \left(\mathrm{n}\mathrm{S}\right)$	2.317	3.2	3.5
$R_3$ (kΩ)	2.424	3.31	3.6
$g_{m4} \left(\mathrm{n}\mathrm{S}\right)$	420.25	683.2	710
$R_4$ (kΩ)	437.03	757.75	794.83
$g_{m5} \left(\mathrm{n}\mathrm{S}\right)$	198.54	108.5	76.54
$R_5$ (kΩ)	200.9	109.9	77.49
$g_{m6} \left(\mathrm{n}\mathrm{S}\right)$	197.67	96.124	54.4
$R_6$ (kΩ)	200.9	97.3	55.102
$R_{a1} \left(\mathrm{k}\mathrm{\Omega }\right)$	5	5	5
$R_{a2 }(\mathrm{\Omega }$)	26	23	20
$I_B$ (nA)	150

4.1. Amplitude Response

The ideal and simulated amplitude response of the Inverse Chebyshev FOF for orders 1.3, 1.6, and 1.9, obtained from MATLAB and by simulating the circuit of Figure 5 using Cadence Spectre, is depicted in Figure 6. The passband dc gain for fractional orders 1.3, 1.6, and 1.9 was found to be −8.7 dB, −6.18 dB, and −7.74 dB, respectively. The DC gain of the Spectre simulated amplitude response in Figure 6 is less than 0 dB due to finite output resistance of the transconductors used.

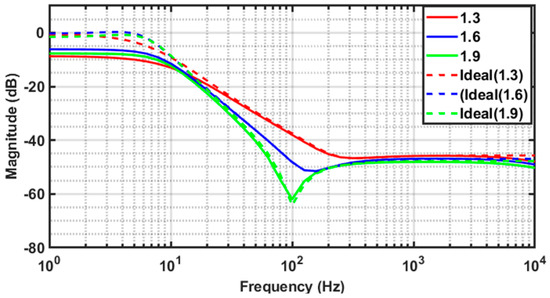
Figure 6. Ideal and simulated amplitude response of Inverse Chebyshev FOF of order 1.3, 1.6, and 1.9 obtained using MATLAB and Cadence Spectre.

The corresponding ideal and simulated phase response obtained by MATLAB and Cadence Spectre is shown in Figure 7. From the phase response plot in Figure 7, it can be observed that the phase reversal (phase shift jump) occurs at 100 Hz notch frequency as expected.

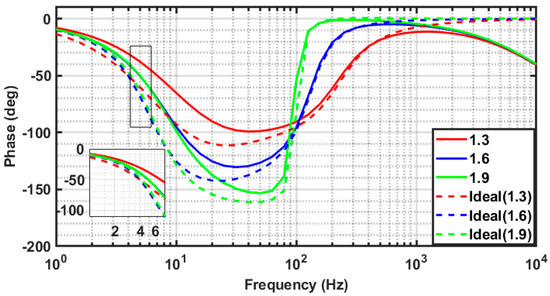
Figure 7. Ideal and simulated phase response of Inverse Chebyshev FOF of order 1.3, 1.6, and 1.9 obtained using MATLAB and Cadence Spectre.

4.2. Transient Characteristics

The time–domain behavior of the FO Inverse Chebyshev filter (FOICF) is studied by applying a sinusoidal signal of different frequencies 2, 4 and 6 Hz and 200 mV peak-to peak at the input. The input and output waveforms are shown in Figure 8a–c, which confirms the correctness of the working of the filter.

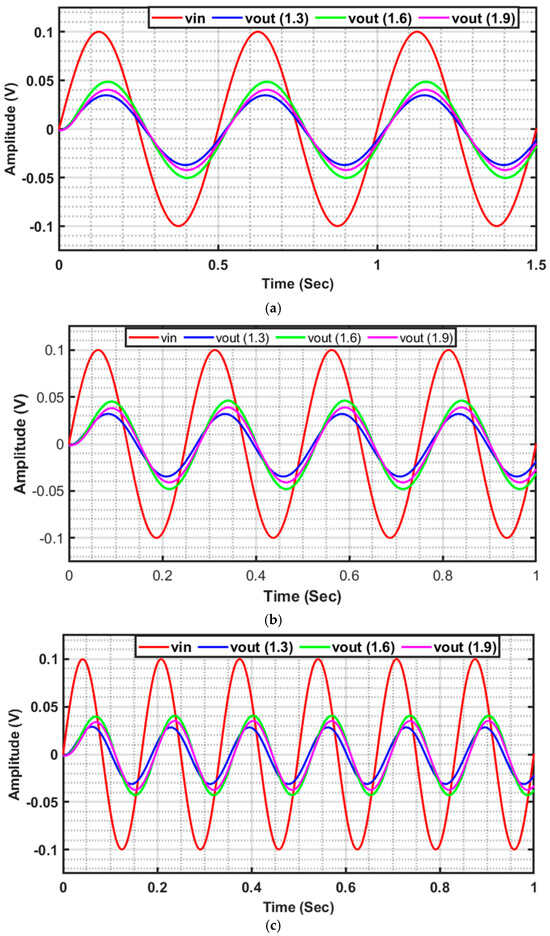
Figure 8. Transient response of fractional-order Inverse Chebyshev filter of order 1.3, 1.6, and 1.9 with 200 mV peak-to peak input at (a) 2 Hz, (b) 4 Hz, (c) 6 Hz.

The phase difference (in degrees) between input and output for FOICF of order 1.3, 1.6 and 1.9 at different input frequencies 2 Hz, 4 Hz and 6 Hz, obtained from ideal phase plot (MATLAB), simulated phase plot (Cadence Spectre) and transient plot (Cadence Spectre) are compared in Table 5. It can be observed that there is a difference between the phase values obtained from ideal and simulated phase plots for different orders and frequencies. The general trend observed is that the difference in phase values decreases as the order increases. The change in phase values for Cadence simulated plots in comparison to ideal values is believed to be due to the non-ideal finite output resistance of OTAs used.

Table 5. Phase difference between the input and output waveforms of FOICF of order1.3, 1.6, and 1.9 at different frequencies.

Frequency	Filter Order	Phase Difference (Degree)
		Phase Plot (MATLAB)	Phase Plot (Cadence Spectre)	Transient Plot (Cadence Spectre)
2 Hz	1.3	−26.3	−15.7	−16.7
	1.6	−19.97	−20.99	−21.88
	1.9	−19.7	−18.7	−19.44
4 Hz	1.3	−30.6	−49.8	−48.9
	1.6	−39.2	−49.7	−47.22
	1.9	−38.8	−46.16	−45.98
6 Hz	1.3	−71	−40	−43.1
	1.6	−80	−63	−64.6
	1.9	−70	−59	−58.39

4.3. THD and Harmonic Spectrum

The simulated plot of %THD (total harmonic distortion) variation of the FO Inverse Chebyshev LP filter for order of 1.3, 1.6, and 1.9, as a function of input voltage is presented in Figure 9. For a sinusoidal input voltage of 100 mV (−20 dB) and frequency of 2 Hz, THD is found to be less than 1%.

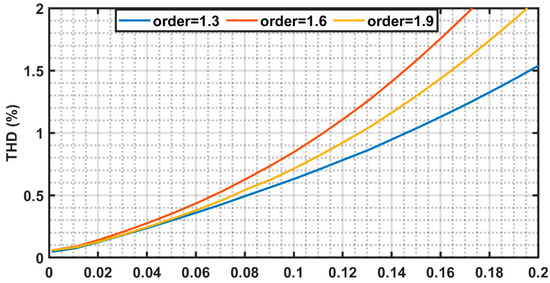
Figure 9. Plot of THD (%) versus input sweep for Inverse Chebyshev FOF of order 1.3, 1.6 and 1.9.

The ${\mathrm{I}\mathrm{R}\mathrm{N}}_{\mathrm{r}\mathrm{m}\mathrm{s}}$ (rms Input-Referred Noise) voltage over the passband of the Inverse Chebyshev FOF for an order of 1.3, 1.6, and 1.9 are 4.9 µV, 4.114 µV and 3.48 µV, respectively. The respective values of the dynamic range (DR) are found to be 83.04, 86.13, 84.71 dB, respectively. The plot of the harmonic spectrum is shown in Figure 10.

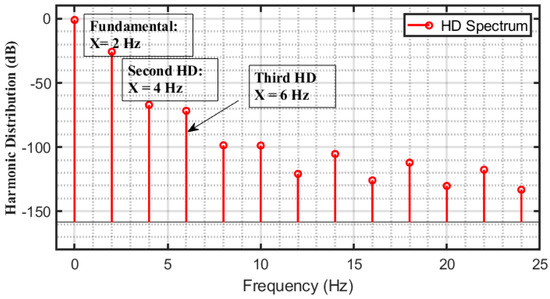
Figure 10. Simulated harmonic spectrum of Inverse Chebyshev FOF of order 1.9 with a 200 mV p-p input signal at 2 Hz.

Figure-Of-Merit (FOM) parameter [26] for the filter is given by

$$\mathrm{F}\mathrm{O}\mathrm{M}={\displaystyle \frac{\mathrm{P}}{\mathrm{D}\mathrm{R}\ast f_c\ast \mathrm{N}}}$$

(14)

where P, DR, $f_c$ and N are power consumption, dynamic range, cut-off frequency, and order of the filter, respectively. The FOM for fractional orders 1.3, 1.6, and 1.9 are found to be 101.64, 52.73, and 49.18 pJ, respectively.

4.4. Monte Carlo Plot

Monte Carlo simulations are performed for Inverse Chebyshev filter of order 1.3, 1.6 and 1.9 in Figure 5 for 1000 runs considering the effect of both the process variations and device mismatch on cut-off frequency and the resulting plots are presented in Figure 11a–c. Here, the blue curve represents Gaussian (or normal) distribution curve. From the plots, it is evident that there is no large variation in the pole frequency of the filter due to process variations. The values of mean cut-off frequency for fractional orders 1.3, 1.6 and 1.9 are 7.04, 7.83, and 8.414 Hz, respectively. The standard deviation (SD) values of cut-off frequency for fractional orders 1.3, 1.6 and 1.9 are 355.3, 219.5, and 207.3 mHz, respectively.

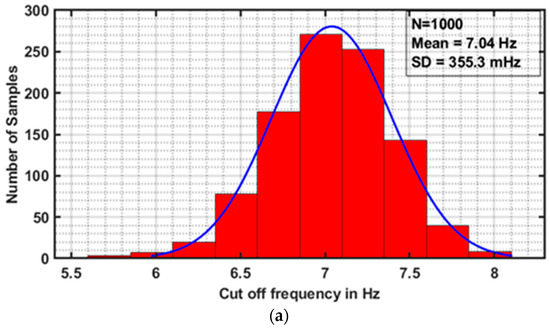
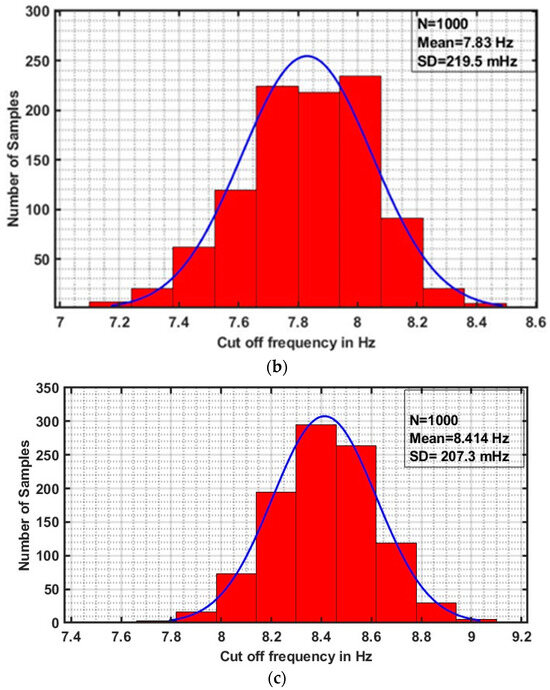
Figure 11. Monte Carlo simulation plots of Inverse Chebyshev FOF of order (a) 1.3, (b) 1.6, and (c) 1.9 with respect to cut-off frequency ${\mathrm{f}}_{\mathrm{c}}$.

4.5. Output Noise

The simulated output referred noise voltage response of the FO Inverse Chebyshev filter in Figure 5 is shown in Figure 12. The flicker noise is more dominant up to a frequency of 10 Hz, and thermal noise dominates after that. The equivalent output noise at 2 Hz for the orders 1.3, 1.6 and 1.9 are 429 µV, 409 µV and 395 µV, respectively, and is less than 125 µV within −3 dB bandwidth for 100 mV input.

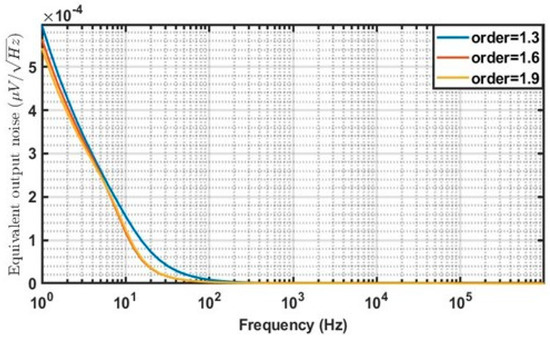
Figure 12. Output noise response of Inverse Chebyshev FOF in Figure 5.

4.6. PVT Plots

The Inverse Chebyshev filter of fractional-order 1.9 in Figure 5 is simulated across five main process corners like FF, SNFP, TT, FNSP and SS, and the resulting amplitude response plots obtained are presented in Figure 13a. At the notch frequency, the magnitude variation is found to 5.96% (from −59.7 dB (SS) to −63.38 dB (FF). The simulations are carried out across voltage variations (${\mathrm{V}}_{\mathrm{D}\mathrm{D}}$ (5%) and ${\mathrm{V}}_{\mathrm{S}\mathrm{S}}$ (5%)) and temperature variations (0, 27, 40 °C), and the resulting amplitude response plots obtained are presented in Figure 13b and Figure 13c, respectively. From Figure 13b, the magnitude variation at notch frequency with respect to voltage variations is 8.29% (from −59.2 dB (1.62 V) to −64.3 dB (1.98 V)). From Figure 13c, the magnitude variation at notch frequency with respect to temperature variations is seen to be 2% (from −61.5 dB (0 °C) to −60.3 dB (40 °C).

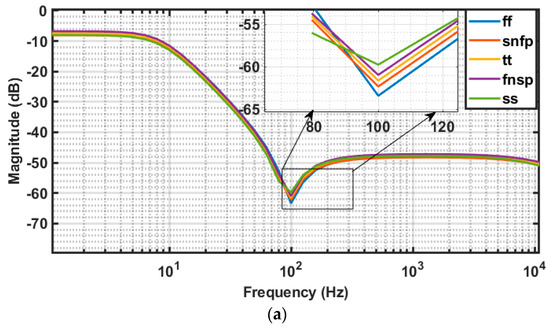
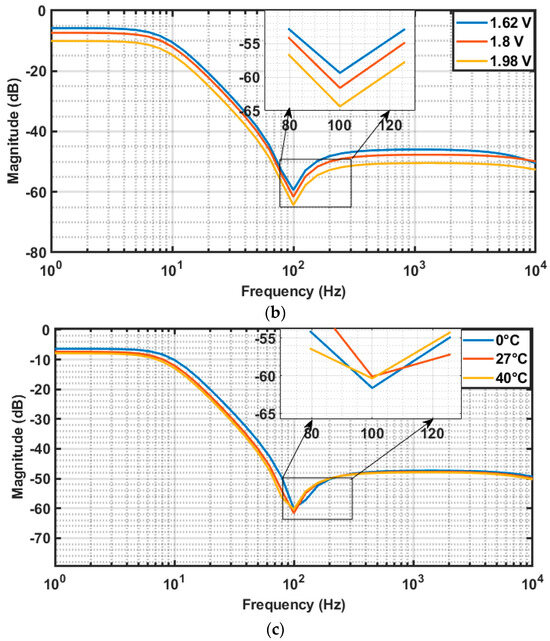
Figure 13. Magnitude response of Inverse Chebyshev filter of fractional-order 1.9 with respect to (a) process (P) corners (FF, SNFP, TT, FNSP and SS), (b) voltage (V) variations (10%), (c) temperature (T) variations (0 °C, 27 °C, 40 °C).

5. Performance Evaluation

The performance parameters of FO Inverse Chebyshev FOF circuit in Figure 4 obtained from Cadence simulation have been summarized in Table 6.

Table 6. Summary of performance characteristics of the Inverse Chebyshev FOF circuit in Figure 5.

Performance Parameter	Order
	1.3	1.6	1.9
Power $\left(\mu W\right)$ at $V_{DD}=1.8 \mathrm{V}$	13.5	13.5	13.5
The cut off frequency ${\mathrm{f}}_{\mathrm{c}}$ (Hz)	7.2	7.9	8.4
Attenuation rate (dB/dec)	−32.21	−35.75	−49.65
Attenuation $A_N$ at notch point ($\mathrm{d}\mathrm{B})$	38	48.2	62
Stopband ripple $A_S$ at 1 kHz $\left(\mathrm{d}\mathrm{B}\right)$	45.8	46.9	48
IRN $\left(\mathsf{\mu }\mathrm{V}/\sqrt{\mathrm{H}\mathrm{z}}\right)$	4.114	3.48	4.98
Dynamic range DR (dB)	83.04	86.13	84.71
FOM (picojoules)	101.64	52.73	49.18

Table 7 compares the performance parameters of the implemented Inverse Chebyshev FOF (i.e., P, THD, IRN, DR, FOM) with some of the FO filter types that have been previously reported in the literature. The DR of the Inverse Chebyshev FOF filter is better compared to [25,26]. It can be seen that the FoM of the current work is better than the FoM of the FOF in [35].

Table 7. Comparison with some fractional-order filters in the literature.

Ref/Fig	[5], Figure 2	[22], Figure 3	[26], Figure 15	[25], Figure 8	[35], Figure 3	This Paper, Figure 5
Filter type	LP FOF	LP FOF	Class AB log-domain LP FOF	Power law LP FOF	LP/HP/AP/AE FOF	LP FOF
Filter approximation type	Inverse Chebyshev	Inverse Chebyshev	Butterworth	Butterworth	Butterworth	Inverse Chebyshev
Fractional order approximation method used	CFE	CFE	CFE	-	Oustaloup	CFE
Curve fit optimization techniques used	Least-squares	Particle swarm	Least-squares	Sanathanan–Koerner (S-K) Least-squares	-	Least-squares
Filter order	1.2, 1.5, 1.8	1.2, 1.8	1.3, 1.5, 1.7	1.5	0.7, 0.8, 0.9	1.3, 1.6, 1.9
Cut off frequency (Hz)	100	100	11.7, 11.9, 11.5	1000	1000	7.2, 7.9, 8.4
Active element used	Opamp (LF411/AD844)	Opamp (741)	Nonlinear transconductor	CFOA (AD844 AN)	MO-CCCII	OTA
CMOS Technology	-	-	180 nm TSMC	-	-	180 nm UMC
Supply voltage	-	-	0.5 V	12 V	2.5 V	1.8 V
Power (P)	-	-	10.6, 10.11, 9.87 nW	-	1 mW	13.5 µW
THD	-	-	-	≤0.21%	≤0.8%	<1%
IRN	-	-	0.36, 0.64, 0.65 pA	-	129.4 pA/√Hz	4.114, 3.48, 4.98 μV⁄ √Hz
DR	-	-	44.7, 44.7, 44.8 dB	60.35 dBc (SFDR)	>60	83.04, 86.13, 84.71 dB
FOM (pJ)	-	-	4.7, 3.9, 3.7	-	1111.11	101.64, 52.73, 49.18

SFDR: Spurious-Free Dynamic Range; dBc: dB relative to the carrier; MO-CCCII: Multi-Output Second-Generation Current-Controlled Conveyor.

6. Conclusions

An Inverse Chebyshev FO LPF of order (1 + α) with α = {0.3, 0.6, 0.9} is synthesized using CFE approximation method. The magnitude ripple characteristics in the stopband are approximated using the least-squares curve fit optimization technique. The FO LPF circuit is designed for a cut-off frequency of 8 Hz with 1.8 V power supply using CC-OTA with resistor-averaged CMFB circuit. The circuit was simulated, and performance factors were evaluated using Cadence IC design suite 6.1.8 (Virtuoso and Spectre) and 180 nm UMC CMOS process models. The Spectre simulated magnitude responses are in good agreement with the MATLAB-simulated responses. From Monte Carlo plots, it is evident that the frequency deviation is within acceptable limits. Furthermore, the THD is found to be lower than 1% and DR value is larger than 83 dB. The curve fit optimization can also be carried out using minimum-phase state-space model by ‘fitmagfrd’ MATLAB routine, as a part of our future work. The work can be extended to implement the Inverse Chebyshev FOF of order (n + α).