Integral Operators in b-Metric and Generalized b-Metric Spaces and Boundary Value Problems

Abstract

We study fixed-point theorems of contractive mappings in b-metric space, cone b-metric space, and the newly introduced extended b-metric space. To generalize an existence and uniqueness result for the so-called ${\mathsf{\Phi }}_s$ functions in the b-metric space to the extended b-metric space and the cone b-metric space, we introduce the class of ${\mathsf{\Phi }}_M$ functions and apply the Hölder continuous condition in the extended b-metric space. The obtained results are applied to prove the existence and uniqueness of solutions and positive solutions for nonlinear integral equations and fractional boundary value problems. Examples and numerical simulation are given to illustrate the applications.

1. Introduction

Fixed-point theorems in metric spaces are fundamental for operator equations, including differential, difference, and integral equations. For example, in studying solutions for various boundary value problems, a common approach is to convert the problem into an integral equation and then apply fixed-point theorems.

In the literature, the traditional metric spaces have been generalized in different directions such as partial metric space [1], 2-metric space [2], G-metric space [3], cone metric spaces [4], complex-valued metric spaces [5], and generalized symmetric spaces [6]. The definition of a b-metric space given in [7] is as follows.

Let X be a space and let ${\mathbb{R}}^{+}$ denote the set of all nonnegative numbers. A function $d:X\times X\to {\mathbb{R}}^{+}$ is said to be a b-metric if for all $x,y,z\in X$ and all $r>0$, the following conditions are satisfied:

$$\begin{array}{c}d(x,y)=0\mathrm{if}x=y\end{array}$$

(1)

$$\begin{array}{c}d(x,y)=d(y,x)\end{array}$$

(2)

$$\begin{array}{c}d(x,y)<r\mathrm{and}d(x,z)<r\mathrm{imply}d(y,z)<2r.\end{array}$$

(3)

A pair $(X,d)$ is called an b-metric space.

In [7], Condition (3) was replaced by the following weaker condition:

$$d(y,z)\le 2d(x,y)+2d(x,z)\mathrm{for} \mathrm{all}x,y,z\in X.$$

(4)

Thus, a function $d:X\times X\to {\mathbb{R}}^{+}$ is said to be a b-metric if for all $x,y,z\in X$, Conditions (1), (2), and (4) are satisfied. Banach’s fixed-point theorem was generalized to the so-called b-metric space in [7].

In fact, in earlier work [8], to extend the estimates of Calderon and Zygmund on certain singular integrals to homogeneous spaces, the following condition (5) was imposed:

$$\rho (x,y)\le k\left(\rho \right(x,z)+\rho (z,y\left)\right)\mathrm{for}\mathrm{all}x,y,z\in X,$$

(5)

where k is a constant. In [8], Conditions (1), (2), and (5) are referred to as a quasi-metric space or a b-metric space.

Just as a normed space is a metric space, a quasi-normed space is a quasi-metric space. Due to the relaxation of the triangle condition, some results in the standard metric space may not hold in a quasi-metric space, or a b-metric space. For example, the ‘open’ balls in a b-metric space may not be open sets [9]. For the topology of b-metric space, including compactness, metrizability, contraction, and fixed points, we refer to the most recent work by Navascués and Mohapatra [9]. Moreover, the concept of b-metric space has been further generalized to extended b-metric space [10].

In applications, b-metric spaces have been applied to similarity and pattern recognition [11], string matching and trademark shapes [12], ice floe tracking [13], optimal transport path in probability measures [14], and other areas. The application in pattern recognition, in particular, is a major topic in data analytics and machine learning algorithms.

To extend the Banach contraction principle in a metric space to b-metric spaces, the following class of functions is fundamental [15].

Definition 1. 

Let S be a family of all functions $\alpha :[0,\infty )\to [0,1)$ satisfying the property:

$$\underset{n\to \infty }{lim}\alpha \left(t_n\right)=1\mathit{implies}\underset{n\to \infty }{lim}{t}_n=0.$$

On the basis of Definition 1, the class of ${\mathsf{\Phi }}_s$ function is essential for fixed points in b-metric spaces.

Definition 2 

([16]). For $s\ge 1$, let ${\mathsf{\Phi }}_s$ denote the family of functions φ: $[0,\infty )\to \left[0,{\displaystyle \frac{1}{s}}\right)$ satisfying the condition:

$$\underset{n\to \infty }{lim}\phi \left({\nu }_n\right)={\displaystyle \frac{1}{s}}\mathit{implies}\mathit{that}\underset{n\to \infty }{lim}{v}_n=0.$$

We will apply the following fixed-point theorem in b-metric spaces to integral equations to obtain results on the existence and uniqueness of solutions.

Theorem 1 

([17]). Let $(X,d)$ be a complete b-metric space with parameter $k\ge 1$ and $\psi :X\to X$ a self-mapping such that

$$k^{2}d(\psi \left(x\right),\psi \left(y\right))\le \phi \left(d(x,y)\right)d(x,y)$$

for all $x,y\in X$ and some $\phi \in {\mathsf{\Phi }}_s$. Then, ψ has a unique fixed point.

The class of ${\mathsf{\Phi }}_s$ functions is also referred to as $G_1$ functions in [11] and S functions in [17]. We adopt the notation ${\mathsf{\Phi }}_s$ functions in this paper because we will introduce the parallel class of ${\mathsf{\Phi }}_M$ functions to extend the results to the extended b-metric spaces. In addition, we also consider positive solutions via the cone b-metric spaces [18]. Our results generalize some previous work on this topic [17]. The rest of this paper follows the approach from abstract to concrete. Section 2 considers the general equations involving the Urysohn integral operator [19]. Then, positive solutions in cone b-metric spaces are obtained in Section 3. Next, in Section 4, to generalize the results to the extended b-metric spaces, the Hölder continuous condition in the extended b-metric space is employed. Lastly, in Section 5, the results are applied to a fractional boundary value problem that has been widely studied previously. In addition, a numerical simulation example is provided to intuitively illustrate the results.

2. The Urysohn Integral Operator

The Urysohn integral operator in a metric space has been widely studied, for example, in the earlier work of [19]. We will consider the existence and uniqueness of solutions for equations involving the Urysohn operator in a b-metric space. The following definition for a b-metric space is given in [9].

Definition 3 

([9]). A b-metric space X is a set endowed with a mapping $d:X\times X\to {\mathbb{R}}^{+}$ with the following properties:

• $d(x,y)\ge 0,d(x,y)=0$ if and only if $x=y$.
• $d(x,y)=d(y,x)$ for any $x,y\in X$.
• There exists $k\ge 1$ such that $d(x,y)\le k\left(d\right(x,z)+d(z,y\left)\right)$ for any $x,y,z\in X$.

The constant k is the index of the b-metric space, and d is called a b-metric.

Obviously, a usual metric space is a b-metric space with the index $k=1$.

Consider $X=C[0,\ell ]$, all continuous functions on the interval $[0,\ell ]$. It is known that $(X,d)$ is a complete b-metric space with parameter $k=2^{p-1}$ [17], where $p>1$ and d is defined by

$$d(f,g)=\underset{0\le x\le \ell }{max}{|f\left(x\right)-g\left(x\right)|}^p.$$

Let $F:[0,\ell ]\times [0,\ell ]\to \mathbb{R}$, $g:[0,\ell ]\times [0,\ell ]\times \mathbb{R}\to \mathbb{R}$, and $h:[0,\ell ]\to \mathbb{R}$ be continuous functions. Our first result is on the integral equations defined with the Urysohn integral operator:

$$z\left(t\right)=h\left(t\right)+{\int }_0^{\ell }F(t,s)g(t,s,z\left(s\right))ds.$$

(6)

Theorem 2. 

Assume that $\theta \in {\mathsf{\Phi }}_s$ with $s=k=2^{p-1}$ for $p>1$. If the following two conditions hold:

• For all $t,s\in [0,\ell ]$ and $u,v\in X$,

  $$|g(t,s,u\left(s\right))-g(t,s,v\left(s\right))|\le {\left({\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{k^2}}\right)}^{{\displaystyle \frac{1}{p}}};$$
• For all $t,s\in [0,\ell ]$,

  $$\underset{0\le t\le \ell }{max}{\int }_0^{\ell }{|F(t,s)|}^{n}ds\le {\displaystyle \frac{1}{{\ell }^{\frac{n}{m}}}},$$

  where $n,m\in [1,\infty )$ with ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$;

then Equation (6) has a unique solution $z\in X$.

Proof. 

Define the mapping $G:X\to X$ as follows

$$Gu\left(t\right)=h\left(t\right)+{\int }_0^{\ell }F(t,s)g(t,s,u\left(s\right))ds.$$

Then, we have

$$\begin{array}{cc}\hfill d(Gu,Gv)& =\underset{t\in [0,\ell ]}{max}{|Gu\left(t\right)-Gv\left(t\right)|}^p\hfill \\ & =\underset{t\in [0,\ell ]}{max}\left\{{\left|h\left(t\right)+{\int }_0^{\ell }F(t,s)g(t,s,u\left(s\right))ds-h\left(t\right)-{\int }_0^{\ell }F(t,s)g(t,s,v\left(s\right))ds\right|}^p\right\}\hfill \\ & =\underset{t\in [0,\ell ]}{max}\left\{{\left|{\int }_0^{\ell }F(t,s)[g(t,s,u\left(s\right))-g(t,s,v\left(s\right))]ds\right|}^p\right\}.\hfill \end{array}$$

From Hölder’s inequality, we obtain

$$\begin{array}{cc}\hfill d(Gu,Gv)& \le \underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{|F(t,s)|}^{n}ds\right)}^{{\displaystyle \frac{p}{n}}}{\left({\int }_0^{\ell }{|g(t,s,u\left(s\right))-g(t,s,v\left(s\right))|}^{m}ds\right)}^{{\displaystyle \frac{p}{m}}}\right\}\hfill \\ & \le \underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{|F(t,s)|}^{n}ds\right)}^{{\displaystyle \frac{p}{n}}}\right\}\underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{|g(t,s,u\left(s\right))-g(t,s,v\left(s\right))|}^{m}ds\right)}^{{\displaystyle \frac{p}{m}}}\right\},\hfill \end{array}$$

where $n,m\in [1,\infty )$ and ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$. Conditions 1 and 2 ensure that

$$\begin{array}{cc}\hfill d(Gu,Gv)& \le {\displaystyle \frac{1}{{\ell }^{\frac{p}{m}}}}\underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{\left({\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{k^2}}\right)}^{{\displaystyle \frac{m}{p}}}ds\right)}^{{\displaystyle \frac{p}{m}}}\right\}\hfill \\ & ={\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{k^2}}.\hfill \end{array}$$

Hence, we obtain

$$k^{2}d(Gu,Gv)\le \theta \left(d(u,v)\right)d(u,v).$$

Theorem 1 implies that G has a unique solution in X. □

As corollaries of Theorem 2, we obtain the following results that are related to Theorems 5 and 6 of [17].

Theorem 3. 

Assume that the following conditions hold:

• For all $t,s\in [0,\ell ]$ and $u,v\in X$, we have

  $$|g(t,s,u\left(s\right))-g(t,s,v\left(s\right){|}^p\le {\displaystyle \frac{e^{-d(u,v)}d(u,v)}{8^{p-1}}};$$
• For all $t,s\in [0,\ell ]$ we have

  $$\underset{0\le t\le \ell }{max}{\int }_0^{\ell }F{(s,t)}^{2}ds\le {\displaystyle \frac{1}{\ell }}.$$

Then, Equation (6) has a unique solution $z\in X$.

Proof. 

In Theorem 2, let $\theta \left(t\right)={\displaystyle \frac{1}{k}}{e}^{-t},t>0$ and $\theta \left(0\right)\in \left[0,{\displaystyle \frac{1}{k}}\right)$; then, $\theta \in {\mathsf{\Phi }}_s$. Condition 1 is equivalent to

$$|g(t,s,u\left(s\right))-g(t,s,v\left(s\right){|}^p\le {\displaystyle \frac{e^{-d(u,v)}d(u,v)}{k^3}}\le {\displaystyle \frac{e^{-d(u,v)}d(u,v)}{8^{p-1}}}.$$

Condition 2 of Theorem 3 is a special case of Condition 2 of Theorem 2 when $m=n=2$. □

Theorem 4. 

Suppose that

• For all $t,s\in [0,l]$ and $u,v\in X$, we have

  $$|g(t,s,u\left(s\right))-g(t,s,v\left(s\right){|}^p\le {\displaystyle \frac{ln(1+|u\left(s\right)-v\left(s\right){|}^p)}{8^{p-1}}};$$
• For all $t,s\in [0,l]$, we have

  $$\underset{0\le t\le \ell }{max}{\int }_0^{\ell }{|F(t,s)|}^{n}ds\le {\displaystyle \frac{1}{{\ell }^{\frac{n}{m}}}},$$
  where $n,m\in [1,\infty )$ with ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$. Then, Equation (6) has a unique solution $z\in X$.

Proof. 

From Condition 1, we have

$$2^{2p-2}{|g(t,s,u\left(s\right))-g(t,s,v\left(s\right)|}^p\le {\displaystyle \frac{ln(1+|u\left(s\right)-v\left(s\right){|}^p)}{2^{p-1}}}\le {\displaystyle \frac{d(u,v)}{2^{p-1}}}.$$

Thus, both conditions of Theorem 2 are satisfied for $k=2^{p-1}$ and $\theta \left(t\right)={\displaystyle \frac{1}{2^{p-1}}}$. □

Remark 1. 

Theorems 3 and 4 are parallel to Theorems 5 and 6 of [17], respectively, in the way that $d(u,v)$ is in the position of $M(u,v)$ defined as

$$M(u,v)=max\left\{d\right(u,v),d(u,Gu),d(v,Gv\left)\right\}.$$

3. Positive Solutions

Positive solutions are particular important in some modelling applications. In a b-metric space, a partial order can be introduced by a cone defined below.

Definition 4 

([18]). Let X be a real Banach space with zero element denoted by 0. A subset C of X is called a cone when the following conditions hold:

• C is closed, nonempty, and $C\ne \left\{0\right\}$;
• If $a,b\in {\mathbb{R}}^{+}$ and $x,y\in C$ then $ax+by\in C$;
• $C\cap -C=\left\{0\right\}$.

Given a cone C, a partial ordering ≤ with respect to C by $x\le y$ if and only if $y-x\in C$. Let $x<y$ denote that $x\le y$ but $x\ne y$.

Definition 5 

([18]). Let C be a cone of X. Then, C is said to be normal if there exists a real number $K>0$ such that for all $x,y\in X$, $0\le x\le y$ implies $\parallel x\parallel \le K\parallel y\parallel$.

Definition 6 

([18]). Let C be a cone of X and A be a nonempty set. A mapping $d:A\times A\to C$ is called a cone b-metric if the conditions of Definition 3 are satisfied with respect to the inequality induced by C.

The following theorem shows that the contraction mapping theorem for fixed points in a Banach space holds true in a complete cone b-metric space.

Theorem 5 

([18]). Let $(X,d)$ be a complete cone b-metric space with the coefficient $k\ge 1$. Suppose the mapping $\psi :X\to X$ satisfies the contractive condition

$$d\left(\psi \right(x),\psi (y\left)\right)\le \lambda d(x,y),forx,y\in X,$$

where $\lambda \in [0,1)$ is a constant. Then, ψ has a unique fixed point in X. Furthermore, the iterative sequence $\left\{{\psi }^{n}x\right\}$ converges to the fixed point.

Let $X=C[0,\ell ]$ with the commonly applied supremum norm $\parallel f\parallel =sup\{|f\left(x\right)|:x\in [0,\ell \left]\right\}$. A natural cone $P\subset C[0,\ell ]$ is defined as

$$P=\{f\in X:f(x)\ge 0\mathrm{for}\mathrm{all}x\in [0,\ell \left]\right\}.$$

(7)

Let $d:X\times X\to K$ be defined by $d(f,g)\left(t\right)={|f\left(t\right)-g\left(t\right)|}^p$, denoted as $d(f,g)={|f-g|}^p$ for $p\ge 1$. Then, Conditions 1 and 2 of Definition 3 are trivially satisfied. We will show that Property 3 holds for $k=2^{p-1}$. First, consider

$$d(f,h)={|f-h+g-g|}^p={|(f-g)+(g-h)|}^p;$$

it is clear that

$${|x+y|}^p\le 2^{p-1}{(|x|}^p+{|y|}^p).$$

With a sufficient substitution, we arrive at

$${|f-h|}^p\le 2^{p-1}{(|f-g|}^p{+|g-h|}^p).$$

This is equivalent to Condition 3 of Definition 3.

More examples of cone b-metric spaces can be found in [4,6].

Theorem 6. 

Let $X=C[0,\ell ]$ and P be the cone defined by (7). Then, $(X,d)$ is a complete cone b-metric space with coefficient $2^{p-1}$ where $d:X\times X\to K$ is defined by

$$d(x,y)={|x-y|}^p$$

for some $p\ge 1$. Furthermore, let $F:[0,\ell ]\times [0,\ell ]\to \mathbb{R}$, $g:[0,\ell ]\times [0,\ell ]\times \mathbb{R}\to \mathbb{R}$, and $h:[0,\ell ]\to \mathbb{R}$ be continuous and $\theta \in {\mathsf{\Phi }}_s$ for $s={\displaystyle \frac{1}{2^{p-1}}}$. Assume that the following conditions hold:

• For all $t,s\in [0,1]$ and $u,v\in X$, there exists a constant $r>{\displaystyle \frac{1}{2^{p-1}}}$ such that

  $$|g(t,s,u\left(s\right)-g(t,s,v\left(s\right))|\le {\left({\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{r}}\right)}^{{\displaystyle \frac{1}{p}}};$$
• For all $t,s\in [0,\ell ]$,

  $${\int }_0^{\ell }{|F(t,s)|}^{n}ds\le {\displaystyle \frac{1}{{\ell }^{\frac{n}{m}}}},$$

where $n,m\in [1,\infty )$ with ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$. Then, the integral equation

$$z\left(t\right)=|h\left(t\right)|+\left|{\int }_0^{\ell }F(t,s)g(t,s,z\left(s\right))ds\right|$$

has a unique solution $z\in P$.

Proof. 

The cone b-metric space $(X,d)$ is complete as P is closed regarding the cone b-metric [17,18]. Suppose the mapping $T:X\to P$ is defined by

$$Tu\left(t\right)=|h\left(t\right)|+\left|{\int }_0^{\ell }F(t,s)g(t,s,u\left(s\right))ds\right|$$

for $u\in X$ and $s,t\in [0,\ell ]$. Then,

$$\begin{array}{cc}\hfill d(Tu,Tv)\left(t\right)& ={|Tu\left(t\right)-Tv\left(t\right)|}^p\hfill \\ & ={\left||h\left(t\right)|+\left|{\int }_0^{\ell }F(t,s)g(t,s,u\left(s\right))ds\right|-|h\left(t\right)|-\left|{\int }_0^{\ell }F(t,s)g(t,s,v\left(s\right))ds\right|\right|}^p\hfill \\ & \le {\left|{\int }_0^{\ell }F(t,s)[g(t,s,u\left(s\right))-g(t,s,v\left(s\right))]ds\right|}^p\hfill \end{array}$$

by the reverse triangle inequality. From Hölder’s inequality, we can obtain

$$\begin{array}{cc}\hfill d(Tu,Tv)\left(t\right)& \le {\left({\int }_0^{\ell }{|F(t,s)|}^{n}ds\right)}^{{\displaystyle \frac{p}{n}}}{\left({\int }_0^{\ell }{|g(t,s,u\left(s\right))-g(t,s,v\left(s\right))|}^{m}ds\right)}^{{\displaystyle \frac{p}{m}}}\hfill \end{array}$$

where $n,m\in [1,\infty )$ satisfy ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$. From Assumptions 1 and 2, we have

$$\begin{array}{cc}\hfill d(Tu,Tv)& \le {\displaystyle \frac{1}{{\ell }^{\frac{p}{m}}}}{\left({\int }_0^{\ell }{\left({\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{r}}\right)}^{{\displaystyle \frac{m}{p}}}ds\right)}^{{\displaystyle \frac{p}{m}}}\hfill \\ & ={\displaystyle \frac{\theta \left(d\right(u,v\left)\right)d(u,v)}{r}}.\hfill \end{array}$$

Hence,

$$d(Tu,Tv)\le {\displaystyle \frac{1}{2^{p-1}r}}d(u,v).$$

Theorem 5 ensures that T has a unique solution in P. □

4. Extension to the Extended b-Metric Spaces

The concept of b-metric space was generalized to the so-called extended b-metric space recently; see [10,20], for example.

Definition 7 

([10]). Let X be a nonempty set, $f:X\times X\to [1,\infty )$, and $d_f:X\times X\to [0,\infty )$. If for all $x, y, z\in X$ we have

• $d_f(x,y)=0$ if and only if $x=y$,
• $d_f(x,y)=d_f(y,x)$,
• $d_f(x,z)\le f(x,z)[d_f(x,y)+d_f(y,z)],$

then $d_f$ is called an extended b-metric and the pair $(X,d_f)$ is called an extended b-metric space. We will denote f as a b-function.

For definitions such as convergence, Cauchy sequence, and complete, we refer to [10]. The following fixed-point theorem in a extended b-metric space was given in [10,20].

Theorem 7 

([10]). Let $(X,d_f)$ be a complete extended b-metric space such that $d_f$ is a continuous functional. Let $T:X\to X$ satisfy

$$d_f(Tx,Ty)\le k{d}_f(x,y)$$

for all $x,y\in X$ and some $k\in [0,1)$. Furthermore, for every $x_0\in X$, suppose that

$$\underset{n,m\to \infty }{lim}f(x_n,x_m)<{\displaystyle \frac{1}{k}}$$

where $x_n=T^n{x}_0$. Then, T has a unique fixed point and $T^n{x}_0$ converges to this fixed point.

To extend results from Section 2 to an extended b-metric space, we introduce the following class of ${\mathsf{\Phi }}_M$ functions that is analogous to the class of ${\mathsf{\Phi }}_s$ functions for the b-metric spaces.

Definition 8. 

Let $(X,d)$ be an extended complete b-metric space with a bounded b-function γ. Let $M={sup}_{x,y\in X}\gamma (x,y)$ and $\vartheta :[0,\infty )\to \left[0,{\displaystyle \frac{1}{M}}\right)$ be a function satisfying the following condition: if there exists a sequence $\left\{a_n\right\}$,

$$\underset{n\to \infty }{lim}\vartheta \left(a_n\right)={\displaystyle \frac{1}{M}}$$

then

$$\underset{n\to \infty }{lim}{a}_n=0.$$

We define ${\mathsf{\Phi }}_M$ to be the set of all functions of this form.

Corollary 1. 

Let $(X,d_f)$ be a complete extended b-metric space with a bounded b-function f such that $d_f$ is a continuous functional, and let ϑ be a ${\mathsf{\Phi }}_M$ function. Let $T:X\to X$ satisfy

$$d_f(Tx,Ty)\le \vartheta \left(d_f(x,y)\right)d_f(x,y)$$

for all $x,y\in X$. Furthermore, for every $x_0\in X$, suppose that

$$\underset{n,m\to \infty }{lim}f(x_n,x_m)<{\displaystyle \frac{1}{{sup}_{x\in [0,\infty )}\vartheta \left(x\right)}}$$

where $x_n=T^n{x}_0$. Then, T has a unique fixed point and $T^n{x}_0$ converges to this fixed point.

Proof. 

Since $\vartheta \in {\mathsf{\Phi }}_M$, we know that $\vartheta \left(x\right)\in \left[0,{\displaystyle \frac{1}{M}}\right)$ for all $x\in [0,\infty )$ where

$$M=sup\left\{f\right(u,v):u,v\in X\}\ge sup\left\{f\right(u,u):u\in X\}.$$

Thus, by Theorem 7, the result holds true. □

Remark 2. 

If $T^n{x}_0$ diverges for some $x_0$, then T has no fixed point; hence, it is safe to assume that $T^n{x}_0$ converges to some u, which simplifies the requirement to

$$f(u,u)<{\displaystyle \frac{1}{{sup}_{x\in [0,\infty )}\vartheta \left(x\right)}}$$

for all u.

The following result is an extension of Theorem 2 to the extended b-metric spaces.

Theorem 8. 

Let $X=C[0,\ell ]$ and $(X,d_{\gamma })$ be a complete extended b-metric space where $d_{\gamma }$ is defined by

$$d_{\gamma }(f,g)=\underset{0\le x\le \ell }{max}{|f\left(x\right)-g\left(x\right)|}^p$$

for $p\ge 1$ and $\gamma (f,g)$ be the b-function and suppose $\gamma (f,g)$ is bounded above. Let $F:[0,\ell ]\times [0,\ell ]\to \mathbb{R}$, $g:[0,\ell ]\times [0,\ell ]\times \mathbb{R}\to \mathbb{R}$, and $h:[0,\ell ]\to \mathbb{R}$ be continuous functions. Let ϑ be a ${\mathsf{\Phi }}_M$ function with

$$\underset{x\in [0,\infty )}{sup}\left\{\vartheta \left(x\right)\right\}\underset{f\in X}{sup}\left\{\gamma (f,f)\right\}<1.$$

Condition 2

Suppose that the following two conditions hold:

• For all $t,s\in [0,\ell ]$ and $u,v\in X$,

  $$|g(t,s,u\left(s\right))-g(t,s,v\left(s\right))|\le {\left(\vartheta \left(d_{\gamma }(u,v)\right)d_{\gamma }(u,v)\right)}^{{\displaystyle \frac{1}{p}}};$$
• For all $t,s\in [0,\ell ]$,

  $$\underset{0\le t\le \ell }{max}{\int }_0^{\ell }{|F(t,s)|}^{n}ds\le {\displaystyle \frac{1}{{\ell }^{\frac{n}{m}}}}$$

for $m,n\in [1,\infty )$ with ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}=1$. Then, the integral equation

$$z\left(t\right)=h\left(t\right)+{\int }_0^{\ell }F(t,s)g(t,s,z\left(s\right))ds$$

has a unique solution $z\in X$.

Proof. 

Define the mapping $T:X\to X$ by

$$Tu\left(t\right)=h\left(t\right)+{\int }_0^{\ell }F(t,s)g(t,s,u\left(s\right))ds.$$

We observe that

$$\underset{n,m\to \infty }{lim}\gamma (T^n{u}_0,T^m{u}_0)\le \underset{f\in X}{sup}\left\{\gamma (f,f)\right\}<{\displaystyle \frac{1}{{sup}_{x\in [0,\infty )}\left\{\vartheta \left(x\right)\right\}}}$$

for any $u_0\in X$. From Condition 2 , it is straightforward that we will obtain

$$d_{\gamma }(Tu,Tv)\le \vartheta \left(d_{\gamma }(u,v)\right)d_{\gamma }(u,v);$$

hence, T has a unique fixed point. Furthermore, $T^n{u}_0$ converges to this fixed point from Corollary 1. □

Remark 3. 

In Theorem 8, $\gamma (f,g)$ is not empty since the constant function $2^{p-1}\in \gamma (f,g)$.

Remark 4. 

Similarly to Section 3, the result can be extended to an extended cone b-metric space for a mapping $T:X\to X$ with a cone P [21].

5. Applications to Boundary Value Problems

Many boundary value problems can be converted to fixed-point problems for the Hammerstein integral operator that is a special case of the Urysohn operator. In this section, we apply the general results for the Urysohn operator to the Hammerstein integral operator, which then provides solutions for some boundary value problems, for example, the fractional boundary value problem that has been widely studied previously [12]. We first extend the Hölder continuous functions or Lipschitz conditions defined for a metric space [22] to the extended b-metric spaces.

Definition 9. 

Let $(X,d_X)$ and $(Y,d_Y)$ be extended b-metric spaces. A function $f:X\to Y$ is said to be Hölder continuous of order $\alpha >0$ or satisfy the Hölder condition of order $\alpha >0$ also known as the Uniform Lipschitz condition of order $\alpha >0$ if there exists an $M\ge 0$ such that for all $x,y\in X$,

$$d_Y(f\left(x\right),f\left(y\right))\le M{d}_X{(x,y)}^{\alpha }.$$

Theorem 9. 

Let $X=C[0,\ell ]$ and define extended b-metric

$$d(u,v)=\underset{s\in [0,1]}{max}{|u\left(s\right)-v\left(s\right)|}^p$$

where $p\ge 1$ and $(X,d)$ has b-function γ. Let $G:[0,\ell ]\times [0,\ell ]\to \mathbb{R}$, $h:[0,\ell ]\to \mathbb{R}$, $g:[0,\ell ]\to \mathbb{R}$ and $f:C[0,\ell ]\to \mathbb{R}$ be continuous functions and $c=inf\left\{\vartheta \right(x):x\in [0,\infty \left)\right\}$ where $\vartheta \in {\mathsf{\Phi }}_M$. Assume that the following conditions hold:

• $$\underset{x\in [0,\infty )}{sup}\left\{\vartheta \left(x\right)\right\}\underset{u\in X}{sup}\left\{\gamma (u,u)\right\}<1.$$
• f is Hölder continuous of order ${\displaystyle \frac{1}{p}}$ with respect to the extended b-metric d above and $M\le c$ for all $u,v\in C[0,\ell ]$.
• For all $t,s\in [0,\ell ]$ we have

  $$\underset{t\in [0,\ell ]}{max}{\int }_0^{\ell }{|G(t,s)|}^{n}ds\le {\displaystyle \frac{1}{{\ell }^{\frac{n}{p}}}}.$$
• $${\int }_0^{\ell }{|h\left(s\right)|}^{m}ds\le 1,$$

where $m,n\in [1,\infty )$ are such that ${\displaystyle \frac{1}{m}}+{\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{p}}=1$. Then, the Hammerstein integral equation

$$u\left(t\right)=g\left(t\right)+{\int }_0^{\ell }G(t,s)h\left(s\right)f\left(u\left(s\right)\right)ds$$

has a unique solution $u\in X$.

Proof. 

We define the mapping $T:X\to X$ by

$$Tu\left(t\right)=g\left(t\right)+{\int }_0^{\ell }G(t,s)h\left(s\right)f\left(u\left(s\right)\right)ds.$$

Then,

$$\begin{array}{cc}\hfill d(Tu,Tv)& =\underset{t\in [0,\ell ]}{max}{|Tu\left(t\right)-Tv\left(t\right)|}^p\hfill \\ & =\underset{t\in [0,\ell ]}{max}\left\{{\left|g\left(t\right)+{\int }_0^{\ell }G(t,s)h\left(s\right)f\left(u\left(s\right)\right)ds-g\left(t\right)-{\int }_0^{\ell }G(t,s)h\left(s\right)f\left(v\left(s\right)\right)ds\right|}^p\right\}\hfill \\ & =\underset{t\in [0,\ell ]}{max}\left\{{\left|{\int }_0^{\ell }G(t,s)h\left(s\right)[f\left(u\left(s\right)\right)-f\left(v\left(s\right)\right)]ds\right|}^p\right\}.\hfill \end{array}$$

From the generalized Hölder’s inequality,

$$\begin{array}{cc}\hfill d(Tu,Tv)& \le \underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{|G(t,s)|}^{n}ds\right)}^{{\displaystyle \frac{p}{n}}}{\left({\int }_0^{\ell }{|h\left(s\right)|}^{m}ds\right)}^{{\displaystyle \frac{p}{m}}}{\int }_0^{\ell }{|f\left(u\left(s\right)\right)-f\left(v\left(s\right)\right)|}^{p}ds\right\}\hfill \\ & ={\left({\int }_0^{\ell }{|h\left(s\right)|}^{m}ds\right)}^{{\displaystyle \frac{p}{m}}}{\int }_0^{\ell }{|f\left(u\left(s\right)\right)-f\left(v\left(s\right)\right)|}^{p}ds\underset{t\in [0,\ell ]}{max}\left\{{\left({\int }_0^{\ell }{|G(t,s)|}^{n}ds\right)}^{{\displaystyle \frac{p}{n}}}\right\},\hfill \end{array}$$

where $n,m\in [1,\infty )$ are arbitrary and ${\displaystyle \frac{1}{n}}+{\displaystyle \frac{1}{m}}+{\displaystyle \frac{1}{p}}=1$. From Assumptions 2, 3, and 4, we have

$$\begin{array}{cc}\hfill d(Tu,Tv)& \le {\displaystyle \frac{1}{\ell }}{\int }_0^{\ell }\underset{s\in [0,\ell ]}{max}{|f\left(u\left(s\right)\right)-f\left(v\left(s\right)\right)|}^{p}ds\hfill \\ & \le {\displaystyle \frac{1}{\ell }}{\int }_0^{\ell }M\underset{s\in [0,\ell ]}{max}{|u\left(s\right)-v\left(s\right)|}^{p}ds\hfill \\ & \le {\displaystyle \frac{1}{\ell }}{\int }_0^{\ell }c\underset{s\in [0,\ell ]}{max}{|u\left(s\right)-v\left(s\right)|}^{p}ds.\hfill \end{array}$$

Hence,

$$d(Tu,Tv)\le cd(u,v)\le \theta \left(d\right(u,v\left)\right)d(u,v).$$

Furthermore, Condition (1) guarantees us that

$$\underset{n,m\to \infty }{lim}\gamma (T^n{u}_0,T^m{u}_0)\le \underset{u\in X}{sup}\left\{\gamma (u,u)\right\}<{\displaystyle \frac{1}{{sup}_{x\in [0,\infty )}\left\{\vartheta \left(x\right)\right\}}}$$

for any $u_0$. So by Theorem 8, T has a unique fixed point. □

Theorem 9 can be applied to boundary value problems via the Hammerstein integral operator. A typical example is given below.

Example 1. 

Consider the following nonlinear fractional boundary value problem:

$$\begin{array}{c}{D}_{0+}^{\alpha }u\left(t\right)+\lambda h\left(t\right)f\left(u\left(t\right)\right)=0,0<t<1,2<\alpha <3,\\ u\left(0\right)=u^{\prime }\left(0\right)=u^{\prime }\left(1\right)=0,\end{array}$$

where $D_{0+}^{\alpha }$ denotes the Riemann–Liouvillle fractional derivative, $\lambda >0$ is a parameter, $h:(0,1)\to {\mathbb{R}}^{+}$ and $f:\mathbb{R}\to {\mathbb{R}}^{+}$ are nonnegative and continuous, and ${\int }_0^{1}h\left(s\right)ds>0$. It is known that $u\in C(0,1)$ is a solution of this boundary value problem (BVP) if and only if

$$u\left(t\right)=\lambda {\int }_0^{1}G(t,s)h\left(s\right)f\left(u\left(s\right)\right)ds,0\le t\le 1,$$

where

$$G(t,s)=\left\{\begin{array}{cc}{\displaystyle \frac{{(1-s)}^{\alpha -2}{t}^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}}\hfill & \mathit{if}0\le t\le s\le 1,\hfill \\ {\displaystyle \frac{{(1-s)}^{\alpha -2}{t}^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}}-{\displaystyle \frac{{(t-s)}^{\alpha -1}}{\mathsf{\Gamma }\left(\alpha \right)}}\hfill & \mathit{if}0\le s\le t\le 1,\hfill \end{array}\right.$$

and $0\le G(t,s)<1$ for all $t,s\in [0,1]$ [12]. Hence, Condition 3 of Theorem 9 is satisfied. We also know that $(X,d)$ is an extended b-metric space with b-function $\gamma (u,v)=d(u,v)+1$, where $X=C[0,1]$ and

$$d(u,v)=\underset{s\in [0,1]}{max}|u\left(s\right)-v\left(s\right)|.$$

We pick $\vartheta \left(x\right)=1-\epsilon$ for $1>\epsilon >0$ so that Condition 1 is satisfied. Let $\lambda =1$, $h\left(s\right)={\displaystyle \frac{s}{s+1}}$, and $f\left(u\right)={\displaystyle \frac{1}{1-\epsilon }}sin\left(u\left(s\right)\right)+{\displaystyle \frac{1}{1-\epsilon }}$. Then, Condition 4 is satisfied. Note that for all $u,v\in X$,

$$\left|{\displaystyle \frac{1}{1-\epsilon }}sin\left(u\left(s\right)\right)+{\displaystyle \frac{1}{1-\epsilon }}-{\displaystyle \frac{1}{1-\epsilon }}sin\left(v\left(s\right)\right)-{\displaystyle \frac{1}{1-\epsilon }}\right|={\displaystyle \frac{1}{1-\epsilon }}\left|sin\left(u\right(s\left)\right)-sin\left(v\right(s\left)\right)\right|,$$

and by the mean value theorem,

$${\displaystyle \frac{1}{1-\epsilon }}\left|sin\left(u\right(s\left)\right)-sin\left(v\right(s\left)\right)\right|\le |u\left(s\right)-v\left(s\right)|.$$

Thus,

$$|f(u\left(s\right))-f(v\left(s\right))|\le (1-\epsilon )|u(s)-v(s)|$$

for all $s\in [0,1]$ and so we have

$$d\left(f\right(u),f(v\left)\right)\le (1-\epsilon )d(u,v).$$

Hence, Condition 2 is satisfied, and the boundary value problem

$$\begin{array}{c}{D}_{0+}^{\alpha }u\left(t\right)+{\displaystyle \frac{tsin\left(u\right(t\left)\right)+t}{(1-\epsilon )(t+1)}}=0,0<t<1,2<\alpha <3,\\ u\left(0\right)=u^{\prime }\left(0\right)=u^{\prime }\left(1\right)=0,\end{array}$$

has a unique solution $u\left(t\right)\in X$.

In Example 1, let $h\left(s\right)={\displaystyle \frac{\lambda s}{s+1}}$, and $\lambda \le {\displaystyle \frac{1}{1-ln\left(2\right)}}$ would satisfy the conditions. Figure 1 and Figure 2 show the plots of the solutions obtained using MATLAB R2023b.

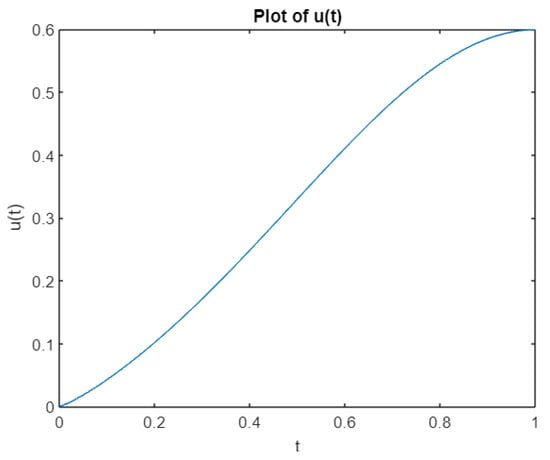
Figure 1. $\lambda =2.9,\alpha =2.4,\epsilon =0.01$.

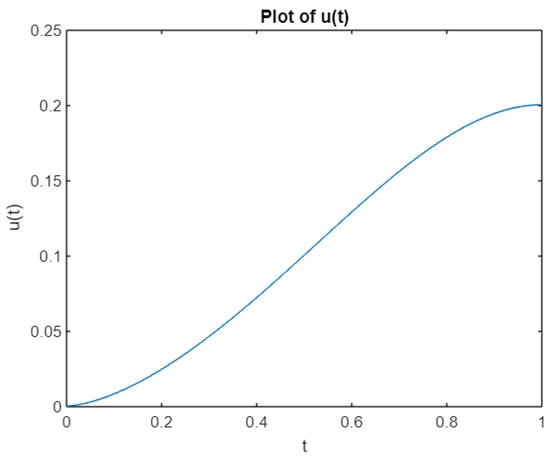
Figure 2. $\lambda =2.9,\alpha =2.8,\epsilon =0.01$.