Approximate Solution of a Kind of Time-Fractional Evolution Equations Based on Fast L1 Formula and Barycentric Lagrange Interpolation

Abstract

In this paper, an effective numerical approach that combines the fast L1 formula and barycentric Lagrange interpolation is proposed for solving a kind of time-fractional evolution equations. This type of equation contains a nonlocal term involving the time variable, resulting in extremely high computational complexity of numerical discrete formats in general. To reduce the computational burden, the fast L1 technique based on the L1 formula and sum-of-exponentials approximation is employed to evaluate the Caputo time-fractional derivative. Meanwhile, a fast and unconditionally stable time semi-discrete format is obtained. Subsequently, we utilize the barycentric Lagrange interpolation and its differential matrices to achieve spatial discretizations so as to deduce fully discrete formats. Then error estimates of related fully discrete formats are explored. Eventually, some numerical experiments are simulated to testify to the effective and fast behavior of the presented method.

1. Introduction

Fractional calculus is an extension of the classical integer order calculus, and fractional calculus has received considerable attention in varieties of applied science, such as electrochemistry, physics, and biology [1,2,3,4]. Fractional order models in practical problems are generally described as fractional order differential and integro-differential equations. Fractional differential operators possess nonlocality, which can better simulate some special phenomena with memory and hereditary characteristics than local operators. However, plenty of fractional differential equations cannot be settled explicitly under most circumstances. Though the exact solutions of some fractional differential equations can be expressed analytically via some special functions, which are usually complicated to evaluate. Consequently, efficient and accurate numerical solutions of fractional differential equations turn into a theme of deep investigations.

Since the initial conditions of the Caputo fractional differential operator have definite physical significance, the mathematical models in practice are generally depicted by the Caputo time-fractional differential equations. This paper takes into account the following kind of time-fractional evolution equations given by

$$\begin{array}{cc}\hfill {}_0{}^{C}D_t^{\alpha }u(\mathit{x},t)-\Delta u(\mathit{x},t)+\kappa u(\mathit{x},t)=f(\mathit{x},t),& \mathit{x}\in \Omega ,t\in (0,T],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill u(\mathit{x},0)=u_0\left(\mathit{x}\right),& \mathit{x}\in \overline{\Omega }=\Omega \cup \partial \Omega ,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill u(\mathit{x},t)=0,& \mathit{x}\in \partial \Omega ,t\in [0,T],\hfill \end{array}$$

(3)

where $\Omega$ is a bounded domain in ${\mathbb{R}}^d$ with $d=1,2,$  $\partial \Omega$ is the boundary of $\Omega$, $\kappa$ is a non-negative constant, $f(\mathit{x},t)$ and $u_0\left(\mathit{x}\right)$ are given functions, and ${}_0{}^{C}D_t^{\alpha }$ is the $\alpha$-order Caputo fractional derivative relating t as follows:

$${}_0{}^{C}D_t^{\alpha }u(\mathit{x},t)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }{\displaystyle \frac{\partial u(\mathit{x},s)}{\partial s}}\mathrm{d}s,0<\alpha <1,$$

(4)

where $\Gamma (·)$ is the common Gamma function, and $\Delta$ is the classic Laplacian operator. Since the nonlocal nature of Caputo fractional derivatives, the numerical simulations for solving Caputo fractional differential equations normally need large storage capacity and calculation workload. On the basis of efficient numerical solutions, the fast algorithm for solving different types of differential equations is still a hot subject. For example, Gu et al. reduced the computational effort of calculating the weakly singular integral (4) by the fast convolution quadrature in [5]. Compared to the traditional block forward substitution approach, a faster direct approach based on the divide-and-conquer strategy combined with the fast Fourier transforms has been used to handle the discrete block triangular Toeplitz-like linear systems, which are obtained from time-fractional partial differential equations [6]. These excellent fruits turn out that fast computation for fractional differential operators is an active investigation subject.

The wonderful L1 scheme based on piecewise linear interpolation is a typical and successful technique for approximating the Caputo fractional derivative [7,8,9,10]. There are plenty of grid partition points required to acquire a highly precise approximation of the fractional Caputo derivative by the L1 approximation due to the nonlocal behavior, which leads to large computation storage and arithmetic operations. It is necessary to speed up the computational efficiency of the L1 method for a more valuable employment. The fast L1 method is an algorithm based on the L1 scheme and sum-of-exponentials (SOE) approximation, which improves the computational speed and keeps the numerical accuracy. Its primary thought is to divide the weakly singular integral in (4) into a sum of the local term and history term, which are treated by the L1 scheme and SOE approximation, respectively. The storage $O\left(N\right)$ and total computational cost $O\left(N^2\right)$ of the L1 scheme are reduced $O\left({\mathcal{N}}_{exp}\right)$ and $O\left(N{\mathcal{N}}_{exp}\right)$ by the fast L1 formula, respectively. Commonly, ${\mathcal{N}}_{exp}$ is much smaller than N. Qiao et al. established a fast Crank-Nicolson L1 finite difference scheme for solving 2D time-varying fractional order movable/immovable diffusion equations [11]. Yu et al. proposed a fast L1 formula for solving 2D convective-diffusion equations and modified the algorithm for the positivity-preserving principle [12]. Jiang et al. used the fast L1 method to discretize Caputo-time-fractional derivatives, which is combined to solve fractional diffusion equations [13], the time-fractional Allen-Cahn equation [14], the time-fractional Cahn-Hilliard problem [15], and nonlinear time-space fractional parabolic equations [16]. Inspired by these achievements, we consider utilizing the fast L1 scheme to handle the time-fractional derivative in (1)–(3) by the fast L1 method.

In addition, we consider discretizing spatial variables by barycentric Lagrange interpolation (BLI), which is an improved format of classic Lagrange interpolation. The BLI not only reduces the computational expense of Lagrange interpolation but also has remarkable numerical stability under some special nodal distributions and can obtain a highly accurate numerical solution with small interpolation node numbers [17,18,19,20]. At the same time, it is not necessary to partition grids when the differential matrix of BLI is utilized to discretize differential operators, and the computational program is easy to perform. For these remarkable advantages, the BLI has been put into many mathematical models of applied sciences extensively. In [21], a fast summation of particle interactions was achieved by a fast multipole approach based on BLI and dual tree traversal. In [22], the time-fractional telegraph equation was solved by high-dimensional BLI and its differential matrix. In [23], the approximate solution of initial boundary value problems in the Sine-Gordon equations was discussed by the BLI collocation method combined with two linearized iterative techniques. In [24,25], a high precision approximate solution of Fredholm integral equations of the second kind was obtained by the barycentric interpolation collocation method. The BLI combined with some numerical treatments can expand its application extensively.

This paper acquires the approximate solution of Equations (1)–(3) by the fast L1 formula in the temporal direction and the BLI method in the spatial direction. The arrangement is outlined as follows systematically. In Section 2, the fast L1 formula and BLI are introduced to make some preparations for deriving a fully discrete format. In Section 3, we give the temporally semi-discretized format of Equations (1)–(3) and analyze the temporal stability and convergence. In Section 4, we deduce the fully discrete format of Equations (1)–(3) in 1D and 2D spaces and analyze related error estimations. In Section 5, some numerical experiments are implemented to testify the theoretical results. Ultimately, a brief conclusion is made in Section 6.

2. Preparations

Before implementing the time and space discretizations of Equations (1)–(3), we first display some preparations.

2.1. Fast L1 Formula for Caputo Fractional Derivative

The fast L1 formula is an effective and fast numerical treatment based on the L1 scheme and SOE approximation. We first state a brief introduction of the L1 scheme for approximating the Caputo fractional derivative

$${}_0{}^{C}D_t^{\alpha }v\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{(t-s)}^{-\alpha }{\displaystyle \frac{\partial v\left(s\right)}{\partial s}}\mathrm{d}s,t\in [0,T].$$

(5)

Let $N\in {\mathbb{N}}^{+}$, we partition $[0,T]$ into $0=t_0<t_1<\cdots <t_{k-1}<t_k<\cdots <t_N=T$. For $1\le k\le N$, let the k-th time-step size be ${\tau }_k:=t_k-t_{k-1}$ and ${\nabla }_{\tau }{v}^k:=v^k-v^{k-1},$  ${\delta }_t{v}^{k-{\displaystyle \frac{1}{2}}}:={\nabla }_{\tau }{v}^k/{\tau }_k$, $v^k=v\left(t_k\right)$. Then the maximum step size is $\tau :=\underset{1\le k\le N}{max}{\tau }_k$. Meanwhile, let ${\Pi }_{1,k}v:=\left({\Pi }_{1,k}v\right)\left(t\right)$ express the linear interpolation of $v\left(t\right)$ on $[t_{k-1},t_k]$, namely,

$$\begin{array}{c}\hfill \left({\Pi }_{1,k}v\right)\left(t\right)={\displaystyle \frac{t_k-t}{{\tau }_k}}v\left(t_{k-1}\right)+{\displaystyle \frac{t-t_{k-1}}{{\tau }_k}}v\left(t_k\right).\end{array}$$

Then the L1 formula to ${}_0{}^{C}D_t^{\alpha }v\left(t_n\right)$ is denoted by

$${\partial }_t^{\alpha }{v}^n:={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_{t_0}^{t_n}{\displaystyle \frac{\left({\Pi }_{1,k}^{\prime }v\right)\left(s\right)}{{(t_n-s)}^{\alpha }}}\mathrm{d}s=\sum _{k=1}^n{a}_{n-k}^{\left(n\right)}{\nabla }_{\tau }{v}^k,$$

(6)

where ${\partial }_t^{\alpha }{v}^n:={\partial }_t^{\alpha }v\left(t_n\right)$ is the discrete Caputo derivative at $t=t_n$ by the L1 scheme, $a_{n-k}^{\left(n\right)}$ are the related discrete convolution kernels with

$$a_{n-k}^{\left(n\right)}:={\displaystyle \frac{1}{{\tau }_k}}{\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_{t_{k-1}}^{t_k}{\displaystyle \frac{1}{{(t_n-s)}^{\alpha }}}\mathrm{d}s,1\le k\le n.$$

(7)

According to [26,27], $a_{n-k}^{\left(n\right)}$ in (7) satisfy the following properties

$$a_{n-k-1}^{\left(n\right)}\ge {\displaystyle \frac{1}{\Gamma (1-\alpha )}}{(t_n-t_k)}^{-\alpha }\ge a_{n-k}^{\left(n\right)},1\le k\le n-1.$$

(8)

Although the L1 formula is effective, it is too expensive to simulate over long periods of time. It is necessary to accelerate the computation of (6) to enhance efficiency. We now give the discrete format of (5) by the fast L1 formula, which is implemented through the above L1 scheme and the next SOE technique.

Lemma 1

([13]). For $0<\alpha <1$, absolute tolerance $\epsilon >0$, and a parameter $\widehat{\tau }$ with $\widehat{\tau }\in (0,T)$, there is a positive integer ${\mathcal{N}}_{exp}$, positive nodes $s_{\ell }^{\left(\alpha \right)}$, and the related positive weights ${\omega }_{\ell }^{\left(\alpha \right)}$ such that

$$|t^{-\alpha }-\sum _{\ell =1}^{{\mathcal{N}}_{exp}}{\omega }_{\ell }^{\left(\alpha \right)}{e}^{-s_{\ell }^{\left(\alpha \right)}t}|\le \epsilon ,\forall t\in [\widehat{\tau },T],$$

(9)

where the number ${\mathcal{N}}_{exp}=\mathcal{O}\left((log{\displaystyle \frac{1}{\epsilon }})(loglog{\displaystyle \frac{1}{\epsilon }}+log{\displaystyle \frac{T}{\widehat{\tau }}})+(log{\displaystyle \frac{1}{\widehat{\tau }}})(loglog{\displaystyle \frac{1}{\epsilon }}+log{\displaystyle \frac{T}{\widehat{\tau }}})\right)$.

Next, we give the fast L1 format of (5). We split the integral of (5) into a local term and a history term, which are handled by the L1 formula (6) and SOE approximation (9), respectively. Concretely,

$$\begin{array}{cc}\hfill {}_0{}^{C}D_t^{\alpha }v\left(t_n\right)& ={\displaystyle \frac{1}{\Gamma (1-\alpha )}}\left[\sum _{k=1}^{n-1}{\int }_{t_{k-1}}^{t_k}{v}^{\prime }\left(s\right){(t_n-s)}^{-\alpha }\mathrm{d}s+{\int }_{t_{n-1}}^{t_n}{\displaystyle \frac{v^{\prime }\left(s\right)}{{(t_n-s)}^{\alpha }}}\mathrm{d}s\right]\hfill \\ \hfill & \approx {\displaystyle \frac{1}{\Gamma (1-\alpha )}}[\sum _{k=1}^{n-1}{\int }_{t_{k-1}}^{t_k}\left({\Pi }_{1,k}^{\prime }v\right)\left(s\right)\sum _{\ell =1}^{{\mathcal{N}}_{exp}}{\omega }_{\ell }^{\left(\alpha \right)}{e}^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s\hfill \\ \hfill & +{\int }_{t_{n-1}}^{t_n}\left({\Pi }_{1,n}^{\prime }v\right)\left(s\right){(t_n-s)}^{-\alpha }\mathrm{d}s]\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (1-\alpha )}}\left(\sum _{\ell =1}^{{\mathcal{N}}_{exp}}{\omega }_{\ell }^{\left(\alpha \right)}{F}_{\ell }^n\right)+a_0^{\left(n\right)}{\nabla }_{\tau }{v}^n\hfill \\ \hfill & \equiv {}^{\mathcal{F}}\partial _t^{\alpha }{v}^n,\hfill \end{array}$$

(10)

where ${}^{\mathcal{F}}\partial _t^{\alpha }{v}^n:={}^{\mathcal{F}}\partial _t^{\alpha }v\left(t_n\right)$ is the discrete Caputo derivative at $t=t_n$ by the fast L1 formula, for $1\le \ell \le {\mathcal{N}}_{exp},$

$$F_{\ell }^1=0,F_{\ell }^n=\sum _{k=1}^{n-1}{\int }_{t_{k-1}}^{t_k}\left({\Pi }_{1,k}^{\prime }v\right)\left(t\right)e^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s,2\le n\le N.$$

The key to computing ${}^{\mathcal{F}}\partial _t^{\alpha }{v}^n$ is evaluating $F_{\ell }^n$. A recursive method is used to solve $F_{\ell }^n$, then

$$\begin{array}{cc}\hfill F_{\ell }^n& =\sum _{k=1}^{n-2}{\int }_{t_{k-1}}^{t_k}\left({\Pi }_{1,k}^{\prime }v\right)\left(s\right)e^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s+{\int }_{t_{n-2}}^{t_{n-1}}\left({\Pi }_{1,k}^{\prime }v\right)\left(s\right)e^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s\hfill \\ \hfill & =e^{-s_{\ell }^{\left(\alpha \right)}{\tau }_n}\sum _{k=1}^{n-2}{\int }_{t_{k-1}}^{t_k}\left({\Pi }_{1,k}^{\prime }v\right)\left(s\right)e^{-s_{\ell }^{\left(\alpha \right)}(t_{n-1}-s)}\mathrm{d}s+{\delta }_t{v}^{n-{\displaystyle \frac{3}{2}}}{\int }_{t_{n-2}}^{t_{n-1}}{e}^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s\hfill \\ \hfill & =e^{-s_{\ell }^{\left(\alpha \right)}{\tau }_n}{F}_{\ell }^{n-1}+B_{\ell }^n\left[v\left(t_{n-1}\right)-v\left(t_{n-2}\right)\right],\hfill \end{array}$$

where

$$\begin{array}{c}\hfill B_{\ell }^n={\displaystyle \frac{1}{{\tau }_{n-1}}}{\int }_{t_{n-2}}^{t_{n-1}}{e}^{-s_{\ell }^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s.\end{array}$$

The formula (10) is referred to as the fast L1 approximation of (5). Conveniently, we rewrite Equation (10) as

$$\begin{array}{c}\hfill {}^{\mathcal{F}}\partial _t^{\alpha }{v}^n=A_0^{\left(n\right)}v\left(t_n\right)-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)v\left(t_k\right)-A_{n-1}^{\left(n\right)}v\left(t_0\right)=\sum _{k=1}^n{A}_{n-k}^{\left(n\right)}{\nabla }_{\tau }{v}^k,\end{array}$$

(11)

where $\left\{A_{n-k}^{\left(n\right)}|1\le n\le N,1\le k\le n\right\}$ are the related discrete convolution coefficients with

$${\displaystyle A_0^n:=a_0^{\left(n\right)},A_{n-k}^{\left(n\right)}:={\displaystyle \frac{1}{{\tau }_k\Gamma (1-\alpha )}}{\int }_{t_{k-1}}^{t_k}\sum _{l=1}^{{\mathcal{N}}_{\exp }}{\omega }_l^{\left(\alpha \right)}{e}^{-s_l^{\left(\alpha \right)}(t_n-s)}\mathrm{d}s,1\le k\le n-1,}$$

(12)

and $a_0^{\left(n\right)}$ is defined in (7). Similar to the property (8), $A_{n-k}^{\left(n\right)}$ satisfy the property below.

Lemma 2

([28]). The coefficients $A_{n-k}^{\left(n\right)}$ defined by (12) satisfy the inequality

$$0\le A_{n-1}^{\left(n\right)}\le A_{n-2}^{\left(n\right)}\le \cdots \le A_1^{\left(n\right)}\le A_0^{\left(n\right)}.$$

Lemma 3

([13]). Assume that $v\left(t\right)\in C^2[0,t_n]$, for $0<\alpha <1$, then,

$$\begin{array}{cc}\hfill \left|R_t{v}^n\right|& =|{}_0{}^{C}D_t^{\alpha }v\left(t_n\right)-{}^{\mathcal{F}}\partial _t^{\alpha }{v}^n|\hfill \\ \hfill & \le {\displaystyle \frac{1}{\Gamma (2-\alpha )}}\left[{\displaystyle \frac{1-\alpha }{12}}+{\displaystyle \frac{2^{2-\alpha }}{2-\alpha }}-(1+2^{-\alpha })\right]\underset{0\le t\le t_n}{max}\left|v^{″}\left(t\right)\right|{\tau }^{2-\alpha }\hfill \\ \hfill & +{\displaystyle \frac{\alpha \epsilon t_{n-1}}{\Gamma (1-\alpha )}}\underset{0\le t\le t_{n-1}}{max}\left|v\left(t\right)\right|.\hfill \end{array}$$

Remark 1.

The fast L1 technique for the Caputo fractional derivative is also applicable to non-uniform meshes. For brevity, uniform meshes in time will be employed in Section 3, with ${\tau }_k=\tau$.

2.2. Barycentric Lagrange Interpolations and Their Differentiation Matrices

For analytical convenience, we set $\Omega =[-1,1]$ and $\Omega ={[-1,1]}^2$ in the 1D and 2D spatial directions, respectively. Next, we give the related barycentric Lagrange interpolations (BLIs) and their differential matrices.

About 1D space, for a given function $u\left(x\right),x\in \Omega =[-1,1]$. Let $M\in {\mathbb{N}}^{+}$, $\Omega$ is partitioned into M parts by the grid ${\left\{x_q\right\}}_{q=0}^M$, then $u\left(x\right)$ can be approximated by

$$u_M\left(x\right)=\sum _{q=0}^M{\varphi }_q\left(x\right)u_q,{\varphi }_q\left(x\right)={\displaystyle \frac{{\omega }_q}{x-x_q}}/\sum _{k=0}^M{\displaystyle \frac{{\omega }_k}{x-x_k}},{\omega }_q={\displaystyle \frac{1}{\prod _{q\ne k}(x_q-x_k)}},$$

(13)

where $u_q=u\left(x_q\right)$, $u_M\left(x\right)$ is called BLI in [17], ${\varphi }_q\left(x\right)$ is the q-th BLI basic function and ${\varphi }_q\left(x_p\right)={\delta }_{pq}$ with ${\delta }_{pq}$ being the Kronecker-Delta functions, ${\omega }_q$ is the q-th BLI weight. Particularly, based on points

$$X_M:={\left\{x_q|x_q=cos\left({\displaystyle \frac{q}{M}}\pi \right)\right\}}_{q=0,1,\cdots ,M},$$

(14)

and $x_q$ are the Chebyshev points of the second kind, there are

$${\omega }_q={(-1)}^q{\vartheta }_q,{\vartheta }_q=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}},\hfill & q=0\mathrm{or}M\hfill \\ 1,\hfill & q=1,\cdots ,M-1,\hfill \end{array}\right.$$

The BLI is a slight variant of Lagrange interpolation, which is fast and stable for some special types of interpolation points [18]. The next lemma gives an error estimation of $u-u_M$ based on the points in (14).

Lemma 4.

Assume that $u^{(M+1)}\left(x\right)$ exists and is continuous on $[-1,1]$. Let $u_M\left(x\right)$ be the BLI (13) of $u\left(x\right)$ based on the points in (14). Then, for large enough M,

$$\parallel u-u_M{\parallel }_{\infty }\le c_1{\left({\displaystyle \frac{e}{2M}}\right)}^M\parallel u^{(M+1)}{\parallel }_{\infty },$$

where $c_1={\displaystyle \frac{2e}{\sqrt{2\pi }}}$ is a constant.

Proof. 

From [29], there exists $\xi \in (-1,1)$, which is dependent on x such that $u_M\left(x\right)$ has the remainder term

$$u\left(x\right)-u_M\left(x\right)={\displaystyle \frac{u^{(M+1)}\left(\xi \right)}{(M+1)!}}\prod _{q=0}^M(x-x_j).$$

(15)

As $M\to \infty$, Stirling’s formula indicates that

$$M!\cong \sqrt{2\pi }{M}^{M+{\displaystyle \frac{1}{2}}}{e}^{-M}.$$

(16)

And according to [22], based upon the Chebyshev points $x_q=cos\left({\displaystyle \frac{q}{M}}\pi \right)$, it implies that

$$\left|\prod _{q=0}^M(x-x_q)\right|\le {\displaystyle \frac{M}{2^{M-1}}}.$$

(17)

It follows from (15)–(17) that

$$\begin{array}{cc}\hfill \parallel u-u_M{\parallel }_{\infty }& =\underset{-1\le x\le 1}{max}|u-u_M|\hfill \\ \hfill & \le \underset{-1\le x\le 1}{max}{\displaystyle \frac{\left|u^{(M+1)}\left(\xi \right)\right|}{(M+1)!}}\left|\prod _{q=0}^M(x-x_q)\right|\hfill \\ \hfill & \le {\displaystyle \frac{M}{2^{M-1}(M+1)!}}\underset{-1\le x\le 1}{max}\left|u^{(M+1)}\left(\xi \right)\right|\hfill \\ \hfill & \cong {\displaystyle \frac{M}{2^{M-1}\sqrt{2\pi }{(M+1)}^{M+\frac{3}{2}}{e}^{-(M+1)}}}\parallel u^{(M+1)}{\parallel }_{\infty }\hfill \\ \hfill & \le {\displaystyle \frac{2e}{\sqrt{2\pi }}}{\left({\displaystyle \frac{e}{2M}}\right)}^M\parallel u^{(M+1)}{\parallel }_{\infty }.\hfill \end{array}$$

The proof is accomplished. □

Further, we introduce the BLI differentiation matrix based on $u_M\left(x\right)$. From (13), $u_M\left(x\right)$ is linear with respect to $u_q$. Thus, the derivatives of $u_M\left(x\right)$ can be obtained by taking the derivatives of ${\varphi }_q\left(x\right)$ directly. Then the second derivative of $u\left(x\right)$ can be approximated as

$$u_M^{″}\left(x\right)=\sum _{q=0}^M{\varphi }_q^{″}\left(x\right)u_q.$$

Then, the approximate values of $u^{″}\left(x\right)$ at points $\{x_p,p=0,1,\cdots ,M\}$ are

$$u_M^{″}\left(x_p\right)=\sum _{q=0}^M{\varphi }_q^{″}\left(x_p\right)u_q.$$

(18)

From [17], a slight calculation shows that ${\varphi }_q^{″}\left(x_p\right)$ are

$${\varphi }_q^{″}\left(x_p\right)=\left\{\begin{array}{cc}-2{\displaystyle \frac{{\omega }_q/{\omega }_p}{x_p-x_q}}\left(\sum _{k\ne i}{\displaystyle \frac{{\omega }_k/{\omega }_p}{x_p-x_k}}-{\displaystyle \frac{1}{x_p-x_q}}\right),\hfill & p\ne q,\hfill \\ -\sum _{p\ne q}{\varphi }_q^{″}\left(x_p\right),\hfill & p=q.\hfill \end{array}\right.$$

For a general expression, let $D_{pq}^{\left(2\right)}={\varphi }_q^{″}\left(x_p\right)$, which are normally known as the entries of second-order BLI differentiation matrix ${\mathbf{D}}^{\left(2\right)}$, namely, ${\mathbf{D}}^{\left(2\right)}={\left[D_{pq}^{\left(2\right)}\right]}_{p,q=0}^M$. Let ${\mathbf{u}}^{\left(2\right)}$, ${\mathbf{u}}_M^{\left(2\right)}$, and $\mathbf{u}$ be vectors of corresponding function values associated with the points $x_p$, respectively. Then Equation (18) can be indicated as matrix form

$${\mathbf{u}}_M^{\left(2\right)}={\mathbf{D}}^{\left(2\right)}\mathbf{u}.$$

(19)

Lemma 5.

Assume that $u^{(M+1)}\left(x\right)$ exists and is continuous on $[-1,1]$. Let $u_M\left(x\right)$ be the BLI (13) of $u\left(x\right)$ based on the points in (14). Then, for large enough M,

$$\parallel u^{″}-u_M^{″}{\parallel }_{\infty }\le c_1\parallel u^{(M+1)}{\parallel }_{\infty }{\left({\displaystyle \frac{e}{2(M-2)}}\right)}^{M-2}.$$

Proof. 

From [30], there exists $\xi \in (-1,1)$, which is dependent on x such that $u_M^{″}\left(x\right)$ has the remainder term

$$u^{″}\left(x\right)-u_M^{″}\left(x\right)={\displaystyle \frac{u^{(M+1)}\left(\xi \right)}{(M-1)!}}\prod _{q=0}^{M-2}(x-x_q).$$

Referring to the proof of Lemma 4, using the Stirling’s formula (16) and inequality (17), then

$$\begin{array}{cc}\hfill \parallel u^{″}-u_M^{″}{\parallel }_{\infty }& =\underset{-1\le x\le 1}{max}|u^{″}-u_M^{″}|\hfill \\ \hfill & \le \underset{-1\le x\le 1}{max}{\displaystyle \frac{\left|u^{(M+1)}\left(\xi \right)\right|}{(M-1)!}}\left|\prod _{q=0}^{M-2}(x-x_q)\right|\hfill \\ \hfill & \le {\displaystyle \frac{2e}{\sqrt{2\pi }}}{\left({\displaystyle \frac{e}{2(M-2)}}\right)}^{M-2}\parallel u^{(M+1)}{\parallel }_{\infty }.\hfill \end{array}$$

The proof is accomplished. □

The BLI is a nodal interpolation method, which is easy to be utilized to construct high-dimensional BLI by tensor product points.

About 2D space, for a function $u(x,y)$, $(x,y)\in \Omega ={[-1,1]}^2$. For fixed y, let $\{x_{q_1},q_1=0,1,\cdots ,M_1\}$ be $M_1+1$ distinct nodes on $[-1,1]$ in the x direction, $x_{q_1}\in X_{M_1}$, then $u(x,y)$ can be approximated by

$$u_{M_1}(x,y)=\sum _{q_1=0}^{M_1}{\varphi }_{q_1}\left(x\right)u_{q_1}\left(y\right),{\varphi }_{q_1}\left(x\right)={\displaystyle \frac{{\omega }_{q_1}}{x-x_{q_1}}}/\sum _{k=0}^{M_1}{\displaystyle \frac{{\omega }_k}{x-x_k}},$$

(20)

where $u_{q_1}\left(y\right)=u(x_{q_1},y)$. Further, let $\{y_{q_2},q_2=0,1,\cdots ,M_2\}$ be $M_2+1$ distinct nodes on $[-1,1]$ in the y direction, $y_{q_2}\in X_{M_2}$; then $u_{q_1}\left(y\right)$ can be approximated as

$$u_{q_1}\left(y\right)\approx \sum _{q_2=0}^{M_2}{\varphi }_{q_2}\left(y\right)u_{q_1{q}_2},{\varphi }_{q_2}\left(y\right)={\displaystyle \frac{{\omega }_{q_2}}{y-y_{q_2}}}/\sum _{k=0}^{M_2}{\displaystyle \frac{{\omega }_k}{y-y_k}},$$

(21)

where $u_{q_1{q}_2}=u_{q_1}\left(y_{q_2}\right)=u(x_{q_1},y_{q_2})$. According to (20) and (21), it yields

$$u_{M_1{M}_2}(x,y)=\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\varphi }_{q_1}\left(x\right){\varphi }_{q_2}\left(y\right)u_{q_1{q}_2},$$

(22)

Here, $u_{M_1{M}_2}(x,y)$ can be regarded as 2D BLI in relation to tensor product points

$$X_{M_1{M}_2}:={\left\{(x_{q_1},y_{q_2})|x_{q_1}=cos\left({\displaystyle \frac{q_1}{M_1}}\pi \right),y_{q_2}=cos\left({\displaystyle \frac{q_2}{M_2}}\pi \right)\right\}}_{\begin{array}{c}{q}_1=0,1\dots ,M_1\\ q_2=0,1,\dots ,M_2\end{array}},$$

(23)

where ${\varphi }_{q_1}\left(x\right)$ and ${\varphi }_{q_2}\left(y\right)$ are BLI basis functions with regard to the points ${\left\{x_{q_1}\right\}}_{q_1=0}^{M_1}$ and ${\left\{y_{q_2}\right\}}_{q_2=0}^{M_2}$, respectively. The following lemma gives an error estimation of $u(x,y)-u_{M_1{M}_2}(x,y)$ based upon the points in (23).

Theorem 1.

Assume that ${\displaystyle \frac{{\partial }^{M_1+1}u(x,y)}{\partial x^{M_1+1}}}$ and ${\displaystyle \frac{{\partial }^{M_2+1}u(x,y)}{\partial y^{M_2+1}}}$ exist and are continuous on $\Omega ={[-1,1]}^2$. Let $u_{M_1{M}_2}(x,y)$ be the 2D BLI (22) of $u(x,y)$ based on the tensor product points in (23). Then, for large enough $M_1,M_2$,

$$\parallel u-u_{M_1{M}_2}{\parallel }_{\infty }\le c_1\left[{\left({\displaystyle \frac{e}{2M_1}}\right)}^{M_1}+\left(1+{\displaystyle \frac{2}{\pi }}log{M}_1\right){\left({\displaystyle \frac{e}{2M_2}}\right)}^{M_2}\right]\parallel u^{(\ast )}{\parallel }_{\infty },$$

(24)

where $\parallel u^{(\ast )}{\parallel }_{\infty }=max\left\{\parallel {\displaystyle \frac{{\partial }^{M_1+1}u}{\partial {\xi }^{M_1+1}}}{\parallel }_{\infty },\parallel {\displaystyle \frac{{\partial }^{M_2+1}u}{\partial {\eta }^{M_2+1}}}{\parallel }_{\infty }\right\}$ with $(\xi ,\eta )\in {(-1,1)}^2$.

Proof. 

According to the above discussion, we know that

$$\begin{array}{cc}\hfill u(x,y)-u_{M_1{M}_2}(x,y)& =\left(u(x,y)-\sum _{q_1=0}^{M_1}{\varphi }_{q_1}\left(x\right)u_{q_1}\left(y\right)\right)\hfill \\ \hfill & +\sum _{q_1=0}^{M_1}{\varphi }_{q_1}\left(x\right)\left(u_{q_1}\left(y\right)-\sum _{q_2=0}^{M_2}{\varphi }_{q_2}\left(y\right)u_{q_1{q}_2}\right).\hfill \end{array}$$

Using the triangle inequality and Lemma 4, then

$$\begin{array}{cc}\hfill & \parallel u-u_{M_1{M}_2}{\parallel }_{\infty }\hfill \\ \hfill & =\underset{-1\le x,y\le 1}{max}|u(x,y)-u_{M_1{M}_2}(x,y)|\hfill \\ \hfill & \le \underset{-1\le x,y\le 1}{max}\left\{|u(x,y)-\sum _{j_1=0}^{M_1}{\varphi }_{q_1}\left(x\right)u_{q_1}\left(y\right)|+\sum _{q_1=0}^{M_1}|{\varphi }_{q_1}\left(x\right)||u_{q_1}\left(y\right)-\sum _{q_2=0}^{M_2}{\varphi }_{q_2}\left(y\right)u_{q_1{q}_2}|\right\}\hfill \\ \hfill & \le \underset{-1\le x,y\le 1}{max}\left\{{\displaystyle \frac{|{\displaystyle \prod _{q_1=0}^{M_1}}(x-x_{q_1})|}{(M_1+1)!}}|{\displaystyle \frac{{\partial }^{M_1+1}u(\xi ,y)}{\partial {\xi }^{M_1+1}}}|+{\Lambda }_{M_1}{\displaystyle \frac{|{\displaystyle \prod _{q_2=0}^{M_2}}(y-y_{q_2})|}{(M_2+1)!}}|{\displaystyle \frac{{\partial }^{M_2+1}u(\xi ,\eta )}{\partial {\eta }^{M_2+1}}}|\right\}\hfill \\ \hfill & \le \underset{-1\le x,y\le 1}{max}\left\{c_1{\left({\displaystyle \frac{e}{2M_1}}\right)}^{M_1}|{\displaystyle \frac{{\partial }^{M_1+1}u(\xi ,y)}{\partial {\xi }^{M_1+1}}}|+{\Lambda }_{M_1}{c}_1{\left({\displaystyle \frac{e}{2M_2}}\right)}^{M_2}|{\displaystyle \frac{{\partial }^{M_2+1}u(\xi ,\eta )}{\partial {\eta }^{M_2+1}}}|\right\}\hfill \\ \hfill & \le c_1\left[{\left({\displaystyle \frac{e}{2M_1}}\right)}^{M_1}+{\Lambda }_{M_1}{\left({\displaystyle \frac{e}{2M_2}}\right)}^{M_2}\right]\parallel u^{(\ast )}{\parallel }_{\infty },\hfill \end{array}$$

where ${\Lambda }_{M_1}:=\underset{-1\le x\le 1}{max}{\displaystyle \sum _{q_1=0}^{M_1}}\left|{\varphi }_{q_1}\left(x\right)\right|$ is the Lebesgue constant relating to ${\varphi }_{q_1}\left(x\right)$ at ${\left\{x_{q_1}\right\}}_{q_1=0}^{M_1}$. From [31], ${\Lambda }_{M_1}$ at the points in (14) can be bounded by ${\Lambda }_{M_1}\le 1+{\displaystyle \frac{2}{\pi }}log{M}_1$, then (24) can be derived. □

Similar to the derivatives of $u_M\left(x\right)$, for $m_1+m_2=2$ with $m_1,m_2\in \mathbb{N}$, the second-order partial derivatives of $u_{M_1{M}_2}(x,y)$ at points $(x_{p_1},y_{p_2})$ can be articulated as

$$\begin{array}{c}\hfill u_{M_1{M}_2}^{″}(x_{p_1},y_{p_2})=\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\varphi }_{q_1}^{\left(m_1\right)}\left(x_{p_1}\right){\varphi }_{q_2}^{\left(m_2\right)}\left(y_{p_2}\right)u_{q_1{q}_2}=\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{D}_{p_1{q}_1}^{\left(m_1\right)}{D}_{p_2{q}_2}^{\left(m_2\right)}{u}_{q_1{q}_2},\end{array}$$

(25)

with $D_{p_1{q}_1}^{\left(m_1\right)}={\varphi }_{q_1}^{\left(m_1\right)}\left(x_{p_1}\right)$ and $D_{p_2{q}_2}^{\left(m_2\right)}={\varphi }_{q_2}^{\left(m_2\right)}\left(y_{p_2}\right)$, where $p_1=0,1\dots ,M_1,$  $p_2=0,1,\dots ,M_2$. Let ${\mathbf{u}}^{\left(2\right)}$, ${\mathbf{u}}_M^{\left(2\right)}$ and $\mathbf{u}$ be vectors of corresponding function values associated with the points $(x_{p_1},y_{p_2})$, respectively. Similar to (19), Equation (25) can be simplified in matrix form.

$${\mathbf{u}}_{M_1{M}_2}^{\left(2\right)}=\left({\mathbf{D}}_1^{\left(m_1\right)}\otimes {\mathbf{D}}_2^{\left(m_2\right)}\right)\mathbf{u},$$

where ${\mathbf{D}}_1^{\left(m_1\right)}={\left[D_{p_1{q}_1}^{\left(m_1\right)}\right]}_{p_1,q_1=0}^{M_1}$ and ${\mathbf{D}}_2^{\left(m_2\right)}={\left[D_{p_2{q}_2}^{\left(m_2\right)}\right]}_{p_2,q_2=0}^{M_2}$ are individually called $m_1$-order and $m_2$-order BLI differentiation matrix, ⊗ signifies the tensor product operation.

For any bounded interval $[a,b]$, the Chebyshev points on $[-1,1]$ can be transformed into points with the same distribution on $[a,b]$ using the transformation $y={\displaystyle \frac{b-a}{2}}x+{\displaystyle \frac{b+a}{2}}$.

3. Temporal Discretization

Now, we primarily deduce the temporally semi-discretized form of Equations (1)–(3) by the fast L1 format (11) and analyze the stable and convergent features of the discrete format.

3.1. Time Semi-Discretization Format

Then, we discretize the time fractional term of Equations (1)–(3) by the format (11). Let us fix the space variable and record $u^n\left(\mathit{x}\right)=u(\mathit{x},t_n)$, $f^n\left(\mathit{x}\right)=f(\mathit{x},t_n)$, $n=1,\dots ,N$, then Equations (1)–(3) can be approximated by

$${}^{\mathcal{F}}\partial _t^{\alpha }{u}^n\left(\mathit{x}\right)-\Delta u^n\left(\mathit{x}\right)+\kappa u^n\left(\mathit{x}\right)=f^n\left(\mathit{x}\right)+R_t{u}^n\left(\mathit{x}\right),$$

(26)

and $R_t{u}^n\left(\mathit{x}\right)={}_0{}^{C}D_t^{\alpha }{u}^n\left(\mathit{x}\right)-{}^{\mathcal{F}}\partial _t^{\alpha }{u}^n\left(\mathit{x}\right)$ indicates truncation error. From Lemma 3, there is

$$|R_t{u}^n\left(\mathit{x}\right)|\le \mathcal{O}({\tau }^{2-\alpha }+\epsilon ).$$

(27)

On the basis of (11), the discrete format (26) can be equivalently expressed as

$$\begin{array}{cc}\hfill & \left[A_0^{\left(n\right)}{u}^n\left(\mathit{x}\right)-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u^k\left(\mathit{x}\right)-A_{n-1}^{\left(n\right)}{u}^0\left(\mathit{x}\right)\right]-\Delta u^n\left(\mathit{x}\right)+\kappa u^n\left(\mathit{x}\right)\hfill \\ & =f^n\left(\mathit{x}\right)+R_t{u}^n\left(\mathit{x}\right),\hfill \end{array}$$

(28)

We discard $R_t{u}^n\left(\mathit{x}\right)$ and take $U^n\left(\mathit{x}\right)$ instead of $u^n\left(\mathit{x}\right)$. So the temporally semi-discretized form of Equation (1) is

$$\begin{array}{c}\hfill \left[A_0^{\left(n\right)}{U}^n\left(\mathit{x}\right)-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U^k\left(\mathit{x}\right)-A_{n-1}^{\left(n\right)}{U}^0\left(\mathit{x}\right)\right]-\Delta U^n\left(\mathit{x}\right)+\kappa U^n\left(\mathit{x}\right)=f^n\left(\mathit{x}\right).\end{array}$$

(29)

Concurrently, the initial value is $U^0\left(\mathit{x}\right)=u_0\left(\mathit{x}\right)$, and the boundary value at $t_n$ is $U^n\left(\mathit{x}\right){|}_{\partial \Omega }=0$ for $n=0,1,\cdots ,N$. So far, the temporal discretization of Equations (1)–(3) is completed.

3.2. Stability and Convergence Analyses

Next, the stable and convergent behaviors of the time semi-discrete format (29) are discussed. For convenience, we first mark some notations. The $L^2(\Omega )$ space is defined by

$$L^2(\Omega )=\left\{u:\Omega \to \mathbb{R}|u\mathrm{is}\mathrm{measurable}\mathrm{and}{\int }_{\Omega }{\left|u\left(\mathit{x}\right)\right|}^2\mathrm{d}\mathit{x}<\infty \right\}.$$

For $u,v\in L^2(\Omega )$, the inner product and $L^2$-norm are respectively defined by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill (u,v)={\int }_{\Omega }u\left(\mathit{x}\right)v\left(\mathit{x}\right)\mathrm{d}\mathit{x},\end{array}\begin{array}{c}\hfill {\parallel u\parallel }_{L^2(\Omega )}={\left({\int }_{\Omega }{\left|u\left(\mathit{x}\right)\right|}^2\mathrm{d}\mathit{x}\right)}^{1/2}.\end{array}\end{array}$$

Further, the Green’s first formula is

$$(u,\Delta v)+(\nabla u,\nabla v)={\oint }_{\partial \Omega }u(\nabla v·\mathbf{n})\mathrm{d}S,$$

(30)

where ∇ denotes the gradient-operator and $\mathbf{n}$ is the outward pointing unit normal of $\mathrm{d}S$.

Lemma 6

(Young’s inequality). For $a,b>0$, $\mu >0$, and $1<\zeta ,\eta <\infty$, ${\displaystyle \frac{1}{\zeta }}+{\displaystyle \frac{1}{\eta }}=1$,

$$ab=({\mu }^{{\displaystyle \frac{1}{\zeta }}}a)({\mu }^{-{\displaystyle \frac{1}{\zeta }}}b)\le \mu {\displaystyle \frac{a^{\zeta }}{\zeta }}+{\mu }^{-{\displaystyle \frac{\eta }{\zeta }}}{\displaystyle \frac{b^{\eta }}{\eta }}.$$

(31)

After that, we present the main consequences of this subsection. Let $u^n\left(\mathit{x}\right)$ and $U^n\left(\mathit{x}\right)$ be the solutions of Equations (1)–(3) and (29), respectively. For avoiding confusion, we record $u^n:=u^n\left(\mathit{x}\right)$ and $U^n:=U^n\left(\mathit{x}\right)$.

Theorem 2.

Assume that $U^n\in L^2(\Omega )$, then the discrete format (29) is unconditionally stable.

Proof. 

We first take the inner product of Equation (29) together with $2U^n$, it yields that

$$\begin{array}{cc}\hfill & 2\left(A_0^{\left(n\right)}{U}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U^k-A_{n-1}^{\left(n\right)}{U}^0,U^n\right)-2(\Delta U^n,U^n)+2\kappa (U^n,U^n)\hfill \\ \hfill & =2(f^n,U^n).\hfill \end{array}$$

(32)

For the first part of the right in (32), we apply $(a,b)\le {\displaystyle \frac{1}{2}}(a^2+b^2)$ and derive that

$$\begin{array}{cc}\hfill & 2\left(A_0^{\left(n\right)}{U}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U^k-A_{n-1}^{\left(n\right)}{U}^0,U^n\right)\hfill \\ \hfill & =2A_0^{\left(n\right)}(U^n,U^n)-2\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)(U^k,U^n)-2A_{n-1}^{\left(n\right)}(U^0,U^n)\hfill \\ \hfill & \ge 2A_0^{\left(n\right)}{\parallel U^n\parallel }_{L^2(\Omega )}^2-\sum _{k=1}^{n-1}\left(A_{n-k-1}^n-A_{n-k}^{\left(n\right)}\right)\left(\parallel U^k{\parallel }_{L^2(\Omega )}^2+{\parallel U^n\parallel }_{L^2(\Omega )}^2\right)\hfill \\ \hfill & -A_{n-1}^{\left(n\right)}\left(\parallel U^0{\parallel }_{L^2(\Omega )}^2+{\parallel U^n\parallel }_{L^2(\Omega )}^2\right)\hfill \\ \hfill & =A_0^{\left(n\right)}\parallel U^n{\parallel }_{L^2(\Omega )}^2-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)\parallel U^k{\parallel }_{L^2(\Omega )}^2-A_{n-1}^{\left(n\right)}{\parallel U^0\parallel }_{L^2(\Omega )}^2\hfill \\ \hfill & \ge A_{n-1}^{\left(n\right)}\left(\parallel U^n{\parallel }_{L^2(\Omega )}^2-{\parallel U^0\parallel }_{L^2(\Omega )}^2\right).\hfill \end{array}$$

(33)

For the second part of the right in (32), we use Green’s first formula (30) and notice $U^n{|}_{\partial \Omega }=0$, then

$$\begin{array}{cc}\hfill -(\Delta U^n,U^n)& =(\nabla U^n,\nabla U^n)-{\oint }_{\partial \Omega }{U}^n(\nabla U^n·\mathbf{n})\mathrm{d}S=(\nabla U^n,\nabla U^n)\ge 0.\hfill \end{array}$$

(34)

For the left part in (32), the following inequalities can be derived from Lemma 6,

$$\begin{array}{c}\hfill (f^n,U^n)\le {\displaystyle \frac{1}{2\kappa }}\parallel f^n{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{\kappa }{2}}{\parallel U\parallel }_{L^2(\Omega )}^2\le {\displaystyle \frac{1}{2\kappa }}\parallel f^n{\parallel }_{L^2(\Omega )}^2+\kappa {\parallel U^n\parallel }_{L^2(\Omega )}^2.\end{array}$$

(35)

We substitute (33)–(35) into (32) and get the following estimation

$$A_{n-1}^{\left(n\right)}\parallel U^n{\parallel }_{L^2(\Omega )}^2\le A_{n-1}^{\left(n\right)}\parallel U^0{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{1}{\kappa }}{\parallel f^n\parallel }_{L^2(\Omega )}^2,$$

which implies that the time semi-discrete format (29) is unconditionally stable. □

Next, we analyze the convergence of the time semi-discrete format (29). Let $e^n=u^n-U^n$; we subtract Equation (29) from Equation (28) and gain the following error equation

$$\begin{array}{c}\hfill \left[A_0^{\left(n\right)}{e}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)e^k-A_{n-1}^{\left(n\right)}{e}^0\right]-\Delta e^n+\kappa e^n=R_t{u}^n,\end{array}$$

(36)

with $e^n{|}_{\partial \Omega }=0$ for $n=0,1,\cdots ,N$ and $e^0=0$.

Theorem 3.

Assume that $U^n\in L^2(\Omega )$, then discrete format (29) is convergent with $\mathcal{O}({\tau }^{2-\alpha }+\epsilon )$ in $L^2$-norm.

Proof. 

We refer to the proof of Theorem 2 and take inner product of Equation (36) with $2e^n$,

$$\begin{array}{c}\hfill 2\left(A_0^{\left(n\right)}{e}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)e^k-A_{n-1}^{\left(n\right)}{e}^0,e^n\right)-2(\Delta e^n,e^n)+2\kappa (e^n,e^n)=2(R_t{u}^n,e^n).\end{array}$$

According to Green’s first formula (30), Young’s inequality (31), and inequality $(a,b)\le {\displaystyle \frac{1}{2}}(a^2+b^2)$, it yields that

$$A_{n-1}^{\left(n\right)}\parallel e^n{\parallel }_{L^2(\Omega )}^2-A_{n-1}^{\left(n\right)}\parallel e^0{\parallel }_{L^2(\Omega )}^2\le {\displaystyle \frac{1}{\kappa }}{\parallel R_t^n\parallel }_{L^2(\Omega )}^2.$$

Further, according to Lemma 3, we obtain that

$$\begin{array}{cc}\hfill A_{n-1}^{\left(n\right)}{\parallel e^n\parallel }_{L^2(\Omega )}^2& \le A_{n-1}^{\left(n\right)}\parallel e^0{\parallel }_{L^2(\Omega )}^2+{\displaystyle \frac{1}{\kappa }}{\parallel R_t^n\parallel }_{L^2(\Omega )}^2\le \mathcal{O}({\tau }^{2-\alpha }+\epsilon ).\hfill \end{array}$$

The proof is accomplished. □

4. Spatial Discretization

This section is devoted to spatial discretizations of Equations (1)–(3) in 1D and 2D cases. We primarily achieve the implementations of 1D and 2D spatial approximations for Equation (28) by the 1D and 2D BLIs, respectively. Thus, the related fully discrete formats of Equations (1)–(3) are obtained, and the related error estimations are provided.

4.1. 1D Space Discretization

In this subsection, we treat the spatial approximation of Equation (28) in 1D case with Laplace operator $\Delta ={\displaystyle \frac{{\partial }^2}{\partial x^2}}$. For a more obvious statement, Equation (28) is firstly rewritten as

$$\begin{array}{cc}\hfill & \left[A_0^{\left(n\right)}{u}^n\left(x\right)-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u^k\left(x\right)-A_{n-1}^{\left(n\right)}{u}^0\left(x\right)\right]-{\displaystyle \frac{{\partial }^2{u}^n\left(x\right)}{\partial x^2}}+\kappa u^n\left(x\right)\hfill \\ \hfill & =f^n\left(x\right)+R_t{u}^n\left(x\right),\hfill \end{array}$$

where $u^n\left(x\right)=u(x,t_n)$, $f^n\left(x\right)=f(x,t_n)$ and $|R_t{u}^n\left(x\right)|\le \mathcal{O}({\tau }^{2-\alpha }+\epsilon )$. Then, $u^n\left(x\right)$ is approximated by (13), which leads to

$$\begin{array}{cc}\hfill & \sum _{q=0}^M{\varphi }_q\left(x\right)\left[A_0^{\left(n\right)}{u}_q^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u_q^k-A_{n-1}^{\left(n\right)}{u}_q^0\right]-\sum _{q=0}^M{\varphi }_q^{″}\left(x\right)u_q^n+\kappa \sum _{q=0}^M{\varphi }_q\left(x\right)u_q^n\hfill \\ \hfill & =f^n\left(x\right)+R_t{u}^n\left(x\right)+R_1{u}^n\left(x\right)+R_x{u}^n\left(x\right),\hfill \end{array}$$

(37)

with $u_q^n=u^n\left(x_q\right)$, $R_1{u}^n\left(x\right)=u^n\left(x\right)-u_M^n\left(x\right),$  $R_x{u}^n\left(x\right)={\left(u^n\left(x\right)\right)}^{″}-{\left(u_M^n\left(x\right)\right)}^{″}$. From Lemmas 4 and 5, $R_1{u}^n$ and $R_x{u}^n$ satisfy

$$\begin{array}{cc}\hfill & \parallel R_1{u}^n{\parallel }_{\infty }\le c_1{\left({\displaystyle \frac{e}{2M}}\right)}^M\parallel u^{(M+1)}{\parallel }_{\infty },{\parallel R_x{u}^n\parallel }_{\infty }\le c_1{\left({\displaystyle \frac{e}{2(M-2)}}\right)}^{M-2}\parallel u^{(M+1)}{\parallel }_{\infty }.\hfill \end{array}$$

(38)

Let Equation (37) be equal at ${\left\{x_p\right\}}_{p=0}^M$ (based on the property ${\varphi }_q\left(x_p\right)={\delta }_{pq}$ and ${\varphi }_q^{″}\left(x_p\right)=D_{pq}^{\left(2\right)}$); it reduces that

$$\begin{array}{cc}\hfill & \sum _{q=0}^M{\delta }_{pq}\left[A_0^{\left(n\right)}{u}_q^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u_q^k-A_{n-1}^{\left(n\right)}{u}_q^0\right]-\sum _{q=0}^M{D}_{pq}^{\left(2\right)}{u}_q^n+\kappa \sum _{j=0}^M{\delta }_{pq}{u}_q^n\hfill \\ \hfill & =f_p^n+R_t{u}_p^n+R_1{u}_p^n+R_x{u}_p^n,\hfill \end{array}$$

where $f_p^n=f(x_p,t_n)$, $R_t{u}_p^n=R_t{u}^n\left(x_p\right)$, $R_1{u}_p^n=R_1{u}^n\left(x_p\right)$, $R_x{u}_p^n=R_x{u}^n\left(x_p\right)$. We discard the remainders $R_t{u}_p^n$, $R_1{u}_p^n$, and $R_x{u}_p^n$ and replace $u_q^n$ by $U_q^n$; the 1D fully discrete format of Equation (1) can be expressed as

$$\begin{array}{cc}\hfill & \sum _{q=0}^M{\delta }_{pq}\left[A_0^{\left(n\right)}{U}_q^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U_q^k-A_{n-1}^{\left(n\right)}{U}_q^0\right]-\sum _{q=0}^M{D}_{pq}^{\left(2\right)}{U}_q^n+\kappa \sum _{q=0}^M{\delta }_{pq}{U}_q^n=f_p^n.\hfill \end{array}$$

(39)

Further, we rearrange the above equation and get that

$$\sum _{q=0}^M\left[\left(A_0^{\left(n\right)}+\kappa \right){\delta }_{pq}-D_{pj}^{\left(2\right)}\right]U_q^n=f_p^n+\sum _{q=0}^M{\delta }_{pq}\left[\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U_q^k+A_{n-1}^{\left(n\right)}{U}_q^0\right],$$

(40)

Let ${\mathbf{U}}^n={[U_0^n,U_1^n,\dots ,U_M^n]}^{\top }$, ${\mathbf{f}}^n={[f_0^n,f_1^n,\dots ,f_M^n]}^{\top }$; the system of Equation (40) can be expressed by

$$\mathbf{L}{\mathbf{U}}^n={\mathbf{f}}^n+\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right){\mathbf{U}}^k+A_{n-1}^{\left(n\right)}{\mathbf{U}}^0,$$

where $\mathbf{L}=\left(A_0^{\left(n\right)}+\kappa \right){\mathbf{I}}_{M+1}-{\mathbf{D}}^{\left(2\right)}$, ${\mathbf{I}}_{M+1}$ be $(M+1)$-order unit matrix, ${\mathbf{D}}^{\left(2\right)}={\left[D_{pq}^{\left(2\right)}\right]}_{p,q=0}^M$. Equations (39) or (40) together with the discrete initial and boundary conditions

$$\begin{array}{cc}\hfill & U_p^0=u_0\left(x_p\right),p=0,1,\cdots ,M,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & U_0^n=U_M^n=0,n=0,1,\cdots ,N,\hfill \end{array}$$

(42)

which yields the approximate solution $U_p^n$.

Now, we give the error estimation based on the 1D fully discrete format (39). Let $u_p^n=u(x_p,t_n)$ and $U_p^n$ be the analytical and numerical solutions of Equations (1)–(3), respectively. Set $e_p^n=u_p^n-U_p^n$, we subtract Equation (39) from Equations (1)–(3) and can get the error equation of the fully discrete scheme as follows

$$\begin{array}{cc}\hfill & {}_0{}^{C}D_t^{\alpha }{u}_p^n-\sum _{q=0}^M{\delta }_{pq}\left[A_0^{\left(n\right)}{U}_q^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U_q^k-A_{n-1}^{\left(n\right)}{U}_q^0\right]\hfill \\ \hfill & -\left({\displaystyle \frac{{\partial }^2{u}_p^n}{\partial x^2}}-\sum _{q=0}^M{D}_{pq}^{\left(2\right)}{U}_q^n\right)+\kappa \left(u_p^n-\sum _{q=0}^M{\delta }_{pq}{U}_q^n\right)=0.\hfill \end{array}$$

Then we obtain error equation

$$\begin{array}{cc}\hfill & \left[A_0^{\left(n\right)}{e}_p^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)e_p^k-A_{n-1}^{\left(n\right)}{e}_p^0\right]+\kappa e_p^n=R_t{u}_p^n+R_1{u}_p^n+R_x{u}_p^n,\hfill \\ \hfill & n=1,\cdots ,N,p=1,\cdots ,M-1,\hfill \\ \hfill & e_p^0=0,p=0,1,\cdots ,M,\hfill \\ \hfill & e_0^n=e_M^n=0,n=0,1,\cdots ,N.\hfill \end{array}$$

(43)

Theorem 4.

If $u(x,t)\in C_{x,t}^{M+1,2}([-1,1]\times (0,T])$ is the solution to Equations (1)–(3), $\{U_p^n,p=0,1,\cdots ,M,n=0,1,\cdots ,N\}$ is obtained by the fully discrete Equation (39) together with (41) and (42), then for large enough $M,N$,

$$\parallel e_p^n{\parallel }_{\infty }\le \mathcal{O}({\tau }^{2-\alpha }+\epsilon )+c_2\left[{\left({\displaystyle \frac{e}{2M}}\right)}^M+{\left({\displaystyle \frac{e}{2(M-2)}}\right)}^{M-2}\right]\parallel u^{(M+1)}{\parallel }_{\infty },$$

(44)

where $c_2=c_1/(A_{n-k-1}^{\left(n\right)}+\kappa )$ is a nonnegative constant.

Proof. 

For the first part of the right in Equation (43) and $e_p^0=0$, it is easy to deduce that

$$\begin{array}{c}\hfill \parallel A_0^{\left(n\right)}{e}_p^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)e_p^k-A_{n-1}^{\left(n\right)}{e}_p^0{\parallel }_{\infty }\ge A_{n-1}^{\left(n\right)}\parallel e_p^n-e_p^0{\parallel }_{\infty }=A_{n-1}^{\left(n\right)}{\parallel e_p^n\parallel }_{\infty }.\end{array}$$

(45)

For the left part of Equation (43), by the triangle inequality, there is

$$\begin{array}{c}\hfill \parallel R_t{u}_p^n+R_1{u}_p^n+R_x{u}_p^n{\parallel }_{\infty }\le \parallel R_t{u}_p^n{\parallel }_{\infty }+\parallel R_1{u}_p^n{\parallel }_{\infty }+{\parallel R_x{u}_p^n\parallel }_{\infty }.\end{array}$$

(46)

We take Equations (45) and (46) into Equation (43); we have

$$\left(A_{n-1}^{\left(n\right)}+\kappa \right)\parallel e_p^n{\parallel }_{\infty }\le \parallel R_t{u}_p^n{\parallel }_{\infty }+\parallel R_1{u}_p^n{\parallel }_{\infty }+{\parallel R_x{u}_p^n\parallel }_{\infty }.$$

In combination with the estimations (27) and (38), we can obtain (44). □

4.2. 2D Space Discretization

In this subsection, we treat the spatial approximation of Equation (28) in 2D case, with Laplace operator $\Delta ={\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}$. Similarly, Equation (28) is firstly rewritten as

$$\begin{array}{cc}\hfill & \left[A_0^{\left(n\right)}{u}^n(x,y)-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u^k(x,y)-A_{n-1}^{\left(n\right)}{u}^0(x,y)\right]\hfill \\ \hfill & -\left({\displaystyle \frac{{\partial }^2{u}^n(x,y)}{\partial x^2}}+{\displaystyle \frac{{\partial }^2{u}^n(x,y)}{\partial y^2}}\right)+\kappa u^n(x,y)=f^n(x,y)+R_t{u}^n(x,y),\hfill \end{array}$$

where $u^n(x,y)=u(x,y,t_n)$, $f^n(x,y)=f(x,y,t_n)$, $|R_t{u}^n(x,y)|\le \mathcal{O}({\tau }^{2-\alpha }+\epsilon )$. Then, $u^n(x,y)$ is approximated by the Equation (22), which leads to

$$\begin{array}{cc}\hfill & \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\varphi }_{q_1}\left(x\right){\varphi }_{q_2}\left(y\right)\left[A_0^{\left(n\right)}{u}_{q_1{q}_2}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u_{q_1{q}_2}^k-A_{n-1}^{\left(n\right)}{u}_{q_1{q}_2}^0\right]\hfill \\ \hfill & -\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}\left({\varphi }_{q_1}^{″}\left(x\right){\varphi }_{q_2}\left(y\right)+{\varphi }_{q_1}\left(x\right){\varphi }_{q_2}^{″}\left(y\right)\right)u_{q_1{q}_2}^n+\kappa \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\varphi }_{q_1}\left(x\right){\varphi }_{q_2}\left(y\right)u_{q_1{q}_2}^n\hfill \\ \hfill & =f^n(x,y)+R_t{u}^n(x,y)+R_2{u}^n(x,y)+R_{xx}{u}^n(x,y)+R_{yy}{u}^n(x,y),\hfill \end{array}$$

(47)

where $u_{q_1{q}_2}^n=u^n(x_{q_1},y_{q_2})$, $R_2{u}^n(x,y)=u^n(x,y)-u_{M_1{M}_2}^n(x,y)$, $R_{xx}{u}^n(x,y)={\displaystyle \frac{{\partial }^2{u}^n(x,y)}{\partial x^2}}-{\displaystyle \frac{{\partial }^2{u}_{M_1{M}_2}^n(x,y)}{\partial x^2}}$ and $R_{yy}{u}^n(x,y)={\displaystyle \frac{{\partial }^2{u}^n(x,y)}{\partial y^2}}-{\displaystyle \frac{{\partial }^2{u}_{M_1{M}_2}^n(x,y)}{\partial y^2}}$. From Theorem 1 and Lemma 5, there are

$$\begin{array}{cc}\hfill \parallel R_2{u}^n{\parallel }_{\infty }& \le c_1\left[{\left({\displaystyle \frac{e}{2M_1}}\right)}^{M_1}+\left(1+{\displaystyle \frac{2}{\pi }}log{M}_1\right){\left({\displaystyle \frac{e}{2M_2}}\right)}^{M_2}\right]\parallel u^{(\ast )}{\parallel }_{\infty },\hfill \\ \hfill \parallel R_{xx}{u}^n+R_{yy}{u}^n{\parallel }_{\infty }& \le c_1\left[{\left({\displaystyle \frac{e}{2(M_1-2)}}\right)}^{M_1-2}+{\left({\displaystyle \frac{e}{2(M_2-2)}}\right)}^{M_2-2}\right]\parallel u^{(\ast )}{\parallel }_{\infty }.\hfill \end{array}$$

(48)

Let (47) be equal at the points $\left\{(x_{p_1},y_{p_2})\right|p_1=0,1,\cdots ,M_1,p_2=0,1,\cdots ,M_2\}$, combined with the properties ${\varphi }_{q_1}\left(x_{p_1}\right)={\delta }_{p_1{q}_1}$, ${\varphi }_{q_2}\left(y_{p_2}\right)={\delta }_{p_2{q}_2}$, and ${\varphi }_{q_1}^{″}\left(x_{p_1}\right)=D_{p_1{q}_1}^{\left(2\right)}$, ${\varphi }_{q_2}^{″}\left(y_{p_2}\right)=D_{p_2{q}_2}^{\left(2\right)}$. Then

$$\begin{array}{cc}\hfill & \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}\left[A_0^{\left(n\right)}{u}_{q_1{q}_2}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)u_{q_1{q}_2}^k-A_{n-1}^{\left(n\right)}{u}_{q_1{q}_2}^0\right]\hfill \\ \hfill & -\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}\left(D_{p_1{q}_1}^{\left(2\right)}{\delta }_{p_2{q}_2}+{\delta }_{p_1{q}_1}{D}_{p_2{q}_2}^{\left(2\right)}\right)u_{q_1{q}_2}^n+\kappa \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}{u}_{q_1{q}_2}^n\hfill \\ \hfill & =f_{p_1{p}_2}^n+R_t{u}_{p_1{p}_2}^n+R_2{u}_{p_1{p}_2}^n+R_{xy}{u}_{p_1{p}_2}^n.\hfill \end{array}$$

and $f_{p_1{p}_2}^n=f(x_{p_1},y_{p_2},t_n)$, $R_t{u}_{p_1{p}_2}^n=R_t{u}^n(x_{p_1},y_{p_2})$, $R_2{u}_{p_1{p}_2}^n=R_2{u}^n(x_{p_1},y_{p_2})$, $R_{xx}{u}_{p_1{p}_2}^n=R_{xx}{u}^n(x_{p_1},y_{p_2})$ and $R_{yy}{u}_{p_1{p}_2}^n=R_{yy}{u}^n(x_{p_1},y_{p_2})$. We discard $R_t{u}_{p_1{p}_2}^n$, $R_2{u}_{p_1{p}_2}^n$, $R_{xx}{u}_{p_1{p}_2}^n$, $R_{yy}{u}_{p_1{p}_2}^n$ and replace $u_{q_1{q}_2}^n$ with $U_{q_1{q}_2}^n$; the 2D fully discrete format of Equation (1) is

$$\begin{array}{cc}\hfill & \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}\left[A_0^{\left(n\right)}{U}_{q_1{q}_2}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U_{q_1{q}_2}^k-A_{n-1}^{\left(n\right)}{U}_{q_1{q}_2}^0\right]\hfill \\ \hfill & -\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}\left(D_{p_1{q}_1}^{\left(2\right)}{\delta }_{p_2{q}_2}+{\delta }_{p_1{q}_1}{D}_{p_2{q}_2}^{\left(2\right)}\right)U_{q_1{q}_2}^n+\kappa \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}{U}_{q_1{q}_2}^n=f_{p_1{p}_2}^n.\hfill \end{array}$$

(49)

We rearrange the Equation (49) and obtain that

$$\begin{array}{cc}\hfill & \sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}\left[\left(A_0^{\left(n\right)}+\kappa \right){\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}-\left(D_{p_1{q}_1}^{\left(2\right)}{\delta }_{p_2{q}_2}+{\delta }_{p_1{q}_1}{D}_{p_2{q}_2}^{\left(2\right)}\right)\right]U_{q_1{q}_2}^n\hfill \\ \hfill & =f_{p_1{p}_2}^n+\sum _{q_1=0}^{M_1}\sum _{q_2=0}^{M_2}{\delta }_{p_1{q}_1}{\delta }_{p_2{q}_2}\left[\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)U_{q_1{q}_2}^k+A_{n-1}^{\left(n\right)}{U}_{q_1{q}_2}^0\right].\hfill \end{array}$$

(50)

Let

$$\begin{array}{cc}\hfill {\mathbf{U}}^n& ={\left[U_{00}^n,U_{01}^n,\dots ,U_{0M_2}^n,\dots ,U_{M_{1}0}^n,U_{M_{1}1}^n,\dots ,U_{M_1{M}_2}^n\right]}^{\top },\hfill \\ \hfill {\mathbf{f}}^n& ={\left[f_{00}^n,f_{01}^n,\dots ,f_{0M_2}^n,\cdots ,f_{M_{1}0}^n,f_{M_{1}1}^n,\dots ,f_{M_1{M}_2}^n\right]}^{\top },\hfill \end{array}$$

then the matrix form of the above fully discrete format (50) can be formulated as

$$\mathbf{E}{\mathbf{U}}^n={\mathbf{f}}^n+\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right){\mathbf{U}}^k+A_{n-1}^{\left(n\right)}{\mathbf{U}}^0,$$

with $\mathbf{E}=\left(A_0^{\left(n\right)}+\kappa \right)\left({\mathbf{I}}_{M_1+1}\otimes {\mathbf{I}}_{M_2+1}\right)-\left({\mathbf{D}}_1^{\left(2\right)}\otimes {\mathbf{I}}_{M_2+1}+{\mathbf{I}}_{M_1+1}\otimes {\mathbf{D}}_2^{\left(2\right)}\right)$, ${\mathbf{D}}_1^{\left(2\right)}={\left[D_{p_1{q}_1}^{\left(2\right)}\right]}_{p_1,q_1=0}^{M_1}$ and ${\mathbf{D}}_2^{\left(2\right)}={\left[D_{p_2{q}_2}^{\left(2\right)}\right]}_{p_2,q_2=0}^{M_2}$. Equations (49) or (50) together with the discrete initial and boundary conditions

$$\begin{array}{cc}\hfill U_{p_1{p}_2}^0& =u_0(x_{p_1},y_{p_2}),\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill U_{p_{1}0}^n& =U_{p_1{M}_2}^n=0,U_{0p_2}^n=U_{M_1{p}_2}^n=0,\hfill \end{array}$$

(52)

for $p_1=0,1,\cdots ,M_1,p_2=0,1,\cdots ,M_2,n=0,1,\cdots ,N$, which yields the approximate solution $U_{p_1{p}_2}^n$.

Now, we give the error estimation based on the 2D fully discrete format Equation (49). Let $u_{p_1{p}_2}^n=u(x_{p_1},y_{p_2},t_n)$ and $U_{p_1{p}_2}^n$ be the exact and approximate solutions of Equations (1)–(3). Similar to (43), set $e_{p_1{p}_2}^n=u_{p_1{p}_2}^n-U_{p_1{p}_2}^n$. Then we can derive the error equation

$$\begin{array}{cc}\hfill & \left[A_0^{\left(n\right)}{e}_{p_1{p}_2}^n-\sum _{k=1}^{n-1}\left(A_{n-k-1}^{\left(n\right)}-A_{n-k}^{\left(n\right)}\right)e_{p_1{p}_2}^k-A_{n-1}^{\left(n\right)}{e}_{p_1{p}_2}^0\right]+\kappa e_{p_1{p}_2}^n=R_t{u}_{p_1{p}_2}^n+R_2{u}_{p_1{p}_2}^n+R_{xy}{u}_{p_1{p}_2}^n,\hfill \\ \hfill & n=1,\cdots ,N,p_1=1,\cdots ,M_1-1,p_2=1,\cdots ,M_2-1,\hfill \\ \hfill & e_{p_1{p}_2}^0=0,p_1=0,1,\cdots ,M_1,p_2=0,1,\cdots ,M_2,\hfill \\ \hfill & e^n{|}_{\partial \Omega }=0,n=0,1,\cdots ,N.\hfill \end{array}$$

Theorem 5.

If $u(x,y,t)\in C_{x,y,t}^{M_1+1,M_2+1,2}({[-1,1]}^2\times (0,T])$ is the solution of Equations (1)–(3), $\{U_{p_1{p}_2}^n,p_1=0,1,\cdots ,M_1,p_2=0,1,\cdots ,M_2,n=0,1,\cdots ,N\}$ is obtained by the fully discrete Equation (49) together with discrete conditions (51) and (52), then for large enough $M_1,M_2,N$,

$$\begin{array}{cc}\hfill \parallel e_{p_1{p}_2}^n{\parallel }_{\infty }& \le \mathcal{O}({\tau }^{2-\alpha }+\epsilon )+c_2[{\left({\displaystyle \frac{e}{2M_1}}\right)}^{M_1}+\left(1+{\displaystyle \frac{2}{\pi }}log{M}_1\right){\left({\displaystyle \frac{e}{2M_2}}\right)}^{M_2}\hfill \\ \hfill & +{\left({\displaystyle \frac{e}{2(M_1-2)}}\right)}^{M_1-2}+{\left({\displaystyle \frac{e}{2(M_2-2)}}\right)}^{M_2-2}]\parallel u^{(\ast )}{\parallel }_{\infty },\hfill \end{array}$$

where $c_2=c_1/(A_{n-k-1}^{\left(n\right)}+\kappa )$, $\parallel u^{(\ast )}{\parallel }_{\infty }=max\left\{\parallel {\displaystyle \frac{{\partial }^{M_1+1}u}{\partial {\xi }^{M_1+1}}}{\parallel }_{\infty },\parallel {\displaystyle \frac{{\partial }^{M_2+1}u}{\partial {\eta }^{M_2+1}}}{\parallel }_{\infty }\right\}$.

Proof. 

Similar to the proof of Theorem 4, the result can be derived by the estimations (27) and (48). □

5. Numerical Experiments

In this section, some numerical experiments are reported to support theoretical results. The temporal discretization is accomplished by the fast L1 format, with absolute tolerance being taken $\epsilon ={10}^{-14}$ in SOE treatment. It expects that the convergent order is near $2-\alpha$ for a smooth enough solution. We compare the CPU time(s) for the L1 and fast L1 formulas to display the fast behavior of the latter. The spatial discretization is handled by the BLI based on the Chebyshev points of the second kind. The high numerical precision in space is depicted via the maximum absolute errors. For brevity, let $u^n$ and $U^n$ be the exact and numerical solutions at $t_n$, respectively. The maximum absolute error is denoted as

$$\mathrm{E}\left(N\right):=\underset{1\le n\le N}{max}|u^n-U^n|,$$

and the temporal convergence rate is calculated by

$$\mathrm{Rate}:={\displaystyle \frac{log\left(\mathrm{E}\right(N)/\mathrm{E}(2N\left)\right)}{log\left(\tau \right(N)/\tau (2N\left)\right)}},$$

where $\tau \left(N\right)$ expresses the maximum time-step size for whole N sub-intervals.

Example 1.

Considering the following 1D time-fractional evolution equation

$${}_0{}^{C}D_t^{\alpha }u(x,t)={\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}+f(x,t),x\in (0,1),t\in (0,1],$$

where the inhomogeneous term is

$$f(x,t)={\displaystyle \frac{\Gamma (3+\alpha )}{2}}{e}^x{x}^2{(1-x)}^2{t}^2-t^{2+\alpha }{e}^x\left(2-8x+x^2+6x^3+x^4\right),$$

with homogeneous initial and boundary conditions. The exact solution is

$$u(x,t)=t^{2+\alpha }{e}^x{x}^2{(1-x)}^2.$$

By choosing different values of $\alpha =0.3,0.5,0.7$ in Table 1 and Figure 1, we fix $M=20$ for testing the temporal numerical performance by the fast L1 formula. Table 1 provides the maximum errors and convergence orders in time, which indicates that the convergence orders reach near $2-\alpha$. In Figure 1, the CPU time of L1 and fast L1 formulas are compared under the same circumstances. For small values of N, there is little difference in calculation time between the two formulas. However, as N increases, the calculation time of the L1 formula increases significantly while the fast L1 formula remains computationally efficient. This validates the advantage of the fast L1 scheme. In addition, the numerical findings in Table 1 are in accordance with Table 1 in [32], which is obtained by the box-type scheme. The method in [32] requires 20,000 nodes in the spatial domain, while our method only needs 20 nodes. This indicates that the computational burden of the current approach is significantly lower. In Table 2, we fix $N=2048$ for testing the spatial numerical accuracy by the BLI. Table 2 displays that the maximum errors and CPU time in space, showing that the high numerical accuracy can be reached in space with a small number of interpolation nodes by the BLI method.

Table 1. Maximum errors and convergent rates in temporal direction with $M=20$ in Example 1.

N	$\mathit{\alpha }=0.3$		$\mathit{\alpha }=0.5$		$\mathit{\alpha }=0.7$
	$\mathbf{E}\left(\mathit{N}\right)$	Rate	$\mathbf{E}\left(\mathit{N}\right)$	Rate	$\mathbf{E}\left(\mathit{N}\right)$	Rate
10	4.08  $\times {10}^{-4}$	-	1.20 $\times {10}^{-3}$	-	3.00 $\times {10}^{-3}$	-
20	1.34  $\times {10}^{-4}$	1.60	4.54  $\times {10}^{-4}$	1.43	1.20 $\times {10}^{-3}$	1.26
40	4.34 $\times {10}^{-5}$	1.63	1.66   $\times {10}^{-4}$	1.46	5.11  $\times {10}^{-4}$	1.28
80	1.39 $\times {10}^{-5}$	1.65	5.98 $\times {10}^{-5}$	1.47	2.10  $\times {10}^{-4}$	1.28
160	4.40 $\times {10}^{-6}$	1.66	2.14 $\times {10}^{-5}$	1.48	8.58 $\times {10}^{-5}$	1.29
320	1.39 $\times {10}^{-6}$	1.67	7.66 $\times {10}^{-6}$	1.49	3.50 $\times {10}^{-5}$	1.29
640	4.35 $\times {10}^{-7}$	1.67	2.73 $\times {10}^{-6}$	1.49	1.42 $\times {10}^{-5}$	1.30
1280	1.36 $\times {10}^{-9}$	1.68	9.68 $\times {10}^{-7}$	1.49	5.79 $\times {10}^{-6}$	1.30

Figure 1. CPU time of L1 and fast L1 formulas with $M=20$ in Example 1.

Table 2. Maximum errors and CPU time in spatial direction with $N=2048$ in Example 1.

M	$\mathit{\alpha }=0.3$		$\mathit{\alpha }=0.5$		$\mathit{\alpha }=0.7$
	$\mathbf{E}\left(\mathit{N}\right)$	CPU	$\mathbf{E}\left(\mathit{N}\right)$	CPU	$\mathbf{E}\left(\mathit{N}\right)$	CPU
6	7.11  $\times {10}^{-4}$	0.04	6.46  $\times {10}^{-4}$	0.06	5.89  $\times {10}^{-4}$	0.06
8	2.46  $\times {10}^{-6}$	0.04	2.69  $\times {10}^{-6}$	0.05	5.07  $\times {10}^{-6}$	0.04
10	6.38  $\times {10}^{-8}$	0.07	4.80  $\times {10}^{-7}$	0.05	3.14  $\times {10}^{-6}$	0.05
12	6.16  $\times {10}^{-8}$	0.05	4.79  $\times {10}^{-7}$	0.05	3.14  $\times {10}^{-6}$	0.04
14	6.17  $\times {10}^{-8}$	0.05	4.79  $\times {10}^{-7}$	0.06	3.15  $\times {10}^{-6}$	0.10

Example 2.

Considering the following 2D time-fractional evolution equation

$${}_0{}^{C}D_t^{\alpha }u(x,y,t)-\Delta u(x,y,t)+u(x,y,t)=f(x,y,t),(x,y)\in {(-1,1)}^2,t\in (0,1],$$

where the inhomogeneous term is

$$f(x,y,t)=\left({\displaystyle \frac{2t^{-\alpha }}{\Gamma (3-\alpha )}}+2{\pi }^2+1\right)t^{2}sin\left(\pi x\right)sin\left(\pi y\right),$$

with homogeneous initial and boundary conditions. The exact solution is

$$u(x,y,t)=t^{2}sin\left(\pi x\right)sin\left(\pi y\right).$$

By choosing the same values of $\alpha =0.3,0.5,0.7$ and setting the number of spatial discrete nodes equal in different directions, i.e., $M=M_1=M_2$ in Table 3 and Figure 2, we fix $M=20$ to observe the temporal numerical performance by the fast L1 method. Similar to the above 1D case, we can see that the convergence rate is in agreement with the theoretical estimate $2-\alpha$ in temporal direction from Table 3. Simultaneously, Table 3 also records the temporal maximum errors and convergent rates by L1-ADI in [33], which demonstrates that our method is more accurate and efficient. From Figure 2, it still implies that the fast L1 scheme can vastly reduce the computational cost. By fixing $N=2048$, Table 4 tests the spatial numerical accuracy using 2D BLI. The numerical results demonstrate that highly numerical accuracy can be achieved in a space with a small number of interpolation nodes using the provided method.

Table 3. Maximum errors and convergent rates in temporal direction with $M=20$ in Example 2.

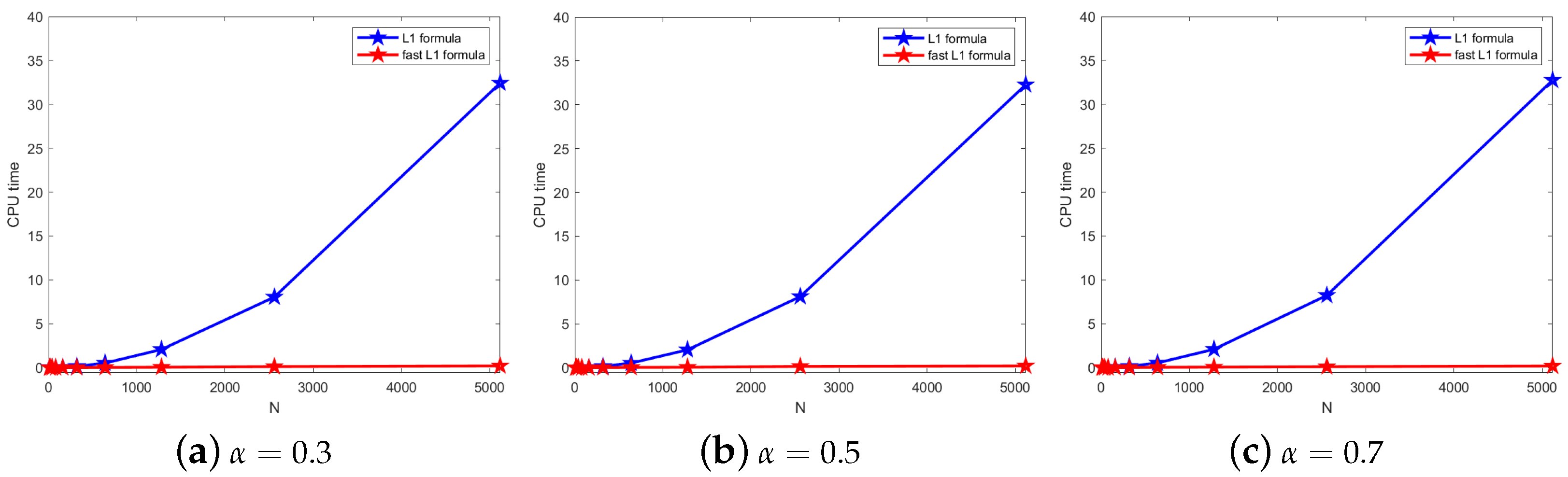
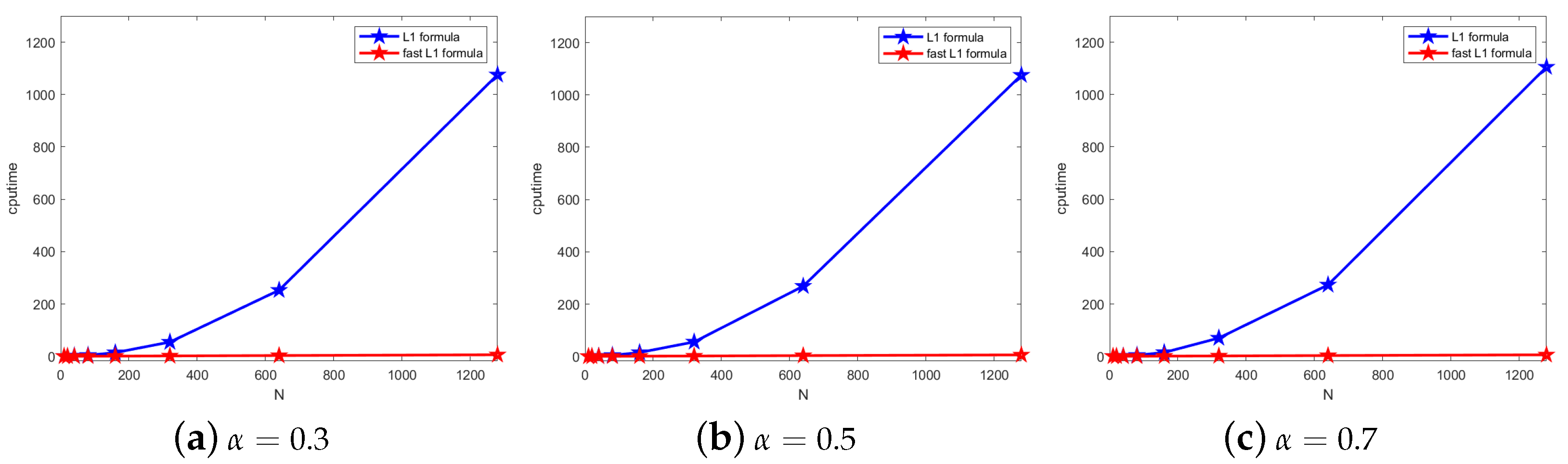
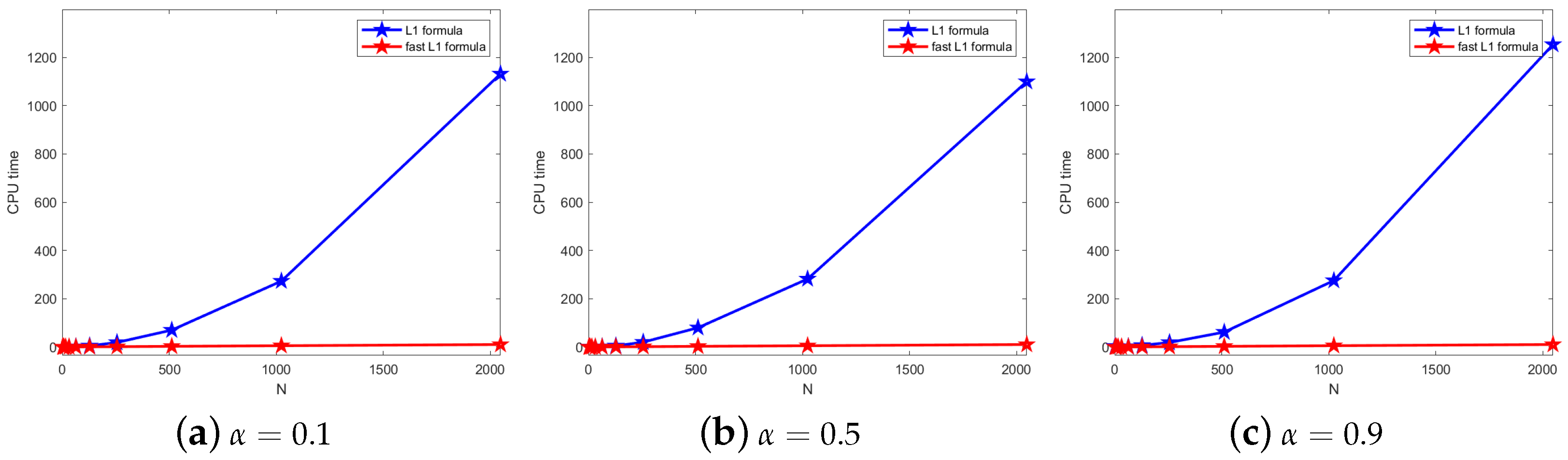
$\mathit{\alpha }$	N	L1-ADI [33]		Present Method
		$\mathbf{E}\left(\mathit{N}\right)$	Rate	$\mathbf{E}\left(\mathit{N}\right)$	Rate
0.3	10	3.68  $\times {10}^{-1}$	-	5.90  $\times {10}^{-4}$	-
	20	2.64  $\times {10}^{-1}$	0.4824	1.90  $\times {10}^{-4}$	1.6329
	40	1.79  $\times {10}^{-1}$	0.5551	6.07  $\times {10}^{-5}$	1.6478
	80	1.18  $\times {10}^{-1}$	0.6052	1.92  $\times {10}^{-5}$	1.6590
0.5	10	2.11  $\times {10}^{-1}$	-	1.60  $\times {10}^{-3}$	-
	20	1.09  $\times {10}^{-7}$	1.0363	5.81  $\times {10}^{-4}$	1.4705
	40	5.34  $\times {10}^{-2}$	1.0292	2.08  $\times {10}^{-4}$	1.4796
	80	2.58  $\times {10}^{-2}$	1.0518	7.44  $\times {10}^{-5}$	1.4900
0.7	10	1.13  $\times {10}^{-1}$	-	3.80  $\times {10}^{-3}$	-
	20	4.28  $\times {10}^{-2}$	1.4040	1.50  $\times {10}^{-3}$	1.2895
	40	1.58  $\times {10}^{-2}$	1.4425	6.31  $\times {10}^{-4}$	1.2936
	80	5.81  $\times {10}^{-3}$	1.4407	2.57  $\times {10}^{-4}$	1.2976

Figure 2. CPU time of L1 and fast L1 formulas with $M=20$ in Example 2.

Table 4. Maximum errors and CPU time in spatial direction with $N=2048$ in Example 2.

M	$\mathit{\alpha }=0.3$		$\mathit{\alpha }=0.5$		$\mathit{\alpha }=0.7$
	$\mathbf{E}\left(\mathit{N}\right)$	CPU	$\mathbf{E}\left(\mathit{N}\right)$	CPU	$\mathbf{E}\left(\mathit{N}\right)$	CPU
6	3.30  $\times {10}^{-3}$	0.28	3.30  $\times {10}^{-3}$	0.29	3.30  $\times {10}^{-3}$	0.30
8	1.51  $\times {10}^{-4}$	0.47	1.51  $\times {10}^{-4}$	0.51	1.51  $\times {10}^{-4}$	0.50
10	2.31  $\times {10}^{-6}$	0.94	2.40  $\times {10}^{-6}$	0.89	3.60  $\times {10}^{-6}$	0.88
12	4.73  $\times {10}^{-8}$	1.30	2.50  $\times {10}^{-7}$	1.28	1.55  $\times {10}^{-6}$	1.26
14	3.25  $\times {10}^{-8}$	1.87	2.27  $\times {10}^{-7}$	1.79	1.47  $\times {10}^{-6}$	1.78

Example 3

([34]). Considering the following 2D time-fractional evolution equation

$${}_0{}^{C}D_t^{\alpha }u(x,y,t)-\Delta u(x,y,t)+u(x,y,t)=f(x,y,t),(x,y)\in {(0,\pi )}^2,t\in (0,1],$$

where the inhomogeneous term is

$$f(x,y,t)=\left({\displaystyle \frac{\alpha \pi csc\left(\alpha \pi \right)}{\Gamma (1-\alpha )}}+3t^{\alpha }\right)sin\left(x\right)sin\left(y\right),$$

with homogeneous initial and boundary conditions. The exact solution is

$$u(x,y,t)=t^{\alpha }sin\left(x\right)sin\left(y\right).$$

Let $\alpha =0.1,0.5,0.9$ and $M=M_1=M_2=20$ in Table 5 and Figure 3. Since the solution is dependent on $\alpha$ and possesses weak singularity at $t=0$, Table 5 displays that the convergence order is near $\alpha$. Figure 3 compares the CPU time of the L1 and fast L1 formulas. For a sufficiently large N, the CPU time of the latter is much less than the former, which is consistent with the tested results of the above two examples. In Table 6, with N fixed at 2048, the maximum error and CPU time in space are displayed. The numerical results indicate that a high-precision numerical solution is obtained using the 2D BLI method.

Table 5. Maximum errors and convergent rates in temporal direction with $M=20$ in Example 3.

	$\mathit{\alpha }=0.1$		$\mathit{\alpha }=0.5$		$\mathit{\alpha }=0.9$
	$\mathbf{E}\left(\mathit{N}\right)$	Rate	$\mathbf{E}\left(\mathit{N}\right)$	Rate	$\mathbf{E}\left(\mathit{N}\right)$	Rate
16	2.02  $\times {10}^{-2}$	-	3.22  $\times {10}^{-2}$	-	5.80  $\times {10}^{-3}$	-
32	1.98  $\times {10}^{-2}$	0.03	2.58  $\times {10}^{-2}$	0.32	3.60  $\times {10}^{-3}$	0.67
64	1.93  $\times {10}^{-2}$	0.03	2.01  $\times {10}^{-2}$	0.36	2.20  $\times {10}^{-3}$	0.72
128	1.89  $\times {10}^{-2}$	0.04	1.54  $\times {10}^{-2}$	0.39	1.30  $\times {10}^{-3}$	0.76
256	1.84  $\times {10}^{-2}$	0.04	1.15  $\times {10}^{-2}$	0.42	7.57  $\times {10}^{-4}$	0.79
512	1.79  $\times {10}^{-2}$	0.04	8.50  $\times {10}^{-3}$	0.44	4.31  $\times {10}^{-4}$	0.81
1024	1.74  $\times {10}^{-2}$	0.04	6.20  $\times {10}^{-3}$	0.46	2.42  $\times {10}^{-4}$	0.83
2048	1.69  $\times {10}^{-2}$	0.04	4.50  $\times {10}^{-3}$	0.47	1.34  $\times {10}^{-4}$	0.85

Figure 3. CPU time of L1 and fast L1 formulas with $M=20$ in Example 3.

Table 6. Numerical results for spatial direction with $N=2048$ in Example 3.

M	$\mathit{\alpha }=0.1$		$\mathit{\alpha }=0.5$		$\mathit{\alpha }=0.9$
	$\mathrm{E}\left(\mathit{N}\right)$	CPU	$\mathrm{E}\left(\mathit{N}\right)$	CPU	$\mathrm{E}\left(\mathit{N}\right)$	CPU
6	1.69  $\times {10}^{-2}$	0.31	4.50  $\times {10}^{-3}$	0.31	1.34  $\times {10}^{-4}$	0.34
8	1.69  $\times {10}^{-2}$	0.46	4.50  $\times {10}^{-3}$	0.50	1.34  $\times {10}^{-4}$	0.51
10	1.69  $\times {10}^{-2}$	0.94	4.50  $\times {10}^{-3}$	0.96	1.34  $\times {10}^{-4}$	1.01
12	1.69  $\times {10}^{-2}$	1.23	4.50  $\times {10}^{-3}$	1.26	1.34  $\times {10}^{-4}$	1.32
14	1.69  $\times {10}^{-2}$	1.82	4.50  $\times {10}^{-3}$	1.80	1.34  $\times {10}^{-4}$	1.77

6. Conclusions

In this paper, a general kind of time-fractional evolution equation with Caputo fractional derivatives is solved efficiently by the fast L1 formula in time and the BLI method in space. The time semi-discrete format obtained from the fast L1 scheme is shown to be unconditionally stable and capable of maintaining the expected convergent behavior. Further, the fully discrete format is derived in combination with the BLI based on the Chebyshev nodes of the second kind in spatial direction. Additionally, related error estimations are demonstrated. Some numerical examples are presented to validate the fast behavior in time and high precision in space.