On Extended Class of Totally Ordered Interval-Valued Convex Stochastic Processes and Applications

Abstract

The intent of the current study is to explore convex stochastic processes within a broader context. We introduce the concept of unified stochastic processes to analyze both convex and non-convex stochastic processes simultaneously. We employ weighted quasi-mean, non-negative mapping $\gamma$, and center-radius ordering relations to establish a class of extended $cr$-interval-valued convex stochastic processes. This class yields a combination of innovative convex and non-convex stochastic processes. We characterize our class by illustrating its relationships with other classes as well as certain key attributes and sufficient conditions for this class of processes. Additionally, leveraging Riemann–Liouville stochastic fractional operators and our proposed class, we prove parametric fractional variants of Jensen’s inequality, Hermite–Hadamard’s inequality, Fejer’s inequality, and product Hermite–Hadamard’s like inequality. We establish an interesting relation between means by means of Hermite–Hadamard’s inequality. We utilize the numerical and graphical approaches to showcase the significance and effectiveness of primary findings. Also, the proposed results are powerful tools to evaluate the bounds for stochastic Riemann–Liouville fractional operators in different scenarios for a larger space of processes.

1. Introduction and Preliminaries

The development, modification, and extension of new and classical mathematical concepts from different strategies is a fascinating subject of research. Originally, modifications were always made to fulfill the limitations of already established results and theories. One of the robust concepts is convexity of sets and mappings, which lay the foundations for advanced analysis. Based on the utility of convexity, numerous approaches have been deployed for the ramifications of convexity to conclude some new refinements and fulfill the limitations of classical concepts. The subject of convexity is a power tool for the derivation of various integral inequalities. To list all the applications of inequalities is not possible, but they play a vital role in analyzing the complex systems and crucial problems of optimization and error analysis of numerical quadrature procedures. Let us retrospect at trapezium inequality for convex function, Let $\mathcal{F}:[{\sigma }_1,{\sigma }_2]\subset \mathbb{R}\to \mathbb{R}$ be a convex mapping with ${\sigma }_1<{\sigma }_2$, then

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}}\right)\le {\displaystyle \frac{1}{{\sigma }_2-{\sigma }_1}}{\int }_{{\sigma }_1}^{{\sigma }_2}\mathcal{F}\left(\mu \right)\mathrm{d}\mu \le {\displaystyle \frac{\mathcal{F}\left({\sigma }_1\right)+\mathcal{F}\left({\sigma }_2\right)}{2}}.\end{array}$$

For a comprehensive study, see [1,2,3,4].

Wu et al. introduced the idea of unified convexity by means of weighted quasi-mean in [5].

Definition 1 

([5]). A mapping $\mathcal{F}:{\mathfrak{K}}_1\to \mathbb{R}$ is said to be θ-convex with respect to an invertible mapping θ, if

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left(\mu \right)+\ell \theta \left(y\right))\right)\le (1-\ell )\mathcal{F}\left(\mu \right)+\ell \mathcal{F}\left(y\right)\forall \mu ,y\in {\mathfrak{K}}_1\ell \in [0,1].\end{array}$$

Interval-valued calculus and analysis is a specific field of set-valued analysis that is beneficial to tackle with uncertain data and quantities in deterministic problems. Moore looked into the subject in an innovative manner, demonstrating its relevance in error estimations, and he wrote extremely fascinating monographs on interval analysis in both real and fuzzy environments. These books set the precedent for subsequent advances. For additional details, visit [6]. His exceptional contributions to the interval realm inspired scholars to examine numerous challenges in the interval environment. Recently, authors utilized fractional interval-valued terminologies to explore neural networking, dynamical systems of differential equations, combinatorics, and inequalities. Breckner [7] purported the idea of set-valued convexity.

Now, we recover some useful results of interval analysis, which are quite helpful in the determination of principle findings.

Theorem 1 

([6]). Presume that $\mathcal{F} : [{\sigma }_1,{\sigma }_2]\to \mathbb{R}$ is an interval-valued mapping such that $\mathcal{F}(\ell )=[{\mathcal{F}}_{*},{\mathcal{F}}^{*}],\mathcal{F}\in I{R}_{[{\sigma }_1,{\sigma }_2]}\iff {\mathcal{F}}_{*},{\mathcal{F}}^{*}\in R_{[{\sigma }_1,{\sigma }_2]}$ and

$$\begin{array}{c}\hfill \left(IR\right){\int }_{{\sigma }_1}^{{\sigma }_2}\mathcal{F}(\ell )\mathrm{d}\ell =\left[\left(R\right){\int }_{{\sigma }_1}^{{\sigma }_2}{\mathcal{F}}_{*}(\ell )\mathrm{d}\ell ,\left(R\right){\int }_{{\sigma }_1}^{{\sigma }_2}{\mathcal{F}}^{*}(\ell )\mathrm{d}\ell \right].\end{array}$$

One of the crucial problems is the ranking of intervals; for this, several partial orderings such as left-right or Kulish–Miranker and up–down orderings have been heavily investigated. In [8], Bhunia et al. introduced the total ordering via center and radius of intervals, which is reported as

$$\begin{array}{c}\hfill \mathcal{E}=⟨{\mathcal{E}}_c,{\mathcal{E}}_r⟩=⟨{\displaystyle \frac{{\mathcal{E}}_{*}+{\mathcal{E}}^{*}}{2}},{\displaystyle \frac{{\mathcal{E}}^{*}-{\mathcal{E}}_{*}}{2}}⟩.\end{array}$$

Moreover, the center radius ($cr$)-ranking relation is described as

Definition 2 

([8]). For two intervals $\mathcal{E}=\left[{\mathcal{E}}_{*},{\mathcal{E}}^{*}\right]=⟨{\mathcal{E}}_c,{\mathcal{E}}_r⟩$ and $\mathcal{W}=\left[{\mathcal{W}}_{*},{\mathcal{W}}^{*}\right]=⟨{\mathcal{W}}_c,{\mathcal{W}}_r⟩$, we define the $cr$-order relation as

$$\begin{array}{c}\hfill \mathcal{E}{⪯}_{cr}\mathcal{W}\iff \left\{\begin{array}{c}{\mathcal{E}}_c<{\mathcal{W}}_c,if{\mathcal{E}}_c\ne {\mathcal{W}}_c\\ {\mathcal{E}}_r\le {\mathcal{W}}_r,if{\mathcal{E}}_c={\mathcal{W}}_c.\end{array}\right.\end{array}$$

Shi et al. [9] proved the monotone property concerning $cr$-ordering for the integral.

Theorem 2 

([9]). Consider $\mathcal{F},\xi : [{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ to be two I.V. mappings such that $\mathcal{F}\left(y\right)=\left[{\mathcal{F}}_{*}\left(y\right),{\mathcal{F}}^{*}\left(y\right)\right],\xi \left(y\right)=\left[{\xi }_{*}\left(y\right),{\xi }^{*}\left(y\right)\right]$. If $\mathcal{F},\xi \in I{R}_{\left(\left[{\sigma }_1,{\sigma }_2\right]\right)}$ and $\mathcal{F}\left(y\right){⪯}_{cr}\xi \left(y\right)$, then

$$\begin{array}{c}\hfill \underset{{\sigma }_1}{\overset{c_2}{\int }}\mathcal{F}\left(y\right)dy{⪯}_{cr}\underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\xi \left(y\right)dy.\end{array}$$

Zhao et al. [10,11] discovered Jensen’s, trapezium, and Chebyshev kinds of inequalities associated with interval-valued h-convex functions. Budak et al. [12] computed the fractional counterparts of classical inequalities for interval-valued convex mappings. Author [13] introduced a potential class of convexity relying on $\beta$-connected sets in a fuzzy environment and computed the fractional versions of Jensen’s and Hadamard’s like inequalities. Bin-Mohsin et al. [14] demonstrated the conception of parametric convexity based on quasi-mean and non-negative mapping h. They computed a fractional blended form of Hadamard-type inequalities associated with containment relations. In [15], Rahman et al. purported the idea of $cr$ interval-valued convex mappings and presented its utility in optimization problems with non-linear constraints. Shi et al. [9] extended the class of interval-valued $cr$ convex functions incorporated with non-negative mapping h and computed several interesting classical inequalities. Liu et al. [16] investigated the $cr$ interval-valued harmonic convex mappings and provided new counterparts of existing inequalities based on this class. Soubhagya et al. constructed several integral inequalities associated with preinvex $cr$-convex mappings in [17]. Vivas-Cortez et al. [18] developed the idea of $cr$-$\gamma$ convex functions and explored its application in inequalities. In 2022, Du and Zhou [19] investigated the exponential fractional forms of coordinated trapezium like inequalities. In [20,21], the authors have analyzed the interval-valued Ostrwoski’s like inequalities with applications in error analysis. In [22], Costa and Roman-Flores established fuzzy interval-valued integral inequalities. In 2017, Costa and Roman-Flores [23] formulated some fundamental inequalities incorporated with interval-valued mappings. Bin-Mohsin [24] examined the coordinated Hadamard’s like inequalities associated with Raina’s fractional operators and harmonic convex mappings. In 2023, Bin-Mohsin et al. [25] deployed the multi-parameter fractional operators to explore the trapezium like inequalities. Recently, Fahad et al. [26] initiated the idea of totally ordered $GA$ convex mappings and presented its some crucial properties and applications.

Next, we provide some facts about second-order stochastic processes, which are useful for future proceedings.

Stochastic Analysis

Stochastic processes are regarded as a family of random variables depending on parameters and probability measure space. Techniques related to stochastic calculus played a critical role in studying mathematical models with randomness. In [27], the authors explored deterministic and stochastic class–age-structured rumour propagation models, focusing on media coverage and age-dependent education, using differential equations, Lyapunov function, and numerical simulations. In [28,29], Zhang et al. analyzed the output feedback finite-time stabilization in probability for a family of high-order stochastic non-linear feed-forward systems and fuzzy stochastic sliding mode control systems, respectively. In [30], the author addressed asynchronous sliding-mode control for non-linear singular Markovian jump systems leveraging Takagi–Sugeno fuzzy models and presented a novel adaptive technique. In [31], the authors studied the mean square admissibility problem for a family of stochastic singular systems that use Poisson switching. In [32,33], the authors investigated the finite-time stochastic and singular non-linear systems based on an observer controller and output constraints, respectively. This theory has expanded at a high rate since its emergence in diverse directions, specifically convexity processes, which is an intriguing sight of research. Convex stochastic processes received significant attention due to their immense utility in optimal design, optimization and approximation theory.

Let $(\Omega ,A,P)$ be a probability space. Any measurable function $\mathcal{F}:\Omega \to \mathbb{R}$ is known as a random variable. A function $\mathcal{F}:I\times \Omega \to \mathbb{R}$ is known as a stochastic process if for all $\mu \in I\subset \mathbb{R}$, the function $\mathcal{F}(\mu ,·)$ is random variable.

A stochastic process $\mathcal{F}:I\times \Omega \to \mathbb{R}$ is known as

• P-upper bounded on $A\subset I$ if

  $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\underset{\ell \in A}{sup}\left\{P\left(\{\theta \in \Omega :\mathcal{F}(\ell ,\theta )\ge n\}\right)\right\}=0,\end{array}$$
• P-lower bounded on $A\subseteq I$ if

  $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\underset{\ell \in A}{sup}\left\{P\left(\{\theta \in \Omega :\mathcal{F}(\ell ,\theta )\le -n\}\right)\right\}=0,\end{array}$$
• P-bounded if it is P-upper and lower bounded on $A\subset I$.
• Continuous on I, if $\forall \mu \in I$,

  $$\begin{array}{c}\hfill P-\underset{\mu \to {\mu }_{\circ }}{lim}\mathcal{F}(\mu ,·)=\mathcal{F}({\mu }_{\circ },·),\end{array}$$

  where P-limit denotes the limit in probability space.
• Mean square continuous in I, if

  $$\begin{array}{c}\hfill \underset{\mu \to {\mu }_{\circ }}{lim}E\left[{(\mathcal{F}(\mu ,·)-\mathcal{F}({\mu }_{\circ },·))}^2\right]=0,\end{array}$$

  and $E\left[\mathcal{F}\right(\mu ,·\left)\right]$ represents the expectation of random variable $\mathcal{F}(\mu ,·)$.
• Mean square differentiable at ${\mu }_{\circ }$ if there exists a random variable ${\mathcal{F}}^{\prime }(\mu ,·):I\times \Omega :\to \mathbb{R}$, such that

  $$\begin{array}{c}\hfill {\mathcal{F}}^{\prime }({\mu }_{\circ },·)=P-\underset{\mu \to {\mu }_{\circ }}{lim}{\displaystyle \frac{\mathcal{F}(\mu ,·)-\mathcal{F}({\mu }_{\circ },·)}{\mu -{\mu }_{\circ }}}.\end{array}$$
• Process $\mathcal{F}(\mu ,·)$ is a mean square integrable with $E\left[\mathcal{F}\right(\mu ,·\left)\right]<\infty$. The random variable $Z:\Omega \to \mathbb{R}$ is a mean square integral of $\mathcal{F}(\mu ,·)$ if for each partition of $I=[{\sigma }_1,{\sigma }_2]$ such that ${\sigma }_1=u_0\le u_1\le u_2\le ,\cdots ,\le u_n={\sigma }_2$ and for all ${\ell }_k\in [u_{k-1},u_k]$, we have

  $$\begin{array}{c}\hfill \underset{n\to \infty }{lim}E\left[{\left(\sum _{k=1}^n\mathcal{F}({\ell }_k,·)(u_k-u_{k-1})-z(.)\right)}^2\right]=0.\end{array}$$

From the above expression, we have

$$\begin{array}{c}\hfill Z(.)={\int }_{{\sigma }_1}^{{\sigma }_2}\mathcal{F}(\mu ,·)\mathrm{d}\mu (a.e).\end{array}$$

Now, we report the notion of a center-radius stochastic process

Definition 3 

([34]). Let $h:[0,1]\to {\mathbb{R}}^{+}$. Any interval-valued stochastic process $\mathcal{F}(\mu ,·)=[{\mathcal{F}}_{*}(\mu ,·),{\mathcal{F}}^{*}(\mu ,·)]$ is said to be an $I.V$ center-radius h convex stochastic process, if

$$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}(1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \mathcal{F}({\sigma }_2,·),\ell \in [0,1].\end{array}$$

Next, we give the interval-valued stochastic Riemann–Liouville (RL)-fractional operators.

Definition 4. 

Let $\mathcal{F}(\mu ,·)=[{\mathcal{F}}_{*}\left(\mu \right),{\mathcal{F}}^{*}\left(\mu \right)]$ and ${\mathcal{F}}_{*}(\mu ,·)$ and ${\mathcal{F}}^{*}(\mu ,·)$ be mean square Riemann integrable on $[{\sigma }_1,{\sigma }_2]$. Then

$$\begin{array}{c}\hfill J_{{\mu }^{+}}^{\alpha }\mathcal{F}({\sigma }_2,·)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_{\mu }^{{\sigma }_2}{({\sigma }_2-\ell )}^{\alpha -1}\mathcal{F}(\ell ,·)\mathrm{d}\ell ,{\sigma }_2>\mu \end{array}$$

and

$$\begin{array}{c}\hfill J_{y^{-}}^{\alpha }\mathcal{F}({\sigma }_1,·)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_{{\sigma }_1}^y{(\ell -{\sigma }_1)}^{\alpha -1}\mathcal{F}(\ell ,·)\mathrm{d}\ell ,{\sigma }_1<y\end{array}$$

with $\alpha \ge 0$. We observe that

$$\begin{array}{c}\hfill J_{{\mu }^{+}}^{\alpha }\mathcal{F}({\sigma }_2,·)=\left[J_{{\mu }^{+}}^{\alpha }{\mathcal{F}}_{*}({\sigma }_2,·),J_{{\mu }^{+}}^{\alpha }{\mathcal{F}}^{*}({\sigma }_2,·)\right],\end{array}$$

and

$$\begin{array}{c}\hfill J_{y^{-}}^{\alpha }\mathcal{F}({\sigma }_1,·)=\left[J_{y^{-}}^{\alpha }{\mathcal{F}}_{*}({\sigma }_1,·),J_{y^{-}}^{\alpha }{\mathcal{F}}^{*}({\sigma }_1,·)\right].\end{array}$$

It is necessary to mention the scholarly articles in convex stochastic processes. In 1980, Nikodem expanded the convexity concepts for stochastic processes and presented their essential characterization in [35]. In [36,37], Skowronski developed the classes of J and Wright convex stochastic processes, respectively, and explored some interesting properties. In 2015, Kotrys [38,39] established the Hemite–Hadamard inequality for convex stochastic processes and delivered the concept of strongly convex stochastic processes, respectively. Jarad et al. [40] deployed fractional concepts and convex stochastic processes to investigate Mercer-type inequalities with applications. Agahi and Babakhani [41] explored fractional analogues of the trapezium and Jensen’s type inequalities associated with convex stochastic processes. In 2023, Afzal and Botmart [42] extended the idea of the Godunova–Levin type of convexity bridging with stochastic theory. They established the Trapezium and Jensen’s like inequalities through interval-valued mean square calculus. Afzal et al. [43] investigated the interval-valued Godunova stochastic processes via Kulish Miranker ordering relation to analyze the novel versions of classical inequalities. In [44], the authors studied the totally ordered interval-valued stochastic processes in Godunova sense and derived the Hadamard’s like inequalities.

From the above discussion, we have observed a research gap: how can we investigate all of the above-mentioned convex and convex-like stochastic processes from the perspective of inequalities at the same time within interval-valued fractional concepts? In this regard, we will develop an extended $cr$ interval-valued convex stochastic process incorporated with invertible mapping $\sigma$, non-negative mapping $\gamma$, and total ordered relation. The major objective of this investigation is to explore generalized convex stochastic processes and their role in constructing stochastic fractional analogues of classical inequalities like Jensen’s inequality and Hermite–Hadamard’s kinds of inequalities within the framework of interval analysis. The article’s layout is as follows: the first part is devoted to reviewing the preamble and facts required for the completion of the study. Next, we explain our suggested concept of stochastic processes and obtain novel fractional analogues of classical results of inequalities. Furthermore, we offer a visual explanation of our findings. We anticipate that this study will open up new research opportunities.

2. Results and Discussions

In the following section, we discuss our main results.

2.1. Analysis of Extended Class of Convex Stochastic Process

We give a unified extended class of stochastic processes based on invertible mapping $\sigma$ and non-negative mapping $\gamma$.

Definition 5. 

Let $\gamma :(0,1)\to \mathbb{R}$ be non-negative mapping. Any mapping $\mathcal{F}:I=[{\sigma }_1,{\sigma }_2]\times \Omega \to \mathbb{R}$ is known as an extended convex stochastic process if

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right)\le (1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \gamma (\ell )\mathcal{F}({\sigma }_2,·),\end{array}$$

(1)

where $\ell \in [0,1]$. If the inequality holds in the reverse direction, then $\mathcal{F}$ is said to be an extended concave stochastic process.

Definition 6. 

Let $\gamma :(0,1)\to \mathbb{R}$ be non-negative mapping. Any mapping $\mathcal{F}:I=[{\sigma }_1,{\sigma }_2]\times \Omega \to {\mathbb{R}}_I^{+}$ satisfying $\mathcal{F}(\mu ,·)=[{\mathcal{F}}_{*}(\mu ,·),{\mathcal{F}}^{*}(\mu ,·)]=⟨{\mathcal{F}}_c(\mu ,·),{\mathcal{F}}_r(\mu ,·)⟩$ is known as an extended $cr$-interval-valued convex stochastic process, if

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}(1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \gamma (\ell )\mathcal{F}({\sigma }_2,·),\end{array}$$

where $\ell \in [0,1]$.

Now, we discuss the potential consequences of Definition 6.

• Selecting $\gamma (\ell )=1$ in Definition 6, we obtain a $(\sigma ,cr)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}(1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\gamma (\ell )={\ell }^{s-1}$ in Definition 6, we obtain a $(\sigma ,cr,s)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}{(1-\ell )}^s\mathcal{F}({\sigma }_1,·)+{\ell }^s\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\gamma (\ell )={\displaystyle \frac{1}{{\ell }^2}}$ in Definition 6, we obtain a $(\sigma ,cr)$ Godunova–Levin convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}{\displaystyle \frac{1}{1-\ell }}\mathcal{F}({\sigma }_1,·)+{\displaystyle \frac{1}{\ell }}\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\gamma (\ell )={\ell }^{-s-1}$ in Definition 6, we obtain a $(\sigma ,cr,s)$ Godunova–Levin convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}{(1-\ell )}^{-s}\mathcal{F}({\sigma }_1,·)+{\ell }^{-s}\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\gamma (\ell )=(1-\ell )$ in Definition 6, we obtain a $(\sigma ,cr)$ tgs convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}\ell (1-\ell )\left[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)\right].\end{array}$$
• Selecting $\gamma (\ell )={\displaystyle \frac{1}{\ell }}$ in Definition 6, we obtain a $(\theta ,cr)$ Q-convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·\right){⪯}_{cr}\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )=1$ in Definition 6, we obtain a $cr$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}(1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )={\displaystyle \frac{1}{\ell }}$ in Definition 6, we obtain a $cr-Q$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )={\ell }^{s-1}$ in Definition 6, we obtain a $(cr,s)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}{(1-\ell )}^{s}f\left({\sigma }_1\right)+{\ell }^{s}f\left({\sigma }_2\right).\end{array}$$
• Selecting $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )={\ell }^{-s-1}$ in Definition 6, we obtain a $(cr,s)$ Godunova-Levin convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}{(1-\ell )}^{-s}\mathcal{F}({\sigma }_1,·)+{\ell }^{-s}\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )=(1-\ell )$ in Definition 6, we obtain a $cr$ tgs convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}((1-\ell ){\sigma }_1+\ell {\sigma }_2,·){⪯}_{cr}\ell (1-\ell )[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)].\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ in Definition 6, we obtain $(cr,\gamma )$ a harmonic convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}(1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \gamma (\ell )\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ and $\gamma (\ell )=1$ in Definition 6, we obtain a $cr$ harmonic convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}(1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ and $\gamma (\ell )={\displaystyle \frac{1}{\mu }}$ in Definition 6, we obtain a $(cr,Q)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ and $\gamma (\ell )={\ell }^{s-1}$ in Definition 6, we obtain a $(cr,s)$ harmonic convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}{(1-\ell )}^{s}f\left({\sigma }_1\right)+{\ell }^{s}f\left({\sigma }_2\right).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ and $\gamma (\ell )={\ell }^{-s-1}$ in Definition 6, we obtain a $(cr,s)$ Godunova-Levin harmonic convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}{(1-\ell )}^{-s}\mathcal{F}({\sigma }_1,·)+{\ell }^{-s}\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ and $\gamma (\ell )=(1-\ell )$ in Definition 6, we obtain a $(cr,tgs)$ harmonic convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\sigma }_1{\sigma }_2}{\ell {\sigma }_1+(1-\ell ){\sigma }_2}},·\right){⪯}_{cr}\ell (1-\ell )[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)].\end{array}$$
• Selecting $\theta \left(\mu \right)={\mu }^p$, in Definition 6, we obtain a $(cr,p,\gamma )$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({((1-\ell ){{\sigma }_1}^p+\ell {{\sigma }_2}^p)}^{{\displaystyle \frac{1}{p}}},·\right){⪯}_{cr}(1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \gamma (\ell )\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\mu }^p$ and $\gamma (\ell )={\ell }^{s-1}$ in Definition 6, we obtain a $(cr,p,s)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({((1-\ell ){{\sigma }_1}^p+\ell {{\sigma }_2}^p)}^{{\displaystyle \frac{1}{p}}},·\right){⪯}_{cr}{(1-\ell )}^s\mathcal{F}({\sigma }_1,·)+{\ell }^s\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\mu }^p$ and $\gamma (\ell )={\ell }^{-s-1}$ in Definition 6, we obtain a $(cr,p,s)$ Godunova–Levin convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({((1-\ell ){{\sigma }_1}^p+\ell {{\sigma }_2}^p)}^{{\displaystyle \frac{1}{p}}},·\right){⪯}_{cr}{\displaystyle \frac{1}{{(1-\ell )}^s}}\mathcal{F}({\sigma }_1,·)+{\displaystyle \frac{1}{{\ell }^s}}\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=exp\left(\mu \right)$ and $\gamma (\ell )=1$ in Definition 6, we obtain a $(cr,GA)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({{\sigma }_1}^{1-\ell }{{\sigma }_2}^{\ell },·\right){⪯}_{cr}(1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=exp\left(\mu \right)$ and $\gamma (\ell )={\ell }^{s-1}$ in Definition 6, we obtain a $(cr,GA,s)$ convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({{\sigma }_1}^{1-\ell }{{\sigma }_2}^{\ell },·\right){⪯}_{cr}{(1-\ell )}^s\mathcal{F}({\sigma }_1,·)+{\ell }^s\mathcal{F}({\sigma }_2,·).\end{array}$$
• Selecting $\theta \left(\mu \right)=exp\left(\mu \right)$ and $\gamma (\ell )={\ell }^{-s-1}$ in Definition 6, we obtain a $(cr,GA,s)$ Godunova–Levin convex stochastic process:

  $$\begin{array}{c}\hfill \mathcal{F}\left({{\sigma }_1}^{1-\ell }{{\sigma }_2}^{\ell },·\right){⪯}_{cr}{\displaystyle \frac{1}{{(1-\ell )}^s}}\mathcal{F}({\sigma }_1,·)+{\displaystyle \frac{1}{{\ell }^s}}\mathcal{F}({\sigma }_2,·).\end{array}$$

We have described the collection including the extended convex (concave) stochastic process, extended $cr$-interval-valued convex stochastic process and extended $cr$-interval-valued concave stochastic process by $SEXSP\left(\gamma ,[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I\right)\left(SEVSP\left(\gamma ,[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I\right)\right)$, $SIEXSP$$\left(cr,\gamma ,[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and $SIEVSP\left(cr,\gamma ,[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ respectively.

Now, we are going to address certain important features of Definition 6.

Proposition 1. 

Let $\mathcal{F},\mathcal{G}:[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ be the two I.V. stochastic process. If $\mathcal{F},\mathcal{G}\in SIEXSP$$\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, then

(a) 

$\mathcal{F}+\mathcal{G}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$.

(b) 

$\beta \mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ for $\beta >0$.

Proof. 

The proof is immediately evident from Definition 6. □

Proposition 2. 

Let $\mathcal{F}\in SIEXSP\left(cr-{\gamma }_1-[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and ${\gamma }_1(\ell )\le {\gamma }_2(\ell )$; then, $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$.

Proof. 

We leave the proof for curious readers. □

Proposition 3. 

Let $\mathcal{F},\mathcal{G}$ be the similar order I.V. stochastic processes such that $\mathcal{F}(\mu ,·)\mathcal{G}(y,·)+\mathcal{F}(y,·)\mathcal{G}(\mu ,·){⪯}_{cr}\mathcal{F}(\mu ,·)\mathcal{G}(\mu ,·)+\mathcal{F}(y,·)\mathcal{G}(y,·),\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$. If $\mathcal{F}\in SIEXSP(cr-{\gamma }_1-$$[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+})$ and $\mathcal{G}\in SIEXSP\left(cr-{\gamma }_2-[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and $\ell {\gamma }_1(\ell )+\ell {\gamma }_2(\ell )\le m$ where $\ell \gamma (\ell )=max\{\ell {\gamma }_1(\ell ),\ell {\gamma }_2(\ell )\}$ and $m>0$ then $\mathcal{F}\mathcal{G}\in SIEXSP\left(cr-m\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$.

Proof. 

The proof follows naturally from Definition 6. □

Theorem 3. 

Suppose $\mathcal{F}:[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ is an I.V. stochastic process such that $\mathcal{F}=[{\mathcal{F}}_{*},{\mathcal{F}}^{*}]=⟨{\mathcal{F}}_c\left(\mu \right),{\mathcal{F}}_r\left(\mu \right)⟩$ with ${\mathcal{F}}_{*}\le {\mathcal{F}}^{*}$. Then, $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, if ${\mathcal{F}}_c,{\mathcal{F}}_r\in SEXSP\left([{\sigma }_1,{\sigma }_2],\mathbb{R}\right)$.

Proof. 

Suppose that ${\mathcal{F}}_c,{\mathcal{F}}_r\in SEXSP\left([{\sigma }_1,{\sigma }_2],\mathbb{R}\right)$; then,

$$\begin{array}{c}\hfill {\mathcal{F}}_c({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·)\le \ell \gamma (\ell ){\mathcal{F}}_c(\mu ,·)+(1-\ell )\gamma (1-\ell ){\mathcal{F}}_c(y,.).\end{array}$$

(2)

and

$$\begin{array}{c}\hfill {\mathcal{F}}_r({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·)\le \ell \gamma (\ell ){\mathcal{F}}_r(\mu ,.)+(1-\ell )\gamma (1-\ell ){\mathcal{F}}_r(y,·).\end{array}$$

(3)

If ${\mathcal{F}}_c({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·)\ne \ell \gamma (\ell ){\mathcal{F}}_c(\mu ,·)+(1-\ell )\gamma (1-\ell ){\mathcal{F}}_c(y,.)$, for each $\mu ,y\in [{\sigma }_1,{\sigma }_2]$ and $\ell \in [0,1]$, then

$$\begin{array}{c}\hfill {\mathcal{F}}_c({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·)<\ell \gamma (\ell ){\mathcal{F}}_c(\mu ,·)+(1-\ell )\gamma (1-\ell ){\mathcal{F}}_c(y,.).\end{array}$$

This implies that

$$\begin{array}{c}\hfill \mathcal{F}({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·){⪯}_{cr}\ell \gamma (\ell )\mathcal{F}(\mu ,·)+(1-\ell )\gamma (1-\ell )\mathcal{F}(y,·).\end{array}$$

Otherwise, for each $\mu ,y\in [{\sigma }_1,{\sigma }_2]$ and $\ell \in [0,1]$, then

$$\begin{array}{c}\hfill {\mathcal{F}}_r({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·)\le \ell \gamma (\ell ){\mathcal{F}}_r(\mu ,·)+(1-\ell )\gamma (1-\ell ){\mathcal{F}}_r(y,·).\end{array}$$

This implies that

$$\begin{array}{c}\hfill \mathcal{F}({\theta }^{-1}(\ell \theta \left(\mu \right)+(1-\ell )\theta \left(y\right)),·){⪯}_{cr}\ell \gamma (\ell )\mathcal{F}(\mu ,·)+(1-\ell )\gamma (1-\ell )\mathcal{F}(y,·).\end{array}$$

Hence, the result is achieved. □

Example 1. 

Let $\mathcal{F}:[0,2]\to {\mathbb{R}}_I^{+}$ be an I.V stochastic process such that $\mathcal{F}(\mu ,·)=[-{\mu }^2+8,3{\mu }^2+12]$, where ${\mathcal{F}}_c={\mu }^2+10$ and ${\mathcal{F}}_r=2{\mu }^2+2$ with $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )=1$ be a extended $cr$-interval-valued convex stochastic process.

Here is a visual illustration of the aforementioned example.

Figure 1 gives a visual of Example 1.

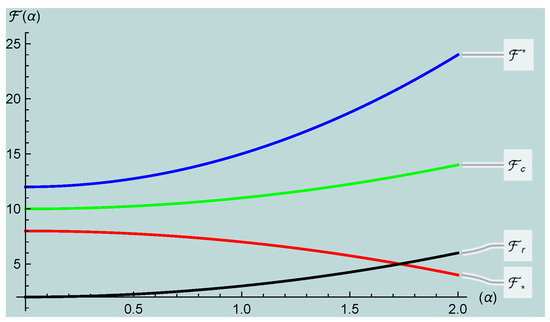
Figure 1. Graphical visualization of $\mathcal{F}(\mu ,·)=[-{\mu }^2+8,3{\mu }^2+12]$.

Now, we present a generalized Jensen’s inequality.

Theorem 4. 

Let $\gamma :(0,1)\to \mathbb{R}$ be a non-negative multiplicative mapping and $\mathcal{F}\in SIEXSP$$\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$; then,

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{1}{{\mathcal{W}}_n}}\sum _{i=1}^n{\ell }_i\theta \left({\mu }_i\right)\right),·\right){⪯}_{cr}\sum _{i=1}^n\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\mathcal{F}({\mu }_i,·),\end{array}$$

(4)

for ${\mu }_i\in [{\sigma }_1,{\sigma }_2]$ and ${\mathcal{W}}_n={\sum }_{i=1}^n{\ell }_i{\mu }_i$.

Proof. 

We deploy the well-known technique of mathematical induction to achieve our result. Suppose $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2]\right)$ and for $n=2$ in (4), then

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{{\ell }_1\theta \left({\mu }_1\right)+{\ell }_2\theta \left({\mu }_2\right)}{{\ell }_1+{\ell }_2}}\right),·\right){⪯}_{cr}\left({\displaystyle \frac{{\ell }_1}{{\ell }_1+{\ell }_2}}\right)\gamma \left({\displaystyle \frac{{\ell }_1}{{\ell }_1+{\ell }_2}}\right)\mathcal{F}({\mu }_1,·)+\left({\displaystyle \frac{{\ell }_2}{{\ell }_1+{\ell }_2}}\right)\gamma \left({\displaystyle \frac{{\ell }_2}{{\ell }_1+{\ell }_2}}\right)\mathcal{F}({\mu }_2,·).\end{array}$$

Now, suppose that the result (4) is true for $n=k-1$ such that

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{1}{{\mathcal{W}}_{k-1}}}\sum _{i=1}^{k-1}{\ell }_i\theta \left({\mu }_i\right)\right),·\right){⪯}_{cr}\sum _{i=1}^{k-1}\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\mathcal{F}({\mu }_i,·).\end{array}$$

(5)

Now, we show that it is true for $n=k$.

$$\begin{array}{cc}\hfill & \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{1}{{\mathcal{W}}_k}}\sum _{i=1}^k{\ell }_i\theta \left({\mu }_i\right)\right),·\right)\hfill \\ \hfill & =\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{1}{{\mathcal{W}}_k}}\sum _{i=1}^{k-1}{\ell }_i\theta \left({\mu }_i\right)+{\displaystyle \frac{{\ell }_k\theta \left({\mu }_k\right)}{{\mathcal{W}}_k}}\right),·\right)=\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}\sum _{i=1}^{k-1}{\displaystyle \frac{{\ell }_i\theta \left({\mu }_i\right)}{{\mathcal{W}}_{k-1}}}+{\displaystyle \frac{{\ell }_k\theta \left({\mu }_k\right)}{{\mathcal{W}}_k}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}\left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\gamma \left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\mathcal{F}({\mu }_k,·)+\left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}\right)\gamma \left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}\right)\mathcal{F}\left({\theta }^{-1}\left(\sum _{i=1}^{k-1}{\displaystyle \frac{{\ell }_i\theta \left({\mu }_i\right)}{{\mathcal{W}}_{k-1}}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}\left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\gamma \left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\mathcal{F}({\mu }_k,·)+\sum _{i=1}^{k-1}\left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}\right)\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\gamma \left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}\right)·\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\mathcal{F}({\mu }_i,·)\hfill \\ \hfill & {⪯}_{cr}\left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\gamma \left({\displaystyle \frac{{\ell }_k}{{\mathcal{W}}_k}}\right)\mathcal{F}({\mu }_k,·)+\sum _{i=1}^{k-1}\left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}·{\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\gamma \left({\displaystyle \frac{{\mathcal{W}}_{k-1}}{{\mathcal{W}}_k}}·{\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_{k-1}}}\right)\mathcal{F}({\mu }_i,·)\hfill \\ \hfill & =\sum _{i=1}^k\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_k}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_k}}\right)\mathcal{F}({\mu }_i,·).\hfill \end{array}$$

Hence, the result is acquired. □

Now, we discuss some potential consequences of Theorem 4.

• Selecting $\theta \left(\mu \right)=\mu$ in Theorem 4, then we acquire Jensen’s inequality for a $cr-\gamma$-convex stochastic process,

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{W}}_n}}\sum _{i=1}^n{\ell }_i{\mu }_i,·\right){⪯}_{cr}\sum _{i=1}^n\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\mathcal{F}({\mu }_i,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\displaystyle \frac{1}{\mu }}$ in Theorem 4, then we acquire the Jensen’s inequality for a harmonically $cr-\gamma$-convex stochastic process,

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{\frac{1}{{\mathcal{W}}_n}{\sum }_{i=1}^n\frac{{\ell }_i}{{\mu }_i}}},·\right){⪯}_{cr}\sum _{i=1}^n\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\mathcal{F}({\mu }_i,·).\end{array}$$
• Selecting $\theta \left(\mu \right)={\mu }^p$, $p\ge -1$ in Theorem 4, then we acquire Jensen’s inequality for a $(cr,p,\gamma )$ convex stochastic process,

  $$\begin{array}{c}\hfill \mathcal{F}\left({\left({\displaystyle \frac{1}{{\mathcal{W}}_n}}\sum _{i=1}^n{\ell }_i{{\mu }_i}^p\right)}^{{\displaystyle \frac{1}{p}}},·\right){⪯}_{cr}\sum _{i=1}^n\sum _{i=1}^n\left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\mathcal{F}({\mu }_i,·).\end{array}$$
• Choosing $\theta \left(\mu \right)=ln\left(\mu \right)$ in Theorem 4, we acquire the Jensen’s inequality for a $(cr,GA,\gamma )$ convex stochastic process,

  $$\begin{array}{c}\hfill \mathcal{F}\left(\prod _{i=1}^n{{\mu }_i}^{{\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}},·\right){⪯}_{cr}\sum _{i=1}^n\gamma \left({\displaystyle \frac{{\ell }_i}{{\mathcal{W}}_n}}\right)\mathcal{F}({\mu }_i,·).\end{array}$$

Remark 1. 

We can obtain several other significant generalizations of Jensen’s inequality by specifying the different values for $\sigma \left(\mu \right)$ and $\gamma (\ell )$.

Now, we deliver a parametric Hermite–Hadamard inequality incorporated with an extended $cr$ interval-valued stochastic process.

Theorem 5. 

Let $\mathcal{F}:[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ be an I.V stochastic process and $\gamma :(0,1)\to (0,\infty )$ with $\gamma \left({\displaystyle \frac{1}{2}}\right)\ne 0$. If $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and a $cr$-interval-valued mean-square integrable on $[{\sigma }_1,{\sigma }_2]$ almost everywhere, then we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}\left(\theta \left({\sigma }_2\right),·\right)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}\alpha [\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]{\int }_0^1{\ell }^{\alpha -1}[\ell \gamma (\ell )+(1-\ell )\gamma (1-\ell )]\mathrm{d}\ell .\hfill \end{array}$$

Proof. 

Since $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, then

$$\begin{array}{c}\hfill \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left(\mu \right)+\theta \left(y\right)}{2}}\right),·\right){⪯}_{cr}{\displaystyle \frac{1}{2}}\gamma \left({\displaystyle \frac{1}{2}}\right)[\mathcal{F}(\mu ,·)+\mathcal{F}(y,·)].\end{array}$$

Replacing $\mu ={\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)$ and $y={\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)$ in the preceding inequality, taking the product by ${\ell }^{\alpha -1}$, and by the process of integration, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)}}{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell .\hfill \end{array}$$

(6)

Now,

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \hfill \\ \hfill & =\left[\left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}_{*}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell ,\left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}^{*}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{1}{\alpha }}{\mathcal{F}}_{*}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)+{\displaystyle \frac{1}{\alpha }}{\mathcal{F}}^{*}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{\alpha }}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{2\theta \left({\sigma }_1\right),\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right)}{2}}\right),·\right).\hfill \end{array}$$

Also

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ & +\left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & =\left[\left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}_{*}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \right.\hfill \\ & +\left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}_{*}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell ,\hfill \\ \hfill & \left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}^{*}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ & \left.+\left(R\right){\int }_0^1{\ell }^{\alpha -1}{\mathcal{F}}^{*}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(\theta \left({\sigma }_2\right)-u)}^{\alpha -1}{\mathcal{F}}_{*}\circ {\theta }^{-1}(u,·)\mathrm{d}u\right.\hfill \\ & +{\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}{\mathcal{F}}_{*}\circ {\theta }^{-1}(u,·)\mathrm{d}u,\hfill \\ \hfill & {\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(\theta \left({\sigma }_2\right)-u)}^{\alpha -1}{\mathcal{F}}^{*}\circ {\theta }^{-1}(u,·)\mathrm{d}u\hfill \\ & \left.+{\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}{\mathcal{F}}^{*}\circ {\theta }^{-1}(u,·)\mathrm{d}u\right].\hfill \end{array}$$

We obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)\alpha }}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(\theta \left({\sigma }_2\right)-u)}^{\alpha -1}\mathcal{F}\circ {\theta }^{-1}(u,·)\mathrm{d}u\right.\hfill \\ \hfill & \left.+{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}\mathcal{F}\circ {\theta }^{-1}(u,·)\mathrm{d}u\right].\hfill \end{array}$$

(7)

Comparing (6) and (7), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right){⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}\left(\theta \left({\sigma }_2\right),·\right)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right].\hfill \end{array}$$

To attain a second inequality, we incorporate with a $(\theta ,cr-\gamma )$ I.V. convexity of $\mathcal{F}$.

$$\begin{array}{cc}\hfill & \mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·){⪯}_{cr}\ell \gamma (\ell )\mathcal{F}({\sigma }_1,·)+(1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_2,·).\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·){⪯}_{cr}(1-\ell )\gamma (1-\ell )\mathcal{F}({\sigma }_1,·)+\ell \gamma (\ell )\mathcal{F}({\sigma }_2,·).\hfill \end{array}$$

(9)

Summing (8) and (9), taking the product of the resulting inequality by ${\ell }^{\alpha -1}$, and employing the integration on both sides with respect to ℓ on $[0,1]$, then we achieve our desired finding. □

Here, we demonstrate some deductions of Theorem 5.

• Selecting $\gamma (\ell )=1$ in Theorem 5, we achieve

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{2{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}\left(\theta ({\sigma }_2,·)\right)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\circ (\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)}{2}}.\hfill \end{array}$$
• Selecting $\gamma (\ell )={\ell }^{s-1}$ in Theorem 5, we obtain

  $$\begin{array}{cc}\hfill & 2^s\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\circ {\theta }^{-1}\left(\theta ({\sigma }_2,·)\right)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\circ (\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)\left[{\displaystyle \frac{\alpha }{\alpha +s}}+\alpha B(\alpha ,s+1)\right],\hfill \end{array}$$

  where $B(.,·)$ is a well-known beta function.
• Choosing $\theta (\ell )={\ell }^p$, $p\ge -1$ in Theorem 5, we acquire

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}}\right)}^{{\displaystyle \frac{1}{p}}},·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{{({{\sigma }_2}^p-{{\sigma }_1}^p)}^{\alpha }}}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\circ k({{\sigma }_2}^p,·)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\mathcal{F}\circ k({{\sigma }_1}^p,·)\right]\hfill \\ \hfill & {⪯}_{cr}\alpha [\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]{\int }_0^1{\ell }^{\alpha -1}[\ell \gamma (\ell )+(1-\ell )\gamma (1-\ell )]\mathrm{d}\ell .\hfill \end{array}$$
• Choosing $\theta (\ell )={\ell }^p$, $p\ge -1$ and $\gamma (\ell )=1$ in Theorem 5, we acquire

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}}\right)}^{{\displaystyle \frac{1}{p}}},·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{2{({{\sigma }_2}^p-{{\sigma }_1}^p)}^{\alpha }}}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\circ k({{\sigma }_2}^p,·)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\mathcal{F}\circ k({{\sigma }_1}^p,·)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]}{2}},\hfill \end{array}$$

  where $k\left(\mu \right)={\mu }^{{\displaystyle \frac{1}{p}}}$.

Remark 2. 

By utilizing different values of $\sigma \left(\mu \right)$ and $\gamma (\ell )$ in Theorem 5, a series of trapezium-like inequalities for stochastic processes can be obtained.

Example 2. 

Let $\mathcal{F}(\ell ,·)=[-{\ell }^2+8,3{\ell }^2+12]$ with $[{\sigma }_1,{\sigma }_2]=[0,2],\theta (\ell )=\ell$ be an extended $cr$-interval-valued convex stochastic process. It satisfies all conditions of Theorem 5; then,

$$\begin{array}{cc}\hfill & L\left(\alpha \right)={\displaystyle \frac{2^{\alpha +1}}{\Gamma (\alpha +1)}}\mathcal{F}\left(1,·\right)=\left[{\displaystyle \frac{7\left(2^{\alpha +1}\right)}{\Gamma (\alpha +1)}},{\displaystyle \frac{152^{\alpha +1}}{\Gamma (\alpha +1)}}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & M\left(\alpha \right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\left[{\int }_0^2\left({(2-\ell )}^{\alpha -1}+{\ell }^{\alpha -1}\right)\mathcal{F}(\ell ,·)\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{2^{\alpha +2}\left(\frac{4}{\alpha }-\frac{1}{\alpha +2}-\frac{2\Gamma \left(\alpha \right)}{\Gamma (\alpha +3)}\right)}{\Gamma \left(\alpha \right)}},{\displaystyle \frac{3\left(2^{\alpha +2}\right)(\alpha (3\alpha +7)+6)}{\left(\alpha \right(\alpha +1\left)\right(\alpha +2\left)\right)\Gamma \left(\alpha \right)}}\right],\hfill \end{array}$$

also

$$\begin{array}{cc}\hfill & U\left(\alpha \right)={\displaystyle \frac{2^{\alpha +1}(\mathcal{F}(0,·)+\mathcal{F}(2,·))}{2\Gamma (\alpha +1)}}=\left[{\displaystyle \frac{6\left(2^{\alpha +1}\right)}{\Gamma (\alpha +1)}},{\displaystyle \frac{18\left(2^{\alpha +1}\right)}{\Gamma (\alpha +1)}}\right].\hfill \end{array}$$

For graphical visualization, we vary $0<\alpha \le 5$.

Figure 2 provides the graphical visualization of Theorem 5, where $L.L.F, L.U.F, M.L.F,$$M.U.F, R.L.F$ and $R.U.F$ represent the lower and upper functions of left, middle and right sides of Theorem 5.

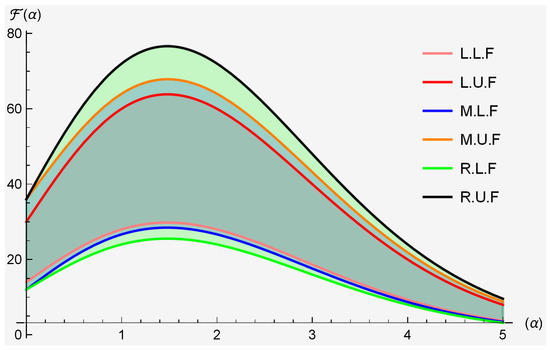
Figure 2. Clearly substantiates the accuracy of Theorem 5.

Now, we give a tabular illustration of Theorem 5.

Table 1 clearly demonstrates the accuracy of Theorem 5 depending on $\alpha$.

Table 1. Comparison of all the sides of Theorem 5.

$\mathit{\alpha }$	${\mathit{L}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{L}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{M}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{M}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}^{*}\left(\mathit{\alpha }\right)$
$0.5$	$22.3408$	$47.8731$	$20.8514$	$52.3412$	$19.1492$	$57.4477$
$1.5$	$29.7877$	$63.8308$	$28.4503$	$67.843$	$25.5323$	$76.5969$
$2.5$	$23.8302$	$51.0646$	$22.5873$	$54.7931$	$20.4258$	$61.2775$
$3.5$	$13.6172$	$29.1798$	$12.7723$	$31.7146$	$11.6719$	$35.0157$
$4.5$	$6.0521$	$12.9688$	$5.62283$	$14.2566$	$5.18752$	$15.5625$

Now, we report the fractional version of weighted Hermite–Hadamard inequality, which is known as the Hermite–Hadamard–Fejer inequality for an extended class of $cr$ interval-valued stochastic processes.

Theorem 6. 

Let $\mathcal{F}:[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ be an I.V. stochastic process and $\xi :[{\sigma }_1,{\sigma }_2]\to \mathbb{R}$ be a symmetric stochastic process with respect to ${\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}}$. If $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and there is a $cr$-interval-valued mean-square integrable on $[{\sigma }_1,{\sigma }_2]$ almost everywhere, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{\theta {\left({\sigma }_2\right)}^{-}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}{\Gamma \left(\alpha \right)}}\left({\int }_0^1{\ell }^{\alpha -1}[\ell \gamma (\ell )+(1-\ell )\gamma (1-\ell )]\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]\mathrm{d}\ell \right),\hfill \end{array}$$

$\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.

Proof. 

If $\mathcal{F}\in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, then we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left(\mu \right)+\theta \left(y\right)}{2}}\right),·\right){⪯}_{cr}\mathcal{F}(\mu ,·)+\mathcal{F}(y,·).\hfill \end{array}$$

Replacing $\mu ={\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right))$ and $y={\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right))$ in the aforementioned inequality, taking the product of the resulting inequality by ${\ell }^{\alpha -1}\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)$, then we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\gamma \left(\frac{1}{2}\right)}}{\int }_0^1{\ell }^{\alpha -1}\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \hfill \\ \hfill & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell .\hfill \end{array}$$

(10)

Now, we use the fact that $\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)=\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)$

$$\begin{array}{cc}\hfill & {\int }_0^1{\ell }^{\alpha -1}\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left[{\int }_0^1{\ell }^{\alpha -1}\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \right.\hfill \\ \hfill & \left.+{\int }_0^1{\ell }^{\alpha -1}\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \right]\hfill \\ \hfill & ={\displaystyle \frac{1}{2{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(\theta \left({\sigma }_2\right)-u)}^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \circ {\theta }^{-1}(u,·)\mathrm{d}u\right.\hfill \\ & \left.+{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \circ {\theta }^{-1}(u,·)\mathrm{d}u\right]\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\alpha \right)}{2{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),)\right.\hfill \\ \hfill & \left.+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right].\hfill \end{array}$$

(11)

And

$$\begin{array}{cc}\hfill & {\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right),·)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right),·)\mathrm{d}\ell \hfill \\ \hfill & ={\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(\theta \left({\sigma }_2\right)-u)}^{\alpha -1}\mathcal{F}({\theta }^{-1}\left(u\right),·)\xi ({\theta }^{-1}\left(u\right),·)\mathrm{d}u\right.\hfill \\ \hfill & \left.+{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}\mathcal{F}({\theta }^{-1}\left(u\right),·)\xi ({\theta }^{-1}\left(u\right),·)\mathrm{d}u\right]\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\alpha \right)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right].\hfill \end{array}$$

(12)

Combining (10)–(12) yields the required result.

To achieve a second relation, we sum (8) and (9) and multiply both sides of the resulting by ${\ell }^{\alpha -1}\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right),·)$. Then, by applying the integration with respect to ℓ on $[0,1]$,

$$\begin{array}{cc}\hfill & {\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}[\ell \gamma (\ell )+(1-\ell )\gamma (1-\ell )]\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]\mathrm{d}\ell .\hfill \end{array}$$

Through simple computations, we achieve our desired result. □

Now, we discuss some special cases of Theorem 6.

• Choosing $\gamma (\ell )=1$ in Theorem 6, we have

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{\theta {\left(\theta \left({\sigma }_2\right)\right)}^{-}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{1-\alpha }{{\sigma }_2\left(\alpha \right)}}(\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)+\mathcal{F}\xi \circ {\theta }^{-1}\left(\theta \left({\sigma }_2\right)\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)}{2}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{\theta {\left(\theta \left({\sigma }_2\right)\right)}^{-}}^{\alpha }\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right],\hfill \end{array}$$
  $\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.
• Choosing $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )=1$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}},·\right)\left[J_{{{\sigma }_1}^{+}}^{\alpha }\xi ({\sigma }_2,·)+J_{{{\sigma }_2}^{-}}^{\alpha }\xi ({\sigma }_1,·)\right]{⪯}_{cr}\left[J_{{{\sigma }_1}^{+}}^{\alpha }\mathcal{F}\xi ({\sigma }_2,·)+J_{{{\sigma }_2}^{-}}^{\alpha }\mathcal{F}\xi ({\sigma }_1,·)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)}{2}}\left[J_{{{\sigma }_1}^{+}}^{\alpha }\xi ({\sigma }_2,·)+J_{{{\sigma }_2}^{-}}^{\alpha }\xi ({\sigma }_1,·)\right],\hfill \end{array}$$
  $\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.
• Choosing $\theta \left(\mu \right)={\mu }^p$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\gamma \left(\frac{1}{2}\right)}}\mathcal{F}\left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}}\right)}^{{\displaystyle \frac{1}{p}}}\right)\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\xi \circ k\left({{\sigma }_2}^p\right)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\xi \circ k\left({{\sigma }_1}^p\right)\right]\hfill \\ \hfill & {⪯}_{cr}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_2}^p\right)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_1}^p\right)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}{\Gamma \left(\alpha \right)}}\left({\int }_0^1{\ell }^{\alpha -1}[\ell \gamma (\ell )+(1-\ell )\gamma (1-\ell )]\xi \circ k(\ell {{\sigma }_1}^p+(1-\ell ){{\sigma }_2}^p)[\mathcal{F}({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)]\mathrm{d}\ell \right),\hfill \end{array}$$
  $\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.
• If we choose $\theta \left(\mu \right)={\mu }^p$ and $\gamma (\ell )=1$ in Theorem 6, then

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}}\right)}^{{\displaystyle \frac{1}{p}}}\right)\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\xi \circ k\left({{\sigma }_2}^p\right)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\xi \circ k\left({{\sigma }_1}^p\right)\right]\hfill \\ \hfill & {⪯}_{cr}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_2}^p\right)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_1}^p\right)\right]\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\mathcal{F}\left({{\sigma }_1}^p\right)+\mathcal{F}\left({{\sigma }_2}^p\right)}{2}}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\xi \circ k\left({{\sigma }_2}^p\right)+J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\xi \circ k\left({{\sigma }_1}^p\right)\right],\hfill \end{array}$$
  $\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.

Now, we utilize the graphical approach to demonstrate the correctness of Theorem 6.

Example 3. 

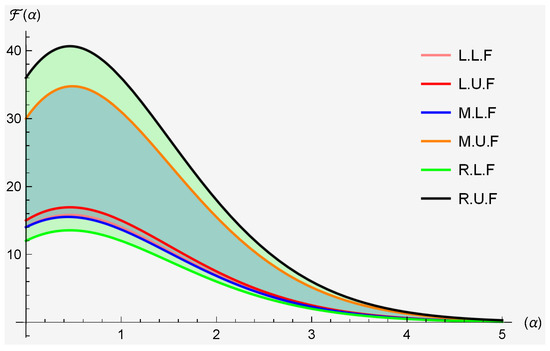
Let $\mathcal{F}(\ell ,·)=[-{\ell }^2+8,3{\ell }^2+12]$ with $[{\sigma }_1,{\sigma }_2]=[0,2],\theta (\ell )=\ell$ be an extended $cr$-interval-valued convex stochastic process and symmetric stochastic process $\xi (\ell ,·)$ at $\left({\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}},·\right)$. Admiring the property $\xi ({\sigma }_1+{\sigma }_2-\mu )=\xi \left(\mu \right),\mu \in [0,2]$ and $\xi (\ell )$ is defined as:

$$\begin{array}{c}\hfill \xi (\ell ,·)=\left\{\begin{array}{c}\ell ,\ell \in [0,1]\hfill \\ 2-\ell ,\ell \in [1,2].\hfill \end{array}\right.\end{array}$$

They satisfy all conditions of Theorem 6; then, we obtain

$$\begin{array}{cc}\hfill & L\left(\alpha \right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\mathcal{F}\left(1,·\right)\left[{\int }_0^1({\ell }^{\alpha -1}+{(1-\ell )}^{\alpha -1})\ell \mathrm{d}\ell +{\int }_1^2({(\ell -1)}^{\alpha -1}+{(2-\ell )}^{\alpha -1})(2-\ell )\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{14}{\Gamma (\alpha +1)}},{\displaystyle \frac{15}{\Gamma (\alpha +1)}}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & M\left(\alpha \right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\left[{\int }_0^1({\ell }^{\alpha -1}+{(1-\ell )}^{\alpha -1})\ell \mathcal{F}(\ell ,·)\mathrm{d}\ell +{\int }_1^2({(\ell -1)}^{\alpha -1}+{(2-\ell )}^{\alpha -1})(2-\ell )\mathcal{F}(\ell ,·)\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{\frac{7\alpha +24}{{\alpha }^2+3\alpha }-\frac{5}{{\alpha }^2+3\alpha +2}+\frac{7}{\alpha }-\frac{6\Gamma \left(\alpha \right)}{\Gamma (\alpha +4)}}{\Gamma \left(\alpha \right)}},{\displaystyle \frac{\frac{15\alpha +36}{{\alpha }^2+3\alpha }+15\left(\frac{1}{{\alpha }^2+3\alpha +2}+\frac{1}{\alpha }\right)+\frac{18\Gamma \left(\alpha \right)}{\Gamma (\alpha +4)}}{\Gamma \left(\alpha \right)}}\right],\hfill \end{array}$$

also

$$\begin{array}{cc}\hfill & U\left(\alpha \right)={\displaystyle \frac{\mathcal{F}\left(0,·\right)+\mathcal{F}\left(1,·\right)}{2\Gamma \left(\alpha \right)}}\left[{\int }_0^1({\ell }^{\alpha -1}+{(1-\ell )}^{\alpha -1})\ell \mathrm{d}\ell +{\int }_1^2({(\ell -1)}^{\alpha -1}+{(2-\ell )}^{\alpha -1})(2-\ell )\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{12}{\Gamma (\alpha +1)}},{\displaystyle \frac{36}{\Gamma (\alpha +1)}}\right].\hfill \end{array}$$

For graphical visualization, we vary $0<\alpha \le 5$.

Figure 3 provides the graphical visualization of Theorem 6, where $L.L.F, L.U.F, M.L.F,$$M.U.F, R.L.F$ and $R.U.F$ represent the lower and upper functions of left, middle and right sides of Theorem 6.

Figure 3. Clearly demonstrates the graphical visualization of Theorem 6.

Now, we deliver a tabular illustration of Theorem 6.

Table 2 clearly illustrates the accuracy of Theorem 6 depending $\alpha$.

Table 2. Comparison of all the sides of Theorem 6.

$\mathit{\alpha }$	${\mathit{L}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{L}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{M}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{M}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}^{*}\left(\mathit{\alpha }\right)$
$0.5$	$15.7973$	$33.8514$	$15.4964$	$34.7541$	$13.5406$	$40.6217$
$1.5$	$10.5315$	$22.5676$	$10.2736$	$23.3413$	$9.02703$	$27.0811$
$2.5$	$4.21262$	$9.02703$	$4.11709$	$9.31361$	$3.61081$	$10.8324$
$3.5$	$1.2036$	$2.57915$	$1.17929$	$2.6521$	$1.03166$	$3.09498$
$4.5$	$0.267468$	$0.573145$	$0.262658$	$0.587574$	$0.229258$	$0.687774$

Theorem 7. 

Let $\mathcal{F},\xi :[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ represent I.V. stochastic processes. If $\mathcal{F},\xi \in SIEXSP$$\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$ and there is a $cr$-interval-valued mean-square integrable on $[{\sigma }_1,{\sigma }_2]$ almost everywhere, then we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{2{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\left(\theta \left({\sigma }_2\right)\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}[{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )]{\mathcal{P}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\ell (1-\ell )[{\gamma }_1(\ell ){\gamma }_2(1-\ell )+{\gamma }_1(1-\ell ){\gamma }_2(\ell )]{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell .\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\mathcal{P}}_1({\sigma }_1,{\sigma }_2)=\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_1,·)+\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_2,·),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)=\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_2,·)+\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_1,·).\hfill \end{array}$$

(14)

$\alpha >0$ and $\forall \mu ,y\in [{\sigma }_1,{\sigma }_2]$.

Proof. 

Since $\mathcal{F},\xi \in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, then

$$\begin{array}{cc}\hfill & \mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·){⪯}_{cr}\ell {\gamma }_1(\ell )\mathcal{F}({\sigma }_1,·)+(1-\ell ){\gamma }_1(1-\ell )\mathcal{F}({\sigma }_2,·).\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·){⪯}_{cr}\ell {\gamma }_2(\ell )\xi ({\sigma }_1,·)+(1-\ell ){\gamma }_2(1-\ell )\xi ({\sigma }_2,·).\hfill \end{array}$$

(16)

Taking the product of (15) and (16), then we have

$$\begin{array}{cc}\hfill & \mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\hfill \\ \hfill & {⪯}_{cr}{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_1,·)+\ell (1-\ell ){\gamma }_1(\ell ){\gamma }_2(1-\ell )\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_2,·)\hfill \\ \hfill & +\ell (1-\ell ){\gamma }_1(1-\ell ){\gamma }_2(\ell )\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_1,·)+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_2,·).\hfill \end{array}$$

(17)

Similarly, we have

$$\begin{array}{cc}\hfill & \mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\hfill \\ \hfill & {⪯}_{cr}{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_1,·)+\ell (1-\ell ){\gamma }_1(1-\ell ){\gamma }_2(\ell )\mathcal{F}({\sigma }_1,·)\xi ({\sigma }_2,·)\hfill \\ \hfill & +\ell (1-\ell ){\gamma }_1(\ell ){\gamma }_2(1-\ell )\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_1,·)+{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )\mathcal{F}({\sigma }_2,·)\xi ({\sigma }_2,·).\hfill \end{array}$$

(18)

Taking the sum of (17) and (18), multiplying both sides of the resulting inequality by ${\ell }^{\alpha -1}$ and integrating with respect to ℓ on $[0,1]$, then we have

$$\begin{array}{cc}\hfill & {\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}[{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )]{\mathcal{P}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\ell (1-\ell )[{\gamma }_1(\ell ){\gamma }_2(1-\ell )+{\gamma }_1(1-\ell ){\gamma }_2(\ell )]{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell .\hfill \end{array}$$

(19)

Now, by comparing with the stochastic Riemann–Liouville fractional operators, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\left(\theta \left({\sigma }_2\right)\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\int }_0^1{\ell }^{\alpha -1}[{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )]{\mathcal{P}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\ell (1-\ell )[{\gamma }_1(\ell ){\gamma }_2(1-\ell )+{\gamma }_1(1-\ell ){\gamma }_2(\ell )]{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)\mathrm{d}\ell .\hfill \end{array}$$

Hence, the proof is completed. □

Here, we report the consequences of Theorem 7.

• Choosing ${\gamma }_1(\ell )=1={\gamma }_1(\ell )$ in Theorem 7, then

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·)+J_{{\left(\theta \left({\sigma }_2\right)\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)\right]\hfill \\ \hfill & {⪯}_{cr}{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{2}{(\alpha +1)(\alpha +2)}}.\hfill \end{array}$$
• Choosing $\theta \left(\mu \right)=\mu$ and ${\gamma }_1(\ell )=1={\gamma }_1(\ell )$ in Theorem 7, then

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{{({\sigma }_2-{\sigma }_1)}^{\alpha }}}\left[J_{{{\sigma }_1}^{+}}^{\alpha }\mathcal{F}\xi ({\sigma }_2,·)+J_{{\left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi ({\sigma }_1,·)\right]\hfill \\ \hfill & {⪯}_{cr}{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{2}{(\alpha +1)(\alpha +2)}}.\hfill \end{array}$$
• Choosing $\theta \left(\mu \right)={\mu }^p$ and ${\gamma }_1(\ell )=1={\gamma }_1(\ell )$ in Theorem 7, then

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{{({{\sigma }_2}^p-{{\sigma }_1}^p)}^{\alpha }}}\left[J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\xi \circ k({{\sigma }_2}^p,·)+J_{{\left({{\sigma }_2}^p\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ k({{\sigma }_1}^p,·)\right]\hfill \\ \hfill & {⪯}_{cr}{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{2}{(\alpha +1)(\alpha +2)}}.\hfill \end{array}$$

Example 4. 

Let $\mathcal{F}(\ell ,·)=[-{\ell }^2+8,3{\ell }^2+12]$ and $\xi (\ell ,·)=[-{\ell }^2+10,3{\ell }^2+10]$ with $[{\sigma }_1,{\sigma }_2]=[0,2]$, $\theta (\ell )=\ell$ being the two extended $cr$-interval-valued convex stochastic processes. They satisfy all assumptions of Theorem 7; then,

$$\begin{array}{cc}\hfill & L\left(\alpha \right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\left[{\int }_0^1\left({(2-\ell )}^{\alpha -1}+{(\ell -1)}^{\alpha -1}\right)\mathcal{F}\xi (\ell )\mathrm{d}\ell \right]\hfill \\ \hfill & =\left[{\displaystyle \frac{2^{\alpha +3}(\alpha (\alpha (\alpha (13\alpha +140)+533)+778)+312)}{2^{\alpha }\left(\alpha (\alpha +1)(\alpha +2)(\alpha +3)(\alpha +4)\right)}}\right.\hfill \\ \hfill & \left.,{\displaystyle \frac{3\left(2^{\alpha +3}\right)(\alpha (\alpha (\alpha (27\alpha +224)+647)+822)+648)}{2^{\alpha }\left(\alpha (\alpha +1)(\alpha +2)(\alpha +3)(\alpha +4)\right)}}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & R\left(\alpha \right)={\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{\alpha (\alpha +2)(\alpha +1)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{2}{(\alpha +1)(\alpha +2)}}\hfill \\ \hfill & =\left[{\displaystyle \frac{104\left({\alpha }^2+\alpha +2\right)+176\alpha }{\alpha (\alpha +2)(\alpha +1)}},{\displaystyle \frac{696\left({\alpha }^2+\alpha +2\right)+1056\alpha }{\alpha (\alpha +2)(\alpha +1)}}\right].\hfill \end{array}$$

For graphical visualization, we vary $0<\alpha \le 5$.

Figure 4 provides the graphical visualization of Theorem 7, where $L.L.F, L.U.F, R.L.F$ and $R.U.F$ represent the lower and upper functions of left and right sides of Theorem 7.

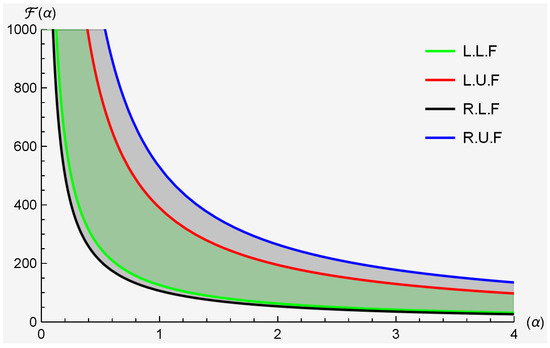
Figure 4. Clearly substantiates the accuracy of Theorem 7.

Now, we deliver a tabular illustration of Theorem 7.

Table 3 clearly demonstrates the accuracy of Theorem 7 depending $\alpha$.

Table 3. Comparison of all the sides of Theorem 7.

$\mathit{\alpha }$	${\mathit{L}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{L}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}^{*}\left(\mathit{\alpha }\right)$
$0.5$	$230.959$	$1016.23$	$199.467$	$1302.4$
$1.5$	$79.215$	$312.478$	$65.6762$	$425.6$
$2.5$	$47.0772$	$192.685$	$39.5683$	$257.067$
$3.5$	$33.1853$	$142.685$	$28.4214$	$185.281$
$4.5$	$25.5033$	$114.509$	$22.216$	$145.268$

Theorem 8. 

Let $\mathcal{F},\xi :[{\sigma }_1,{\sigma }_2]\to {\mathbb{R}}_I^{+}$ be I.V. stochastic processes. If

$$\mathcal{F},\xi \in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$$

and there is a $cr$-interval-valued mean-square integrable on $[{\sigma }_1,{\sigma }_2]$ almost everywhere, then we have

$$\begin{array}{cc}\hfill & \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{{\gamma }_1\left(\frac{1}{2}\right){\gamma }_2\left(\frac{1}{2}\right)\Gamma (\alpha +1)}{4{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·)+J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ (\theta \left({\sigma }_2\right),·)\right]\hfill \\ \hfill & +\alpha {\displaystyle \frac{1}{4}}{\gamma }_1\left({\displaystyle \frac{1}{2}}\right){\gamma }_2\left({\displaystyle \frac{1}{2}}\right)\left[{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\int }_0^1{\ell }^{\alpha -1}\ell (1-\ell )[{\gamma }_1(\ell ){\gamma }_2(1-\ell )+{\gamma }_1(1-\ell ){\gamma }_2(\ell )]\right.\hfill \\ & \left.+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\int }_0^1{\ell }^{\alpha -1}[{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )]\mathrm{d}\ell \right],\hfill \end{array}$$

where ${\mathcal{P}}_1({\sigma }_1,{\sigma }_2)$ and ${\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)$ are given by (13) and (14), respectively.

Proof. 

Since $\mathcal{F},\xi \in SIEXSP\left(cr-\gamma -[{\sigma }_1,{\sigma }_2],{\mathbb{R}}_I^{+}\right)$, then we have

$$\begin{array}{cc}\hfill & \mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{1}{4}}{\gamma }_1\left({\displaystyle \frac{1}{2}}\right){\gamma }_2\left({\displaystyle \frac{1}{2}}\right)\left[\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\right.\hfill \\ \hfill & +\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\hfill \\ \hfill & +\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\hfill \\ \hfill & \left.+\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\right]\hfill \end{array}$$

Taking the product of the preceding inequality by ${\ell }^{\alpha -1}$ and integrating with respect to ′ℓ′ on $[0,1]$, then

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{1}{4}}{\gamma }_1\left({\displaystyle \frac{1}{2}}\right){\gamma }_2\left({\displaystyle \frac{1}{2}}\right)\left[{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \right.\hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & \left.+{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \right].\hfill \end{array}$$

Applying the definition of I.V. convexity, we acquire

$$\begin{array}{cc}\hfill & {\int }_0^1{\ell }^{\alpha -1}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\mathrm{d}\ell \hfill \\ \hfill & ={\displaystyle \frac{1}{\alpha }}\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{1}{4}}{\gamma }_1\left({\displaystyle \frac{1}{2}}\right){\gamma }_2\left({\displaystyle \frac{1}{2}}\right)\left[{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \right.\hfill \\ \hfill & +{\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & +{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\int }_0^1{\ell }^{\alpha -1}\ell (1-\ell )[{\gamma }_1(\ell ){\gamma }_2(1-\ell )+{\gamma }_1(1-\ell ){\gamma }_2(\ell )]\mathrm{d}\ell \hfill \\ \hfill & \left.+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\int }_0^1{\ell }^{\alpha -1}[{\ell }^2{\gamma }_1(\ell ){\gamma }_2(\ell )+{(1-\ell )}^2{\gamma }_1(1-\ell ){\gamma }_2(1-\ell )]\mathrm{d}\ell \right].\hfill \end{array}$$

(20)

Also

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}((1-\ell )\theta \left({\sigma }_1\right)+\ell \theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & ={\displaystyle \frac{1}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{\int }_{\theta \left({\sigma }_1\right)}^{\theta \left({\sigma }_2\right)}{(u-\theta \left({\sigma }_1\right))}^{\alpha -1}\mathcal{F}\xi \circ {\theta }^{-1}(u,·)\mathrm{d}u\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\alpha \right)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{J}_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_1\right),·).\hfill \end{array}$$

(21)

and

$$\begin{array}{cc}\hfill & \left(IR\right){\int }_0^1{\ell }^{\alpha -1}\mathcal{F}({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\xi ({\theta }^{-1}(\ell \theta \left({\sigma }_1\right)+(1-\ell )\theta \left({\sigma }_2\right)),·)\mathrm{d}\ell \hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\alpha \right)}{{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}{J}_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}(\theta \left({\sigma }_2\right),·).\hfill \end{array}$$

(22)

Combining (20)–(22) leads to the desired outcome. □

Now, we report the consequences of Theorem 8.

• Choosing $\gamma (\ell )=1$ in Theorem 8, then

  $$\begin{array}{cc}\hfill & 2\mathcal{F}\left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\xi \left({\theta }^{-1}\left({\displaystyle \frac{\theta \left({\sigma }_1\right)+\theta \left({\sigma }_2\right)}{2}}\right),·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{2{(\theta \left({\sigma }_2\right)-\theta \left({\sigma }_1\right))}^{\alpha }}}\left[J_{{\theta \left({\sigma }_2\right)}^{-}}^{\alpha }\mathcal{F}\xi \circ {\theta }^{-1}\left(\theta \left({\sigma }_1\right)\right)+J_{\theta {\left({\sigma }_1\right)}^{+}}^{\alpha }\mathcal{F}\xi \circ \left(\theta \left({\sigma }_2\right)\right)\right]\hfill \\ \hfill & +{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{\alpha }{(\alpha +1)(\alpha +2)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)}},\hfill \end{array}$$

  where ${\mathcal{P}}_1({\sigma }_1,{\sigma }_2)$ and ${\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)$ are given by (13) and (14), respectively.
• Choosing $\theta \left(\mu \right)=\mu$ and ${\gamma }_1(\ell )=1={\gamma }_2(\ell )$ in Theorem 8, then

  $$\begin{array}{cc}\hfill & 2\mathcal{F}\left({\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}},·\right)\xi \left({\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}},·\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{2{({\sigma }_2-{\sigma }_1)}^{\alpha }}}\left[J_{{{\sigma }_2}^{-}}^{\alpha }\mathcal{F}\xi ({\sigma }_1,·)+J_{{{\sigma }_1}^{+}}^{\alpha }\mathcal{F}\xi ({\sigma }_2,·)\right]\hfill \\ \hfill & +{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{\alpha }{(\alpha +1)(\alpha +2)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)}},\hfill \end{array}$$

  where ${\mathcal{P}}_1({\sigma }_1,{\sigma }_2)$ and ${\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)$ are given by (13) and (14), respectively.
• Choosing $\theta \left(\mu \right)={\mu }^p$ and ${\gamma }_1(\ell )=1={\gamma }_2(\ell )$ in Theorem 8, then

  $$\begin{array}{cc}\hfill & 2\mathcal{F}\left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}},·\right)}^{{\displaystyle \frac{1}{p}}}\right)\xi \left({\left({\displaystyle \frac{{{\sigma }_1}^p+{{\sigma }_2}^p}{2}},·\right)}^{{\displaystyle \frac{1}{p}}}\right)\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (\alpha +1)}{2{({{\sigma }_2}^p-{{\sigma }_1}^p)}^{\alpha }}}\left[J_{{{{\sigma }_2}^p}^{-}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_1}^p\right)+J_{{{{\sigma }_1}^p}^{+}}^{\alpha }\mathcal{F}\xi \circ k\left({{\sigma }_2}^p\right)\right]\hfill \\ \hfill & +{\mathcal{P}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{\alpha }{(\alpha +1)(\alpha +2)}}+{\mathcal{Q}}_1({\sigma }_1,{\sigma }_2){\displaystyle \frac{{\alpha }^2+\alpha +2}{2(\alpha +2)(\alpha +1)}},\hfill \end{array}$$

  where ${\mathcal{P}}_1({\sigma }_1,{\sigma }_2)$ and ${\mathcal{Q}}_1({\sigma }_1,{\sigma }_2)$ are given by (13) and (14), respectively.

Example 5. 

Let $\mathcal{F}(\ell ,·)=[-{\ell }^2+8,3{\ell }^2+12]$ and $\xi (\ell ,·)=[-{\ell }^2+10,3{\ell }^2+10]$ with $[{\sigma }_1,{\sigma }_2]=[0,2]$, ${\gamma }_1(\ell )=1={\gamma }_2(\ell )$ being the two extended $cr$-interval-valued convex stochastic processes. They satisfy all assumptions of Theorem 8; then,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\alpha }}\mathcal{F}\left(1\right)\xi \left(1\right)=\left[{\displaystyle \frac{126}{\alpha }},{\displaystyle \frac{390}{\alpha }}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2^{\alpha +1}}}\left[{\int }_0^2\left({(2-\ell )}^{\alpha -1}+{(\ell -1)}^{\alpha -1}\right)\mathcal{F}\xi (\ell )\mathrm{d}\ell \right]+{\mathcal{P}}_1(0,2){\displaystyle \frac{1}{\alpha (\alpha +1)(\alpha +2)}}+{\mathcal{Q}}_1(0,2){\displaystyle \frac{{\alpha }^2+2\alpha +4}{2\alpha (\alpha +2)(\alpha +1)}}\hfill \\ \hfill & =\left[{\displaystyle \frac{48{\alpha }^2+148\alpha +88}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{2^{\alpha +3}(\alpha (\alpha (\alpha (13\alpha +140)+533)+778)+312)}{2^{\alpha +1}\left(\alpha (\alpha +1)(\alpha +2)(\alpha +3)(\alpha +4)\right)}}\right.\hfill \\ \hfill & \left.,{\displaystyle \frac{264{\alpha }^2+960\alpha +528}{\alpha (\alpha +1)(\alpha +2)}}+{\displaystyle \frac{32^{\alpha +3}(\alpha (\alpha (\alpha (27\alpha +224)+647)+822)+648)}{2^{\alpha +1}\left(\alpha (\alpha +1)(\alpha +2)(\alpha +3)(\alpha +4)\right)}}\right].\hfill \end{array}$$

For graphical visualization, we vary $0<\alpha \le 4$. Now, we deliver a tabular illustration of Theorem 8.

Figure 5 provides the graphical visualization of Theorem 8, where $L.L.F, L.U.F, R.L.F$ and $R.U.F$ represent the lower and upper functions of left and right sides of Theorem 5.

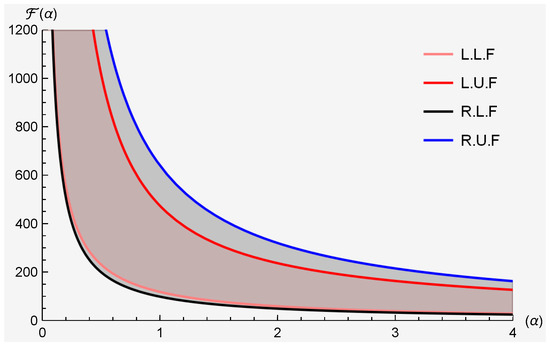
Figure 5. Clearly substantiates the accuracy of Theorem 8.

Table 4 clearly demonstrates the accuracy of Theorem 8 depending $\alpha$.

Table 4. Comparison of all the sides of Theorem 8.

$\mathit{\alpha }$	${\mathit{L}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{L}}^{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}_{*}\left(\mathit{\alpha }\right)$	${\mathit{R}}^{*}\left(\mathit{\alpha }\right)$
$0.5$	252	780	208	1080
$1.5$	84	260	71	351
$2.5$	50	156	42	212
$3.5$	36	111	30	153
$4.5$	28	86	23	120

2.2. Applicable Analysis

Now, we offer a relation between special means by taking into account the $cr$-interval-valued stochastic version of Hermite–Hadamard’s inequality.

• The arithmetic mean:

  $$A({\sigma }_1,{\sigma }_2)={\displaystyle \frac{{\sigma }_1+{\sigma }_2}{2}},$$
• The generalized log-mean:

  $$L_r({\sigma }_1,{\sigma }_2)={\left[{\displaystyle \frac{{{\sigma }_2}^{r+1}-{{\sigma }_1}^{r+1}}{(r+1)({\sigma }_2-{\sigma }_1)}}\right]}^{{\displaystyle \frac{1}{r}}};r\in \mathbb{Z}\setminus \{-1,0\}.$$

Proposition 4. 

For ${\sigma }_1,{\sigma }_2>0$, then

$$\begin{array}{cc}\hfill \left[-A^2({\sigma }_1,{\sigma }_2)+10,3A^2({\sigma }_1,{\sigma }_2)+10\right]& {⪯}_{cr}\left[{-Ł}_2^2({\sigma }_1,{\sigma }_2)+10,{3Ł}_2^2({\sigma }_1,{\sigma }_2)+10\right]\hfill \\ \hfill & {⪯}_{cr}\left[-A({{\sigma }_1}^2,{{\sigma }_2}^2)+10,3A({{\sigma }_1}^2,{{\sigma }_2}^2)+10\right].\hfill \end{array}$$

Proof. 

The claim follows immediately by applying $\mathcal{F}(\mu ,·)=\left[{\mu }^2+10,6{\mu }^2+10\right]$ and $\theta \left(\mu \right)=\mu$ and $\gamma (\ell )=1$ in Theorem 5. □

3. Conclusions

In our study, we explored the notion of a generic stochastic process connected with totally ordered relations and mean square interval-valued calculus. Also, we offered several characterizations of our proposed space of processes. The main advantage of this class is that it allows us to construct a family of innovative stochastic process classes. In addition, we delivered parametric Jensen’s inequality and fractional Hadamard’s-like inequalities incorporated with a newly suggested class of convexity in the context of mean square interval analysis. Also, we discuss numerous significant consequences of primary findings to enhance the existing literature. We hope that the ideas offered in this paper will motivate further investigation in optimization and other applied sciences domains. By applying similar strategies, several classes of convex stochastic processes can be obtained. Another interesting problem in the realm of stochastic interval-valued analysis is how fractional reverse Minkowski’s and Hölder’s-like inequalities can be obtained utilizing the $cr$-ordering relation. In the future, we try to investigate this class of stochastic processes in a fuzzy environment. Also, these results can be utilized to investigate sampled-data stabilization of chaotic non-linear systems and fixed-point techniques. For more details, see [45,46]. We hope that this will serve as a starting point for subsequent investigations.