Shear Mechanism and Optimal Estimation of the Fractal Dimension of Glass Bead-Simulated Sand
Abstract
1. Introduction
2. Test Preparations
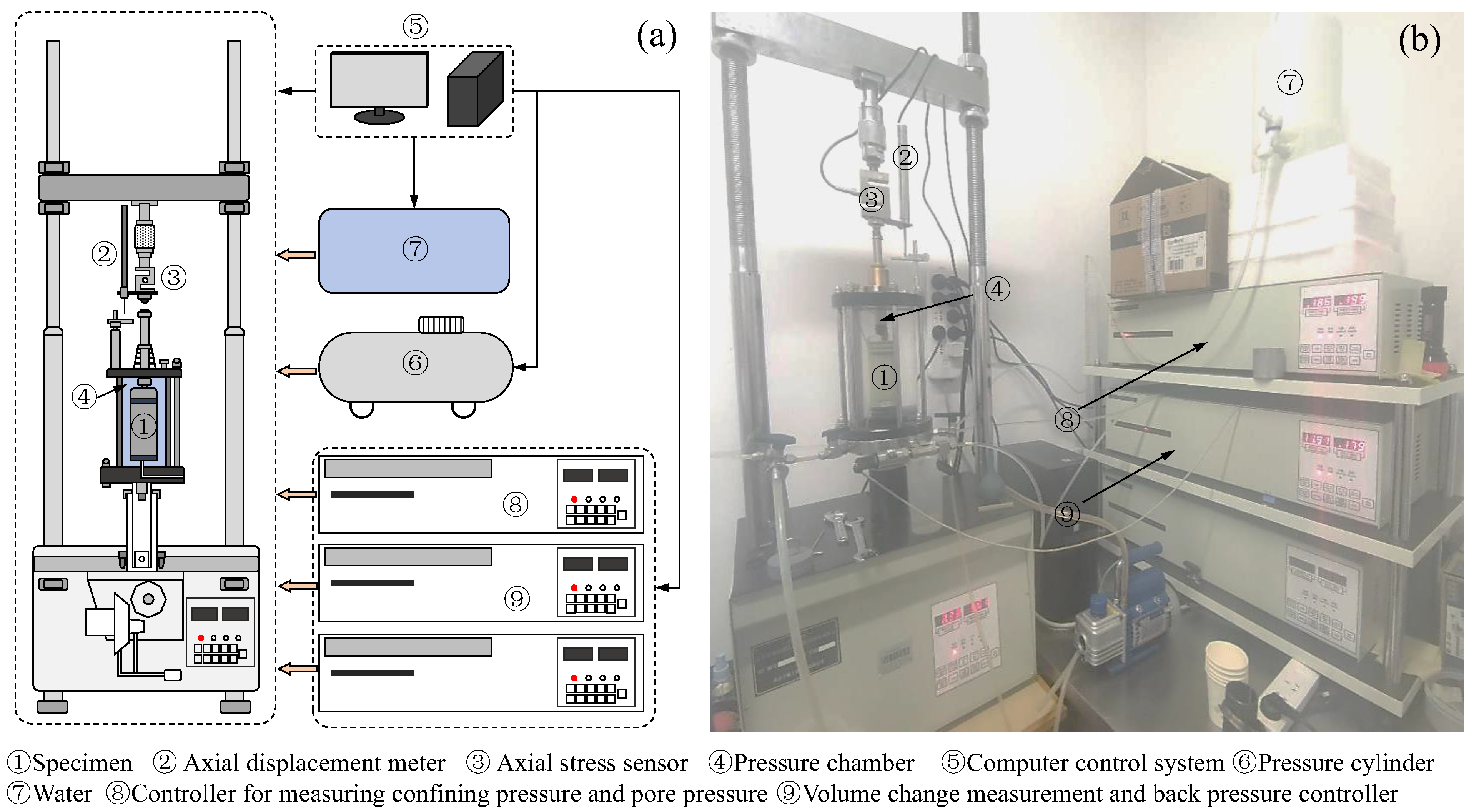
2.1. Test Apparatus and Materials
2.2. Test Procedure and Scheme
3. Test Results and Mechanism Analysis
3.1. Analysis of Test Results
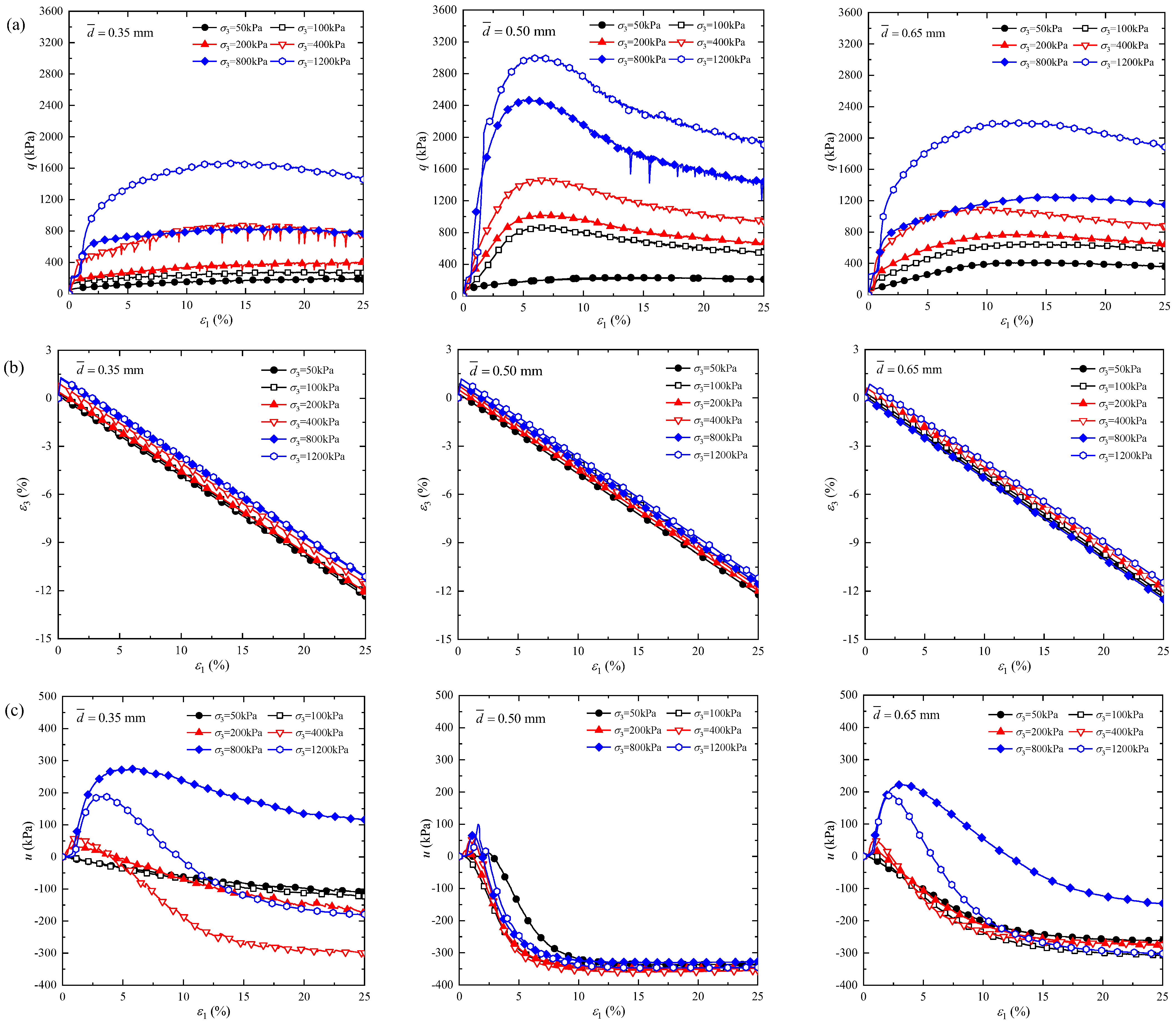
3.1.1. The Variety Rule of q, ε3, and u
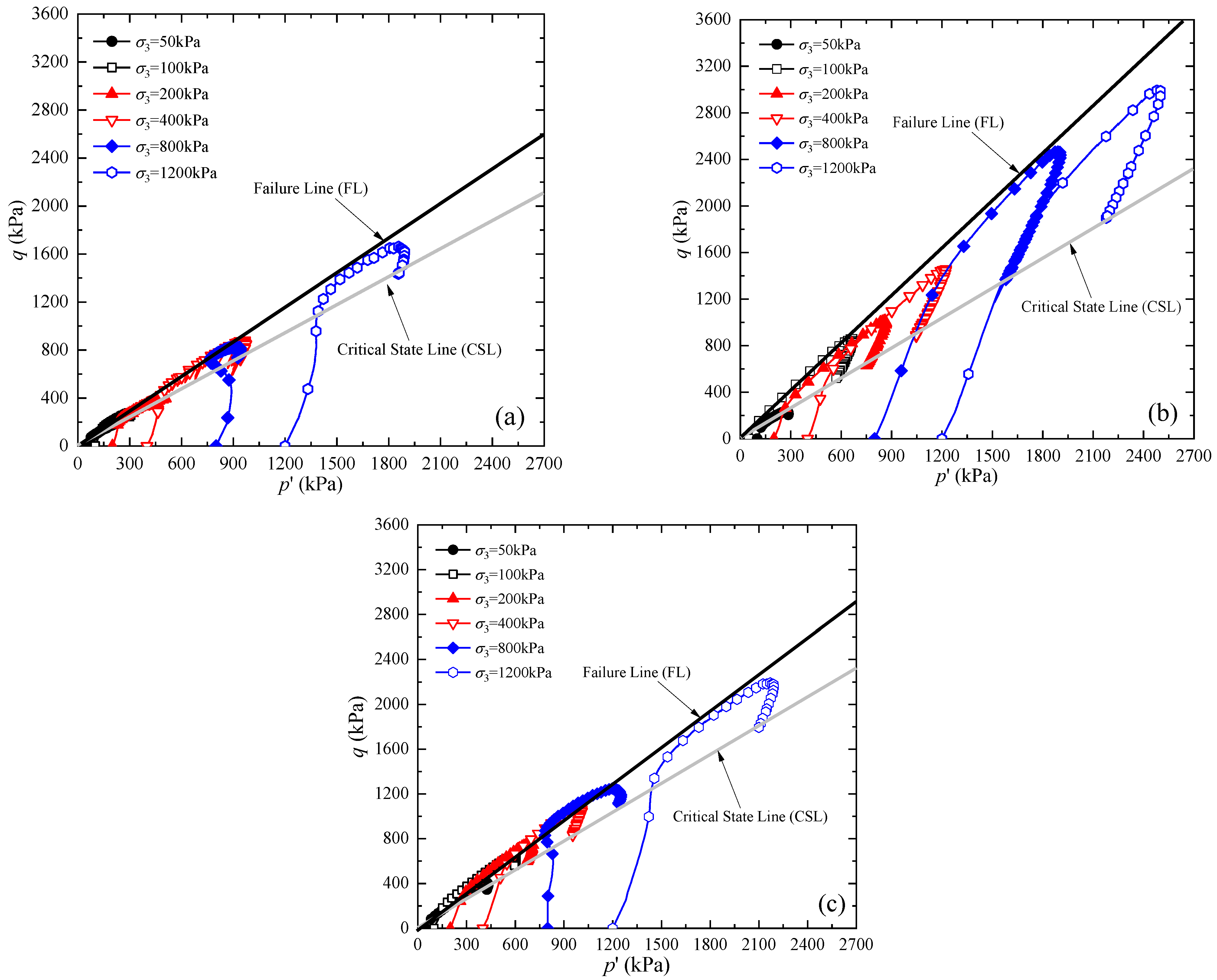
3.1.2. The Relationship between q and p’
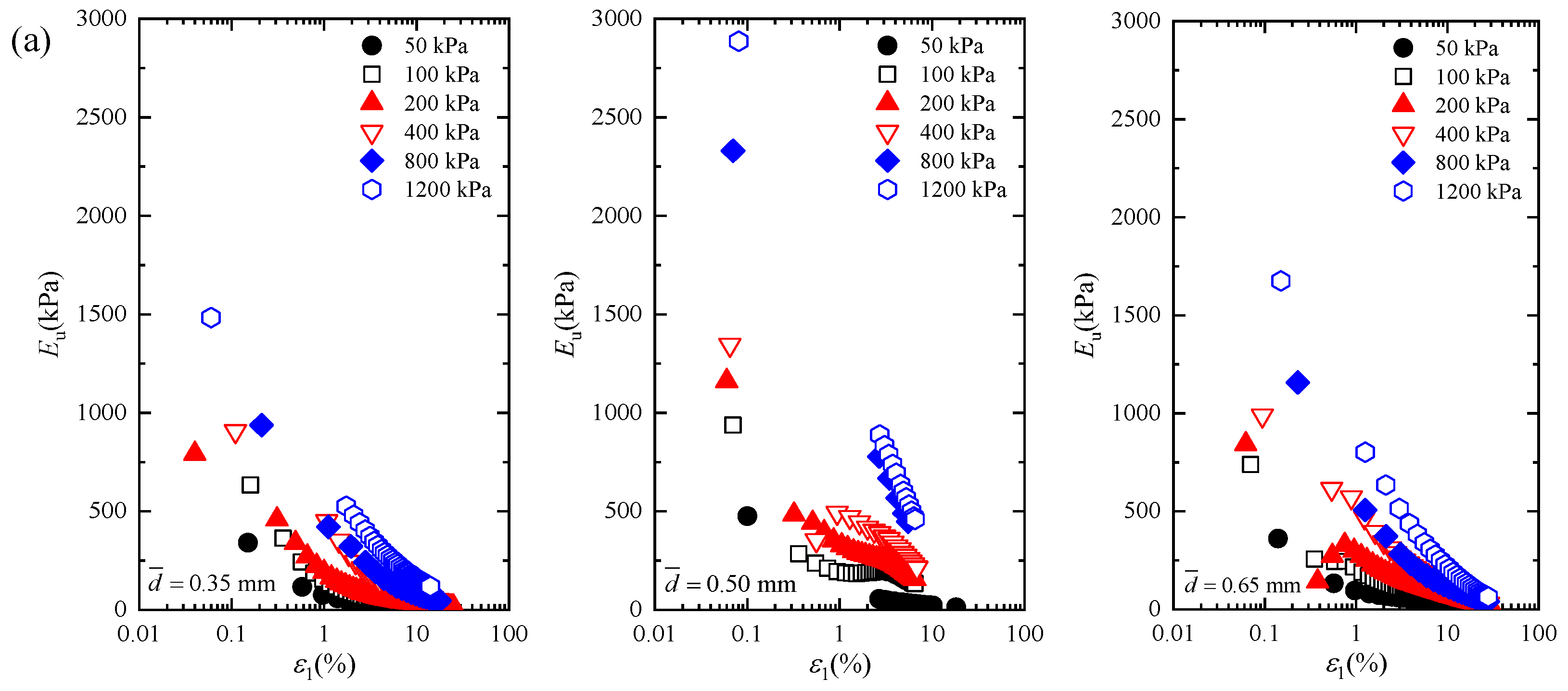
3.1.3. Nonlinear Analysis of the Secant Modulus Eu
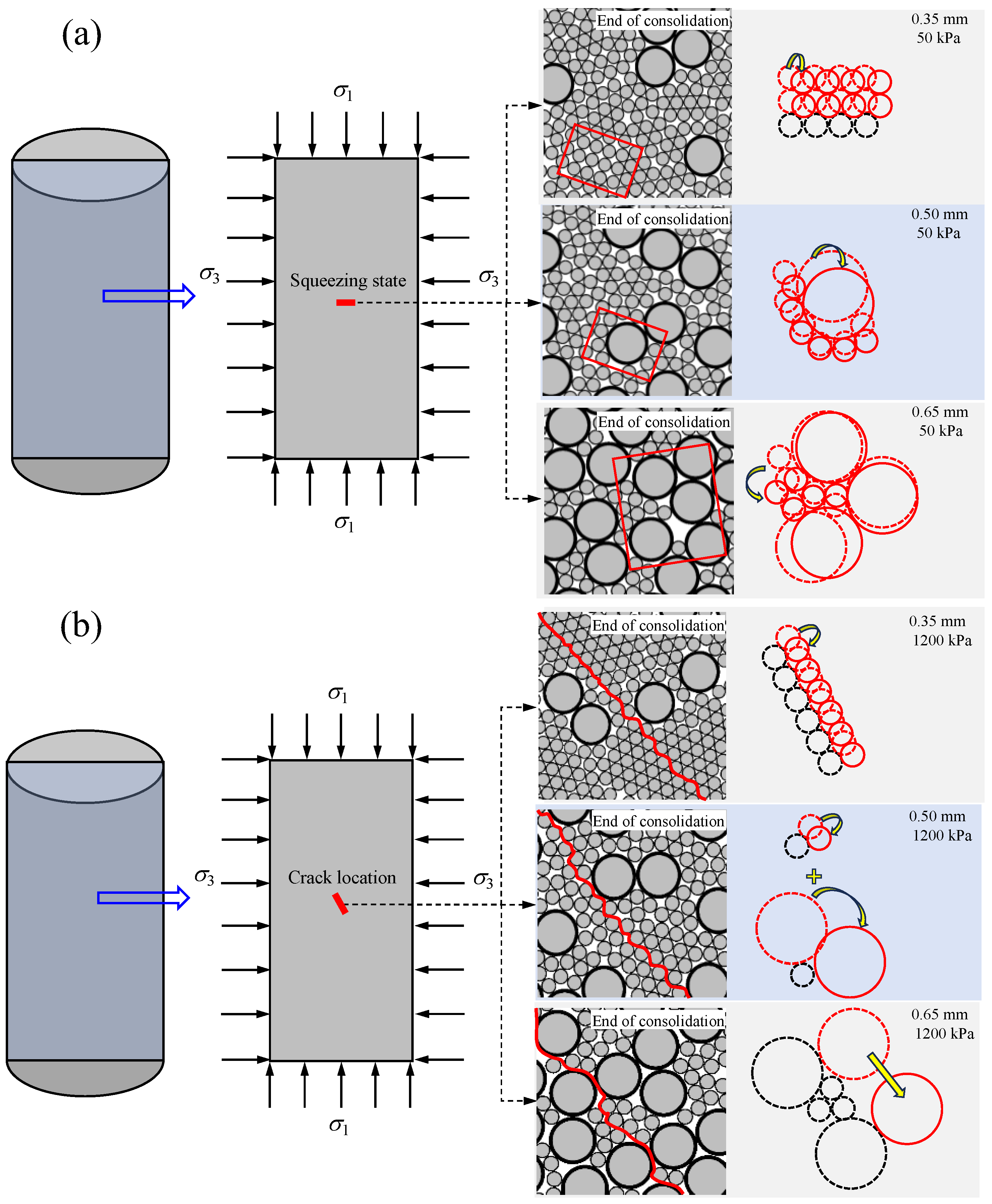
3.2. Mechanism Analysis
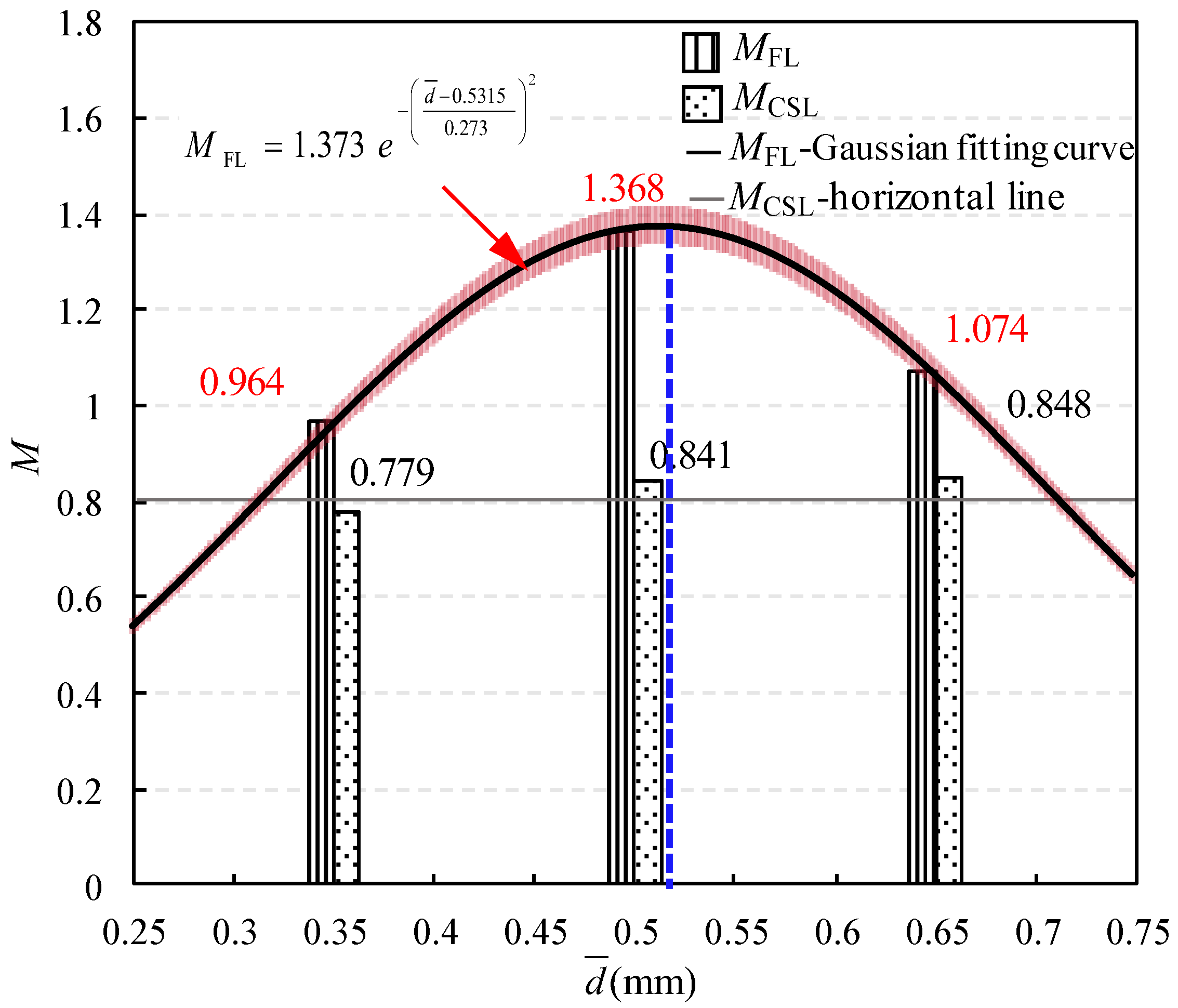
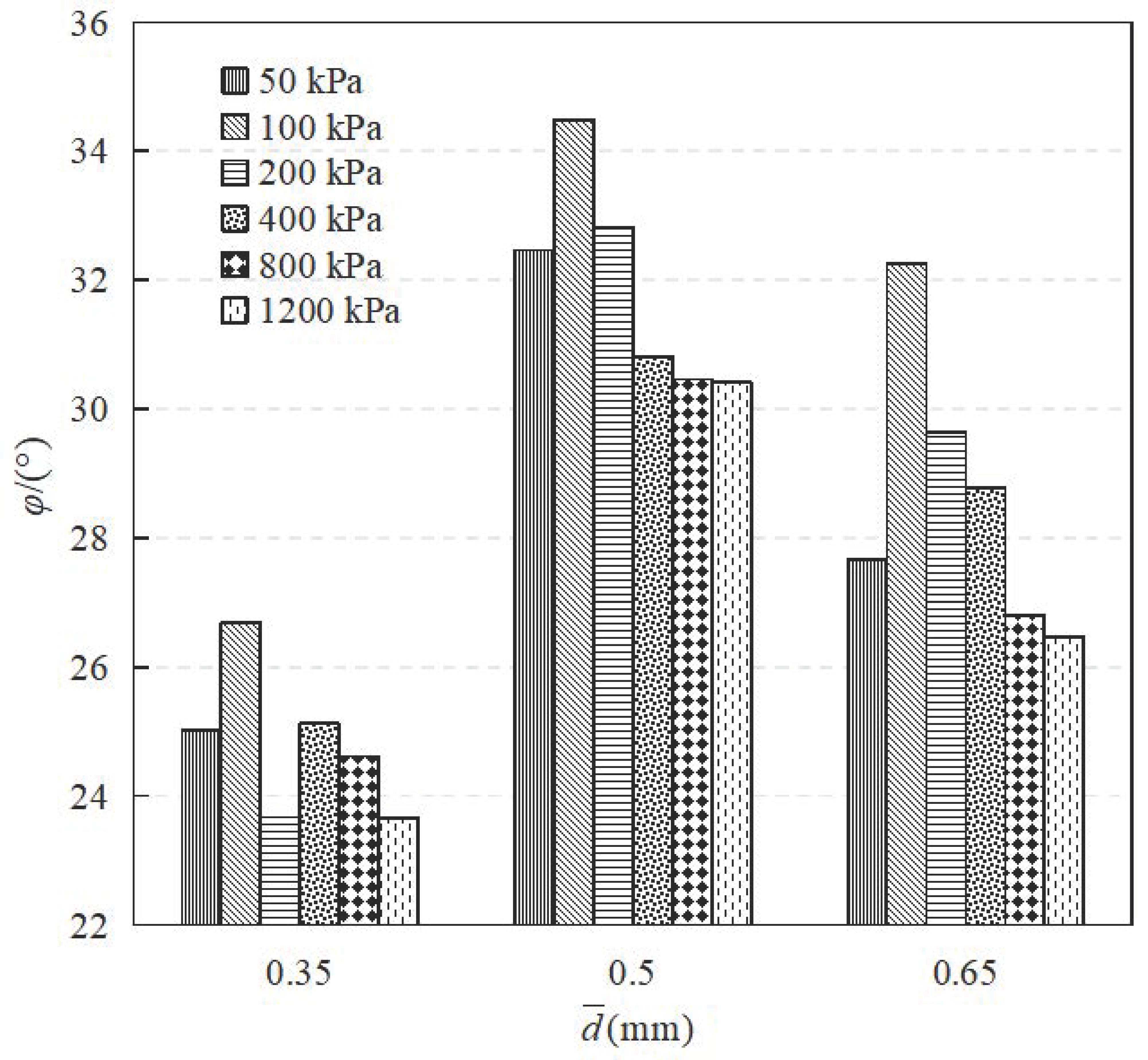
4. Parameters of Shear Strength
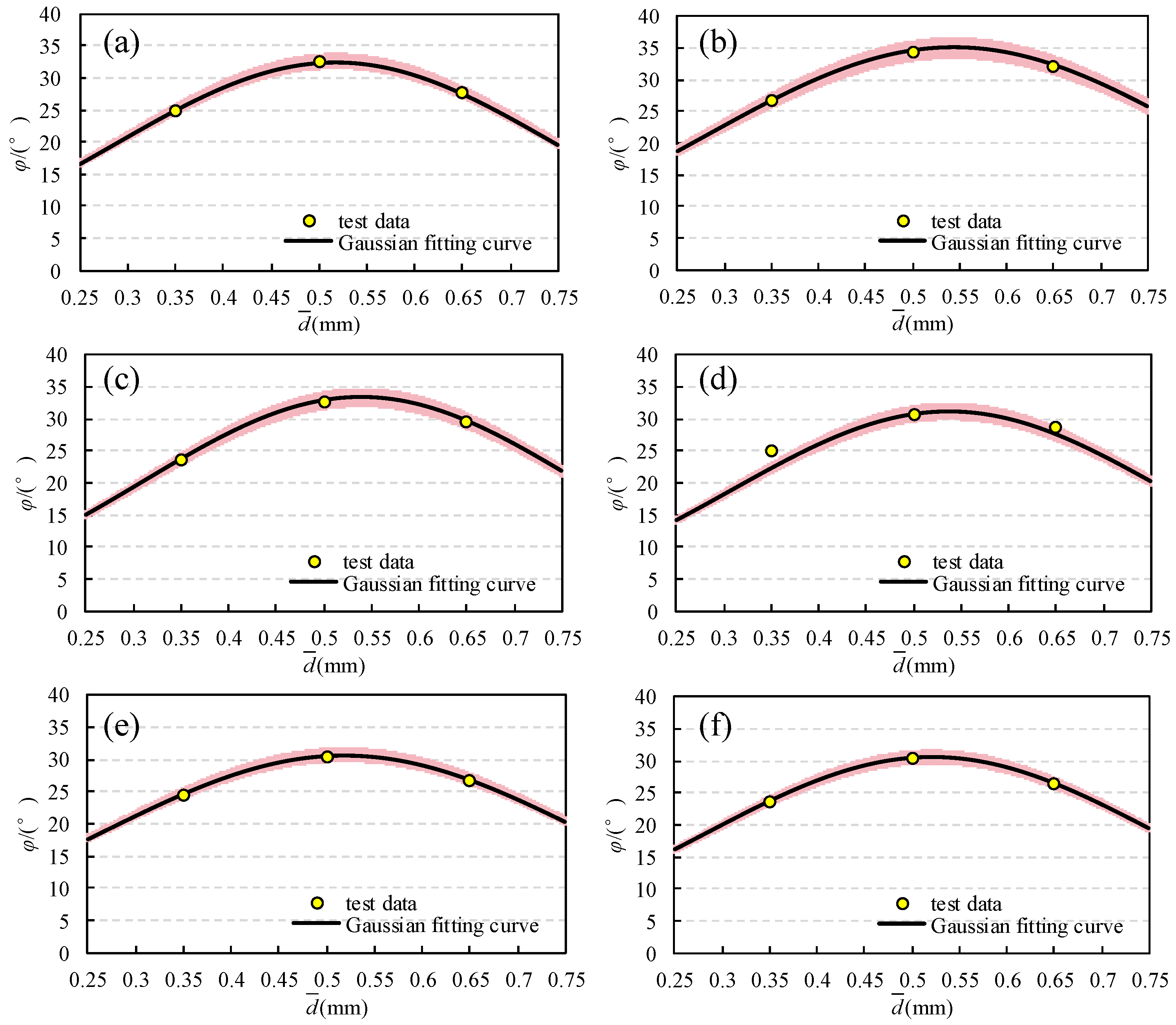
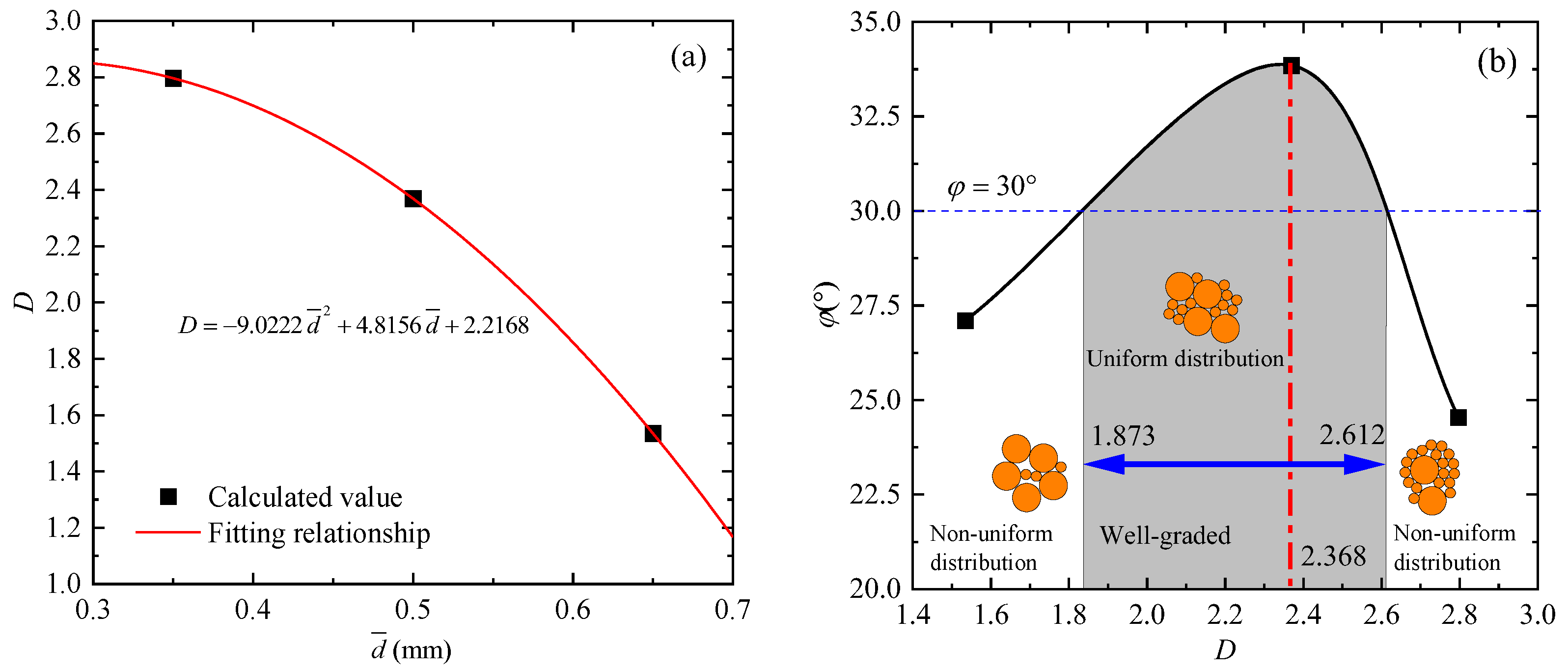
5. Discussion of Fractal Dimension D
6. Conclusions
- (1)
- Strain-softening under a high confining pressure is more pronounced than under a low confining pressure. Under a high confining pressure, the peak shear stress first increases and then decreases as the average particle size increases.
- (2)
- As the effective confining pressure increases, the secant modulus Eu gradually increases, while the pore water pressure first increases and then decreases. Before the specimen reaches the peak shear stress, the normalized modulus ratio Eu/Eu50 first decreases and then increases as the average particle size increases. The particle ratio and arrangement are fundamental reasons for the different macroscopic shear behaviors of particles.
- (3)
- The peak effective internal friction angle φ ranges from 23° to 35° and first increases and then decreases with the increase in effective confining pressure. With the increase in average particle size, the peak shear stress and peak effective internal friction angle φ first increase and then decrease, both of which can be expressed by a Gaussian function.
- (4)
- The range of the fractal dimension D for well-graded particles is 1.873 to 2.612, and the corresponding average particle size ranges from 0.433 to 0.598. Under the optimal mechanical properties of glass beads, the particle size ratio of 0.25 mm to 0.75 mm is 23:27, and the fractal dimension D is 2.368.
- (5)
- In this paper, the average particle size and fractal dimension D of glass beads with optimal shear properties are determined, aiming to provide parameter support for geotechnical engineering design and simulation, such as sandy soil subgrade, while considering the influence of grading factors. Meanwhile, it is of great significance to reveal the relationship between the macroscopic particle friction mechanism and sand particle size distribution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Tian, C.; Wen, L.; Chen, A.; Wang, L.; Qiu, W.; Zhou, H. A study of the overtopping breach of a sand-gravel embankment dam using experimental models. Eng. Fail. Anal. 2021, 124, 105360. [Google Scholar] [CrossRef]
- Chen, J.; Cai, X.; Lale, E.; Yang, J.; Cusatis, G. Centrifuge modeling testing and multiscale analysis of cemented sand and gravel (csg) dams. Constr. Build. Mater. 2019, 223, 605–615. [Google Scholar] [CrossRef]
- Shen, D.; Shi, Z.; Zheng, H.; Yang, J.; Hanley, K.J. Effects of grain composition on the stability, breach process, and breach parameters of landslide dams. Geomorphology 2022, 413, 108362. [Google Scholar] [CrossRef]
- Jafarian, Y.; Mehrzad, B.; Lee, C.; Haddad, A. Centrifuge modeling of seismic foundation-soil-foundation interaction on liquefiable sand. Soil Dyn. Earthq. Eng. 2017, 97, 184–204. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, R.; Lv, P.; Zhang, H. Model tests on jacking installation and lateral loading performance of a new skirted foundation in sand. Ocean Eng. 2020, 197, 106914. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, J.; Chen, X.; Wang, X.; Jia, Y. Experimental investigation on static and dynamic characteristics of granulated rubber-sand mixtures as a new railway subgrade filler. Constr. Build. Mater. 2021, 273, 121955. [Google Scholar] [CrossRef]
- Arulrajah, A.; Yaghoubi, E.; Imteaz, M.; Horpibulsuk, S. Recycled waste foundry sand as a sustainable subgrade fill and pipe-bedding construction material: Engineering and environmental evaluation. Sustain. Cities Soc. 2017, 28, 343–349. [Google Scholar] [CrossRef]
- Shen, J.; Wang, X.; Shan, Y.; Cui, J.; Chen, X.; Wang, X.; Zhu, C. Particle breakage and shape analysis of calcareous sand under consolidated—Undrained triaxial shear. Bull. Eng. Geol. Environ. 2022, 81, 232. [Google Scholar] [CrossRef]
- Abdallah, K.; Abdelkader, B.; Djamel Eddine, B.; Benali, N.; Basma, L.; Ahmed, A. Effect of Non-plastic Fines Content and Gradation on the Liquefaction Response of Chlef Sand. Transp. Infrastruct. Geotechnol. 2024, 11, 2638–2670. [Google Scholar] [CrossRef]
- Liang, J.; Lu, D.; Du, X.; Wu, W.; Ma, C. Non-orthogonal elastoplastic model for sand with dilatancy. Comput. Geotech. 2020, 117, 103329. [Google Scholar] [CrossRef]
- Fan, G.-W.; Li, X.-F. Hypoplastic constitutive model of inherently anisotropic sand. Comput. Geotech. 2024, 175, 106645. [Google Scholar] [CrossRef]
- Fan, G.W.; Li, X.F. On anisotropic local bifurcation based on hypoplastic model. Int. J. Mech. Sci. 2024, 284, 109733. [Google Scholar] [CrossRef]
- Lu, D.; Zhou, X.; Du, X.; Wang, G. A 3D fractional elastoplastic constitutive model for concrete material. Int. J. Solids Struct. 2019, 165, 160–175. [Google Scholar] [CrossRef]
- Abduljabbar, A.; Mohyaldinn, M.; Younis, O.; Alghurabi, A. A numerical cfd investigation of sand screen erosion in gas wells: Effect of fine content and particle size distribution. J. Nat. Gas Sci. Eng. 2021, 95, 104228. [Google Scholar] [CrossRef]
- Lv, Y.; Wang, Y.; Zuo, D. Effects of particle size on dynamic constitutive relation and energy absorption of calcareous sand. Powder Technol. Int. J. Sci. Technol. Wet Dry Part. Syst. 2019, 356, 21–30. [Google Scholar] [CrossRef]
- Adegbule, A.O.; Yan, S.; Papelis, C.; Kibbey, T.C. The effect of sand grain roughness on the grain-scale spatial distribution of grain-surface precipitates formed by evaporation. Colloids Surf. A Physicochem. Eng. Asp. 2018, 548, 134–141. [Google Scholar] [CrossRef]
- Yang, H.; Baudet, B.A. Characterisation of the roughness of sand particles. Procedia Eng. 2016, 158, 98–103. [Google Scholar] [CrossRef][Green Version]
- Kimura, S.; Kaneko, H.; Ito, T.; Minagawa, H. The effect of effective normal stress on particle breakage, porosity and permeability of sand: Evaluation of faults around methane hydrate reservoirs. Tectonophysics 2014, 630, 285–299. [Google Scholar] [CrossRef]
- Molaikbasi, H.; Saberian, M.; Li, J. Prediction of compressive and tensile strengths of zeolite-cemented sand using porosity and composition. Constr. Build. Mater. 2019, 202, 784–795. [Google Scholar] [CrossRef]
- Jena, H.; Sahoo, B.; Roy, G.; Meikap, B. Characterization of hydrodynamic properties of a gas–liquid–solid three-phase fluidized bed with regular shape spherical glass bead particles. Chem. Eng. J. 2008, 145, 50–56. [Google Scholar] [CrossRef]
- Enferad, S.; Pillitteri, S.; Lumay, G.; Gaiani, C.; De Richter, S.K.; Marck, M.; Umbetov, S.; Vandewalle, N.; Jenny, M. Powder flow behavior governed by the surface properties of glass beads. Powder Technol. 2021, 388, 425–433. [Google Scholar] [CrossRef]
- Hazzar, L.; Nuth, M.; Chekired, M. Dem simulation of drained triaxial tests for glass-beads. Powder Technol. 2019, 364, 123–134. [Google Scholar] [CrossRef]
- Xu, W.; Li, X.; Yang, W.; Jia, H. Triaxial test on glass beads simulating coarse-grained soil. Res. Cold Arid Reg. 2022, 14, 274–280. [Google Scholar] [CrossRef]
- Xiao, Y.; Hu, J.; Shi, J.; Liang, F. Static and cyclic liquefaction of granular materials considering grain morphology. Transp. Geotech. 2023, 42, 101107. [Google Scholar] [CrossRef]
- Gong, J.; Pang, X.; Tang, Y.; Liu, M.; Jiang, J.; Ou, X. Effects of particle shape, physical properties and particle size distribution on the small-strain stiffness of granular materials: A DEM study. Comput. Geotech. 2024, 165, 105903. [Google Scholar] [CrossRef]
- Manmatharajan, M.V.; Ingabire, E.-P.; Sy, A.; Ghafghazi, M. Effect of particle size and particle size distribution on the post-liquefaction strength of granular soils. Soils Found. 2023, 63, 101336. [Google Scholar] [CrossRef]
- Wang, J.; Lin, G.; Tang, R.; Zhang, Y.; Yao, Z.; Feng, K.; Tian, N.; Chen, Z.; He, C. A particle-scale insight into the face stability of shallow EPB shield tunnels in dry cobble-rich soil. Tunn. Undergr. Space Technol. 2024, 144, 105516. [Google Scholar] [CrossRef]
- Andrianatrehina, N.L.; Souli, H.; Rech, J.; Fry, J.-J.; Fleureau, J.-M.; Taibi, S. Influence of the percentage of sand on the behavior of gap-graded cohesionless soils. Comptes Rendus. Mec. 2016, 344, 536–546. [Google Scholar] [CrossRef]
- Dutta, T.; Otsubo, M.; Kuwano, R. Stress wave transmission and frequency-domain responses of gap-graded cohesionless soils. Soils Found. 2021, 61, 857–873. [Google Scholar] [CrossRef]
- Ghali, M.; Chekired, M.; Karray, M. A laboratory-based study correlating cone penetration test resistance to the physical parameters of uncemented sand mixtures and granular soils. Eng. Geol. 2019, 255, 11–25. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Lv, L. Glass Beads Test with True Triaxial Stress Path Achieved by Conventional Triaxial Apparatus. Fractal Fract. 2024, 8, 193. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Deng, Y.; Chang, C.S.; Gokce, A. Strength–dilatancy and critical state behaviours of binary mixtures of graded sands influenced by particle size ratio and fines content. Géotechnique 2021, 73, 202–217. [Google Scholar] [CrossRef]
- Zuo, K.; Gu, X.; Hu, C.; Hu, J.; Gao, G. Shear stiffness of sand-fines binary mixtures: Effects of sand gradation and fines content. Constr. Build. Mater. 2023, 383, 131364. [Google Scholar] [CrossRef]
- Li, Y.; Aydin, A.; Xu, Q.; Chen, J. Constitutive behavior of binary mixtures of kaolin and glass beads in direct shear. Ksce J. Civ. Eng. 2012, 16, 1152–1159. [Google Scholar] [CrossRef]
- Fedakar, H.I.; Cetin, B.; Rutherford, C.J. Deformation characteristics of medium-dense sand-clay mixtures under a principal stress rotation. Transp. Geotech. 2021, 30, 100616. [Google Scholar] [CrossRef]
- Shen, Y.; Rui, X.; Ma, Y.; Shen, J.; Xu, J. Anisotropic behaviors of calcareous sand dependent on loading direction and initial shear stress. Appl. Ocean. Res. 2023, 141, 103775. [Google Scholar] [CrossRef]
- Chitravel, S.; Otsubo, M.; Kuwano, R. Effects of seepage flow on liquefaction resistance of uniform sand and gap-graded soil under undrained cyclic torsional shear. Soils Found. 2023, 63, 101363. [Google Scholar] [CrossRef]
- Umar, M.; Kiyota, T.; Chiaro, G.; Duttine, A. Post-liquefaction deformation and strength characteristics of sand in torsional shear tests. Soils Found. 2021, 61, 1207–1222. [Google Scholar] [CrossRef]
- Ma, Z.; Li, X. Experiments on the State Boundary Surface of Aeolian Sand for Road Building in the Tengger Desert. Appl. Sci. 2023, 13, 879. [Google Scholar] [CrossRef]
- Wang, R.; Guo, J.; Lei, S.; Wang, X.; Rong, W.; Yu, Z. A study on the cyclic shear and particle breakage characteristics of the interface between steel and calcareous sand. Mar. Georesources Geotechnol. 2022, 41, 1426–1439. [Google Scholar] [CrossRef]
- Mohamad, H.M.; Zainorabidin, A.; Mohamad, M.I. Maximum strain effect and secant modulus variation of hemic peat soil at large deformation due to cyclic loading. Civil Eng. J. 2022, 8, 2243–2260. [Google Scholar] [CrossRef]
- Koseki, J.; Kawakami, S.; Nagayama, H.; Sato, T. Chance of Small Strain Quasi-elastic Deformation Properties During Undrained Cyclic Torsional Shear and Triaxial Tests of Toyoura Sand. J. Jpn. Geotech. Soc. 2008, 40, 101–110. [Google Scholar] [CrossRef]
- Kantesaria, N.; Sachan, A. Small Strain Shear Modulus and Yielding Characteristics of Compacted High Plasticity Clay. Géotechnique 2021, 72, 424–437. [Google Scholar] [CrossRef]
- Gao, Y.; Luo, W.; Luo, J.; Qian, J.; Zhang, H. Nonlinear characteristics and comparison of triaxial undrained shear moduli of soft soils under two consolidation states. Chin. J. Geotech. Eng. 2021, 43, 64–67. (In Chinese) [Google Scholar]
- Vikash, G.; Prashant, A. Calibration of 3-d failure criteria for soils using plane strain shear strength data. Geotech. Spec. Publ. 2010, 200, 86–91. [Google Scholar] [CrossRef]
- Li, X.F.; Fan, G.W. On strain localization of aeolian sand in true triaxial apparatus. Acta Geotech. 2024, 19, 3115–3128. [Google Scholar] [CrossRef]
- Xu, P.; Sun, Z.; Shao, S.; Fang, L. Comparative analysis of common strength criteria of soil materials. Materials 2021, 14, 4302. [Google Scholar] [CrossRef]
- Lan, G.; Sun, W.; Zhang, X.; Chen, Y.; Tan, W.; Li, X. A three-dimensional fractal model of the normal contact characteristics of two contacting rough surfaces. AIP Adv. 2021, 11, 055023. [Google Scholar] [CrossRef]
- Al-Raeei, M. Morse potential specific bond volume: A simple formula with applications to dimers and soft-hard slab slider. J. Phys. Condens. Matter. 2022, 34, 284001. [Google Scholar] [CrossRef]
- Kumar, A. Dynamic behaviour and semi-analytical solution of nonlinear fractional-order Kuramoto–Sivashinsky equation. Pramana 2024, 98, 48. [Google Scholar] [CrossRef]
- Talbot, A.N.; Richart, F.E. The strength of concrete-its relation to the cement, aggregates and water. Ill. Univ Eng Exp Sta Bull. 1923, 137, 117–118. [Google Scholar]
- Yang, D.; Chu, X. The Effects of the Particle Size Ratio on the Behaviors of Binary Granular Materials. CMES Comput. Model. Eng. Sci. 2023, 136, 63–85. [Google Scholar] [CrossRef]
- Li, G.X. Advanced Soil Mechanics; Tsinghua University Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Yu, F. Characteristics of particle breakage of sand in triaxial shear. Powder Technol. 2017, 320, 656–667. [Google Scholar] [CrossRef]
- Liu, J.; Wang, G.; Kamai, T.; Zhang, F.; Yang, J.; Shi, B. Static liquefaction behavior of saturated fiber-reinforced sand in undrained ring-shear tests. Geotext. Geomembr. 2011, 29, 462–471. [Google Scholar] [CrossRef]
- Fu, X.-J.; Zhao, Z.-H. Laboratory study of the instability of saturated silty sand. Rock Soil Mech. 2008, 29, 381–385. (In Chinese) [Google Scholar]
- Zhang, Z.-T. Dynamic Behaviors and the Evolution of Particle Breakage for Coal Gangue Subgrade Filler under Cyclic Loading; University of Science and Technology of Hunan: Xiangtan, China, 2021. [Google Scholar]




| Drained Condition | Average Particle Sizes (mm) | Effective Confining Pressures (kPa) |
|---|---|---|
| undrained | 0.35 | 50 |
| 100 | ||
| 200 | ||
| 400 | ||
| 800 | ||
| 1200 | ||
| 0.50 | 50 | |
| 100 | ||
| 200 | ||
| 400 | ||
| 800 | ||
| 1200 | ||
| 0.65 | 50 | |
| 100 | ||
| 200 | ||
| 400 | ||
| 800 | ||
| 1200 |
| σ3 (kPa) | (mm) | Tengger Desert Sand [39] | Schematic Diagram | ||
|---|---|---|---|---|---|
| 0.35 | 0.5 | 0.65 | |||
| 50 | 194.6 (0.040) | 235.7 (0.142) | 410.4 (0.169) | 1052 (0.136) | 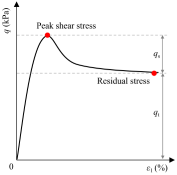 |
| 100 | 277.4 (0.076) | 868.2 (0.559) | 647.4 (0.178) | 1243 (0.058) | |
| 200 | 403.9 (0.094) | 1018.3 (0.616) | 770.7 (0.259) | 1368 (0.061) | |
| 400 | 886.1 (0.181) | 1463.0 (0.642) | 1097.3 (0.298) | 1732 (0.027) | |
| 800 | 830.5 (0.137) | 2470.7 (0.669) | 1250.2 (0.124) | 2103 (0.016) | |
| 1200 | 1679.9 (0.199) | 3007.5 (0.594) | 2197.1 (0.225) | − | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, R. Shear Mechanism and Optimal Estimation of the Fractal Dimension of Glass Bead-Simulated Sand. Fractal Fract. 2024, 8, 578. https://doi.org/10.3390/fractalfract8100578
Li X, Wang R. Shear Mechanism and Optimal Estimation of the Fractal Dimension of Glass Bead-Simulated Sand. Fractal and Fractional. 2024; 8(10):578. https://doi.org/10.3390/fractalfract8100578
Chicago/Turabian StyleLi, Xuefeng, and Rui Wang. 2024. "Shear Mechanism and Optimal Estimation of the Fractal Dimension of Glass Bead-Simulated Sand" Fractal and Fractional 8, no. 10: 578. https://doi.org/10.3390/fractalfract8100578
APA StyleLi, X., & Wang, R. (2024). Shear Mechanism and Optimal Estimation of the Fractal Dimension of Glass Bead-Simulated Sand. Fractal and Fractional, 8(10), 578. https://doi.org/10.3390/fractalfract8100578






