A Compact Scheme Combining the Fast Time Stepping Method for Solving 2D Fractional Subdiffusion Equations

Abstract

In this paper, in order to improve the calculation accuracy and efficiency of α-order Caputo fractional derivative (0 < α ≤ 1), we developed a compact scheme combining the fast time stepping method for solving 2D fractional nonlinear subdiffusion equations. In the temporal direction, a time stepping method was applied. It can reach second-order accuracy. In the spatial direction, we utilized the compact difference scheme, which can reach fourth-order accuracy. Some properties of coefficients are given, which are essential for the theoretical analysis. Meanwhile, we rigorously proved the unconditional stability of the proposed scheme and gave the sharp error estimate. To overcome the intensive computation caused by the fractional operators, we combined a fast algorithm, which can reduce the computational complexity from O(N²) to O(Nlog(N)), where N represents the number of time steps. Considering that the solution of the subdiffusion equation is weakly regular in most cases, we added correction terms to ensure that the solution can achieve the optimal convergence accuracy.

1. Introduction

Fractional differential equations (FDEs) have been widely studied because of their memory effects [1,2]. Many important physical problems can finally be transformed into the solution of FDEs, such as the fractional subdiffusion equation and fractional wave equation [3,4,5]. However, in most cases, it is extremely difficult or even impossible to solve FDEs directly. This inspires us to develop numerical methods to solve FDEs. These numerical methods include the finite difference method [6,7,8], finite element method [9,10,11], finite volume method [12,13,14], Galerkin spectral method [15,16,17] and so forth. The fractional subdiffusion equations, as essential FDEs, have been widely applied in many fields, such as simulation engineering, physics and biology, and researchers have demonstrated that the use of FDEs has performed better than integer ones in the above areas [18,19,20].

In this paper, we consider the following fractional nonlinear subdiffusion equation:

$$\left\{\begin{array}{cc}{u}_t+D_{0,t}^{\alpha }u=D_{0,t}^{\beta }\Delta u+g\left(u\right)+f(x,y,t)\hfill & (x,y,t)\in \mathrm{\Omega }\times (0,T]\hfill \\ u(x,y,0)={\mathrm{\Phi }}_0(x,y),u_t(x,y,0)={\mathrm{\Phi }}_1(x,y)\hfill & (x,y)\in \overline{\mathrm{\Omega }}\hfill \\ u(x,y,t)=0,\hfill & (x,y,t)\in \partial \mathrm{\Omega }\times (0,T]\hfill \end{array}\right.$$

(1)

where $\mathrm{\Omega }=[0,L_1]\times [0,L_2]$ is a bounded domain, the initial value ${\mathrm{\Phi }}_0,{\mathrm{\Phi }}_1$ and the source term $f(x,y,t)$ are given functions, the nonlinear term satisfies $|g(u)|\le C\left|u\right|$ with $|g^{\prime }(u)|\le C$ and C is a positive constant. $\Delta u=\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}.$ $D_{0,t}^{\alpha }u,D_{0,t}^{\beta }\Delta u$ are Caputo fractional derivatives of order $0<\alpha <1$, which is defined as follows [21]:

$$D_{0,t}^{\alpha }u(x,y,t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-s)}^{-\alpha }\frac{\partial u(x,y,s)}{\partial s}\mathrm{d}s.$$

(2)

In addition, we know that

$$D_{0,t}^{\alpha }{t}^p=\frac{\mathrm{\Gamma }(1+p)}{\mathrm{\Gamma }(1+p-\alpha )}{t}^{p-\alpha },p>0.$$

(3)

The time stepping method plays an important role in the process of solving FDEs. Many researchers have investigated the time stepping method. Li et al. [22] utilized the time stepping method for the nonlinear fluid–fluid interaction. Zeng et al. [23] proposed a fast algorithm for the time stepping method. Alzahrani et al. [24] developed a high-order time stepping method for space fractional reaction diffusion equations. The method used in this paper in time discretization is the shifted convolution quadrature method [25], which belongs to the time stepping method. Usually, the subdiffusion equations have an initial singularity for non-smooth solutions. We improved the accuracy by adding correction terms. Due to the fact that fractional operators spend much time in computation due to their nonlocality, the fast algorithm was implemented to reduce the computational cost. Liu et al. [26] proposed a fast high-order compact difference method that can help to reduce the computational work from $O(N^2)$ to $O(Nlo{g}^{2}N)$ in the temporal direction. We also utilized a fast algorithm that can reduce the computational work from $O(N^2)$ to $O(Nlog(N))$, where N represents the number of time steps. To the best of the authors’ knowledge, there are few papers utilizing the fast algorithm for the problem (1). The highlights of this paper can be summarized as

• Our numerical schemes have temporal second-order accuracy and spatial fourth-order accuracy, which are relatively high.
• We developed a fast time stepping method for solving the nonlinear fractional subdiffusion equation, which improves the computation efficiency.
• We recovered the optimal convergence accuracy for non-smooth solutions by adding correction terms.

This paper is organized in several sections. In Section 2, we introduce some lemmas and notations. In Section 3, the fully discrete scheme is given. In Section 4, we rigorously prove the stability of the fully discrete scheme and give the sharp error estimate. In Section 5, we derive the approximation formulas with the correction terms, which can help to improve the optimal convergence accuracy. In Section 6, we combine a fast algorithm to reduce the computational cost from $O(N^2)$ to $O(Nlog(N))$. Finally, we make a conclusion.

2. Preparations

$L_1$ and $L_2$ are evenly divided into $M_1$ and $M_2$, respectively. Let $h_1=L_1/M_1$, $h_2=L_2/M_2$, $\tau =T/N$, where $M_1,M_2,N$ are positive integers, $h_1,h_2$ are the step sizes in space along the x direction and y direction, respectively, and $\tau$ is the temporal step size. Define $x_i=i{h}_1(0\le i\le M_1),y_j=j{h}_2(0\le j\le M_2),t_k=k\tau (0\le k\le N)$; thus, we obtain a uniform discretization in space and time.

Define ${\overline{\mathrm{\Omega }}}_h=\left\{(x_i,y_j)\right|0\le i\le M_1,0\le j\le M_2\}$, and $\mathrm{\Omega }$ is covered by ${\overline{\mathrm{\Omega }}}_h$. ${\mathrm{\Omega }}_h={\overline{\mathrm{\Omega }}}_h\cap \mathrm{\Omega },\partial {\mathrm{\Omega }}_h={\overline{\mathrm{\Omega }}}_h\cap \partial \mathrm{\Omega },\omega =\left\{(i,j)\right|(x_i,y_j)\in {\mathrm{\Omega }}_h\},\partial \omega =\left\{(i,j)\right|(x_i,y_j)\in \partial {\mathrm{\Omega }}_h\},\overline{\omega }=\omega \cup \partial \omega$, ${\mathrm{\Omega }}_{\tau }=\left\{t_k\right|0\le k\le N\}$, and [0,T] is covered by ${\mathrm{\Omega }}_{\tau }$.

We define the grid functions as follows:

$${\mathcal{V}}_h=\left\{u\right|u=\left\{u_{ij}\right|(i,j)\in \overline{\omega }\}\mathrm{is}\mathrm{the}\mathrm{grid}\mathrm{function}\mathrm{on}{\overline{\mathrm{\Omega }}}_h\},$$

(4)

$${\mathring{\mathcal{V}}}_h=\left\{u\right|u\in {\mathcal{V}}_h,u_{ij}=0,\mathrm{when}(i,j)\in \partial \omega \}.$$

(5)

For any $u\in {\mathcal{V}}_h$, we have

$$u_{i+\frac{1}{2},j}=\frac{1}{2}(u_{i,j}+u_{i+1,j}),u_{i,j+\frac{1}{2}}=\frac{1}{2}(u_{i,j}+u_{i,j+1})$$

(6)

Introduce the notations

$$\begin{array}{c}{\delta }_x{u}_{i-\frac{1}{2},j}=\frac{1}{h_1}(u_{ij}-u_{i-1,j}),{\delta }_y{u}_{i,j-\frac{1}{2}}=\frac{1}{h_2}(u_{ij}-u_{i,j-1})\hfill \\ {\delta }_x^2{u}_{ij}=\frac{1}{h_1}({\delta }_x{u}_{i+\frac{1}{2},j}-{\delta }_x{u}_{i-\frac{1}{2},j}),\hfill \\ {\delta }_x{\delta }_y{u}_{i-\frac{1}{2},j-\frac{1}{2}}=\frac{1}{h_1}({\delta }_y{u}_{i,j-\frac{1}{2}}-{\delta }_y{u}_{i-1,j-\frac{1}{2}})\hfill \\ {\delta }_y^2{u}_{ij}=\frac{1}{h_2}({\delta }_y{u}_{i,j+\frac{1}{2}}-{\delta }_y{u}_{i,j-\frac{1}{2}}),\hfill \\ {\delta }_x^2{\delta }_y^2{u}_{ij}=\frac{1}{h_1^2}({\delta }_y^2{u}_{i-1,j}-2{\delta }_y^2{u}_{ij}+{\delta }_y^2{u}_{i+1,j})\hfill \end{array}$$

(7)

Define compact operator [27]

$${\mathcal{A}}_x{u}_{ij}=\left\{\begin{array}{cc}(I+\frac{h_1^2}{12}{\delta }_x^2)u_{ij}\hfill & 1\le i\le M_1-1\hfill \\ u_{ij}\hfill & i=0\mathrm{or}i=M_1\hfill \end{array}\right.,0\le j\le M_2$$

(8)

$${\mathcal{A}}_y{u}_{ij}=\left\{\begin{array}{cc}(I+\frac{h_2^2}{12}{\delta }_y^2)u_{ij}\hfill & 1\le j\le M_2-1\hfill \\ u_{ij}\hfill & j=0\mathrm{or}j=M_2\hfill \end{array}\right.,0\le i\le M_1$$

(9)

Inner products and the responding norms are given as follows:

$$\begin{array}{c}(u,v)=h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}{u}_{ij}{v}_{ij},\left|\right|u\left|\right|=\sqrt{(u,u)}\hfill \\ ({\delta }_{x}u,{\delta }_{x}v)=h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}({\delta }_x{u}_{i-\frac{1}{2},j}){\delta }_x{v}_{i-\frac{1}{2},j},\left|\right|{\delta }_{x}u\left|\right|=\sqrt{({\delta }_{x}u,{\delta }_{x}u)}\hfill \\ ({\delta }_{y}u,{\delta }_{y}v)=h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2}({\delta }_y{u}_{i,j-\frac{1}{2}}){\delta }_y{v}_{i,j-\frac{1}{2}},\left|\right|{\delta }_{y}u\left|\right|=\sqrt{({\delta }_{y}u,{\delta }_{y}u)}\hfill \\ ({\delta }_x{\delta }_{y}u,{\delta }_x{\delta }_{y}v)=h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2}({\delta }_x{\delta }_y{u}_{i-\frac{1}{2},j-\frac{1}{2}})({\delta }_x{\delta }_y{v}_{i-\frac{1}{2},j-\frac{1}{2}}),\hfill \\ \left|\right|{\delta }_x{\delta }_{y}u\left|\right|=\sqrt{({\delta }_x{\delta }_{y}u,{\delta }_x{\delta }_{y}u)}\hfill \end{array}$$

(10)

We have

$$\begin{array}{c}(-{\delta }_x^{2}u,v)=h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}(-{\delta }_x^2{u}_{ij})v_{ij}=({\delta }_{x}u,{\delta }_{x}v),\hfill \\ (-{\delta }_y^{2}u,v)=h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}(-{\delta }_y^2{u}_{ij})v_{ij}=({\delta }_{y}u,{\delta }_{y}v),\hfill \\ ({\delta }_x^2{\delta }_y^{2}u,v)=h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}({\delta }_x^2{\delta }_y^2{u}_{ij})v_{ij}=({\delta }_x{\delta }_{y}u,{\delta }_x{\delta }_{y}v).\hfill \end{array}$$

(11)

For any $u,v\in {\mathring{\mathcal{V}}}_h$, we define

$$\begin{array}{cc}\hfill {(u,v)}_A& =({\mathcal{A}}_x{\mathcal{A}}_{y}u,v)\hfill \\ & =\left(\left(I+\frac{h_1^2}{12}{\delta }_x^2\right)\left(I+\frac{h_2^2}{12}{\delta }_y^2\right)u,v\right)\hfill \\ & =(u,v)-\frac{h_1^2}{12}({\delta }_{x}u,{\delta }_{x}v)-\frac{h_2^2}{12}({\delta }_{y}u,{\delta }_{y}v)+\frac{h_1^2{h}_2^2}{144}({\delta }_x{\delta }_{y}u,{\delta }_x{\delta }_{y}v)\hfill \end{array}$$

(12)

and the responding norm is ${\left|\right|u\left|\right|}_A=\sqrt{{(u,u)}_A}$.

Finally, we define the grid function

$$U_{ij}^n=u(x_i,y_j,t_n),f_{ij}^n=f(x_i,y_j,t_n),(i,j)\in \overline{\omega },0\le n\le N.$$

(13)

Lemma 1 

([28]). For any $u\in {\mathring{\mathcal{V}}}_h$, we have

$$\left|\right|{\delta }_x{\delta }_y{u\left|\right|}^2\le \frac{4}{h_1^2}\left|\right|{\delta }_y{u\left|\right|}^2,\left|\right|{\delta }_y{\delta }_x{u\left|\right|}^2\le \frac{4}{h_2^2}\left|\right|{\delta }_{x}u{\left|\right|}^2.$$

(14)

Lemma 2 

([27]). For any $u\in {\mathring{\mathcal{V}}}_h$, we have

$$\frac{1}{3}{\left|\right|u\left|\right|}^2\le {\left|\right|u\left|\right|}_A^2\le {\left|\right|u\left|\right|}^2.$$

(15)

3. Fully Discrete Compact Scheme

Lemma 3 

([29]). The Caputo fractional derivative $D_{0,t}^{\alpha }u(0<\alpha <1)$ is approximated at $t_{n-\theta }$

$$\begin{array}{cc}\hfill D_{0,t}^{\alpha }u(t_{n-\theta })& =D_{\tau ,\alpha }^{n,\theta }u+E_{n-\theta }^{(\alpha )}\hfill \\ & ={\tau }^{-\alpha }\sum _{k=0}^n{\omega }_{n-k}^{(\alpha )}(u^k-u^0)+E_{n-\theta }^{(\alpha )},\hfill \end{array}$$

(16)

where $E_{n-\theta }^{(\alpha )}=O(t_{n-\theta }^{\sigma -\alpha -2}{\tau }^2)$, and the coefficients ${\omega }_k^{(\alpha )}$ are as follows:

$${\omega }_k^{(\alpha )}=\left\{\begin{array}{cc}2/[2(1+\theta )-\alpha ],\hfill & k=0\hfill \\ 4W_1^1/{[2(1+\theta )-\alpha ]}^2,\hfill & k=1\hfill \\ (W_k^1{\omega }_{k-1}^{(\alpha )}+W_k^2{\omega }_{k-2}^{(\alpha )})/k/(1-\alpha /2+\theta ),\hfill & k\ge 2\hfill \end{array}\right.$$

(17)

$$\begin{array}{c}{W}_k^1=-\alpha +(\alpha -1)(\alpha /2-\theta )-(k-1)(\alpha -\theta -1),\hfill \\ W_k^2=-(\alpha -1)(\alpha /2-\theta )-(k-2)(\theta -\alpha /2).\hfill \end{array}$$

Lemma 4 

([10,29]). The first-order derivative $u_t$ is approximated at $t_{n-\theta }$

$$\begin{array}{c}{u}_t(t_{n-\theta })=u_{\tau ,\theta }^n+E_{\tau ,\theta }^{(n)}\hfill \\ =\left\{\begin{array}{ccc}& \frac{u^1-u^0}{\tau }+E_{\tau ,\theta }^{(1)},\hfill & n=1\hfill \\ & \frac{3-2\theta }{2\tau }{u}^n-\frac{2-2\theta }{\tau }{u}^{n-1}+\frac{1-2\theta }{2\tau }{u}^{n-2}+E_{\tau ,\theta }^{(n)},\hfill & n\ge 2\hfill \end{array}\right.\hfill \end{array}$$

(18)

where $E_{\tau ,\theta }^{(n)}=O(t_{n-\theta }^{\tilde{\sigma }-3}{\tau }^2),\tilde{\sigma }=min\{{\sigma }_2,{\sigma }_3,\cdots \}$\{2}.

Consider Equation (1) at nodes $(x_i,y_j,t_{n-\theta })$. We obtain

$$\begin{array}{cc}\hfill u_t(x_i,y_j,t_{n-\theta })+D_{0,t}^{\alpha }u(x_i,y_j,t_{n-\theta })=& D_{0,t}^{\beta }\left(\frac{{\partial }^{2}u}{\partial x^2}(x_i,y_j,t_{n-\theta })+\frac{{\partial }^{2}u}{\partial y^2}(x_i,y_j,t_{n-\theta })\right)\hfill \\ & +g_{ij}^{n-\theta }+f_{ij}^{n-\theta },\hfill \end{array}$$

(19)

where $(i,j)\in \overline{\omega },1\le n\le N$, $f_{ij}^{n-\theta }=f(x_i,y_j,t_{n-\theta }),g_{ij}^{n-\theta }=g(u(x_i,y_j,t_{n-\theta }))$.

Act the operator ${\mathcal{A}}_x{\mathcal{A}}_y$ on both sides of Equation (19). We obtain

$$\begin{array}{cc}& {\mathcal{A}}_x{\mathcal{A}}_y{u}_t(x_i,y_j,t_{n-\theta })+{\mathcal{A}}_x{\mathcal{A}}_y{D}_{0,t}^{\alpha }u(x_i,y_j,t_{n-\theta })\hfill \\ \hfill =& D_{0,t}^{\beta }{\mathcal{A}}_y{\delta }_x^2{U}_{ij}^{n-\theta }+D_{0,t}^{\beta }{\mathcal{A}}_x{\delta }_y^2{U}_{ij}^{n-\theta }\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{n-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta }+r_{ij},\hfill \end{array}$$

(20)

where $|r_{ij}|\le C(h_1^4+h_2^4)$.

Using (16) and (18), we can obtain

Case $n=1$:

$$\begin{array}{cc}& {\mathcal{A}}_x{\mathcal{A}}_y\frac{U_{ij}^1-U_{ij}^0}{\tau }+{\tau }^{-\alpha }\sum _{k=0}^1{\omega }_{1-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(U_{ij}^k-U_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(U_{ij}^k-U_{ij}^0)+{\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(U_{ij}^k-U_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{1-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{1-\theta }+r_{ij}^1,\hfill \end{array}$$

(21)

Case $n\ge 2$:

$$\begin{array}{cc}& \frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{U}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{U}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{U}_{ij}^{n-2}\hfill \\ & +{\tau }^{-\alpha }\sum _{k=0}^n{\omega }_{n-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(U_{ij}^k-U_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(U_{ij}^k-U_{ij}^0)+{\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(U_{ij}^k-U_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{n-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta }+r_{ij}^n,\hfill \end{array}$$

(22)

where $r_{ij}^n=E_{\tau ,\theta }^{(n)}+E_{n-\theta }^{(\alpha )}+E_{n-\theta }^{(\beta )}+r_{ij}$.

Omit the error term $r_{ij}^n$, replace the exact solution $U_{ij}^n$ with the numerical solution $u_{ij}^n$ and obtain numerical schemes for solving Equation (1) as follows:

Case $n=1$:

$$\begin{array}{cc}& {\mathcal{A}}_x{\mathcal{A}}_y\frac{u_{ij}^1-u_{ij}^0}{\tau }+{\tau }^{-\alpha }\sum _{k=0}^1{\omega }_{1-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^k-u_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^k-u_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{1-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{1-\theta },(i,j)\in \omega \hfill \end{array}$$

(23)

Case $n\ge 2$:

$$\begin{array}{cc}& \frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-2}\hfill \\ & +{\tau }^{-\alpha }\sum _{k=0}^n{\omega }_{n-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^k-u_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^k-u_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{n-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta },(i,j)\in \omega \hfill \\ & u_{ij}^0={\mathrm{\Phi }}_0(x_i,y_j),(i,j)\in \omega \hfill \\ & u_{ij}^n=0,(i,j)\in \partial \omega ,0\le n\le N\hfill \end{array}$$

(24)

4. Stability and Convergence Analysis

Lemma 5 

([29]). ${\omega }_k^{(\alpha )}$ are defined in (16). For any vector $(u^1,..,u^M)\in {\mathbb{R}}^M$ with $M\ge 1$, it satisfies

$$\sum _{k=1}^M\sum _{i=1}^k{\omega }_{k-i}^{(\alpha )}{u}^i{u}^k\ge 0,$$

(25)

where $\alpha \in (0,1)$, $\theta \in (\frac{\alpha -1}{2},1]$.

Lemma 6 

([29]). $u_{\tau ,\theta }^j$ are defined in (18). For any vector $(u^1,...,u^M)\in {\mathbb{R}}^M$ with $M\ge 2$, it satisfies

$$\sum _{j=1}^M{u}^j{u}_{\tau ,\theta }^j\ge \frac{1}{4\tau }{(u^M)}^2-\frac{1}{2\tau }{(u^1)}^2,$$

(26)

where $\theta \in [0,1]$.

Theorem 1. 

The schemes (21) and (22) derived by our method are unconditionally stable, and they have the following estimate:

$$\begin{array}{c}\hfill \left|\right|u_{ij}^N{\left|\right|}_A\le C(||u_{ij}^0{\left|\right|}_A+\underset{0\le n\le N}{max}\left|\right|f_{ij}^n{\left|\right|}_A).\end{array}$$

(27)

Proof of Theorem 1. 

For simplicity, define $v_{ij}^n:=u_{ij}^n-u_{ij}^0$, and we can derive by (16) and (18) that

$$\begin{array}{cc}& {\mathcal{A}}_x{\mathcal{A}}_y\frac{v_{ij}^1-v_{ij}^0}{\tau }={\mathcal{A}}_x{\mathcal{A}}_y\frac{u_{ij}^1-u_{ij}^0}{\tau },\hfill \\ & \frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-2}\hfill \\ \hfill =& \frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-2},\hfill \\ & D_{\tau ,\alpha }^{n,\theta }{v}_{ij}^n=D_{\tau ,\alpha }^{n,\theta }{u}_{ij}^n,D_{\tau ,\beta }^{n,\theta }\Delta v_{ij}^n=D_{\tau ,\beta }^{n,\theta }\Delta u_{ij}^n.\hfill \end{array}$$

(28)

We take the inner product of (23) and (24) with $v_{ij}^l$. Then, we replace l with n and sum both sides for n from 1 to N ($N\ge 2$ ). We obtain

$$\begin{array}{cc}& \frac{1}{\tau }\left({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^1,v_{ij}^1\right)+\frac{3-2\theta }{2\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^n,v_{ij}^n)\hfill \\ & -\frac{2-2\theta }{\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-1},v_{ij}^n)+\frac{1-2\theta }{2\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-2},v_{ij}^n)\hfill \\ & +{\tau }^{-\alpha }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\alpha )}({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^k,v_{ij}^n)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\mathcal{A}}_x{\delta }_y^2{v}_{ij}^k,v_{ij}^n)+{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\mathcal{A}}_y{\delta }_x^2{v}_{ij}^k,v_{ij}^n)\hfill \\ & +\sum _{n=1}^N({\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{n-\theta },v_{ij}^n)+\sum _{n=1}^N({\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta },v_{ij}^n)\hfill \end{array}$$

(29)

Using the Lemmas 1, 5 and 6 and the Cauchy–Schwarz inequality, we have

$$\begin{array}{c}\frac{1}{\tau }\left({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^1,v_{ij}^1\right)+\frac{3-2\theta }{2\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^n,v_{ij}^n)\hfill \\ -\frac{2-2\theta }{\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-1},v_{ij}^n)+\frac{1-2\theta }{2\tau }\sum _{n=2}^N({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^{n-2},v_{ij}^n)\hfill \\ \ge \frac{1}{4\tau }\left|\right|v_{ij}^N{\left|\right|}_A^2-\frac{1}{2\tau }\left|\right|v_{ij}^1{\left|\right|}_A^2,\hfill \end{array}$$

(30)

$${\tau }^{-\alpha }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\alpha )}({\mathcal{A}}_x{\mathcal{A}}_y{v}_{ij}^k,v_{ij}^n)\ge 0$$

(31)

$$\begin{array}{cc}& {\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\mathcal{A}}_x{\delta }_y^2{v}_{ij}^k,v_{ij}^n)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}\left(\left(I+\frac{h_1^2}{12}{\delta }_x^2\right){\delta }_y^2{v}_{ij}^k,v_{ij}^n\right)\hfill \\ \hfill =& -{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_y{v}_{ij}^k,{\delta }_y{v}_{ij}^n)+\frac{h_1^2}{12}{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_x{\delta }_y{v}_{ij}^k,{\delta }_x{\delta }_y{v}_{ij}^n)\hfill \\ \hfill \le & -\frac{2}{3}{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_y{v}_{ij}^k,{\delta }_y{v}_{ij}^n)\le 0\hfill \end{array}$$

(32)

$$\begin{array}{cc}& {\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\mathcal{A}}_y{\delta }_x^2{v}_{ij}^k,v_{ij}^n)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}\left(\left(I+\frac{h_2^2}{12}{\delta }_y^2\right){\delta }_x^2{v}_{ij}^k,v_{ij}^n\right)\hfill \\ \hfill =& -{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_x{v}_{ij}^k,{\delta }_x{v}_{ij}^n)+\frac{h_2^2}{12}{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_y{\delta }_x{v}_{ij}^k,{\delta }_y{\delta }_x{v}_{ij}^n)\hfill \\ \hfill \le & -\frac{2}{3}{\tau }^{-\beta }\sum _{n=1}^N\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}({\delta }_x{v}_{ij}^k,{\delta }_x{v}_{ij}^n)\le 0\hfill \end{array}$$

(33)

$$\begin{array}{cc}& \sum _{n=1}^N({\mathcal{A}}_x{\mathcal{A}}_{y}g(v_{ij}^{n-\theta }),v_{ij}^n)+\sum _{n=1}^N({\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta },v_{ij}^n)\hfill \\ \hfill \le & \frac{1}{2}\sum _{n=1}^N\left|\right|g(v_{ij}^{n-\theta }){\left|\right|}_A^2+\frac{1}{2}\sum _{n=1}^N\left|\right|v_{ij}^n{\left|\right|}_A^2+\frac{1}{2}\sum _{n=1}^N\left|\right|f_{ij}^{n-\theta }{\left|\right|}_A^2+\frac{1}{2}\sum _{n=1}^N\left|\right|v_{ij}^n{\left|\right|}_A^2\hfill \\ \hfill \le & C\sum _{n=0}^N\left|\right|v_{ij}^n{\left|\right|}_A^2+C\sum _{n=0}^N\left|\right|f_{ij}^n{\left|\right|}_A^2.\hfill \end{array}$$

(34)

Ignoring the non-negative terms, we obtain

$$\begin{array}{c}\hfill \left|\right|v_{ij}^N{\left|\right|}_A^2\le 2\left|\right|v_{ij}^1{\left|\right|}_A^2+C\tau \sum _{n=0}^N\left|\right|v_N^n{\left|\right|}_A^2+C\tau \sum _{n=0}^N\left|\right|f_{ij}^n{\left|\right|}_A^2.\end{array}$$

(35)

Similarly, for $n=1$, with (21) and the Cauchy–Schwarz inequality, we have

$$\left|\right|v_{ij}^1{\left|\right|}^2\le C\tau \sum _{n=0}^1(||v_{ij}^n{\left|\right|}_A^2)+C\tau \sum _{n=0}^1(||f_{ij}^n{\left|\right|}_A^2).$$

(36)

Using Grönwall’s inequality, we obtain

$$\left|\right|v_{ij}^N{\left|\right|}_A^2\le C(\tau \sum _{n=0}^N\left|\right|f_{ij}^n{\left|\right|}_A^2).$$

(37)

where C is independent of n and $\tau$.

Finally, using the triangular inequality $\left|\right|u_{ij}^N{\left|\right|}_A\le \left|\right|v_{ij}^N{\left|\right|}_A+\left|\right|u_{ij}^0{\left|\right|}_A$, we obtain Theorem 1. □

Next, we prove the convergence of (21) and (22).

Theorem 2. 

Assume that $\left\{U_{ij}^n\right|(i,j)\in \overline{\omega },0\le n\le N\}$ is the exact solution of Equation (1). Let $\left\{u_{ij}^n\right|(i,j)\in \overline{\omega },0\le n\le N\}$ be the numerical solution of the fully discrete scheme. We have the error estimate

$$\begin{array}{cc}\hfill \left|\right|U_{ij}^n-u_{ij}^n{\left|\right|}_A& \le \tilde{C}{\tau }^2+C{\tau }^{\tilde{\sigma }-\frac{1}{2}}+C{\tau }^{\sigma -\alpha -1}+C{\tau }^{\sigma -\beta -1}+C(h_1^4+h_2^4),\hfill \end{array}$$

where C is independent of $n,h$ and τ.

Proof of Theorem 2. 

For simplicity, define $e_{ij}^n=U_{ij}^n-u_{ij}^n$. Note that $e_{ij}^0=0$. Using Equation (21) minus (23) and Equation (22) minus (24), we have

Case $n=1$:

$$\begin{array}{c}{\mathcal{A}}_x{\mathcal{A}}_y\frac{e_{ij}^1}{\tau }+{\tau }^{-\alpha }\sum _{k=0}^1{\omega }_{1-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^k={\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2{e}_{ij}^k\hfill \\ +{\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2{e}_{ij}^k+{\mathcal{A}}_x{\mathcal{A}}_y(g(U_{ij}^{1-\theta })-g(u_{ij}^{1-\theta }))+r_{ij}^1\hfill \end{array}$$

(38)

Case $n\ge 2$:

$$\begin{array}{c}\frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{n-2}\hfill \\ +{\tau }^{-\alpha }\sum _{k=0}^n{\omega }_{n-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^k={\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2{e}_{ij}^k\hfill \\ +{\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2{e}_{ij}^k+{\mathcal{A}}_x{\mathcal{A}}_y(g(U_{ij}^{n-\theta })-g(u_{ij}^{n-\theta }))+r_{ij}^n\hfill \end{array}$$

(39)

Both integrate $e_{ij}^n$, then replace n with l and sum l from 1 to n. We can obtain

$$\begin{array}{cc}& \frac{1}{\tau }\left({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^1,e_{ij}^1\right)+\frac{3-2\theta }{2\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^l,e_{ij}^l)\hfill \\ & -\frac{2-2\theta }{\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{l-1},e_{ij}^l)+\frac{1-2\theta }{2\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{l-2},e_{ij}^l)\hfill \\ & +{\tau }^{-\alpha }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\alpha )}({\mathcal{A}}_y{\delta }_x^2{e}_{ij}^k,e_{ij}^l)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\mathcal{A}}_x{\delta }_y^2{e}_{ij}^k,e_{ij}^l)+{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\mathcal{A}}_y{\delta }_x^2{e}_{ij}^k,e_{ij}^l)\hfill \\ & +\sum _{l=1}^n({\mathcal{A}}_x{\mathcal{A}}_y(g(U_{ij}^{l-\theta })-g(u_{ij}^{l-\theta })),e_{ij}^l)+\sum _{l=1}^n(r_{ij}^l,e_{ij}^l)\hfill \end{array}$$

(40)

$$\begin{array}{cc}& \frac{1}{\tau }\left({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^1,e_{ij}^1\right)+\frac{3-2\theta }{2\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^l,e_{ij}^l)\hfill \\ & -\frac{2-2\theta }{\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{l-1},e_{ij}^l)+\frac{1-2\theta }{2\tau }\sum _{l=2}^n({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^{l-2},e_{ij}^l)\hfill \\ \hfill \ge & \frac{1}{4\tau }\left|\right|e_{ij}^n{\left|\right|}_A^2-\frac{1}{2\tau }\left|\right|e_{ij}^1{\left|\right|}_A^2,\hfill \end{array}$$

(41)

$$\begin{array}{c}{\tau }^{-\alpha }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\alpha )}({\mathcal{A}}_x{\mathcal{A}}_y{e}_{ij}^k,e_{ij}^l)\ge 0,\hfill \end{array}$$

(42)

$$\begin{array}{cc}& {\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\mathcal{A}}_x{\delta }_y^2{e}_{ij}^k,e_{ij}^l)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}((I+\frac{h_1^2}{12}{\delta }_x^2){\delta }_y^2{e}_{ij}^k,e_{ij}^l)\hfill \\ \hfill =& -{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_y{e}_{ij}^k,{\delta }_y{e}_{ij}^l)+\frac{h_1^2}{12}{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_x{\delta }_y{e}_{ij}^k,{\delta }_x{\delta }_y{e}_{ij}^l)\hfill \\ \hfill \le & -\frac{2}{3}{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_y{e}_{ij}^k,{\delta }_y{e}_{ij}^l)\le 0,\hfill \end{array}$$

(43)

$$\begin{array}{cc}& {\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\mathcal{A}}_y{\delta }_x^2{e}_{ij}^k,e_{ij}^l)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}((I+\frac{h_2^2}{12}{\delta }_y^2){\delta }_x^2{e}_{ij}^k,e_{ij}^l)\hfill \\ \hfill =& -{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_x{e}_{ij}^k,{\delta }_x{e}_{ij}^l)+\frac{h_2^2}{12}{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_y{\delta }_x{e}_{ij}^k,{\delta }_y{\delta }_x{e}_{ij}^l)\hfill \\ \hfill \le & -\frac{2}{3}{\tau }^{-\beta }\sum _{l=1}^n\sum _{k=1}^l{\omega }_{l-k}^{(\beta )}({\delta }_x{e}_{ij}^k,{\delta }_x{e}_{ij}^l)\le 0,\hfill \end{array}$$

(44)

$$\begin{array}{cc}& \sum _{l=1}^n({\mathcal{A}}_x{\mathcal{A}}_y(g(U_{ij}^{l-\theta })-g(u_{ij}^{l-\theta })),e_{ij}^l)\hfill \\ \hfill \le & \frac{1}{2}\sum _{l=1}^n\left|\right|g(U_{ij}^{l-\theta })-g(u_{ij}^{l-\theta }){\left|\right|}_A^2+\frac{1}{2}\sum _{l=1}^n\left|\right|e_{ij}^l{\left|\right|}_A^2\hfill \\ \hfill \le & \frac{1}{2}\sum _{l=1}^n\left|\right|g^{\prime }{(\mu )\left|\right|}_A^2\left|\right|e_{ij}^{l-\theta }{\left|\right|}_A^2+\frac{1}{2}\sum _{l=1}^n\left|\right|e_{ij}^l{\left|\right|}_A^2\hfill \\ \hfill \le & C\sum _{l=0}^n\left|\right||e_{ij}^l{\left|\right|}_A^2.\hfill \end{array}$$

(45)

We know that

$$\tau \sum _{j=1}^n{t}_{j-\theta }^s=\left\{\begin{array}{cc}O(1),\hfill & s>-1\hfill \\ O(logn),\hfill & s=-1\hfill \\ O({\tau }^{1+s}),\hfill & s<-1\hfill \end{array}\right.$$

(46)

$$\begin{array}{c}\tau \sum _{l=1}^n\left|\right|E_{\tau ,\theta }^{(l)}{\left|\right|}^2\le {\tilde{E}}_{n-\theta }^{(1)}\hfill \\ :=C{\tau }^5\sum _{j=1}^n{t}_{j-\theta }^{2\tilde{\sigma }-6}=\left\{\begin{array}{ccc}& O({\tau }^4),\hfill & \tilde{\sigma }>2.5\hfill \\ & O({\tau }^{4}logn),\hfill & \tilde{\sigma }=2.5\hfill \\ & O({\tau }^{2\tilde{\sigma }-1}),\hfill & \tilde{\sigma }<2.5\hfill \end{array}\right.\hfill \end{array}$$

(47)

$$\begin{array}{c}\tau \sum _{l=1}^n\left|\right|E_{n-\theta }^{(\alpha )}{\left|\right|}^2\le {\tilde{E}}_{n-\theta }^{(2)}\hfill \\ :=C{\tau }^5\sum _{j=1}^n{t}_{j-\theta }^{2\sigma -2\alpha -4}=\left\{\begin{array}{ccc}& O({\tau }^4),\hfill & \sigma >\alpha +1.5\hfill \\ & O({\tau }^{4}logn),\hfill & \sigma =\alpha +1.5\hfill \\ & O({\tau }^{2\sigma -2\alpha +1}),\hfill & \sigma <\alpha +1.5\hfill \end{array}\right.\hfill \end{array}$$

(48)

$$\begin{array}{c}\tau \sum _{l=1}^n\left|\right|E_{n-\theta }^{(\beta )}{\left|\right|}^2\le {\tilde{E}}_{n-\theta }^{(3)}\hfill \\ :=C{\tau }^5\sum _{j=1}^n{t}_{j-\theta }^{2\sigma -2\beta -4}=\left\{\begin{array}{ccc}& O({\tau }^4),\hfill & \sigma >\beta +1.5\hfill \\ & O({\tau }^{4}logn),\hfill & \sigma =\beta +1.5\hfill \\ & O({\tau }^{2\sigma -2\beta +1}),\hfill & \sigma <\beta +1.5\hfill \end{array}\right.\hfill \end{array}$$

(49)

$$\begin{array}{cc}& \tau \sum _{l=1}^n(r_{ij}^l,e_{ij}^l)\hfill \\ \hfill =& \tau \sum _{l=1}^n(E_{\tau ,\theta }^{(l)},e_{ij}^l)+\tau \sum _{l=1}^n(E_{l-\theta }^{(\alpha )},e_{ij}^l)+\tau \sum _{l=1}^n(E_{l-\theta }^{(\beta )},e_{ij}^l)+\tau \sum _{l=1}^n(r_{ij},e_{ij}^l)\hfill \\ \hfill \le & \frac{\tau }{2}\sum _{l=1}^n\left|\right|E_{\tau ,\theta }^{(l)}{\left|\right|}^2+\frac{\tau }{2}\sum _{l=1}^n\left|\right|E_{l-\theta }^{(\alpha )}{\left|\right|}^2+\frac{\tau }{2}\sum _{l=1}^n\left|\right|E_{l-\theta }^{(\beta )}{\left|\right|}^2+\frac{\tau }{2}\sum _{l=1}^n\left|\right|r_{ij}{\left|\right|}^2+2\tau \sum _{l=1}^n\left|\right|e_{ij}^l{\left|\right|}^2\hfill \\ \hfill \le & {\tilde{E}}_{n-\theta }^{(1)}+{\tilde{E}}_{n-\theta }^{(2)}+{\tilde{E}}_{n-\theta }^{(3)}+C^2{(h_1^4+h_2^4)}^2+6\tau \sum _{l=1}^n\left|\right|e_{ij}^l{\left|\right|}_A^2,\hfill \end{array}$$

(50)

$$\begin{array}{c}\hfill \frac{1}{4}\left|\right|e_{ij}^n{\left|\right|}_A^2\le \frac{1}{2}\left|\right|e_{ij}^1{\left|\right|}_A^2+C\tau \sum _{l=0}^n\left|\right|e_{ij}^l{\left|\right|}_A^2+{\tilde{E}}_{n-\theta }^{(1)}+{\tilde{E}}_{n-\theta }^{(2)}+{\tilde{E}}_{n-\theta }^{(3)}+C^2{(h_1^4+h_2^4)}^2.\end{array}$$

(51)

For $n=1$, we can similarly derive that

$$(1-C\tau )\left|\right|e_{ij}^1{\left|\right|}_A^2\le C^2(h_1^4+h_2^4)+{\tilde{E}}_{1-\theta }^{(1)}+{\tilde{E}}_{1-\theta }^{(2)}+{\tilde{E}}_{1-\theta }^{(3)}.$$

(52)

Using Grönwall’s inequality, we obtain

$$\left|\right|e_{ij}^n{\left|\right|}_A^2\le \tilde{C}{\tau }^4+C{\tau }^{2\tilde{\sigma }-1}+C{\tau }^{2\sigma -2\alpha +1}+C{\tau }^{2\sigma -2\beta +1}+C^2{(h_1^4+h_2^4)}^2,$$

(53)

where C is independent of $n,h$ and $\tau$. $\tilde{C}$ is defined by

$$\tilde{C}=\left\{\begin{array}{cc}O(\sqrt{logn}),\hfill & \tilde{\sigma }=2.5\mathrm{or}\sigma =\alpha +1.5\mathrm{or}\sigma =\beta +1.5\hfill \\ O(1),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(54)

Finally, by using the triangle inequality, we obtain Theorem 2. □

5. Analysis for Non-Smooth Solutions

By reading references [30,31], we rewrite the approximation formula with correction terms.

$$\left\{\begin{array}{c}{D}_{0,t}^{\alpha }u(t_{n-\theta })\approx D_{\tau ,\alpha }^{n,\theta }u+{\tau }^{-\alpha }\sum _{l=1}^m{w}_{n,l}^{(\alpha )}(u^l-u^0),\hfill \\ D_{0,t}^{\beta }u(t_{n-\theta })\approx D_{\tau ,\beta }^{n,\theta }u+{\tau }^{-\beta }\sum _{l=1}^m{w}_{n,l}^{(\beta )}(u^l-u^0),\hfill \\ u_t(t_{n-\theta })\approx u_{\tau ,\theta }^n+{\tau }^{-1}\sum _{l=1}^m{w}_{n,l}^{(1)}(u^l-u^0),\hfill \end{array}\right.$$

(55)

where the correction terms can be obtained by solving the following linear systems:

$$\left\{\begin{array}{c}\sum _{l=1}^m{w}_{n,l}^{(\alpha )}{t}_l^{{\sigma }_r}={\tau }^{\alpha }\frac{\mathrm{\Gamma }({\sigma }_r+1)}{\mathrm{\Gamma }({\sigma }_r+1-\alpha )}{t}_{n-\theta }^{{\sigma }_r-\alpha }-\sum _{k=1}^n{\omega }_{n-k}^{(\alpha )}{t}_k^{{\sigma }_r},\hfill \\ \sum _{l=1}^m{w}_{n,l}^{(\beta )}{t}_l^{{\sigma }_r}={\tau }^{\beta }\frac{\mathrm{\Gamma }({\sigma }_r+1)}{\mathrm{\Gamma }({\sigma }_r+1-\beta )}{t}_{n-\theta }^{{\sigma }_r-\beta }-\sum _{k=1}^n{\omega }_{n-k}^{(\beta )}{t}_k^{{\sigma }_r},\hfill \\ \sum _{l=1}^m{w}_{1,l}^{(1)}{t}_l^{{\sigma }_r}=\tau {\sigma }_r{t}_{1-\theta }^{{\sigma }_r-1}-t_1^{{\sigma }_r},\hfill \\ \sum _{l=1}^m{w}_{n,l}^{(1)}{t}_l^{{\sigma }_r}=\tau {\sigma }_r{t}_{n-\theta }^{{\sigma }_r-1}-\frac{3-2\theta }{2}{t}_n^{{\sigma }_r}+(2-2\theta )t_{n-1}^{{\sigma }_r}-\frac{1-2\theta }{2}{t}_{n-2}^{{\sigma }_r},\hfill & n\ge 2\hfill \end{array}\right.$$

(56)

Combining (55), we rewrite the schemes (23) and (24) as follows:

Case $n=1$:

$$\begin{array}{cc}& {\mathcal{A}}_x{\mathcal{A}}_y\frac{u_{ij}^1-u_{ij}^0}{\tau }+{\tau }^{-1}\sum _{l=1}^m{w}_{1,l}^{(1)}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^l-u_{ij}^0)\hfill \\ & +{\tau }^{-\alpha }\sum _{k=0}^1{\omega }_{1-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^k-u_{ij}^0)+{\tau }^{-\alpha }\sum _{l=1}^m{w}_{n,l}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^l-u_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{l=1}^m{w}_{n,l}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^l-u_{ij}^0)\hfill \\ & +{\tau }^{-\beta }\sum _{k=0}^1{\omega }_{1-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{l=1}^m{w}_{n,l}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^l-u_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{1-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{1-\theta },\hfill \end{array}$$

(57)

Case $n\ge 2$:

$$\begin{array}{cc}& \frac{3-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^n-\frac{2-2\theta }{\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-1}+\frac{1-2\theta }{2\tau }{\mathcal{A}}_x{\mathcal{A}}_y{u}_{ij}^{n-2}\hfill \\ & +{\tau }^{-1}\sum _{l=1}^m{w}_{n,l}^{(1)}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^l-u_{ij}^0)+{\tau }^{-\alpha }\sum _{k=0}^n{\omega }_{n-k}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^k-u_{ij}^0)\hfill \\ & +{\tau }^{-\alpha }\sum _{l=1}^m{w}_{n,l}^{(\alpha )}{\mathcal{A}}_x{\mathcal{A}}_y(u_{ij}^l-u_{ij}^0)\hfill \\ \hfill =& {\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{l=1}^m{w}_{n,l}^{(\beta )}{\mathcal{A}}_x{\delta }_y^2(u_{ij}^l-u_{ij}^0)\hfill \\ & +{\tau }^{-\beta }\sum _{k=0}^n{\omega }_{n-k}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^k-u_{ij}^0)+{\tau }^{-\beta }\sum _{l=1}^m{w}_{n,l}^{(\beta )}{\mathcal{A}}_y{\delta }_x^2(u_{ij}^l-u_{ij}^0)\hfill \\ & +{\mathcal{A}}_x{\mathcal{A}}_y{g}_{ij}^{n-\theta }+{\mathcal{A}}_x{\mathcal{A}}_y{f}_{ij}^{n-\theta }.\hfill \end{array}$$

(58)

5.1. Fast Algorithm

We can obtain the following formula by referring to [29,32].

$$\begin{array}{cc}& {\tau }^{-\alpha }\sum _{n=0}^{\infty }{\omega }_n^{(\alpha )}{\xi }^n={\tau }^{-\alpha }\omega (\xi ,\alpha )\hfill \\ \hfill =& F_{\alpha }(\frac{1-\xi }{\tau })=\frac{1}{2\pi i}{\int }_C{\left(\frac{1-\xi }{\tau }-\lambda \right)}^{-1}{F}_{\alpha }(\lambda )\mathrm{d}\lambda \hfill \end{array}$$

(59)

We define $e_n(z)$ such that

$$\sum _{n=0}^{\infty }{e}_n(z){\xi }^n:={(1-\xi -z)}^{-1}$$

(60)

Then, we can obtain

$${\omega }_n^{(\alpha )}=\frac{{\tau }^{\alpha +1}}{2\pi i}{\int }_C{e}_n(\tau \lambda )F_{\alpha }(\lambda )\mathrm{d}\lambda$$

(61)

(60) also shows that

$$e_n(z)=q(z)r{(z)}^n,$$

(62)

where $r(z)=\frac{1}{1-z},q(z)=\frac{1}{1-z}$.

We choose base B, and $[0,T]$ is divided into a series of small intervals $I_l$ as follows:

$$I_l=[B^{l-1}\tau ,(2B^l-2)\tau ].$$

(63)

where B is an integer.

Next, we need to find the approximate formula for (61). In particular, we choose the Talbot contour as the integral pat. The Talbot contour is given as

$$(-\pi ,\pi )\to C:\vartheta \mapsto \varrho (\vartheta )=\frac{K}{T_l}((\vartheta cot(\vartheta )+ik\vartheta )v+\sigma ),$$

(64)

where $T_l=(2B^l-2)\tau ,k,v,\sigma$ are parameters that we decided for ourselves. Here, we choose $k=0.5653,v=0.6443,\sigma =-0.4814$ [29]. For the selection of parameters, readers can refer to [33] for more details.

The integral along the Talbot contour C, (61) can be approximated as

$${\omega }_n^{(\alpha )}\approx {\tau }^{\alpha +1}\sum _{j=-K}^K{w}_j^{(l)}{e}_n(\tau {\lambda }_j^{(l)})F_{\alpha }({\lambda }_j^{(l)}),n\tau \in I_l$$

(65)

where the weights $w_j^{(l)}$ and quadrature points ${\lambda }_j^{(l)}$ are given by

$$w_j^{(l)}=-\frac{i}{2(K+1)}{\varrho }^{\prime }({\vartheta }_j),{\lambda }_j^{(l)}=\varrho ({\vartheta }_j),{\vartheta }_j=\frac{j\pi }{K+1}.$$

(66)

The choice of K has an effect on the approximation of (61). Generally, the larger the K selected, the better the approximation between different small intervals $I_l$.

Since (63) overlaps the adjacent interval $I_l$, $L-1$ points $b_l$ are introduced to divide the interval $[0,n\tau ]$. $b_l$ satisfy

$$n=b_0>b_1>b_2>\cdots >b_{L-1}>b_L=0,$$

(67)

and $[(n-b_{l-1}+1)\tau ,(n-b_l)\tau ]\subset I_l$. L is the smallest integer such that $n+2\le 2B^L$.

Now, we can rewrite the approximation Formula (16) with $b_l$ as follows

$$D_{\tau ,\alpha }^{n,\theta }u={\tau }^{-\alpha }{\omega }_0^{(\alpha )}(u^n-u^0)+{\tau }^{-\alpha }\sum _{l=1}^L\sum _{k=b_l}^{b_{l-1}-1}{\omega }_{n-k}^{(\alpha )}(u^k-u^0).$$

(68)

For convenience, we define $v_{n,\alpha }^{(l)}$ as

$$v_{n,\alpha }^{(l)}=\left\{\begin{array}{cc}{\tau }^{-\alpha }{\omega }_0^{(\alpha )}(u^n-u^0),\hfill & l=0,\hfill \\ {\tau }^{-\alpha }\sum _{k=b_l}^{b_{l-1}-1}{\omega }_{n-k}^{(\alpha )}(u^k-u^0),\hfill & l=1,2,\cdots ,L.\hfill \end{array}\right.$$

(69)

Combining (62) and (65), we can obtain

$$\begin{array}{cc}\hfill v_{n,\alpha }^{(l)}\approx & \sum _{j=-K}^K{w}_j^{(l)}\left[\tau \sum _{k=b_l}^{b_{l-1}-1}{e}_{n-k}(\tau {\lambda }_j^{(l)})(u^k-u^0)\right]F_{\alpha }({\lambda }_j^{(l)})\hfill \\ \hfill =& \sum _{j=-K}^K{w}_j^{(l)}\left[\tau \sum _{k=b_l}^{b_{l-1}-1}q(\tau {\lambda }_j^{(l)})r{(\tau {\lambda }_j^{(l)})}^{n-k-1}(u^k-u^0)\right]F_{\alpha }({\lambda }_j^{(l)})\hfill \\ \hfill =& \sum _{j=-K}^K{w}_j^{(l)}\tau e_{n-b_{l-1}+2}\left[\sum _{k=b_l}^{b_{l-1}-1}r{(\tau {\lambda }_j^{(l)})}^{b_{l-1}-2-k}(u^k-u^0)\right]F_{\alpha }({\lambda }_j^{(l)})\hfill \\ \hfill =& \sum _{j=-K}^K{w}_j^{(l)}\tau e_{n-b_{l-1}+2}{y}_j^{(i)}{F}_{\alpha }({\lambda }_j^{(l)})\hfill \end{array}$$

(70)

where $y_j$ is

$$y_j=y_j(b_l,b_{l-1},{\lambda }_j^{(l)})=\sum _{k=b_l}^{b_{l-1}-1}r{(\tau {\lambda }_j^{(l)})}^{b_{l-1}-2-k}(u^k-u^0).$$

(71)

Because $y_j$ has a recursive structure, (71) can be rewritten as

$$\begin{array}{cc}\hfill y_j(b_l,b_s,{\lambda }_j^{(l)})=& \sum _{k=b_l}^{b_m-1}r{(\tau {\lambda }_j^{(l)})}^{b_s-2-k}(u^k-u^0)+y_j(b_m,b_s,{\lambda }_j^{(l)})\hfill \\ \hfill =& r{(\tau {\lambda }_j^{(l)})}^{b_s-b_m}{y}_j(b_l,b_m,{\lambda }_j^{(l)})+y_j(b_m,b_s,{\lambda }_j^{(l)}).\hfill \end{array}$$

(72)

The first few weights cannot be accurately approximated by (65) [18,23,34]; thus, introduce an integer M to denote the first weights computed by (17). Then, the fast algorithm can be summarized as follows:

$$\begin{array}{cc}\hfill D_{\tau ,\gamma }^{n,\theta }u& =\sum _{l=0}^M{v}_{n,\gamma }^{(l)}+\sum _{l=M+1}^L{v}_{n,\gamma }^{(l)}\hfill \\ & \approx \sum _{l=0}^M{v}_{n,\gamma }^{(l)}+\sum _{l=M+1}^L\sum _{j=-K}^K{w}_j^{(l)}{r}_0^{n-(b_{l-1}-1)}(\tau {\lambda }_j^{(l)})y_j^{(0)}{F}_{\alpha }({\lambda }_j^{(l)})\hfill \end{array}$$

(73)

5.2. Numerical Experiments

Case 1: We consider (1) with homogeneous initial condition ${\mathrm{\Phi }}_1(x,y)=0,{\mathrm{\Phi }}_2(x,y)=0$.

Its exact solution is $u(x,y,t)=t^{4}sin(\pi x)sin(\pi y)$, the nonlinear term is $g(u)=u^2$ and the responding forcing term is $f(x,y,t)=(4t^3+\frac{\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\alpha )}{t}^{4-\alpha }+\frac{2{\pi }^2\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\beta )}{t}^{4-\beta }-t^{8}sin(\pi x)$$sin(\pi y))sin(\pi x)sin(\pi y)$. The corresponding results are given in Table 1 and Table 2. We also present the pictures of the numerical solution and exact solution with $t=1,\alpha =0.7$, $\beta =0.8,\theta =0.2,\tau =1/320,h_1=h_2=1/50$ in Figure 1.

Table 1. Errors and temporal convergence orders with $h_1=h_2=\frac{1}{50}$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\theta })$	$\mathit{\tau }$	${\left|\right|\mathit{E}(\mathit{\tau })\left|\right|}_2$	Order	${\left|\right|\mathit{E}(\mathit{\tau })\left|\right|}_{\mathit{\infty }}$	Order
(0.1, 0.2, 0.7)	$1/20$	3.2036 $\times {10}^{-1}$		$1.2815\times {10}^{-2}$
	$1/40$	$8.3145\times {10}^{-2}$	1.95	$3.3258\times {10}^{-3}$	1.95
	$1/80$	$2.1174\times {10}^{-2}$	1.97	$8.4695\times {10}^{-4}$	1.97
	$1/160$	$5.3414\times {10}^{-3}$	1.99	$2.1366\times {10}^{-4}$	1.99
	$1/320$	$1.3405\times {10}^{-3}$	1.99	$5.3620\times {10}^{-5}$	1.99
(0.4, 0.5, 0.4)	$1/20$	$7.2448\times {10}^{-2}$		$2.8979\times {10}^{-3}$
	$1/40$	$1.8434\times {10}^{-2}$	1.98	$7.3735\times {10}^{-4}$	1.98
	$1/80$	$4.6481\times {10}^{-3}$	1.99	$1.8592\times {10}^{-4}$	1.99
	$1/160$	$1.1661\times {10}^{-3}$	2.00	$4.6643\times {10}^{-5}$	2.00
	$1/320$	$2.9110\times {10}^{-4}$	2.00	$1.1644\times {10}^{-5}$	2.00
(0.7, 0.8, 0.2)	$1/20$	$3.7499\times {10}^{-2}$		$1.4999\times {10}^{-3}$
	$1/40$	$9.5613\times {10}^{-3}$	1.97	$3.8245\times {10}^{-4}$	1.97
	$1/80$	$2.4149\times {10}^{-3}$	1.99	$9.6597\times {10}^{-5}$	1.99
	$1/160$	$6.0778\times {10}^{-4}$	1.99	$2.4311\times {10}^{-5}$	1.99
	$1/320$	$1.5341\times {10}^{-4}$	1.99	$6.1364\times {10}^{-6}$	1.99

Table 2. Errors and spatial convergence orders with $\tau =\frac{1}{4000},\alpha =\beta$ and $\theta =\frac{\alpha }{2}$.

$(\mathit{\alpha })$	h	Order	${\left|\right|\mathit{E}(\mathit{h})\left|\right|}_{\mathit{\infty }}$
0.5	$1/5$	5.1624 × ${10}^{-4}$
	$1/10$	$3.5246\times {10}^{-5}$	3.87
	$1/20$	$2.1883\times {10}^{-6}$	4.01
	$1/40$	$1.2850\times {10}^{-7}$	4.09
0.8	$1/5$	$5.3326\times {10}^{-4}$
	$1/10$	$3.6395\times {10}^{-5}$	3.87
	$1/20$	$2.2463\times {10}^{-6}$	4.02
	$1/40$	$1.1864\times {10}^{-7}$	4.24
0.2	$1/5$	$4.9280\times {10}^{-4}$
	$1/10$	$3.3663\times {10}^{-5}$	3.87
	$1/20$	$2.1062\times {10}^{-6}$	4.00
	$1/40$	$1.3998\times {10}^{-7}$	3.91

Figure 1. Numerical solution and exact solution for Case 1 at the final time $t=1$ with $\alpha =0.7$, $\beta =0.8,\theta =0.2,\tau =1/320,h_1=h_2=1/50$. (a) Numerical solution. (b) Exact solution.

Case 2: We consider (1) with non-homogeneous initial condition ${\mathrm{\Phi }}_1(x,y)=sin(\pi x)sin(\pi y),$${\mathrm{\Phi }}_2(x,y)=0$. Its exact solution is $u(x,y,t)=(t^4+1)sin(\pi x)sin(\pi y)$, the nonlinear term is $g(u)=u^2$ and the responding forcing term is $f(x,y,t)=(4t^3+\frac{\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\alpha )}{t}^{4-\alpha }+\frac{2{\pi }^2\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\beta )}{t}^{4-\beta }-(t^8+2t^4+1)sin(\pi x)sin(\pi y))sin(\pi x)sin(\pi y)$.

The responding results are shown in Table 3. We present the pictures of the numerical solution and exact solution with $t=1,\alpha =0.7,\beta =0.8,\theta =0.2,\tau =1/320$, $h_1=h_2=1/50$ in Figure 2. We can see that the numerical scheme is still applicable to the equations with initial conditions, which reflects the stability of our method.

Table 3. Errors and temporal convergence orders with $h_1=h_2=\frac{1}{50}$ for non-homogeneous initial condition.

$(\mathit{\alpha },\mathit{\beta },\mathit{\theta })$	$\mathit{\tau }$	${\left|\right|\mathit{E}(\mathit{\tau })\left|\right|}_2$	Order	${\left|\right|\mathit{E}(\mathit{\tau })\left|\right|}_{\mathit{\infty }}$	Order
(0.1, 0.2, 0.7)	$1/20$	3.2036 × ${10}^{-1}$		$1.2815\times {10}^{-2}$
	$1/40$	$8.3145\times {10}^{-2}$	1.95	$3.3258\times {10}^{-3}$	1.95
	$1/80$	$2.1174\times {10}^{-2}$	1.97	$8.4695\times {10}^{-4}$	1.97
	$1/160$	$5.3414\times {10}^{-3}$	1.99	$2.1366\times {10}^{-4}$	1.99
	$1/320$	$1.3405\times {10}^{-3}$	1.99	$5.3620\times {10}^{-5}$	1.99
(0.4, 0.5, 0.4)	$1/20$	$7.2448\times {10}^{-2}$		$2.8979\times {10}^{-3}$
	$1/40$	$1.8434\times {10}^{-2}$	1.98	$7.3735\times {10}^{-4}$	1.98
	$1/80$	$4.6481\times {10}^{-3}$	1.99	$1.8592\times {10}^{-4}$	1.99
	$1/160$	$1.1661\times {10}^{-3}$	2.00	$4.6643\times {10}^{-5}$	2.00
	$1/320$	$2.9110\times {10}^{-4}$	2.00	$1.1644\times {10}^{-5}$	2.00
(0.7, 0.8, 0.2)	$1/20$	$3.7499\times {10}^{-2}$		$1.4999\times {10}^{-3}$
	$1/40$	$9.5613\times {10}^{-3}$	1.97	$3.8245\times {10}^{-4}$	1.97
	$1/80$	$2.4149\times {10}^{-3}$	1.99	$9.6597\times {10}^{-5}$	1.99
	$1/160$	$6.0778\times {10}^{-4}$	1.99	$2.4311\times {10}^{-5}$	1.99
	$1/320$	$1.5341\times {10}^{-4}$	1.99	$6.1364\times {10}^{-6}$	1.99

Figure 2. Numerical solution and exact solution for Case 2 at the final time $t=1$ with $\alpha =0.7$, $\beta =0.8,\theta =0.2,\tau =1/320,h_1=h_2=1/50$. (a) Numerical solution. (b) Exact solution.

Case 3: We consider the (1) with homogeneous initial condition ${\mathrm{\Phi }}_1(x,y)=0,{\mathrm{\Phi }}_2(x,y)=0$. Its exact solution is $f(x,y,t)=(4t^3+\frac{2}{3}{t}^{\frac{1}{2}}+\frac{\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\alpha )}{t}^{4-\alpha }+\frac{\mathrm{\Gamma }(\frac{5}{2})}{\mathrm{\Gamma }(\frac{5}{2}-\alpha )}{t}^{\frac{3}{2}-\alpha }+\frac{2{\pi }^2\mathrm{\Gamma }(5)}{\mathrm{\Gamma }(5-\beta )}{t}^{4-\beta }+\frac{2{\pi }^2\mathrm{\Gamma }(\frac{5}{2})}{\mathrm{\Gamma }(\frac{5}{2}-\beta )}{t}^{\frac{3}{2}-\beta }-(t^8+t^3)sin(\pi x)sin(\pi y))sin(\pi x)sin(\pi y)$.

Table 4 compares the results using (21), (22) and (57), (58). The standard method in Table 4 refers to the method solved directly by using the compact scheme. Because the solution has weak regularity, the convergence accuracy is not optimal and, with correction terms, it is better than the results of scheme (21) and (22).

Table 4. Temporal convergence orders with $h_1=h_2=\frac{1}{40}$.

$(\mathit{\alpha },\mathit{\beta },\mathit{\theta })$	$\mathit{\tau }$	Standard	Order	Correction	Order
(0.6, 0.7, 0.2)	$1/20$	0.0015		0.0014
	$1/40$	3.9957 $\times {10}^{-4}$	1.94	$3.6003\times {10}^{-4}$	1.99
	$1/80$	$1.0451\times {10}^{-4}$	1.93	$8.9871\times {10}^{-5}$	2.00
	$1/160$	$2.7687\times {10}^{-5}$	1.92	$2.2446\times {10}^{-5}$	2.00
(0.4, 0.5, 0.2)	$1/20$	$5.2178\times {10}^{-4}$		$4.6290\times {10}^{-4}$
	$1/40$	$1.4013\times {10}^{-4}$	1.90	$1.1713\times {10}^{-4}$	1.98
	$1/80$	$3.8036\times {10}^{-5}$	1.88	$2.9186\times {10}^{-5}$	2.00
	$1/160$	$1.0677\times {10}^{-5}$	1.83	$7.2925\times {10}^{-6}$	2.00
(0.1, 0.3, 0.1)	$1/20$	$8.5825\times {10}^{-4}$		$7.4914\times {10}^{-4}$
	$1/40$	$2.2442\times {10}^{-4}$	1.94	$1.8595\times {10}^{-4}$	2.01
	$1/80$	$5.8913\times {10}^{-5}$	1.93	$4.5577\times {10}^{-5}$	2.03
	$1/160$	$1.5787\times {10}^{-5}$	1.90	$1.1222\times {10}^{-5}$	2.02

Case 4: We consider the (1) with homogeneous initial condition ${\mathrm{\Phi }}_1(x)=0,{\mathrm{\Phi }}_2(x)=0$. Its exact solution and the responding forcing term are the same as with the first case. We use $u_{i,j_S}^n$ for numerical solutions obtained by the standard method and $u_{i,j_F}^n$ for numerical solutions obtained by the fast algorithm. We calculate the pointwise error

$$E(\alpha ,N)=\underset{(i,j)\in \omega ,0\le n\le N}{max}|u_{i,j_S}^n-u_{i,j_F}^n|$$

(74)

for ${\mathrm{Fast}}_{10}$ and ${\mathrm{Fast}}_{30}$, where ${\mathrm{Fast}}_{10}$ and ${\mathrm{Fast}}_{30}$ represent $K=10$ and $K=30$ in (73), respectively. The results are shown in Table 5. We plot the numerical solutions obtained by the standard method and the fast algorithm at $\alpha =0.2,N=4000,K=30$, as shown in Figure 3, and the contours of pointwise error are given in Figure 4. We can clearly see that, when the time division is dense enough, the fast algorithm can reduce the calculation time and ensure the accuracy of the calculation results.

Table 5. Pointwise error with $\alpha =\beta$ and $\theta =\frac{\alpha }{2}$.

$\mathit{\alpha }$	N	Standard	Fast10	$\mathit{E}(\mathit{\alpha },\mathit{N})$	Fast30	$\mathit{E}(\mathit{\alpha },\mathit{N})$
$0.5$	$1\times {10}^3$	34.27 s	8.37 s	2.8207 $\times {10}^{-5}$	14.23 s	9.3092 $\times {10}^{-13}$
	$2\times {10}^3$	242.69 s	20.76 s	4.4986 $\times {10}^{-5}$	35.83 s	1.2712 $\times {10}^{-12}$
	$3\times {10}^3$	768.54 s	35.68 s	5.6412 $\times {10}^{-5}$	61.05 s	1.5155 $\times {10}^{-12}$
	$4\times {10}^3$	1807.78 s	54.05 s	6.7789 $\times {10}^{-5}$	87.66 s	1.7977 $\times {10}^{-12}$
$0.8$	$1\times {10}^3$	37.95 s	8.65 s	4.7046 $\times {10}^{-5}$	14.96 s	4.6401 $\times {10}^{-8}$
	$2\times {10}^3$	245.22 s	20.51 s	1.4745 $\times {10}^{-4}$	33.84 s	7.1265 $\times {10}^{-12}$
	$3\times {10}^3$	795.33 s	35.41 s	2.1211 $\times {10}^{-4}$	56.39 s	9.9941 $\times {10}^{-12}$
	$4\times {10}^3$	1880.17 s	53.69 s	2.7975 $\times {10}^{-4}$	80.75 s	1.2794 $\times {10}^{-11}$
$0.2$	$1\times {10}^3$	34.06 s	8.38 s	1.5528 $\times {10}^{-5}$	13.57 s	1.1113 $\times {10}^{-13}$
	$2\times {10}^3$	233.63 s	20.01 s	2.3424 $\times {10}^{-5}$	34.49 s	1.1524 $\times {10}^{-13}$
	$3\times {10}^3$	752.88 s	33.42 s	2.4674 $\times {10}^{-5}$	60.22 s	1.2723 $\times {10}^{-13}$
	$4\times {10}^3$	1754.31 s	51.04 s	3.0534 $\times {10}^{-5}$	87.92 s	1.2524 $\times {10}^{-13}$

Figure 3. Numerical solution for Case 4 at the final time $t=1$ with $\alpha =0.2,N=4000,K=30$. (a) Numerical solution by standard method. (b) Numerical solution by fast algorithm.

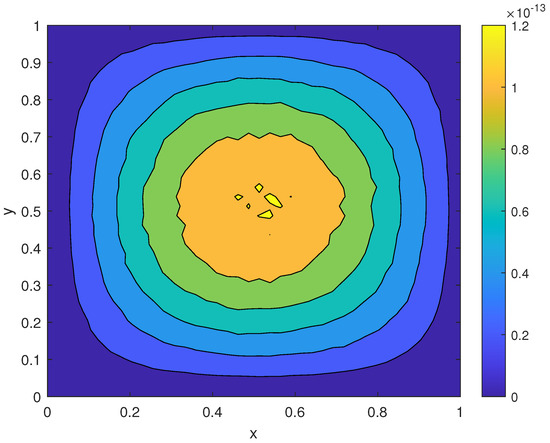
Figure 4. Contours of pointwise error for Case 4 at the final time $t=1$ with $\alpha =0.2,N=4000,K=30$.

6. Conclusions

In this study, we developed a compact scheme combining the fast time stepping method for solving fractional nonlinear subdiffusion equations. To overcome the weak regularity of nonsmooth solutions, we added the correction terms to recover the optimal convergence accuracy. We had the stability analysis for Equation (1) and gave a sharp estimate. Several numerical experiments were implemented to validate the theoretical results and confirm the efficiency and accuracy of the fast algorithm. In the future, we will use fast algorithms to solve systems composed of fractional differential equations, possibly in three dimensions. We will explore more efficient approximations for fractional operators.