Fractional View Study of the Brusselator Reaction–Diffusion Model Occurring in Chemical Reactions

Abstract

In this paper, we study a fractional Brusselator reaction–diffusion model with the help of the residual power series transform method. Specific reaction–diffusion chemical processes are modeled by applying the fractional Brusselator reaction–diffusion model. It should be mentioned that many problems in nonlinear science are characterized by fractional differential equations, where an unknown term occurs when a fractional-order derivative is operating on it. The analytic method of this problem is rarely discussed in the literature, despite numerous scholars having researched its application and usefulness. To validate our proposed method’s accuracy, we compare the numerical results of the residual power series transform method and the exact result with different fractional orders. The solution shows that the introduced approach is a good tool for solving linear and nonlinear fractional system differential equations. Finally, we provide two and three-dimensional graphical plots to support the impact of the fractional derivative on the behavior of the achieved profile results to the proposed equations.

1. Introduction

Fractional calculus, which includes fractional order derivatives and fractional integrals, has attracted interest in the areas of natural sciences and technology due to its vast implementations in electromagnetic waves, viscoelasticity, diffusion of biological population, nanotechnology, image and signal processing, random walk, control theory of dynamical systems, anomalous transport, and anomalous diffusion [1,2,3]. Nonlinear ordinary and partial differential equations (PDEs) are used to represent the majority of real-world scientific and engineering phenomena [4]. In the mathematical modeling of numerous natural phenomena, fractional nonlinear differential equations are particularly helpful. The essential quality of fractional derivatives is their nonlocality, which emphasizes the fact that the future state derives from the current state and all prior states. The study of nonlinear ordinary differential equations is required to observe the behavior of a system. However, evaluating the analytical solution for these types of situations is difficult. As a result, they are dealt with by utilizing approximate numeric techniques [5,6,7].

Chemical reactions play an essential function, as shown by the Brusselsator reaction–diffusion system. The reaction terms in this model come from the modeling of the chemical structures, which includes plasma and laser physics, enzyme reactions, and other processes. This nonlinear partial differential equation develops since chemical reactions involve two unstable intermediates with controllable output and input compounds. Ozone generation by atomic oxygen is one of the physical issues the Brusselsator reaction–diffusion system solves. Specific chemical reaction–diffusion processes are modeled using the fractional Brusselator reaction–diffusion system. It should be mentioned that many models in nonlinear science are characterized by fractional differential equations, where an unknown function occurs when a fractional-order derivative is operating on it. The approximate analysis of this system is rarely discussed in the literature, despite numerous scholars having researched its application and usefulness [8,9,10,11]. Recently, the development of numerical schemes for the numerical solutions of reaction–diffusion Brusselator systems has received considerable attention, such as the decomposition method [12,13], the finite-difference method [14], the Runge–Kutta–Chebyshev technique [15], the dual-reciprocity boundary element technique [16], the differential quadrature technique [17], the collocation technique applying the radial basis function [18], the homotopy perturbation method [19], the residual power series method [20] and the variational iteration method [21].

The residual power series method is a semianalytical tool for investigating many types of fuzzy, partial, ordinary, and fractional-order integrodifferential problems. It is an effective optimization method, since it delivers solutions in the closed type of available features. Various fractional differential and integral equations and fuzzy fractional differential equations have been effectively solved using the residual power series technique, for example, the Newell–Whitehead–Segel fractional order equations [22] and the fractional Fokker–Planck equations [23]. Researchers have coupled the fractional resonant Schrodinger equation [24], massive fractional Thirring and Kundu–Eckhaus problems [25], and particular categories of fractional fuzzy differential equations [26,27]. The Yang transform (YT), which Xiao-Jun Yang introduced, can be used to resolve a variety of differential equations with constant coefficients. This article aims to analyze the analytic and approximated solution for a nonlinear system’s fractional partial differential equations by applying the residual power series transform method. The residual power series transform method is a combination of the Yang transformation and the residual power series method, which provides the analytical results as a easily fractional power series solution by converting the suggested problems to Yang space and creating the results for the equations. Finally, the result can be achieved by the inverse Yang transform of the achieved solutions. Using the limit concept, the unknown coefficients in a Yang expansion can be determined, as opposed to the residual power series transform method, which relies on the fractional derivative and may require time to determine the fractional derivatives to identify the results. The residual power series transform method requires fewer processing resources and less time and provides more precision.

This work is arranged as follows: Section 2 contains some useful basic definitions of the Yang transform. The suggested method is explained in terms of achieving the results for the fractional partial differential equations schemes in Section 3. In Section 4, numerical solutions are presented for some problems. Lastly, concluding remarks are drawn in Section 2.

2. Preliminaries

This section is concerned with the fundamental concept of fractional calculus along with the Yang transform theory.

2.1. Definition

The fractional Caputo derivative is given as [28]

$$\begin{array}{cc}\hfill & D_{\vartheta }^{\wp }U(\mathfrak{y},\vartheta )=\frac{1}{\mathsf{\Gamma }(k-\wp )}{\int }_0^{\vartheta }{(\vartheta -\wp )}^{k-\wp -1}{U}^{(k)}(\mathfrak{y},\wp )d\wp ,k-1<\wp \le k,k\in N.\hfill \end{array}$$

(1)

2.2. Definition

The Yang transform is stated as [28]

$$Y\left\{U(\vartheta )\right\}=M(u)={\int }_0^{\infty }{e}^{\frac{-\vartheta }{u}}U(\vartheta )d\vartheta ,\vartheta >0,u\in (-{\vartheta }_1,{\vartheta }_2),$$

(2)

and the inverse Yang transform is

$$Y^{-1}\left\{M(u)\right\}=U(\vartheta ).$$

(3)

2.3. Definition

The nth derivative Yang transform is stated as [28]

$$Y\left\{U^n(\vartheta )\right\}=\frac{M(u)}{u^n}-\sum _{k=0}^{n-1}\frac{U^k(0)}{u^{n-k-1}},\forall n=1,2,3,\dots$$

(4)

2.4. Definition

The Yang transform in connection with the fractional-order derivative is stated as [28]

$$Y\left\{U^{\wp }(\vartheta )\right\}=\frac{M(u)}{u^{\wp }}-\sum _{k=0}^{n-1}\frac{U^k(0)}{u^{\wp -(k+1)}},n-1<\wp \le n.$$

(5)

3. Methodology

In this section, we present the suggested methodology of the fractional partial differential equations [29]

$$\begin{array}{cc}\hfill D_{\tau }^{\wp }{\omega }_1(\phi ,\tau )& ={\aleph }_1\left({\omega }_1,{\omega }_2,\dots ,{\omega }_m\right)+f_1(\phi ,\tau )\hfill \\ \hfill D_{\tau }^{\wp }{\omega }_2(\phi ,\tau )& ={\aleph }_2\left({\omega }_1,{\omega }_2,\dots ,{\omega }_m\right)+f_2(\phi ,\tau )\hfill \\ \hfill ⋮& \\ \hfill D_{\tau }^{\wp }{\omega }_m(\phi ,\tau )& ={\aleph }_m\left({\omega }_1,{\omega }_2,\dots ,{\omega }_m\right)+f_m(\phi ,\tau )\hfill \end{array}$$

(6)

subject to:

$${\omega }_i(\phi ,0)=g_i(\phi ),i=1,2,\dots ,m,$$

(7)

where $D_{\tau }^{\wp }$ refers to the $\mathrm{CD}$ of order $\wp ,\wp \in (0,1],{\aleph }_i,i=$$1,2,\dots ,m$ are well-known nonlinear analytic functions, and $f_i,i=1,2,\dots ,m$ can be represented as

Now, the technique for the RPSM solution of the fractional partial differential equations in (6) and (7) can be constructed through the following steps.

Step 1. We write the fractional nonlinear differential equation as in Equations (6) and (7) in the following short form:

$$D_{\tau }^{\wp }{\omega }_j(\phi ,\tau )-{\aleph }_j\left({\omega }_1,{\omega }_2,\dots ,{\omega }_m\right)-f_j(\phi ,\tau )=0,j=1,2,\dots ,m,$$

(8)

subject to:

$${\omega }_j(\phi ,0)=g_j(\phi ),j=1,2,\dots ,m.$$

(9)

Step 2. Applying the Yang transform to both sides of Equation (8), it becomes:

$$W_j(\phi ,s)-s{\omega }_j(\phi ,0)-s^{\wp }{N}_j(\phi ,s)-s^{\wp }{F}_j(\phi ,s)=0,$$

(10)

where $W_j(\phi ,s)={\mathcal{Y}}_{\tau }\left[{\omega }_j(\phi ,\tau )\right],N_j(\phi ,s)={\mathcal{Y}}_{\tau }\left[{\mathbf{N}}_j\left({\omega }_1,{\omega }_2\right.\right.$, $\left.\left.\dots ,{\omega }_m\right)\right]$, and $F_j(\phi ,s)={\mathcal{Y}}_{\tau }\left[f_j(\phi ,\tau )\right]$.

Step 3. Suppose that the solutions of fractional partial differential equations in Equation (10) are in the form:

$$W_j(\phi ,s)=\sum _{n=0}^{\infty }{s}^{n\wp +1}{g}_{jn}(\phi ),s>0,j=1,2,\dots ,m.$$

(11)

Applying Equation (9), we have $g_j(\phi )={\omega }_j(\phi ,0)={lim}_{s\to \infty }s{W}_j(\phi ,s)=g_{j0}(\phi )$. Therefore, the series form solutions can be represented as:

$$W_j(\phi ,s)=s{g}_j(\phi )+\sum _{n=1}^{\infty }{s}^{n\wp +1}{g}_{jn}(\phi ),s>0,j=1,2,\dots ,m.$$

(12)

Step 4. We define the k th-truncated series of $W_j(\phi ,s)$ as follows:

$$W_j^k(\phi ,s)=s{g}_j(\phi )+\sum _{n=1}^k{s}^{n\phi +1}{g}_{jn}(\phi ),s>0j=1,2,\dots ,m.$$

(13)

Step 5. We define the Yang residual functions of Equation (10) and the k th-Yang residual functions, respectively, as follows:

$${\mathcal{Y}\mathrm{Res}}_j(\phi ,s)=W_j(\phi ,s)-s{\omega }_j(\phi ,0)-s^{\wp }{N}_j(\phi ,s)-s^{\wp }{F}_j(\phi ,s).$$

(14)

$${\mathcal{Y}\mathrm{Res}}_j^k(\phi ,s)=W_j^k(\phi ,s)-s{\omega }_j(\phi ,0)-s^{\wp }{N}_j(\phi ,s)-s^{\wp }{F}_j(\phi ,s).$$

(15)

Step 6. We substitute the form of $W_j^k(\phi ,s)$ as in Equation (13) into Equation (15).

Step 7. We multiply Equation (15) by $s^{ka+1},k=1,2,\dots ,j=$$1,2,\dots ,m$.

Step 8. We solve the following algebraic equations recursively:

$$\underset{s\to \infty }{lim}{s}^{k\wp +1}L{Res}_j^k(\phi ,s)=0,k=1,2,3,\dots j=1,2,\dots ,m;$$

(16)

then, we obtain the forms of the unknown coefficients, $g_{j1}(\phi ),g_{j2}(\phi ),\dots ,g_{j(k-1)}(\phi )$, respectively.

Step 9. We substitute the obtained forms of $g_{ji}(\phi ),i=$$1,2,\dots ,m$ to obtain the $k^{th}$ series form solutions of Equation (10).

Step 10. We operate the inverse YT on the final form of $W_j^k(\phi ,s),j=1,2,\dots ,m$ to obtain the $k^{th}$ series form solution, ${\omega }_j^k(\phi ,\tau ),j$$=1,2,\dots ,m$, of Equations (6) and (7).

4. Results

Example 1.

We considered the system of the fractional reaction–diffusion equation

$$\begin{array}{cc}\hfill & D_{\tau }^{\wp }u=u-u^2-uv+u_{\phi \phi },\hfill \\ \hfill & D_{\tau }^{\wp }v=v_{\phi \phi }-uv,0<\wp \le 1,\tau >0,\hfill \end{array}$$

(17)

with the initial conditions

$$\begin{array}{cc}\hfill & u(\phi ,0)=\frac{e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2},\hfill \\ \hfill & v(\phi ,0)=\frac{1}{1+e^{0.5p\phi }},\hfill \end{array}$$

(18)

where p is constant.

Using the Yang transformation on Equation (17) and applying Equation (18), we obtained

$$\begin{array}{cc}\hfill & \mathcal{Y}\left[D_{\tau }^{\wp }u\right]=\mathcal{Y}[u-u^2-uv+u_{\phi \phi }],\hfill \\ \hfill & \mathcal{Y}\left[D_{\tau }^{\wp }v\right]=\mathcal{Y}[v_{\phi \phi }-uv],\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & U(\phi ,\varrho )=\varrho u(\phi ,0)+{\varrho }^{\wp }\mathcal{Y}[u-u^2-uv+u_{\phi \phi }],\hfill \\ \hfill & V(\phi ,\varrho )=\varrho v(\phi ,0)+{\varrho }^{\wp }\mathcal{Y}[v_{\phi \phi }-uv].\hfill \end{array}$$

(20)

The $K^{th}$-truncated term series were

$$\begin{array}{cc}\hfill & U(\phi ,\varrho )=\frac{\varrho e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2}+\sum _{n=1}^{\mathsf{ß}}{\varrho }^{n\wp +1}{f}_n(\phi ),\hfill \\ \hfill & V(\phi ,\varrho )=\frac{\varrho }{\left(1+e^{0.5p\phi }\right)}+\sum _{n=1}^{\mathsf{ß}}{\varrho }^{n\wp +1}{g}_n(\phi ),\hfill \end{array}$$

(21)

and the $k^{th}$-Yang residual functions were

$$\begin{array}{cc}\hfill {\mathcal{Y}}_{\tau }Re{s}_{u,k}(\phi ,\varrho )=& U_{\mathsf{ß}}(\phi ,\varrho )-\frac{\varrho e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2}-{\varrho }^{\wp }{\mathcal{Y}}_{\tau }[{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}(\phi ,\varrho )\right)-{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}^2(\phi ,\varrho )\right)\hfill \\ \hfill & -{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}(\phi ,\varrho )\right){\mathcal{Y}}_{\tau }^{-1}\left(V_{\mathsf{ß}}(\phi ,\varrho )\right)+{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß},\phi \phi }(\phi ,\varrho )\right)],\hfill \\ \hfill {\mathcal{Y}}_{\tau }Re{s}_{u,k}(\phi ,\varrho )=& V_{\mathsf{ß}}(\phi ,\varrho )-\frac{\varrho }{\left(1+e^{0.5p\phi }\right)}-{\varrho }^{\wp }{\mathcal{Y}}_{\tau }\left[{\mathcal{Y}}_{\tau }^{-1}\left(V_{\mathsf{ß},\phi \phi }(\phi ,\varrho )\right)-{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}(\phi ,\varrho )\right){\mathcal{Y}}_{\tau }^{-1}\left(V_{\mathsf{ß}}(\phi ,\varrho )\right)\right].\hfill \end{array}$$

(22)

Now, to find $f_{\mathsf{ß}}(\phi )$, and $g_{\mathsf{ß}}(\phi )$, $k=1,2,3,\dots$, we substituted the $k^{th}$-truncated series Equation (21) into the $k^{th}$-Yang residual function Equation (22), multiplied the achieved solutions by ${\varrho }^{k\wp +1}$, and then recursively investigated the relations ${lim}_{\varrho \to \infty }({\varrho }^{k\wp +1}{\mathcal{Y}}_{\tau }Re{s}_{u,k}(\phi ,\varrho ))=0$ and ${lim}_{\varrho \to \infty }({\varrho }^{k\wp +1}{\mathcal{Y}}_{\tau }Re{s}_{v,k}(\phi ,\varrho ))=0$, $k=1,2,3,\dots$. The first few functions were

$$\begin{array}{cc}\hfill f_0(\phi )=& \frac{e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2},\hfill \\ \hfill g_0(\phi )=& \frac{1}{1+e^{0.5p\phi }},\hfill \\ \hfill f_1(\phi )=& \frac{(p^2{e}^{0.5p\phi }-2p^2-2e^{0.5p\phi })e^{p\phi }}{{(1+e^{0.5p\phi })}^4},\hfill \\ \hfill g_1(\phi )=& -\frac{0.25(4e^{p\phi }+p^2{e}^{0.5p\phi }-p^2{e}^{p\ast x})}{{(1+e^{0.5p\phi })}^3},\hfill \\ \hfill f_2(\phi )=& \frac{1}{8{(1+e^{0.5p\phi })}^6}(-32p^2{e}^{2p\phi }+16e^{2p\phi }+28e^{1.5p\phi }{p}^2-33p^4{e}^{1.5p\phi }+4p^2{e}^{2.5p\phi }+18p^4{e}^{2p\phi }-p^4{e}^{2.5p\phi }\hfill \\ \hfill & +8p^4{e}^{p\phi }),\hfill \\ \hfill g_2(\phi )=& \frac{1}{16{(1+e^{0.5p\phi })}^5}(p^4{e}^{2p\phi }+16e^{2p\phi }-8p^2{e}^{2p\phi }+11p^2{e}^{p\phi }-11p^4{e}^{1.5p\phi }+40p^2{e}^{1.5p\phi }-p^4{e}^{0.5p\phi }\hfill \\ \hfill & -32p^2{e}^{p\phi }-16e^{1.5p\phi }).\hfill \end{array}$$

(23)

Putting the values of $f_{\mathsf{ß}}(\phi )$ and $g_{\mathsf{ß}}(\phi )$, $k=1,2,3,\dots$ into Equation (21), we obtained

$$\begin{array}{cc}\hfill U(\phi ,\varrho )=& \frac{\varrho e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2}+{\varrho }^{\wp +1}\left(\frac{(p^2{e}^{0.5p\phi }-2p^2-2e^{0.5p\phi })e^{p\phi }}{{(1+e^{0.5p\phi })}^4}\right)+(\frac{{\varrho }^{2\wp +1}}{8{(1+e^{0.5p\phi })}^6}(-32p^2{e}^{2p\phi }+16e^{2p\phi }+28e^{1.5p\phi }{p}^2\hfill \\ & -33p^4{e}^{1.5p\phi }+4p^2{e}^{2.5p\phi }+18p^4{e}^{2p\phi }-p^4{e}^{2.5p\phi }+8p^4{e}^{p\phi })),\hfill \\ \hfill V(\phi ,\varrho )=& \frac{\varrho }{\left(1+e^{0.5p\phi }\right)}-{\varrho }^{\wp +1}\left(\frac{0.25(4e^{p\phi }+p^2{e}^{0.5p\phi }-p^2{e}^{p\ast x})}{{(1+e^{0.5p\phi })}^3}\right)+(\frac{{\varrho }^{2\wp +1}}{16{(1+e^{0.5p\phi })}^5}(p^4{e}^{2p\phi }+16e^{2p\phi }-8p^2{e}^{2p\phi }\hfill \\ & +11p^2{e}^{p\phi }-11p^4{e}^{1.5p\phi }+40p^2{e}^{1.5p\phi }-p^4{e}^{0.5p\phi }-32p^2{e}^{p\phi }-16e^{1.5p\phi })).\hfill \end{array}$$

(24)

Using the inverse Yang transform, we obtained

$$\begin{array}{cc}\hfill u(\phi ,\tau )=& \frac{e^{p\phi }}{{\left(1+e^{0.5p\phi }\right)}^2}+\left(\frac{(p^2{e}^{0.5p\phi }-2p^2-2e^{0.5p\phi })e^{p\phi }}{{(1+e^{0.5p\phi })}^4}\right)\frac{{\tau }^{\wp }}{\mathsf{\Gamma }(\wp +1)}+(\frac{1}{8{(1+e^{0.5p\phi })}^6}(-32p^2{e}^{2p\phi }+16e^{2p\phi }\hfill \\ & +28e^{1.5p\phi }{p}^2-33p^4{e}^{1.5p\phi }+4p^2{e}^{2.5p\phi }+18p^4{e}^{2p\phi }-p^4{e}^{2.5p\phi }+8p^4{e}^{p\phi }))\frac{{\tau }^{2\wp }}{\mathsf{\Gamma }(2\wp +1)},\hfill \\ \hfill v(\phi ,\tau )=& \frac{1}{\left(1+e^{0.5p\phi }\right)}-\left(\frac{0.25(4e^{p\phi }+p^2{e}^{0.5p\phi }-p^2{e}^{p\ast x})}{{(1+e^{0.5p\phi })}^3}\right)\frac{{\tau }^{\wp }}{\mathsf{\Gamma }(\wp +1)}+(\frac{1}{16{(1+e^{0.5p\phi })}^5}(p^4{e}^{2p\phi }+16e^{2p\phi }-8p^2{e}^{2p\phi }\hfill \\ & +11p^2{e}^{p\phi }-11p^4{e}^{1.5p\phi }+40p^2{e}^{1.5p\phi }-p^4{e}^{0.5p\phi }-32p^2{e}^{p\phi }-16e^{1.5p\phi }))\frac{{\tau }^{2\wp }}{\mathsf{\Gamma }(2\wp +1)}.\hfill \end{array}$$

(25)

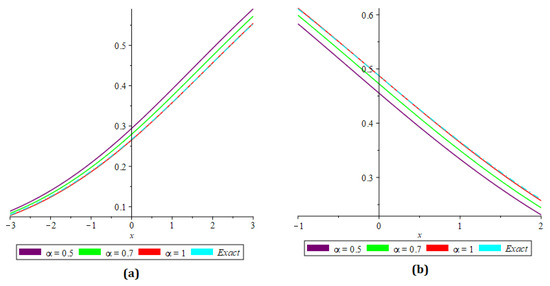
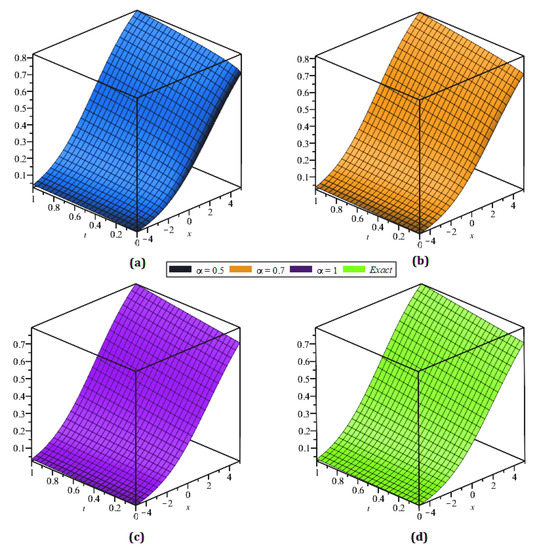
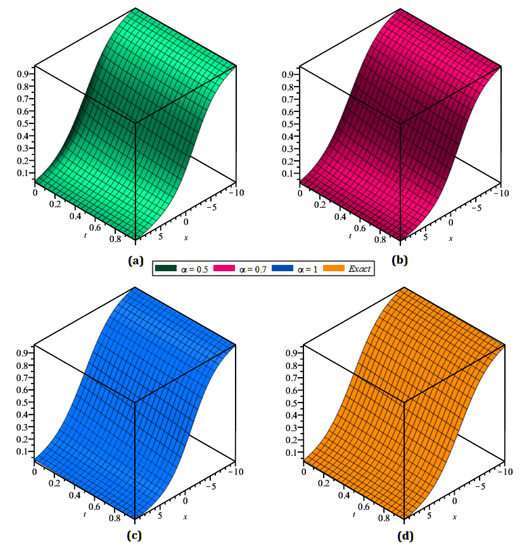
The residual power series transformation method was implemented to achieve the analytical and exact results for the strongly nonlinear fractional reaction–diffusion equation with the initial conditions. In Figure 1, the analytical solutions of (a) $u(\phi ,(\tau ))$ and (b) $v(\phi ,(\tau ))$ of Example 1 are shown. In Figure 2, (a) the fractional order $0.5$, (b) $0.7$, (c) the actual result and (d) analytical solution of Eaxample 1 of $u(\phi ,\tau )$. Similarly, in Figure 3, (a) the fractional order $0.5$, (b) $0.7$, (c) the actual result and (d) analytical solution of Eaxample 1 of $v(\phi ,\tau )$. In the above, the figures showed that in the residual power series transformation method, the analytical results were close to each other. Table 1 and Table 2 detail the numerical analysis of $u(\phi ,\tau )$ and $v(\phi ,\tau )$ of the given example from Example 1, with different values of φ, τ, and $p=\frac{2}{3}$.

Figure 1. The analytical solution for $u(\phi ,(\tau ))$ and $v(\phi ,(\tau ))$ from Example 1.

Figure 2. The actual and analytical results for $u(\phi ,\tau )$ at $k=\frac{2}{3}$, $c=1$, and different values of ℘ from Example 1.

Figure 3. The actual and analytical solutions for $v(\phi ,\tau )$ at $p=\frac{2}{3}$, $c=1$, and different values of ℘ from Example 1.

Table 1. Numerical analysis of $u(\phi ,\tau )$ of the example given in Example 1 with different values of $\phi$, $\tau$, and $p=\frac{2}{3}$.

$\mathit{\tau }$	$\mathit{\phi }$	AE at $\mathit{\wp }=0.5$	AE at $\mathit{\wp }=0.75$	AE at $\mathit{\wp }=1$	AE at $\mathit{\wp }=1$ [20]
	0.2	0.0805629452	0.0502204062	0.0325020875	0.0325020875
	0.4	0.0825454718	0.0515331039	0.0334241734	0.0334241734
0.1	0.6	0.0839111844	0.0524787587	0.0341170570	0.0341170570
	0.8	0.0846437383	0.0530448606	0.0345706478	0.0345706478
	1	0.0847452771	0.0532295274	0.0347813764	0.0347813764
	0.2	0.1386150391	0.1064055404	0.0816294703	0.0816294703
	0.4	0.1421027846	0.1091805284	0.0838571430	0.0838571430
0.25	0.6	0.1445063572	0.1111623891	0.0855012205	0.0855012205
	0.8	0.1457962927	0.1123251454	0.0865387309	0.0865387309
	1	0.1459764695	0.1126662559	0.0869633834	0.0869633834

Table 2. Numerical analysis of $v(\phi ,\tau )$ of the example given in Example 1 with different values of $\phi$, $\tau$, and $p=\frac{2}{3}$.

$\mathit{\tau }$	$\mathit{\phi }$	$\mathbf{AEat}\mathit{\wp }=0.5$	$\mathbf{AEat}\mathit{\wp }=0.75$	$\mathbf{AEat}\mathit{\wp }=1$	$\mathbf{AEat}\mathit{\wp }=1$
	0.2	0.0365409370	0.0162647517	0.0044485940	0.0044485940
	0.4	0.0372349264	0.0167576585	0.0047433264	0.0047433264
0.1	0.6	0.0378161928	0.0172017544	0.0050225392	0.0050225392
	0.8	0.0382802895	0.0175933608	0.0052838629	0.0052838629
	1	0.0386242276	0.0179294469	0.0055251728	0.0055251728
	0.2	0.0493801887	0.0277102702	0.0109897476	0.0109897476
	0.4	0.0502167121	0.0285674155	0.0116808654	0.0116808654
0.25	0.6	0.0508790642	0.0293301937	0.0123303104	0.0123303104
	0.8	0.0513628857	0.0299925619	0.0129326754	0.0129326754
	1	0.0516662223	0.0305498127	0.0134832205	0.0134832205

Example 2.

We considered the fractional order reaction–diffusion Brusselator equation

$$\begin{array}{cc}\hfill D_{\tau }^{\wp }u(\phi ,\rho ,\tau )=& u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )-u(\phi ,\rho ,\tau )(A+1)+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right)+B,\hfill \\ \hfill D_{\tau }^{\wp }v(\phi ,\rho ,\tau )=& -u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )+Au(\phi ,\rho ,\tau )+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right),\hfill \end{array}$$

(26)

with the initial conditions

$$\begin{array}{cc}\hfill u(\phi ,\rho ,0)=& 2+\frac{1}{4}\rho ,\hfill \\ \hfill v(\phi ,\rho ,0)=& 1+\frac{4}{5}\phi ,\hfill \end{array}$$

(27)

where $u(\phi ,\rho ,\tau )$ and $v(\phi ,\rho ,\tau )$ represent the chemical concentrations of the intermediate reaction products, and A and B are the constant concentrations of the input reagents, where $A=\frac{17}{5}$ and $B=1$.

Using the Yang transformation on Equation (26) and applying Equation (27), we obtained

$$\begin{array}{cc}\hfill \mathcal{Y}\left[D_{\tau }^{\wp }u(\phi ,\rho ,\tau )\right]=& \mathcal{Y}[u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )-u(\phi ,\rho ,\tau )(A+1)+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right)+B],\hfill \\ \hfill \mathcal{Y}\left[D_{\tau }^{\wp }v(\phi ,\rho ,\tau )\right]=& \mathcal{Y}[-u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )+Au(\phi ,\rho ,\tau )+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right)],\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & U(\phi ,\rho ,\varrho )=\varrho u(\phi ,\rho ,0)+{\varrho }^{\wp }\mathcal{Y}[u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )-u(\phi ,\rho ,\tau )(A+1)+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right)+B],\hfill \\ \hfill & V(\phi ,\rho ,\varrho )=\varrho v(\phi ,\rho ,0)+{\varrho }^{\wp }\mathcal{Y}[-u^2(\phi ,\rho ,\tau )v(\phi ,\rho ,\tau )+Au(\phi ,\rho ,\tau )+\frac{1}{500}\left(u_{\phi \phi }(\phi ,\rho ,\tau )+u_{\rho \rho }(\phi ,\rho ,\tau )\right)].\hfill \end{array}$$

(29)

The $k^{th}$ truncate series terms were

$$\begin{array}{cc}\hfill & U(\phi ,\varrho )=\varrho (2+\frac{1}{4}\rho )+\sum _{n=1}^{\mathsf{ß}}{\varrho }^{n\wp +1}{f}_n(\phi ,\rho ),\hfill \\ \hfill & V(\phi ,\varrho )=\varrho (1+\frac{4}{5}\phi )+\sum _{n=1}^{\mathsf{ß}}{\varrho }^{n\wp +1}{g}_n(\phi ,\rho ),\hfill \end{array}$$

(30)

and the $k^{th}$-Yang residual functions were

$$\begin{array}{cc}\hfill {\mathcal{Y}}_{\tau }Re{s}_{u,k}(\phi ,\rho ,\varrho )=& U_{\mathsf{ß}}(\phi ,\rho ,\varrho )-\varrho 2+\frac{1}{4}\rho -\frac{1}{{\varrho }^{\wp }}{\mathcal{Y}}_{\tau }[{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}^2(\phi ,\rho ,\varrho )\right){\mathcal{Y}}_{\tau }^{-1}\left(V_{\mathsf{ß}}(\phi ,\rho ,\varrho )\right)-{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}(\phi ,\rho ,\varrho )\right)(A+1)\hfill \\ \hfill & +\frac{1}{500}\left({\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß},\phi \phi }(\phi ,\rho ,\varrho )\right)+{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß},\rho \rho }(\phi ,\rho ,\varrho )\right)\right)+B],\hfill \\ \hfill {\mathcal{Y}}_{\tau }Re{s}_{v,k}(\phi ,\rho ,\varrho )=& V_{\mathsf{ß}}(\phi ,\rho ,\varrho )-\varrho 1+\frac{4}{5}\phi -\frac{1}{{\varrho }^{\wp }}{\mathcal{Y}}_{\tau }[-{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}^2(\phi ,\rho ,\varrho )\right){\mathcal{Y}}_{\tau }^{-1}\left(V_{\mathsf{ß}}(\phi ,\rho ,\varrho )\right)+A{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß}}(\phi ,\rho ,\varrho )\right)\hfill \\ \hfill & +\frac{1}{500}\left({\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß},\phi \phi }(\phi ,\rho ,\varrho )\right)+{\mathcal{Y}}_{\tau }^{-1}\left(U_{\mathsf{ß},\rho \rho }(\phi ,\rho ,\varrho )\right)\right)].\hfill \end{array}$$

(31)

Now, to calculate $f_{\mathsf{ß}}(\phi ,\rho )$ and $g_{\mathsf{ß}}(\phi ,\rho )$, $k=1,2,3,\dots ,$ we put the $k^{th}$-truncate series (Equation (30)) into the $k^{th}$-Yang residual function (Equation (31)), multiplied the solution equation by ${\varrho }^{k\wp +1}$, and then recursively analyzed the relations ${lim}_{\varrho \to \infty }({\varrho }^{k\wp +1}{\mathcal{Y}}_{\tau }Re{s}_{u,k}(\phi ,\psi ,\varrho ))=0$, and ${lim}_{\varrho \to \infty }({\varrho }^{k\wp +1}{\mathcal{Y}}_{\tau }Re{s}_{v,k}(\phi ,\psi ,\varrho ))=0$, $k=1,2,3,\dots$. The first few terms were defined as:

$$\begin{array}{cc}\hfill f_0(\phi ,\rho )=& 2+\frac{\rho }{4},\hfill \\ \hfill g_0(\phi ,\rho )=& 1+\frac{4\phi }{5},\hfill \\ \hfill f_1(\phi ,\rho )=& -\frac{1899}{500}+\frac{16\phi }{5}-\frac{\rho }{10}+\frac{4\phi \rho }{5}+\frac{1{\rho }^2}{16}+\frac{{\rho }^2\phi }{20},\hfill \\ \hfill g_1(\phi ,\rho )=& \frac{1401}{500}-\frac{16\phi }{5}-\frac{3\rho }{20}-\frac{4\rho \phi }{5}-\frac{{\rho }^2}{16}-\frac{{\rho }^2\phi }{20},\hfill \\ \hfill f_2(\phi ,\rho )=& \frac{66261}{5000}-\frac{36667\phi }{1250}+\frac{256{\rho }^2}{251}-\frac{13{\rho }^3}{320}-\frac{{\rho }^4}{256}-\frac{{\rho }^3\phi }{20}+\frac{\rho }{2}+\frac{96{\phi }^2\rho }{25}+\frac{16\phi }{5}+\frac{12{\phi }^2{\rho }^2}{25}\hfill \\ \hfill & +\frac{{\rho }^3{\phi }^2}{50}-\frac{{\rho }^4\phi }{320}-\frac{33{\rho }^2\phi }{50}-\frac{9199\rho \phi }{1250}-\frac{2}{5}-\frac{2399{\rho }^2}{8000}-\frac{157\rho }{1000}+\frac{2\rho \phi }{5},\hfill \\ \hfill g_2(\phi ,\rho )=& -\frac{44021}{5000}+\frac{{\rho }^3\phi }{20}-\frac{96\rho {\phi }^2}{25}-\frac{12{\rho }^2{\phi }^2}{25}+\frac{{\rho }^4\phi }{320}-\frac{{\rho }^3\ast {\phi }^2}{50}+\frac{28917\phi }{1250}-\frac{256{\phi }^2}{25}+\frac{13{\rho }^3}{320}\hfill \\ & +\frac{{\rho }^4}{256}+\frac{1899{\rho }^2}{8000}+\frac{7699\rho \phi }{1250}+\frac{61{\rho }^2\phi }{100}-\frac{243\rho }{1000},\hfill \\ \hfill & ⋮.\hfill \end{array}$$

(32)

Putting the value of $f_{\mathsf{ß}}(\phi ,\rho )$ and $g_{\mathsf{ß}}(\phi ,\rho )$, $k=1,2,3,\dots$, into Equation (30), we obtained

$$\begin{array}{cc}\hfill U(\phi ,\rho ,\varrho )=& \varrho (2+\frac{1}{4}\rho )+\left[-\frac{1899}{500}+\frac{16\phi }{5}-\frac{\rho }{10}+\frac{4\phi \rho }{5}+\frac{1{\rho }^2}{16}+\frac{{\rho }^2\phi }{20}\right]{\varrho }^{\wp +1}+[\frac{66261}{5000}-\frac{36667\phi }{1250}+\frac{256{\rho }^2}{251}\hfill \\ \hfill & -\frac{13{\rho }^3}{320}-\frac{{\rho }^4}{256}-\frac{{\rho }^3\phi }{20}+\frac{\rho }{2}+\frac{96{\phi }^2\rho }{25}+\frac{16\phi }{5}+\frac{12{\phi }^2{\rho }^2}{25}+\frac{{\rho }^3{\phi }^2}{50}-\frac{{\rho }^4\phi }{320}-\frac{33{\rho }^2\phi }{50}-\frac{9199\rho \phi }{1250}\hfill \\ \hfill & -\frac{2}{5}-\frac{2399{\rho }^2}{8000}-\frac{157\rho }{1000}+\frac{2\rho \phi }{5}]{\varrho }^{2\wp +1}+\dots ,\hfill \\ \hfill V(\phi ,\rho ,\varrho )=& \varrho (1+\frac{4}{5}\phi )+\left[\frac{1401}{500}-\frac{16\phi }{5}-\frac{3\rho }{20}-\frac{4\rho \phi }{5}-\frac{{\rho }^2}{16}-\frac{{\rho }^2\phi }{20}\right]{\varrho }^{\wp +1}+[-\frac{44021}{5000}+\frac{{\rho }^3\phi }{20}-\frac{96\rho {\phi }^2}{25}\hfill \\ \hfill & -\frac{12{\rho }^2{\phi }^2}{25}+\frac{{\rho }^4\phi }{320}-\frac{{\rho }^3{\phi }^2}{50}+\frac{28917\phi }{1250}-\frac{256{\phi }^2}{25}+\frac{13{\rho }^3}{320}+\frac{{\rho }^4}{256}+\frac{1899{\rho }^2}{8000}+\frac{7699\rho \phi }{1250}\hfill \\ \hfill & +\frac{61{\rho }^2\phi }{100}-\frac{243\rho }{1000}]{\varrho }^{2\wp +1}+\dots .\hfill \end{array}$$

(33)

Now, applying the inverse Yang transform, we obtained

$$\begin{array}{cc}\hfill u(\phi ,\rho ,\tau )=& 2+\frac{1}{4}\rho +\left[-\frac{1899}{500}+\frac{16\phi }{5}-\frac{\rho }{10}+\frac{4\phi \rho }{5}+\frac{{\rho }^2}{16}+\frac{{\rho }^2\phi }{20}\right]\frac{{\tau }^{\wp }}{\mathsf{\Gamma }(\wp +1)}+[\frac{66261}{5000}-\frac{36667\phi }{1250}+\frac{256{\rho }^2}{251}\hfill \\ \hfill & -\frac{13{\rho }^3}{320}-\frac{{\rho }^4}{256}-\frac{{\rho }^3\phi }{20}+\frac{\rho }{2}+\frac{96{\phi }^2\rho }{25}+\frac{16\phi }{5}+\frac{12{\phi }^2{\rho }^2}{25}+\frac{{\rho }^3{\phi }^2}{50}-\frac{{\rho }^4\phi }{320}-\frac{33{\rho }^2\phi }{50}-\frac{9199\rho \phi }{1250}\hfill \\ \hfill & -\frac{2}{5}-\frac{2399{\rho }^2}{8000}-\frac{157\rho }{1000}+\frac{2\rho \phi }{5}]\frac{{\tau }^{2\wp }}{\mathsf{\Gamma }(2\wp +1)}+\dots ,\hfill \\ \hfill v(\phi ,\rho ,\tau )=& 1+\frac{4}{5}\phi +\left[\frac{1401}{500}-\frac{16\phi }{5}-\frac{3\rho }{20}-\frac{4\rho \phi }{5}-\frac{{\rho }^2}{16}-\frac{{\rho }^2\phi }{20}\right]\frac{{\tau }^{\wp }}{\mathsf{\Gamma }(\wp +1)}+[-\frac{44021}{5000}+\frac{{\rho }^3\phi }{20}-\frac{96\rho {\phi }^2}{25}\hfill \\ \hfill & -\frac{12{\rho }^2{\phi }^2}{25}+\frac{{\rho }^4\phi }{320}-\frac{{\rho }^3{\phi }^2}{50}+\frac{28917\phi }{1250}-\frac{256{\phi }^2}{25}+\frac{13{\rho }^3}{320}+\frac{{\rho }^4}{256}+\frac{1899{\rho }^2}{8000}+\frac{7699\rho \phi }{1250}\hfill \\ \hfill & +\frac{61{\rho }^2\phi }{100}-\frac{243\rho }{1000}]\frac{{\tau }^{2\wp }}{\mathsf{\Gamma }(2\wp +1)}+\dots .\hfill \end{array}$$

(34)

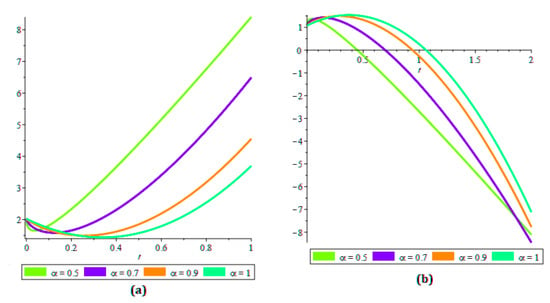
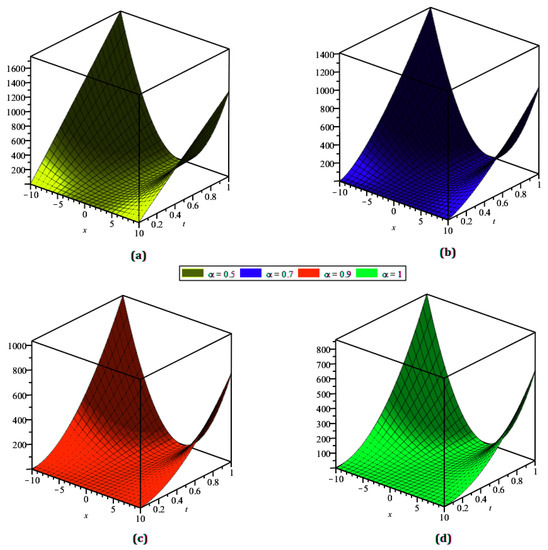
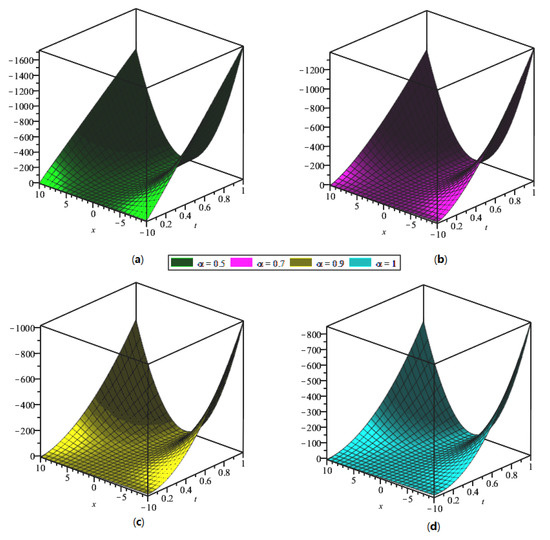
The residual power series transformation method was implemented to achieve the analytical and exact results of the strongly nonlinear fractional reaction–diffusion equation with the initial conditions. In Figure 4, the analytical solutions of (a) $u(\phi ,(\tau ))$ and (b) $v(\phi ,(\tau ))$ of Example 2 are shown. In Figure 5, (a) the fractional order $0.5$, (b) $0.7$, (c) the actual result and (d) analytical solution of Eaxample 2 of $u(\phi ,\tau )$. Similarly, in Figure 6, (a) the fractional order $0.5$, (b) $0.7$, (c) the actual result and (d) analytical solution of Example 2 of $v(\phi ,\tau )$. These figures showed that in using the residual power series transformation method, the analytical results were close to each other. Table 3 and Table 4 detail the numerical analysis of $u(\phi ,\tau )$ and $v(\phi ,\tau )$ from Example 2 with different values of φ, τ, and $p=\frac{2}{3}$.

Figure 4. The analytical solution (a) $u(\phi ,(\tau ))$ and subplot (b) $v(\phi ,(\tau ))$ at $A=\frac{17}{5}$, $B=1$, $x=0.1$, and $y=0.1$, respectively, from Example 2.

Figure 5. The analytical solution for $u(\phi ,\tau )$ at $A=\frac{17}{5}$, $B=1$, and $y=1$ for distinct values of ℘ from Example 2.

Figure 6. The analytical solution for $v(\phi ,\tau )$ at $A=\frac{17}{5}$, $B=1$, and $y=1$ for different values of ℘ from Example 2.

Table 3. Numerical analysis of $u(\phi ,\tau )$ of the example given in 2 with different values of $\phi$, $\tau$, and $p=\frac{2}{3}$.

$\mathit{\tau }$	$\mathit{\phi }$	Numerical Simulation at $\mathit{\wp }=0.5$	Numerical Simulation at $\mathit{\wp }=0.75$	Numerical Simulation at $\mathit{\wp }=1$
	0.2	1.837707373	1.917052547	1.980814044
	0.4	1.625576979	1.975701657	2.036756119
0.1	0.6	1.530086586	2.045377487	2.098530194
	0.8	1.551236193	2.126080036	2.166136269
	1	1.689025800	2.217809305	2.239574344
	0.2	1.713577815	1.674859093	1.702150273
	0.4	1.553928691	1.670189950	1.748038242
0.25	0.6	1.503958022	1.722897876	1.830376211
	0.8	1.563665809	1.832982869	1.949164180
	1	1.733052051	2.000444931	2.104402148

Table 4. Numerical analysis of $v(\phi ,\tau )$ of the example given in 2 with different values of $\phi$, $\tau$, and $p=\frac{2}{3}$.

$\mathit{\tau }$	$\mathit{\phi }$	Numerical Simulation at $\mathit{\wp }=0.5$	Numerical Simulation at $\mathit{\wp }=0.75$	Numerical Simulation at $\mathit{\wp }=1$
	0.2	1.459238898	1.424447874	1.321163456
	0.4	1.754369291	1.528622455	1.421371381
0.1	0.6	1.932859684	1.605050337	1.515747306
	0.8	1.994710077	1.653731523	1.604291231
	1	1.939920471	1.674666009	1.687003156
	0.2	1.324648176	1.528861254	1.499959102
	0.4	2.088050864	1.776106048	1.590008633
0.25	0.6	2.559853552	1.913672387	1.643608164
	0.8	2.740056238	1.941560270	1.660757695
	1	2.628658925	1.859769698	1.641457227

5. Conclusions

This paper examined the fractional reaction–diffusion and reaction–diffusion Brusselator equations in terms of the Caputo fractional derivative. With the aid of the RPSM, the series solution of the investigated model was successfully attained. Plots were made of the numerical simulations of the proposed solution using various fractional values of ℘. The technique was applied to the suggested fractional-order systems to investigate its analytical solutions. The solutions showed that the method was inexpensive and suitable for achieving analytical solutions. We, therefore, conclude that the suggested fractional models connected to the Caputo fractional derivative are very helpful in efficiently investigating the problems arising in science and engineering.