Transient Heat Conduction in a Semi-Infinite Domain with a Memory Effect: Analytical Solutions with a Robin Boundary Condition

Abstract

The Robin boundary condition initial value problem for transient heat conduction with the time-fractional Caputo derivative in a semi-infinite domain with a convective heat transfer (Newton’s law) at the boundary has been solved and analyzed by two analytical approaches. The uniqueness and the stability of the solution on the half-axis have been analyzed. The problem solutions by application of the operational method (Laplace transform in the time domain) and the integral-balance method (double integration technique) have been developed analytically.

1. Introduction

Transport processes in non-local media are mainly modeled by the time-fractional diffusion equations [1,2,3,4] which macroscopically perform the fractal natures of the materials as non-localities in time [5,6]. Especially in the case of heat conduction and anomalous diffusion, the transient heat conduction via the application of the time-fractional Caputo derivative has been thermodynamically formulated in [7,8] applying the fading memory formalism. Recently, various techniques upon various initial and boundary conditions have been applied to solve time-fractional heat transfer equations [1,2,3,4,5,6,7,8,9,10,11,12,13,14] but a review of these studies is beyond the scope of this work.

The present analysis, and solutions developed, address the time-fractional heat conduction (which can also be considered as an anomalous diffusion equation) with the Robin boundary condition. The Robin boundary condition appears in many applied diffusion problems such as solute rejection [9,14,15], solidification of alloys [16,17], and heat transfer at the boundary by convection (as in this article) [18], and the dominating solutions are numerical [6,9,10,11,12,15,16,17] considering finite domains [11,14,15,16,17], while solutions in the semi-infinite domain are rare [9]. Moreover, estimates concerning the existence and uniqueness of the problem solution have been developed in [9,11,19].

1.1. Aim

This work addresses the analysis and analytical solutions to transient heat conduction in a semi-infinite domain with hereditary effects modeled by the time-fractional Caputo derivative and the Robin boundary condition considering a convective term of the heat flux. The task has been developed by a solution applying the Laplace transform in the time domain and an approximate integral-balance method (double integration technique).

The main idea of applying two distinct, by nature, analytical solutions is to demonstrate, from one side, the straightforwardness of the formal exact analytical solution developed in the Laplace domain and how hard it could be to analyze from a physical point of view, and the sound results of the approximate integral-balance method allowing the meaning of the exact solution to be explained.

1.2. Further Paper Organization

The following part of the article considers the Robin boundary condition formulation. As a first step, Section 2 considers the general formulation of the Robin boundary condition (Section 2.1) and the problem to be resolved (Section 2.2). The existence and uniqueness of the solution are considered in Section 3. An analytical solution by application of the Laplace transform in the time domain and analysis of the temperature profile together with the surface temperature and flux evolutions in time is developed in Section 4. The second step applied is the development of an approximate integral-balance solution (Section 5) and analysis of the results concerning the surface temperature and heat flux time evolutions and related outcomes. Section 6 considers and analyzes common problems emerging from the developed analytical solutions with relevant comments on the physical significance of the results and draws emerging open problems expecting to be resolved.

2. Mathematical Statement of the Problem

2.1. The Robin Boundary Condition

2.1.1. The General Formulation

If there is a domain S on which a certain modeling equation (in the present case a heat diffusion equation) has to be solved and $S$ marks the boundary with the surrounding medium (commonly a fluid), the Robin boundary condition is defined as a weighted combination of the Dirichlet and Neumann boundary conditions, namely

$$aT+b\frac{\partial T}{\partial n}=g,$$

(1)

where $a$ and $b$ are nonzero constants, $\frac{\partial T}{\partial n}$ is the normal derivative to the boundary.

In a domain $S=[0,1]$, the Robin conditions are

$$aT\left(0,t\right)-b\frac{\partial T\left(0,t\right)}{\partial n}=g\left(0,t\right),$$

(2)

$$aT\left(1,t\right)+b\frac{\partial T\left(1,t\right)}{\partial n}=g\left(1,t\right),$$

(3)

bearing in mind that at the end of the domain the $\frac{\partial T}{\partial n}$ changes the sign.

If the Robin condition is applied to an insulating boundary $G$ then the diffusive and the convective fluxes sum to zero

$$aT\left(G,t\right)-b\frac{\partial T\left(G,t\right)}{\partial n}=g\left(G,t\right)=0,$$

(4)

2.1.2. Heat Conduction with Convective Flux at the Boundary

Considering a convective heat exchange at the boundary, the Robin boundary condition defines the thermal flux q as a weighted combination of the Newton boundary condition (h is the heat exchange coefficient with a dimension $W/m^{2}K$)

$$q=h\cdot (T_f-T_0),$$

(5)

and the Neuman boundary condition ($\lambda$ is the thermal conductivity $\left[W/\left(m\cdot K\right)\right]$)

$$q=-k\cdot \mathrm{grad}T.$$

(6)

Here, $T_f$ denotes the temperature of the fluid, while $T_0$ is the temperature at the fluid-solid interface, i.e., at $x=0$.

For a semi-infinite medium exhibiting non-local in-time transport properties concerning thermal energy, with initial temperature $T_0$, the Robin boundary condition (3) at $x=0$, and applied at $t=0_{+}$ in its homogeneous form of (4), is:

$$-k\cdot \mathrm{grad}T=h\cdot \left(T_f-T_s\right)\Rightarrow k\cdot \mathrm{grad}T+h\cdot \left(T_f-T_s\right)=0.$$

(7)

If it is positive, i.e., $T_f>T_s$ there is a heating of the medium by the fluid. To this moment, we restrict ourselves to this case. The situation $T_f<T_s$ corresponding to the medium cooling is commented on in Section 5.

2.2. Transient Heat Conduction with Memory Effects in a Semi-Infinite Domain

In a semi-infinite domain $D=\{(x,\tau ):0<x<\infty ,0<t\le T\}$, the model of transient heat conduction (8) involving memory effects through the time-fractional Caputo derivative [12] is:

$${\partial }_{0t}^{\alpha }T(x,\tau )=a\frac{{\partial }^2}{\partial x^2}T(x,\tau ), \tau >0,0<x<\infty , 0<\alpha \le 1$$

(8)

$${\partial }_{0t}^{\alpha }T(x,t)=\frac{1}{\Gamma (1-\alpha )}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{T_t^{}(x,s)}{{(t-s)}^{\alpha }}}ds, 0<\alpha \le 1.$$

(9)

Introducing a time scale $t_0$ the Caputo derivative can be presented as [5,20]:

$${\partial }_{0t}^{\alpha }T(x,\tau )=\frac{1}{t_0^{\alpha }}\frac{1}{\Gamma (1-\alpha )}{\displaystyle \underset{0}{\overset{\tau }{\int }}\frac{T_t^{}(x,s)}{{(\tau -s)}^{\alpha }}}ds.$$

(10)

Then, (8) can be presented as

$${\partial }_{0t}^{\alpha }T(x,\tau )=\overline{a}\frac{{\partial }^2}{\partial x^2}T(x,\tau ).$$

(11)

Here, $\overline{a}=a{t}_0^{\alpha }$ has a dimension of $m^2$ bearing in mind that in (8) the dimension of the thermal diffusivity $a$ is $m^2/s^{\alpha }$ since this is a subdiffusion model.

For a complete statement of the problem, we set the initial and boundary conditions:

$$T(x,0)=T_0, T\left(0,\tau \right)=T_s,$$

(12)

$$k\frac{\partial T\left(0,\tau \right)}{\partial x}+h\cdot \left[T_f-T_s\right]=0, T(\infty ,\tau )=T_0, \frac{\partial T(\infty ,\tau )}{\partial x}=0.$$

(13)

That is, the non-dimensalization affects only the time variable. However, bearing in mind that in a semi-infinite medium, there is no characteristic length scale, we may consider the results in [5,13] where the length scale in such a case of a fractional diffusion equation can be defined as $x_0=\sqrt{a{t}^{\alpha }}$ with a dimension of length $\left[m\right]$; for $\alpha =1$, we obtain the length scale in the classical diffusion equation. On this basis, we may define a similarity variable ${\eta }_{\alpha }=x/\sqrt{a{t}^{\alpha }}$; with $\alpha =1$, it matches the Boltzmann similarity variable $\eta =x/\sqrt{at}$.

3. Existence and Uniqueness of a Solution

Theorem 1.

Let the conditions $T(\xi ,\tau )\in C^{2,0}(D)\cap C^{1,0}(\overline{D})$, ${\partial }_{0t}^{\alpha }u(x,t)\in C(\overline{D})$ be satisfied; then, for solving the problem (8)–(13) there is an a priori valid estimate:

$${‖T‖}_0^2+D_{0\tau }^{-\alpha }{‖T_x‖}_0^2\le M\left({‖T_0(x)‖}_0^2+{\left(\frac{h}{\kappa }{T}_f\right)}^2\right),$$

(14)

where $M=const$, which depends on the input data of the problem.

Proof of Theorem 1.

Let $M_i=const,i=1,2,\dots$, which depends on the input data. Multiplying Equation (8) by $T(x,\tau )$, we get:

$$\left({\partial }_{0\tau }^{\alpha }T(x,\tau ),T(x,\tau )\right)=\left(T_{xx}(x,\tau ),T(x,\tau )\right),$$

(15)

where $(g,h)={\displaystyle \underset{0}{\overset{\infty }{\int }}ghdx}$, ${‖g‖}_0^2=(g,g)$, for the functions given in the domain $[0,+\infty )$.

Let us transform each of the terms of the Robin condition expressed as (13) and then use the Cauchy inequality with $\epsilon$ [19].

$$\left({\partial }_{0\tau }^{\alpha }T,T\right)=\frac{1}{\Gamma (1-\alpha )}{\displaystyle \underset{0}{\overset{\infty }{\int }}Tdx{\displaystyle \underset{0}{\overset{t}{\int }}{T}_{\tau }{(t-\tau )}^{-\alpha }d\tau \ge \frac{1}{2}(1,{\partial }_{0t}^{\alpha }{T}^2)=\frac{1}{2}{\partial }_{0\tau }^{\alpha }{‖T‖}_0^2}},$$

(16)

$$\left(T_{xx},T\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{T}_{xx}Tdx}={\left.T(x,\tau )T_x(x,\tau )\right|}_0^{\infty }-{\displaystyle \underset{0}{\overset{\infty }{\int }}{T}_x{T}_{x}d\xi =T(0,\tau )\frac{\alpha }{\lambda }}[T_f-T(0,\tau )]-{‖T_x‖}_0^2,$$

(17)

Now let us estimate the first term on the right side of (17):

$$\begin{array}{l}{\left.T(x,\tau )T_x(x,\tau )\right|}_0^{\infty }=\frac{h}{\kappa }T(0,\tau )[T_f-T(0,\tau )]=\frac{h}{\kappa }{T}_f\cdot T(0,\tau )-\frac{h}{\kappa }{T}^2(0,\tau )\\ \le -\frac{h}{\kappa }{T}^2(0,\tau )+\frac{1}{2}\left(T^2(0,\tau )+{\left(\frac{h}{\kappa }{T}_f\right)}^2\right)\le M_2^{\epsilon }{‖T‖}_0^2+\frac{1}{2}{\left(\frac{h}{\kappa }{T}_f\right)}^2.\end{array}$$

(18)

Substituting (17) and (18) into (15), we obtain:

$$\frac{1}{2}{\partial }_{0\tau }^{\alpha }{‖T‖}_0^2+{‖T_x‖}_0^2\le M_3{‖T‖}_0^2+\frac{1}{2}{\left(\frac{h}{\kappa }{T}_f\right)}^2.$$

(19)

In Inequality (19), we apply the fractional differentiation operator $D_{0\tau }^{-\alpha }$ to both sides. Then, based on Lemma 2 from [19] (see Appendix A for details), we obtain the following estimate:

$${‖T‖}_0^2+D_{0\tau }^{-\alpha }{‖T_x‖}_0^2\le M_4{‖T_0(x)‖}_0^2+D_{0\tau }^{-\alpha }{\left(\frac{h}{\kappa }{T}_f\right)}^2,$$

(20)

or

$${‖T‖}_0^2+D_{0\tau }^{-\alpha }{‖T_x‖}_0^2\le M\left({‖T_0(x)‖}_0^2+{\left(\frac{h}{\kappa }{T}_f\right)}^2\right).$$

(21)

where $M=\mathrm{const}$, which depends on the input data.

From (21), it follows the uniqueness and stability of the solution to Problems (8)–(13) concerning the initial data. □

4. Solution to the Heating Problem: Laplace Transform Approach

The solution to Model (8)–(13) will be developed by applying the Laplace transforms in the time domain. Thus, applying the Laplace transform we obtain

$$T_L^{//}(x,p)-\frac{p^{\alpha }}{a}T(x,p)+\frac{p^{\alpha -1}}{a}{T}_0=0.$$

(22)

The boundary conditions in the Laplace domain will take the form:

$$T_L^{/}(0,p)+\beta \left[\frac{T_f}{p}-T_L(0,p)\right]=0, T_L(\infty ,p)=0,$$

(23)

where $\beta =\frac{h}{k}$ is the ratio of the heat transfer coefficients.

The characteristic equation of (22) is

$${\mu }^2-\frac{p^{\alpha }}{a}=0.$$

(24)

Then, using the roots of (24), the general solution to (22) can be expressed as:

$$T_L(x,p)=C_1{e}^{\sqrt{\frac{p^{\alpha }}{a}}x}+C_2{e}^{-\sqrt{\frac{p^{\alpha }}{a}}x}+\frac{1}{p}{T}_0.$$

(25)

Applying the second boundary condition of (23) we have:

$$0=T_L(\infty ,p)=\sqrt{\frac{p^{\alpha }}{a}}{C}_1\exp \left(+\infty \right)+C_2\sqrt{\frac{p^{\alpha }}{a}}\exp \left(+\infty \right).$$

(26)

Since physically the temperature becomes unchanged at infinity, and the temperature profiles are decaying in space, the first term in the RHS of (26) has no physical meaning, and the reasonable solution is $C_1=0$.

Further, $C_2$ can be determined from the boundary condition at the interface $x=0$, namely

$$-\sqrt{\frac{p^{\alpha }}{a}}{C}_2+\beta \left[\frac{T_f}{p}-\frac{T_0}{p}-C_2\right]=0.$$

(27)

Therefore,

$$C_2=\frac{T_f-T_0}{p\left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}.$$

(28)

Then, the final solution in the Laplace domain is:

$$T_L(x,p)=\frac{T_f-T_0}{p\left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}{e}^{-\sqrt{\frac{p^{\alpha }}{a}}x}+\frac{T_0}{p}.$$

(29)

We can transform (29) as

$$T_L(x,p)=(T_f-T_0)\cdot \frac{\beta \sqrt{a}}{p\left(1-(-\beta \sqrt{a}\cdot p^{-\alpha /2}\right)}\cdot \frac{1}{p^{\alpha /2}}{\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\frac{p^{\alpha /2}}{\sqrt{a}}x\right)}^n}{n!}}+\frac{T_0}{p}.$$

(30)

Then, the following takes place

$$\begin{array}{ll}\frac{\beta \sqrt{a}}{p^{\alpha /2}\left(1-(-\beta \sqrt{a}\cdot p^{-\alpha /2}\right)}& =\beta \sqrt{a}{\displaystyle \underset{0}{\overset{+\infty }{\int }}{t}^{\alpha /2-1}{\displaystyle \sum _{k=0}^{\infty }\frac{{\left(-\beta \sqrt{a}\cdot t^{\alpha /2}\right)}^k}{\Gamma \left(\frac{\alpha }{2}k+\frac{\alpha }{2}\right)}}}\cdot e^{-pt}dt\\ & =\beta \sqrt{a}{\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{\alpha /2-1}{E}_{\alpha /2,\alpha /2}\left(-\beta \sqrt{a}\cdot t^{\alpha /2}\right)\cdot e^{pt}dt},\end{array}$$

(31)

$$\begin{array}{l}\frac{1}{p}{\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\frac{p^{\alpha /2}}{\sqrt{a}}x\right)}^n}{n!}}={\displaystyle \underset{0}{\overset{+\infty }{\int }}{\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\frac{1}{\sqrt{a}}x\cdot t^{-\alpha /2}\right)}^n}{n!\cdot \Gamma \left(-\frac{\alpha }{2}n+1\right)}}}\cdot e^{-pt}dt\\ ={\displaystyle \underset{0}{\overset{+\infty }{\int }}\varphi \left(-\frac{\alpha }{2},1,-\frac{1}{\sqrt{a}}x\cdot t^{-\alpha /2}\right)\cdot e^{-pt}dt.}\end{array}$$

(32)

Here, $E_{\alpha /2,\alpha /2}(-z^{\alpha /2})={\displaystyle \sum _{k=0}^{\infty }\frac{{(-z^{\alpha /2})}^k}{\Gamma \left(\frac{\alpha }{2}k+\frac{\alpha }{2}\right)}}$ is the Mittag-Leffler function, and $\varphi \left(-\frac{\alpha }{2},1,-\lambda \cdot t^{-\alpha /2}\right)={\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\lambda \cdot t^{-\alpha /2}\right)}^n}{n!\cdot \Gamma \left(-\frac{\alpha }{2}n+1\right)}}$ is Wright’s function [13,21].

From (31) and (32), for the original expression

$$\frac{T_f-T_0}{p\left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}{e}^{-\sqrt{\frac{p^{\alpha }}{a}}x}$$

(33)

one obtains (see Appendix B for details)

$$\begin{array}{l}{L}^{-1}\left(\frac{(T_f-T_0)}{p\cdot \left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}{e}^{-\sqrt{\frac{p^{\alpha }}{a}}x}\right)\\ =(T_f-T_0)\cdot \beta \sqrt{a}\cdot {\displaystyle \underset{0}{\overset{\tau }{\int }}\varphi \left(-\frac{\alpha }{2},1,-\frac{1}{\sqrt{a}}x\cdot {\tau }^{-\alpha /2}\right){(\tau -s)}^{\alpha /2-1}\cdot E_{\alpha /2,1}(-\beta \sqrt{a}{(\tau -s)}^{\alpha /2})}ds.\end{array}$$

(34)

Applying the convolution properties in the Laplace domain to (35), we obtain

$$\begin{array}{l}T(x,\tau )=T_0+(T_f-T_0)\times \\ \beta \sqrt{a}\cdot {\displaystyle \underset{0}{\overset{\tau }{\int }}\varphi \left(-\frac{\alpha }{2},1,-\frac{1}{\sqrt{a}}x\cdot s^{-\alpha /2}\right)\cdot {(\tau -s)}^{\alpha /2-1}\times E_{\alpha /2,\alpha /2}(-\beta \sqrt{a}{(\tau -s)}^{\alpha /2})}ds\end{array}$$

(35)

The dimensionless form of (35) is:

$$\begin{array}{l}\frac{T(x,\tau )-T_0}{(T_f-T_0)}=\Theta (x,\tau )=\\ \beta \sqrt{a}\cdot {\displaystyle \underset{0}{\overset{\tau }{\int }}\varphi \left(-\frac{\alpha }{2},1,-\frac{1}{\sqrt{a}}x\cdot s^{-\alpha /2}\right)\cdot {(\tau -s)}^{\alpha /2-1}\times E_{\alpha /2,\alpha /2}(-\beta \sqrt{a}{(\tau -s)}^{\alpha /2})}ds.\end{array}$$

(36)

Remark 1:

The dimensionless form (36) reveals that the temperature scale can be chosen as $\left(T_f-T_0\right)$. From the point of view of nondimensalization, it is possible to use only $T_f$ as a temperature scale, since just shifting the temperature scale by $T_0$ we obtain zero initial condition. Moreover, $T_f$ is the maximal temperature in the system under consideration. Then, we may use the dimensionless variable $u=T\left(x,t\right)/T_f$$u=T\left(x,t\right)/T_f$ (this approach is used in Section 5). When the surface temperature $T_s$ becomes equal to $T_f$, the heat transfer process stops which simply explains this approach.

4.1. Laplace Transform Solution to the Heating Problem: An Analysis of the Outcomes

In the case when the heat transfer coefficient $h$ is very large, then $\beta \to \infty$. Then from the boundary Condition (13), it follows that $T(0,\tau )\to T_s=\mathrm{const}$. This is a well-known case with high Biot numbers (see the relationship between $\beta$ and the Biot number in Section 5, Remark 3) when at the interface the situation approaches the Dirichlet boundary condition.

The temperature profiles shown in Figure 1 and Figure 2 reveal the effects of the fractional order at selected time moments for various values of the fractional order; the decrease in the fractional order results in the deceleration of the heat conduction process, an expected damping effect when a hereditary, i.e., a finite speed of the heat diffusion, is taken into account. Moreover, the plots indicate that after a certain distance, the temperature becomes practically negligible; that is, at a fixed time, the propagation of the temperature profile is controlled by the fractional order $\alpha$: the low values of $\alpha$ represent shorter distances at which the temperature becomes practically zero. These points could be considered as fronts of the solution propagation albeit the problem considers boundary conditions at infinity (mathematically facilitating the solution but physically unrealistic). We will discuss the concept of a finite front of the solution in Section 5.

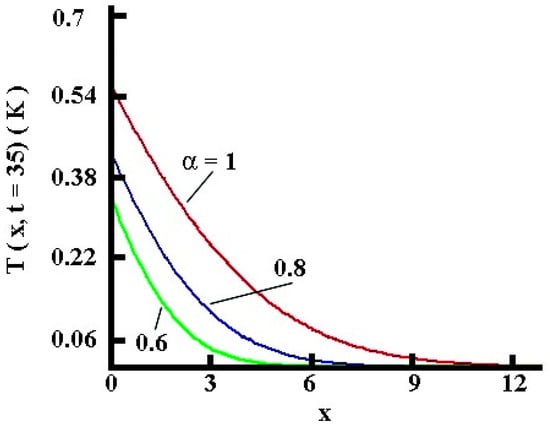
Figure 1. (color online). Temperature profiles, Solution (36), for various values of the fractional order $\alpha$.

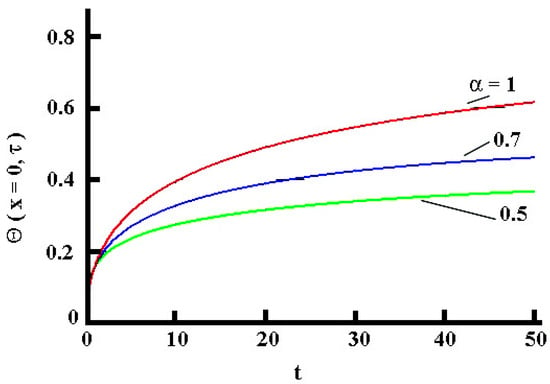
Figure 2. (color online). Dimensionless surface temperature $\Theta \left(x=0,\tau \right)$ evolution in time for various values of the fractional derivative parameter: (1) $\alpha =0.5$, (2) $\alpha =0.7$, (3) $\alpha =1$.

4.2. Surface Temperature Evolution in Time

The surface temperature grows in time, in the regime of heating, but the retardation, that is, its growth in time towards the fluid temperature ${\Theta }_f\left({\Theta }_f=\Theta \left(T_s=T_f\right)\right)$ is controlled by the fractional order $\alpha$.

4.3. Surface Flux Evolution in Time

Differentiating (35) concerning $x$, we obtain the expression about the temperature gradient in the Laplace domain

$$\frac{\partial T_L(x,p)}{\partial x}=\frac{T_f-T_0}{p^{1-\alpha }\sqrt[]{a}\cdot \left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}{e}^{-\sqrt{\frac{p^{\alpha }}{a}}x}.$$

(37)

Then, setting $x=0$, we obtain the temperature gradient at the interface, namely:

$$\frac{\partial T_L(0,p)}{\partial x}=\frac{T_f-T_0}{p^{1-\alpha /2}\sqrt{a}\cdot \left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}.$$

(38)

Further, from the expression

$$\frac{\partial T_L(0,p)}{\partial x}=\frac{T_f-T_0}{p^{1-\alpha /2}\sqrt{a}\cdot \left(1+\frac{1}{\beta }\sqrt{\frac{p^{\alpha }}{a}}\right)}=-\beta (T_f-T_0){\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\beta \sqrt{a}\cdot {\tau }^{\alpha /2}\right)}^n}{\Gamma (\alpha /2n+1)}}}{e}^{-pt}dt$$

(39)

we obtain the expression in the original physical coordinates

$$\frac{\partial T_L(0,\tau )}{\partial x}=-\beta (T_c-T_0)\cdot E_{\alpha /2,1}(-\beta \sqrt{a}\cdot {\tau }^{\alpha /2}).$$

(40)

Therefore, the heat flux density equals:

$$q=h\cdot \left(T_f-T_0\right)\cdot E_{\alpha /2,1}\left(-\beta \sqrt{a}\cdot {\tau }^{\alpha /2}\right).$$

(41)

or in a dimensionless form as

$$\frac{q}{h\cdot \left(T_f-T_0\right)}=E_{\alpha /2,1}\left(-\beta \sqrt{a}\cdot {\tau }^{\alpha /2}\right).$$

(42)

Here, $h$ is the heat transfer coefficient following the general definition of the Robin boundary condition (see Equation (1)).

As can be seen from Figure 3, the heat flux density is maximum at the first moments, and then gradually decreases, tending to zero when $\tau \to \infty$. At the same time, with a decrease in the order of the time derivative, this process slows down. At the initial moment, the heat flux density is maximum, and from (42) we obtain that it is equal to (the Mittag-Leffler function for $\tau =0$ equals $1$):

$$q_{\max }=b\cdot (T_f-T_0).$$

(43)

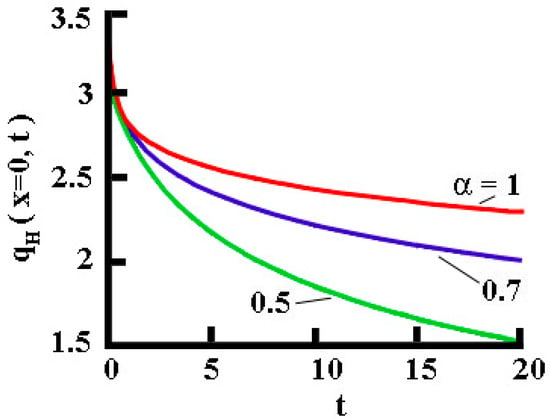
Figure 3. (color online). Surface heat flux evolution. Effect of the fractional order $\alpha$.

For $\alpha =1$, we have:

$$E_{1/2,1/2}\left(-z^{1/2}\right)={\displaystyle \sum _{k=0}^{\infty }\frac{{\left(-z^{1/2}\right)}^k}{\Gamma \left(\frac{1}{2}k+\frac{1}{2}\right)}}=\frac{1}{\sqrt{\pi }}\left(1-z^{1/2}{e}^{z}erf\left(z^{1/2}\right)\right),$$

(44)

$$\varphi \left(-\frac{1}{2},1,-\lambda \cdot t^{-1/2}\right)={\displaystyle \sum _{n=0}^{\infty }\frac{{\left(-\lambda \cdot t^{-1/2}\right)}^n}{n!\cdot \Gamma \left(-\frac{1}{2}n+1\right)}}=\frac{1}{\sqrt{\pi }}{e}^{-{\lambda }^{2}t}.$$

(45)

The behavior of the surface heat flux shown in Figure 3 cannot be explained physically if the Solution (42) is used despite their mathematical correctness. The impossibility of extracting physical insights from these solutions is compensated in this work by the outcomes of the approximate analytical solutions developed in Section 5.

Using Equalities (43) and (44), the solutions (36) and (37) take the form:

$$\frac{T(x,\tau )-T_0}{(T_f-T_0)}=\Theta (x,\tau )=\mathrm{erfc}\left(\frac{x}{2\sqrt{a\tau }}\right)-e^{\beta x+{\beta }^{2}a\tau }\mathrm{erfc}\left(\frac{x}{2\sqrt{a\tau }}+\beta \sqrt{a\tau }\right).$$

(46a)

In terms of the similarity variable $\eta =x/\sqrt{a\tau }$ and the dimensionless product $\beta \sqrt{a\tau }$ (see comments in Section 5), we have

$$\frac{T(x,\tau )-T_0}{(T_f-T_0)}=\Theta (x,\tau )=\mathrm{erfc}\left(\frac{\eta }{2}\right)-e^{\beta x+{\beta }^{2}a\tau }\mathrm{erfc}\left(\frac{\eta }{2}+\beta \sqrt{a\tau }\right).$$

(46b)

5. SOLUTION TO THE PROBLEM: Approximate Integral-Balance Approach

Model (8) is a subdiffusion equation well-known in the literature. However, before applying the integral-balance method with the Robin boundary condition, we have to clarify the method of nondimensalization of the model equations and the related boundary conditions. Some moments were touched on in the solution performed with the help of the Laplace transform, but now we stress the attention on the physical meaning of both the boundary conditions and the results developed.

In what follows, we consider two cases: heating and cooling by forced convection.

5.1. The Dimensionless Heat Transfer Model Reconsidered

5.1.1. The Dimensionless Convective Boundary Condition at $x=0$

The forced convective boundary condition implies

$$-k{\left(\frac{\partial T}{\partial x}\right)}_{x=0}=h\left(T_f-T_s\right).$$

(47a)

The relationship (47a) implies that $T_f>T_s$, i.e., the fluid temperature is higher than that of the body and we have convective heating. In the opposite case, that is the convective cooling with $T_f<T_s$, the boundary condition is

$$-k\left(T\right){\left(\frac{\partial T}{\partial x}\right)}_{x=0}=h\left(T_s-T_f\right).$$

(47b)

In the case of such conditions, the reference temperature is $T_f$ [22], so after nondimensalization of the boundary Conditions (47a) and (47b), we have (48a) and (48b), respectively.

$$-{\left(\frac{\partial u}{\partial \tilde{x}}\right)}_{x=0}=\frac{hL}{k}\left(1-u_s\right)\Rightarrow -{\left(\frac{\partial u}{\partial \tilde{x}}\right)}_{x=0}=Bi\left(1-u_s\right)$$

(48a)

$${\left(\frac{\partial u}{\partial \tilde{x}}\right)}_{x=0}=\frac{hL}{k_0}\left(u_s-1\right)\Rightarrow -{\left(\frac{\partial u}{\partial \tilde{x}}\right)}_{x=0}=Bi\left(u_s-1\right)$$

(48b)

The temperature $T_f$ is chosen as a reference scale in the nondimensalization procedure instead of the common difference $\left(T_f-T_s\right)$ because the surface temperature $T_s$ changes in time and cannot be used for such purposes. Some comments about this approach were made in Remark 1.

Remark 2:

In the non-dimensalization procedure resulting in (48a) and (48b), we suggested that a length scale $L$ exists. It was conducted especially to show clearly that the Biot number $Bi=\frac{hL}{\lambda }$ controls the heat transfer across the solid-fluid interface and how it represents the heat transfer resistance when the heat flux is supplied (released) by convection and transported through the body by heat conduction.

However, in the cases of semi-infinite media, the diffusion processes have no length and time scales. In such cases, the non-dimensalizations of the boundary Conditions (47a) and (47b) are possible concerning the temperature only, namely

$$-{\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\frac{h}{k}\left(1-u_s\right)\Rightarrow -{\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\beta \left(1-u_s\right).$$

(49a)

$${\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\frac{hx}{k}\left(u_s-1\right)\Rightarrow -{\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\beta \left(u_s-1\right)$$

(49b)

Here, the ratio $\beta =h/k$ is not dimensionless and has a dimension $\left[m^{-1}\right]$ and $1/\beta =k/h$ is with a dimension of length $\left[m\right]$. Hence, in some circumstances this can be used as a length scale. In addition, in $Bi=\beta L$, the length scale $L$ can be defined for the problem of interest.

5.1.2. Dimensionless Model Equation Reconsidered

With the variable $u=T/T_f$, we have the dimensionless model of transient heat conduction (50a) with convection boundary conditions for heating (50b) and cooling (50c):

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=a\frac{{\partial }^{2}u}{\partial x^2}.$$

(50a)

Convective heating:

$$-u_s{\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\beta \left(1-u_s\right).$$

(50b)

Convective cooling:

$$-u_s{\left(\frac{\partial u}{\partial x}\right)}_{x=0}=\beta \left(u_s-1\right).$$

(50c)

5.2. The Integral Balance Method

5.2.1. The Integral-Balance Method: The Concept of Finite Penetration Depth

The integral-balance approach used in this work to solve (1) suggests a finite depth of penetration $\delta$ (a sharp front) that evolves in time, i.e., $\delta \left(t\right)$. Beyond the point $x=\delta \left(t\right)$, the medium is undisturbed and the following Goodman’s boundary conditions [23] are imposed on the assumed profile $u_a\left(x,t\right)$:

$$u_a\left(\delta ,t\right)=\frac{\partial u_a\left(\delta ,t\right)}{\partial x}=0,x\ge \delta , \delta \left(t=0\right)=0.$$

(51)

In the context of subdiffusion, the concept of a final penetration depth is motivated by experimental facts of almost sharp fronts of penetration of the diffusion substances [24,25,26]. Moreover, in the fractional diffusion equation referring to sub-diffusion problems [4], the heat (mass) propagation (diffusion) is so slow [27,28] that the concept of the penetration layer becomes essential since it exists [24,25,27,28].

Following the heat-balance concept [29] to the time-fractional diffusion equation at any time $t$, the integral of both sides (50a) from $0$ to $\delta$ should be

$${\displaystyle \underset{0}{\overset{\delta }{\int }}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}dx}=-a{\left(\frac{\partial u}{\partial x}\right)}_{x=0}.$$

(52)

The idea of the integral-balance method is to replace $u\left(x,t\right)$ in (52) with an assumed profile $u_a\left(x,t\right)$ expressed as a function of the dimensionless coordinate $x/\delta$ and satisfying Goodman’s boundary conditions (51). The integration in (52) yields an equation defining the penetration depth $\delta \left(t\right)$ and consequently the approximate distribution of temperature. The simpler form of the method (52) is known as the heat-balance integral method (HBIM) [23]. It has been conceived [13] to develop approximate closed-form solutions to fractional subdiffusion equations and further apply them to solve other complex models involving time-fractional derivatives [29]. The integral of the left-side in (52) was termed—fractional-time heat-balance Integral (FT-HBI) [29]. The main drawback of HBIM applied to either integer-order or fractional differential equations is that the gradient at $x=0$, in the right-hand side of (52), should be determined through the assumed approximate profile. This drawback can be avoided by the double-integration method (DIM) presented briefly in the next section. The method has been conceived for integer-order problems and then applied to time-fractional equations [29] as explained next.

5.2.2. Double-Integration Method to Time-Fractional Diffusion Equation

The first step of DIM is the integration of (1) from $x$ to $\delta$, namely [29]

$${\displaystyle \underset{x}{\overset{\delta }{\int }}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}dx}=-a{\left(\frac{\partial u\left(x,t\right)}{\partial x}\right)}_{x=0}.$$

(53)

and integrating (53) again from $0$ to $\delta$, we obtain [29]

$${\displaystyle \underset{0}{\overset{\delta }{\int }}\left({\displaystyle \underset{x}{\overset{\delta }{\int }}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}dx}\right)}=a\cdot u\left(0,t\right).$$

(51)

Therefore, the right side of (54) depends on the boundary condition at $x=0$ and, in contrast to (52), is independent of the choice of the assumed profile.

Equation (54) is the principle relationship of the double integration method when the differential equation is of fractional order. It is general and does not specify the time of the time-fractional derivative $\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}$ [30]. For the coherence in the solutions developed here, we consider the time-fractional Caputo derivative. Following the terminology established [29], the left side of (54) is termed hereafter as fractional-time double-balance integral (FT-DBI).

5.2.3. Convective Boundary Conditions and Applications of the Integral-Balance Method

To clarify the literature background we will comment on some integral balance solutions (single integration approach, i.e., HBIM) to the case of a forced convection boundary condition developed in a few studies available in the literature. Davis and Worthington [31] have developed a solution using a quadratic polynomial profile and a linear boundary condition $\partial \theta \left(0,t\right)/\partial x=Bi{\left({\theta }_s-{\theta }_a\right)}^p$, where $1\le p\le 4/3$, ${\theta }_s=T_s/T_0$, ${\theta }_a=T_a/T_0$; with $p=1$ we have forced convection, whilst $p=4/3$ corresponding to upward-facing surface cooling due to turbulent natural convection. This solution has met difficulties in the complete implementation of the integral-balance method because the surface temperature should be determined through the boundary condition; for a given Biot number, the Newton-Raphson method has been applied and the solution then used in the approximate profile in case of low Biot numbers $\left(0.1\le Bi\le 10\right)$.

Myers [32] also mentioned a similar problem in the solution of the equation of the penetration depth when applying the classical heat-balance integral method (HBIM) and the double integration method (DIM) to the case of forced convection for $Bi=1$. Braga et al. [33] have solved the same problem, without specifying $Bi$ and developed an expression about the penetration depth in terms of the Lambert W function.

5.3. DIM Solution to the Problem

5.3.1. Assumed Profile

The dimensionless parabolic profile (with unspecified exponent) becomes [29]

$$u_a=u_s{\left(1-x/\delta \right)}^n.$$

(55)

with Goodman’s boundary conditions

$$u\left(0,t\right)=u_s.$$

(56a)

$$u\left(\delta ,t\right)=u_0=0 \mathrm{or} k{\left(\frac{\partial u}{\partial x}\right)}_{x=\delta }=0.$$

(56b)

Recall, that the surface temperature $u_s$ should be defined through the boundary condition (49a) or (49b) and the profile (55), a problem developed in the next section. The exponent $n$$n$ is not specified here and will be discussed in the sequel when the approximate solutions will be analyzed.

5.3.2. Surface Temperature Determination with the Assumed Profile

At this point of the analysis, we will discuss two cases: convective heating and convective cooling, which mathematically alter the temperature difference in the flux expression. The equations defining the surface temperature in these cases are:

• Convective heating

From (47a) we have

$$-u_s\frac{n}{\delta }=\beta \left(1-u_s\right)\Rightarrow u_s\left(\frac{n}{\delta }\right)+\beta u_s-\beta =0.$$

(57)

From (57) we get

$$u_s=\frac{\beta \delta }{n+\beta \delta }.$$

(58)

The case has been solved by Braga et al. [33] (the case with $\alpha =1$) and the penetration depth can be expressed by the Lambert W function.

If $\beta$ is large, that means large Biot numbers due to intensive mixing, or more realistic due to large body size with a temperature gradient in it, we have $u_s\approx 1$. Otherwise, for small Biot numbers, we have $u_s\approx \beta \delta /n$. For the specific case with $\beta =1$ we get

$$u_{s\left(\beta =1\right)}=\frac{\delta }{n+\delta }.$$

(59)

This case has been analyzed by Myers [33] (the case $\alpha =1$).

• Convective cooling

From (49b) we have

$$-u_s\frac{n}{\delta }=\beta \left(u_s-1\right)\Rightarrow u_s\left(\frac{n}{\delta }\right)-\beta u_s+\beta =0$$

(60)

and

$$u_s\frac{n}{\delta }=\beta \left(u_s-1\right)\Rightarrow u_s=\frac{\beta \delta }{\left(\beta \delta -n\right)}.$$

(61)

For small values of $\beta$, $u_s$ tends to be negative, so the condition $\beta \delta -n>0$ should be satisfied. However, for large $\beta$ we have $u_s\to 1$, that is the case with a fixed temperature boundary condition.

5.3.3. Penetration Depth

Therefore, following the integral relation (54) and the assumed profile (55)

$${\displaystyle \underset{0}{\overset{\delta }{\int }}\left({\displaystyle \underset{x}{\overset{\delta }{\int }}\frac{{\partial }^{\alpha }{u}_a\left(x,t\right)}{\partial t^{\alpha }}dx}\right)}=\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left[N{\delta }^2\right]=N\frac{{\partial }^{\alpha }\left(u_s{\delta }^2\right)}{\partial t^{\alpha }},$$

(62)

where $N{\left[\left(n+1\right)\left(n+2\right)\right]}^{-1}$ and $u_s$ is defined by (57) or (58).

Then, the integral relation (62) yields

$$\frac{{\partial }^{\alpha }\left(u_s{\delta }^2\right)}{\partial t^{\alpha }}=aN{u}_s.$$

(63)

Now, bearing in mind that the surface temperature is a non-zero value we may solve (63), and the physical condition $\delta \left(t=0\right)=0$, since there is heat conduction before $t=0$.

$${\delta }^2=a\left(n+1\right)\left(n+2\right)\frac{t^{\alpha }}{\Gamma \left(1+\mu \right)}\Rightarrow \delta \left(t\right)=\sqrt{a{t}^a}\sqrt{\frac{\left(n+1\right)\left(n+2\right)}{\Gamma \left(1+\alpha \right)}}.$$

(64)

For $\alpha =1$ we obtain the integer order relationship ${\delta }_0=\sqrt{at}\sqrt{\left(n+1\right)\left(n+2\right)}$ [34].

Simulations of the evolution of the penetration depth in different time intervals and demonstrating the retardation effect (Figure 4d) of the fractional order $\alpha$ are shown in Figure 4.

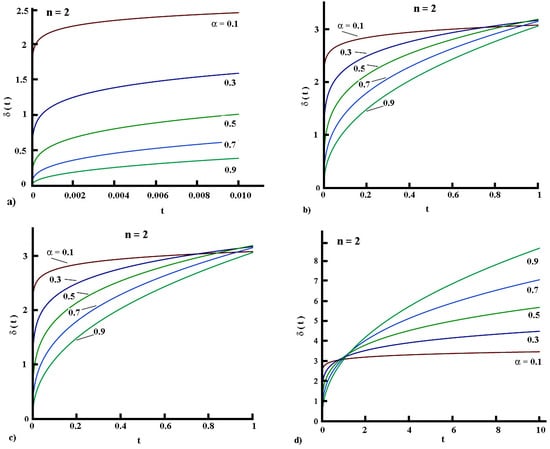
Figure 4. (color online). Penetration depth evolution in different time intervals and various values of the fractional order $\alpha$: (a) Very short time; (b) Short times; (c) Times less than $t\le 1$; (d) Longer times.

For the sake of simplicity and clarity in the presentation of the results obtained in the solution simulations, it was accepted $a=1$ and $n=2$ (the value $n=2$ comes from classical integral-balance solutions [23] and is too close to the optimal values of the profile exponents [29]). They facilitate the presentations, making it easy to demonstrate the qualitative behavior of the solutions, even though $a=1$ is physically incorrect. The problems emerging with the profile exponent $n$ are discussed at the end of this article.

5.3.4. Approximate Temperature Profiles

Now, we may construct the approximate solutions with the two types of convective boundary conditions:

• Convective heating

$$u_a=\frac{\beta \delta }{n+\beta \delta }{\left(1-\frac{x}{\delta }\right)}^n,$$

(65)

• Convective cooling

$$u_a=\frac{\beta \delta }{\beta \delta -n}{\left(1-\frac{x}{\delta }\right)}^n.$$

(66)

The solutions for a fixed time ($t=0.1$) are presented in the Figure 5.

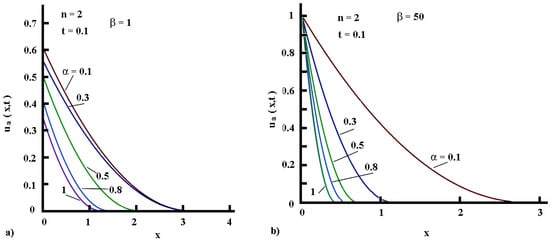
Figure 5. (color online). Temperature profiles for a fixed time ($t=0.1$) and cases of heating (a) and cooling (b) regimes. Notes: (1) for the cooling regime the condition $\beta \delta >n$ is obeyed; (2) The points where the profiles cross the abscissa denote the fronts of the penetration depths.

Before studying the approximate profiles for various values of the parameter $\beta$, we have to see what the behaviors of the surface temperature and flux are, thus assessing the physical adequacy of the developed approximate solutions.

5.3.5. Surface Temperature Evolution in Time

• For the regime of heating

$$u_s=\frac{\beta \delta }{n+\beta \delta }.$$

(67)

For large values of $\beta$, which correspond to large Biot numbers due to either large $h$ or small $k$, we obtain

$$u_s=\frac{\beta \delta }{n+\beta \delta }=\frac{\delta }{\frac{n}{\beta }+\delta }\approx 1.$$

(68)

That is, when the ratio $n/\beta$ becomes negligible and $\delta$ evolves in time, we obtain a regime close to the case of the Dirichlet boundary condition; from another point of view, as the product $\beta \delta$ becomes large, we approach this boundary condition too. This comment is consistent with the estimations at the beginning of Section 4.1 related to high values of $\beta$. Another extreme case for small values of $\beta$ appears with bodies having a high-temperature conductivity $k$ that finally results in an almost missing temperature gradient in the medium. In such a case, we have short times (i.e., for a thin thermal layer) with $\beta \delta <<1$ for which we obtain $u_s{\left(t\right)}_{\beta \delta <<1}\approx 1/n$. However, as the penetration depth $\delta \left(t\right)$ evolves, we may approximate

$$u_s\left(t\right)=\frac{1}{\frac{n}{\beta \delta }+1}\approx 1.$$

(69)

That is, when the ratio $n/\delta$ becomes negligible and $\delta$ evolves in time, we obtain a regime close to the case of the Dirichlet boundary condition.

5.3.6. Surface Flux Evolution in Time

From the construction of the assumed profile (55), it follows that

$$-\frac{\partial u_a}{\partial x}=u_s\frac{1}{\delta }n.$$

(70)

Then, the surface fluxes are:

• For the regime of heating

$$q_H=-k\frac{\partial u_a}{\partial x}=k\frac{\beta \delta }{n+\delta \beta }\frac{1}{\delta }n\Rightarrow q_H=k\frac{\beta }{n+\delta \beta }n=\frac{h}{n+\delta \beta }n,$$

(71)

bearing in mind that $\beta =h/k$.

For large values of $\beta$ and fixed $n$, we have $q_H\approx \frac{n}{\delta }$, i.e., a decreasing heat flux. For small values of $\beta$, we obtain $q_H\approx \frac{\beta n}{n}\approx \beta$, meaning that the heat flux is almost constant due to the negligible temperature gradient in the medium.

• For the regime of cooling

$$q_C=-k\frac{\partial u_a}{\partial x}=k\frac{\beta \delta }{\left(\beta \delta -n\right)}\frac{1}{\delta }n\Rightarrow q_C=k\frac{\beta }{\beta \delta -n}n=\frac{h}{\beta \delta -n}n.$$

(72)

For large $\beta$ and fixed $n$, we obtain $q_C=k\frac{\beta }{\beta \delta -n}n\approx k\frac{\beta n}{\beta \delta }=k\frac{n}{\delta }$.

Otherwise, for small values $\beta$ and short times, we have $q_C=k\frac{\beta }{\beta \delta -n}n\approx k\beta \approx h$ which is physically reasonable since the heat flux is directed from the medium to the fluid. When the condition $\beta \delta -n>0$ is obeyed, and $\beta \delta <<n$, after a certain period, then $q_C\approx k\frac{n}{\delta }$.

For the plotting of the time variations of the surface flux and to better explain the results obtained, we will recast (71) and (72) as

$$\frac{q_H}{h}=\frac{n}{n+\delta \beta },\frac{q_C}{h}=\frac{n}{\delta \beta -n},$$

(73)

bearing in mind that under certain hydrodynamic conditions, the value of the heat transfer coefficient $h$ is accepted as a constant. Recall that the ratio $q/h$ has a dimension of temperature.

In light of the approximate solutions developed, the convective part of the Robin boundary condition can be presented as $q=h{T}_f\left(T_s/T_f-1\right)=h{T}_f\left(u_s-1\right)$, where $u_s=T_s/T_f$ is the dimensionless surface temperature used in the solution (see the first line in Section 5.1.2 and the comments in Remark 2). As $u_s\left(t\right)$ rises in time and approaches unity, as demonstrated by the plots in Figure 6, Figure 7 and Figure 8, the difference $\left(u_s-1\right)$ diminishes, and the surface heat flux also diminishes, accordingly. At this point, we have to recall that for large values of the product $\beta \delta$, due to high values of $\beta$ or for longer times, the surface temperature mimics the Dirichlet boundary condition. In such a case, the heat flux through the medium should be constant in time. The analysis of the surface heat flux for the regime of cooling is analogous.

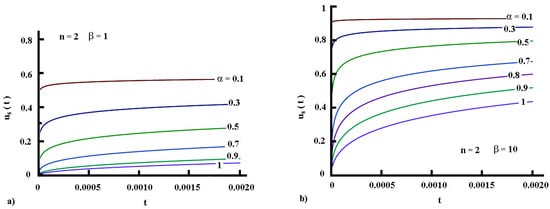
Figure 6. (color on-line). Surface temperature evolution for very short times: (a) $\beta =1$; (b) $\beta =10$.

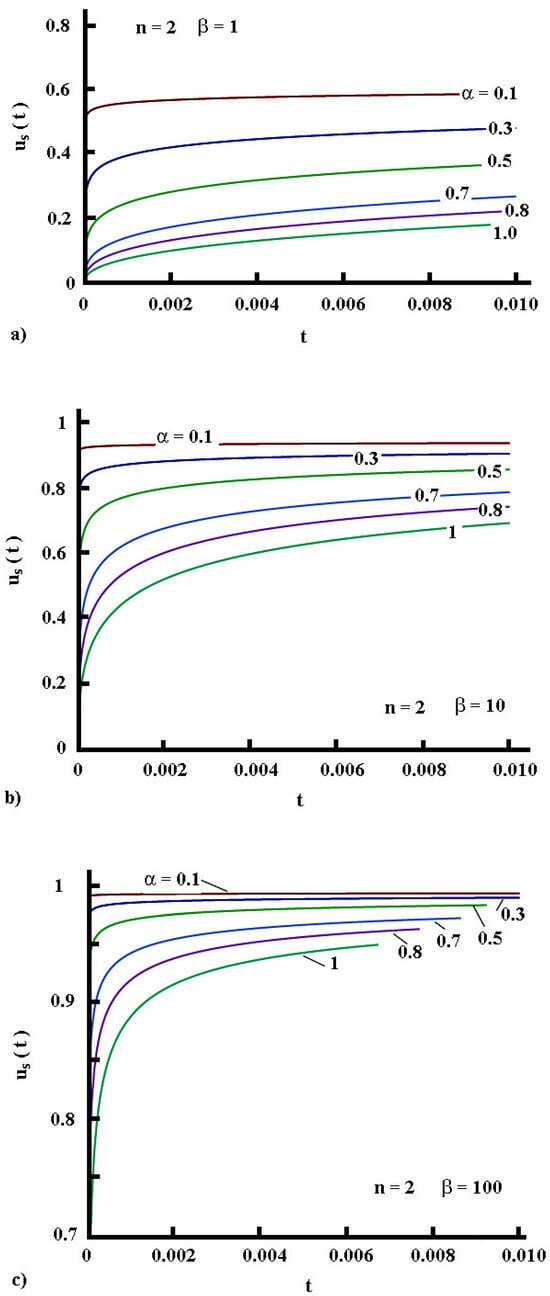
Figure 7. (color online). Surface temperature evolution for short times: (a) $\beta =1$; (b) $\beta =10$; (c) $\beta =100$.

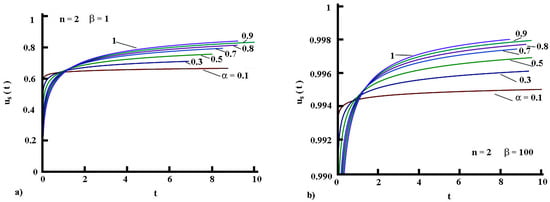
Figure 8. (color online). Surface temperature evolution for longer times: (a) $\beta =1$; (b) $\beta =100$.

The plots in Figure 9 and Figure 10 reveal a steady decrease in the time of the surface heat flux, precisely per unit heat transfer coefficient. Similar behavior was obtained with a formal solution obtained through the Laplace transform (see Figure 3). Further, bearing in mind that, from the side of the fluid, $q_{{}_H}=h\left(T_s-T_f\right)$, the increase in the surface temperature, for the regime of heating, for instance, reduces the difference $\left(T_s\left(t\right)-T_f\right)$ since $T_s\left(t\right)\to T_f$ for $t>0$ and consequently $q_{{}_H}$ decreases in time up to a moment when $\Delta T_{sf}=\left(T_s\left(t\right)-T_f\right)$ attaining a certain minimal value after a long time which, as a result, yields a heat flux that is almost unchanging in time.

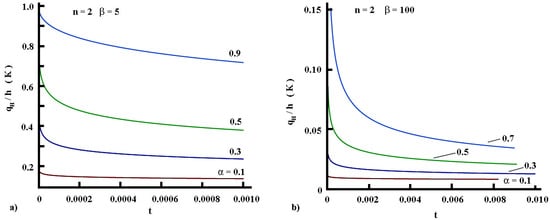
Figure 9. (color online). Surface flux time evolution in the regime of heating: (a) Very short times; (b) Short times. Effects of the parameter $\beta$.

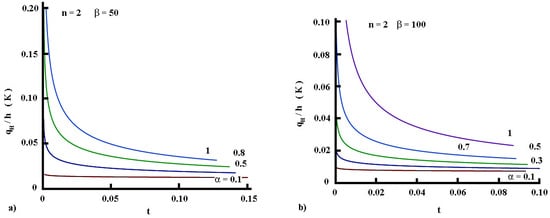
Figure 10. (color online). Surface flux time evolution in the regime of heating (short times): Behavior for large values of $\beta$.

In the context of the results developed, it is worth noting that in both cases, heating or cooling, concerning the heat conduction in the solid medium, the heat flux decreases as the penetration depth $\delta \left(t\right)$ evolves in time. This can be simply explained by accepting the thermal penetration layer as a slab, where the Fourier law can be expressed by the well-known integral relation, for a certain moment.

$$q=\frac{k}{\delta }\left(T_s-T_{\delta }\right).$$

(74)

It must be borne in mind that there is a continuity of the heat flux across the boundary $x=0$; that is, the increased penetration depth $\delta$ results in a decreased heat flux.

Now, concerning the solution through the Laplace transform, we may say that such a physical analysis is, to a greater extent, impossible due to its formality, despite the mathematical correctness. Thus, approximate solutions with a well-formulated physical basis allow an understanding of the results and the behavior of the formal solution.

5.3.7. Thermal Impedance

The thermal impedance is the ratio of the temperature difference to the heat flux, namely

$$Z=\frac{\Delta T}{q}.$$

(75)

From the above results we obtain:

For the heating regime, using (65) and (71) we have

$${}_{H}Z_t^{\alpha }=\frac{u_a\left(x=0\right)}{q_H}=\frac{1}{k}\frac{\delta }{n}=\frac{\sqrt{a{t}^{\alpha }}}{n}\sqrt{\frac{\left(n+1\right)\left(n+2\right)}{\Gamma \left(1+\alpha \right)}}.$$

(76)

For the cooling regime, using (66) and (72) we obtain

$${}_{C}Z_{\alpha }^t=\frac{u_a\left(x=0\right)}{q_C}=\frac{\left(\frac{\beta \delta }{\beta \delta -n}\right)}{k\frac{\beta }{\beta \delta -n}n}=\frac{1}{k}\frac{\delta }{n}=\frac{1}{k}\frac{\sqrt{a{t}^{\alpha }}}{n}\sqrt{\frac{\left(n+1\right)\left(n+2\right)}{\Gamma \left(1+\alpha \right)}}.$$

(77)

The results (76) and (77) are identical and independent of the parameter $\beta$. We may extract from them the most important issues explaining some moments of the transient heat transfer. From (76) and (77), we have the thermal impedance $Z_t^{\alpha }=Z\left(\alpha ,t,k\right)$:

$$Z_t^{\alpha }\equiv \frac{1}{k}\frac{\sqrt{a{t}^{\alpha }}}{\sqrt{\Gamma \left(1+\alpha \right)}}.$$

(78)

The obvious fact is that with the decrease in thermal conductivity $k$, the resistance concerning the heat energy transferred to/from the medium increases, which is a physically reasonable result. Bearing in mind that $\beta =h/k$, a decrease in $k$ means high values of $\beta$ (high Bio numbers) and an increasing temperature gradient in the medium.

Further, the decrease in the fractional order $\alpha$, that is the increase in the medium damping effect, yields an increased $Z_t^{\alpha }$ due to the denominator depending on $\Gamma \left(1+\alpha \right)$. Bearing in mind that $\Gamma \left(1+\alpha \right)$ is of an order of magnitude of unity, in the range $0<\alpha <1$, this effect is not significant. However, since $Z_t^{\alpha }$ is time-dependent, $Z_t^{\alpha }\equiv t^{\alpha /2}$, the decrease in $\alpha$, i.e., the increase in the damping effect results in a slower increase in $Z_t^{\alpha }$ and vice versa.

Results similar to (73)–(75) can be obtained from the solution developed by the Laplace transform, but evaluation of the thermal resistance $Z_t^{\alpha }$ using (36), (37), and (41) is not so obvious and it is hard to see the physical meaning behind it.

Remark 3:

After these results, we are interested in the effect of the parameter $\beta$. To clarify the results developed before this remark, we have to remember that the dimension of $\beta =h/k$ is $m^{-1}$, thus we have a dimensionless product $\beta \delta$. Moreover, since $\delta \equiv \sqrt{a{t}^{\alpha }}$, we have a product $\delta \equiv \beta \sqrt{a{t}^{\alpha }}=\frac{h}{k}\sqrt{a{t}^{\alpha }}$ that is also dimensionless (this dimensionless product appears in the solutions (40)–(42) and more explicitly in (46a), taking into account that in these results the dimension of the thermal diffusivity is $m^2/s^{\alpha }$).

6. Outcomes, Comparative Analysis, and Open Problems

At the end of this study where two analytical solutions to transient heat conduction in a semi-infinite medium with a Robin boundary condition were developed, we have to strike the balance and outline the main outcomes.

6.1. Outcomes and Comparative Analysis

The two solutions developed provide outcomes that are physically sound and balance each other in terms of accuracy and the ability to physically interpret the results. Precisely, the solution by Laplace transform in time (Section 4) provides solutions that are hard to explain, i.e., the rise of the surface temperature in time and the reduction in the surface heat flux. In contrast, the approximate integral-balance solution has a primary clearly defined physical basis concerning the finite penetration depth, since there are no physical reasons for the temperature field to propagate into the medium with infinite speed as it follows from the exact solution. It is worth noting that the idea of a front of the solution could come to mind from the profiles in Figure 1 where after a certain distance from the interface $x=0$ the temperature becomes negligible and could be accepted as zero.

Further, the surface temperature and flux variations in time are more physically clear when the results of the approximate solution are interpreted and this allows us to understand the meaning of the results of the exact solution.

6.2. Open Problem

The approximate solution was developed by the assumed parabolic profile with an unspecified exponent (55). In this study, we used $n=2$. This approach had the only view to present clear and explainable results. However, we have to remember that the assumed profile $u_a$ (55) satisfies the integral relation (54) (DIM solution) but not the original heat conduction model (50a). Hence, if the approximate solution is replaced in the model (50a), we obtain

$$\frac{{\partial }^{\alpha }{u}_a}{\partial t^{\alpha }}-a\frac{{\partial }^2{u}_a}{\partial x^2}\ne 0.$$

(79)

That is, the residual function $R\left(x,t,\alpha ,n\right)$:

$$R\left(x,t,\alpha ,n\right)=\frac{{\partial }^{\alpha }{u}_a}{\partial t^{\alpha }}-a\frac{{\partial }^2{u}_a}{\partial x^2}.$$

(80)

should attain a minimum within the interval defined by the thermal layer, i.e., for $0\le x\le 1$ and for $t>0$. This means that we have to look for an optimal value of the exponent $n$ where there are two parameters: the fractional order $\alpha$ and the ratio $\beta =h/k$. In this direction, we have two approaches:

Minimization of the norm $\left|R\left(x,t,\alpha ,n\right)\right|$

$${\displaystyle \underset{0}{\overset{\delta }{\int }}\left|R\left(x,t,\alpha ,n\right)\right|}dx={\displaystyle \underset{0}{\overset{\delta }{\int }}\left|\frac{{\partial }^{\alpha }{u}_a}{\partial t^{\alpha }}-a\frac{{\partial }^2{u}_a}{\partial x^2}\right|dx}.$$

(81)

Minimization of the squared residual function $\left[R^2\left(x,t,\alpha ,n\right)\right]$

$${\displaystyle \underset{0}{\overset{\delta }{\int }}\left[R^2\left(x,t,\alpha ,n\right)\right]}dx={\displaystyle \underset{0}{\overset{\delta }{\int }}{\left(\frac{{\partial }^{\alpha }{u}_a}{\partial t^{\alpha }}-a\frac{{\partial }^2{u}_a}{\partial x^2}\right)}^{2}dx}.$$

(82)

Therefore, we have to expect $n\left(\alpha ,\beta \right)$ depending in a complex way on $\alpha$ and $\beta$. This task addresses an open problem beyond the scope of the present work and draws new studies, but we have to mention that similar problems have been resolved in [13,29].

7. Conclusions

Transient heat conduction in a hereditary semi-infinite medium with a Robin boundary condition has been considered and solved by two analytical methods: exact solution by application of the Laplace transform, and approximate integral-balance solution. The results obtained allow direct physical interpretations which is an important moment in mathematical modeling. Both solutions provide similar results, not compared from a quantitative point of view but allowing a comparative analysis. The latter especially envisages the phenomena at the interface $x=0$, i.e., the surface temperature and flux. It was demonstrated that the thermal impedance at the boundary depends on the fractional order $\alpha$.

From the authors’ point of view, the present study presents alternative approaches to solve the transient heat conduction in a hereditary semi-infinite medium with Robin boundary conditions and allows clear physical explanations of the results developed.