Fractional Order Weighted Mixed Sensitivity-Based Robust Controller Design and Application for a Nonlinear System
Abstract
:1. Introduction
1.1. The Contex of Research
1.2. Literature Review
1.3. Research Gaps
1.4. Authors’ Contribution
- Fractional-order small signal modeling for IM is undertaken for the first time, achieved through the approximation of experimental data.
- The fractional Laplace operator is incorporated in weighting functions, following to the general guidelines of mixed sensitivity.
- Optimal parameters are determined to enhance the robust stability and nominal performance of the closed-loop system with the designed controller.
- Three distinct robust controllers (Robust PID Controller, FOPID Based H∞ Controller and Fixed-structure H∞ controller) are designed and compared in terms of robustness and tracking performances.
1.5. Chapter Organization
2. Modeling of Induction Motor System
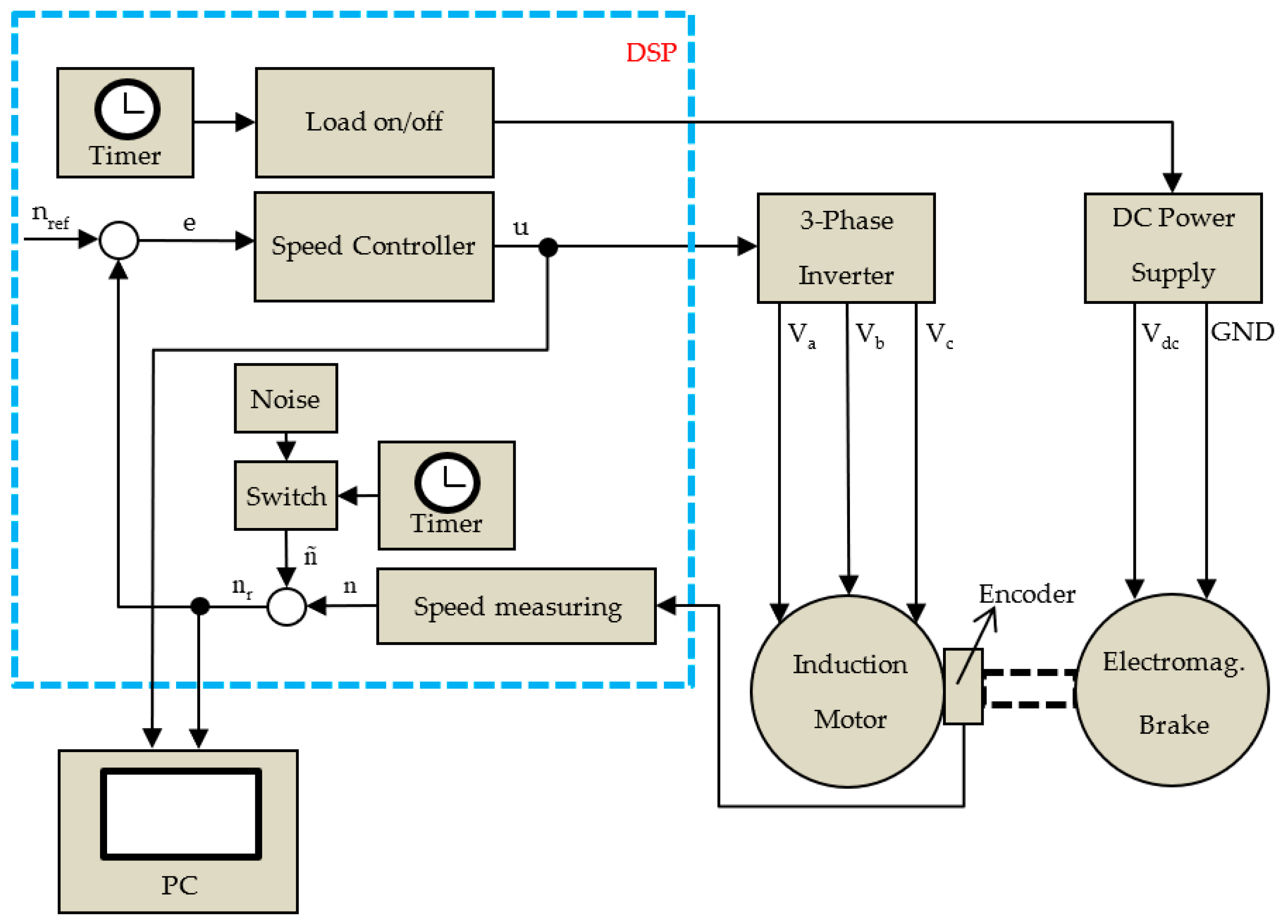
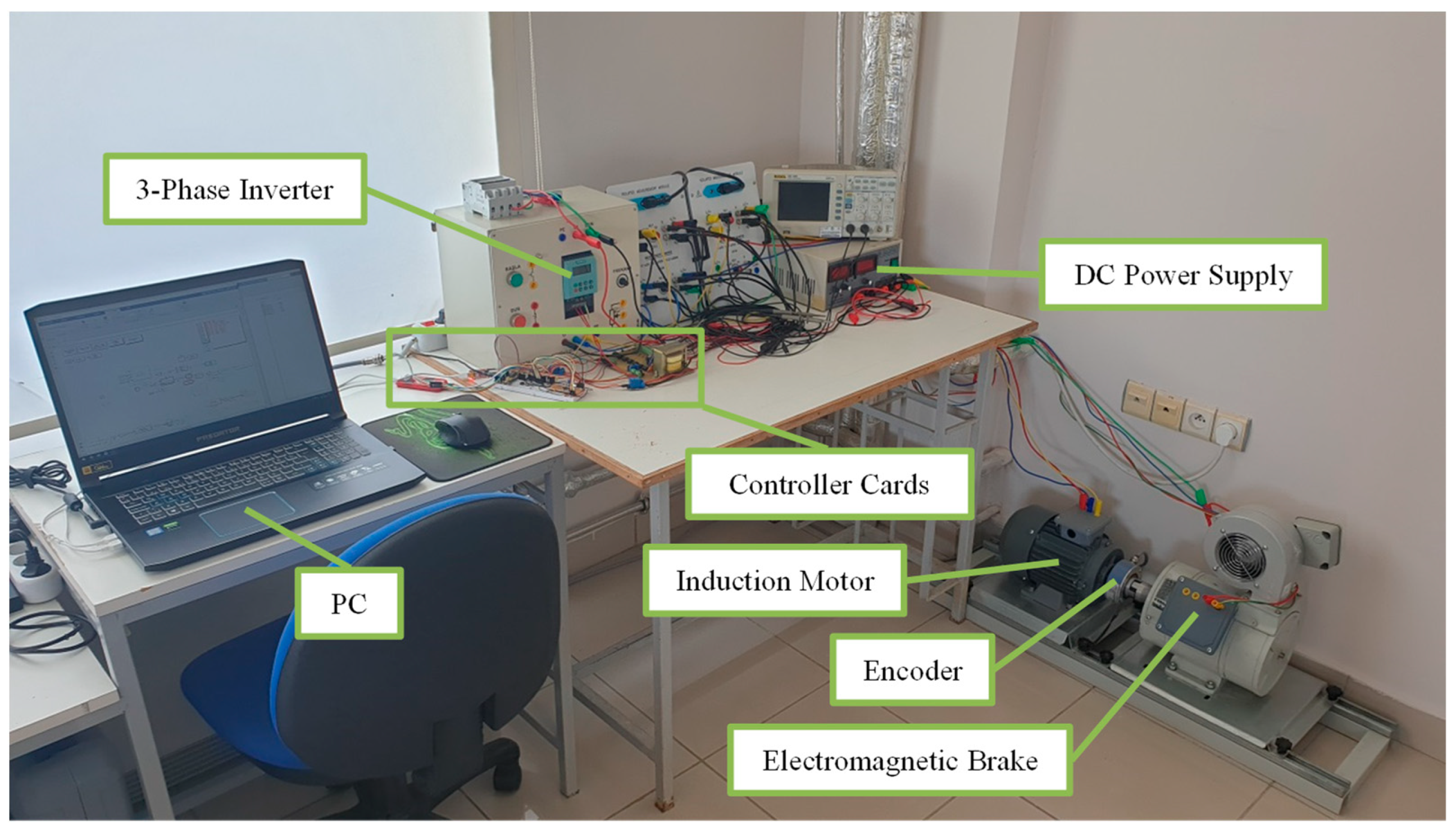
2.1. Description of Experimental Setup
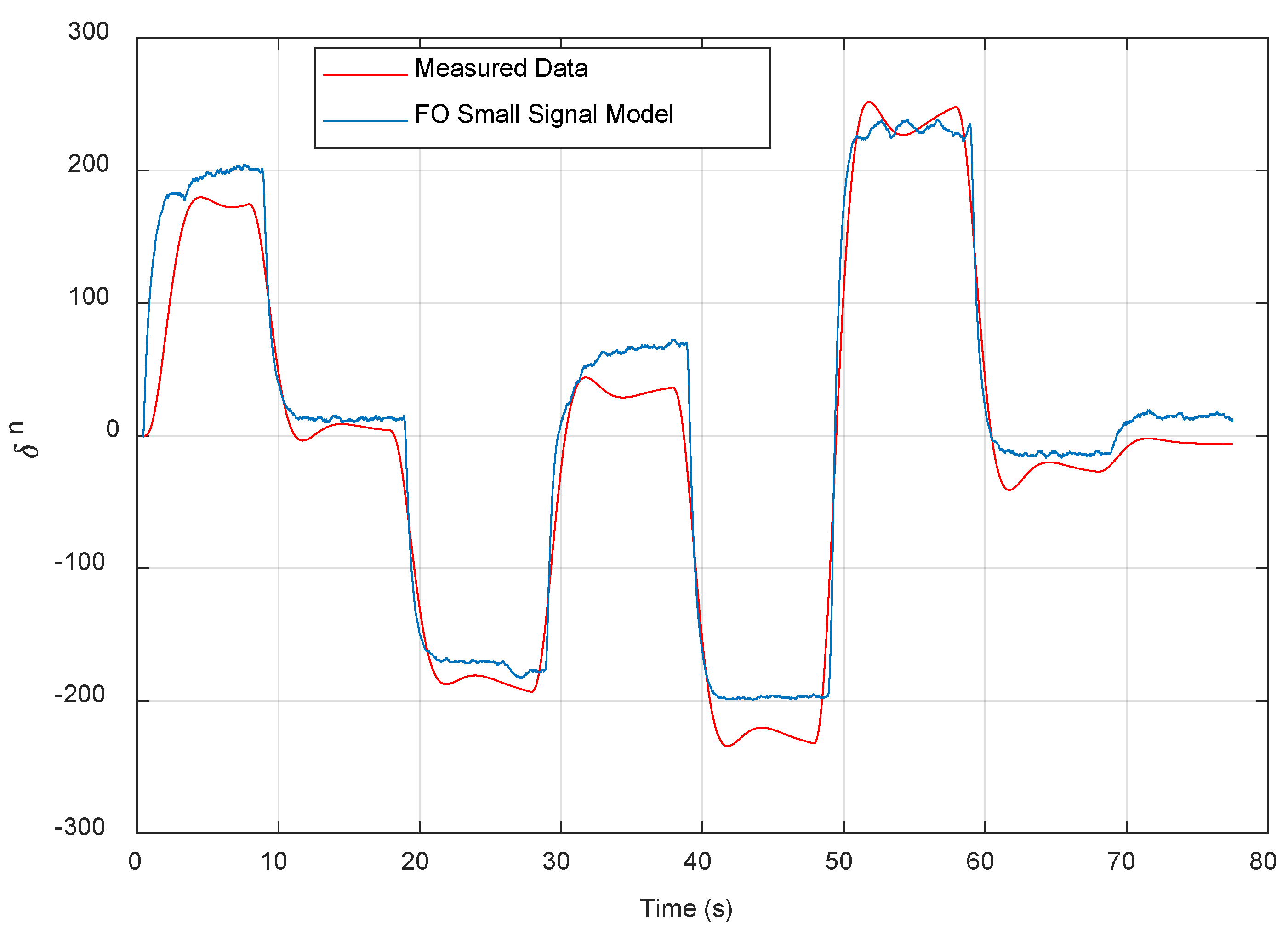
2.2. Fractional Order Small Signal Modeling of IM
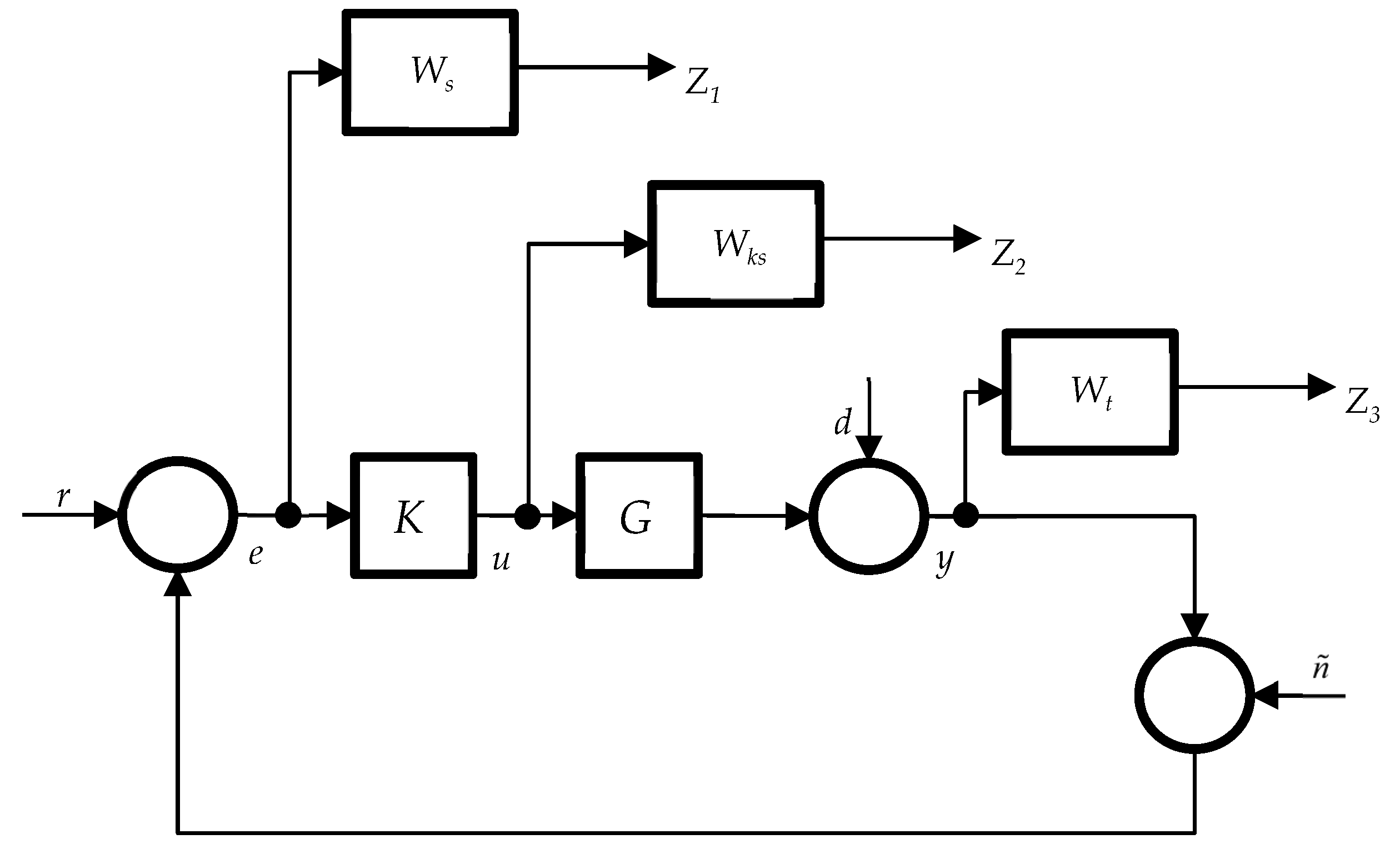
3. Weighting Mixed-Sensitivity-Based H∞ Controller Design
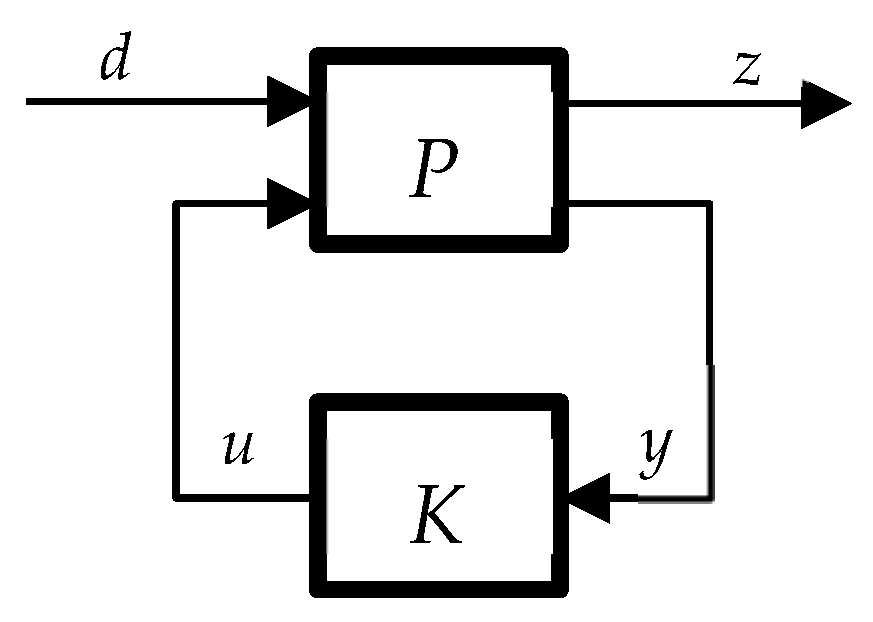
3.1. Main Concepts of H∞ Control Based on Weighted Mixed Sensitivity
3.2. Fractional Order Weighted Mixed Sensitivity Problem
- It is recommended to have and to ensure that the frequency responses of weighting functions are maximally flat in the high and low frequency ranges.
- High-performance tracking dynamics with acceptable noise levels are achieved with .
- Effective disturbance attenuation is achieved by increasing ωBP as much as possible until it no longer causes a peak in the sensitivity curve.
- When considering measurement noise, it becomes necessary to decrease ωBT until it starts affecting tracking performance.
3.3. Selecting of Weighting Functions
3.4. Design of Proposed Robust Controllers
3.4.1. Robust PID Controller
- The suitable bandwidth ωol = 0.1676 rad/s;
- The appropriate phase margin ∆ϕ = 70.2°.
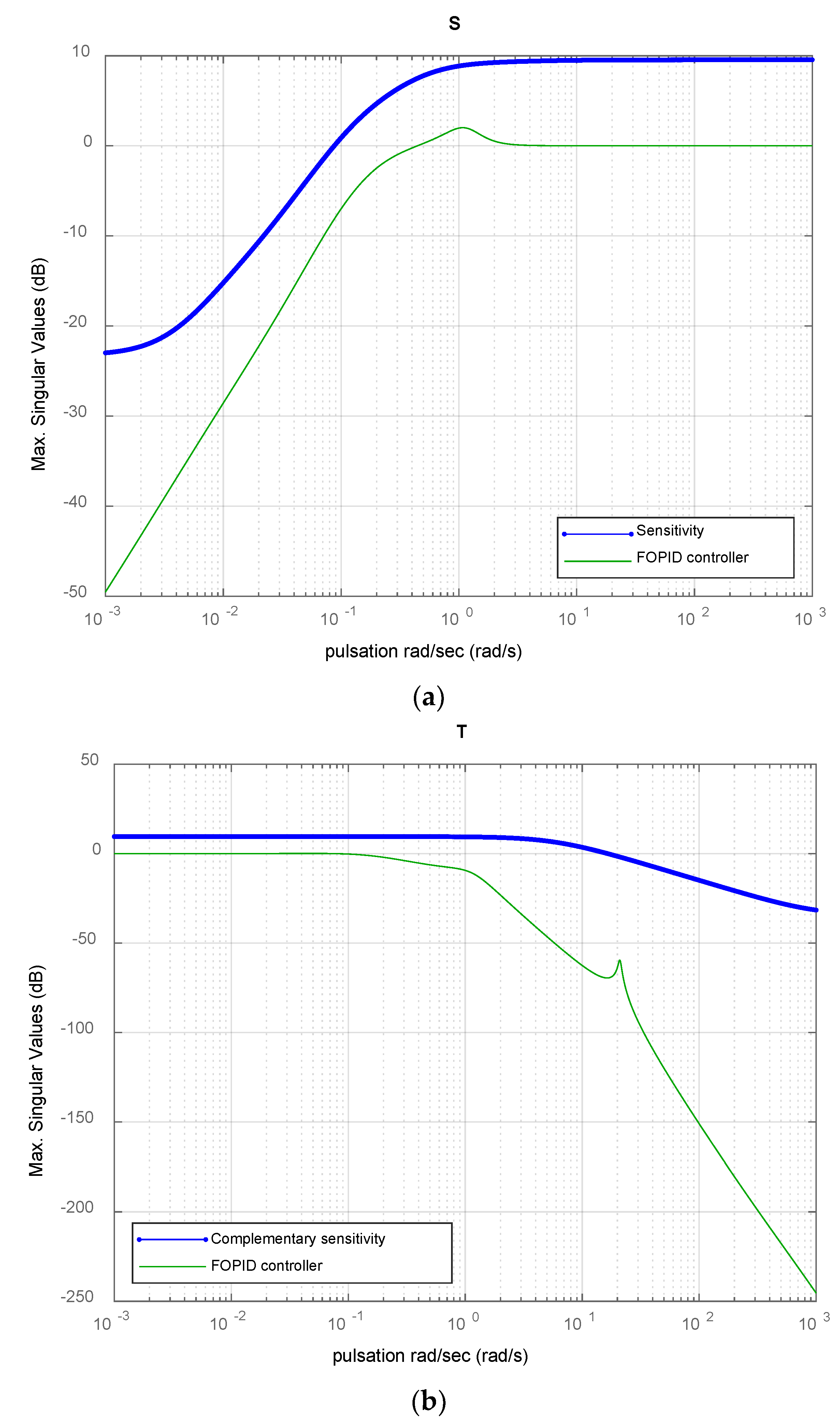
3.4.2. FOPID Based H∞ Controller
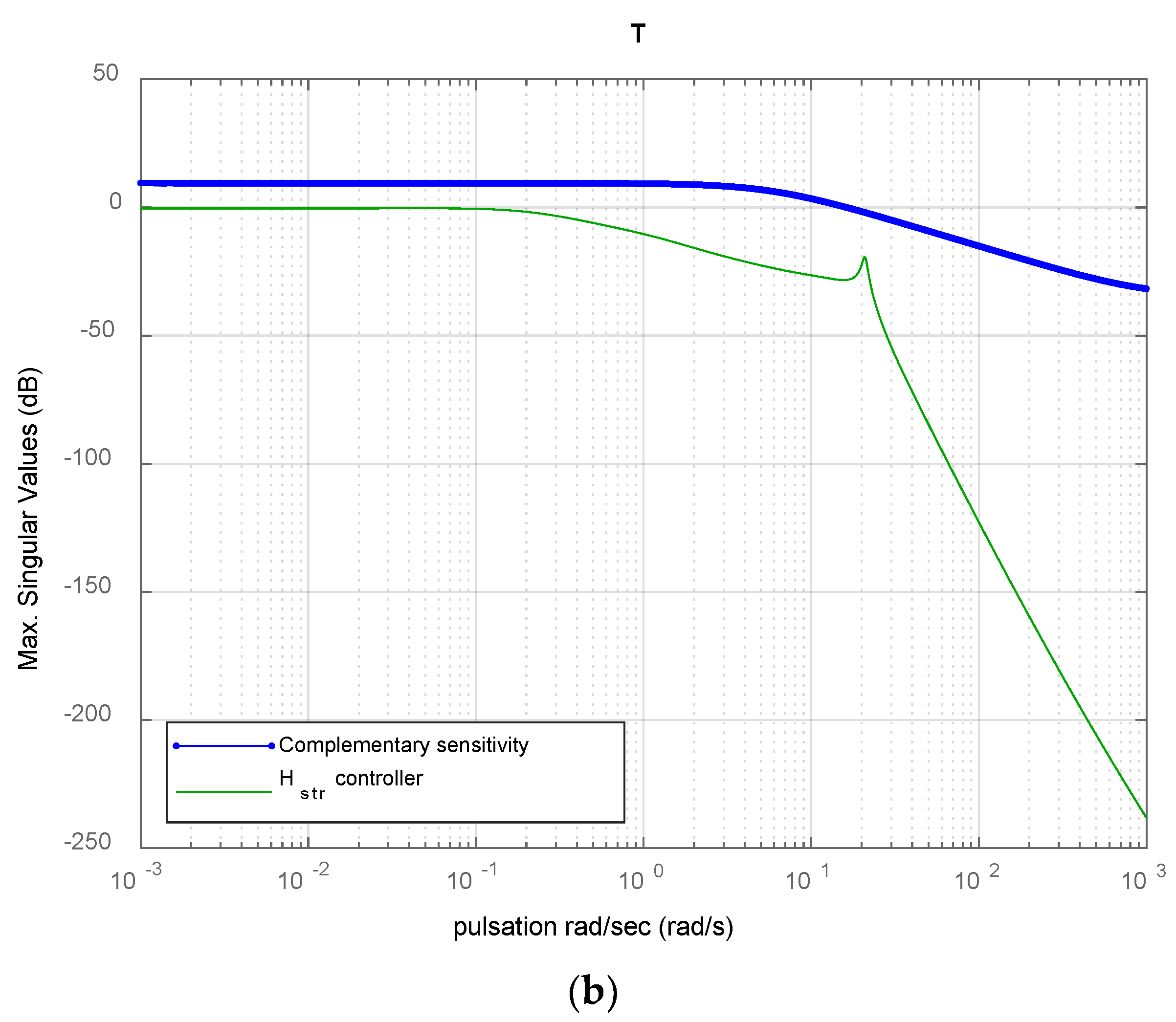
3.4.3. Fixed-Structure H∞ Controller
- ‘Targetgain = 0′ stops the optimization once the target H∞ is achieved.
- ‘Randomstart = 10′ prevents local minima.
- ‘Display final’ indicates the optimization results at each iteration.
- ‘tunableSS (‘Hstr’,5,1,1)’ selects controller ‘Hstr’ with a single input-single output.
- Construction of sensitivity functions.
- ‘blkdiag’ forms a block diagonal matrix from production of weighting functions and sensitivity functions.
- ‘hinfstruct’ tunes the controller.
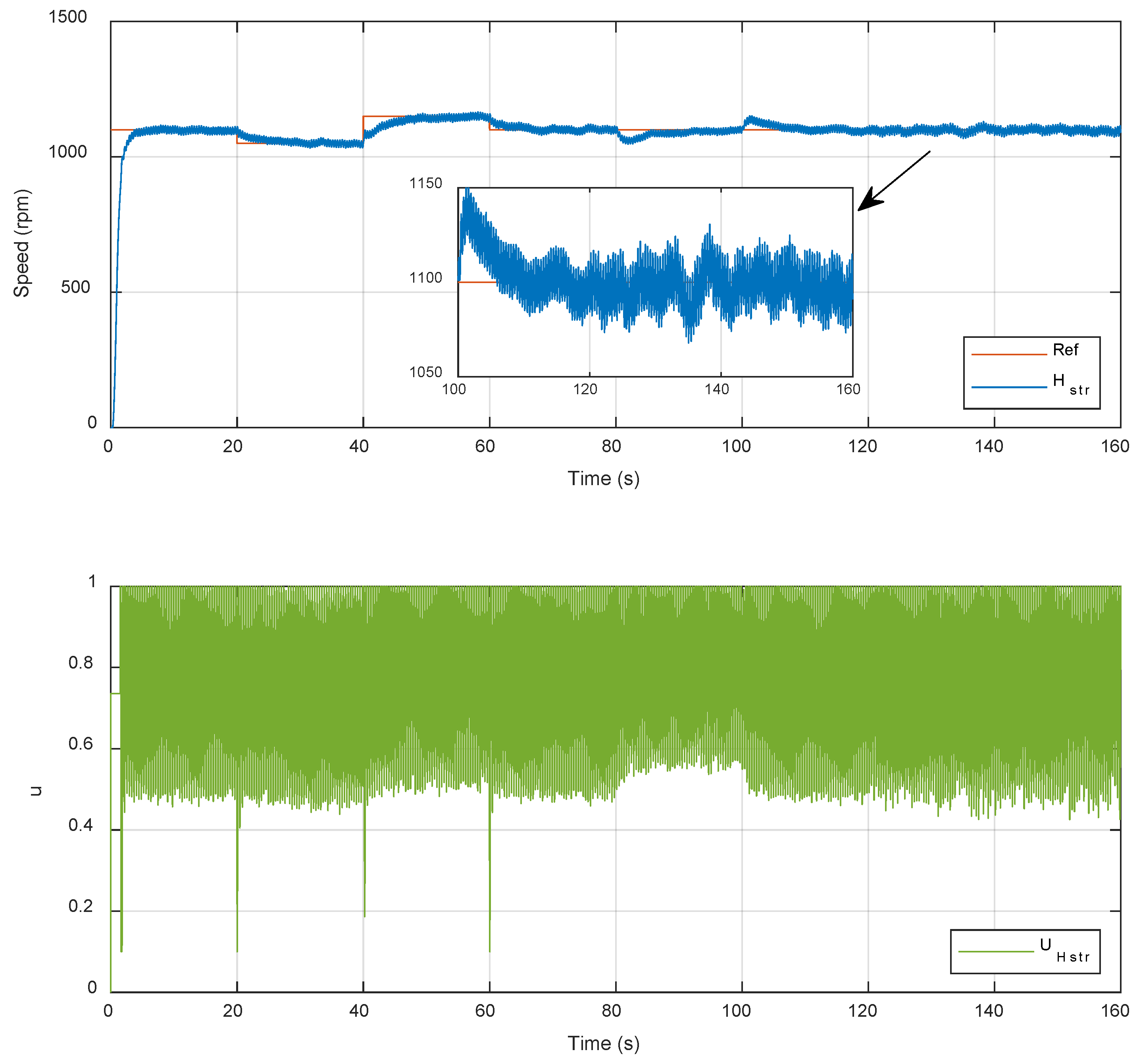
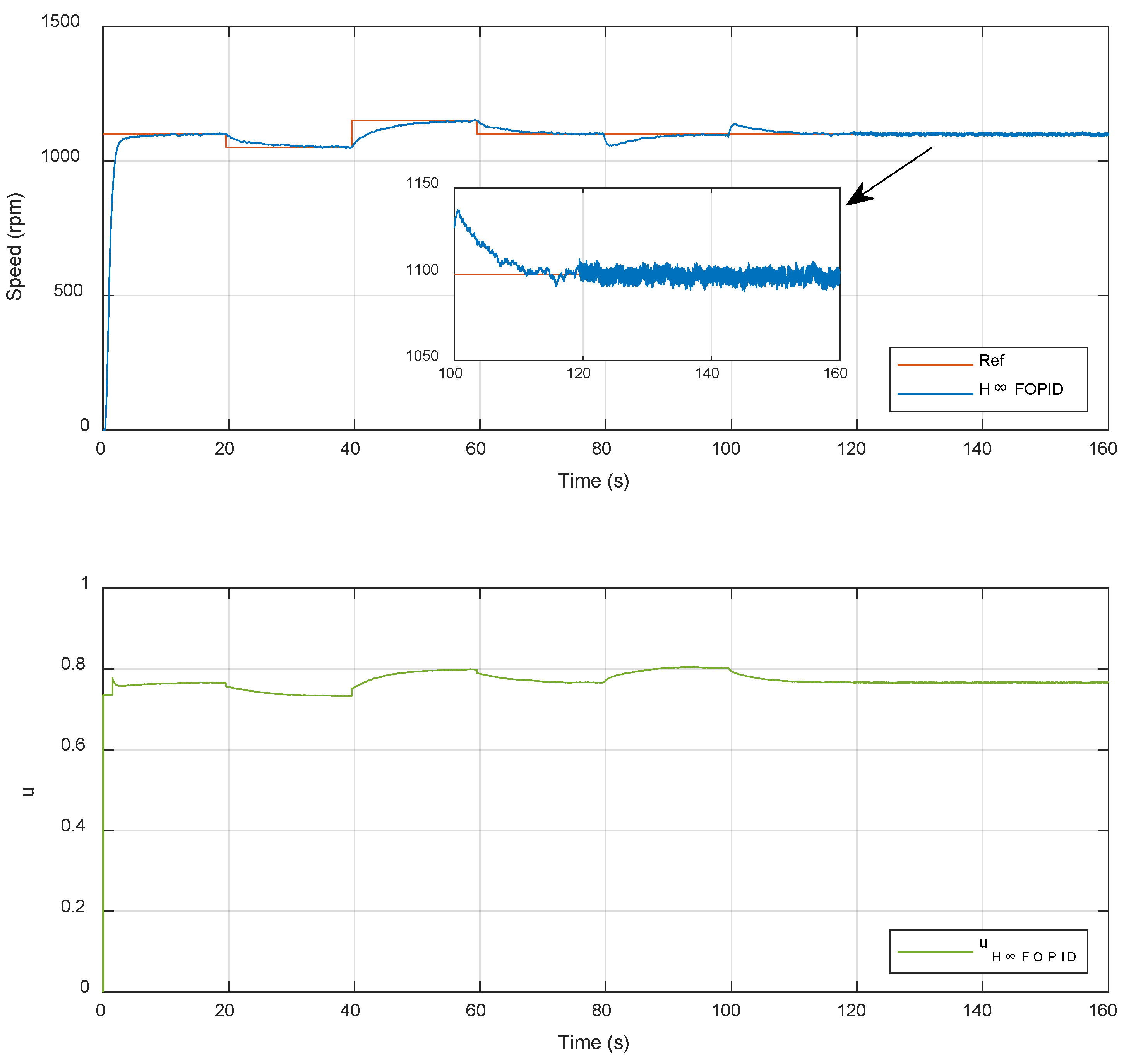
4. Results and Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value |
|---|---|
| CreationFcn | @pswcreationuniform |
| Display | ‘final’ |
| FunctionTolerance | 1.0000 × 106 |
| HybridFcn | [] |
| InertiaRange | [0.1000,1.1000] |
| InitialSwarmMatrix | [] |
| InitialSwarmSpan | 2000 |
| MaxIterations | ‘200*numberofvariables’ |
| MaxStallIterations | 20 |
| MaxStallTime | Inf |
| MaxTime | Inf |
| MinNeighborsFraction | 0.2500 |
| ObjectiveLimit | -Inf |
| OutputFcn | [] |
| PlotFcn | @pswplotbestf |
| SelfAdjustmentWeight | 1.4900 |
| SocialAdjustmentWeight | 1.4900 |
| SwarmSize | ‘min(100,10*numberofvariables)’ |
| UseParallel | 0 |
| UseVectorized | 0 |
References
- Ilten, E. Conformable Fractional Order Controller Design and Implementation for Per-Phase Voltage Regulation of Three-Phase SEIG Under Unbalanced Load. Electr. Power Compon. Syst. 2022, 50, 636–648. [Google Scholar] [CrossRef]
- Demirtas, M.; Ilten, E.; Calgan, H. Pareto-Based Multi-objective Optimization for Fractional Order PIλ Speed Control of Induction Motor by Using Elman Neural Network. Arab. J. Sci. Eng. 2019, 44, 2165–2175. [Google Scholar] [CrossRef]
- Talla, J.; Leu, V.Q.; Šmídl, V.; Peroutka, Z. Adaptive speed control of induction motor drive with inaccurate model. IEEE Trans. Ind. Electron. 2018, 65, 8532–8542. [Google Scholar] [CrossRef]
- Sung, W.; Shin, J.; Jeong, Y. Energy-efficient and robust control for high-performance induction motor drive with an application in electric vehicles. IEEE Trans. Veh. Technol. 2012, 61, 3394–3405. [Google Scholar] [CrossRef]
- Lin, F.-J.; Wai, R.-J. Robust control using neural network uncertainty observer for linear induction motor servo drive. IEEE Trans. Power Electron. 2002, 17, 241–254. [Google Scholar]
- Alonge, F.; Cirrincione, M.; D’Ippolito, F.; Pucci, M.; Sferlazza, A. Robust active disturbance rejection control of induction motor systems based on additional sliding-mode component. IEEE Trans. Ind. Electron. 2017, 64, 5608–5621. [Google Scholar] [CrossRef]
- Pohl, L.; Vesely, I. Speed control of induction motor using H∞ linear parameter varying controller. IFAC-PapersOnLine 2016, 49, 74–79. [Google Scholar] [CrossRef]
- Qu, H.; Zhao, J. Event-triggered H∞ control for switched interval type-2 fuzzy systems under denial-of-service. Int. J. Robust Nonlinear Control 2023, 33, 2219–2237. [Google Scholar] [CrossRef]
- Ilten, E.; Calgan, H.; Demirtas, M. Design of induction motor speed observer based on long short-term memory. Neural Comput. Appl. 2022, 34, 18703–18723. [Google Scholar] [CrossRef]
- Acevedo, S.S.; Giraldo, E.; Giraldo, D. Speed control of induction motor using robust control with lsdp. In Proceedings of the Electronics, Robotics and Automotive Mechanics Conference, Online, 30 September–3 October 2008; IEEE: New York, NY, USA, 2008; pp. 350–353. [Google Scholar]
- Mohamed, A. Modern robust control of a CSI-fed induction motor drive system. In Proceedings of the 1998 American Control Conference ACC, Philadelphia, PA, USA, 24–26 June 1998; (IEEE Cat. No. 98CH36207). IEEE: New York, NY, USA, 1998; Volume 6, pp. 3803–3808. [Google Scholar]
- Allag, M.; Allag, A.; Zeghib, O.; Hamidani, B. Robust h∞ control based on the mean value theorem for induction motor drive. J. Control Autom. Electr. Syst. 2019, 30, 657–665. [Google Scholar] [CrossRef]
- Kaitwanidvilai, S.; Olranthichachart, P.; Ngamroo, I. PSO based automatic weight selection and fixed structure robust loop shaping control for power system control applications. Int. J. Innov. Comput. Inf. Control 2011, 7, 1549–1563. [Google Scholar]
- Kaur, R.; Ohri, J. PSO based weight selection and fixed structure robust loop shaping control for pneumatic servo system with 2DOF controller. Int. J. Electr. Comput. Eng. 2015, 8, 1365–1373. [Google Scholar]
- Amieur, T.; Bechouat, M.; Sedraoui, M.; Kahla, S.; Guessoum, H. A new robust tilt-PID controller based upon an automatic selection of adjustable fractional weights for permanent magnet synchronous motor drive control. Electr. Eng. 2021, 103, 1881–1898. [Google Scholar] [CrossRef]
- Avci, D.; Ozdemir, N.; Yavuz, M. Fractional Optimal Control of Diffusive Transport Acting on a Spherical Region; CRC Press: Boca Raton, FL, USA, 2019; Volume 1. [Google Scholar]
- Daraz, A.; Malik, S.A.; Basit, A.; Aslam, S.; Zhang, G. Modified FOPID controller for frequency regulation of a hybrid interconnected system of conventional and renewable energy sources. Fractal Fract. 2023, 7, 89. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Alqahtani, M.H.; Aljumah, A.S.; Aly, M.; Almutairi, S.Z.; Mohamed, E.A. Design Optimization of Improved Fractional-Order Cascaded Frequency Controllers for Electric Vehicles and Electrical Power Grids Utilizing Renewable Energy Sources. Fractal Fract. 2023, 7, 603. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A new intelligent fractional-order load frequency control for interconnected modern power systems with virtual inertia control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Makhbouche, A.; Boudjehem, B.; Birs, I.; Muresan, C.I. Fractional-order PID controller based on immune feedback mechanism for time-delay systems. Fractal Fract. 2023, 7, 53. [Google Scholar] [CrossRef]
- Rahman, M.Z.U.; Leiva, V.; Martin-Barreiro, C.; Mahmood, I.; Usman, M.; Rizwan, M. Fractional transformation-based intelligent H-infinity controller of a direct current servo motor. Fractal Fract. 2022, 7, 29. [Google Scholar] [CrossRef]
- Sedraoui, M.; Amieur, T.; Bachir Bouiadjra, R.; Sahnoune, M. Robustified fractional-order controller based on adjustable fractional weights for a doubly fed induction generator. Trans. Inst. Meas. Control 2017, 39, 660–674. [Google Scholar] [CrossRef]
- Amieur, T.; Younsi, A.; Aidoud, M.; Sedraoui, M.; Amieur, O. Design of robust fractional order PID controller using fractional weights in the mixed sensitivity problem. In Proceedings of the 2017 14th International Multi-Conference on Systems, Signals & Devices, Marrakech, Morocco, 28–31 March 2017; IEEE: New York, NY, USA, 2017; pp. 549–553. [Google Scholar]
- Menak, R.; Tan, N. Design of Robust Integer/Fractional Order PID Controller Based on Bode’s Ideal Transfer Function and H-Infinity Robust Performance Condition. In Proceedings of the 2023 International Conference on Fractional Differentiation and Its Applications, Ajman, United Arab Emirates, 14–16 March 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Yaghi, M.; Efe, M.Ö. H2/H∞-Neural-Based FOPID Controller Applied for Radar-Guided Missile. IEEE Trans. Ind. Electron. 2019, 67, 4806–4814. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N. FOPID controller design for robust performance using particle swarm optimization. Fract. Calc. Appl. Anal. 2007, 10, 169–187. [Google Scholar]
- Demirtas, M.; Calgan, H.; Toufik, A.; Sedraoui, M. Small-signal modeling and robust multi-loop PID and H∞ controllers synthesis for a self-excited induction generator. ISA Trans. 2021, 117, 234–250. [Google Scholar] [CrossRef] [PubMed]
- Tepljakov, A. Fractional-Order Calculus Based Identification and Control of Linear Dynamic Systems. Master’s Thesis, Tallinn University of Technology, Tallinn, Estonia, 2011. [Google Scholar]
- Yan, Z.; Utkin, V. Sliding mode observers for electric machines-an overview. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society, IECON 02, Sevilla, Spain, 5–8 November 2002; IEEE: New York, NY, USA, 2002; Volume 3, pp. 1842–1847. [Google Scholar]
- Ilten, E. Conformable fractional order controller design and optimization for sensorless control of induction motor. COMPEL- Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 1528–1541. [Google Scholar] [CrossRef]
- Dey, N.; Mondal, U.; Mondal, D. Design of a H-infinity robust controller for a DC servo motor system. In Proceedings of the 2016 International Conference on Intelligent Control Power and Instrumentation, Kolkata, India, 21–23 October 2016; IEEE: New York, NY, USA, 2016; pp. 27–31. [Google Scholar]
- Ortega, M.G.; Rubio, F.R. Systematic design of weighting matrices for the H∞ mixed sensitivity problem. J. Process Control 2004, 14, 89–98. [Google Scholar] [CrossRef]
- Papalambrou, G.; Karlis, E.; Kyrtatos, N. Robust control of manifold air injection in a marine diesel engine. IFAC-PapersOnLine 2015, 48, 438–443. [Google Scholar] [CrossRef]
- Oloomi, H.; Shafai, B. Weight selection in mixed sensitivity robust control for improving the sinusoidal tracking performance. In Proceedings of the 42nd IEEE International Conference on Decision and Control, MAUI, HI, USA, 9–12 December 2003; (IEEE Cat. No. 03CH37475). IEEE: New York, NY, USA, 2003; Volume 1, pp. 300–305. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
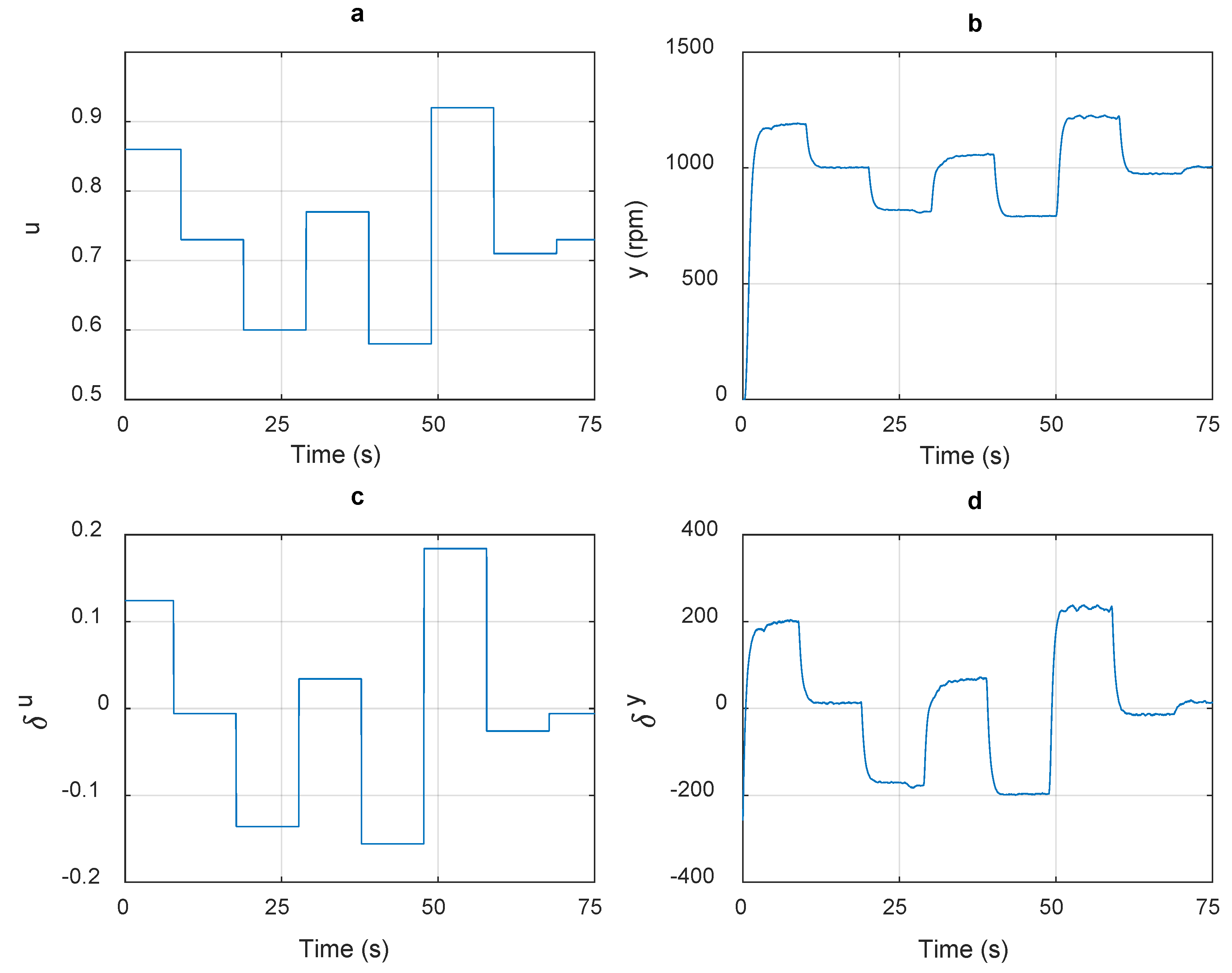





| Parameter | Value |
|---|---|
| Rated Voltage (VL-N) | 220 V |
| Rated Current | 2.7 A |
| Rated Power | 1.1 kW |
| Frequency | 50 Hz |
| Cosine (φ) | 0.80 |
| Rated Speed | 1380 rpm |
| Pole pairs (p) | 2 |
| Stator Resistance (Rs) | 7.8 Ω |
| Stator Inductance (Ls) | 55 mH |
| Friction Factor (B) | 0.072 N·m·s |
| Rotor Inertia (J) | 0.0088 kg·m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilten, E. Fractional Order Weighted Mixed Sensitivity-Based Robust Controller Design and Application for a Nonlinear System. Fractal Fract. 2023, 7, 769. https://doi.org/10.3390/fractalfract7100769
Ilten E. Fractional Order Weighted Mixed Sensitivity-Based Robust Controller Design and Application for a Nonlinear System. Fractal and Fractional. 2023; 7(10):769. https://doi.org/10.3390/fractalfract7100769
Chicago/Turabian StyleIlten, Erdem. 2023. "Fractional Order Weighted Mixed Sensitivity-Based Robust Controller Design and Application for a Nonlinear System" Fractal and Fractional 7, no. 10: 769. https://doi.org/10.3390/fractalfract7100769
APA StyleIlten, E. (2023). Fractional Order Weighted Mixed Sensitivity-Based Robust Controller Design and Application for a Nonlinear System. Fractal and Fractional, 7(10), 769. https://doi.org/10.3390/fractalfract7100769








