An ε-Approximate Approach for Solving Variable-Order Fractional Differential Equations
Abstract
1. Introduction
2. Preliminaries
2.1. Homogenization
2.2. Space Introduction
3. Algorithm and Convergence Analysis
3.1. The -Approximate Approach
3.2. Stability Results for the Problem
3.3. Convergence Analysis
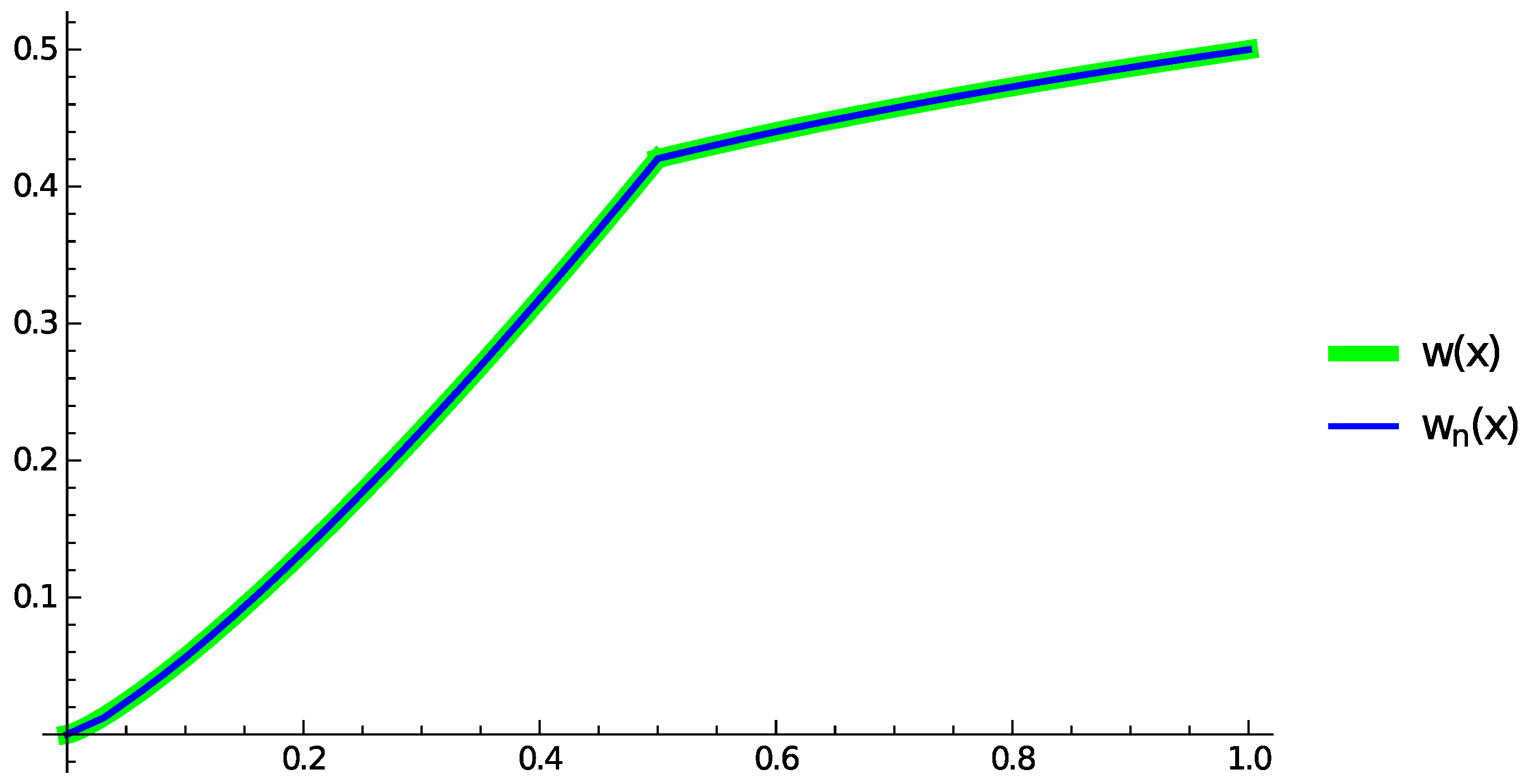
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, C277–C300. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Phanikumar, M.S.; Meerschaert, M.M. A novel numerical method for the time variable fractional order mobile–Cimmobile advection–Cdispersion model. Comput. Math. Appl. 2013, 66, 693–701. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gorenflo, R.; Sokolov, I.M. Fractional diffusion in inhomogeneous media. J. Phys. A Math. Gen. 2005, 38, L679. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Kumar, P.; Chaudhary, S.K. Analysis of fractional order control system with performance and stability. Int. J. Eng. Sci. 2017, 9, 408–416. [Google Scholar]
- Obembe, A.D.; Hossain, M.E.; Abu-Khamsin, S.A. Variable-order derivative time fractional diffusion model for heterogeneous porous media. J. Pet. Sci. Eng. 2017, 152, 391–405. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Fang, J.; Holm, S. A survey on fractional derivative modeling of power-law frequency-dependent viscous dissipative and scattering attenuation in acoustic wave propagation. Appl. Mech. Rev. 2018, 70, 030802. [Google Scholar] [CrossRef]
- Leith, J.R. Fractal scaling of fractional diffusion processes. Signal Process. 2003, 83, 2397–2409. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wu, L. An operational matrix of fractional differentiation of the second kind of Chebyshev polynomial for solving multiterm variable order fractional differential equation. Math. Probl. Eng. 2016, 2016, 7126080. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M. On spectral methods for solving variable-order fractional integro-differential equations. Comput. Appl. Math. 2018, 37, 3937–3950. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Agarwal, P. Numerical solution of multiterm variable-order fractional differential equations via shifted Legendre polynomials. Math. Methods Appl. Sci. 2019, 42, 3978–3991. [Google Scholar] [CrossRef]
- Ali, K.K.; Mohamed, E.M.; Nisar, K.S.; Khashan, M.M.; Zakarya, M. A collocation approach for multiterm variable-order fractional delay-differential equations using shifted Chebyshev polynomials. Alex. Eng. J. 2022, 61, 3511–3526. [Google Scholar] [CrossRef]
- Li, X.; Gao, Y.; Wu, B. Approximate solutions of Atangana-Baleanu variable order fractional problems. AIMS Math. 2020, 5, 2285. [Google Scholar] [CrossRef]
- Singh, A.K.; Mehra, M.; Gulyani, S. Learning parameters of a system of variable order fractional differential equations. Numer. Methods Partial. Differ. Equ. 2021, 1–15. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Li, B.; Sun, Y. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Amin, R.; Shah, K.; Ahmad, H.; Ganie, A.H.; Abdel-Aty, A.H.; Botmart, T. Haar wavelet method for solution of variable order linear fractional integro-differential equations. AIMS Math. 2022, 7, 5431–5443. [Google Scholar] [CrossRef]
- Yang, J.; Yao, H.; Wu, B. An efficient numerical method for variable order fractional functional differential equation. Appl. Math. Lett. 2018, 76, 221–226. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wu, L. An operational matrix technique for solving variable order fractional differential-integral equation based on the second kind of Chebyshev polynomials. Adv. Math. Phys. 2016, 2016, 6345978. [Google Scholar] [CrossRef]
- Wu, B.Y.; Lin, Y.Z. Application of the Reproducing Kernel Space, Beijing; Science Press: Beijing, China, 2012. [Google Scholar]
- Wang, Y.; Zhou, H.; Mei, L.; Lin, Y. A Numerical Method for Solving Fractional Differential Equations. Math. Probl. Eng. 2022, 2022, 3778016. [Google Scholar] [CrossRef]
- Jia, Y.T.; Xu, M.Q.; Lin, Y.Z. A numerical solution for variable order fractional functional differential equation. Appl. Math. Lett. 2017, 64, 125–130. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Wang, Z. Solving the nonlinear variable order fractional differential equations by using Euler wavelets. Comput. Model. Eng. Sci. 2019, 118, 339–350. [Google Scholar]
| xi | ||||||||
|---|---|---|---|---|---|---|---|---|
| [23] | Ours | [23] | Ours | [23] | Ours | [23] | Ours | |
| 0.2 | ||||||||
| 0.4 | 0 | |||||||
| 0.6 | ||||||||
| 0.8 | ||||||||
| 1.0 | ||||||||
| R | Method in [19] | The Proposed Method | ||||
|---|---|---|---|---|---|---|
| n = 3 | n = 4 | n = 5 | n = 3 | n = 4 | n = 5 | |
| 1 | - | |||||
| 2 | ||||||
| 4 | ||||||
| 8 | ||||||
| AEs | AEs | ||
|---|---|---|---|
| 0.1 | 0.6 | ||
| 0.2 | 0.7 | ||
| 0.3 | 0.8 | ||
| 0.4 | 0.9 | ||
| 0.5 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, W.; Mei, L.; Lin, Y.; Sun, H. An ε-Approximate Approach for Solving Variable-Order Fractional Differential Equations. Fractal Fract. 2023, 7, 90. https://doi.org/10.3390/fractalfract7010090
Wang Y, Wang W, Mei L, Lin Y, Sun H. An ε-Approximate Approach for Solving Variable-Order Fractional Differential Equations. Fractal and Fractional. 2023; 7(1):90. https://doi.org/10.3390/fractalfract7010090
Chicago/Turabian StyleWang, Yahong, Wenmin Wang, Liangcai Mei, Yingzhen Lin, and Hongbo Sun. 2023. "An ε-Approximate Approach for Solving Variable-Order Fractional Differential Equations" Fractal and Fractional 7, no. 1: 90. https://doi.org/10.3390/fractalfract7010090
APA StyleWang, Y., Wang, W., Mei, L., Lin, Y., & Sun, H. (2023). An ε-Approximate Approach for Solving Variable-Order Fractional Differential Equations. Fractal and Fractional, 7(1), 90. https://doi.org/10.3390/fractalfract7010090







