Fuzzy Analysis of Artificial Drug Transmission Model with Optimal Control

Abstract

This article presents an artificial drug abusers system consolidating the impact of treatment with psychological and physiological addicts under fuzzy parameters. In the fuzzy model, all of the parameters are considered to be triangular fuzzy numbers to represent the uncertainty that pervaded the dynamics. To handle the arrangements while avoiding problems, the fuzzy model is turned into a defuzzified model using the utility function method. The fuzzy model’s positivity and boundedness are carefully explored, and an equilibrium analysis is also completed. Both the drug-addict equilibrium and the drug-free equilibrium have established stability analyses. This article explains fuzzy optimum control using Pontryagin’s maximum principle. Finally, it is shown that the treatment alongside counselling and conducting awareness programs is more fruitful and drug-related controlling is more viable in the fuzzy nature. Likewise, we plot the 3D associations with fuzzy parameters which show the inventiveness and appropriateness of the results.

1. Introduction

Artificial drugs such as ecstasy, ketamine, and crystal methamphetamine are more popular in drug markets as they essentially appear in entertainment venues [1]. What is worse is that artificial drugs are more addictive because they directly affect the central nervous system and exhibit a higher level of psychological reliance than conventional narcotics such as heroin, morphine, and marijuana, among others. Moreover, artificial drugs are continually advancing and have extraordinary fluctuation. Drugs such as amphetamine are for the most part utilized in unambiguous districts such as Goa and Ahmedabad in India [2]. A new report shows that medication use in India continues to develop quickly, and all the more shockingly, heroin has supplanted normal opium [3,4,5]. Most artificial drugs are fabricated in an illegal laboratory, and there are no security estimates utilized in the manufacture of artificial drugs. At the point when a dependent individual endeavors to stop, he/she might encounter truly disagreeable withdrawal side effects which can bring down their determination to continue with forbearance and in any case entangle early recuperation. In this manner it is exceptionally vital for rational measures to check the present spread of artificial drugs.

Most of the time, studying drug misuse and how it affects everyone is an impossible task. According to a report, the number of people using artificial drugs is currently increasing. The global standard is that there are one to five explicit drug addicts for every implicit one. The true drug addicts in every nation are significantly more than just those registered at such levels. Another tendency of the spread of fake pharmaceuticals is the rising death of young people. Many researchers [6,7,8,9,10,11] have alluded to drug use spreading like an infectious disease. Their focus has mainly been on modelling epidemics. The elements of smoking and alcoholic models examined the effects on general wellbeing places. A mathematical model was created by Nyabadza [12] to show how methamphetamine spread across a South African region. According to their findings, a relapse is inevitable in hard drug users after a person has recovered if the fundamental reproduction number is more than one. Subsequently, it is important to expect that backsliding can happen among people who have history of illicit drug use. Liu [1] formed an artificial drugs transmission model with treatment and concentrated on the stability and bifurcation investigation of the model. Wang [13] utilized a second compound lattice hypothesis to concentrate on worldwide asymptotically stable drug-free and drug-use equilibrium points. Samantha [5] developed a non-independent medications model and obtained the adequate states of the worldwide asymptotic dependability of the model.

The survey carried out has produced some graphs (From Figure 1, Figure 2 and Figure 3) showing that the number of artificial drug users is constantly increasing. For example, since 2019, the number of drug users in the world has increased by 29.5%, and by the end of 2021, there were almost 8.746 million drug users in the world, including 4.98 million artificial drug users, representing 54.6% of all drug users. World practice shows that the ratio of overt and hidden drug addicts is 1:5. Thus, in each country the number of registered drug addicts is much lower than the number of real drug addicts. In addition, young people are increasingly becoming victims, which increases the artificial transfer of drugs. Some people may think that they will not become addicted after one use, but this is a misconception. As the literature shows, just one use can lead to addiction. Drug treatment and psychotherapy are the main methods of treatment for drug addicts.

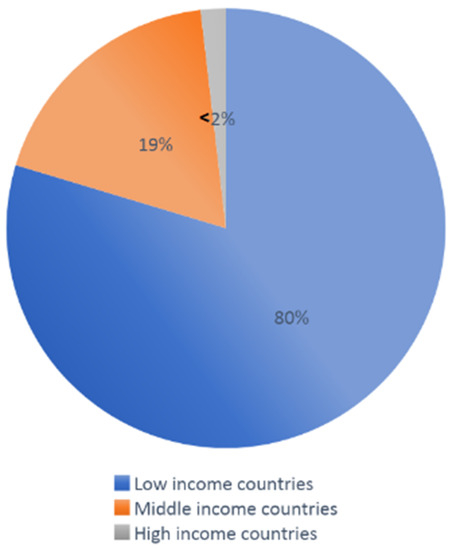
Figure 1. Global distribution of drugs and mode of transportation in 2020 [3].

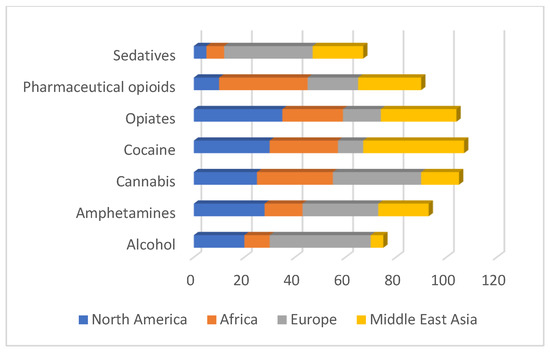
Figure 2. Global statistics of artificial drug usage in North America, Middle East Asia, Europe, and Africa [3].

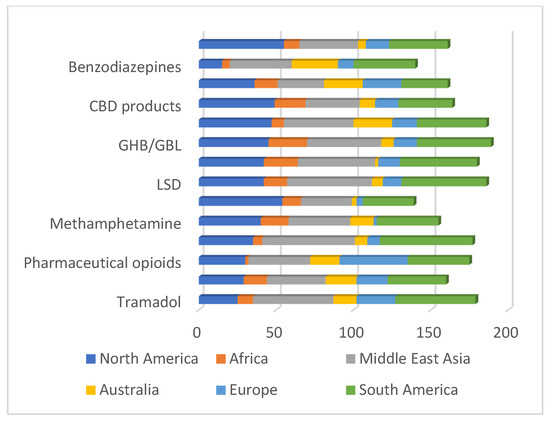
Figure 3. Global Statistics of artificial drugs, precursors, and new psychoactive substances [3].

As far as we are aware, there is no effective treatment for drug addiction anywhere in the world. Prescription drugs are the mainstay of treatment for drug users, just like they are for other fixation infections. When an addict comes forward to a medical organization, they first must go through detoxification to restore their brain’s neurons and relax, and then they can undergo psychotherapy to repeatedly practice using drugs. In any case, from the continuing addicts, we find the impact is not great. Many organic boundaries may vary cooperatively with an occasionally changing climate that has an indispensable impact on psychological addicts, physiological addicts, acceleration rate, treatment rate, relapse rate, etc. To manage the issue, a few methodologies, such as interval approach, fuzzy methodology, stochastic methodology, and dispersion approach, have been used by scientists to portray the loose boundaries. Researchers have utilized the interval approach, fuzzy approach, stochastic approach, and diffusion approach to show the imprecise parameters; however, the majority of these vulnerabilities stem from both regular variables and human elements. These uncertainties are mostly caused by natural and human factors, including climatic change, measurement error, and equipment limits. In a previous study, Bassanezi [14] laid out a framework by examining the stability of dynamical systems using fuzzy differential conditions. Mizukoshi [15], by virtue of beginning circumstances under fuzzy differential circumstances, examined the dependability of fuzzy dynamical system. Bede and Lady [16], in consideration of the summed up differentiability, thought about the arrangements of fuzzy differential conditions. Guo [17] applied fuzzy impulsive functional differential conditions to a strategic model. The model combined with ill-defined biological characteristics can be used to study the distinctive behaviors brought on by this uniqueness. Through fuzzy analysis, Zhang [18] examined the SVIRS illness system with a Holling type-II functional response, saturated incidence rate, and saturated treatment. The results are reflected to be near to the nature of the system.

In order to determine the best control approach, optimal control theory is currently extensively used in the research of infectious disease dynamics. Numerous authors [19,20,21,22,23] have recently used the infectious disease dynamics model to examine addictions to drugs, tobacco, video games, social media, and other behaviors. In order to comprehend how the spread of the aforementioned addictions may be controlled with optimal implementation, they employed optimal control approaches. According to Guo [24], the best control method calls for the simultaneous employment of three different types of measures. Alemneh [25] looked at ways to properly manage social media addiction for a predetermined amount of time. A delay differential equation model with optimal control that describes how HIV interacts with the cell-mediated response was examined by Hattaf [26]. A dynamical model of the Zika virus with optimum control analysis was put forth by Khan [27]. Similar studies related to smoking, tumor, predator–prey, and hepatitis can be seen in [28,29,30,31]. However, this work investigated fuzzy optimum control of artificial drug transformation.

In this study, we created an artificial drug abuser model using the control interventions as a form of drug-induced therapy. All of the parameters have to be adjusted to deal with uncertainties. We think about the fuzziness in terms of numbers. This fuzzy model is more accurate in capturing the unpredictability of everyday life. Here, we examine the fuzzy model’s positivity, boundedness, analysis of the equilibrium, stability, and ideal control. Fuzzy artificial drug abuser model numerical simulations are run, and the results of optimal control are graphically displayed.

Pre-Requisites of Fuzzy Model

Definition 1.

Triangular Fuzzy Number

A membership function of a triangular fuzzy number is defined as follows

$$M_{\tilde{F}}\left(w\right)=\left\{\begin{array}{l}\frac{w-p}{q-p},p\le w\le q;\\ \frac{r-w}{r-q},\hspace{0.17em}q\le w\le r;\\ 0,\hspace{0.17em}\hspace{0.17em}otherwise.\end{array}\right.$$

Definition 2.

$\eta$-Cut of a Fuzzy Number

$\eta$-Cut of a fuzzy number $\tilde{F}$ is defined as

$$F_{\eta }=\left\{w/M_{\tilde{F}}\left(w\right)\ge \eta ,\hspace{0.17em}w\in W,\eta \in \left[0,1\right]\right\},$$

where $F_{\eta }=\left[F_L\left(\eta \right),F_U\left(\eta \right)\right]$, $F_L\left(\eta \right),F_U\left(\eta \right)$ are the lower and upper limits of the fuzzy number, respectively.

Definition 3.

Utility Function Method

Utility function is defined as the weighted sum of the objectives $U={\displaystyle \sum _{i=1}^n{w}_i{a}_i},w_i\ge 0$subject to the condition ${\displaystyle \sum _{i=1}^n{w}_i}=1.$

2. Fuzzy Formulation of Artificial Drug Transmission

In the fuzzy artificial drug transmission model, we divide the total population into susceptible ($\tilde{S}$), psychological addicts ($\tilde{C}$), physiological addicts ($\tilde{P}$), and drug users under treatment ($\tilde{T}$). The fuzzy parameters meanings in the drug transmission model are given in Table 1. Based on the concept of fuzzy differential equations [15], the artificial drug transmission model with fuzzy parameters is described in the following manner:

$$\left\{\begin{array}{l}{\tilde{S}}^1=\tilde{\Delta }-\tilde{\alpha }SC-\tilde{\beta }SP-\tilde{M}S,\\ {\tilde{C}}^1=\tilde{\alpha }SC+\tilde{\beta }SP-\tilde{\gamma }C-\tilde{\delta }C-\tilde{M}C,\\ {\tilde{P}}^1=\tilde{\gamma }C+\tilde{\epsilon }T-\tilde{\psi }P-\tilde{M}P,\\ {\tilde{T}}^1=\tilde{\delta }C+\tilde{\psi }P-\tilde{\epsilon }T-\tilde{M}T.\end{array}\right.$$

(1)

Table 1. Physical interpretation of the parameters.

Parameters	Physical Description of the Parameters	TFN
$\tilde{\Delta }$	Fuzzy susceptible population	(2, 4, 6)
$\tilde{\alpha }$	Fuzzy contact rate between the susceptible population and psychological addicts	(0.5, 0.7, 0.9)
$\tilde{\beta }$	Fuzzy contact rate between the susceptible population and physiological addicts	(0.5, 0.7, 0.9)
$\tilde{\gamma }$	Fuzzy escalation rate from the psychological addicts	(0.01, 0.05, 0.1)
$\tilde{\delta }$	Fuzzy treatment rate of the physiological addicts	(0.1, 0.3, 0.5)
$\tilde{\epsilon }$	Fuzzy relapse rate of the drug users in treatment	(0.1, 0.4, 0.8)
$\tilde{\psi }$	Fuzzy treatment rate of the physiological addicts	(0.2, 0.4, 0.6)
$\tilde{M}$	Fuzzy natural mortality of all populations	(2, 4, 6)

3. Analysis of the Fuzzy System

In this section, we provide the positivity, boundedness, existence, and stability analysis of fuzzy artificial drug transmission.

3.1. Positivity and Boundedness Fuzzy Artificial Drug Model

Let the solution of system (1) be ${\left[{\tilde{x}}^1\right]}_{\eta }=\left[{\left(x^1\right)}_l^{\eta },{\left(x^1\right)}_u^{\eta }\right]$, then the deterministic system of the fuzzy artificial drug transmission model is reduced into

$$\left\{\begin{array}{l}{\left(S^1\right)}_L^{\eta }={\left({\Delta }_L\right)}^{\eta }-{\left({\alpha }_U\right)}^{\eta }SC-{\left({\beta }_U\right)}^{\eta }SP-{\left(M_U\right)}^{\eta }S,\\ {\left(S^1\right)}_U^{\eta }={\left({\Delta }_U\right)}^{\eta }-{\left({\alpha }_L\right)}^{\eta }SC-{\left({\beta }_L\right)}^{\eta }SP-{\left(M_L\right)}^{\eta }S,\\ {\left(C^1\right)}_L^{\eta }={\left({\alpha }_L\right)}^{\eta }SC+{\left({\beta }_L\right)}^{\eta }SP-{\left({\gamma }_U\right)}^{\eta }C-{\left({\delta }_U\right)}^{\eta }C-{\left(M_U\right)}^{\eta }C,\\ {\left(C^1\right)}_U^{\eta }={\left({\alpha }_U\right)}^{\eta }SC+{\left({\beta }_U\right)}^{\eta }SP-{\left({\gamma }_L\right)}^{\eta }C-{\left({\delta }_L\right)}^{\eta }C-{\left(M_L\right)}^{\eta }C,\\ {\left(P^1\right)}_L^{\eta }={\left({\gamma }_L\right)}^{\eta }C+{\left({\epsilon }_L\right)}^{\eta }T-{\left({\psi }_U\right)}^{\eta }P-{\left(M_U\right)}^{\eta }P,\\ {\left(P^1\right)}_U^{\eta }={\left({\gamma }_U\right)}^{\eta }C+{\left({\epsilon }_U\right)}^{\eta }T-{\left({\psi }_L\right)}^{\eta }P-{\left(M_L\right)}^{\eta }P,\\ {\left(T^1\right)}_L^{\eta }={\left({\delta }_L\right)}^{\eta }C+{\left({\psi }_L\right)}^{\eta }P-{\left({\epsilon }_U\right)}^{\eta }T-{\left(M_U\right)}^{\eta }T,\\ {\left(T^1\right)}_U^{\eta }={\left({\delta }_U\right)}^{\eta }C+{\left({\psi }_U\right)}^{\eta }P-{\left({\epsilon }_L\right)}^{\eta }T-{\left(M_L\right)}^{\eta }T.\end{array}\right.$$

(2)

According to utility function method, the system (2) is reduced into

$$\left\{\begin{array}{l}{S}^1={\eta }_1{\left(S^1\right)}_L^{\eta }+{\eta }_2{\left(S^1\right)}_U^{\eta },\\ C^1={\eta }_1{\left(C^1\right)}_L^{\eta }+{\eta }_2{\left(C^1\right)}_U^{\eta },\\ P^1={\eta }_1{\left(P^1\right)}_L^{\eta }+{\eta }_2{\left(P^1\right)}_U^{\eta },\\ T^1={\eta }_1{\left(T^1\right)}_L^{\eta }+{\eta }_2{\left(T^1\right)}_U^{\eta }.\end{array}\right.$$

(3)

where ${\eta }_1,{\eta }_2$ are the two weight functions such that ${\eta }_1+{\eta }_2=1$ and ${\eta }_1,{\eta }_2\ge 0$, then the system (3) can be rewritten as

$$\left\{\begin{array}{l}{S}^1=m_{11}-m_{12}SC-m_{13}SP-m_{14}S,\\ C^1=m_{21}SC+m_{22}SP-m_{23}C,\\ P^1=m_{31}C+m_{32}T-m_{33}P,\\ T^1=m_{41}C+m_{42}P-m_{43}T.\end{array}\right.$$

(4)

where

$$\begin{array}{l}{m}_{11}={\eta }_1{\left({\Delta }_L\right)}^{\eta }+{\eta }_2{\left({\Delta }_U\right)}^{\eta };m_{12}={\eta }_1{\left({\alpha }_U\right)}^{\eta }+{\eta }_2{\left({\alpha }_L\right)}^{\eta };\\ m_{13}={\eta }_1{\left({\beta }_U\right)}^{\eta }+{\eta }_2{\left({\beta }_L\right)}^{\eta };m_{14}={\eta }_1{\left(T_U\right)}^{\eta }+{\eta }_2{\left(T_L\right)}^{\eta };\\ m_{21}={\eta }_1{\left({\alpha }_L\right)}^{\eta }+{\eta }_2{\left({\alpha }_U\right)}^{\eta };m_{22}={\eta }_1{\left({\beta }_L\right)}^{\eta }+{\eta }_2{\left({\beta }_U\right)}^{\eta };\\ m_{23}={\eta }_1{\left({\gamma }_U\right)}^{\eta }+{\eta }_2{\left({\gamma }_L\right)}^{\eta };m_{31}={\eta }_1{\left({\gamma }_L\right)}^{\eta }+{\eta }_2{\left({\gamma }_U\right)}^{\eta };\\ m_{32}={\eta }_1{\left({\epsilon }_L\right)}^{\eta }+{\eta }_2{\left({\epsilon }_U\right)}^{\eta };m_{33}={\eta }_1{\left({\psi }_U+T_U\right)}^{\eta }+{\eta }_2{\left({\psi }_L+T_L\right)}^{\eta };\\ m_{41}={\eta }_1{\left({\delta }_L\right)}^{\eta }+{\eta }_2{\left({\delta }_U\right)}^{\eta };m_{42}={\eta }_1{\left({\psi }_L\right)}^{\eta }+{\eta }_2{\left({\psi }_U\right)}^{\eta };\\ m_{43}={\eta }_1{\left({\epsilon }_U+T_U\right)}^{\eta }+{\eta }_2{\left({\epsilon }_L+T_L\right)}^{\eta }.\end{array}$$

Theorem 1.

At any given moment, all of the system (1)s in $R_{+}^4$solution trajectories are non-negative.

Proof. 

From system (1), we obtain

$${\tilde{S}}^1{}_{at\hspace{0.17em}S=0}=m_{11},\hspace{0.17em}{\tilde{C}}^1{}_{at\hspace{0.17em}C=0}=m_{22}SP,{\tilde{P}}^1{}_{atP=0}=m_{31}C+m_{32}T,{\tilde{T}}^1=m_{41}C+m_{42}P.$$

In the boundary plane region $R_{+}^4$, we observe that all rates are non-negative. As a result, every solution trajectory for system (1) is non-negative in $R_{+}^4$. □

Theorem 2.

If $\mathrm{\Gamma }=\min \left\{m_{14},m_{33},m_{23}-m_{31}-m_{41},m_{21}-m_{12},m_{22}-m_{13},m_{32}-m_{43}\right\}$, and satisfy the conditions $m_{21}>m_{12},m_{22}>m_{13},m_{32}>m_{43},m_{23}>m_{31}+m_{41}$, then all the solution trajectories of the system (1) are bounded in the region$R_{+}^4$.

Proof. 

Let us define an auxiliary function

$$\pi =S+C+P+T.$$

(5)

Differentiating Equation (5) with respect to t on both sides, we have

$$\frac{d\pi }{dt}=\frac{dS}{dt}+\frac{dC}{dt}+\frac{dP}{dt}+\frac{dT}{dt}$$

$$\begin{array}{l}\frac{d\pi }{dt}=m_{11}-m_{12}SC-m_{13}SP-m_{13}S+m_{21}SC+m_{22}SP-m_{23}C+m_{31}C+m_{32}T-m_{33}P+m_{41}C+m_{42}P-m_{43}T,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

$$\begin{array}{l}\frac{d\pi }{dt}+N\pi =m_{11}+(N-m_{14})S+(N-m_{33})P+(L-(m_{23}-m_{31}-m_{41}))C+(m_{21}-m_{12})SC+(m_{22}-m_{13})SP+(m_{32}-m_{43})T.\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

If $\mathrm{\Gamma }=\min \left\{m_{14},m_{33},m_{23}-m_{31}-m_{41},m_{21}-m_{12},m_{22}-m_{13},m_{32}>m_{43}\right\}$, then $\frac{d\pi }{dt}+N\pi \le m_{11}$. Solving the above, we obtain $\pi \le \frac{m_{11}}{N}+L{e}^{-\mathrm{\Gamma }t}$. Therefore, it can be written as $S\left(t\right)\le \frac{m_{11}}{N},$ $C\left(t\right)\le \frac{m_{11}}{N},$ $P\left(t\right)\le \frac{m_{11}}{N},$ $T\left(t\right)\le \frac{m_{11}}{N}.$ Thus, the solution of the system (1) is bounded. □

3.2. Existence, Basic Reproduction Number and Stability Analysis of Fuzzy Artificial Drug Transmission

3.2.1. Existence of Fuzzy Artificial Drug Transmission

The system (1) has two positive equilibrium points: (i) fuzzy artificial drug-free equilibrium point $\left(D_0^f\right)=\left(\frac{m_{11}}{m_{14}},0,0,0\right)$ and (ii) fuzzy artificial drug addiction equilibrium point $\left(D_1^f\right)=\left(S_D^f,C_D^f,P_D^f,T_D^f\right),$ where

$$\begin{array}{c}{S}_D^f=\frac{m_{23}\left(m_{33}{m}_{43}-m_{32}{m}_{42}\right)}{m_{21}{m}_{33}{m}_{43}+m_{22}{m}_{31}{m}_{43}+m_{22}{m}_{32}{m}_{41}-m_{21}{m}_{32}{m}_{42}},C_D^f=\frac{m_{33}{m}_{43}-m_{32}{m}_{42}}{m_{31}{m}_{43}+m_{32}{m}_{41}}\\ P_D^f=\frac{\theta {\theta }_1\left(m_{11}{m}_{21}-m_{14}{m}_{23}\right)+m_{11}{m}_{22}{\theta }^2}{m_{12}{m}_{23}{\theta }_1^2+\theta {\theta }_1{m}_{13}{m}_{23}}, T_D^f=\frac{m_{41}{m}_{33}+m_{31}{m}_{42}}{m_{31}{m}_{43}+m_{32}{m}_{41}}.\\ \theta =m_{31}{m}_{43}+m_{32}{m}_{41},\hspace{0.17em}{\theta }_1=m_{33}{m}_{43}-m_{32}{m}_{42}.\end{array}$$

3.2.2. Basic Reproduction Number

The basic reproduction number $\left(R_0^f\right)$ for system (4) is determined using the next generation matrix method [10]

$$R_0^f=\frac{m_{12}\left(m_{33}{m}_{43}+m_{31}{m}_{43}+m_{41}{m}_{32}-m_{32}{m}_{42}\right)}{m_{23}\left(m_{33}{m}_{43}-m_{32}{m}_{42}\right)}.$$

3.2.3. Stability Analysis

Theorem 3.

The system (4) is asymptotically stable locally at artificial drug-free equilibrium point if $R_0^f<1$and unstable if $R_0^f>1$.

Theorem 4.

The system (4) is asymptotically stable locally at artificial drug addiction equilibrium point if $R_0^f>1$and unstable $R_0^f<1$.

4. Optimal Control of Artificial Drug Addiction

Finding the best control measures requires the use of optimal strategies. To reduce the number of psychological addicts and physiological addicts in drug control and cost engaged with counselling and awareness programs, we use optimal control systems as treatment. The total cost of the disease burden brought on by drug users is provided by

$$J\left(\tilde{D}\left(t\right)\right)={\displaystyle \underset{0}{\overset{t_f}{\int }}\left[J_{1}C\left(t\right)+J_{2}P\left(t\right)+J_3{\tilde{D}}^2\left(S\left(t\right)+C\left(t\right)+P\left(t\right)+T\left(t\right)\right)\right]}\hspace{0.17em}dt,$$

(6)

subject to the following model

$$\left\{\begin{array}{l}{S}^1=m_{11}-m_{12}SC-m_{13}SP-m_{14}S-{\tilde{\Omega }}_1\tilde{D}S,\\ C^1=m_{21}SC+m_{22}SP-m_{23}C-{\tilde{\Omega }}_2\tilde{D}C,\\ P^1=m_{31}C+m_{32}T-m_{33}P-{\tilde{\Omega }}_3\tilde{D}P,\\ T^1=m_{41}C+m_{42}P-m_{43}T+\left({\tilde{\Omega }}_{1}S+{\tilde{\Omega }}_{2}C+{\tilde{\Omega }}_{3}P\right)\tilde{D}.\end{array}\right.$$

(7)

with the initial conditions $S_0\ge 0,C_0\ge 0,P_0\ge 0\hspace{0.17em},\hspace{0.17em}{T}_0\ge 0$. The terms $J_{1}C\left(t\right),J_{2}P\left(t\right)$ represent the cost associated with psychological and physiological addicts. The term $J_3{\tilde{D}}^2$ represents the cost function of the drug control because control of drug addicts works in all populations.

$$J\left(\tilde{D}\left(t\right)\right)=\underset{D\in \mathbb{Q}}{\min }{\displaystyle \underset{0}{\overset{t_f}{\int }}\left[J_{1}C\left(t\right)+J_{2}P\left(t\right)+J_3{\tilde{D}}^2\left(S\left(t\right)+C\left(t\right)+P\left(t\right)+T\left(t\right)\right)\right]}\hspace{0.17em}dt.$$

(8)

4.1. Existence of Optimal Control

Now we will discuss whether there is an ideal control variable that minimizes the cost function in a finite amount of time in this section.

Theorem 5.

There exists an optimal control ${\tilde{D}}^{*}$in  $\mathbb{Q}$ such that $J\left({\tilde{D}}^{*}\right)=\min \left\{J\left(\tilde{D}\right)\right\}$ corresponding to the control system (6) and (7).

Proof. 

We use the following conditions to prove the theorem

I.

System (7) has a set of solutions with control variable $\left({\tilde{D}}^{*}\right)$ in $\mathbb{Q}$ is non-empty.

II.

The region $\mathbb{Q}$ is closed and convex.

III.

The integrand I is convex on $\mathbb{Q}$ and $I\left(S,C,P,T.\tilde{D}\right)\ge \Omega \left(\tilde{D}\right)$, where $\Omega \left(\tilde{D}\right)$ is continuous and ${\left|\tilde{D}\right|}^{-1}\Omega \left(\tilde{D}\right)\to \infty$, whenever $\left|\tilde{D}\right|\to \infty$, then $\left|•\right|$ represents the $L\left(0,t_f\right)$ norm.

$$I\left(S,C,P,T.\tilde{D}\right)=J_{1}C\left(t\right)+J_{2}P\left(t\right)+J_3{\tilde{D}}^2\left(S\left(t\right)+C\left(t\right)+P\left(t\right)+T\left(t\right)\right).$$

Artificial drug total population $\left(\mathbb{N}\right)=S^1+C^1+P^1+T^1$. □

This gives us $\underset{n\to \infty }{lim}\hspace{0.17em}\sup \mathbb{N}\le \frac{m_{11}}{\mathbb{N}}$. As a result, we obtain the Picard–Lindelöf theorem’s proof that the system is bounded in the area of (7). Lipschitz’s condition is satisfied by the right-hand side of (8). As a result, condition (i) is met. The definition satisfies the conditions for closed and convex region. Condition (ii) is therefore verified. Now, the quadratic character of D guarantees the convexity of the function I, where $I\left(S,C,P,T.\tilde{D}\right)=J_{1}C\left(t\right)+J_{2}P\left(t\right)+J_3{\tilde{D}}^2\ge J_3{\tilde{D}}^2$. Let $\Theta \left(\tilde{D}\right)=J_3{\tilde{D}}^2$, then $I\left(S,C,P,T.\tilde{D}\right)\ge J_3{\tilde{D}}^2$. Here, $\Theta \left(\tilde{D}\right)$ is a continuous function and ${\left|\tilde{D}\right|}^{-1}\Omega \tilde{D}$ $\to$$\infty$ as $\left|\tilde{D}\right|\to \infty$. Thus, condition (iii) is verified. Therefore, the optimal control variable ${\tilde{D}}^{*}$ exists. Hence, we have $\Omega \left({\tilde{D}}^{*}\right)=\min \Omega \left(\tilde{D}\right)$.

4.2. Features of the Optimal Control Function

We develop the essential conditions for system (6) and system (7) optimal control functions in accordance with the Pontryagin’s maximal principle. The corresponding Hamiltonian function is defined as

$$\begin{array}{l}H\left(S,C,P,T,\tilde{D},\theta \right)=I\left(S,C,P,T.D\right)+{\theta }_1{S}^1+{\theta }_2{C}^1+{\theta }_3{P}^1+{\theta }_4{T}^1,\\ H\left(S,C,P,T,\tilde{D},\theta \right)=J_{1}C\left(t\right)+J_{2}P\left(t\right)+J_3{D}^2+{\theta }_1\left(m_{11}-m_{12}SC-m_{13}SP-m_{14}S-{\tilde{\Omega }}_1\tilde{D}S\right)\\ +{\theta }_2\left(m_{21}SC+m_{22}SP-m_{23}C-{\tilde{\Omega }}_2\tilde{D}C\right)+{\theta }_3\left(m_{31}C+m_{32}T-m_{33}P-{\tilde{\Omega }}_3\tilde{D}P\right)\\ +{\theta }_4\left(m_{41}C+m_{42}P-m_{43}T-\left({\tilde{\Omega }}_{1}S+{\tilde{\Omega }}_{2}C+{\tilde{\Omega }}_{3}P\right)\tilde{D}\right)\end{array}$$

where ${\theta }_1,{\theta }_2,{\theta }_3\hspace{0.17em}and\hspace{0.17em}{\theta }_4$ are called adjoint variables.

Theorem 6.

We assume that the optimal control variables ${\tilde{D}}^{*}$and corresponding state variables of control system (6) and (7) are $S_{*},C_{*},P_{*},T_{*}$. These reduce the functional cost. Then,$\exists$adjoint variable ${\theta }_1,{\theta }_2,{\theta }_3\hspace{0.17em}and\hspace{0.17em}{\theta }_4$satisfy the following canonical equations$\frac{d{\theta }_1}{dt}=-\frac{\partial H}{\partial S};\frac{d{\theta }_2}{dt}=-\frac{\partial H}{\partial C};\frac{d{\theta }_3}{dt}=-\frac{\partial H}{\partial P};\frac{d{\theta }_4}{dt}=-\frac{\partial H}{\partial T}$with transversality condition${\theta }_w\left(t\right)=0$for w = 1, 2, 3 then we obtain

$${\tilde{D}}^{*}=\min \left\{\max \left\{\frac{{\tilde{\Omega }}_{1}S\left({\theta }_1-{\theta }_4\right)+{\tilde{\Omega }}_{2}C\left({\theta }_2-{\theta }_4\right)+{\tilde{\Omega }}_{3}P\left({\theta }_3-{\theta }_4\right)}{2J_3\left(S+C+P+T\right)},0\right\},1\right\}.$$

Proof. 

Let ${\tilde{D}}^{*}$ be the optimal value of the control variables, and $S_{*},C_{*},P_{*},T_{*}$ are the corresponding values of the variable $S\left(t\right),C\left(t\right),P\left(t\right),T\left(t\right)$ of the control system (7), which reduce the cost function given in Equation (8). By Pontryagin’s maximum principle, the adjoint variables ${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4$ satisfy the conditions

$$\frac{d{\theta }_1}{dt}=-\frac{\partial H}{\partial S};\frac{d{\theta }_2}{dt}=-\frac{\partial H}{\partial C};\frac{d{\theta }_3}{dt}=-\frac{\partial H}{\partial P};\frac{d{\theta }_4}{dt}=-\frac{\partial H}{\partial T}$$

Therefore, we have

$$\begin{array}{l}\frac{\partial {\theta }_1}{\partial t}=-\frac{\partial H}{\partial S}=-J_3{\tilde{D}}^2+{\theta }_1\left(m_{12}C+m_{13}P+m_{14}\right)-{\theta }_2\left(m_{21}C+m_{22}P\right)+{\Omega }_1\tilde{D}\left({\theta }_1-{\theta }_4\right),\\ \frac{\partial {\theta }_2}{\partial t}=-\frac{\partial H}{\partial C}=-J_1-J_3{\tilde{D}}^2+{\theta }_1\left(m_{12}S\right)+{\theta }_2\left(m_{23}-m_{21}S\right)-{\theta }_3{m}_{31}+{\tilde{\Omega }}_2\tilde{D}\left({\theta }_1-{\theta }_4\right),\\ \frac{\partial {\theta }_3}{\partial t}=-\frac{\partial H}{\partial C}=-J_2-J_3{\tilde{D}}^2+{\theta }_1\left(m_{13}S\right)-{\theta }_2\left(m_{22}S\right)+{\theta }_3{m}_{33}-{\theta }_4{m}_{42}+{\tilde{\Omega }}_3\tilde{D}\left({\theta }_3-{\theta }_4\right),\\ \frac{\partial {\theta }_4}{\partial t}=-\frac{\partial H}{\partial T}=-J_3{\tilde{D}}^2-{\theta }_3{m}_{32}+{\theta }_4{m}_{43}.\end{array}$$

From the optimality condition ${\frac{\partial H}{\partial \tilde{D}}}_{at\hspace{0.17em}\left(S=S_{*},C=C_{*},P=P_{*},T=T_{*}\right)}=0$, we obtain

$${\tilde{D}}^{*}=\frac{{\tilde{\Omega }}_{1}S\left({\theta }_1-{\theta }_4\right)+{\tilde{\Omega }}_{2}C\left({\theta }_2-{\theta }_4\right)+{\tilde{\Omega }}_{3}P\left({\theta }_3-{\theta }_4\right)}{2J_3\left(S+C+P+T\right)}$$

By definition, the highest and the lowest value of the control are 1 and 0, respectively. That is, if ${\tilde{D}}^{*}\le 0$ then ${\tilde{D}}^{*}=0$, and if ${\tilde{D}}^{*}\ge 1$ then ${\tilde{D}}^{*}=1$. Therefore, for ${\tilde{D}}^{*}$ we obtain the fuzzy optimum value of J for the system (7). Hence, the theorem is proved. □

5. Numerical Simulations

In this section, we place a focus on numerical simulations of the artificial drug transmission model using the parameter values from Table 1.

6. Numerical Observations

Figure 4 shows that the time series evaluation dynamics of populations for different initial values. It is clear from the figure that the system exhibits steadiness for a very short span of time and the system comes to steadiness after certain period of time. The time varies for different initial values.

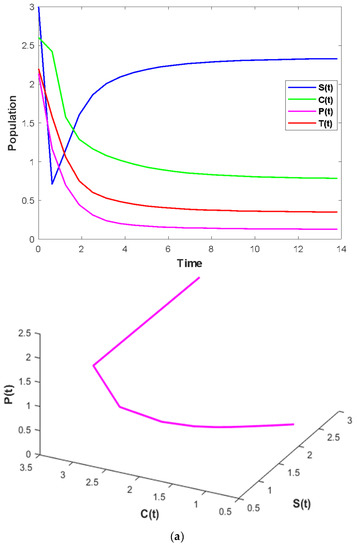
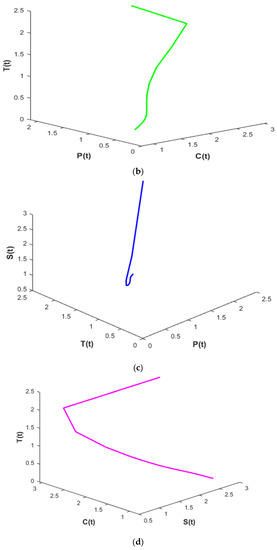
Figure 4. The time series evolution for the population S(t), C(t), P(t), and T(t) with the values of attributes from Table 1. (a) The phase portrait projection of S(t), C(t), and P(t) along with the values of attributes from Table 1. (b) The phase portrait projection of C(t), P(t), and T(t) along with the values of attributes from Table 1. (c) The phase portrait projection of T(t), P(t), and S(t) along with the values of attributes from Table 1. (d) The phase portrait projection of S(t), C(t), and T(t) along with the values of attributes from Table 1.

Figure 5a–d show that the time series evaluation dynamics for S(t), C(t), P(t), and T(t), respectively, for different values of fuzzy contact rates between the susceptible population and psychological addicts ($\alpha$). Figure 5a clearly shows that the system demonstrates steadiness over a very short length of time and that it attains steadiness after a specific amount of time unlike the rest of Figure 5b–d. Those change over time depending on the original initial numeric. Additionally, it is observed that the density of S(t) decreases (Figure 5a), the density of C(t) increases (Figure 5b), the density of P(t) increases (Figure 5c), and the density of T(t) increases (Figure 5d).

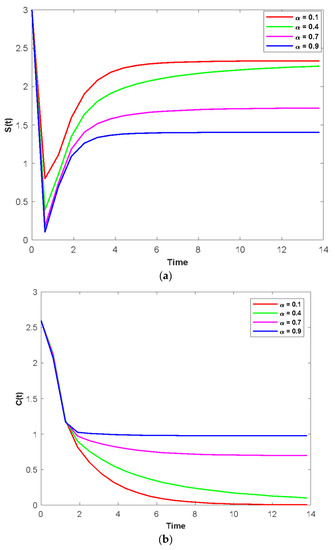
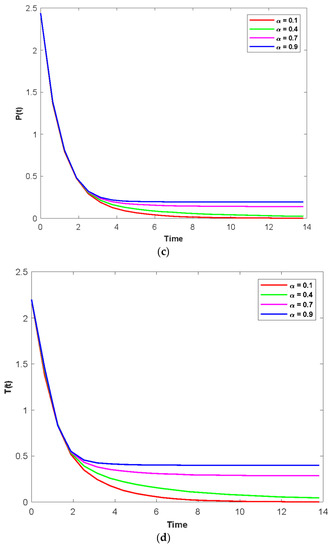
Figure 5. (a) The time series evolution for the population S(t) for various values of $\alpha$ and remaining values of attributes from Table 1. (b) The time series evolution for the population C(t) for various values of $\alpha$ and remaining values of attributes from Table 1. (c) The time series evolution for the population P(t) for various values of $\alpha$ and remaining values of attributes from Table 1. (d) The time series evolution for the population T(t) for various values of $\alpha$ and remaining values of attributes from Table 1.

Figure 6a–d show that the time series evaluation dynamics for S(t), C(t), P(t), and T(t), respectively for different values of fuzzy contact rates between the susceptible population and physiological addicts of populations ($\beta$). Figure 6a clearly shows that the system demonstrates steadiness over a very short length of time and that it attains constancy after a short time, unlike in Figure 6b–d. They might change over time depending on the starting values. Additionally, it is noted that when the attribute $\beta$ varies from 0.1 to 0.9, the density of S(t) decreases (Figure 6a) and the population densities of C(t), P(t), and T(t) increase (Figure 6b–d).

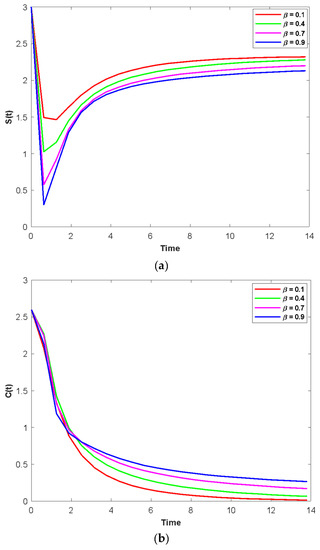
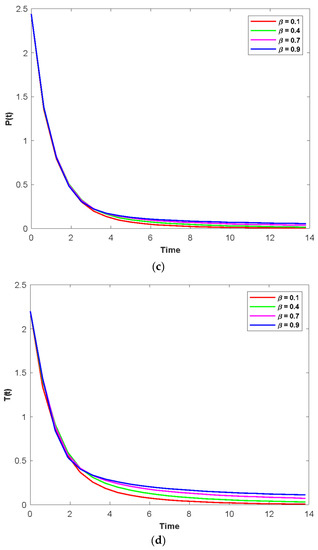
Figure 6. (a) The time series evolution for the population S(t) for various values of $\beta$ and remaining values of attributes from Table 1. (b) The time series evolution for the population C(t) for various values of $\beta$ and remaining values of attributes from Table 1. (c) The time series evolution for the population P(t) for various values of $\beta$ and remaining values of attributes from Table 1. (d) The time series evolution for the population T(t) for various values of $\beta$ and remaining values of attributes from Table 1.

Figure 7a–d display the time series evaluation dynamics for S(t), C(t), P(t), and T(t), respectively, for various values of the physiological addicts’ fuzzy treatment rates ($\delta$). Unlike Figure 7b–d, Figure 7a clearly displays that the system exhibits steadiness for a very short amount of time, rises up to a certain length, and then eventually achieves constancy after a short time. The beginning values will determine whether they change over time. It is also noted that when the attribute $\delta$ caries from 0.1 to 0.9, the density of S(t) decreases (Figure 4a) and the population densities of C(t), P(t), and T(t) increase (Figure 7b–d).

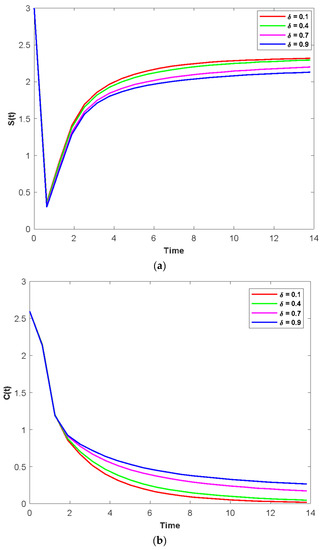
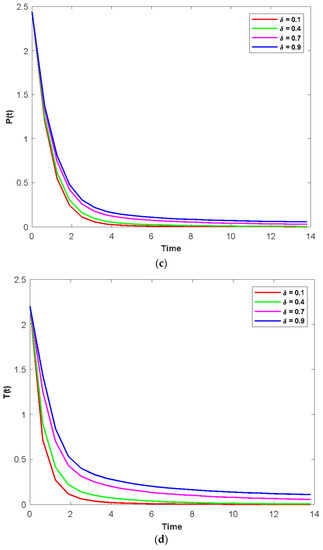
Figure 7. (a) The time series evolution for the population S(t) for various values of $\delta$ and remaining values of attributes from Table 1. (b) The time series evolution for the population C(t) for various values of $\delta$ and remaining values of attributes from Table 1. (c) The time series evolution for the population P(t) for various values of $\delta$ and remaining values of attributes from Table 1. (d) The time series evolution for the population T(t) for various values of $\delta$ and remaining values of attributes from Table 1.

Figure 8a–d illustrate the time series assessment dynamics for S(t), C(t), P(t), and T(t), respectively, for various values of the psychological addicts’ fuzzy treatment rates ($\psi$). Unlike Figure 8b–d, Figure 8a clearly reveals that the system exhibits steadiness after a very short period of time and that it attains steadiness after a certain amount of time. Depending on the original initial number, they evolve over time. When the attribute $\psi$ varies from 0.1 to 0.4, the densities of populations of S(t), C(t), P(t), and T(t) increase (Figure 8a–d).

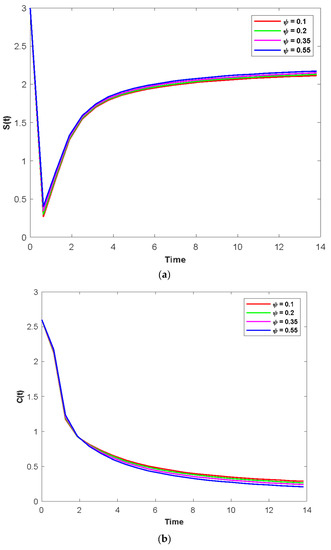
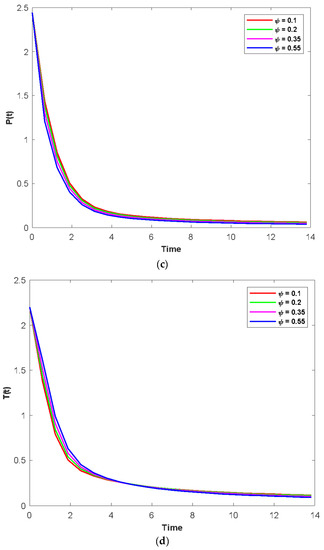
Figure 8. (a) The time series evolution for the population S(t) for various values of $\psi$ and remaining values of attributes from Table 1. (b) The time series evolution for the population C(t) for various values of $\psi$ and remaining values of attributes from Table 1. (c) The time series evolution for the population P(t) for various values of $\psi$ and remaining values of attributes from Table 1. (d) The time series evolution for the population T(t) for various values of $\psi$ and remaining values of attributes from Table 1.

7. Conclusions and Remarks

Artificial drugs include new drugs such as k2 (spice), ecstasy (Molly), and bath salts, which are quite acceptable among drug addicts. Some people believe that traditional drugs have more toxicity than artificial ones, meaning that they may believe that if someone uses an artificial drug a little, they will not become addicted. Based on this incorrect psychological belief, many people forget to take the proper precautions and can be captured by an addiction to artificial drugs gradually. Many people, especially the young generation, are exposed drugs due to various reasons. These people can be considered to be susceptible populations. The importance of health education in schools and families is to create awareness in youth. This education should be initiated by the government Artificial drugs are ideal for drug addicts, who are physically and psychologically addicted to their drug of choice. Thus, we planned an artificial drug victimizers model pertaining to the treatment of drug clients in fuzzy form. The fuzzy model’s positivity, boundedness, and equilibrium analysis are all thoroughly examined. We used the next generation matrix method to determine the fundamental reproduction number for the fuzzy artificial drug abuser model. The stability of the drug-free and drug-addicted equilibrium is a topic of discussion. To reduce drug addiction and the expense of treatment, counselling, and awareness campaigns, a fuzzy optimal control issue related to the drug abuse transmission model was used in accordance with Pontryagin’s Maximum Principle. The impact of fuzzy optimal response brought on by counselling programs can reduce both the financial burden and the number of addicts. This strategy can also reduce the overall financial load. This will ensure that a genuine control approach is carried out in a practical and conservative manner.