Abstract
In this paper, we extend the Petviashvili method (PM) to the fractional nonlinear Schrödinger equation (fNLSE) for the construction and analysis of its soliton solutions. We also investigate the temporal dynamics and stabilities of the soliton solutions of the fNLSE by implementing a spectral method, in which the fractional-order spectral derivatives are computed using FFT (Fast Fourier Transform) routines, and the time integration is performed by a 4th order Runge–Kutta time-stepping algorithm. We discuss the effects of the order of the fractional derivative, , on the properties, shapes, and temporal dynamics of the soliton solutions of the fNLSE. We also examine the interaction of those soliton solutions with zero, photorefractive and q-deformed Rosen–Morse potentials. We show that for all of these potentials, the soliton solutions of the fNLSE exhibit a splitting and spreading behavior, yet their dynamics can be altered by the different forms of the potentials and noise considered.
1. Introduction
The applications of fractional calculus to the Schrödinger equation, which serves as a model in various fields including, but not limited to, quantum physics, optics, hydrodynamics, and elastic body dynamics, are many. The fractional Schrödinger equation was first derived in [1], and since then its many possible applications have been proposed and studied. A Galerkin-Legendre spectral scheme that satisfies mass and energy conservation is studied in [2]. The contraction mapping principle is applied and the wave functions with their energy levels are studied in [3]. The existence of the ground states for an asymptotically linear fractional Schrödinger equation by variational methods is proven in [4]. The fractional Schrödinger–Poisson system of equations is also studied, and it is shown that a ground state solution and a sign-changing solution exist for such a system [5]. In a semi-classical analysis of the fractional Schrödinger equation, it is shown that the non-negative continuous potential can decay arbitrarily [6]. The fractional Schrödinger equation is still the subject of many ongoing studies [1,7,8,9].
On the other hand, the Petviashvili method (PM) is one of the commonly used methods for obtaining the soliton solutions of nonlinear systems. PM was first introduced in [10], and later was extended to spectral renormalization method [11] to serve as a numerical scheme that can be applied to many nonlinear systems including nonlinearities not necessarily restricted to fixed homogeneities. To the best of our knowledge, the extension of PM to the fNLSE remains an open research problem. Additionally, the analysis of the interaction of the soliton solutions of the fNLSE with various forms of potentials also remains to be investigated. With these motivations, we propose a numerical PM for the construction of soliton solutions of the fNLSE. The organization of this paper is as follows: in Section 2 of this paper, a review of the fNLSE equation and the PM method for finding its soliton solution are introduced. Additionally, for the time-stepping purposes, the usage of the Runge–Kutta 4 algorithm is discussed, where the spatial derivatives are evaluated spectrally using the efficient FFT routines. In Section 3, results and our findings are discussed. More specifically, we construct one and two soliton solutions of the fNLSE using the aforementioned numerical scheme and discuss their properties and the effects of fractional order derivative on these solitons’ characteristics and dynamics. Both q-deformed algebras [12,13] and potentials [14] have been considered in various areas from quantum computing [15,16] to quantum metrology [17], quantum thermodynamics [18] and so on. Therefore, in addition to zero potential and photorefractive potential, we consider q-deformed Rosen–Morse potentials and discuss their effects on soliton behavior and dynamics at Section 3. In Section 4, we discuss our findings and comment on their possible usage areas and future research directions in applied sciences.
2. Materials and Methods
Mathematical Formulation of the Petviashvili’s Method for the Solution of the Fractional Nonlinear Schrödinger Equation
The fractional order Schrödinger equation was first derived in [1] and became a common tool for modeling various processes in quantum mechanics, optics, and hydrodynamics, just to name a few areas of its applications. The fractional order Schrödinger can be written as
where the dependent variable denotes the complex wavefunction, i is the imaginary unity, ħ denotes the reduced Planck’s constant, is the position vector, t is the time and the Hamiltonian is given by where is a constant in dimensions of , which reduces to for where m denotes the mass of atomic particle, is the Laplacian, is the potential function and shows the order of the fractional derivative. The fractional Laplacian in this equation is used as a model to represent different heat kernels or Levy processes [19], thus it is commonly used in modeling different diffusive and stochastic processes in the nature as discussed in the introduction part of this paper. Thus, in the full form the fractional Schrödinger equation can be written as
Here, the 3D Riesz fractional derivative can be written as
where is the 3D Fourier transform of the wavefunction . In 1D and dimensionless form, the governing fractional Schrödinger equation given in Equation (1) reduces to [9]
We confine ourselves with time-independent potentials, , and we also take the effect of nonlinearity on the wavefunction, thus the 1D fractional nonlinear Schrödinger equation (fNLSE) becomes
Here, is a constant controlling the strength of the nonlinearity and is taken to be throughout this study in conjunction with the existing literature [20,21,22,23].
Although there are many techniques proposed in the literature to solve dynamic equations involving fractional Schrödinger-types of equations including, but not limited to, finite differences [24,25] and mass conservative spectral methods [26], there are a few techniques in the literature for the construction of soliton solutions of nonlinear equations such as shooting, self-consistency, and relaxation methods [10,11], which are not extended to fractional equations to our best knowledge. One of the commonly used methods with this aim is the Petviashvili’s method (PM) [10]. PM relies on transforming the governing dynamic equation into the wavenumber domain via FFT routines. After such a transformation, starting from the initial conditions, the iterations are continued until a nonlinearity-dependent convergence criterion is satisfied [10,11,27]. An energy conservation principle is used to check the convergence of the scheme [10,11]. The method summarized here is first proposed by Petviashvili and applied to the Kadomtsev–Petviashvili (KP) equation for the construction of its soliton solutions [10]. Later, PM is extended to account for nonlinearities not necessarily restricted to fixed homogeneity and named as the spectral renormalization method (SRM) [11,27]. The literature which utilizes PM and SRM is vast. These methods are commonly used to analyze the characteristics and dynamics of various phenomena such as lattice vortices, dark and gray solitons, the effect of various types of nonlinearities, and wave blocking [11,28,29]. The reader can refer to the papers [10,11,29,30,31] and the references therein for more detailed discussions of PM and SRM and their applications.
In this part, we extend the PM method for the solution of the fNLSE given in Equation (5). One can rewrite Equation (5) as
where the nonlinear term reads as . Using the ansatz, , where is the soliton eigenvalue, the fNLSE with becomes
The Fourier transform of parameter can be found using
where F denotes the Fourier transform. Thus, the Fourier transform of the fractional order derivative in Equation (6) can be computed using
where the parameter k is the wavenumber array, which has N multiples of the fundamental wavenumber as its entries. Fourier inverting the expression in Equation (9) via IFFTs, the fractional-order derivative can be computed [9,32,33]. The number of spectral components should be selected as a power of 2 for the efficient computations of FFT and IFFT routines.
The iteration equation in the wavenumber domain can be obtained by taking the 1D Fourier transform of Equation (6); however, it is well-known that such an iteration equation would have a singularity [10,11]. This is also true for the fNLSE investigated in this paper. To avoid such a singularity, we add and subtract a term to the Equation (6). Here, p denotes a positive real number, which is selected to be throughout this study [10,11]. After such an operation, the 1D Fourier transform of Equation (6) yields
which becomes the PM iteration scheme for the fNLSE. Following other studies on PM and SRM, we introduce the parameter defined by to obtain a convergence condition. The Fourier transform of this new parameter can be computed by . With such a substitution, the iteration formula given for the fNLSE in Equation (10) becomes
By multiplying both sides of Equation (11) with the term and integrating for the calculation of the total energy, the convergence criteria for the PM proposed for fNLSE becomes
The energy terms in the Equation (12) can be calculated via ordinary summation operations in the wavenumber domain, which generally yields to different values. A parameter can be introduced into this equation, and the ratio of the energy terms from the two sides of the equation can be obtained. Thus, the convergence of the scheme can be tested using the parameter calculated at every time step, enabling the construction of converged soliton solutions of the fNLSE. Starting from the initial conditions described in terms of Gaussians, Equations (11) and (12) are applied iteratively, until the parameter convergences to a relative error bound, which is selected as in this study.
PM is a powerful method for the efficient computation of the soliton solutions of the various dynamic equations. However, the stability of the solitons obtained via PM is not guaranteed, thus it is necessary to analyze their stability dynamics. It is well-known that a necessary, but not sufficient, condition for the soliton stability is the Vakhitov–Kolokolov slope condition [34]. Vakhitov–Kolokolov slope condition dictates that for a soliton to be stable, the condition must be satisfied for the positive values of the soliton eigenvalues, . In this formula, the soliton power parameter can be calculated using . The second condition for the soliton stability is the spectral condition, which is introduced and discussed analytically in [35,36]. Another approach commonly used to test the spectral condition is the numerical approach. The complexity of the different equations involving complicated potential functions and defect modes make the numerical approach a popular choice. When the spectral condition is tested numerically, starting from the soliton solutions constructed by PM, the time-stepping is performed for the next times using a time integration technique. With this aim, we implement a Fourier spectral scheme for the solution of the fNLSE. For the time-stepping, we use a 4th order Runge–Kutta time integrator. For this purpose, the fNLSE presented in Equation (5) can be rewritten as
Here, the function denotes the right-hand-side of the expression given in Equation (13). The fractional order Laplacian in Equation (13) can be computed using the expression given in Equation (9) and IFFT routines. All products in Equation (13) are calculated by ordinary multiplication in the physical domain. Time stepping of this equation is performed using a 4th order Runge–Kutta algorithm. The four slopes of the Runge–Kutta at each time step are computed by
where are the time index and the time step, respectively. The dimensionless time step is selected to be throughout this paper, which satisfies the stability and convergence conditions. Starting from the soliton solutions of the fNLSE obtained by the PM, the complex wavefunction and time parameter at later time steps are found by
At every time step, the soliton power, P, is computed and time versus soliton power, , graphs are plotted for the investigation of the stability characteristics of the solitons of the fNLSE. Additionally, the effect of potential terms on the characteristics and dynamics of these solitons are also investigated. The potentials considered for this purpose are photorefractive and q-deformed Rosen–Morse potentials, as described in the coming section of this paper.
3. Results and Discussion
3.1. Results for Zero Potential,
In this section, we present the characteristics and dynamics of the soliton solution of the fNLSE under the effect of zero optical potential, . Starting from a Gaussian in the form of initially, the one soliton solution of the fNLSE can be obtained numerically using the PM method suggested above for various values of the fractional order, . The computational domain is set to be where the value of is used for the length of the computational domain. The number of spectral components for this and all other simulations is selected as for utilizing the full computational efficiency of the FFT and IFFT algorithms. The one soliton solution of the fNLSE obtained by the proposed PM is shown in Figure 1 for various values of fractional order .
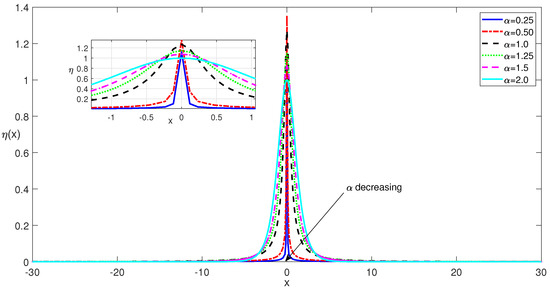
Figure 1.
Self-localized one soliton solutions of the fNLSE for various values of for a zero potential of .
In this figure, the amplitude of the one soliton solution of the fNLSE obtained for the fractional-order is used as the normalization amplitude. Figure 1 confirms that a decrease in the fractional-order, , leads to significant changes in the soliton profile. The solitons obtained for smaller values are more peaked and slender, leading to a higher nonlinearity parameter. This increased slenderness behavior and significantly reduced soliton width can lead to many important applications in applied sciences. In nonlinear and fiber optics, and in hydrodynamics, the success of pulse/wave positioning, pinpointing, and matched filtering can be enhanced by adjusting the order of the fractional derivative, . Additionally, the increased slenderness of the solitons enhances their sparsity in the spatial and temporal domains. Higher sparsity of the soliton signals makes the usage of smart algorithms such as compressive sensing possible, bringing up many challenges [37,38]. Efficient analysis, measurement, interpolation, and extrapolation of solitons of the fNLSE are a few of the problems involving those challenges.
When the aforementioned computational approach is initiated using two Gaussians in the form of , the PM converges to self-localized two soliton solutions of the fNLSE. Two solitons of the fNLSE obtained this way are displayed in Figure 2 for various values of the fractional order, . Similar to the one soliton solutions, the two solitons presented in Figure 2 become more slender as the fractional order parameter, , decreases.
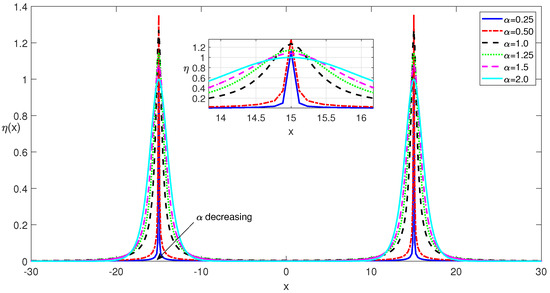
Figure 2.
Self-localized two soliton solutions of the fNLSE for various values of for a zero potential of .
Although the solitons of the fNLSE with 1,2, or multi-peaks can be constructed using the PM method summarized above, their stability characteristics should also be investigated. For this reason, we refer to some studies in the literature that investigate the stability characteristics of solitons (see, e.g., refs. [34,35,36] and the references therein). Vakhitov–Kolokolov condition, also known as the slope condition [34], is one of the necessary conditions to be satisfied for the soliton stability. This condition dictates that for the soliton to be stable, the condition should hold true for the positive values of the soliton eigenvalue, [34]. Here, denotes the soliton power. To examine if the Vakhitov–Kolokolov condition is satisfied, we depict the soliton eigenvalue vs. power graphs in Figure 3 and Figure 4 for the one soliton and two soliton solutions of the fNLSE, respectively. For the range of soliton eigenvalues considered, which is , we observe that the Vakhitov–Kolokolov condition is satisfied with the exceptional regions and spikes in Figure 3 and Figure 4. The behavior and trend in the graphs are quite similar for the different values of the derivative fractional order, . Especially the graph for the one soliton case exhibits a smoother behavior. Since for the soliton eigenvalue of , the Vakhitov–Kolokolov is satisfied, the value of is used for computations presented in this paper.
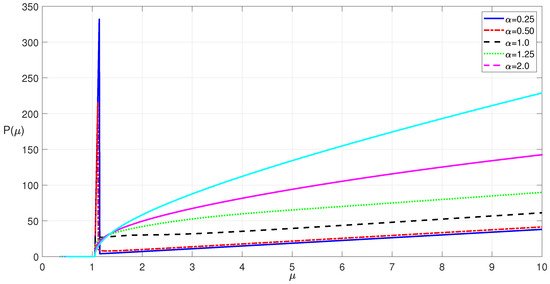
Figure 3.
Self-localized one soliton power vs. soliton eigenvalue, , for various values of for a zero potential of .
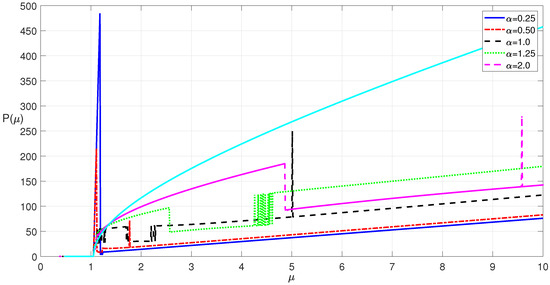
Figure 4.
Self-localized two soliton power vs. soliton eigenvalue, , for various values of for a zero potential of .
In the soliton stability theory, it is known that the Vakhitov–Kolokolov slope condition is necessary for the soliton stability; however, it is not a sufficient condition. Thus, the spectral condition should be investigated either analytically or numerically [35,36]. For this purpose, we use the spectral method with the 4th order Runge–Kutta time-stepping algorithm and analyze the temporal soliton characteristics and profiles numerically starting from the soliton shapes obtained by the PM method proposed for fNLSE and presented in Figure 1 and Figure 2. We depict the one soliton profile at different times in Figure 5 and two soliton profiles at different times in Figure 6. For both of these figures, the derivative fractional order is selected as .
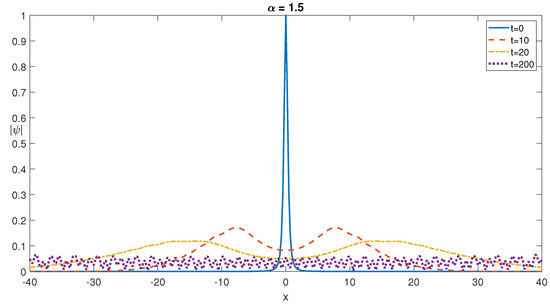
Figure 5.
Self-localized one soliton profiles at different times for for a zero potential of .
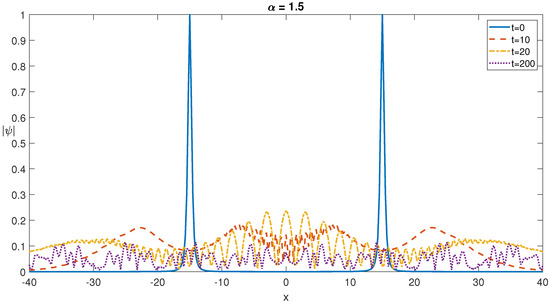
Figure 6.
Self-localized two soliton profiles at different times for for a zero potential of .
Checking Figure 5 and Figure 6, we can observe both of the one and two soliton profiles are exhibiting a splitting and spreading behavior. Such a splitting and spreading behavior is observed for all derivative fractional orders in the interval of . In the long-time limit, both the one and two soliton profiles evolve into sinusoidal-looking waveforms. These splitting and spreading dynamics is also commensurate with the findings presented in [9]. For the fractional order of , well-defined initial soliton shapes are preserved during the temporal evolution as expected, since the governing fNLSE reduces to the NLSE for this fractional derivative value.
In order to examine the stabilities or instability characteristics of the solitons, if any, we plot the time vs. soliton power graph in Figure 7. Since both of the one and two soliton graphs give similar results, only the graph for the one soliton dynamics is presented in Figure 7. Checking this figure, it is possible to conclude that soliton power becomes stabilized after some adjustment time and in the long-time limit exhibit a steady-in-the-mean behavior. The low amplitude oscillations observed in the long time limit in the graphs presented in Figure 7 are due to the last forms of the profiles exhibiting a sinusoidal-like behavior. We observe similar results for different values of ; however, for the sake of brevity and clarity of the presentation, only the graph for is presented.
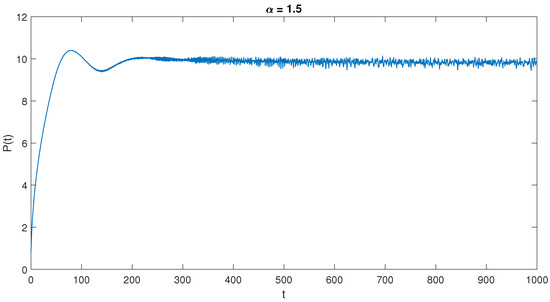
Figure 7.
Self-localized one soliton power as a function of time for for a zero potential of .
Next, we test the robustness of the soliton solutions against the noisy perturbations. With this motivation, we impose a white noise in the form to the wavefunction at every time step of temporal evolution, where the noise terms are and includes uniformly distributed random numbers in the interval of . As Figure 8 confirms, the soliton solutions of the fNLSE are robust against such perturbations and they remain bounded. No rogue wave patterns triggered by modulational instability are observed, including the long-time limiting case at which the profile resembles a sinusoidal waveform. In Figure 8, in the first subplot, the self-localized one soliton shape at different times under the effect of noisy perturbations is depicted. In the second subplot of Figure 8, the denoised soliton profiles at various times are presented. For the denoising process, we used a 3rd order Savitzky–Golay filter. As the figure indicates, the denoising filter can be used to filter the noise to obtain the fundamental characteristics and profiles of the solutions; however, such a denoising process can cause some reduction in the peak amplitudes of the solitons, which become even more pronounced for the lower values of the fractional-order . Similar behavior is also observed for the two soliton cases.
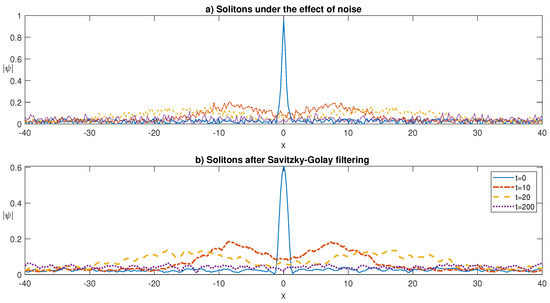
Figure 8.
Self-localized one soliton profiles at different times for for a zero potential of . (a) Under the effect of noise. (b) After the noise is filtered out by Savitzky–Golay filter.
3.2. Results for Photorefractive Potential,
Various forms of the potential functions are commonly used to model the effects of different phenomena on nonlinear processes. In quantum mechanics parabolic traps [20,21], linear potentials [9] and q-deformed potentials [14,27,39,40,41] are well-studied forms of the potentials. In nonlinear and fiber optics, the photorefractive and saturable photorefractive potentials with/without defects are commonly investigated [11,27,29]. In hydrodynamics, the blocking effect of opposing currents is modeled using constant, linear, sinusoidal, and other types of potentials [28,42]. In Bose–Einstein condensation, repulsive and attractive potentials are used to model ultracold atomic system dynamics with optical traps [43,44,45]. This brief list is intended to provide the reader a starting point, and is by no means complete.
In this section, we investigate the effects of the photorefractive potentials on the soliton solutions of the fNLSE. With this aim, we use a potential function in the form of , and follow the similar steps described above. Starting from a Gaussian initial condition, the one soliton solution of the fNLSE with the photorefractive potential is constructed and depicted in Figure 9 for various values of the fractional order, .
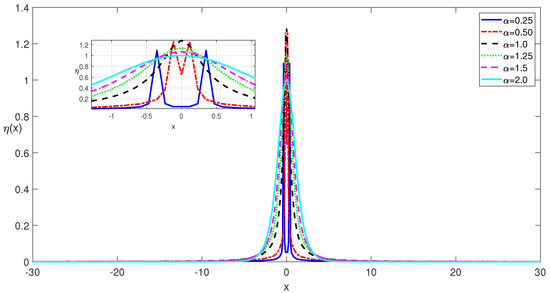
Figure 9.
Self-localized one soliton solutions of the NLSE for various values of for a photorefractive potential of .
Compared to the solitons depicted in Figure 1, the ones depicted in Figure 9 have some differences. The striking effect of the photorefractive potential is that, although one soliton shape is preserved at the base of the soliton, some of them begin exhibiting two peaks. This finding is also confirmed by the results presented in [11,27,29]. These two peaked one soliton shapes become more prominent for the lower values of such as , which lead to more slender profiles.
Next, we analyze the effect of the photorefractive potential on the temporal dynamics of the soliton shapes of the fNLSE. Running the time-stepping algorithm for the fNLSE for the derivative fractional order of with this photorefractive potential, we obtain the soliton shapes, which are depicted in Figure 10. As before, the splitting and spreading behavior for the solitons are experienced. However, a comparison of Figure 5 and Figure 10 indicate that the photorefractive potential causes the generation of higher wavenumber components appearing as shorter wavelength undulations on the main soliton profiles, which is especially clear for shorter times of evolution. Additionally, it is possible to conclude that photorefractive potential decreases the spreading of the one soliton. This is clear in Figure 10, since the peaks are mainly confined to a region closer to the origin .
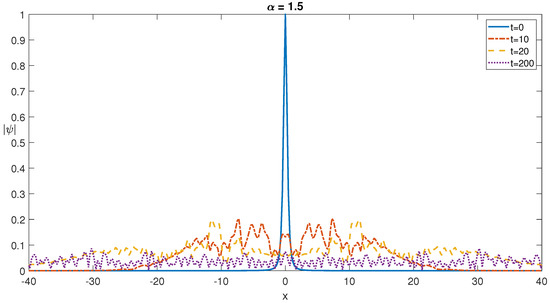
Figure 10.
Self-localized one soliton profiles at different times for for a photorefractive potential of .
The two soliton solutions of the fNLSE under the effect of a photorefractive potential in the form of is depicted in Figure 11. After comparison of Figure 6 and Figure 11, it is possible to state that on the shorter time scales short-wavelength undulations on the main soliton profiles are significantly trapped near two initial peaks. The graphs and graphs obtained for the soliton solutions of the fNLSE under the effect of a photorefractive potential are similar and for the sake of brevity are not presented, but the steady-in-the-mean state is achieved earlier around the dimensionless time of . They are also stable and robust against noisy perturbations.
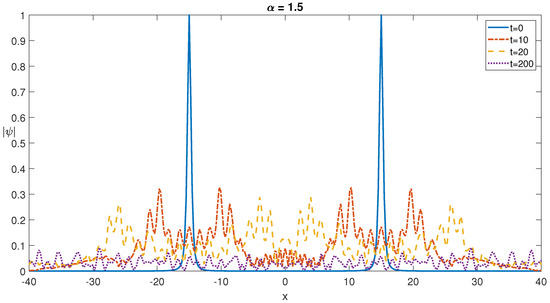
Figure 11.
Self-localized two soliton profiles at different times for for a photorefractive potential of .
3.3. Results for q-Deformed Rosen-Morse Potential,
Another type of potential function commonly used to effects of shifts and asymmetry in the medium under investigation is the q-deformed potentials [46]. Various analytical solutions of the nonlinear systems with q-deformed potential are present in the literature [46]; however, the majority of the solutions are valid for models other than fNLSE and valid for steady-state conditions. In order to investigate the effects of q-deformation on the solitons of the fNLSE, we use a q-deformed Rosen–Morse potential. For this purpose, we use a potential function in the form of where q-deformed hyperbolic functions are formulated as and [46]. The parameters of the q-deformed potential functions are selected as as the typical parameters used in the literature [27,46].
In Figure 12, we depict the one soliton solutions of the fNLSE with the q-deformed Rosen–Morse potential term with the parameter obtained for various values of the fractional-order . Compared to the solitons depicted in Figure 1 and Figure 9, which are obtained for the zero potential and for the photorefractive potential cases, respectively, the solitons depicted in Figure 12 have distinctive features. The dip in the peak or two peaked solitons observed for the photorefractive potentials are not observed for the q-deformed Rosen–Morse and their shapes are more similar to the ones obtained for the zero potential case. However, as an important difference, the location of the peak is shifted and the profile exhibits skewness due to the q-deformed Rosen–Morse type potential used in their construction.
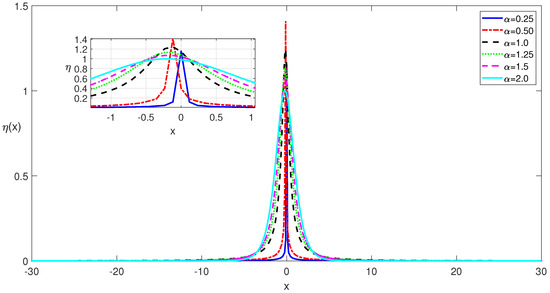
Figure 12.
Self-localized one soliton solutions of the fNLSE with a Rosen–Morse potential of with for various values of .
After a careful inspection of Figure 13, it is possible to state that during the temporal dynamics of the fNLSE with q-deformed Rosen–Morse potential, the shifts in soliton peak positions and their profile skewnesses can be observed. Additionally, about an axis passing through the origin, the wavefield exhibits an asymmetric distribution of the wavefunction. This asymmetry can be useful for the implementation of filtering–tunneling potentials of the optical and quantum processes modeled in the frame of the fNLSE.
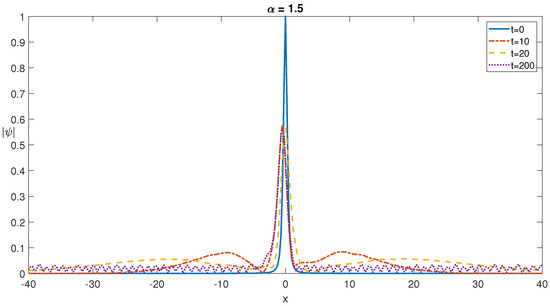
Figure 13.
Self-localized one soliton profiles at different times for for a Rosen–Morse potential of with .
Lastly, we examine the effect of parameter of the q-deformed Rosen–Morse potential. The value of is reduced from 1 to 0.1, and solitons of the fNLSE obtained by PM and then time-evolved by fractional spectral method with 4th order Runge–Kutta time-integrator are depicted in Figure 14. Such a reduction in the parameters leads to a significant increase in the q-deformed Rosen Morse potential, and similar to the photorefractive potential case, low amplitude undulations with shorter wavenumber components become apparent on the main soliton profile. However, skewness and asymmetry of the wavefield are still observed.
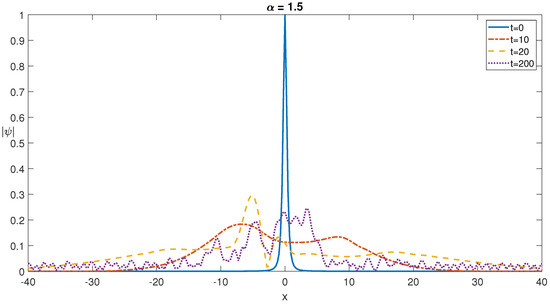
Figure 14.
Self-localized one soliton profiles at different times for for a Rosen–Morse potential of with .
4. Conclusions
In this paper, we extended the Petviashvili method (PM), which can be used to construct the soliton solutions of the fractional nonlinear Schrödinger equation (fNLSE). We investigated the characteristics and the effects of fractional order processes on those solitons. Additionally, the stabilities and temporal dynamics of those solitons of the fNLSE are investigated via a Fourier spectral algorithm with a 4th order Runge–Kutta time integrator, where the fractional derivatives are computed spectrally. We showed that the fractional derivative order parameter controls the slenderness of the soliton peak profiles, soliton profiles more slender as reduced. We showed that under zero potential, photorefractive potential, and q-deformed Rosen–Morse potential, the fNLSE admits soliton solutions. These solitons exhibit a splitting and spreading behavior; however, various forms of the potentials can be used to alter their dynamics. We also showed that those solitons are robust against noisy perturbations, and the effect of noise on these solitons can be removed by a Savitzky–Golay filter. For the zero potential case, solitons of the fNLSE split into two pieces initially, then spread. However, in the photorefractive and q-deformed Rosen–Morse potential cases, shorter wavelength components are generated. This effect is more prominent in the case of the photorefractive potential. For the q-deformed Rosen–Morse potential case, the shifts in soliton peak location and skewness in their profiles are observed.
The fractional-order soliton dynamics reported in this work are promising. The fractional-order derivative controls the slenderness of the solitons and their peakedness. Thus, the physical processes described by fractional derivatives can be used to fine-tune the soliton profiles to increase the resolution of the solutions, enabling pulse pinpointing and matched filtering with a better performance. Additionally, the photorefractive and q-deformed potentials can be used for multi-frequency wavefield generation as well as tunneling, shifting, and adjusting the skewness of those solitons. Our findings can be used in many disciplines, including, but not limited to, quantum physics, nonlinear optics and hydrodynamics, Bose–Einstein condensation, and quantum control theory.
There are many possible research directions based on the research presented in this paper. First of all, our results can be easily generalized to N-soliton solutions. The effects of other types of potentials of fNLSE can also be investigated within the frame of the approach presented herein. Some of these potentials are Eckart, Coulomb, Yukawa, parity-time symmetric Rosen–Morse, and -deformed an-harmonic potentials. Fractional order equations with other forms of nonlinearities such as Kundu–Eckhaus or Sasa–Satsuma type extensions of the NLSEcan also be studied within our numerical framework. Additionally, many interesting phenomena observed in the nonlinear sciences such as quantum tunneling, wave blocking, entanglement, and wave–wave and wave–particle interactions can be investigated under the effect of fractional processes using the methodology presented in this paper. Such future works on this subject would contribute to significant improvements and new insights in various branches of science, some of which are mentioned above.
Author Contributions
Conceptualization, C.B., S.F., A.A.A. and F.O.; methodology, C.B. and S.F.; software, C.B. and S.F.; validation, C.B., S.F., A.A.A. and F.O.; formal analysis, C.B., S.F., A.A.A. and F.O.; investigation, C.B., S.F., A.A.A. and F.O.; resources, C.B. and S.F.; writing—original draft preparation, C.B., S.F., A.A.A. and F.O.; visualization, C.B. and S.F.; supervision, C.B.; funding acquisition, F.O. All authors have read and agreed to the published version of the manuscript.
Funding
F.O. acknowledge Personal Research Fund of Tokyo International University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the results can be reproduced through the presented methods.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PM | Petviashvili method |
| fNLSE | fractional nonlinear Schrödinger equation |
| KP | Kadomtsev-Petviashvili |
| SRM | spectral renormalization method |
| CSRM | compressive spectral renormalization method |
References
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [PubMed]
- Fei, M.; Zhang, G.; Wang, N.; Huang, C. A linearized conservative Galerkin–Legendre spectral method for the strongly coupled nonlinear fractional Schrödinger equations. Adv. Differ. Equ. 2020, 2020, 661. [Google Scholar] [CrossRef]
- Shao, J.; Guo, B. The Cauchy problem for Schrödinger-damped Boussinesq system. J. Math. Anal. Appl. 2021, 494, 124639. [Google Scholar] [CrossRef]
- Chen, P.; Liu, X. Ground states for asymptotically linear fractional Schrödinger–Poisson systems. J. -Pseudo-Differ. Oper. Appl. 2021, 12, 8. [Google Scholar] [CrossRef]
- Gu, G.; Tang, X.; Shen, J. Multiple solutions for fractional Schrödinger–Poisson system with critical or supercritical nonlinearity. Appl. Math. Lett. 2021, 111, 106605. [Google Scholar] [CrossRef]
- An, X.; Lipeng, D.; Peng, Y. Semi-classical analysis for fractional Schrödinger equations with fast decaying potentials. Appl. Anal. 2021, 101, 5138–5155. [Google Scholar] [CrossRef]
- Jamshir, N.; Lari, B.; Hassanabadi, H. The time independent fractional Schrödinger equation with position-dependent mass. Phys. A Stat. Mech. Appl. 2021, 565, 125616. [Google Scholar] [CrossRef]
- Alouini, B. Finite dimensional global attractor for a fractional Schrödinger type equation with mixed anisotropic dispersion. J. Dyn. Differ. Equ. 2022, 34, 1237–1268. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Fractional Schrödinger equation in the presence of the linear potential. Mathematics 2016, 4, 31. [Google Scholar] [CrossRef]
- Petviashvili, V.I. Equation of an extraordinary soliton. Fiz. Plazmy 1976, 2, 469–472. [Google Scholar]
- Ablowitz, M.J.; Musslimani, Z.H. Spectral renormalization method for computing self-localized solutions to nonlinear systems. Opt. Lett. 2005, 30, 2140–2142. [Google Scholar] [CrossRef] [PubMed]
- Bonatsos, D.; Lenis, D.; Raychev, P.; Terziev, P. Deformed harmonic oscillators for metal clusters: Analytic properties and supershells. Phys. Rev. A 2002, 65, 033203. [Google Scholar] [CrossRef]
- Altintas, A.A.; Arik, M.; Arikan, A.S.; Dil, E. Inhomogeneous quantum invariance group of multi-dimensional multi-parameter deformed boson algebra. Chin. Phys. Lett. 2012, 29, 010203. [Google Scholar] [CrossRef]
- Molaee, Z.; Ghominejad, M.; Hassanabadi, H.; Zarrinkamar, S. S-wave solutions of spin-one DKP equation for a deformed Hulthén potential in (1+ 3) dimensions. Eur. Phys. J. Plus 2012, 127, 116. [Google Scholar] [CrossRef]
- Altintas, A.A.; Ozaydin, F.; Yesilyurt, C.; Bugu, S.; Arik, M. Constructing quantum logic gates using q-deformed harmonic oscillator algebras. Quantum Inf. Process. 2014, 13, 1035–1044. [Google Scholar] [CrossRef]
- Altintas, A.A.; Ozaydin, F.; Bayındır, C. q-Deformed three-level quantum logic. Quantum Inf. Process. 2020, 19, 247. [Google Scholar] [CrossRef]
- Hasegawa, H. Quantum Fisher Information and q-Deformed Relative Entropies: Additivity vs Nonadditivity. Prog. Theor. Phys. 2006, 162, 183–189. [Google Scholar] [CrossRef]
- Güvenilir, E.; Ozaydin, F.; Müstecaplıoğlu, Ö.E.; Hakioğlu, T. Work harvesting by q-deformed statistical mutations in an Otto engine. arXiv 2022, arXiv:2208.08565. [Google Scholar]
- Kwaśnicki, M. Ten Equivalent Definitions of the Fractional Laplace Operator. Fract. Calc. Appl. Anal. 2017, 20, 7–51. [Google Scholar] [CrossRef]
- Bayındır, C. Rogue quantum harmonic oscillations. Phys. A Stat. Mech. Appl. 2020, 547, 124462. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Alexander, T.J.; Turitsyn, S.K. Nonlinear modes of a macroscopic quantum oscillator. Phys. Lett. A 2001, 278, 225–230. [Google Scholar] [CrossRef]
- Bayındır, C.; Ozaydin, F. Freezing optical rogue waves by Zeno dynamics. Opt. Commun. 2018, 413, 141–146. [Google Scholar] [CrossRef]
- Bayındır, C.; Ozaydin, F. Self-localized soliton solutions of the nonlinear quantum harmonic oscillator. TWMS J. Appl. Eng. Math. 2022, 12, 412. [Google Scholar]
- Wang, Y.; Hao, Z.; Du, R. A Linear Finite Difference Scheme for the Two-Dimensional Nonlinear Schrödinger Equation with Fractional Laplacian. J. Sci. Comput. 2021, 90, 24. [Google Scholar] [CrossRef]
- Li, M.; Gu, X.M.; Huang, C.; Fei, M.; Zhang, G. A fast linearized conservative finite element method for the strongly coupled nonlinear fractional Schrödinger equations. J. Comput. Phys. 2018, 358, 256–282. [Google Scholar] [CrossRef]
- Duo, S.; Zhang, Y. Mass-conservative Fourier spectral methods for solving the fractional nonlinear Schrödinger equation. Comput. Math. Appl. 2016, 71, 2257–2271. [Google Scholar] [CrossRef]
- Bayındır, C.; Altintas, A.A.; Ozaydin, F. Self-localized solitons of a q-deformed quantum system. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105474. [Google Scholar] [CrossRef]
- Bayındır, C. Self-localized solitons of the nonlinear wave blocking problem. Dyn. Atmos. Ocean. 2021, 93, 101189. [Google Scholar] [CrossRef]
- Fibich, G. The Nonlinear Schrödinger Equation; Springer: Berlin/Heidelberg, Germany, 2015; Volume 192. [Google Scholar] [CrossRef]
- Fokas, A.S.; Cao, Y.; He, J. Multi-Solitons, Multi-Breathers and Multi-Rational Solutions of Integrable Extensions of the Kadomtsev–Petviashvili Equation in Three Dimensions. Fractal Fract. 2022, 6, 425. [Google Scholar] [CrossRef]
- Bayındır, C. Self-localized solutions of the Kundu-Eckhaus equation in nonlinear waveguides. Results Phys. 2019, 14, 102362. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in the medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Weinstein, M.I. Modulational stability of ground states of nonlinear Schrödinger equations. SIAM J. Math. Anal. 1985, 16, 472–491. [Google Scholar] [CrossRef]
- Sivan, Y.; Fibich, G.; Ilan, B.; Weinstein, M. Qualitative and quantitative analysis of stability and instability dynamics of positive lattice solitons. Phys. Rev. E 2008, 78, 046602. [Google Scholar] [CrossRef] [PubMed]
- Bayındır, C. Compressive spectral method for the simulation of the nonlinear gravity waves. Sci. Rep. 2016, 6, 22100. [Google Scholar] [CrossRef] [PubMed]
- Bayındır, C. Compressive spectral renormalization method. TWMS J. Appl. Eng. Math. 2018, 8, 425–437. [Google Scholar]
- Macfarlane, A.J. On q-analogues of the quantum harmonic oscillator and the quantum group SU(2)q. J. Phys. Math. Gen. 1989, 22, 4581–4588. [Google Scholar] [CrossRef]
- Biedenharn, L.C. The quantum group SUq(2) and a q-analogue of the boson operators. J. Phys. Math. Gen. 1989, 22, L873–L878. [Google Scholar] [CrossRef]
- Biedenharn, L.C.; Lohe, M.A. Quantum Group Symmetry and q-Tensor Algebras; World Scientific: Singapore, 1995. [Google Scholar]
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech.—B/Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a matter-wave bright soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef]
- Nguyen, J.H.; Luo, D.; Hulet, R.G. Formation of matter-wave soliton trains by modulational instability. Science 2017, 356, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Falaye, B.; Oyewumi, K.; Abbas, M. Exact solution of Schrödinger equation with q-deformed quantum potentials using Nikiforov—Uvarov method. Chin. Phys. B 2013, 22, 110301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).