On the Existence and Stability of a Neutral Stochastic Fractional Differential System

Abstract

The main purpose of this paper is to investigate the existence and Ulam-Hyers stability (U-Hs) of solutions of a nonlinear neutral stochastic fractional differential system. We prove the existence and uniqueness of solutions to the proposed system by using fixed point theorems and the Banach contraction principle. Also, by using fundamental schemes of fractional calculus, we study the (U-Hs) to the solutions of our suggested system. Besides, we study an example, best describing our main result.

1. Introduction

As we know, modeling natural phenomena is one of the ways to understand and interpret them. Therefore, the discovery of new modeling tools has always been of interest to researchers. Fractional calculus is one of these useful and new tools. Fractional differential equations have been used in different fields, such as control theory, biomath [1,2], thermodynamics, signal processing, and so on [3,4]. The application of fractional calculus by new researchers has been developed in the field of time-dependent damping behavior in the viscoelastic behavior sciences. Furthermore, fractional differential equations (FDEs) also have great applications in the nonlinear oscillation of earthquakes, with several physical phenomena such as fluid dynamics, traffic models, seepage flow in porous media, etc. [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Disavowing FDEs is like saying that irrational numbers do not exist. In addition, boundary value problems play a special role in solving and interpreting real-world problems, for example, population dynamics, thermoplasticity, chemical engineering, blood flow, underground water flow, etc. [24].

The concept of stability is one of the qualitative aspects of dynamic systems. Stability theory is very significant, as each practicable control system is structured to be stable. Additionally, in physical use, the stability of solutions is very beneficial because variations in mathematical models undoubtedly stem from measurement errors. A stable solution may become variable through such variations. The analysis of the stability properties of solutions has captivated a lot of research workers through its promising applications. Specifically, the Ulam–Hyers stability analysis and its uses have been studied by legion researchers. The definition of (U-Hs) has applicable significance; it means if someone is capitalizing upon the (U-Hs), then one does not necessarily need to approach the exact solution. It testifies that there is a consistently exact solution to each of the approximate solutions. This is advantageous in all fields, including economics, numerical analysis, optimizations theory, biology, etc., where finding the exact solution is quite tiring or time-consuming; see [25,26,27,28,29,30].

On the other hand, physical models often fluctuate due to stochastic noise or perturbation, so it makes sense to include stochastic effects into the fractional differential equation to investigate this type of modeling. This leads us to focus on this type of equation in this study. One can find many published works in this area; see, for example, refs. [31,32,33,34].

According to the lack of investigations on the existence and the (U-Hs) of the solutions of a nonlinear neutral stochastic fractional differential system, it is of great interest to perform some investigations in this area. Dai et al. [35] investigated the following fractional differential equation for existence and Ulam–Hyers type stability

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\upsilon }^{\prime }(\mathit{t})+{{}^c\mathcal{D}}_{0^{+}}^{\wp }\upsilon (\mathit{t})=\upsilon (\mathit{t},\upsilon (\mathit{t})),\mathit{t}\in [0,1],\hfill \\ & \upsilon (1)={\mathrm{I}}_{0^{+}}^{\hslash }\upsilon (\beta )=\frac{1}{\Gamma (\hslash )}{\int }_0^{\beta }{(\beta -s)}^{\hslash -1}\upsilon (s)ds,\hfill \end{array}\right.\end{array}$$

where ${{}^c\mathcal{D}}_{0^{+}}^{\wp }(·)$ and ${\mathrm{I}}_{0^{+}}^{\hslash }$ represents the fractional Caputo derivative of order $\wp \in (0,1)$ and the fractional Riemann–Liouville integral such that $\hslash >0$, respectively. The function $\upsilon :[0,1]\times \mathbb{R}\to \mathbb{R}$ is continuous and $\upsilon \in {\mathrm{C}}^1[0,1]$, while $\beta \in (0,1]$ is a fixed number.

Y. Guo et al. [36], investigated the impulsive neutral functional stochastic differential equation for existence and UH stability as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\mathcal{D}}_{0^{+}}^{\alpha }[\upsilon (t)-l(t,{\upsilon }_t)]=\kappa (t,{\upsilon }_t)+\vartheta (t,{\upsilon }_t)\frac{d\omega (t)}{dt},t\in [0,b],t\ne t_k,\hfill \\ & \Delta {\mathrm{I}}_{0^{+}}^{2-\alpha }(\upsilon (t_k))=I_k(\upsilon (t_k^{-})),\Delta {\mathrm{I}}_{0^{+}}^{1-\alpha }(\upsilon (t_k))=J_k(\upsilon (t_k^{-})),\hfill \\ & {\mathrm{I}}_{0^{+}}^{2-\alpha }(\upsilon (0)-l(0,{\upsilon }_0))={\varphi }_1\in {\mathbf{B}}_y,{\mathrm{I}}_{0^{+}}^{1-\alpha }(\upsilon (0)-l(0,{\upsilon }_0))={\varphi }_2\in {\mathbf{B}}_y,\hfill \end{array}\right.\end{array}$$

where ${\mathcal{D}}_{0^{+}}^{(.)}$ represents the Riemann–Liouville fractional derivative of order $\alpha \in (1,2]$, and $k=1,2,\cdots ,m$. We also have $0=t_0<t_1<t_2<\cdots <t_m<t_{m+1}=b$. The functions $\kappa ,l,\vartheta :(0,b]\times {\mathbf{B}}_y$ are continuous and $\omega (t)$ $(t\in (0,b]),$ is the Wiener process, while ${\mathbf{B}}_y$ is a phase space. The notations $I_k,J_k$ represent appropriate functions, and ${\mathrm{I}}_{0^{+}}^{1-\alpha },{\mathrm{I}}_{0^{+}}^{2-\alpha }$ are Riemann–Liouville fractional integrals with orders $1-\alpha$ and $2-\alpha$, respectively. The $\Delta {\mathrm{I}}_{0^{+}}^{1-\alpha },$ $\Delta {\mathrm{I}}_{0^{+}}^{2-\alpha }$ are defined by

$$\begin{array}{ccc}\hfill \Delta {\mathrm{I}}_{0^{+}}^{1-\alpha }(\upsilon (t_k))& =& {\mathrm{I}}_{0^{+}}^{1-\alpha }(\upsilon (t_k^{+}))-{\mathrm{I}}_{0^{+}}^{1-\alpha }(\upsilon (t_k^{-})),\hfill \\ \hfill \Delta {\mathrm{I}}_{0^{+}}^{2-\alpha }(\upsilon (t_k))& =& {\mathrm{I}}_{0^{+}}^{2-\alpha }(\upsilon (t_k^{+}))-{\mathrm{I}}_{0^{+}}^{2-\alpha }(\upsilon (t_k^{-})).\hfill \end{array}$$

Here, the maps $({\upsilon }_t:(-\infty ,b]\to \mathbb{R})\in {\mathbf{B}}_y$ have been defined by ${\upsilon }_t(\upsilon )=\upsilon (t+\upsilon ),$ $\upsilon \le 0$.

Sathiyaraj et al. [37] studied (U-Hs) results of the solutions of the following fractional stochastic differential system involving the Hilfer fractional derivative ${{}^H\mathcal{D}}_{0^{+}}^{\alpha ,\beta }$ of order $\alpha \in [0,1]$ and type $\beta \in (0,1)$ for $t\in [0,T],(T>0)$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {{}^H\mathcal{D}}_{0^{+}}^{\alpha ,\beta }(u(t))=\mathcal{A}u(t)+\vartheta (t,u(t),{{}^H\mathcal{D}}_{0^{+}}^{\alpha ,\beta }(u(t)))+{\int }_0^t\eta (s,u(s),{{}^H\mathcal{D}}_{0^{+}}^{\alpha ,\beta }(u(s)))d\omega (s),\hfill \\ & {\mathrm{I}}_{0^{+}}^{1-\gamma }(u(t))=u_0,\gamma =\alpha +\beta -\alpha \beta ,\hfill \end{array}\right.\end{array}$$

where $u\in {\mathbb{R}}^n$ and $\mathcal{A}$ are a matrix of dimension $n\times n$. The functions $\vartheta ,\eta :(0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ and $\eta :(0,T]\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n\times {\mathbb{R}}^n$ are nonlinear and continuous.

There exists extensive prose about the existence and uniqueness (EU) of solutions related to FDEs involving ordinary and fractional derivatives, etc., while in the setting of a nonlinear neutral stochastic FDEs system involving ordinary derivative, as far as we know, existence, uniqueness, and stability have not been discussed.

Motivated by the above content, in this article we study the EU and (U-Hs) of the following nonlinear stochastic fractional differential system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {{}^c\mathcal{D}}_{0^{+}}^{\wp }[\upsilon (t)-\kappa (t,\upsilon (t))]=\mathrm{A}\upsilon (t)+l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt},t\in \mathrm{J}:=[0,b],\hfill \\ & \upsilon (0)=\mathbf{B},\hfill \end{array}\right.\end{array}$$

(1)

where $\mathrm{A}$ represents the diagonal matrix of dimensions $n\times n$, with the Caputo fractional deferential operators ${{}^c{\mathcal{D}}^{\wp }}_{0^{+}}(·)={({{}^c{\mathcal{D}}^{{\wp }_1}}_{0^{+}},{{}^c{\mathcal{D}}^{{\wp }_2}}_{0^{+}},\cdots ,{{}^c{\mathcal{D}}^{{\wp }_n}}_{0^{+}})}^T$, each of order ${\wp }_{i_{1\le i\le n}}\in (0,1)$. ${(W(t))}_{t\ge 0}$ is a standard Brownian motion on the complete probability space $(\mathrm{\Omega },{\mathbf{F}}_b,\mathbf{P}),$ $b>0$ along with some filtration ${\mathbf{F}}_b={\{{\mathfrak{F}}_t\}}_{t\in \mathrm{J}}$ satisfy some conditions, while ${\mathfrak{F}}_0$ consists of $\mathbf{P}$-null sets. Additionally, $l:={(l_1,l_2,\cdots ,l_n)}^T$, $l_{1\le i\le n}:\mathrm{J}\times R^n\times R^n\to R^n$ and $\kappa :\mathrm{J}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ are n-dimensional locally integrable measurable bounded vector functions on $0<t\le b$ and its entries admit the Laplace transformation. Furthermore, $\upsilon (t)={({\upsilon }_1(t),{\upsilon }_2(t),\cdots ,{\upsilon }_n(t))}^T$ is an unknown vector function, and $\mathbf{B}$ is ${\mathfrak{F}}_0$ measurable $\mathrm{H}$-valued random vector.

The remainder of the article is arranged as follows: In the Section 2, we evoke a few useful definitions and results akin to fractional integrals and fractional derivatives. The EU of solutions to the suggested system (1) and Ulam–Hyres stability results are investigated in Section 3. A precise example is discussed in Section 4.

2. Preliminaries

This portion is dedicated to introducing a few conceptions and recalling helpful definitions and preliminary results employed in the whole article.

Let ${\mathbb{R}}^n$ be endowed with standard Euclidean norm and ${\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ denotes the space of all ${\mathbf{F}}_b$ measurable processes l, satisfying

$${\parallel l\parallel }_{{\mathrm{H}}^2}^2=\underset{t\in \mathrm{J}}{sup}\mathbf{E}{\parallel l(t)\parallel }^2<\infty .$$

It is known that $({\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n),\parallel ·{\parallel }_{{\mathrm{H}}^2})$ is a Banach space and $\kappa :\mathrm{J}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, $l:\mathrm{J}\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ are measurable and bounded functions satisfying the following hypothesis:

(A₁)

There exist positive constants ${\mathcal{L}}_{\kappa },{\mathcal{L}}_l$ such that for all $\upsilon ,\pounds ,\overline{\upsilon },\overline{\pounds }\in ({\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ and $t\in \mathrm{J},$

$$\begin{array}{cc}\hfill \parallel \kappa (t,\upsilon )-\kappa (t,\pounds )\parallel \le & {\mathcal{L}}_{\kappa }\parallel \upsilon -\pounds \parallel ,\hfill \\ \hfill \parallel l(t,\upsilon ,\overline{\upsilon })-l(t,\pounds ,\overline{\pounds })\parallel \le & {\mathcal{L}}_l\left[\parallel \upsilon -\pounds \parallel +\parallel {\int }_0^t\overline{\upsilon }(s)ds-{\int }_0^t\overline{\pounds }(s)ds\parallel \right].\hfill \end{array}$$

(A₂)

Assume that ${sup}_{t\in \mathrm{J}}\parallel \kappa (t,0)\parallel <\infty$ and ${sup}_{t\in \mathrm{J}}\parallel l(t,0,0)\parallel <\infty$. Note that the condition ${sup}_{t\in \mathrm{J}}\parallel \kappa (t,0)\parallel <\infty$ implies ${\int }_0^b{\parallel \kappa (t,0)\parallel }^{2}dt<\infty$.

The next condition is a consequence of $({\mathbf{A}}_1)$, but we list it here because of our easy access.

(A₃)

Let ${\mathcal{L}}_l$, ${\mathcal{L}}_{\kappa }$ be the same constants in $({\mathbf{A}}_1)$ and there exist real numbers $c_1\in (0,1)$, $c_2>0$ such that for all $t\in \mathrm{J}$ and $\upsilon ,\pounds \in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$,

$$\begin{array}{cc}\hfill \parallel \kappa (t,\upsilon )\parallel \le & {\mathcal{L}}_{\kappa }\left[1+\parallel \upsilon \parallel \right],\hfill \\ \hfill \parallel l(t,\upsilon ,\pounds )\parallel \le & {\mathcal{L}}_l\left[c_1\parallel \upsilon \parallel +c_2\parallel {\int }_0^t\pounds (s)ds\parallel \right].\hfill \end{array}$$

Definition 1

([6]). Assume that $f:(0,{\infty }^{+})\to \mathbb{R}$ is a real-valued integrable function and Γ denotes the Gamma function. The fractional Riemann–Liouville integral of order ℘, for which $0<\wp <1$, is defined by

$${\mathrm{I}}_{0^{+}}^{\wp }f(t)=\frac{1}{\Gamma (\wp )}{\int }_0^t{(t-v)}^{\wp -1}f(v)dv,t>0.$$

Definition 2

([6]). Let $f(t)$ be an absolutely continuous function; then, the fractional derivative in the Caputo sense, of order $\wp$, $0<\wp <1$, is defined as:

$${{}^c\mathcal{D}}_{0^{+}}^{\wp }f(t)=\frac{1}{\Gamma (1-\wp )}{\int }_0^t{(t-s)}^{-\wp }f(s)ds.$$

Definition 3

([6]). The 2-parametric Mittag–Leffler matrix function is defined as:

$${\mathrm{E}}_{\wp ,\nu }(t^{\wp }\mathrm{A})=\sum _{k=0}^{\infty }{\mathrm{A}}^k\frac{t^{k\wp }}{\Gamma (\wp k+\nu )},\wp ,\nu ,t\in \mathbb{C},\mathit{and}\Re (\wp ),\Re (\nu )>0.$$

Particularly, ${\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})={\mathrm{E}}_{\wp }(t^{\wp }\mathrm{A})$ has the following property

$${{}^c\mathcal{D}}_{0^{+}}^{\wp }{\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})=\mathrm{A}{\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A}),t>0.$$

We further suppose that there exist constants ${\mathcal{M}}_0$ and ${\mathcal{N}}_0$, where

$$\underset{t\in \mathrm{J}}{max}\parallel {\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A}){\parallel }^2={\mathcal{M}}_0\mathit{and}\underset{t\in \mathrm{J}}{max}{\parallel {\mathrm{E}}_{\wp ,\wp }(t^{\wp }\mathrm{A})\parallel }^2={\mathcal{N}}_0.$$

The last two estimates will be used in the coming results.

Furthermore, let ${{}^c\mathcal{D}}_{0^{+}}^{\wp }f(t)$ be the Caputo fractional derivative of $f(t)$; then, its Laplace transform, where $0<\wp <1$, is

$$\mathrm{L}\{{{}^c\mathcal{D}}_{0^{+}}^{\wp }f(t)\}(s)=s^{\wp }\mathrm{L}\{f(t)\}(s)-s^{\wp -1}f(0).$$

Lemma 1.

For any $t>0$, $\mathrm{{\rm Y}}>0$ and $\frac{1}{2}<\wp <1,$ the following integral inequality

$$\frac{\mathrm{{\rm Y}}}{\Gamma (2\wp -1)}{\int }_0^t{(t-s)}^{2\wp -2}{\mathrm{E}}_{2\wp -1,1}(s^{2\wp -1}\mathrm{{\rm Y}})ds\le {\mathrm{E}}_{2\wp -1,1}(t^{2\wp -1}\mathrm{{\rm Y}})$$

holds.

Proof. 

Consider

$$\begin{array}{cc}\hfill & \frac{\mathrm{{\rm Y}}}{\Gamma (2\wp -1)}{\int }_0^t{(t-s)}^{2\wp -2}{\mathrm{E}}_{2\wp -1,1}(s^{2\wp -1}\mathrm{{\rm Y}})ds\hfill \\ & =\frac{\mathrm{{\rm Y}}}{\Gamma (2\wp -1)}\sum _{j=0}^{\infty }\frac{{\mathrm{{\rm Y}}}^j}{\Gamma (j(2\wp -1)+1)}{\int }_0^t{(t-s)}^{2\wp -2}{s}^{j(2\wp -1)}ds\hfill \\ \hfill & =\sum _{j=0}^{\infty }\frac{{\mathrm{{\rm Y}}}^{j+1}{t}^{(j+1)(2\wp -1)}}{\Gamma (2\wp -1)\Gamma (j(2\wp -1)+1)}\mathcal{B}(2\wp -1,j(2\wp -1)+1)\hfill \\ \hfill & =\sum _{j=0}^{\infty }\frac{{\mathrm{{\rm Y}}}^{j+1}{t}^{(j+1)(2\wp -1)}}{\Gamma ((j+1)(2\wp -1)+1)}\hfill \\ \hfill & =\sum _{j=1}^{\infty }\frac{{\mathrm{{\rm Y}}}^j{t}^{j(2\wp -1)}}{\Gamma (j(2\wp -1)+1)}\hfill \\ \hfill & ={\mathrm{E}}_{2\wp -1,1}(t^{2\wp -1}\mathrm{{\rm Y}})-1\le {\mathrm{E}}_{2\wp -1,1}(t^{2\wp -1}\mathrm{{\rm Y}}).\hfill \end{array}$$

□

The following integral inequality has a vital role in obtaining certain estimates in our main theory throughout the paper.

For any $b>0,$ and $\wp >\frac{1}{2}$, assume that $\mathrm{\Psi }(t)$ is an $\mathrm{H}$-valued process satisfying $\mathbf{E}{\int }_0^b{\parallel \mathrm{\Psi }(t)\parallel }^{2}dt<\infty$. Then, we can find a constant $C_b=\frac{b^{2\wp -1}}{2\wp -1}$, where

$$\underset{t\in \mathrm{J}}{sup}\mathbf{E}\left(\parallel {\int }_0^t{(t-\tau )}^{\wp -1}\mathrm{\Psi }(\tau )dW(\tau ){\parallel }^2\right)\le C_b\mathbf{E}{\int }_0^b{\parallel \mathrm{\Psi }(\tau )\parallel }^{2}d\tau .$$

(2)

Definition 4

([38]). A function l is said to be of exponential order $\hslash ,$ if $\exists M_{\hslash }>0$, where for some $t_0>0,$ we have

$$|l(t)|\le M_{\hslash }{e}^{\hslash t},\mathit{for}t\ge t_0.$$

Lemma 2

([38]). The Laplace transform for a function g, which is piecewise continuous on $[0,\infty )$ and exponential order ℏ, exists for $\Re (s)>\hslash$ and converges absolutely.

Theorem 1

([39] (Krasnoselskii fixed-point theorem)). Let $\mathcal{S}\ne \varnothing$ be a closed and convex subset of Banach space $\mathrm{B}$. Consider two operators ${\mathcal{P}}_1,{\mathcal{P}}_2$ such that

1 

${\mathcal{P}}_{1}u+{\mathcal{P}}_{2}v\in \mathcal{S}$, where $u,v\in \mathcal{S}$.

2 

${\mathcal{P}}_1$ is compact and continuous operator.

3 

${\mathcal{P}}_2$ is contraction operator.

Then $\exists v\in \mathcal{S}$ such that $x={\mathcal{P}}_{1}v+{\mathcal{P}}_{2}v$.

3. Main Results

3.1. Existence and Uniqueness

Before studying the qualitative behavior of solutions to system (1), we consider

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {{}^c\mathcal{D}}_{0^{+}}^{\wp }[\upsilon (t)-\kappa (t,\upsilon (t))]=\mathrm{A}\upsilon (t)+l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt},t\in \mathrm{J}:=[0,b],\hfill \\ & \upsilon (0)=\mathbf{B},\hfill \end{array}\right.\end{array}$$

where ${{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\wp }(.)$ represents the fractional Caputo derivative of order $\wp (0<\wp <1)$ and $\mathrm{A}$ is an $n\times n$ matrix.

Definition 5.

A stochastic process ${\{\upsilon (t),t\in \mathrm{J}\}}_{t\ge 0}$ is said to be a mild solution of the system (1), if

• $(i)$$\upsilon (t)$ is adapted to ${\{{\mathfrak{F}}_t\}}_{\upsilon \ge 0}$ with ${\int }_0^b{\parallel \upsilon (t)\parallel }_{{\mathrm{H}}^2}^{2}dt<\infty$, $a.e.$;
• $(ii)$$\upsilon (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ has a continuous path on $t\in \mathrm{J}$ $a.e.$ and for all $t\in \mathrm{J}$, $\upsilon (t)$ satisfies the following integral equation

  $$\begin{array}{cc}\hfill \upsilon (t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathit{B}-\kappa (0,\mathit{B})]+\kappa (t,\upsilon (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s).\hfill \end{array}$$

Theorem 2.

Let $\upsilon \in {\mathrm{C}}^1(\mathrm{J},{\mathbb{R}}^n)$, $0<\wp \le 1,$ then any mild solution of

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {{}^c\mathcal{D}}_{0^{+}}^{\wp }[\upsilon (t)-\kappa (t,\upsilon (t))]=\mathrm{A}\upsilon (t)+l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt},t\in \mathrm{J}:=[0,b],\hfill \\ & \upsilon (0)=\mathit{B},\hfill \end{array}\right.\end{array}$$

is formulated by

$$\begin{array}{cc}\hfill \upsilon (t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathit{B}-\kappa (0,\mathit{B})]+\kappa (t,\upsilon (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s).\hfill \end{array}$$

Proof. 

Since $\upsilon \in {\mathrm{C}}^1(\mathrm{J},{\mathbb{R}}^n)$, both $\upsilon$ and ${{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\wp }\upsilon$ are bounded. Then, $\forall t\in \mathrm{J}$, $\upsilon$ and ${{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\wp }\upsilon$ are of exponential order. Thus, the Laplace transform of $\upsilon$ and ${{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\wp }y$ exist for $\upsilon \in {\mathrm{C}}^1(\mathrm{J},{\mathbb{R}}^n)$. Consider

$${{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\wp }[\upsilon (t)-\kappa (t,\upsilon (t))]=\mathrm{A}\upsilon (t)+l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt},t\in \mathrm{J}.$$

(3)

By applying the Laplace transform $\mathrm{L}$, on both sides of (3), we find

$$\begin{array}{cc}\hfill & s^{\wp }\mathrm{L}\{\upsilon (t)-\kappa (t,\upsilon (t))\}(s)-s^{\wp -1}[\upsilon (0)-\kappa (0,\upsilon (0))]\hfill \\ & =\mathrm{L}\{\mathrm{A}\upsilon (t)\}(s)+\mathrm{L}\{l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt}\}(s),\hfill \end{array}$$

(4)

where $\Re (s)>0$. In the matrix form, for (4) we obtain

$$\begin{array}{cc}\hfill & \mathrm{K}\mathrm{L}\{\upsilon (t)-\kappa (t,\upsilon (t))\}(s)-s^{-1}\mathrm{K}[\mathbf{B}-\kappa (0,\mathbf{B})]\hfill \\ & =\mathrm{L}\{\mathrm{A}\upsilon (t)\}(s)+\mathrm{L}\{l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt}\}(s),\hfill \end{array}$$

(5)

where the diagonal matrix $\mathrm{K}=$ diag $(s^{{\wp }_1},s^{{\wp }_2},\cdots ,s^{{\wp }_n})$. We can rewrite (5) in the form

$$\begin{array}{cc}\hfill & (\mathrm{K}-\mathrm{A})\mathrm{L}\{\upsilon (t)-\kappa (t,\upsilon (t))\}(s)=s^{-1}\mathrm{K}[\mathbf{B}-\kappa (0,\mathbf{B})]\hfill \\ & +\mathrm{K}\mathrm{L}\{\kappa (t,\upsilon (t))\}(s)+\mathrm{L}\{l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt}\}(s).\hfill \end{array}$$

(6)

By multiplying the inverse matrix ${\mathrm{K}}^{-1}=$ diag $(s^{-{\wp }_1},s^{-{\wp }_2},\cdots ,s^{-{\wp }_n}),$ we find

$$\begin{array}{cc}\hfill (\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})\mathrm{L}\{\upsilon (t)-\kappa (t,\upsilon (t))\}(s)& =s^{-1}[\mathbf{B}-\kappa (0,\mathbf{B})]+\mathrm{L}\{\kappa (t,\upsilon (t))\}(s)\hfill \\ \hfill & +{\mathrm{K}}^{-1}\mathrm{L}\{l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt}\}(s),\hfill \end{array}$$

(7)

where $\mathrm{I}$ is n-th order identity matrix. Clearly, the matrix $(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})$ is invertible. We solve Equation (7) for $\mathrm{L}\{\upsilon (t)\}(s)$ as

$$\begin{array}{cc}\hfill \mathrm{L}\{\upsilon (t)\}(s)& =s^{-1}{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}[\mathbf{B}-\kappa (0,\mathbf{B})]\hfill \\ & +\mathrm{L}\{\kappa (t,\upsilon (t))\}(s)+{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}\mathrm{L}\{\kappa (t,\upsilon (t))\}(s)\hfill \\ \hfill & +{\mathrm{K}}^{-1}{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}\mathrm{L}\{l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt}\}(s).\hfill \end{array}$$

(8)

By applying the inverse Laplace transform to Equation (8) yields

$$\begin{array}{cc}\hfill \upsilon (t)& =\mathbf{X}(t)[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\upsilon (t))\hfill \\ & +\mathbf{Z}(t)\ast \kappa (t,\upsilon (t))+\mathbf{Q}(t)\ast l(t,\upsilon (t),{\upsilon }^{\prime }(t))\frac{dW(t)}{dt},\hfill \end{array}$$

(9)

where the matrix functions $\mathbf{X}(t)$, $\mathbf{Z}(t)$ and $\mathbf{Q}(t)$ are given by

$$\begin{array}{cc}\hfill \mathbf{X}(t)=& {\mathrm{L}}^{-1}[s^{-1}{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}],\hfill \\ \hfill \mathbf{Z}(t)=& {\mathrm{L}}^{-1}[{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}],\hfill \\ \hfill \mathbf{Q}(t)=& {\mathrm{L}}^{-1}[{\mathrm{K}}^{-1}{(\mathrm{I}-{\mathrm{K}}^{-1}\mathrm{A})}^{-1}],\hfill \end{array}$$

while the convolution products ∗ are defined by

$$\mathbf{Z}(t)\ast \kappa (t,\upsilon (t))={\int }_0^t\mathbf{Z}(t-s)\kappa (s,\upsilon (s))ds,$$

and

$$\mathbf{Q}(t)\ast l(t,\upsilon (t),{\upsilon }^{\prime }(t))={\int }_0^t\mathbf{Q}(t-s)l(s,\upsilon (s),{\upsilon }^{\prime }(s))ds.$$

If ${\wp }_1={\wp }_2=\cdots ={\wp }_n=\wp$, then we have

$$\mathbf{X}(t)={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A}),$$

$$\mathbf{Z}(t)=\mathrm{A}{\upsilon }^{\wp -1}{\mathrm{E}}_{\wp ,\wp }(t^{\wp }\mathrm{A}),$$

and

$$\mathbf{Q}(t)={\upsilon }^{\wp -1}{\mathrm{E}}_{\wp ,\wp }(t^{\wp }\mathrm{A}).$$

Thus, Equation (9) becomes

$$\begin{array}{cc}\hfill \upsilon (t)={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+g(t,u(t))& +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s).\hfill \end{array}$$

□

Next, on the basis of Theorem 2, we presume the solution of system (1).

Theorem 3.

Let the assumptions ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ hold. Then, there exists a continuously differentiable unique mild solution $\pounds (t)$ with the same initial condition of system (1) expressed by:

$$\begin{array}{cc}\hfill \pounds (t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s).\hfill \end{array}$$

Proof. 

Let ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)=\{\xi \in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n),\xi (0)=\xi \}$. One can easily check that ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)$ is a closed subspace of the Banach space ${\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$. Define an operator $\mathcal{P}$ on ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)$ by

$$\begin{array}{cc}\hfill (\mathcal{P}\pounds )(t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s)(t\in \mathrm{J}).\hfill \end{array}$$

Obviously, the operator $\mathcal{P}$ is well-defined. Let ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)$ be endowed with the maximum norm ${\parallel ·\parallel }_{\mathbf{B}}$, defined as

$${\parallel \xi \parallel }_{\mathbf{B}}^2=\underset{t\in \mathrm{J}}{sup}\frac{{\mathbf{E}\parallel \xi (t)\parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{u}^{\wp -1})},\mathrm{{\rm Y}}>0,\xi \in {\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n).$$

Since ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)$ is a closed subspace of the Banach space ${\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$, $({\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n),\parallel ·{\parallel }_{\mathbf{B}})$ is also a Banach space. Thus, we can find ${\mathcal{N}}_0>0$ and choose a fixed positive number $\mathrm{{\rm Y}}$ such that $\frac{3{\mathcal{N}}_0^2{\Gamma (2\wp -1)(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{\mathrm{{\rm Y}}(1-3{\mathcal{L}}_{\kappa }^2)}<1,0<{\mathcal{L}}_{\kappa }^2<\frac{1}{3}$.

On the basis of assumption ${\mathbf{A}}_1$ with the use of It${\hat{o}}^{\prime }s$ isometry and Cauchy–Schwartz inequality, we have

$$\begin{array}{cc}& \mathbf{E}\parallel (\mathcal{P}\upsilon )(t)-(\mathcal{P}\pounds )(t){\parallel }^2\le 3\mathbf{E}\parallel \kappa (t,\mathcal{P}\upsilon (t))-\kappa (t,\mathcal{P}\pounds (t)){\parallel }^2\hfill \\ \hfill & +3\mathbf{E}\parallel {\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[\kappa (s,\upsilon (s))-\kappa (s,\pounds (s))]ds{\parallel }^2+3\mathbf{E}\hfill \\ \hfill & \times \parallel {\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[l(s,\upsilon (s),{\upsilon }^{\prime }(s))-l(s,\pounds (s),{\pounds }^{\prime }(s))]dW(s){\parallel }^2\hfill \\ \hfill & \le 3{\mathcal{L}}_{\kappa }^2{\mathbf{E}\parallel \mathcal{P}\upsilon (t)-\mathcal{P}\pounds (t)\parallel }^2+{3b\parallel \mathrm{A}\parallel }^2{\mathcal{N}}_0^2{\mathcal{L}}_{\kappa }^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds\hfill \\ \hfill & +6{\mathcal{N}}_0^2{\mathcal{L}}_l^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds\hfill \\ \hfill & =3{\mathcal{L}}_{\kappa }^2\mathbf{E}\parallel \mathcal{P}\upsilon (t)-\mathcal{P}\pounds (t){\parallel }^2\hfill \\ \hfill & +3{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2){\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds.\hfill \end{array}$$

Thus, by Lemma 1 and the definition of $\mathrm{{\rm Y}}$, we obtain

$$\begin{array}{cc}\hfill \frac{\mathbf{E}\parallel (\mathcal{P}y)(t)-(\mathcal{P}x)(t){\parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}& \le \frac{3{\mathcal{L}}_{\kappa }^2{\mathbf{E}\parallel \mathcal{P}\upsilon (t)-\mathcal{P}\pounds (t)\parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}+\frac{3{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{2\wp -2}\frac{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds.\hfill \end{array}$$

Therefore,

$${\parallel \mathcal{P}\upsilon -\mathcal{P}\pounds \parallel }_{\mathrm{{\rm Y}}}^2\le \frac{3{\mathcal{N}}_0^2{\Gamma (2\wp -1)(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{\mathrm{{\rm Y}}(1-3{\mathcal{L}}_{\kappa }^2)}{\parallel \upsilon -\pounds \parallel }_{\mathrm{{\rm Y}}}^2.$$

Since by the assumption $\frac{3{\mathcal{N}}_0^2{\Gamma (2\wp -1)(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{\mathrm{{\rm Y}}(1-3{\mathcal{L}}_{\kappa }^2)}<1$, then the operator $\mathcal{P}$ is a contraction on ${\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n)$. Hence, due to the contraction mapping principle, the operator $\mathcal{P}$ possesses a unique fixed point, which is the unique solution of system (1). □

Theorem 4.

Let the assumptions ${\mathbf{A}}_1$ to ${\mathbf{A}}_3$ be satisfied $\forall t\in \mathrm{J}$ and $\upsilon ,\pounds ,\overline{\upsilon },\overline{\pounds }\in ({\mathrm{H}}_{\mathbf{B}}^2\mathrm{J},{\mathbb{R}}^n)$. Then, the problem (1) has at least one mild solution, provided that $0<{\mathcal{L}}_{\kappa }<\frac{1}{2\sqrt{2}}$.

Proof. 

To discuss the solvability of system (1), we transform the considered system (1) into an equivalent fixed point problem. Consider a closed ball

$${\mathcal{W}}_{\epsilon }=\{\upsilon \in {\mathrm{H}}_{\mathbf{B}}^2(\mathrm{J},{\mathbb{R}}^n){:\mathbf{E}\parallel \upsilon \parallel }_{\mathrm{{\rm Y}}}^2\le \epsilon \},$$

where

$$0<\frac{8{\mathcal{M}}_0^2\left[\mathbf{E}\parallel \mathbf{B}{\parallel }^2+{\mathcal{L}}_{\kappa }^2(1+\mathbf{E}\parallel \mathbf{B}{\parallel }^2)\right]+8}{{\mathcal{Q}}_{l\kappa }(1-8{\mathcal{L}}_{\kappa }^2)}\le \epsilon ,$$

with

$${\mathcal{Q}}_{l\kappa }=1-\frac{8b^{2\wp -1}\Gamma (2\wp -1)\left[{b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2{\mathcal{M}}_0^2+{\mathcal{N}}_0^2{\mathcal{L}}_l^2(c_1^2+c_2^2)\right]}{\mathrm{{\rm Y}}(1-8{\mathcal{L}}_{\kappa }^2)},$$

and define two operators ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ on ${\mathcal{W}}_{\epsilon }$ by

$$\begin{array}{cc}\hfill ({\mathcal{P}}_1\upsilon )(t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\upsilon (t)),\hfill \\ \hfill ({\mathcal{P}}_2\upsilon )(t)& ={\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s),t\in \mathrm{J}.\hfill \end{array}$$

For any $\upsilon \in {\mathcal{W}}_r,$ we conclude that

$$\begin{array}{cc}\hfill \mathbf{E}\parallel ({\mathcal{P}}_1\upsilon )(t)+({\mathcal{P}}_2\upsilon )(t){\parallel }^2& =4\mathbf{E}\parallel {\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]{\parallel }^2+4\mathbf{E}\parallel \kappa (t,\mathcal{P}\upsilon (t)){\parallel }^2\hfill \\ \hfill & +4\mathbf{E}\parallel {\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds{\parallel }^2\hfill \\ \hfill & +4\mathbf{E}\parallel {\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s){\parallel }^2\hfill \\ \hfill & \le 8{\mathcal{M}}_0^2\left[\mathbf{E}\parallel \mathbf{B}{\parallel }^2+{\mathcal{L}}_{\kappa }^2(1+\mathbf{E}\parallel \mathbf{B}{\parallel }^2)\right]+8{\mathcal{L}}_{\kappa }^2\left[1+\mathbf{E}\parallel \mathcal{P}\upsilon (t){\parallel }^2\right]\hfill \\ \hfill & +8b{\mathcal{M}}_0^2\parallel \mathrm{A}{\parallel }^2{\mathcal{L}}_{\kappa }^2\left[1+\mathbf{E}\parallel \upsilon (t){\parallel }^2\right]{\int }_0^t{(t-s)}^{2\wp -2}ds\hfill \\ \hfill & +8{\mathcal{N}}_0^2{\mathcal{L}}_l^2[c_1^2+c_2^2]\mathbf{E}\parallel y{\parallel }^2{\int }_0^t{(t-s)}^{2\wp -2}ds.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \parallel ({\mathcal{P}}_1\upsilon )+({\mathcal{P}}_2\upsilon ){\parallel }_{\mathrm{{\rm Y}}}^2& \le \frac{8{\mathcal{M}}_0^2\left[\mathbf{E}\parallel \mathbf{B}{\parallel }^2+{\mathcal{L}}_{\kappa }^2(1+\mathbf{E}\parallel \mathbf{B}{\parallel }^2)\right]}{(1-8{\mathcal{L}}_{\kappa }^2)}\hfill \\ & +8{\mathcal{M}}_0^2\parallel \mathrm{A}{\parallel }^2{\mathcal{L}}_{\kappa }^2\left[1+\epsilon \right]\frac{b^{2\wp }\Gamma (2\wp -1)}{\mathrm{{\rm Y}}(1-8{\mathcal{L}}_{\kappa }^2)}\hfill \\ \hfill & +\frac{8{\mathcal{N}}_0^2{b}^{2\wp -1}\Gamma (2\wp -1){\mathcal{L}}_l^2[c_1^2+c_2^2]}{\mathrm{{\rm Y}}(1-8{\mathcal{L}}_{\kappa }^2)}\epsilon +\frac{8}{(1-8{\mathcal{L}}_{\kappa }^2)}\hfill \\ \hfill & \le \epsilon .\hfill \end{array}$$

Thus, ${\mathcal{P}}_1\upsilon +{\mathcal{P}}_2\upsilon \in {\mathcal{W}}_{\epsilon }$. In view of Theorem 3, we conclude that ${\mathcal{P}}_1$ is a contraction mapping if

$$\frac{3{\mathcal{N}}_0^2{\Gamma (2\wp -1)(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{\mathrm{{\rm Y}}(1-3{\mathcal{L}}_{\kappa }^2)}<1.$$

It follows directly from the proof of the Theorem 3.

Next, we show that the operator ${\mathcal{P}}_2$ is continuous as well as compact. First, we show that ${\mathcal{P}}_2$ is continuous. For this, we construct a differentiable uniformly convergent sequence ${\{{\upsilon }_n\}}_{n\in \mathbb{N}}$ in ${\mathcal{W}}_{\epsilon }$ such that ${\upsilon }_n\to \upsilon$ as $n\to \infty$.

$\forall t\in [0,b],$ we have

$$\begin{array}{cc}\hfill & \mathbf{E}\parallel ({\mathcal{P}}_2{\upsilon }_n)(t)-({\mathcal{P}}_2\upsilon )(t){\parallel }^2\hfill \\ \hfill & \le 2\mathbf{E}\parallel {\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[\kappa (s,{\upsilon }_n(s))-\kappa (s,\upsilon (s))]ds{\parallel }^2+2\mathbf{E}\hfill \\ \hfill & \times \parallel {\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[l(s,{\upsilon }_n(s),{\upsilon }_n^{\prime }(s))-l(s,\upsilon (s),{\upsilon }^{\prime }(s))]dW(s){\parallel }^2\hfill \\ \hfill & \le 2b{\mathcal{L}}_{\kappa }^2{\parallel \mathrm{A}\parallel }^2{\mathcal{M}}_0^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}\parallel {\upsilon }_n{-\upsilon \parallel }^{2}ds+4{\mathcal{N}}_0^2{\mathcal{L}}_l^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel {\upsilon }_n-\upsilon \parallel }^{2}ds\hfill \end{array}$$

so

$$\begin{array}{cc}\hfill \frac{\mathbf{E}\parallel ({\mathcal{P}}_2{\upsilon }_n)(t)-({\mathcal{P}}_{2}y)(t){\parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\upsilon t^{2\wp -1})}& \le \frac{{2b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2{\mathcal{M}}_0^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}{\int }_0^t{(t-s)}^{2\wp -2}{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})\frac{\mathbf{E}\parallel {\upsilon }_n{-\upsilon \parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})}ds\hfill \\ \hfill & +\frac{4{\mathcal{N}}_0^2{\mathcal{L}}_l^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}{\int }_0^t{(t-s)}^{2\wp -2}{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})\frac{\mathbf{E}\parallel {\upsilon }_n{-\upsilon \parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp }-1)}ds.\hfill \end{array}$$

Using the weighted maximum norm, we obtain

$$\mathbf{E}\parallel {\mathcal{P}}_2{\upsilon }_n-{\mathcal{P}}_2\upsilon {\parallel }_{\mathrm{{\rm Y}}}^2\le \frac{2\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}\left[b{\mathcal{L}}_{\kappa }^2\parallel \mathrm{A}{\parallel }^2{\mathcal{M}}_0^2+2{\mathcal{N}}_0^2{\mathcal{L}}_l^2\right]\parallel {\upsilon }_n-\upsilon {\parallel }_{\mathrm{{\rm Y}}}\to 0,\mathrm{as}n\to \infty .$$

The last inequality implies the operator ${\mathcal{P}}_2$ is continuous. Moreover, the operator ${\mathcal{P}}_2$ is uniformly bounded, which follows from the start of the proof.

Finally, we show that ${\mathcal{P}}_2$ is equi-continuous. Let $t_1,t_2\in \mathrm{J}$ with $t_1<t_2$. For any $\upsilon \in {\mathcal{W}}_{\epsilon }$, we have

$$\begin{array}{cc}\hfill & \mathbf{E}\parallel ({\mathcal{P}}_2\upsilon )(t_2)-({\mathcal{P}}_2\upsilon )(t_1){\parallel }^2\hfill \\ \hfill & \le 4\mathbf{E}\parallel {\int }_0^{t_1}\mathrm{A}\left[{(t_2-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_2-s)}^{\wp }\mathrm{A})-{(t_1-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_1-s)}^{\wp }\mathrm{A})\right]\hfill \\ \hfill & \times \kappa (s,\upsilon (s))ds{\parallel }^2\hfill \\ \hfill & +4\mathbf{E}\parallel {\int }_{t_1}^{t_2}\mathrm{A}{(t_2-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_2-s)}^{\wp }\mathrm{A})\kappa (s,\upsilon (s))ds{\parallel }^2\hfill \\ \hfill & +4\mathbf{E}\parallel {\int }_0^{t_1}\left[{(t_2-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_2-s)}^{\wp }\mathrm{A})-{(t_1-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_1-s)}^{\wp }\mathrm{A})\right]\hfill \\ \hfill & \times l(s,\upsilon (s),{\upsilon }^{\prime }(s))dW(s){\parallel }^2\hfill \\ \hfill & +4\mathbf{E}\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t_2-s)}^{\wp }\mathrm{A})l(s,\upsilon (s),{\upsilon }^{\prime }(s))ds{\parallel }^2\hfill \\ \hfill & \le 4{\mathcal{L}}_{\kappa }^2{\mathcal{M}}_0^2{\int }_0^{t_1}\left[{(t_2-s)}^{2\wp -2}-{(t_1-s)}^{2\wp -2}\right]\left[1+{\mathbf{E}\parallel \upsilon \parallel }^2\right]ds\hfill \\ \hfill & \times +4{\mathcal{M}}_0^2{\mathcal{L}}_2^2{\parallel \mathrm{A}\parallel }^2{b\parallel \mathrm{A}\parallel }^2{\int }_{t_1}^{t_2}{(t_2-s)}^{2\wp -2}{(1+\mathbf{E}\parallel \upsilon \parallel }^2)ds\hfill \\ \hfill & +4{\mathcal{N}}_0^2{\mathcal{L}}_l^2){\int }_0^{t_1}\left[{(t_2-s)}^{2\wp -2}-{(t_1-s)}^{2\wp -2}\right][(c_1+c_2)\mathbf{E}{\parallel \upsilon \parallel }^{2}ds+4{\mathcal{N}}_0^2{\mathcal{L}}_l^2\hfill \\ \hfill & \times {\int }_{t_1}^{t_2}\left[{(t_2-s)}^{2\wp -2}\right][(c_1+c_2){]\mathbf{E}\parallel \upsilon \parallel }^{2}ds\to 0,\mathrm{as}{t}_1\to t_2.\hfill \end{array}$$

which further implies that $\parallel {\mathcal{P}}_2\upsilon (t_2)-{\mathcal{P}}_2\upsilon (t_1){\parallel }_{\mathrm{{\rm Y}}}^2\to 0$ as $t_1\to t_2$. This shows that the operator ${\mathcal{P}}_2$ is compact. Therefore, in view of the Arzela–Ascoli theorem, ${\mathcal{P}}_2$ is compact. Hence, the problem (1) has at least one solution on $\mathrm{J}$, thanks to Theorem 1. □

3.2. The Ulam–Hyres Stability Results

Now, in the following, we want to examine the (U-Hs) result about the system (1) in ${\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ on the interval $\mathrm{J}=[0,b]$.

Definition 6.

We say that (1) is Ulam–Hyers stable, if for any solution $\pounds (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ of (1), which satisfies the following inequality

$$\underset{t\in [0,b]}{sup}\mathbf{E}\parallel {{}^c\mathcal{D}}_{0^{+}}^{\wp }[\pounds (t)-\kappa (t,\pounds (t))]-\mathrm{A}v(t)-l(t,\pounds (t),{\pounds }^{\prime }(t))\frac{W(t)}{dt}{\parallel }^2\le ϵ,ϵ>0,$$

(10)

then, there exists a solution $\upsilon (t)$ of (1), where

$$\underset{t\in [0,b]}{sup}\mathbf{E}{\parallel \pounds (t)-\upsilon (t)\parallel }^2\le Cϵ,$$

such that C is a constant that is independent of $\pounds (t)$ and $\upsilon (t)$.

Definition 7.

We say that the system (1) posses Ulam–Hyers–Rassias stability, if for any solution $\pounds (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ of (1), which satisfies the following inequality

$$\underset{t\in [0,b]}{sup}\mathbf{E}\parallel {{}^c\mathcal{D}}_{0^{+}}^{\wp }[\pounds (t)-\kappa (t,\pounds (t))]-\mathrm{A}\pounds (t)-l(t,\pounds (t),{\pounds }^{\prime }(t))\frac{W(t)}{dt}{\parallel }^2\le \phi (t),$$

(11)

such that $\phi :\mathrm{J}\to [0,\infty )$ is a continuous function, then there exists a solution $\upsilon (t)$ of (1), where

$$\underset{t\in [0,b]}{sup}\mathbf{E}{\parallel \pounds (t)-\upsilon (t)\parallel }^2\le C\phi (t),$$

and C is a constant, that is independent of $\pounds (t)$ and $\upsilon (t)$.

Remark 1.

A function $\pounds (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ is said to be the solution of the inequality (10) if, and only if, we can find a function $\hslash (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ such that

• $(1)$${\mathbf{E}\parallel \hslash (t)\parallel }^2\le ϵ,$$t\in \mathrm{J};$
• $(2)$

  $$\begin{array}{cc}\hfill \pounds (t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathit{B}-\kappa (0,\mathit{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s)\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\hslash (s)ds.\hfill \end{array}$$

Note: A similar remark can be obtained on considering inequality (11).

Lemma 3.

A function $\pounds (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ satisfying (10) also satisfies the following integral inequality

$$\begin{array}{cc}\hfill & \mathbf{E}\parallel \pounds (t)-{\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathit{B}-\kappa (0,\mathit{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & -{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & -{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s){\parallel }^2\le \frac{b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ.\hfill \end{array}$$

Proof. 

According to Remark 1 $(2),$ we can write

$$\begin{array}{cc}\hfill \pounds (t)& ={\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s)\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\hslash (s)ds.\hfill \end{array}$$

By applying expectation and Cauchy–Schwartz inequality, we obtain

$$\begin{array}{cc}\hfill & \mathbf{E}\parallel \pounds (t)-{\mathrm{E}}_{\wp ,1}(t^{\wp }\mathrm{A})[\mathbf{B}-\kappa (0,\mathbf{B})]+\kappa (t,\pounds (t))\hfill \\ \hfill & -{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\kappa (s,\pounds (s))ds\hfill \\ \hfill & -{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})l(s,\pounds (s),{\pounds }^{\prime }(s))dW(s){\parallel }^2\hfill \\ \hfill & =\mathbf{E}\parallel {\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\hslash (s)ds{\parallel }^2\hfill \\ \hfill & \le {\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}\parallel {\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A}){\parallel }^2\mathbf{E}\parallel \hslash (s){\parallel }^{2}ds\hfill \\ \hfill & \le {\mathcal{N}}_0ϵ{\int }_0^t{(t-s)}^{2\wp -2}ds\hfill \\ \hfill & \le \frac{b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ.\hfill \end{array}$$

□

Theorem 5.

If the assumptions ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ are true, then the system (1) is (U-H) stable, provided that

$$6{\mathcal{L}}_{\kappa }^2+\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}<1,$$

Proof. 

Suppose that $ϵ>0$ and $\pounds (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ be a continuously differentiable function satisfying (10) and $\upsilon (t)\in {\mathrm{H}}^2(\mathrm{J},{\mathbb{R}}^n)$ are the unique solution of system (1). By applying the Ito’s isometry along with the following inequality, we find

$$\parallel \sum _{j=1}^n{\upsilon }_j{\parallel }^2\le n\sum _{j=1}^n\parallel {\upsilon }_j{\parallel }^2$$

and so

$$\begin{array}{cc}\hfill \mathbf{E}\parallel \upsilon (t)-\pounds (t){\parallel }^2& \le 2\mathbf{E}\parallel \kappa (t,\upsilon (t))-\kappa (t,\pounds (t))\hfill \\ \hfill & +{\int }_0^t\mathrm{A}{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[\kappa (s,\upsilon (s))-\kappa (s,\pounds (s))]ds\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})[l(s,\upsilon (s),{\upsilon }^{\prime }(s))-l(s,\pounds (s),{\pounds }^{\prime }(s))]dW(s){\parallel }^2\hfill \\ \hfill & +2\mathbf{E}\parallel {\int }_0^t{(t-s)}^{\wp -1}{\mathrm{E}}_{\wp ,\wp }({(t-s)}^{\wp }\mathrm{A})\hslash (s)ds{\parallel }^2\hfill \\ \hfill & \le 6{\mathcal{L}}_g^2{\mathbf{E}\parallel \upsilon (t)-\pounds (t)\parallel }^2+{6b\parallel \mathrm{A}\parallel }^2{\mathcal{N}}_0^2{\mathcal{L}}_{\kappa }^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds\hfill \\ \hfill & +12{\mathcal{N}}_0^2{\mathcal{L}}_l^2{\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds+\frac{2b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ\hfill \\ \hfill & =6{\mathcal{L}}_{\kappa }^2{\mathbf{E}\parallel \mathcal{P}\upsilon (t)-\mathcal{P}\pounds (t)\parallel }^2+6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2\hfill \\ \hfill & +2{\mathcal{L}}_l^2){\int }_0^t{(t-s)}^{2\wp -2}\mathbf{E}{\parallel \upsilon -\pounds \parallel }^{2}ds+\frac{2b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ.\hfill \end{array}$$

Thus, by using Lemma 1 and the definition of $\mathrm{{\rm Y}}$, we obtain

$$\begin{array}{cc}\hfill \frac{\mathbf{E}\parallel \upsilon (t)-\pounds (t){\parallel }^2}{{\mathrm{E}}_{2\wp -1}(\mathrm{{\rm Y}}{t}^{2\wp -1,1})}& \le \frac{6{\mathcal{L}}_{\kappa }^2{\mathbf{E}\parallel \upsilon (t)-\pounds (t)\parallel }^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}+\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{t}^{2\wp -1})}\hfill \\ \hfill & \times {\int }_0^t{(t-s)}^{2\wp -2}{\mathrm{E}}_{2\wp -1}(\mathrm{{\rm Y}}{s}^{2\wp -1})\frac{{\parallel \upsilon -\pounds \parallel }_{\mathrm{{\rm Y}}}^2}{{\mathrm{E}}_{2\wp -1,1}(\mathrm{{\rm Y}}{s}^{2\wp -1})}ds\hfill \\ \hfill & +\frac{2}{{\mathrm{E}}_{2\wp -1}(\mathrm{{\rm Y}}{t}^{2\wp -1,1})}\frac{b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ\hfill \\ \hfill & \le \left(6{\mathcal{L}}_{\kappa }^2+\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}\right){\parallel \upsilon -\pounds \parallel }_{\mathrm{{\rm Y}}}^2+\frac{2b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0ϵ.\hfill \end{array}$$

By taking maximum over $\mathrm{J}$, and considering the assumption

$$6{\mathcal{L}}_{\kappa }^2+\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}<1,$$

we obtain

$${\parallel \upsilon -\pounds \parallel }_{\mathrm{{\rm Y}}}^2\le \frac{\frac{2b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0}{1-6{\mathcal{L}}_{\kappa }^2-\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}}ϵ=Cϵ,$$

where

$$C=\frac{\frac{2b^{2\wp -1}}{2\wp -1}{\mathcal{N}}_0}{1-6{\mathcal{L}}_{\kappa }^2-\frac{6{\mathcal{N}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}}.$$

By Definition 6, the system (1) is (U-H) stable. □

Remark 2.

The Ulam–Hyers–Rasssias stability can be discussed in the same manner.

4. Example

We now present an example to defend our pivotal results of the theory attained above.

Example 1.

Consider the Cauchy neutral fractional stochastic differential equation system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {{}^{\mathfrak{c}}\mathcal{D}}_{0^{+}}^{\frac{4}{7}}\left[\upsilon (t)+\frac{t}{5}\left(\begin{array}{c}{\upsilon }_1(t)+1\\ {\displaystyle \frac{{cos}^2{\upsilon }_2(t)}{1+{cos}^2{\upsilon }_2(t)}}\end{array}\right)\right]=\left(\begin{array}{cc}0& 4\\ 3& 2\end{array}\right)\upsilon (t)\hfill \\ & +\left(\frac{t}{4}\left(\begin{array}{c}|{\upsilon }_1(t)|+{cos}^2{\upsilon }_1(t)\\ {\upsilon }_2(t)+2\end{array}\right)+\frac{1}{4}{\upsilon }^{\prime }(t)\right)\frac{dW(t)}{dt},(t\in (0,1])\hfill \\ & \upsilon (0)=\left(\begin{array}{c}4\\ 7\end{array}\right),\hfill \end{array}\right.\end{array}$$

where $\mathrm{A}=\left(\begin{array}{cc}0& 4\\ 3& 2\end{array}\right)$, $\upsilon (t)={({\upsilon }_1(t),{\upsilon }_2(t))}^T$, and $W(t)$ is the standard Brownian motion while the measurable functions are given by

$$\kappa (t,\upsilon (t))=\frac{t}{5}\left(\begin{array}{c}{\upsilon }_1(t)+1\\ {\displaystyle \frac{{cos}^2{\upsilon }_2(t)}{1+{cos}^2{\upsilon }_2(t)}}\end{array}\right),$$

and

$$l(t,\upsilon (t),{\upsilon }^{\prime }(t))=\left(\frac{t}{4}\left(\begin{array}{c}|{\upsilon }_1(t)|+{cos}^2{\upsilon }_1(t)\\ {\upsilon }_2(t)+2\end{array}\right)+\frac{1}{4}{\upsilon }^{\prime }(t)\right).$$

Comparing with our considered problem (1), we have

$$\left\{\begin{array}{c}\wp =\frac{4}{7},\hfill \\ {\mathcal{L}}_{\kappa }=\frac{1}{5},\hfill \\ {\mathcal{L}}_l=\frac{1}{2},\hfill \\ b=1.\hfill \end{array}\right.$$

By taking ${\mathcal{N}}_0=\frac{1}{8}$, $\mathrm{{\rm Y}}=1$, ${\mathcal{M}}_0=1$, we obtain

$$\frac{3{\mathcal{N}}_0^2{\Gamma (2\wp -1)(b\parallel A\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)}{\mathrm{{\rm Y}}(1-3{\mathcal{L}}_{\kappa }^2)}=\frac{3\Gamma (\frac{5}{2})[\frac{16}{25}+\frac{1}{4}]}{64(1-\frac{3}{25})}=0.0628<1.$$

Therefore, in view of Theorem 3, Equation (1) has a unique solution.

Furthermore,

$$1-6{\mathcal{L}}_{\kappa }^2-\frac{6{\mathcal{M}}_0^2{(b\parallel \mathrm{A}\parallel }^2{\mathcal{L}}_{\kappa }^2+2{\mathcal{L}}_l^2)\Gamma (2\wp -1)}{\mathrm{{\rm Y}}}=0.6740\ne 0,$$

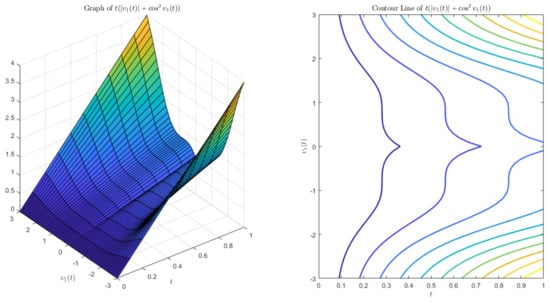
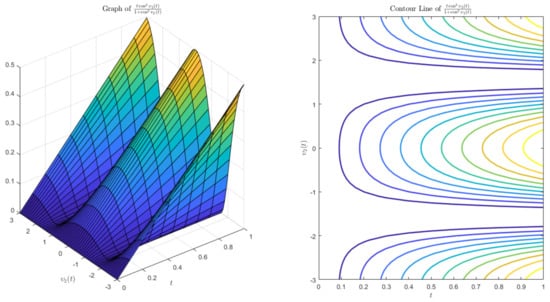
Thus, by Theorem 5, system (1) is Ulam–Hyers stable. To better understand this example, graphs of some functions are provided in Figure 1 and Figure 2.

Figure 1. The graph of $t(|{\upsilon }_1(t)|+{cos}^2{\upsilon }_1(t))$.

Figure 2. The graph of ${\displaystyle \frac{t{cos}^2{\upsilon }_2(t)}{1+{cos}^2{\upsilon }_2(t)}}$.

5. Conclusions

The fractional stochastic neutral differential system has many applications in various fields, such as viscoelasticity, automatic control, electrochemistry, etc. Based on some well-known fixed-point theorems of fractional calculus and the technique of stochastic analysis, the existence of results for the considered system has been obtained. Likewise, under specific assumptions and conditions, we have found the (U-Hs) result for the solution of system (1). We also provided an example and some figures to show the performance of the results that we proved.