New Solutions of Nonlinear Dispersive Equation in Higher-Dimensional Space with Three Types of Local Derivatives
Abstract
:1. Introduction
2. Preliminaries
- ,
- ,
3. Nucci’s Reduction Method
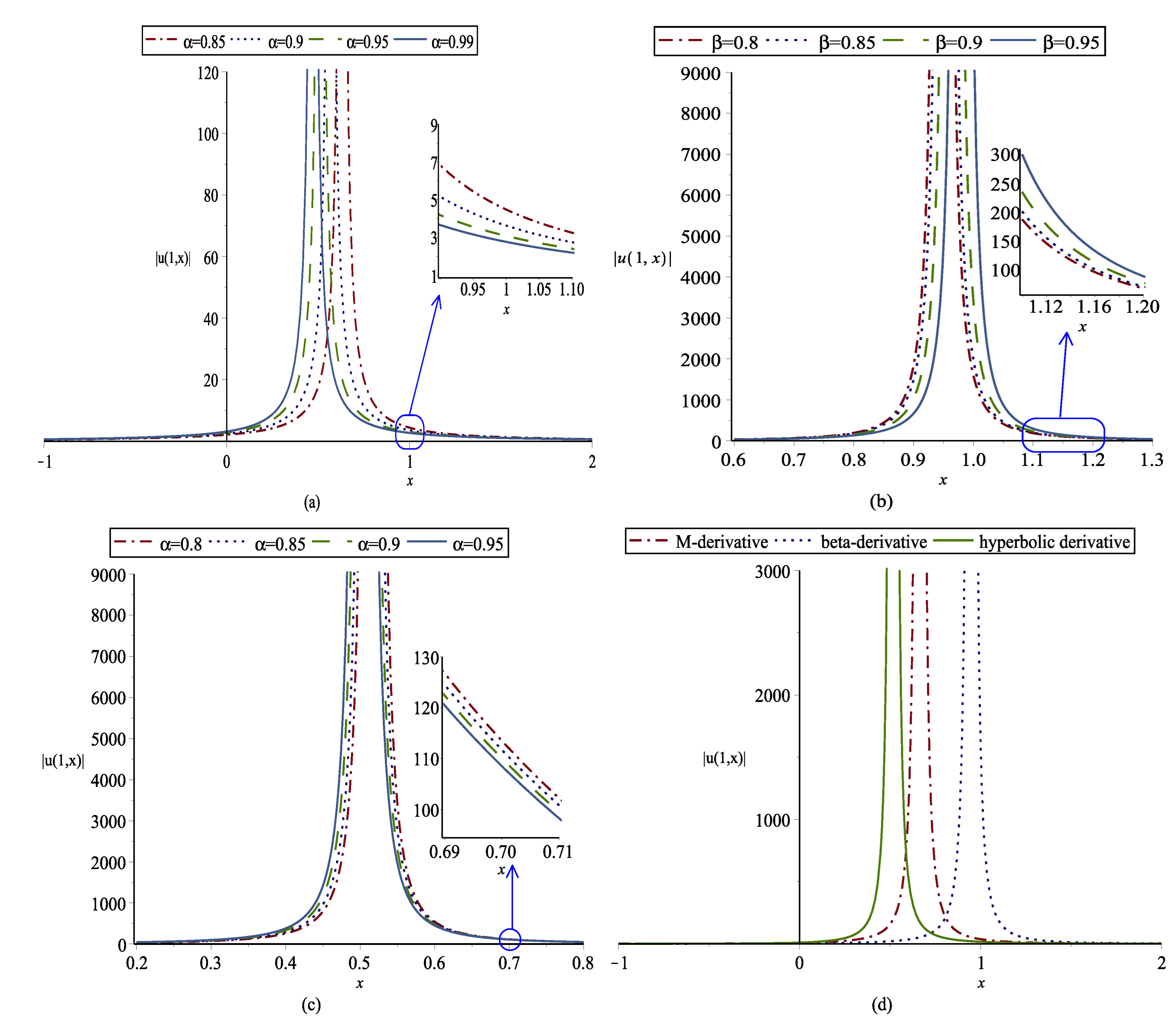
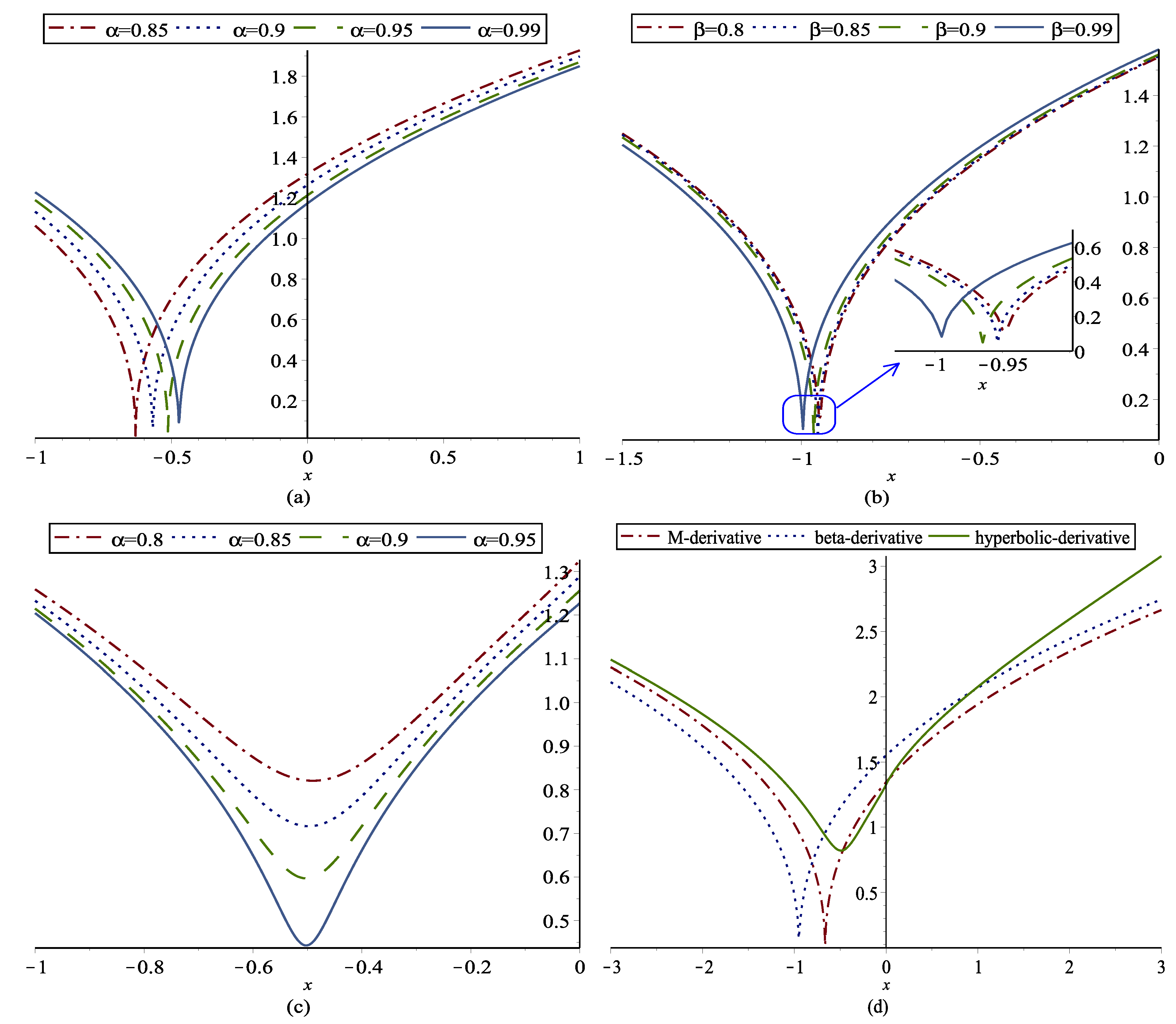
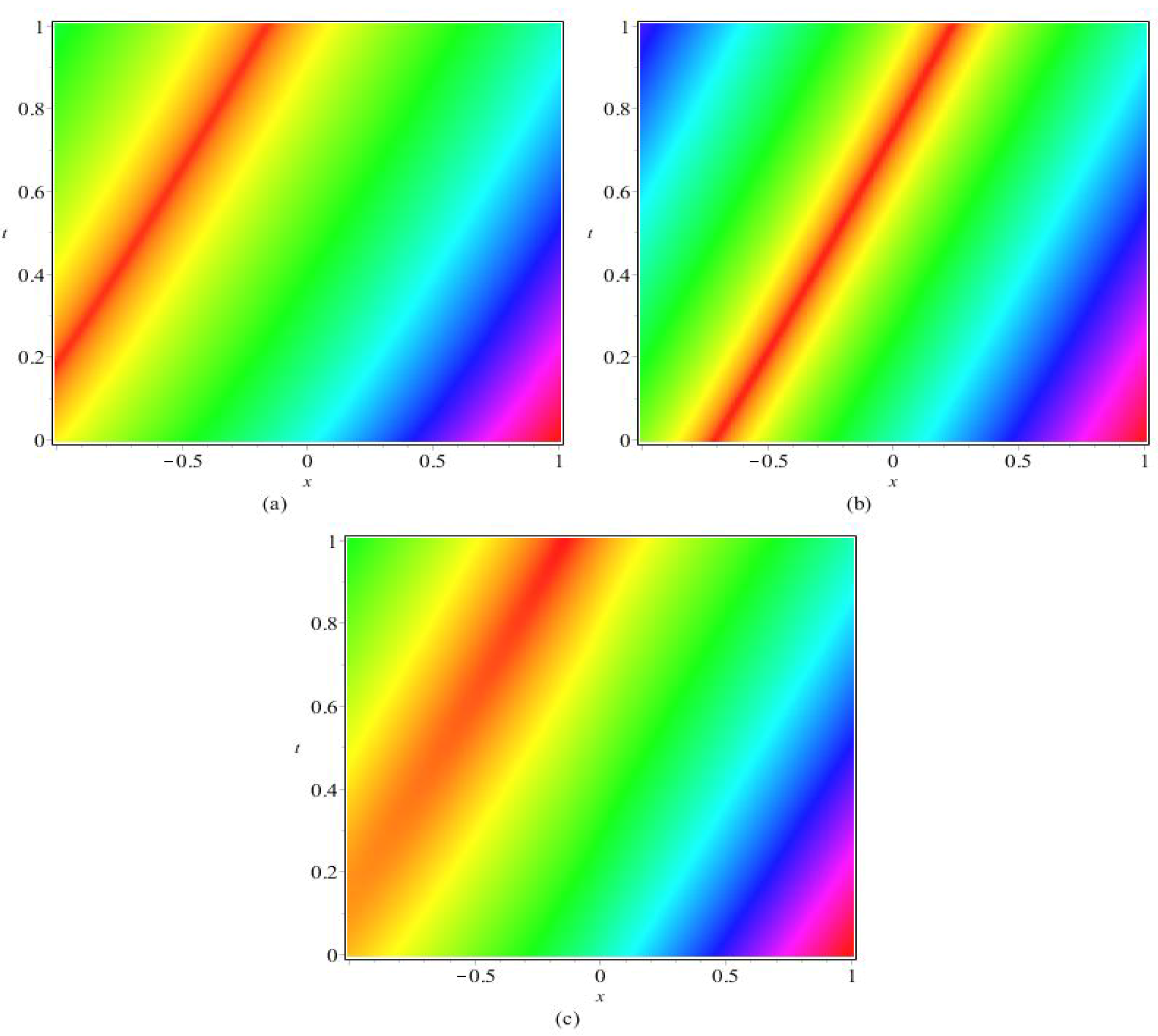
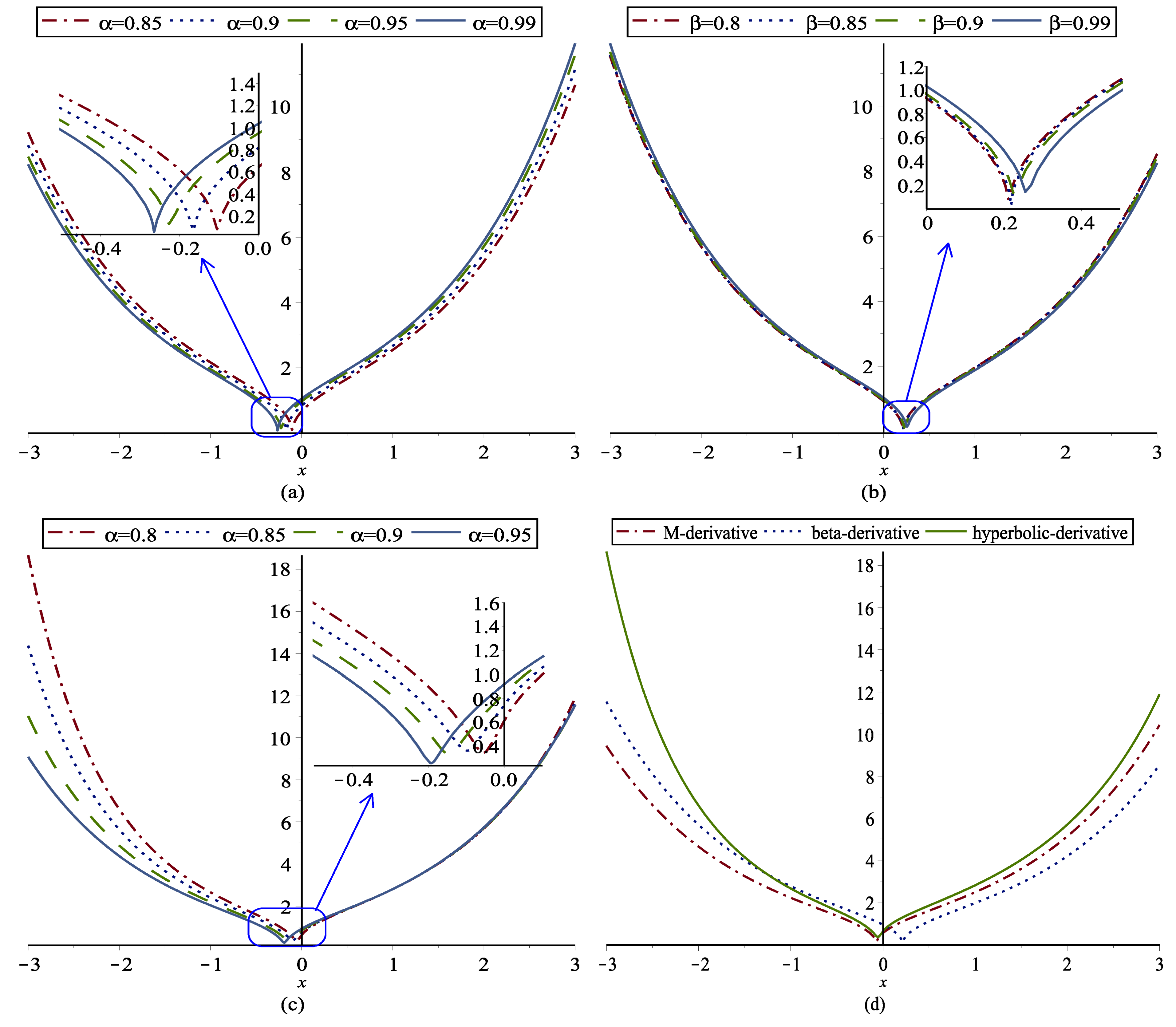
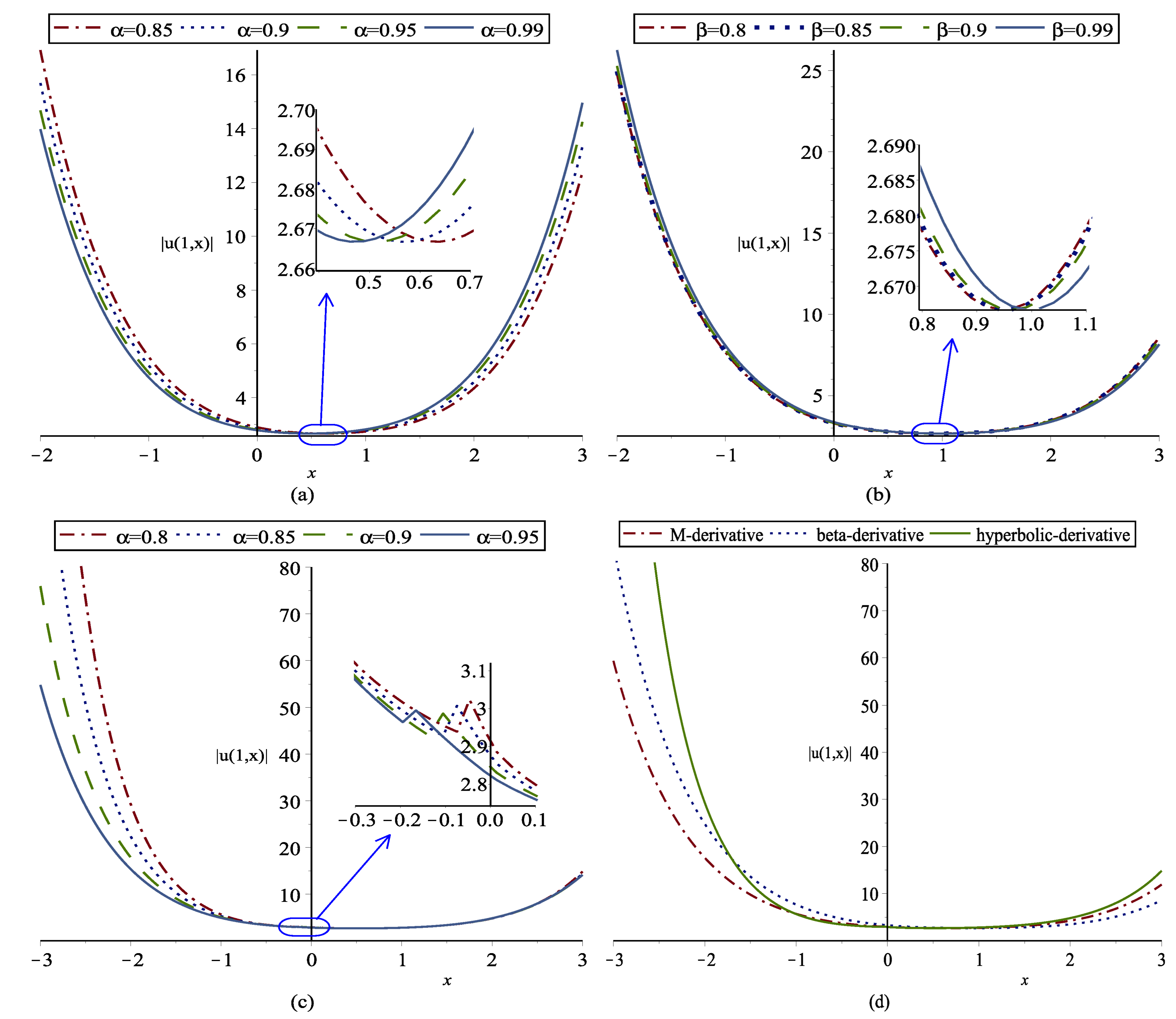
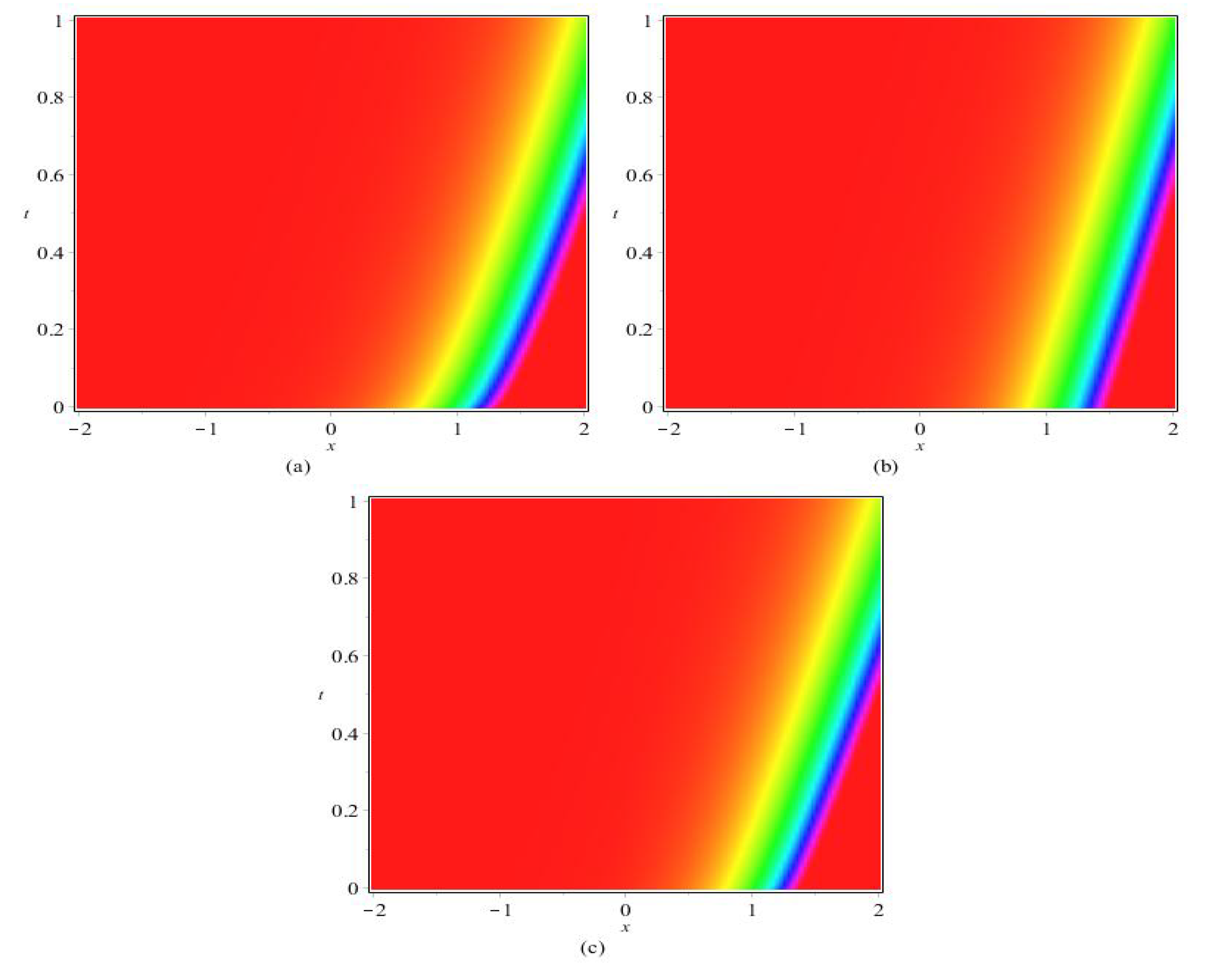
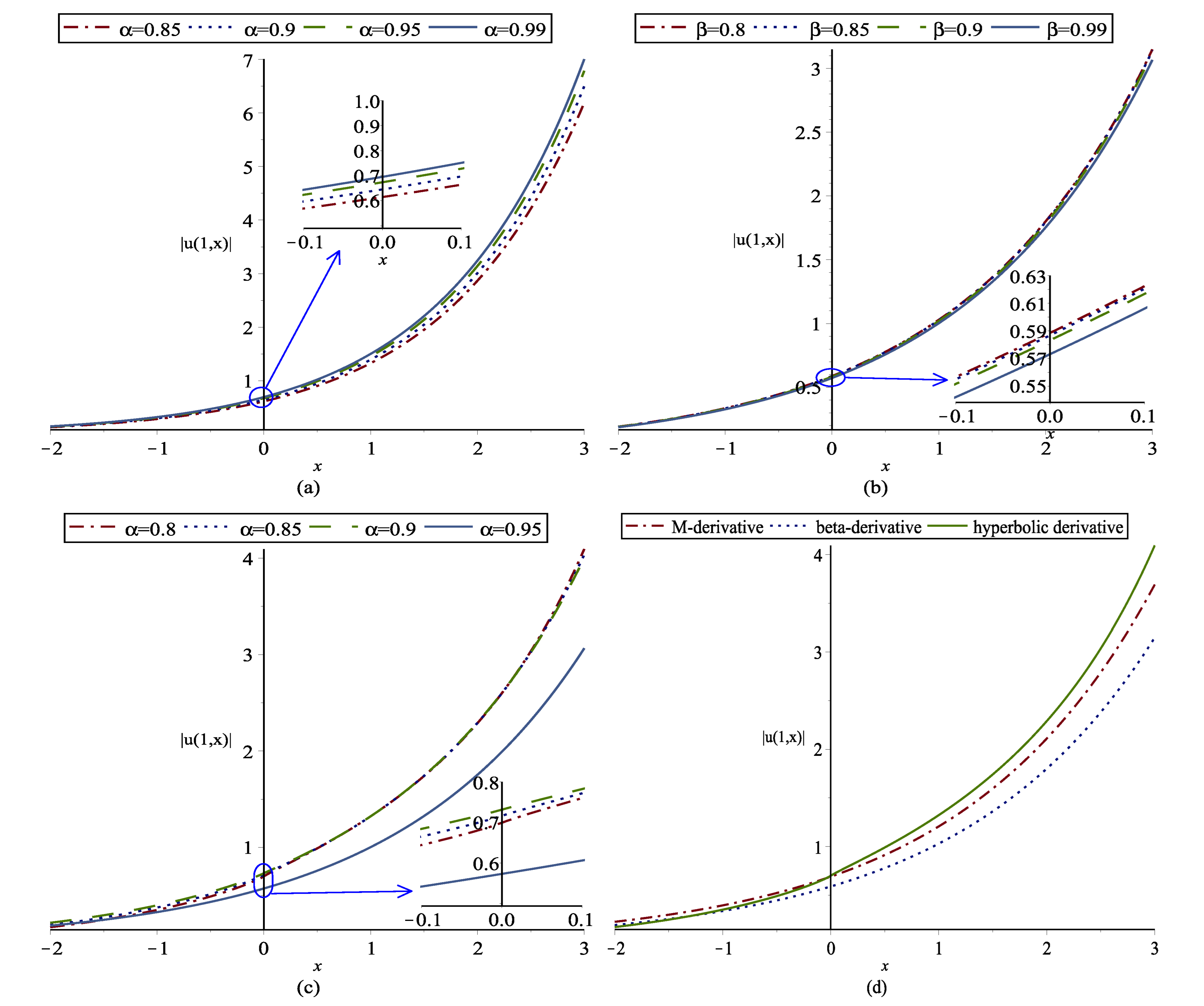
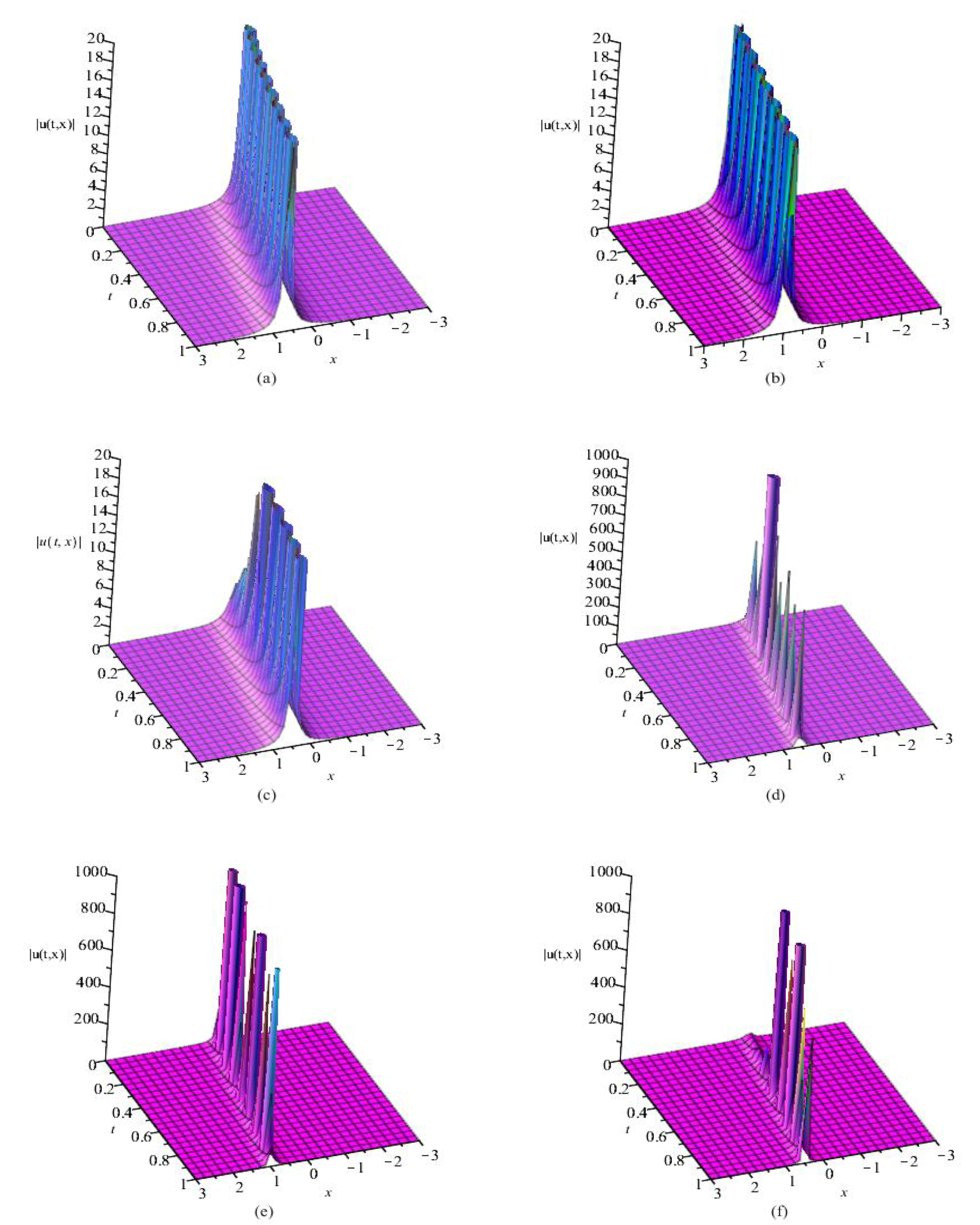
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Khan, M.N.; Ahmad, I.; Ahmad, H.; Abu-Zinadah, H.; Chu, Y.M. Numerical Solution of Traveling Waves in Chemical Kinetics: Time Fractional Fishers Equations. Fractals 2022, 30, 2240051. [Google Scholar] [CrossRef]
- Rashid, S.; Abouelmagd, E.I.; Khalid, A.; Farooq, F.B.; Chu, Y.M. Some Recent Developments on Dynamical ℏ-Discrete Fractional Type Inequalities in the Frame of Nonsingular and Nonlocal Kernels. Fractals 2021, 30, 2240110. [Google Scholar] [CrossRef]
- Jin, F.; Qian, Z.S.; Chu, Y.M.; ur Rahman, M. On nonlinear evolution model for drinking behavior under caputo-fabrizio derivative. J. Appl. Anal. Comput. 2022, 12, 790–806. [Google Scholar] [CrossRef]
- He, Z.Y.; Abbes, A.; Jahanshahi, H.; Alotaibi, N.D.; Wang, Y. Fractional-Order Discrete-Time SIR Epidemic Model with Vaccination: Chaos and Complexity. Mathematics 2022, 10, 165. [Google Scholar] [CrossRef]
- Hajiseyedazizi, S.N.; Samei, M.E.; Alzabut, J.; Chu, Y.M. On multi-step methods for singular fractional q-integro-differential equations. Open Math. 2021, 19, 1378–1405. [Google Scholar] [CrossRef]
- Zhao, T.H.; Zhou, B.C.; Wang, M.K.; Chu, Y.M. On approximating the quasi-arithmetic mean. J. Inequalities Appl. 2019, 2019, 42. [Google Scholar] [CrossRef]
- Sapuppo, F.; Schembri, F.; Fortuna, L.; Bucolo, M. Microfluidic circuits and systems. IEEE Circuits Syst. Mag. 2009, 9, 6–19. [Google Scholar] [CrossRef]
- Sapuppo, F.; Schembri, F.; Fortuna, L.; Llobera, A.; Bucolo, M. A polymeric micro-optical system for the spatial monitoring in two-phase microfluidics. Microfluid. Nanofluidics 2012, 12, 165–174. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Baleanu, D. Lie symmetry analysis and exact solutions of the time fractional Gas dynamics equation. J. Optoelectron. Adv. Mater 2016, 18, 383–388. [Google Scholar]
- Osman, M.S.; Baleanu, D.; Adem, A.R.; Hosseini, K.; Mirzazadeh, M.; Eslami, M. Double-wave solutions and Lie symmetry analysis to the (2+ 1)-dimensional coupled Burgers equations. Chin. J. Phys. 2020, 63, 122–129. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Haji-Badali, A.; Vafadar, P. Group invariant solutions and conservation laws of the Fornberg–Whitham equation. Z. Für Naturforschung A 2014, 69, 489–496. [Google Scholar] [CrossRef]
- Inc, M.; Yusuf, A.; Isa, A.A.; Hashemi, M.S. Soliton solutions, stability analysis and conservation laws for the brusselator reaction diffusion model with time-and constant-dependent coefficients. Eur. Phys. J. Plus 2018, 133, 168. [Google Scholar] [CrossRef]
- Hashemi, M.S. Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals 2018, 107, 161–169. [Google Scholar] [CrossRef]
- Qu, C.; Zhu, C. Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method. J. Phys. A Math. Theor. 2009, 42, 475201. [Google Scholar] [CrossRef]
- Yusuf, A. Symmetry analysis, invariant subspace and conservation laws of the equation for fluid flow in porous media. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050173. [Google Scholar] [CrossRef]
- Bekir, A.; Kaplan, M. Exponential rational function method for solving nonlinear equations arising in various physical models. Chin. J. Phys. 2016, 54, 365–370. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M.; Kaabar, M.K.A. New conservation laws and exact solutions of the special case of the fifth-order KdV equation. J. Ocean. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Wang, Y.; Miah, M.M.; Osman, M.S. Study on Date–Jimbo–Kashiwara–Miwa Equation with Conformable Derivative Dependent on Time Parameter to Find the Exact Dynamic Wave Solutions. Fractal Fract. 2022, 6, 4. [Google Scholar] [CrossRef]
- Arnous, A.H.; Mirzazadeh, M.; Zhou, Q.; Moshokoa, S.P.; Biswas, A.; Belic, M. Soliton solutions to resonant nonlinear schrodinger’s equation with time-dependent coefficients by modified simple equation method. Optik 2016, 127, 11450–11459. [Google Scholar] [CrossRef] [Green Version]
- Savaissou, N.; Gambo, B.; Rezazadeh, H.; Bekir, A.; Doka, S.Y. Exact optical solitons to the perturbed nonlinear Schrödinger equation with dual-power law of nonlinearity. Opt. Quantum Electron. 2020, 52, 318. [Google Scholar] [CrossRef]
- Pinar, Z.; Rezazadeh, H.; Eslami, M. Generalized logistic equation method for Kerr law and dual power law Schrödinger equations. Opt. Quantum Electron. 2020, 52, 504. [Google Scholar] [CrossRef]
- Inc, M.; Hosseini, K.; Samavat, M.; Mirzazadeh, M.; Eslami, M.; Moradi, M.; Baleanu, D. N-wave and other solutions to the B-type Kadomtsev-Petviashvili equation. Therm. Sci. 2019, 23, 2027–2035. [Google Scholar] [CrossRef] [Green Version]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+ 1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Khater, M.M. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F. Application of conservation theorem and modified extended tanh-function method to (1 + 1)-dimensional nonlinear coupled Klein–Gordon–Zakharov equation. Chaos Solitons Fractals 2017, 104, 33–40. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Asif, M.; Hosseini, K.; Mirzazadeh, M.; Akinyemi, L. Some novel integration techniques to explore the conformable M-fractional Schrödinger-Hirota equation. J. Ocean. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Seadawy, A.R.; Eslami, M.; Mirzazadeh, M. Generalized solitary wave solutions to the time fractional generalized Hirota-Satsuma coupled KdV via new definition for wave transformation. J. Ocean Eng. Sci. 2019, 4, 77–84. [Google Scholar] [CrossRef]
- Ma, W.X. Riemann–Hilbert problems and N-soliton solutions for a coupled mKdV system. J. Geom. Phys. 2018, 132, 45–54. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solution and the Hirota condition of a (2 + 1)-dimensional combined equation. Math. Comput. Simul. 2021, 190, 270–279. [Google Scholar] [CrossRef]
- Li, J.; Xia, T. N-soliton solutions for the nonlocal Fokas–Lenells equation via RHP. Appl. Math. Lett. 2021, 113, 106850. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Kadomtsev–Petviashvili hierarchy: N-soliton solutions and distinct dispersion relations. Appl. Math. Lett. 2016, 52, 74–79. [Google Scholar] [CrossRef]
- Dong, H.; Wei, C.; Zhang, Y.; Liu, M.; Fang, Y. The Darboux Transformation and N-Soliton Solutions of Coupled Cubic-Quintic Nonlinear Schrödinger Equation on a Time-Space Scale. Fractal Fract. 2021, 6, 12. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Z.G.; Li, J.J.; Yang, H.W. Analysis of Lie symmetries with conservation laws and solutions of generalized (4 + 1)-dimensional time-fractional Fokas equation. Fractal Fract. 2022, 6, 108. [Google Scholar] [CrossRef]
- Sun, Y.L.; Ma, W.X.; Yu, J.P. N-soliton solutions and dynamic property analysis of a generalized three-component Hirota–Satsuma coupled KdV equation. Appl. Math. Lett. 2021, 120, 107224. [Google Scholar] [CrossRef]
- Rosenau, P.; Hyman, J.M. Compactons: Solitons with finite wavelength. Phys. Rev. Lett. 1993, 70, 564. [Google Scholar] [CrossRef] [PubMed]
- Niu, Z.; Wang, Z. Bifurcation and exact traveling wave solutions for the generalized nonlinear dispersive mk (m, n) equation. J. Appl. Anal. Comput. 2021, 11, 2866–2875. [Google Scholar] [CrossRef]
- Wazwaz, A.M. General compactons solutions and solitary patterns solutions for modified nonlinear dispersive equations mK (n, n) in higher dimensional spaces. Math. Comput. Simul. 2002, 59, 519–531. [Google Scholar] [CrossRef]
- He, B.; Meng, Q.; Rui, W.; Long, Y. Bifurcations of travelling wave solutions for the mK (n, n) equation. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2114–2123. [Google Scholar] [CrossRef]
- Yan, Z. Modified nonlinearly dispersive mK (m, n, k) equations: I. New compacton solutions and solitary pattern solutions. Comput. Phys. Commun. 2003, 152, 25–33. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Rezazadeh, H.; Inc, M.; Akinlar, M.A. New solutions to the fractional perturbed Chen–Lee–Liu equation with a new local fractional derivative. Waves Random Complex Media 2021, 1–36. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: Singapore, 2012. [Google Scholar]
- Kolwankar, K.M.; Gangal, A.D. Fractional differentiability of nowhere differentiable functions and dimensions. Chaos Interdiscip. J. Nonlinear Sci. 1996, 6, 505–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hashemi, M.S.; Baleanu, D. Lie Symmetry Analysis of Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Adda, F.B.; Cresson, J. About non-differentiable functions. J. Math. Anal. Appl. 2001, 263, 721–737. [Google Scholar] [CrossRef] [Green Version]
- Kolwankar, K.M.; Gangal, A.D. Hölder exponents of irregular signals and local fractional derivatives. Pramana 1997, 48, 49–68. [Google Scholar] [CrossRef] [Green Version]
- Carpinteri, A.; Cornetti, P. A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos Solitons Fractals 2002, 13, 85–94. [Google Scholar] [CrossRef]
- Sousa, J.; de Oliveira, E.C. On the local M-derivative. arXiv 2017, arXiv:1704.08186. [Google Scholar]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Salahshour, S.; Ahmadian, A.; Abbasbandy, S.; Baleanu, D. M-fractional derivative under interval uncertainty: Theory, properties and applications. Chaos Solitons Fractals 2018, 117, 84–93. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Nucci, M.C. The complete Kepler group can be derived by Lie group analysis. J. Math. Phys. 1996, 37, 1772–1775. [Google Scholar] [CrossRef]
- Nucci, M.C.; Leach, P.L. The determination of nonlocal symmetries by the technique of reduction of order. J. Math. Anal. Appl. 2000, 251, 871–884. [Google Scholar] [CrossRef] [Green Version]
- Nucci, M.C.; Leach, P.G.L. An integrable SIS model. J. Math. Anal. Appl. 2004, 290, 506–518. [Google Scholar] [CrossRef] [Green Version]
- Marcelli, M.; Nucci, M.C. Lie point symmetries and first integrals: The Kowalevski top. J. Math. Phys. 2003, 44, 2111–2132. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, S.; Chang, M.M.; Shaikh, A.A. Analysis of series RL and RC circuits with time-invariant source using truncated M, atangana beta and conformable derivatives. J. Ocean Eng. Sci. 2021, 6, 217–227. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Nucci, M.C.; Abbasbandy, S. Group analysis of the modified generalized Vakhnenko equation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 867–877. [Google Scholar] [CrossRef]
- Hashemi, M.S. A novel approach to find exact solutions of fractional evolution equations with non-singular kernel derivative. Chaos Solitons Fractals 2021, 152, 111367. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akgül, A.; Hashemi, M.S.; Jarad, F. New Solutions of Nonlinear Dispersive Equation in Higher-Dimensional Space with Three Types of Local Derivatives. Fractal Fract. 2022, 6, 202. https://doi.org/10.3390/fractalfract6040202
Akgül A, Hashemi MS, Jarad F. New Solutions of Nonlinear Dispersive Equation in Higher-Dimensional Space with Three Types of Local Derivatives. Fractal and Fractional. 2022; 6(4):202. https://doi.org/10.3390/fractalfract6040202
Chicago/Turabian StyleAkgül, Ali, Mir Sajjad Hashemi, and Fahd Jarad. 2022. "New Solutions of Nonlinear Dispersive Equation in Higher-Dimensional Space with Three Types of Local Derivatives" Fractal and Fractional 6, no. 4: 202. https://doi.org/10.3390/fractalfract6040202
APA StyleAkgül, A., Hashemi, M. S., & Jarad, F. (2022). New Solutions of Nonlinear Dispersive Equation in Higher-Dimensional Space with Three Types of Local Derivatives. Fractal and Fractional, 6(4), 202. https://doi.org/10.3390/fractalfract6040202