A Study of Generalized Hybrid Discrete Pantograph Equation via Hilfer Fractional Operator

Abstract

Pantograph, a device in which an electric current is collected from overhead contact wires, is introduced to increase the speed of trains or trams. The work aims to study the stability properties of the nonlinear fractional order generalized pantograph equation with discrete time, using the Hilfer operator. Hybrid fixed point theorem is considered to study the existence of solutions, and the uniqueness of the solution is proved using Banach contraction theorem. Stability results in the sense of Ulam and Hyers, and its generalized form of stability for the considered initial value problem are established and we depict numerical simulations to demonstrate the impact of the fractional order on stability.

1. Introduction

Differential equations with delay have a wide range of applications in science and engineering. Pantograph equations, in general referring to differential equations with proportional delays, have their origin in 1971 from the work of Ockendon and Tayler [1]. Since then, continuous and discrete versions of the equation have attracted a large number of physicists and mathematicians to study and analyze the importance of the equations in science, engineering and technology [2,3,4,5,6,7,8,9]. The generalized pantograph equation

$${\upsilon }^{\prime }\left(\zeta \right)=A\upsilon \left(\zeta \right)+B\upsilon \left(\delta \zeta \right)+C{\upsilon }^{\prime }\left(\delta \zeta \right),$$

(1)

where $0<\vartheta <1,$ was proposed by Iserles [10]. Some notable fields of application of pantograph equations include number theory, cell growth, economy, quantum mechanics, biology, electrodynamics, chemical kinetics, physics, medicine and so on.

Fractional calculus was known to mathematicians and scientists for more than three centuries, but the application of fractional calculus in various fields of engineering, science and economics was understood only during last few decades. The reality of nature is better translated by fractional order calculus due its non-local distribution and memory effects. Though different fractional order derivatives and integrals like the Hadamard fractional derivative, Riesz derivative, and so on, are defined, only few derivatives like the Caputo fractional derivative and Riemann Liouville derivative are very widely used to model real life phenomena [11]. Generalization of the Riemann-Liouville and Caputo type derivatives into a fractional order derivative of type $0\le \mu \le 1$ was proposed by R. Hilfer in [12]. The fractional derivative proposed by Hilfer yields Caputo $(\mu =1)$ and Riemann Liouville derivative $(\mu =0)$ as particular cases. Some recent works on fractional order Hilfer derivatives can be found in [13,14,15,16,17,18]. Perturbation techniques are powerful tools in nonlinear analysis for studying diverse aspects of the solution of nonlinear dynamical systems. They are useful in describing, predicting and demonstrating the nonlinear effects caused in vibrating systems. Hybrid fixed point theory is a common approach to tackle perturbed nonlinear equations. Hybrid differential equations are nonlinear differential equations with perturbation of the equation involving multiplication or division by a term (quadratic perturbation) [19]. Hybrid equations of fractional order have attracted researchers in recent times to the extent that they embrace various dynamic systems as particular cases [20,21,22,23,24,25]. The existence of results for the solution of the hybrid pantograph equation with fractional order, given by

$$\begin{array}{cc}\hfill D_{0+}^{\eta }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{f(\zeta ,\upsilon (\zeta ),\upsilon (\delta \zeta \left)\right)}}\right]& =\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\sigma \zeta \left)\right),0<\zeta <1,\hfill \\ \hfill \upsilon \left(0\right)& =0,\hfill \end{array}$$

(2)

was studied in [2]. The generalized hybrid fractional pantograph equation

$$\begin{array}{cc}\hfill D_{0+}^{\eta }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{f(\zeta ,\upsilon (\zeta ),\upsilon (\varphi \left(\zeta \right)\left)\right)}}\right]& =\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\rho \left(\zeta \right)\left)\right),0<\zeta <1,\hfill \\ \hfill \upsilon \left(0\right)& =0,\hfill \end{array}$$

(3)

was considered to study the existence of solution in [26].

Discrete time fractional order calculus was enriched by the contributions of Atici et al. [27,28,29], Anastassiou [30], Goodrich [31,32], Holm [33], and so on. The definition of Hilfer fractional sum and differences are proposed in [34]. As for hybrid equations with discrete fractional operators, the authors in [35] considered the hybrid fractional sum-difference equations and investigated the existence of solutions. The qualitative properties of the discrete fractional hybrid equations are yet to be explored. The stability analysis of Hilfer type hybrid fractional equations has not been studied, to fill this gap, we consider an application of Hilfer fractional sum and difference to generalized hybrid pantograph equation and perform stability analysis.

The paper is formatted as follows: Essential definitions and lemmas are provided in Section 2 and the mathematical representation of the discrete time hybrid fractional pantograph equation is presented in Section 3. The existence of a unique solution for the Hilfer type discrete fractional generalized hybrid pantograph equation is illustrated in Section 4. Section 5 and Section 6 present the stability results and application of the main result is demonstrated with a numerical example, respectively.

2. Prerequisites

Definition 1

([31]). ($\eta th$ Fractional Sum ) Let $\eta >0$ and $\mathfrak{p}:{\mathbb{N}}_{\lambda }\to \mathbb{R}.$ Then the delta fractional sum of $\mathfrak{p}$ is

$${\Delta }_{\lambda }^{-\eta }\mathfrak{p}\left(\zeta \right)=\sum _{\ell =\lambda }^{\zeta -\eta }{h}_{\eta -1}(\zeta ,\sigma (\ell ))\mathfrak{p}(\ell ),$$

(4)

where $h_{\eta }(\zeta ,\ell )={\displaystyle \frac{{(\zeta -\ell )}^{\left(\eta \right)}}{\Gamma (\eta +1)}}$ is the $\eta th$ fractional Taylor monomial, $\sigma (\ell )=\ell +1$ and ${\zeta }^{\left(\eta \right)}={\displaystyle \frac{\Gamma (\zeta +1)}{\Gamma (\zeta -\eta +1)}}$ is the falling factorial function.

Definition 2

([28]). The $\eta th-$ Riemann–Liouville type fractional difference of function $\mathfrak{p}$ is defined by

$$\begin{array}{cc}\hfill {\Delta }_{\lambda }^{\eta }\mathfrak{p}\left(\zeta \right)& ={\Delta }^m{\Delta }_{\lambda }^{-(m-\eta )}\left(\mathfrak{p}\left(\zeta \right)\right),\hfill \\ \hfill & =\sum _{\ell =\lambda }^{\zeta +\eta }{h}_{m-\eta -1}(\zeta ,\sigma (\ell ))\mathfrak{p}(\ell ),\forall \zeta \in {\mathbb{N}}_{\lambda +m-\eta },\hfill \end{array}$$

where $\eta >0,$ $\mathfrak{p}:{\mathbb{N}}_{\lambda }\to \mathbb{R}$ and $m-1<\eta <m$ for $m\in {\mathbb{N}}_1.$

Theorem 1

([36]). Let $\rho ,{\eta }_1>0$ and $\mathfrak{p}:\mathbb{N}\to \mathbb{R}.$ Then the inequalities

(1).

${\Delta }^{-{\eta }_1}\left[{\Delta }^{-\rho }\mathfrak{p}\left(\zeta \right)\right]={\Delta }^{-(\rho +{\eta }_1)}\mathfrak{p}\left(\zeta \right)={\Delta }^{-\rho }\left[{\Delta }^{-{\eta }_1}\mathfrak{p}\left(\zeta \right)\right],$

(2).

${\Delta }^{-{\eta }_1}\Delta \mathfrak{p}\left(\zeta \right)=\Delta {\Delta }^{-{\eta }_1}\mathfrak{p}\left(\zeta \right)-{\displaystyle \frac{{(\zeta -a)}^{({\eta }_1-1)}}{\Gamma \left({\eta }_1\right)}}\mathfrak{p}\left(a\right),$

hold.

Definition 3

([37]). The $\eta th-$ Caputo type fractional difference of function $\mathfrak{p}$ is defined by

$$\begin{array}{cc}\hfill {\phantom{x}}^C{\Delta }_{\lambda }^{\eta }\mathfrak{p}\left(\zeta \right)& ={\Delta }_{\lambda }^{-(m-\eta )}{\Delta }^m\left(\mathfrak{p}\left(\zeta \right)\right),\hfill \\ \hfill & =\sum _{\ell =\lambda }^{\zeta -(m-\eta )}{h}_{m-\eta -1}(\zeta ,\sigma (\ell )){\Delta }^m\mathfrak{p}(\ell )\forall \zeta \in {\mathbb{N}}_{\lambda +m-\eta },\hfill \end{array}$$

where $\eta >0,$ $\mathfrak{p}:{\mathbb{N}}_{\lambda }\to \mathbb{R}$ and $m-1<\eta <m$ for $m\in {\mathbb{N}}_1.$

Definition 4

([34]). The Hilfer fractional difference of order $m-1<\eta <m$ and type $0\le \mu \le 1$ of function $\mathfrak{p}$ is defined by

$${\Delta }_{\lambda }^{\eta ,\mu }\mathfrak{p}\left(\zeta \right)={\Delta }_{\lambda +(1-\mu )(m-\eta )}^{-\mu (m-\eta )}\Delta {\Delta }_{\lambda }^{-(1-\mu )(m-\eta )}\left(\mathfrak{p}\left(\zeta \right)\right),for\zeta \in {\mathbb{N}}_{\lambda +1-\eta }.$$

(5)

where $\mathfrak{p}:{\mathbb{N}}_{\lambda }\to \mathbb{R}.$

Lemma 1

([34]). Assume $0<\eta <1,$ $0\le \mu \le 1,$ and function $\mathfrak{p}:{\mathbb{N}}_{\lambda }\to \mathbb{R}$, then for $\zeta \in {\mathbb{N}}_{\lambda +1}$ the composition properties are

(I).

${\Delta }_{\lambda +1-\eta }^{-\eta }\left[{\Delta }_{\lambda }^{\eta ,\mu }\mathfrak{p}\left(\zeta \right)\right]={\Delta }_{\lambda +(1-\mu )(1-\eta )}^{-(\eta +\mu -\eta \mu )}\Delta {\Delta }_{\lambda }^{-(1-\mu )(1-\eta )}\left(\mathfrak{p}\left(\zeta \right)\right).$

(II).

${\Delta }_{\lambda +1-\eta }^{-\eta }\left[{\Delta }_{\lambda }^{\eta ,\mu }\mathfrak{p}\left(\zeta \right)\right]={\Delta }_{\lambda +(1-\mu )(1-\eta )}^{-(\eta +\mu -\eta \mu )}{\Delta }_{\lambda }^{(\eta +\mu -\eta \mu )}\left(\mathfrak{p}\left(\zeta \right)\right).$

(III).

${\Delta }_{\lambda +\eta }^{\eta ,\mu }\left[{\Delta }_{\lambda }^{-\eta }\mathfrak{p}\left(\zeta \right)\right]={\Delta }_{\lambda +(1-\mu +\eta \mu )}^{-\mu (1-\eta )}{\Delta }_{\lambda }^{\mu (1-\eta )}\left(\mathfrak{p}\left(\zeta \right)\right).$

(IV).

${\Delta }_{\lambda +\eta }^{\eta ,\mu }\left[{\Delta }_{\lambda }^{-\eta }\mathfrak{p}\left(\zeta \right)\right]=\mathfrak{p}\left(\zeta \right)-{\Delta }_{\lambda }^{-(1-\mu (1-\eta \left)\right)}\mathfrak{p}(\lambda +1-\mu (1-\eta ))h_{\mu (1-\eta )-1}(\zeta ,\lambda +1-\mu (1-\eta )).$

Theorem 2

([38]). (Banach Contraction Mapping Principle)

A contraction mapping on a complete metric space has exactly one fixed point.

Theorem 3

([20]). (Hybrid Fixed Point Theorem)

Let $\mathcal{Y}$ be the nonempty, closed, bounded and convex subset of Banach algebra $\mathcal{B}$. Let the operators be ${\mathcal{P}}_1:\mathcal{B}\to \mathcal{B},{\mathcal{P}}_2:\mathcal{Y}\to \mathcal{B}$ such that

(i).

${\mathcal{P}}_1$ is Lipschitz continuous with constants θ.

(ii).

${\mathcal{P}}_2$ is completely continuous.

(iii).

$\upsilon ={\mathcal{P}}_1\upsilon {\mathcal{P}}_{2}y\Rightarrow \upsilon \in \mathcal{Y}\forall y\in \mathcal{Y}$.

(iv).

$\theta A<1,$ where $A=∥{\mathcal{P}}_2\left(\mathcal{Y}\right)∥.$

then, ${\mathcal{P}}_1\upsilon {\mathcal{P}}_2\upsilon =\upsilon$ has a solution.

Theorem 4

([39]). (Arzela-Ascoli Theorem) A set of functions in $\mathcal{C}\left(\right[a,b\left]\right)$ with supremum norm is relatively compact if, and only if, it is uniformly bounded and equicontinuous on $[a,b].$

3. Discrete Fractional Hybrid Pantograph Equation

This section is devoted to the description of the hybrid pantograph model and approximate solution. Stability analysis of fractional hybrid equations by [40] and works on the hybrid pantograph equation by [2,26] have inspired and motivated us to investigate the stability of initial value Hilfer type discrete fractional generalized hybrid pantograph equation (HDFGHPE). Let us denote $\mathbb{D}=[\lambda ,\mathbb{T}]\cap {\mathbb{N}}_{\lambda }$. Let $\vartheta =\eta +\mu -\eta \mu$ with $0<\eta \le 1,$ $0\le \mu \le 1.$ We have

$$\left\{\begin{array}{c}{\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]=w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi (\zeta +\eta -1)\right)),\hfill \\ {\Delta }_{\lambda }^{-(1-\vartheta )}\left[{\displaystyle \frac{\upsilon (\lambda +1-\vartheta )}{\mathrm{\Theta }(\lambda +1-\vartheta ,\upsilon (\lambda +1-\vartheta ),\upsilon (\psi (\lambda +1-\vartheta )\left)\right)}}\right]=\Lambda ,\hfill \end{array}\right.$$

(6)

where $\zeta \in [\lambda +1-\eta ,\mathbb{T}]\cap {\mathbb{N}}_{\lambda +1-\eta }$ with $\lambda \in \mathbb{R}$ and $\mathbb{T}\in \mathbb{N}$ where ${\mathbb{N}}_j=\left\{j,j+1,\dots \right\},j\in \mathbb{R}$. Here ${\Delta }^{\eta ,\mu }$ is Hilfer type fractional difference operator of order $\eta$ and type $\mu$, $\Lambda \in \mathbb{R}$, $\psi ,\phi :\mathbb{D}\to [0,1],$ $\mathrm{\Theta }:\mathbb{D}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}\setminus \left\{0\right\}$ and $w:\mathbb{D}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous functions.

Lemma 2.

Let $0<\eta <1,$ $0\le \mu \le 1,$ $\mathrm{\Theta }:\mathbb{D}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}\setminus \left\{0\right\}$ and $w:\mathbb{D}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$. Then HDFGHPE (6) with initial condition has an unique solution

$$\begin{array}{cc}\hfill \upsilon \left(\zeta \right)=\mathrm{\Theta }(\zeta ,& \upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right)\left)\right[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)],\hfill \end{array}$$

(7)

for $\zeta \in \mathbb{D}.$

Proof. 

Applying ${\Delta }_{\lambda +1-\eta }^{-\eta }$ for (6), we have

$${\Delta }_{\lambda +1-\eta }^{-\eta }\left[{\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]\right]={\Delta }_{\lambda +1-\eta }^{-\eta }\left[w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right].$$

(8)

Apply Lemma (1) to left-hand side of (8) to obtain

$${\Delta }_{\lambda +1-\eta }^{-\eta }\left[{\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]\right]={\Delta }_{\lambda +(1-\eta )(1-\mu )}^{-(\eta +\mu -\eta \mu )}{\Delta }_{\lambda }^{(\eta +\mu -\eta \mu )}\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right].$$

Now, consider

$${\Delta }_{\lambda +(1-\eta )(1-\mu )}^{-(\eta +\mu -\eta \mu )}{\Delta }_{\lambda }^{(\eta +\mu -\eta \mu )}\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]={\Delta }_{\lambda +(1-\vartheta )}^{-\vartheta }\Delta {\Delta }_{\lambda }^{-(1-\vartheta )}\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right].$$

Using the Theorem (1) yields

$${\Delta }_{\lambda +(1-\eta )(1-\mu )}^{-(\eta +\mu -\eta \mu )}{\Delta }_{\lambda }^{(\eta +\mu -\eta \mu )}\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]={\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}-\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta ).$$

Thus, Equation (7) holds. This completes the proof. □

4. Fixed Point Operators of HDFGHPE (6)

This section defines a fixed point operator and establishes the existence of an unique solution of (6). Let $\mathcal{B}$ with norm $∥\upsilon ∥=\underset{\zeta \in \mathbb{D}}{sup}\left|\upsilon \left(\zeta \right)\right|$ be the space of all functions $\upsilon \left(\zeta \right)$. Clearly, $\mathcal{B}$ is a Banach space.

Let us define the operator $\mathsf{{\rm Y}}:\mathcal{B}\to \mathcal{B}$ by

$$\begin{array}{cc}\hfill \mathsf{{\rm Y}}\upsilon \left(\zeta \right)=& \mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & + {\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)],\hfill \end{array}$$

(9)

for $\zeta \in \mathbb{D}.$

For all $\upsilon ,{\upsilon }^{*}\in \mathbb{R}$ and $\zeta \in \mathbb{D}$, we make the following assumptions

(J₁):

There exists ${\chi }_w\left(\zeta \right)\in \mathcal{C}(\mathbb{D},{\mathbb{R}}^{+})$ such that

$$\left|w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi (\zeta +\eta -1)\right))\right|\le {\chi }_w\left(\zeta \right).$$

(J₂):

There exist ${\xi }_1\left(\zeta \right)\in \mathcal{C}(\mathbb{D},{\mathbb{R}}^{+})$ with bound ${\xi }_1$ such that

$$|\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta ,{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \zeta \right))|\le {\xi }_1\left(\zeta \right)max\left\{|\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,|\upsilon \left(\psi \left(\zeta \right)\right)-{\upsilon }^{*}\left(\psi \left(\zeta \right)\right)|\right\}.$$

(J₃):

There exist ${\xi }_2\left(\zeta \right)\in \mathcal{C}(\mathbb{D},{\mathbb{R}}^{+})$ with bound ${\xi }_2$ such that

$$\begin{array}{cc}\hfill \left|w\right(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi \right(\zeta +\eta -1\left)\right))-& w(\zeta +\eta -1,{\upsilon }^{*}(\zeta +\eta -1),{\upsilon }^{*}\left(\phi (\zeta +\eta -1)\right))|\hfill \\ & \le {\xi }_2\left(\zeta \right)max\left\{|\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,|\upsilon \left(\phi \left(\zeta \right)\right)-{\upsilon }^{*}\left(\phi \left(\zeta \right)\right)|\right\}.\hfill \end{array}$$

4.1. Uniqueness of Solution of HDFGHPE (6)

Theorem 5.

Assume that $\left(J_1\right),\left(J_2\right),\left(J_3\right)$ hold and there exists ${\chi }_{\mathrm{\Theta }}\left(\zeta \right)\in \mathcal{C}(\mathbb{D},{\mathbb{R}}^{+})$ such that

$$\left|\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))\right|\le {\chi }_{\mathrm{\Theta }}\left(\zeta \right),$$

(10)

$\forall \upsilon \in \mathbb{R}$ and $\zeta \in \mathbb{D}.$ Then $\upsilon \left(\zeta \right)$ is a unique solution of hybrid fractional difference Equation (6) if

$$\mathsf{\Omega }={\xi }_1\left[\Lambda h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )+{\chi }_w{\displaystyle \frac{{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}\right]+{\chi }_{\mathrm{\Theta }}{\xi }_2{\displaystyle \frac{{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}<1.$$

(11)

Proof. 

Let ${\chi }_w=\underset{\zeta \in \mathbb{D}}{max}\left|{\chi }_w\left(\zeta \right)\right|$ and ${\chi }_{\mathrm{\Theta }}=\underset{\zeta \in \mathbb{D}}{max}\left|{\chi }_{\mathrm{\Theta }}\left(\zeta \right)\right|.$

We aim to prove that the mapping $\mathsf{{\rm Y}}$ defined in (9) is a contraction. For $\upsilon ,{\upsilon }^{*}\in \mathbb{R}$ and $\zeta \in \mathbb{D}$, we have

$$\begin{array}{cc}\hfill |\mathsf{{\rm Y}}\upsilon \left(\zeta \right)-\mathsf{{\rm Y}}{\upsilon }^{*}\left(\zeta \right)|=& \left|\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))\right[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)]\hfill \\ & -\mathrm{\Theta }(\zeta ,{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \left(\zeta \right)\right))[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }^{*}(\zeta +\eta -1),{\upsilon }^{*}\left(\phi (\zeta +\eta -1)\right))\right)]|,\hfill \\ \hfill \le & |{\xi }_1\left(\zeta \right)\left|\right|h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )|\Lambda +|\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta ,{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \left(\zeta \right)\right))|\hfill \\ & {\Delta }_{\lambda +1-\eta }^{-\eta }\left|\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)\right|\hfill \\ & +|\mathrm{\Theta }(\zeta ,{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \left(\zeta \right)\right))|{\Delta }_{\lambda +1-\eta }^{-\eta }|w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi (\zeta +\eta -1)\right))\hfill \\ & -w(\zeta +\eta -1,{\upsilon }^{*}(\zeta +\eta -1),{\upsilon }^{*}\left(\phi (\zeta +\eta -1)\right))|,\hfill \\ \hfill \le & \left({\xi }_1\Lambda h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )+({\chi }_w{\xi }_1+{\chi }_{\mathrm{\Theta }}{\xi }_2){\displaystyle \frac{{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}\right)∥\upsilon -{\upsilon }^{*}∥,\hfill \\ \hfill ∥\mathsf{{\rm Y}}\upsilon -\mathsf{{\rm Y}}{\upsilon }^{*}∥ \le & \mathsf{\Omega }∥\upsilon -{\upsilon }^{*}∥.\hfill \end{array}$$

Thus, the mapping $\mathsf{{\rm Y}}$ is a contraction mapping with $\mathsf{\Omega }<1.$ Therefore, the initial value discrete time Hilfer type fractional generalized pantograph Equation (6) has a unique solution. □

4.2. Existence Results for HDFGHPE (6)

The existence of the solution of HDFGHPE (6) is established using hybrid fixed point theorem (3) due to Dhage [20].

Theorem 6.

Assume that $\left(J_1\right),\left(J_2\right)$ hold. Then HDFGHPE (6) has a solution $\upsilon \left(\zeta \right)$ for $\zeta \in \mathbb{D}$ if

$${\xi }_1\left[\Lambda {(\mathbb{T}-\lambda -1+\vartheta )}^{(\vartheta -1)}\Gamma \left(\eta \right)+{\chi }_w\Gamma \left(\vartheta \right){(\mathbb{T}-\lambda -1+\eta )}^{\left(\eta \right)}\right]<\Gamma \left(\vartheta \right)\Gamma \left(\eta \right).$$

(12)

Proof. 

Let $\mathcal{Y}= \left\{\upsilon \in \mathcal{B}:∥\upsilon ∥\le \mathfrak{S}\right\}$, where $\mathfrak{S}$ is a real number such that

$$\mathfrak{S}\ge {\displaystyle \frac{{\mathrm{\Theta }}_0\left|\mathrm{\Xi }\right|}{1-{\xi }_1\left|\mathrm{\Xi }\right|}},$$

(13)

where ${\mathrm{\Theta }}_0=\underset{\zeta \in \mathbb{D}}{max}\left|\mathrm{\Theta }(\zeta ,0,0)\right|$ and $\mathrm{\Xi }=\Lambda |h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )|+{\chi }_w{\displaystyle \frac{{(\mathbb{T}-\lambda -1+\eta )}^{\left(\eta \right)}}{\Gamma \left(\eta \right)}}$.

Clearly, $\mathcal{Y}$ is a closed, bounded and convex subset of $\mathcal{B}.$ By Lemma (2), let the operators ${\mathcal{P}}_1:\mathcal{B}\to \mathcal{B}$ and ${\mathcal{P}}_2:\mathcal{Y}\to \mathcal{B}$ be

$$\begin{array}{cc}\hfill {\mathcal{P}}_1\upsilon \left(\zeta \right)& =\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right),\hfill \\ \hfill {\mathcal{P}}_2\upsilon \left(\zeta \right)& =\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )+{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right),\hfill \end{array}$$

where $\zeta \in \mathbb{D}$. Thus, solution of (6) is equivalent to

$${\mathcal{P}}_1\upsilon \left(\zeta \right){\mathcal{P}}_2\upsilon \left(\zeta \right)=\upsilon \left(\zeta \right),\zeta \in \mathbb{D}.$$

We shall now prove that the operators ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ satisfy the conditions of the Theorem (3) in following steps.

Step 1:

We shall show that the operator ${\mathcal{P}}_1$ is Lipschitz continuous on $\mathcal{B}.$

From the condition $J_1$, we have,

$$\begin{array}{cc}\hfill \left|{\mathcal{P}}_1\upsilon \left(\zeta \right)-{\mathcal{P}}_1{\upsilon }^{*}\left(\zeta \right)\right|& =|\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta -{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \left(\zeta \right)\right))|,\hfill \\ \hfill & \le |{\xi }_1\left(\zeta \right)|max\left\{|\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,|\upsilon \left(\psi \left(\zeta \right)\right)-{\upsilon }^{*}\left(\psi \left(\zeta \right)\right)|\right\},\hfill \\ \hfill ∥{\mathcal{P}}_1\upsilon -{\mathcal{P}}_1{\upsilon }^{*}∥& \le {\xi }_1∥\upsilon -{\upsilon }^{*}∥.\hfill \end{array}$$

Thus, ${\mathcal{P}}_1$ is lipschitz continuous with constants ${\xi }_1$.

Step 2:

We proceed to prove that the operator ${\mathcal{P}}_2$ is completely continuous on $\mathcal{Y}$.

The continuity of w implies the continuity of operator ${\mathcal{P}}_2$ on $\mathcal{Y}$.

First, we shall prove the uniform boundedness of the operator ${\mathcal{P}}_2$ in $\mathcal{Y}$.

$$\begin{array}{cc}\hfill \left|{\mathcal{P}}_2\upsilon \left(\zeta \right)\right|& = \left|\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )+{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)\right|,\hfill \\ \hfill & \le \Lambda |h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )|+\left|{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)\right|,\hfill \\ \hfill & \le |h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )|\Lambda +{\displaystyle \frac{{\chi }_w\Gamma (\mathbb{T}+\eta -\lambda -1)}{\eta \Gamma \left(\eta \right)}}=\varpi ,\hfill \\ \hfill ∥{\mathcal{P}}_2\upsilon ∥& \le \varpi .\hfill \end{array}$$

Therefore, ${\mathcal{P}}_2$ is uniformly bounded on $\mathcal{Y}$.

We prove the equicontinuity of the the operator ${\mathcal{P}}_2$. For any $\epsilon >0,$ let there exist ${\zeta }_a,{\zeta }_b\in \mathbb{D}({\zeta }_a<{\zeta }_b)$ such that

$$\left|{\displaystyle \frac{\Gamma ({\zeta }_b+\eta )\Gamma \left({\zeta }_a\right)-\Gamma \left({\zeta }_b\right)\Gamma ({\zeta }_a+\eta )}{\Gamma \left({\zeta }_b\right)\Gamma ({\zeta }_a+\eta )}}\right| < \left({\displaystyle \frac{\Gamma (\eta +1)\Gamma \left(\mathbb{T}\right)}{{\chi }_w\Gamma (\mathbb{T}+\eta )}}\right){\displaystyle \frac{\epsilon }{2}},$$

(14)

and

$$\left|{\displaystyle \frac{\Gamma ({\zeta }_b-\lambda +\vartheta )\Gamma ({\zeta }_a-\lambda +1)}{\Gamma ({\zeta }_b-\lambda +1)\Gamma ({\zeta }_a-\lambda -\vartheta )}}-1\right| < \left({\displaystyle \frac{\Gamma (\mathbb{T}-\lambda +1)}{\Lambda \Gamma (\mathbb{T}-\lambda -\vartheta )}}\right){\displaystyle \frac{\epsilon }{2}},$$

(15)

then,

$$\begin{array}{cc}\hfill \left|{\mathcal{P}}_2\upsilon \left({\zeta }_b\right)-{\mathcal{P}}_2\upsilon \left({\zeta }_a\right)\right| =& |\Lambda h_{\vartheta -1}({\zeta }_b,\lambda +1-\vartheta )-\Lambda h_{\vartheta -1}({\zeta }_a,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w({\zeta }_b+\eta -1,\upsilon ({\zeta }_b+\eta -1),\upsilon \left(\phi ({\zeta }_b+\eta -1)\right))\right)\hfill \\ & -{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w({\zeta }_a+\eta -1,\upsilon ({\zeta }_a+\eta -1),\upsilon \left(\phi ({\zeta }_a+\eta -1)\right))\right)|,\hfill \\ \hfill \le & \left|\Lambda \left[{\displaystyle \frac{{({\zeta }_b-\lambda -1+\vartheta )}^{(\vartheta -1)}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{({\zeta }_b-\lambda -1+\vartheta )}^{(\vartheta -1)}}{\Gamma \left(\vartheta \right)}}\right]\right|\hfill \\ & +{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}|\left[\sum _{\ell =\lambda +1-\eta }^{{\zeta }_b-\eta }{({\zeta }_b-\ell -1)}^{(\eta -1)}-{\displaystyle \frac{1}{\Gamma \left(\eta \right)}}\sum _{\ell =\lambda +1-\eta }^{{\zeta }_a-\eta }{({\zeta }_a-\ell -1)}^{(\eta -1)}\right]\hfill \\ & \left(w(\ell +\eta ,\upsilon (\ell +\eta ),\upsilon (\sigma (\ell +\eta )\left)\right)\right)|,\hfill \\ \hfill \le & \left|\Lambda \left[{\displaystyle \frac{{({\zeta }_b-\lambda -1+\vartheta )}^{(\vartheta -1)}}{\Gamma \left(\vartheta \right)}}-{\displaystyle \frac{{({\zeta }_b-\lambda -1+\vartheta )}^{(\vartheta -1)}}{\Gamma \left(\vartheta \right)}}\right]\right|\hfill \\ & +{\displaystyle \frac{{\chi }_w}{\Gamma \left(\eta \right)}}\left|{\displaystyle \frac{\Gamma ({\zeta }_b+\eta )}{\Gamma \left({\zeta }_b\right)}}-{\displaystyle \frac{\Gamma ({\zeta }_a+\eta )}{\Gamma \left({\zeta }_a\right)}}\right|,\hfill \\ \hfill \le & \Lambda {\displaystyle \frac{\Gamma (\mathbb{T}-\lambda -\vartheta )}{\Gamma (\mathbb{T}-\lambda +1)}}\left[{\displaystyle \frac{\Gamma ({\zeta }_b-\lambda +\vartheta )\Gamma ({\zeta }_a-\lambda +1)}{\Gamma ({\zeta }_b-\lambda +1)\Gamma ({\zeta }_a-\lambda -\vartheta )}}-1\right]\hfill \\ & +{\displaystyle \frac{{\chi }_w\Gamma (\mathbb{T}+\eta )}{\Gamma \left(\mathbb{T}\right)\Gamma (\eta +1)}}\left|{\displaystyle \frac{\Gamma ({\zeta }_b+\eta )\Gamma \left({\zeta }_a\right)-\Gamma ({\zeta }_a+\eta )\Gamma \left({\zeta }_b\right)}{\Gamma ({\zeta }_a+\eta )\Gamma \left({\zeta }_b\right)}}\right|,\hfill \\ \hfill ∥{\mathcal{P}}_2\upsilon \left({\zeta }_b\right)-{\mathcal{P}}_2\upsilon \left({\zeta }_a\right)∥& <\epsilon .\hfill \end{array}$$

which implies the equicontinuity of ${\mathcal{P}}_2$ in $\mathcal{B}$. By Arzela Ascoli’s theorem, the operator ${\mathcal{P}}_2$ is completely continuous.

Step 3:

We prove $\upsilon ={\mathcal{P}}_1\upsilon {\mathcal{P}}_{2}y\Rightarrow \upsilon \in \mathcal{Y}\forall y\in \mathcal{Y}$.

Let $\upsilon \in \mathcal{B},y\in \mathcal{Y}$ be arbitrary such that $\upsilon ={\mathcal{P}}_1\upsilon {\mathcal{P}}_{2}y.$

$$\begin{array}{cc}\hfill \left|\upsilon \left(\zeta \right)\right| \le & |{\mathcal{P}}_1\upsilon \left(\zeta \right)\left|\right|{\mathcal{P}}_{2}y\left(\zeta \right)|,\hfill \\ \hfill \le & \left|\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)\right||\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,y(\zeta +\eta -1),y(\phi (\zeta +\eta -1)\left)\right)\right)|,\hfill \\ \hfill \le & \left|\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)-\mathrm{\Theta }(\zeta ,0,0)+\mathrm{\Theta }(\zeta ,0,0)\right||\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,y(\zeta +\eta -1),y(\phi (\zeta +\eta -1)\left)\right)\right)|,\hfill \\ \hfill \le & |{\xi }_1\left(\zeta \right)|\left[\Lambda |h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )|+{\chi }_w{\displaystyle \frac{{(\mathbb{T}-\lambda -1+\eta )}^{\left(\eta \right)}}{\Gamma \left(\eta \right)}}\right]max\left\{\left|\upsilon \right(\zeta \left)\right|,\left|\upsilon \right(\psi \left(\zeta \right)\left)\right|\right\}\hfill \\ & +{\mathrm{\Theta }}_0\left[\Lambda |h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )|+{\chi }_w{\displaystyle \frac{{(\mathbb{T}-\lambda -1+\eta )}^{\left(\eta \right)}}{\Gamma \left(\eta \right)}}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill \le & {\displaystyle \frac{{\mathrm{\Theta }}_0\left|\mathrm{\Xi }\right|}{1-{\xi }_1\left|\mathrm{\Xi }\right|}},\hfill \\ \hfill ∥\upsilon ∥ \le & \mathfrak{S}.\hfill \end{array}$$

Therefore $\upsilon \left(\zeta \right)\in \mathcal{Y}.$

Step 4:

We show that $\theta A<1.$ Here,

$$\begin{array}{cc}\hfill A& =\underset{\zeta \in \mathbb{D}}{sup}\left\{\left|{\mathcal{P}}_2\left(\mathcal{Y}\right)\right|\right\},\hfill \\ \hfill & \le \Lambda |h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )|+{\chi }_w{\displaystyle \frac{{(\mathbb{T}-\lambda -1+\eta )}^{\left(\eta \right)}}{\Gamma \left(\eta \right)}}.\hfill \end{array}$$

With $\theta ={\xi }_1$ and (12), the condition $\theta A<1$ is satisfied.

Evidently, ${\mathcal{P}}_1\upsilon \left(\zeta \right){\mathcal{P}}_{2}y\left(\zeta \right)=\upsilon \left(\zeta \right),\zeta \in \mathbb{D}$ has a solution in $\mathcal{Y}$ which implies that HDFGHPE (6) has a solution $\upsilon \left(\zeta \right)$ for $\zeta \in \mathbb{D}.$ This completes the proof. □

5. Stability of HDFGHPE (6)

Stability is a condition in which trajectories of the system would not exhibit any significant changes under small disturbance. The asymptotic stability analysis of nonlinear discrete fractional equations were studied by Fulai Chen in [36,41]. Several authors have contributed on the stability analysis of various applications of fractional order discrete time equations as in [6,42,43,44,45,46,47]. We devote this section to study the stability of the HDFGHPE (6). Consider the discrete time Hilfer fractional initial value problem (6) and the following inequality

$$\left|{\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{{\upsilon }_1\left(\zeta \right)}{\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))}}\right]-w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))\right|\le \epsilon ,\zeta \in \mathbb{D},$$

(16)

where $\epsilon >0$ and ${\upsilon }_1\in \mathcal{C}(\mathbb{D},\mathbb{R})$.

Definition 5

([48] Ulam–Hyers Stability). The discrete time Hilfer fractional initial value problem (6) is Ulam–Hyers stable if there exists a real constant $\mathbb{V}>0$ such that for each $\epsilon >0$ and for every solution ${\upsilon }_1\in \mathcal{C}(\mathbb{D},\mathbb{R})$ of inequality (16), there exists a solution $\upsilon \in \mathcal{C}(\mathbb{D},\mathbb{R})$ of (6) with

$$\left|{\upsilon }_1\left(\zeta \right)-\upsilon \left(\zeta \right)\right|<\mathbb{V}\epsilon ,\zeta \in \mathbb{D}.$$

(17)

Definition 6

([48] Generalized Ulam–Hyers Stability). The HDFGHPE (6) is generalized Ulam–Hyers stable if $\sigma \in \mathcal{C}({\mathbb{R}}^{+},{\mathbb{R}}^{+})$ with $\sigma \left(0\right)=0$ exists such that for every solution ${\upsilon }_1\in \mathcal{C}(\mathbb{D},\mathbb{R})$ of inequality (16), there exists $\upsilon \in \mathcal{C}(\mathbb{D},\mathbb{R})$ of (6) with

$$\left|{\upsilon }_1\left(\zeta \right)-\upsilon \left(\zeta \right)\right| <\sigma \left(\epsilon \right),\zeta \in \mathbb{D}.$$

(18)

The following remark is essential for proving the stability results.

Remark 1.

A function ${\upsilon }_1\left(\zeta \right)\in \mathcal{B}$ solves (16) iff a function $q:\mathbb{D}\times \mathbb{R}\to \mathbb{R}$ exists satisfying

(H₁):

$\left|q(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1))\right| \le \epsilon ,\zeta \in \mathbb{D}.$

(H₂):

${\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{{\upsilon }_1\left(\zeta \right)}{\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))}}\right]-w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))$ $=q(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1)).$

Lemma 3.

If the function ${\upsilon }_1\left(\zeta \right)$ is the solution of the inequality (16) then

$$\begin{array}{cc}\hfill |{\upsilon }_1\left(\zeta \right)-& \Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))\hfill \\ & {\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))\right)|\le \epsilon {\displaystyle \frac{{\chi }_{\mathrm{\Theta }}{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}},\hfill \end{array}$$

(19)

for $\zeta \in \mathbb{D}.$

Proof. 

If ${\upsilon }_1\left(\zeta \right)$ satisfy (16), using Remark (1) and Lemma (1) the solution of $\left(H_2\right)$ is

$$\begin{array}{cc}\hfill {\upsilon }_1\left(\zeta \right)=& \mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))(\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))+q(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1))\right))\hfill \end{array}$$

where $\zeta \in \mathbb{D}.$

Hence,

$$\begin{array}{cc}\hfill |{\upsilon }_1\left(\zeta \right)-& \mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ \hfill +& {\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))\right)]|\hfill \\ & =\left|\left(\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))\right){\Delta }_{\lambda +1-\eta }^{-\eta }q(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1))\right|,\hfill \\ \hfill & \le \epsilon {\displaystyle \frac{|{\chi }_{\mathrm{\Theta }}\left(\zeta \right)|}{\Gamma \left(\eta \right)}}\sum _{\ell =\lambda +1-\eta }^{\zeta -\eta }{(\zeta -\ell -1)}^{(\eta -1)},\hfill \\ \hfill & \le \epsilon {\displaystyle \frac{{\chi }_{\mathrm{\Theta }}{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}.\hfill \end{array}$$

This completes the proof. □

Theorem 7.

Assume that conditions $\left(J_1\right),\left(J_2\right),\left(J_3\right)$ and (10) hold. Let ${\upsilon }_1\in \mathcal{B}$ solve (16) and let $\upsilon \in \mathcal{B}$ be the solution of

$$\left\{\begin{array}{c}{\Delta }_{\lambda }^{\eta ,\mu }\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]-w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi (\zeta +\eta -1)\right))=0,0<\eta \le 1,\hfill \\ {\Delta }_{\lambda }^{-(1-\vartheta )}{\left[{\displaystyle \frac{\upsilon \left(\zeta \right)}{\mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)}}\right]}_{\zeta =\lambda +1-\vartheta }={\Delta }_{\lambda }^{-(1-\vartheta )}{\left[{\displaystyle \frac{{\upsilon }_1\left(\zeta \right)}{\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))}}\right]}_{\zeta =\lambda +1-\vartheta }.\hfill \end{array}\right.$$

(20)

Then (6) is Ulam-Hyers stable provided

$$\Gamma (\eta +1){\xi }_1\Lambda {(\mathbb{T}-\lambda -1+\vartheta )}^{(\vartheta -1)}+\Gamma \left(\vartheta \right){(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}[{\xi }_1{\chi }_w+{\chi }_{\mathrm{\Theta }}{\xi }_2]<\Gamma (\eta +1)\Gamma \left(\vartheta \right).$$

Proof. 

Using Lemma (2), we have

$$\begin{array}{cc}\hfill \upsilon \left(\zeta \right)=& {\Delta }_{\lambda }^{-(1-\vartheta )}\left[{\displaystyle \frac{{\upsilon }_1(\lambda +1-\vartheta )}{\mathrm{\Theta }(\lambda +1-\vartheta ,{\upsilon }_1(\lambda +1-\vartheta ),{\upsilon }_1\left(\psi (\lambda +1-\vartheta )\right))}}\right]\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))\hfill \\ & +\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right)){\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right),\zeta \in \mathbb{D}.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill \left|{\upsilon }_1\left(\zeta \right)-\upsilon \left(\zeta \right)\right| =& |{\upsilon }_1\left(\zeta \right)-\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))\hfill \\ & -\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right)){\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)|,\hfill \\ \hfill =& |{\upsilon }_1\left(\zeta \right)-\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))\right)]\hfill \\ \hfill \phantom{\left|{\upsilon }_1\left(\zeta \right)-\upsilon \left(\zeta \right)\right|}& -\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\hfill \\ & +{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon (\phi (\zeta +\eta -1)\left)\right)\right)]+\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))\hfill \\ & \left[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )+{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))\right)\right]|,\hfill \\ \hfill \le & |{\upsilon }_1\left(\zeta \right)-[\Lambda h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )+{\Delta }_{\lambda +1-\eta }^{-\eta }\left(w\right(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),\hfill \\ & {\upsilon }_1\left(\phi (\zeta +\eta -1)\right)\left)\right)]\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))|+\Lambda \left|h_{\vartheta -1}(\zeta ,\lambda +1-\vartheta )\right|\hfill \\ & |\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))|+|\mathrm{\Theta }(\zeta ,{\upsilon }_1\left(\zeta \right),{\upsilon }_1\left(\psi \left(\zeta \right)\right))\hfill \\ & {\Delta }^{-\eta }w(\zeta +\eta -1,{\upsilon }_1(\zeta +\eta -1),{\upsilon }_1\left(\phi (\zeta +\eta -1)\right))-\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))\hfill \\ & {\Delta }^{-\eta }w(\zeta +\eta -1,\upsilon (\zeta +\eta -1),\upsilon \left(\phi (\zeta +\eta -1)\right))|,\hfill \end{array}$$

$$\begin{array}{cc}\hfill ∥{\upsilon }_1-\upsilon ∥ \le & \epsilon {\displaystyle \frac{{\chi }_{\mathrm{\Theta }}{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}+[{\xi }_1\left[\Lambda h_{\vartheta -1}(\mathbb{T},\lambda +1-\vartheta )+{\chi }_w{\displaystyle \frac{{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}\right]\hfill \\ & +{\chi }_{\mathrm{\Theta }}{\xi }_2{\displaystyle \frac{{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)}}]∥{\upsilon }_1-\upsilon ∥,\hfill \\ \hfill \le & \mathbb{V}\epsilon ,\hfill \end{array}$$

where $\mathbb{V}={\displaystyle \frac{{\chi }_{\mathrm{\Theta }}{(\mathbb{T}+\eta -\lambda -1)}^{\left(\eta \right)}}{\Gamma (\eta +1)(1-\mathsf{\Omega })}}$ with $\mathsf{\Omega }$ defined in (11) is the stability constant. This completes the proof. The generalized Ulam–Hyers stability of the HDFGHPE (6) is established by replacing $\sigma \left(\epsilon \right)=\mathbb{V}\epsilon$ with $\sigma \left(0\right)=0.$ □

6. Numerical Examples

This section presents a numerical example to illustrate the results obtained in previous sections.

Example 1.

Let us consider the Hilfer type discrete fractional generalized hybrid pantograph equation of the form

$$\begin{array}{cc}\hfill {\Delta }_{0.3}^{0.6,0.5}& \left[{\displaystyle \frac{10\upsilon \left(\zeta \right)}{3+cos\left(\upsilon \right(\zeta \left)\right)}}\right]={\displaystyle \frac{1}{30}}\left[{\displaystyle \frac{1}{2}}+{\left(\upsilon (\zeta -0.4)\right)}^3\right]\hfill \\ \hfill & {\Delta }^{-0.2}\left[{\displaystyle \frac{10\upsilon \left(0.5\right)}{3+cos\left(\upsilon \right(0.5\left)\right)}}\right]=0.9\hfill \end{array}$$

(21)

where $\zeta \in [0,20]\cap {\mathbb{N}}_{0.7}$. We shall now establish the Ulam- Hyers stability of (21). Comparing (21) and (6), we have $\eta =0.6,\mu =0.5,\vartheta =0.8,\lambda =0.3,\Lambda =0.9,\mathbb{T}=20$, $\mathbb{D}=[0.3,20]\cap {\mathbb{N}}_{0.3}$ and

$$\begin{array}{cc}\hfill \mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)& =0.3+{\displaystyle \frac{1}{10}}cos\left(\upsilon \left(\zeta \right)\right),\hfill \\ \hfill w(\zeta -0.4,\upsilon (\zeta -0.4),\upsilon (\phi (\zeta -0.4)\left)\right)& ={\displaystyle \frac{1}{30}}\left[{\displaystyle \frac{1}{2}}+{\left(\upsilon (\zeta -0.4)\right)}^3\right].\hfill \end{array}$$

Let $\underset{\zeta \in \mathbb{D}}{max}\left|\upsilon \left(\zeta \right)\right|\le {\displaystyle \frac{M}{2}},$ where $M\in {\mathbb{R}}^{+}$. Using the conditions $\left(J_1\right),\left(J_2\right),\left(J_3\right)$ and (10), we yield

$$\begin{array}{cc}\hfill & \left|w(\zeta -0.4,\upsilon (\zeta -0.4),\upsilon \left(\phi (\zeta -0.4)\right))\right|\le \left|{\displaystyle \frac{1}{30}}\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{{\left(M\right)}^3}{8}}\right]\right|,\hfill \\ \hfill & |\mathrm{\Theta }(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \left(\zeta \right)\right))-\mathrm{\Theta }(\zeta ,{\upsilon }^{*}\left(\zeta \right),{\upsilon }^{*}\left(\psi \left(\zeta \right)\right))|\le 0.1|\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,\hfill \\ \hfill & |w(\zeta -0.4,\upsilon (\zeta -0.4),\upsilon \left(\phi (\zeta -0.4)\right))-w(\zeta -0.4-{\upsilon }^{*}(\zeta -0.4),{\upsilon }^{*}\left(\phi (\zeta -0.4)\right))|\hfill \\ & \le \left|{\displaystyle \frac{M^2}{40}}\right||\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,\hfill \\ \hfill & \left|\mathrm{\Theta }\right(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \right(\zeta \left)\right)\left)\right|\le 0.4\hfill \end{array}$$

That is ${\chi }_w={\displaystyle \frac{1}{30}}\left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{{\left(M\right)}^3}{8}}\right],{\chi }_{\mathrm{\Theta }}=0.4,{\xi }_1=0.1,{\xi }_2={\displaystyle \frac{M^2}{40}}$, where $M=1.$ From Theorem (5), we get $\mathsf{\Omega }=0.122794<1.$

Using (13), we have $\mathfrak{S}\ge 0.08044$ with ${\mathrm{\Theta }}_0=0.4.$ Thus, (21) has a unique solution.

Ulam–Hyers stability of HDFGHPE (21) is evident from Theorem (7).

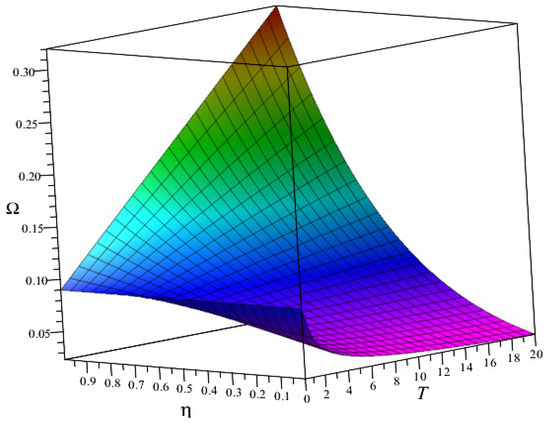
The stability condition (11) thus obtained for HDFGHPE (21) is tabulated for different fractional order $\eta \in (0,1)$ in Table 1 and represented in Figure 1. For an increase in time, the stability condition $\left(\mathsf{\Omega }\right)$ increases gradually for all values of η in $(0,1)$, and the Ω is clearly less than 1 satisfying the condition obtained in Theorem (5). An important observation to be made is when order $\left(\eta \right)$ is small the value of Ω decreases with increasing time. As the order $\left(\eta \right)$ increases, this trend changes with value of Ω increasing for increase in time.

Table 1. Representation of impact of fractional order $\eta$ on stability condition $\mathsf{\Omega }$.

Time	$\mathit{\eta }=0.15$	$\mathit{\eta }=0.30$	$\mathit{\eta }=0.45$	$\mathit{\eta }=0.60$	$\mathit{\eta }=0.75$	$\mathit{\eta }=0.90$
	$\mathsf{\Omega }$
0.3	0.09000	0.09000	0.08999	0.09000	0.09000	0.09000
1.3	0.06383	0.07058	0.07733	0.08408	0.09083	0.09758
2.3	0.05464	0.06397	0.07379	0.08413	0.09497	0.10632
3.3	0.04991	0.06069	0.07258	0.08561	0.09982	0.11526
4.3	0.04694	0.05877	0.07228	0.08761	0.10488	0.12422
5.3	0.04487	0.05753	0.07244	0.08984	0.10998	0.13315
6.3	0.04334	0.05671	0.07285	0.09216	0.11506	0.14202
7.3	0.04214	0.05613	0.07341	0.09452	0.12010	0.15084
8.3	0.04118	0.05574	0.07406	0.09689	0.12508	0.15959
9.3	0.04040	0.05546	0.07477	0.09925	0.12999	0.16829
10.3	0.03974	0.05528	0.07552	0.10158	0.13485	0.17693
11.3	0.03918	0.05516	0.07629	0.10390	0.13964	0.18552
12.3	0.03869	0.05510	0.07707	0.10618	0.14438	0.19406
13.3	0.03827	0.05508	0.07786	0.10843	0.14905	0.20255
14.3	0.03790	0.05509	0.07866	0.11066	0.15368	0.21100
15.3	0.03758	0.05512	0.07946	0.11285	0.15825	0.21940
16.3	0.03729	0.05518	0.08025	0.11502	0.16277	0.22776
17.3	0.03703	0.05525	0.08104	0.11716	0.16724	0.23609
18.3	0.03679	0.05534	0.08183	0.11927	0.17167	0.24437
19.3	0.03658	0.05543	0.08260	0.12135	0.17606	0.25262

Figure 1. Representation of impact of fractional order $\left(\eta \right)$ on the stability condition $\mathsf{\Omega }$.

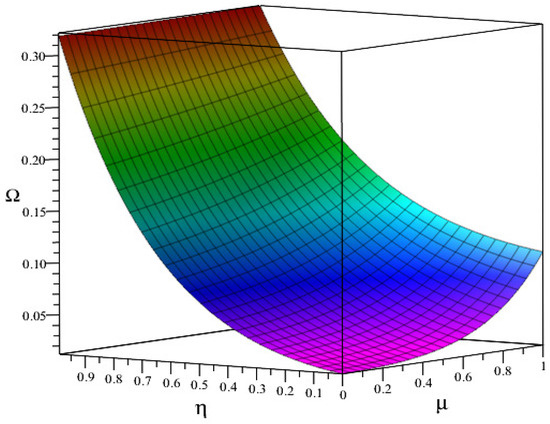
The values in the Table 1 and Table 2 are obtained by substitution of the numerically calculated values that satisfy the conditions $\left(J_1\right),\left(J_2\right),\left(J_3\right)$ and (10) and employing the definition of falling factorial function in the inequality (11). As we already know, the Hilfer operator generalizes both the Riemann– Liouville and Caputo type operator for particular cases of $\mu .$ The analysis of stability condition on varying $\mu \in [0,1]$ is carried out and tabulated in Table 2 with presentation in Figure 2. The change in type μ of the operator between $[0,1]$ results in increase of stability condition $\left(\mathsf{\Omega }\right)$ as in Figure 2.

Table 2. Effect of change in $\mu \in [0,1]$ for different fractional order $\eta \in (0,1)$ on stability condition $\mathsf{\Omega }$.

$\mathit{\mu }$	$\mathit{\eta }=0.15$	$\mathit{\eta }=0.30$	$\mathit{\eta }=0.45$	$\mathit{\eta }=0.60$	$\mathit{\eta }=0.75$	$\mathit{\eta }=0.90$
	$\mathsf{\Omega }$
0	0.02133	0.03646	0.06066	0.09860	0.15705	0.24566
0.2	0.02440	0.04111	0.06701	0.10628	0.16477	0.25050
0.4	0.03100	0.06397	0.07666	0.11651	0.17392	0.25567
0.6	0.04396	0.06341	0.09101	0.12998	0.18472	0.26117
0.8	0.06790	0.08633	0.11191	0.14758	0.19744	0.26704
1.0	0.11018	0.12274	0.14184	0.17037	0.21235	0.27329

Figure 2. Representation of effect of change in $\mu \in [0,1]$ for different fractional order $\eta \in (0,1)$ on stability condition $\mathsf{\Omega }$.

Example 2.

This example establishes the Hyers–Ulam stability of Hilfer type discrete fractional equation of the form

$$\begin{array}{cc}\hfill {\Delta }_{0.4}^{0.5,0.4}& \upsilon \left(\zeta \right)={\displaystyle \frac{1}{10}}\upsilon (\zeta -0.5)+0.01{sin}^2\left(\upsilon (\zeta -0.5)\right)\hfill \\ \hfill & {\Delta }^{-0.3}\left[\upsilon \left(0.7\right)\right]=0.6\hfill \end{array}$$

(22)

where $\zeta \in [0,15]\cap {\mathbb{N}}_{0.9}$. Making an analogy between (22) and (6), we have $\eta =0.5,\mu =0.4,\vartheta =0.7,$ $\lambda =0.4,\Lambda =0.6,\mathbb{T}=15$, $\mathbb{D}=[0.4,15]\cap {\mathbb{N}}_{0.4}$ and

$$\begin{array}{cc}\hfill \mathrm{\Theta }(\zeta ,\upsilon (\zeta ),\upsilon (\psi \left(\zeta \right)\left)\right)& =1,\hfill \\ \hfill w(\zeta -0.5,\upsilon (\zeta -0.5),\upsilon (\phi (\zeta -0.5)\left)\right)& ={\displaystyle \frac{1}{10}}\upsilon (\zeta -0.5)+0.01{sin}^2\left(\upsilon (\zeta -0.5)\right).\hfill \end{array}$$

Let $\underset{\zeta \in \mathbb{D}}{max}\left|\upsilon \left(\zeta \right)\right|\le M,$ where $M\in {\mathbb{R}}^{+}$. Using the conditions $\left(J_1\right),\left(J_2\right),\left(J_3\right)$ and (10), we yield

$$\begin{array}{cc}\hfill & \left|w(\zeta -0.4,\upsilon (\zeta -0.4),\upsilon \left(\phi (\zeta -0.4)\right))\right|\le {\displaystyle \frac{M}{10}}+0.01,\hfill \\ \hfill & |w(\zeta -0.4,\upsilon (\zeta -0.4),\upsilon \left(\phi (\zeta -0.4)\right))-w(\zeta -0.4-{\upsilon }^{*}(\zeta -0.4),{\upsilon }^{*}\left(\phi (\zeta -0.4)\right))|\hfill \\ & \le 0.11|\upsilon \left(\zeta \right)-{\upsilon }^{*}\left(\zeta \right)|,\hfill \\ \hfill & \left|\mathrm{\Theta }\right(\zeta ,\upsilon \left(\zeta \right),\upsilon \left(\psi \right(\zeta \left)\right)\left)\right|\le 1\hfill \end{array}$$

That is ${\chi }_w=0.06,{\chi }_{\mathrm{\Theta }}=1,{\xi }_1=0,{\xi }_2={\displaystyle \frac{M}{10}}+0.01$, where $M=0.5.$ From Theorem (5), we get $\mathsf{\Omega }=0.470225<1.$

Using (13), we have $\mathfrak{S}\ge 0.256486$ with ${\mathrm{\Theta }}_0=1.$ Thus, existence of unique solution for (22) is evident from the numerical calculations. Theorem (7) ensures the stability of Hilfer type discrete fractional problem (22) in the sense of Hyers and Ulam.

7. Conclusions

The article concentrated on obtaining the stability results generalizing Riemann–Liouville and Caputo type fractional derivatives in discrete time with the help of the Hilfer type discrete fractional operator. The application of the generalized discrete fractional operator (Hilfer) to a hybrid pantograph equation was considered in this work. Hybrid fixed point theory was used to develop the existence of a solution, and Banach contraction theorem was used to prove the uniqueness of the solution of the generalized fractional hybrid pantograph equation with discrete time. Stability analysis in the sense of Ulam–Hyers is performed, and the impact of the fractional order $\left(\eta \right)$ and type $\left(\mu \right)$ are carried out as an example, with simulations present supporting the results obtained.