Abstract
In an uncertain situation, data may present in continuous form or discrete form. We have various techniques to deal with continuous data in a realistic situation. However, when data are in discrete form, the existing techniques are inadequate to deal with these situations, and these techniques cannot provide the proper modulation for adequate analysis of the system. In order to provide the proper acceleration to discrete data, we need an appropriate modulation technique that can help us to handle unconditional boundedness on the technique and will operate like the techniques used for continuous data with fractional variables. In this work, we developed an intuitionistic fuzzy fractional knowledge-based expert system using unconditional and qualified fuzzy propositions based on the Z-intuitionistic fuzzy fractional valuation probability density function. In this proposed method, the discrete fractional variables will be converted into intuitionistic fuzzy fractional numbers and then be used in our algorithm. The proposed Z-intuitionistic fuzzy fractional valuation knowledge-based system can easily be applied in the medical field for the diagnosis of diseases in a vague environment due to the ordered-pair characteristics of the Z-intuitionistic fuzzy fractional valuation. In this study, we collected data of dengue patients, which included seven clinical findings: Temperature, sugar, Pulse Rate (PR), age, cough, and Blood Pressure (BP).A numerical example was also carried out to elaborate on the present technique. In addition, a comparative study is discussed in this work. We also provide the managerial implications of the data, with the limitations of the proposed technique presented at the end of this work.
1. Introduction
In real life, information may often be imperfect due to its vague nature. The aspects of imperfect knowledge are uncertain and imprecise. These uncertainties are characterized by the degree of truth in the form of the membership grade. In 1965, L.A. Zadeh [1] introduced the concept of fuzzy set theory. Fuzzy set theory is a useful tool to deal with these types of imprecise factors in the modelling of systems. The fuzzy logic approach has previously been used in the medical field [2,3] in existing studies. Different industrial and medical problems characterized by such uncertainty and imprecision [4,5] can be solved using fuzzy set theory. To solve this type of problem, we have to develop an inference system that will include all the input factors and provide a final output value. The fuzzy inference system used in decision making is essentially based on the experience, intuition, and knowledge of experts. Due to the complexity of real-life problems, sometimes these features cannot address all the uncertainties of the considered problem. The Z-number, introduced by Zadeh [6], is applicable for such types of uncertainties present in a problem. By using the concept of Z-numbers, an estimation of the input and output factors can easily be performed by the concept of fuzzy logic. The Z-number can be represented by an ordered pair (A, B), where A and B are fuzzy sets. The concept of Z-numbers has been used in many real-life problems [7]. Kang et al. [8,9] applied the Z-number in the context of a decision-making problem. Kang et al. [10] also provided a method for converting Z-numbers into the theory of a classical fuzzy number. Xiao [11] also used the concept of the Z-number in multi-criteria decision making. Azadeh et al. [12] provided a mathematical technique based on the analytical hierarchy process with the help of the Z-number extension of fuzzy sets. Many extended techniques of fuzzy logic, such as intuitionistic fuzzy logic [13,14] and mediative fuzzy logic [15], have also been used in engineering and agricultural fields and the medical field [16,17]. Mediative fuzzy logic is also applied in the extension technique [18] for consistent measurement in decision making. The concept of the Z-number is very closely related to the idea of linguistic terms [19]. Yager [20] provided an ordered triple (V, A, B) to represent Z-valuation, which is equal to the statement V is (A, B). The Z-number is used to provide information about variable V. Z-valuation indicates that V takes A with certainty B. Let us consider V is (A, B); here we are assuming V is as random variable. Zadeh [6] suggested that this Z-valuation can also be formed as a restriction on V described as
Prob (V is A) is B
Let P (some probability distribution) be the space of all probability distributions [21] on universal set U. The given information can be handled by using a possibility distribution function. Using Zadeh’s definition of fuzzy probability, we can express the given information as
and
that will give the degree of truth of that satisfies B. In this manner, as a possibility distribution over the space P, we may easily express the information V as (A, B), under the assumption that V is a random variable. In 1986, Atanassov [22] proposed an idea to deal with the current uncertainty present in a problem with the consideration of favorable, as well as unfavorable cases. The intuitionistic fuzzy set defines the membership grade and non-membership grade of an element, regarding its belongings and non-belongings, with a hesitation margin, where the sum of these three values will always be equal to 1. In an intuitionistic environment, we may express the given information as
and
where the first expression gives the degree of truth, and the second expression gives the false values of that will satisfy B. In this work, the application of fuzzy logic in the measurement of disease diagnostic levels is considered. By using unconditional and qualified intuitionistic fuzzy propositions, we developed an intuitionistic fuzzy knowledge-based expert system based on the Z-intuitionistic fuzzy fractional valuation probability density function. We proposed a Z-intuitionistic fuzzy fractional valuation-based inference system that is easily applicable in the medical diagnosis of patients with dengue in an intuitionistic fuzzy environment. Fuzzy set theory and intuitionistic fuzzy logic have many applications [23,24], including in the medical field [25,26]. The calculation of an intuitionistic fuzzy generator [27] is also used and has been applied in medical diagnoses. Dhiman and Sharma [28] provided a truth-value restriction method based on the inference of intuitionistic conditional and qualified fuzzy propositions. Szmidt and Kacprzyk proposed the concept of measuring distances between intuitionistic fuzzy sets [29,30] and provided a similarity measure for intuitionistic fuzzy sets in medical diagnostic [31] reasoning. The intuitionistic fuzzy set has also been applied [32] in the determination of students’ performance. The aim of this proposed work is to generalize the concept of Z-valuation over Z-intuitionistic fuzzy fractional valuation and to apply this concept over an inference system based on unconditional and qualified intuitionistic fuzzy propositions. The proposed method can be applied in the diagnostic process of dengue disease to obtain the various severity levels of patients.
The basic objective of the study contains certain points, as follows:
- (1)
- We will generalize the concept of the Z-number to the Z-intuitionistic number to obtain knowledge about the valuation function.
- (2)
- We will introduce the concept of the Z-intuitionistic fuzzy fractional valuation based on these Z-intuitionistic numbers.
- (3)
- We will develop an intuitionistic fuzzy knowledge-based system based on the Z-intuitionistic fuzzy fractional valuation function by using unconditional and qualified intuitionistic fuzzy propositions in the context of the probability density function.
- (4)
- We will show the applicability of our proposed algorithm in the medical field and discuss the relationship between Z-intuitionistic fuzzy fractional valuation and symptomatic factors of dengue-infected patients.
The present research paper is divided into ten sections. In the Section 2, basic concepts related to our proposed work are defined. In the Section 3, we defined the structure of the proposed inference system. In the Section 4, we developed an algorithm for the proposed Z-intuitionistic fuzzy fractional valuation function. In the Section 5, we defined the mathematical formulation of our proposed work. In the Section 6, we defined the process of collecting dengue-patient data, and in this section, we present the data of fifteen infected patients, as well as their symptomatic structure. The numerical computations of this work are given in the Section 7. In the next section, we present the conclusions of the entire work, we also discussed a comparative study in this section. In Section 9, we give the results and discussions of the proposed work. In the last section, we present the future scope of this work.
2. Basic Concepts
2.1. Fuzzy Logic
The idea of fuzzy logic was first introduced by Lotfi A. Zadeh of the University of California at Berkeley in the 1960s. Fuzzy logic is an approach to computing based on “degrees of truth” rather than the usual “true or false” (1 or 0) Boolean logic. It may help to view fuzzy logic as the way reasoning truly works, and binary or Boolean logic as simply a special case of it.
2.2. Fuzzy Sets
Fuzzy set A is defined based on universal set U, denoted as
where represents the membership value of A given in universal set U.
2.3. Fuzzy Number
Fuzzy set defined on the basis of universal set U is known as a fuzzy number if it satisfies the following three properties:
- a.
- Fuzzy set A should be “normal”, i.e., there exists a point such that .
- b.
- Fuzzy set A should be “convex”, i.e., and
- c.
- Support of A, i.e., {x U: } is bounded.
2.4. Intuitionistic Fuzzy Set
Intuitionistic fuzzy set B is defined on the basis of universal set U, denoted as
where the functions represent the membership and non-membership grades, respectively, and represents the hesitation value of x in B such where
2.5. Intuitionistic Fuzzy Number
Intuitionistic fuzzy set defined on the basis of universal set U, is known as an intuitionistic fuzzy number if it satisfies the following three properties:
- a.
- The intuitionistic fuzzy set must satisfy the normal property, i.e., there exists a point such that .
- b.
- The intuitionistic fuzzy set must satisfy the convexity property, i.e., andand
- c.
- Support of B, i.e., {x U: } is bounded.
2.6. Z-Numbers
If A and B are two fuzzy numbers defined on the basis of universal set U, then the ordered pair (A, B) represents the Z-number. A Z-number can also be viewed as the fuzzy set of probability functions that arise from the malleable restriction of the probability of a fuzzy fact by a fuzzy probability. The representation of the Z-number requires complex calculations and does not reduce down to the original fuzzy fact when the probability is one.
2.7. Z-Intuitionistic Numbers
If A and B are two intuitionistic fuzzy numbers defined on universal set U, then the Z-intuitionistic number can be represented by an ordered pair (A, B). An intuitionistic Z-number can be viewed as the fuzzy set of probability functions that arise from the malleable restriction of the probability of an intuitionistic fuzzy fact by an intuitionistic fuzzy probability.
2.8. Z-Valuations
If A and B are two fuzzy numbers defined on the basis of universal set U, and V is a valuation function, then the ordered triple (V, A, B) will represent the Z-valuation, which deals with the statement “V is (A, B)”.The Z-valuation indicates that V takes A with certainty B. The Z-valuation can also be viewed as a restriction on V, described by previous authors [20] as Prob (V is A) is B.
2.9. Z-Intuitionistic Valuations
If A and B are two intuitionistic fuzzy numbers defined on the basis of universal set U, and V is a valuation function, then the ordered triple (V, A, B) will represent the Z-intuitionistic valuation, which deals with the statement “V is (A, B)”.The Z-intuitionistic valuation indicates that V takes A with certainty B (considering both membership and non-membership values).
2.10. Z-Intuitionistic Fuzzy Fractional Valuations
The Z-intuitionistic fuzzy fractional valuation deals with the statement “V is (A, B)”, and the Z-intuitionistic fuzzy fractional valuation deals with the uncertainty present in the fraction form of the intuitionistic fuzzy probability. We express the given information as
and
where , and represent the numerator and denominator parts of membership values, respectively, and
where , represent the numerator and denominator parts of non-membership values, respectively.
3. Proposed Z-Intuitionistic Fuzzy Fractional Valuation Knowledge-Based System
In this section, we developed an inference system based on the Z-intuitionistic valuation called the “Z-intuitionistic fuzzy fractional valuation knowledge-based system”. The architecture of the proposed system is presented in Figure 1, which consists of eight components.
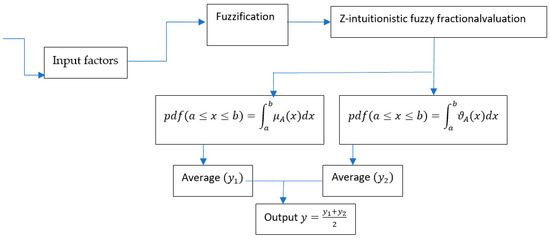
Figure 1.
Proposed inference system using Z-intuitionistic fuzzy fractional valuation.
4. Algorithm of the Proposed Z-Intuitionistic Fuzzy Fractional Valuation-Based Inference System
The proposed algorithm of the system contains seven steps, and the process of each step is given below:
Step 1: Let us consider a set of input factors I = {input-I, input-II,….input N} and an output factor, namely “Out”, which represents the output of the system.
Step 2: Categorize each input and output factor into three linguistic categories, viz low, medium, and high.
Step 3: Fuzzify each input and output factor using triangular- as well as trapezoidal-shaped intuitionistic fuzzy numbers; the selection of a triangular or trapezoidal shape is dependent upon the structure of the data.
Step 4: Now consider a Z-intuitionistic fuzzy fractional valuation for the uncertain variable V to express the knowledge in a probabilistic form, that is “V is input-N is Out”.
Step 5: Now consider intuitionistic fuzzy rules with the help of unconditional and qualified propositions as mentioned above in step 4.
Step 6: To obtain a conventional and numeric value of the intuitionistic fuzzy rules produce probability density function P, as shown in Figure 1.
Step 7: Take the average of all outputs obtained from step 6 (for both membership and non-membership values) to obtain the final crisp output of the proposed system, which shows the specific categories of the output amongst the three linguistic categories.
5. Mathematical Formulation
In this section, we formulate the mathematical model of the symptoms included in our work. Seven symptoms, namely temperature, sugar, pulse rate, age, cough, and blood pressure are categorized into three linguistic categories, in the form of trapezoidal or triangular membership functions, the shape of which is dependent upon the trend of the data:
where on the real line.
where on the real line.
Let us consider probability distribution function P, which shows the space of all probability distributions on universal set U. The possibility distribution function is used to handle the given information. Using Zadeh’s definition of the fuzzy probability, we express the given information as
that provides the degree of truth of , which satisfies
and
that provides the degree of true and false values of , which satisfy B. In this work, the application of intuitionistic fuzzy logic to measure disease diagnostic levels is considered.
For a particular patient with various input factors (symptoms), we must consider an intuitionistic fuzzy rule based on unconditional and qualified intuitionistic fuzzy propositions, in which the antecedent part of input factor ‘I’ is represented by an intuitionistic fuzzy number (which can betrapezoidal or triangular) and the consequent part ‘O’ is represented by the probability distribution function with the help of the Z-intuitionistic fuzzy fractional valuation, given as follows:
is an intuitionistic fuzzy set, is the membership function of , and is the non-membership function of over universal sets , I = 1,2, …n.
A continues this version of the intuitionistic fuzzy rule, while the function with ‘n’ arguments is
6. Data Collection of Dengue Infected Patients
We applied our approach to the data [25], and we collected seven clinical factors: Temperature, sugar, Pulse Rate (PR), age, cough, and Blood Pressure (BP), as shown in Table 1.

Table 1.
Data of dengue-infected patients.
7. Numerical Computation
In this section, we conducted a study based on the data of dengue-infected patients. For the applicability process, we estimated the severity level of dengue-infected patients. In this study, we considered five (out of seven) input factors, which are categorized into three linguistic categories, and their ranges are given in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Furthermore, we also categorized the output factor ‘Out’ into three linguistic categories with the following ranges: Less severe (Out ≤ 25), normal (25 < Out ≤ 40), and severe (40 ≤ Out).
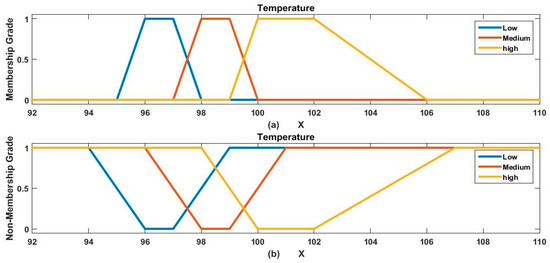
Figure 2.
Three linguistic categories of temperature with their trapezoidal membership (a) and non-membership grades (b).
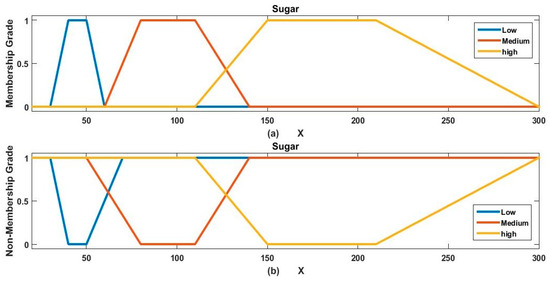
Figure 3.
Three linguistic categories of sugar with their trapezoidal membership (a) and non-membership grades (b).
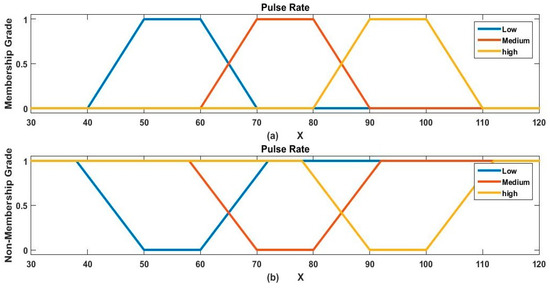
Figure 4.
Three linguistic categories of pulse rate with their trapezoidal membership (a) and non-membership grades (b).
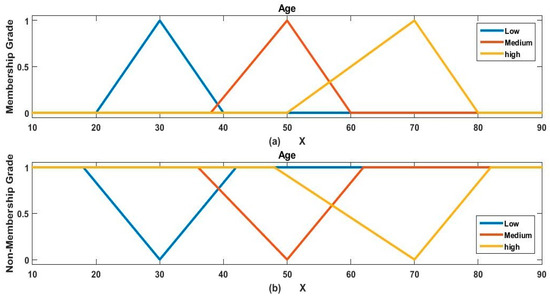
Figure 5.
Three linguistic categories of age with their triangular membership (a) and non-membership grades (b).
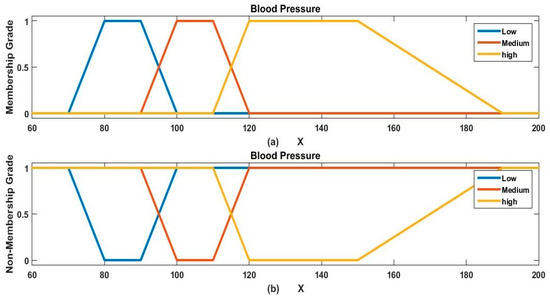
Figure 6.
Three linguistic categories of blood pressure with their trapezoidal membership (a) and non-membership grade (b).
We considered patients with the identities P-XII and P-XIV for the numerical computation as follows:
For patient P-XII, the value of temperature is high
sugar is medium
PR is high
age is low
and BP is high
For patient P-XIV, the value for temperature is medium
sugar is high
PR is medium
age is high
and BP is high
8. Conclusions
Decisions involved in any problem are based upon the available information. The concept of a Z-intuitionistic-number relates to the issue of the reliability of the information in two ways: First, if it considers the membership function of the information, and second, if it considers the non-membership function of the information. We generalized the concept of the Z-number with the computation of Z-intuitionistic fuzzy fractional numbers. The concept of a Z-intuitionistic fuzzy fractional number can be applied in many areas, especially in decision making and risk assessment in the medical field and in many prediction-making problems.
The entire work is illustrated in the following points:
- (1)
- We used the concept of Zadeh’s Z-numbers and generalized the concept of a Z-number to a Z-intuitionistic number to obtain knowledge about a valuation function (uncertain variable) in the context of forming Z-intuitionistic fuzzy fractional valuations (V, A, B).
- (2)
- Z-intuitionistic fuzzy fractional valuation describes the uncertain knowledge in probabilistic form, which indicates the fact that “V is A is equal to B”. We interpreted this as Z-intuitionistic fuzzy fractional valuation demonstrating the knowledge.
- (3)
- We developed an intuitionistic fuzzy knowledge-based system based on the Z-intuitionistic fuzzy fractional valuation function. In this proposed work, we used unconditional and qualified fuzzy propositions in the form of the probability density function.
- (4)
- A comparative study between Z-valuation, Z-intuitionistic valuation, and Z-intuitionistic fuzzy fractional valuation is also discussed in this study (see Table 2).
 Table 2. Comparative study of existing techniques with proposed technique.
Table 2. Comparative study of existing techniques with proposed technique. - (5)
- The utility of the proposed algorithm based on the intuitionistic fuzzy Z-valuation method is established in the medical field. This concept will provide a remarkable landmark in decision making regarding the severity levels of dengue patients. This proposed method shows the relationship between Z-intuitionistic fuzzy fractional valuation and the symptomatic factors of dengue-infected patients.
- (6)
- A numeric computation was carried out to represent the severity level of dengue-infected patients. The numerical computation allowed us to observe that patient P-XII with an output value of 18.0125 belongs to the less-severe category in terms of dengue risk. However, in the case of patient P-XIV, the output value was 45.847, which indicates the patient is affected by dengue disease at a high severity level.
The proposed technique is applicable to various datasets, whether it is provided in an indiscrete or continuous form. The managerial implication of this study is not restricted to the medical field, and it may be applied in engineering, agriculture, economic fields, etc. However, the limitations of this model depend upon the nature, accuracy level, and sample size of the experimental data.
The proposed technique is easily applicable in the diagnostic process of diseases, requiring less computation. Existing intuitionistic fuzzy inference technique-based models may lead to high levels of computation due to the defuzzification and aggregation processes. Throughout this entire work, there was no requirement for any complex computation techniques such as defuzzification in order to obtain the required output of the proposed system.
9. Results and Discussion
In this work, we determined the objective severity levels of dengue-infected patients. In this work, we provide an organized structure, the objective of the research, with conclusive outcomes given in the conclusion section. To make it easy for the reader to understand the whole concept, the mathematical structure, and the methodology, Figure 1 provides a graphical representation of the proposed Z-intuitionistic fuzzy fractional valuation-based inference system with all eight components. During this study, we obtained seven symptoms of the patients, including temperature, sugar, pulse rate, age, cough, and blood pressure, as shown in Table 1, and the various linguistic categories of these input variables are shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 with the help of triangular and trapezoidal intuitionistic fuzzy numbers. The output factors reflect the various categories of severity of dengue patients, with some fixed values in the form of ranges (as discussed earlier in Section 7). The interpretation of the results is important for the proper treatment of infected patients. As a result, physicians and doctors can recommend the exact treatment and dose quantity to an infected patient by determining the exact severity level of dengue disease.
10. Future Aspects of the Work
From a future perspective, we may extend the proposed Z-intuitionistic fuzzy fractional valuation to generalized concepts of fuzzy set theory, such as mediative fuzzy logic or intuitionistic type-II fuzzy logic, to create an inference system that will manage the uncertainty in a more appropriate manner. We may use the inference system based on Sugeno’s approach [33] or Tsukamoto’s approach [34] by taking a certain linear or monotonic function for the consequent part of the knowledge-based fuzzy rules.
Author Contributions
Data collection, Methodology, Inference system methodology and MATLAB software, N.D.; Formal analysis, M.M.G.; Visualization, and Investigation, D.P.S.; Formal technique to analysis, V.; Review and Editing with writing, V.N.M.; Conceptualization, Overall methodology, Supervision and Validation, M.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this work are collected from [24]. https://aip.scitation.org/doi/10.1063/5.0062862, accessed on 23 September 2021.
Acknowledgments
The first author is thankful to the university grants commission (UGC) for financial support. This work is carried out under the grant F.No. 91/2021/2095/Sattar-4-2021-04(17) 2021 dated 11 October 2021 for the Centre of Excellence by Uttar Pradesh Government.
Conflicts of Interest
The authors have no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Sharif, S.; Seno, S.A.; Rowhanimanesh, A. A fuzzy-logic-based fault detection system for medical Internet of Nano Things. Nano Commun. Netw. 2021, 30, 100366. [Google Scholar] [CrossRef]
- Bora, D.J. Contrast Improvement of Medical Images Using Advanced Fuzzy Logic-Based Technique. In Advanced Machine Vision Paradigms for Medical Image Analysis; Academic Press: Cambridge, MA, USA, 2021; pp. 229–257. [Google Scholar]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall of India: New Delhi, India, 2003; ISSN 0-13-101171-5. [Google Scholar]
- Yen, J.; Langari, R.; Zadeh, L.A. Industrial Applications of Fuzzy Logic and Intelligent Systems; IEEE Press Piscataway: Hoboken, NJ, USA, 1995. [Google Scholar]
- Zadeh, L.A. A note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Aliev, R.A.; Huseynov, O.H.; Aliyev, R.R.; Alizadeh, A. Arithmetic on Z-Numbers. The Theory and Application; World Scientific Publishing Co.: Singapore, 2015; ISBN 9789814675291/9814675296. [Google Scholar]
- Aliev, R.A.; Zeinalova, L.M. Decision Making under Z-Information. In Human-Centric Decision-Making Models for Social Sciences; Studies in Computational Intelligence; Guo, P., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 502, pp. 233–252. [Google Scholar]
- Kang, B.; Wei, D.; Li, Y.; Deng, Y. Decision making using z-numbers under uncertain environment. J. Comput. Inf. Syst. 2012, 8, 2807–2814. [Google Scholar]
- Kang, B.; Wei, D.; Li, Y.; Deng, Y. A method of converting z-number to classical fuzzy number. J. Comput. Inf. Syst. 2012, 9, 703–709. [Google Scholar]
- Xiao, Z.Q. Application of Z-numbers in multi-criteria decision making. In Proceedings of the Informative and International Conference on Cybernetics for Computational Social Systems, Qingdao, China, 9–10 October 2014; pp. 91–95. [Google Scholar]
- Azadeh, A.; Saberi, M.; Atashbar, N.Z.; Chang, E.; Pazhoheshfar, P. Z-AHP: A Z-number extension of fuzzy analytical hierarchy process. In Proceedings of the International Conference on Digital Ecosystems and Technologies (DEST), Menlo Park, CA, USA, 24–26 July 2013; pp. 141–147. [Google Scholar]
- Atanassov, K.; Gargov, G. Elements of Intuitionistic fuzzy logic part 1. FuzzySets Syst. 1989, 95, 39–52. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Montiel, O.; Castillo, O.; Melin, P.; Rodríguez, D.A.; Sepúlveda, R. Reducing the cycling problem evolutionary algorithms. In Proceedings of the 2005 International Conference on Artificial Intelligence (ICAI-2005), Las Vegas, NV, USA, 27–30 June 2005; pp. 426–432. [Google Scholar]
- Kumar, S.; Sharma, M.K.; Dhiman, N.; Joshi, D. Meditative fuzzy logic and agricultural production planning: State level investigation of wheat crop in India. Int. J. Agricult. Stat. Sci. 2020, 16, 889–900. [Google Scholar]
- Sharma, M.K.; Dhiman, N.; Mishra, V.N. Mediative fuzzy logic mathematical model: A contradictory management prediction in COVID-19 pandemic. Appl. Soft Comput. 2021, 105, 107285. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.K.; Dhiman, N.; Mishra, L.N.; Mishra, V.N.; Sahani, S.K. Mediative Fuzzy Extension Technique and Its Consistent Measurement in the Decision Making of Medical Application. Math. Probl. Eng. 2021, 2021, 9. [Google Scholar] [CrossRef]
- Yager, R.R. On a View of Zadeh’s Z-Numbers. In Advances in Computational Intelligence. IPMU 2012. Communications in Computer and Information Science; Greco, S., Bouchon-Meunier, B., Coletti, G., Fedrizzi, M., Matarazzo, B., Yager, R.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 299, pp. 90–101. [Google Scholar]
- Yager, R.R. On Z-Valuations using Zadeh’s z-number. Int. J. Intell. Syst. 2012, 27, 259–278. [Google Scholar] [CrossRef]
- Zadeh, L.A. Probability measures of fuzzy events. J. Math. Anal. Appl. 1968, 10, 421–427. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. New operations defined over Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Chaira, T. Fuzzy Set and Its Extension: The Intuitionistic Fuzzy Set; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; ISBN 978-1-119-54422-7. [Google Scholar]
- Zimmermann, L.J. Fuzzy Set Theory-and Its Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 978-94-015-8702-0. [Google Scholar]
- Sharma, M.K.; Dhiman, N.; Verma, S.; Mishra, V.N. Mediative neuro fuzzy inference and mediative fuzzy expert system for the identification of severity diagnosis of the dengue patients. AIP Conf. Proc. 2021, 2364, 020029. [Google Scholar]
- Dhiman, N.; Sharma, M.K. Fuzzy Logic Inference System for Identification and Prevention of Coronavirus (COVID-19). Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2020, 9, 1575–1580. [Google Scholar]
- Dhiman, N.; Sharma, M.K. Calculus of new intuitionistic fuzzy generator: In generated intuitionistic fuzzy sets and its applications in medical diagnosis. Int. J. Adv. Appl. Sci. 2020, 7, 125–130. [Google Scholar] [CrossRef]
- Dhiman, N.; Sharma, M.K. Diabetes Diagnostic Model Based on Truth-value Restrictions Method Using Inference of Intuitionistic Conditional and Qualified Fuzzy Propositions. Int. J. Eng. Adv. Technol. (IJEAT) 2019, 9, 5015–5021. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. On measuring distances between intuitionistic fuzzy sets. Notes Intuit. Fuzzy Sets 1997, 3, 1–3. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Medical diagnostic reasoning using a similarity measure for intuitionistic fuzzy sets. In Proceedings of the 8th International Conference on Intuitionistic Fuzzy Sets, Varna, Bulgaria, 20–21 June 2004; Volume 10, pp. 61–69. [Google Scholar]
- Vasanti, G.; Viswanadham, T. Intuitionistic fuzzy sets and its application in student performance determination of a course via normalized Euclidean distance method. Int. J. Multidiscip. Sci. Emerg. Res. 2015, 4, 1053–1055. [Google Scholar]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K. Takagi–Sugeno fuzzy inference system for modeling stage–discharge relationship. J. Hydrol. 2006, 331, 146–160. [Google Scholar] [CrossRef]
- Wahyuni, I.; Mahmudy, W.F.; Iriany, A. Rainfall prediction in Tengger region Indonesia using Tsukamoto fuzzy inference system. In Proceedings of the 2016 1st International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 23–24 August 2016; pp. 130–135. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).