Dynamics of Different Nonlinearities to the Perturbed Nonlinear Schrödinger Equation via Solitary Wave Solutions with Numerical Simulation

Abstract

This paper investigates the solitary wave solutions for the perturbed nonlinear Schrödinger equation with six different nonlinearities with the essence of the generalized classical derivative, which is known as the beta derivative. The aforementioned nonlinearities are known as the Kerr law, power, dual power law, triple power law, quadratic–cubic law and anti-cubic law. The dark, bright, singular and combinations of these solutions are retrieved using an efficient, simple integration scheme. These solutions suggest that this method is more simple, straightforward and reliable compared to existing methods in the literature. The novelty of this paper is that the perturbed nonlinear Schrödinger equation is investigated in different nonlinear media using a novel derivative operator. Furthermore, the numerical simulation for certain solutions is also presented.

1. Introduction

Finding solitary wave solutions is the most interesting work in soliton theory [1,2]. Many physical phenomena are represented as prototypes in the form of nonlinear partial differential equations (PDEs), particularly in nonlinear Schrödinger equations (NSEs). The NS equation is a generic model that governs the wave evolution in a broad range of physical circumstances including water waves, blood flow in blood vessels, nonlinear optics, magnetic films and plasma physics [3,4,5,6]. These models indicate the parameters that affect the phenomenon, which are not seen directly by observing the phenomenon. Various models have been formulated in the field of science and engineering representing a different phenomenon. For example, most naturally occurring phenomena have been modeled in the structure of NLSEs [7,8,9,10,11]. The NLSE affirms diverse solutions; for instance, dark and bright solitons, localized waves and periodic traveling waves, which have attracted a great deal of interest due to their applications in different physical systems. For the determination of solutions to these models, different techniques have been constructed. For example, the semi-inverse variational method [12] has been employed to determine the two types of solitons for the Perturbed Gerdjikov–Ivanov equation (PGIE). The hyperbolic rational function solutions of the Boussinesq fractional type models have been explored using an exponential rational function scheme [13].

In addition to the above-mentioned models, there is another efficient model, named the perturbed nonlinear Schrödinger equation. A variety of solutions for this model has been determined by using the different schemes [14,15,16,17,18]. A great deal of attention has been devoted to the study of exact solutions of NPDEs for more than two decades. Many efficient approaches have been reported to extract wave solutions [19,20,21,22,23,24,25,26]. There are many ways to derive a series of solutions for $(2+1)$-dimensional FDEs; for example, the $(G^{\prime }/G^2)$ expansion method [27] and the modified extended tanh expansion method [28,29] are efficient approaches to investigate the different types of wave solutions. By using the modified extended tanh expansion method, dark and singular wave solutions of the famous Biswas and Arshed model with full nonlinearity were obtained in [30]. A variety of wave solutions to the $(2+1)$-dimensional integrable non-linear Schrödinger equation is presented in [31].

The main aim of this paper is to determine the solitary wave solutions of the perturbed nonlinear Schrödinger equation with a beta time-fractional derivative by applying the modified extended tanh expansion method. We study the aforementioned equation for different nonlinearities including the Kerr, power, quadratic-cubic, anti-cubic, dual power and triple power laws [32,33,34,35,36]. Moreover, we recall the definition of the $\beta$-time derivative and its properties [37,38,39].

Definition 1.

Suppose $g\left(\tau \right)$ is a function that is defined for all non-negative τ. Then, the $\beta$-time derivative of the function g of order β is given as

$$D^{\beta }\left(g\left(\tau \right)\right)=\frac{d^{\beta }g\left(\tau \right)}{d{\tau }^{\beta }}=\underset{ϵ\to 0}{\lim }\frac{g(\tau +ϵ{(\tau +\frac{1}{\mathsf{\Gamma }(\beta )})}^{1-\beta })-g\left(\tau \right)}{ϵ},0<\beta \le 1.$$

Theorem 1.

Suppose $g\left(\tau \right)$ and $h\left(\tau \right)$ are the $\beta$-time differentiable functions for all $\tau >0$ and $\beta \in (0,1]$. Then,

$$i.D^{\beta }(ag\left(\tau \right)+bh\left(\tau \right))=a{D}^{\beta }\left(g\left(\tau \right)\right)+b{D}^{\beta }\left(h\left(\tau \right)\right),\forall a,b\in R.$$

$$ii.D^{\beta }\left(g\left(\tau \right)h\left(\tau \right)\right)=h\left(\tau \right)D^{\beta }\left(g\left(\tau \right)\right)+g\left(\tau \right)D^{\beta }\left(f\left(\tau \right)\right).$$

$$iii.D^{\beta }(\frac{g\left(\tau \right)}{h\left(\tau \right)})=\frac{f\left(\tau \right)D^{\beta }\left(g\left(\tau \right)\right)-g\left(\tau \right)D^{\beta }\left(h\left(\tau \right)\right)}{{\left(h\left(\tau \right)\right)}^2}.$$

$$iv.D^{\beta }\left(g\left(\tau \right)\right)={(\tau +\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{1-\beta }\frac{dg\left(\tau \right)}{d\tau }.$$

2. Model and Method Description

Consider the following dimensionless form of the perturbed nonlinear Schrödinger equation, given as [40]

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+{\tau G\left(\right|u|}^2)u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2p}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2p})}{\partial x^{\beta }}.$$

(1)

where $u=u(x,t)$ shows the traveling wave profile, depending on the space of the independent variables x and time t. In Equation (1), the first term indicates the linear evaluation of the phenomena, the coefficient of $\sigma$ represents the spatio-temporal dispersion (STD) and the coefficient of $\rho$ shows the group velocity dispersion (GVD). The perturbation terms appear on the right-hand side of Equation (1). The coefficient of $\kappa$ represents the inter-model dispersion, the coefficient of $\delta$ shows the self-steepening perturbation term and the coefficient $\varrho$ indicates the nonlinear dispersion, while p is the full nonlinearity parameter. The coefficient $\tau$ represents the non-Kerr Law nonlinearity term, modeled by the function G.

2.1. The Modified Extended tanh Expansion Method

Let us assume the non-linear PDE of the form:

$$Y(v,v^2{v}_{\gamma },v_{\theta },v_{\theta \theta },v_{\gamma \gamma },v_{\gamma \theta },...)=0,$$

(2)

here $v=v(\gamma ,\theta )$. Let us examine the following transformations:

$$v=V\left(\eta \right),\eta =\gamma -\nu \theta$$

(3)

with $\nu$ is the wave speed. Substituting the Equation (3) in Equation (2) yields the following nonlinear ODE:

$$Z(V\left(\eta \right),V^2\left(\eta \right)V^{\prime }\left(\eta \right),V^{″}\left(\eta \right),...)=0$$

(4)

Moreover, consider the trial solution of Equation (4) in the form:

$$V\left(\eta \right)={\alpha }_0+\sum _{n=1}^m{\alpha }_n{\varphi }^n\left(\eta \right)+\sum _{n=1}^m{\beta }_n{\varphi }^{-n}\left(\eta \right)$$

(5)

In Equation (5), ${\alpha }_0,{\alpha }_n,{\beta }_n,(n=1,2,3,...,m)$ are unknowns and both ${\alpha }_n$ and ${\beta }_n$ are not vanish simultaneously. The homogenous balance method between the nonlinear term and highest derivative term in Equation (4) produces the value of m. The function $\varphi \left(\zeta \right)$ satisfies the following Riccati differential equation

$${\varphi }^{\prime }\left(\zeta \right)=\mathsf{\Omega }+{\varphi }^2\left(\zeta \right)$$

(6)

having the solutions given in [41] depending on the unknown parameter $\mathsf{\Omega }$.

2.2. Mathematical Analysis of the Model

We start with the following wave transformations:

$$u(x,t)=U\left(\eta \right)\times \exp \left(\iota \psi \right(x,t\left)\right),$$

(7)

$$\eta =\frac{1}{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }-\frac{\lambda }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta },$$

(8)

$$\psi (x,t)=-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta .$$

(9)

Here U demonstrates the amplitude portion of the wave solution, $\lambda$ reveals the velocity of the wave solution. The frequency of the wave solution is $\omega$ and $\theta$ exhibits the wave number of the wave solution. Furthermore, the phase constant of the wave solution is given by $\vartheta$ and $\iota =\sqrt{-1}$.

By inserting Equation (7) in Equation (1), we ensure the real and imaginary parts as follows:

Real part:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U-\delta \omega U^{2p+1}+\tau G\left(U^2\right)U=0$$

(10)

Imaginary part:

$$(\lambda (\sigma \omega -1)+\sigma \theta -2\rho \omega -\kappa )+((2p+1)\delta +2p\varrho )U^{2p}=0.$$

(11)

From Equation (11), we grab the speed of the wave solution by taking the coefficient of $U^j$, $j=0,2p$ equal to zero.

$$\lambda =\frac{\sigma \theta -2\rho \omega -\kappa }{1-\sigma \omega }$$

(12)

along with the constraint conditions for the existence of wave solutions.

$$(2p+1)\delta +2p\varrho =0.$$

(13)

We now take up the six forms of nonlinearities in the following subsections.

3. Application of the Method with Different Nonlinear Medias

3.1. Kerr Law

For this law, $G\left(u\right)=u$. Equation (1) for PNLSE with Kerr Law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau {\left|u\right|}^{2}u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2p}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2p})}{\partial x^{\beta }}.$$

(14)

For the Equation (1) to be integrable, put $p=1$ in the Kerr Law nonlinear medium. Equation (10) changes into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U+(\tau -\delta \omega )U^3=0$$

(15)

By using the homogeneous balance technique into the Equation (15), we get $m=1$. For $m=1$, Equation (5) reduces into:

$$U\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}.$$

(16)

Here ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ are unknown parameters. By putting the Equations (16) and (6) into Equation (15) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ and other parameters. Now with the use of symbolic software, we get the following solution sets:

Set 1:

$$\left\{{\alpha }_0=0,{\alpha }_1=\mp \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }},{\beta }_1=0,\theta =\frac{\kappa \omega +2\lambda \sigma \mathsf{\Omega }+\rho \left({\omega }^2-2\mathsf{\Omega }\right)}{\sigma \omega -1}\right\}$$

(17)

We now using the Equations (17) and (16) in Equation (7) and secure the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\{\pm \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(18)

or

$$u_2(x,t)=\{\pm \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(19)

If $\mathsf{\Omega }=0$, then

$$u_3(x,t)=\{\pm \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\frac{1}{\eta }\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(20)

If $\mathsf{\Omega }>0$, then

$$u_4(x,t)=\{\mp \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(21)

or

$$u_5(x,t)=\{\pm \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(22)

Set 2:

$$\left\{{\alpha }_0=0,{\alpha }_1=\mp \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }},{\beta }_1=\pm \frac{\sqrt{2}\sqrt{{\mathsf{\Omega }}^2(\rho -\lambda \sigma )}}{\sqrt{\delta \omega -\tau }},\theta =\frac{\kappa \omega -6\mathsf{\Omega }(\rho -\lambda \sigma )+2\lambda \sigma \mathsf{\Omega }+\rho \left({\omega }^2-2\mathsf{\Omega }\right)}{\sigma \omega -1}\right\}$$

(23)

We now using the Equations (23) and (26) in Equation (7) and grab the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\{\pm \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)+\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(24)

If $\mathsf{\Omega }>0$, then

$$u_2(x,t)=\{\frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\mp \tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\pm \cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(25)

Set 3:

$$\left\{{\alpha }_0=0,{\alpha }_1=0,{\beta }_1=\mp \frac{\sqrt{2}\sqrt{{\mathsf{\Omega }}^2(\rho -\lambda \sigma )}}{\sqrt{\delta \omega -\tau }},\theta =\frac{\kappa \omega +2\lambda \sigma \mathsf{\Omega }+\rho \left({\omega }^2-2\mathsf{\Omega }\right)}{\sigma \omega -1}\right\}$$

(26)

We now using the Equations (23) and (26) in Equation (7) and obtain the following cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\{\mp \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(27)

or

$$u_2(x,t)=\{\mp \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(28)

If $\mathsf{\Omega }>0$, then

$$u_3(x,t)=\{\mp \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(29)

or

$$u_4(x,t)=\{\pm \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(30)

Set 4:

$$\left\{{\alpha }_0=0,{\alpha }_1=\mp \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }},{\beta }_1=\mp \frac{\sqrt{2}\sqrt{{\mathsf{\Omega }}^2(\rho -\lambda \sigma )}}{\sqrt{\delta \omega -\tau }},\theta =\frac{\kappa \omega +6\mathsf{\Omega }(\rho -\lambda \sigma )+2\lambda \sigma \mathsf{\Omega }+\rho \left({\omega }^2-2\mathsf{\Omega }\right)}{\sigma \omega -1}\right\}$$

(31)

We now using the Equations (31) and (26) in Equation (7) and get the following cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\{\pm \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)-\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(32)

or

$$u_2(x,t)=\{\mp \frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)-\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(33)

If $\mathsf{\Omega }>0$, then

$$u_3(x,t)=\{\mp \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)+\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(34)

or

$$u_4(x,t)=\{\pm \frac{\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -\tau }}\left(\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)+\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(35)

Here the $2D$ and $3D$ graphs, by taking $\kappa =\sigma =\delta =1$, $\omega =\mathsf{\Omega }=-1$, $\tau =-2$ are displayed in Figure 1 and Figure 2 for selected solutions to visualized their dynamics.

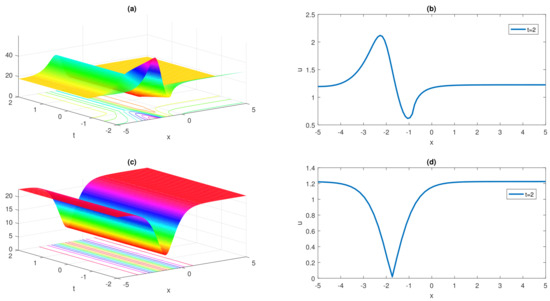
Figure 1. $2D$ and $3D$ wave simulations of dark soliton type solution (18) are presented in (a–d) for fractional parameter $\beta =0.75,1.0$.

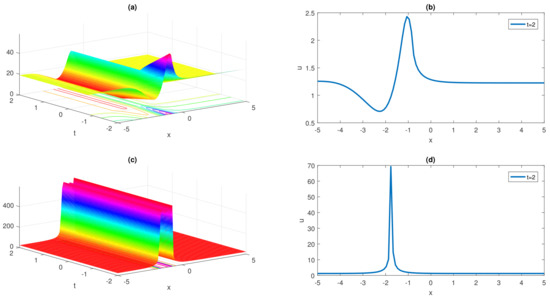
Figure 2. $2D$ and $3D$ wave simulations of bright soliton type solution (19) are presented in (a–d) for fractional parameter $\beta =0.75,1.0$.

3.2. Power Law

For this law, $G\left(u\right)=u^n$, where $0<n<2$, shows the power law nonlinearity factor. If $n=1$, then power law reduces to Kerr law. Equation (1) for PNLSE with Power Law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau {\left|u\right|}^{2n}u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2n}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2n})}{\partial x^{\beta }}.$$

(36)

For the Equation (1) to be integrable, put $p=n$ in the Power Law nonlinear medium. Equation (10) changes into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U+(\tau -\delta \omega )U^{2n+1}=0$$

(37)

To retrieve the solutions, we use the following transformation on the above equation.

$$U\left(\eta \right)=V^{\frac{1}{2n}}\left(\eta \right)$$

(38)

we get the following equation:

$$(1-2n)(\rho -\sigma \lambda ){\left(V^{\prime }\right)}^2+2n(\rho -\sigma \lambda )V{V}^{″}-4n^2(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)V^2+4n^2(\tau -\delta \omega )V^3=0.$$

(39)

By using the homogeneous balance technique into the Equation (39), we get $m=2$. For $m=2$, Equation (5) reduces into:

$$V\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}+{\alpha }_2{\varphi }^2\left(\eta \right)+\frac{{\beta }_2}{{\varphi }^2\left(\eta \right)}$$

(40)

Here ${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$ and ${\beta }_2$ are unknown parameters. By putting the Equations (40) and (6) into Equation (15) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, ${\beta }_2$ and other parameters. We now, with the use of symbolic software, grab the following solution sets:

Set 1:

$$\left\{{\alpha }_0=-\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},{\alpha }_1=0,{\alpha }_2=0,{\beta }_1=0,{\beta }_2=-\frac{(n+1){\mathsf{\Omega }}^2(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},\theta =\frac{\mathsf{\Omega }(\rho -\lambda \sigma )+n^2\omega (\kappa +\rho \omega )}{n^2(\sigma \omega -1)}\right\}$$

(41)

We now using the Equations (41) and (40) in Equation (7) and secure the following cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)={\{\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\mathrm{csch}}^2\left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(42)

or

$$u_2(x,t)={\{-\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\mathrm{sech}}^2\left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(43)

If $\mathsf{\Omega }>0$, then

$$u_3(x,t)={\{-\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\csc }^2\left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(44)

or

$$u_4(x,t)={\{-\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\sec }^2\left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(45)

Set 2:

$$\left\{{\alpha }_0=-\frac{(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},{\alpha }_1=0,{\alpha }_2=-\frac{(n+1)(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},{\beta }_1=0,{\beta }_2=0,\theta =\frac{\mathsf{\Omega }(\rho -\lambda \sigma )+n^2\omega (\kappa +\rho \omega )}{n^2(\sigma \omega -1)}\right\}$$

(46)

We now using the Equations (46) and (40) in Equation (7) and get the following cases.

If $\mathsf{\Omega }=0$, then

$$u_1(x,t)={\{-\frac{(n+1)\left({\eta }^2\mathsf{\Omega }+1\right)(\rho -\lambda \sigma )}{{\eta }^2{n}^2(\tau -\delta \omega )}\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(47)

Set 3:

$$\begin{array}{c}\{{\alpha }_0=-\frac{2(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},{\alpha }_1=0,{\alpha }_2=-\frac{(n+1)(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},{\beta }_1=0,{\beta }_2=-\frac{(n+1){\mathsf{\Omega }}^2(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )},\hfill \\ \hfill \theta =\frac{4\mathsf{\Omega }(\rho -\lambda \sigma )+n^2\omega (\kappa +\rho \omega )}{n^2(\sigma \omega -1)}\}\end{array}$$

(48)

We now using the Equations (48) and (40) in Equation (7) and secure the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)={\{\frac{4(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\mathrm{csch}}^2\left(2\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(49)

if $\mathsf{\Omega }=0$, then

$$u_2(x,t)={\{-\frac{(n+1){\left({\eta }^2\mathsf{\Omega }+1\right)}^2(\rho -\lambda \sigma )}{{\eta }^2{n}^2(\tau -\delta \omega )}\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(50)

if $\mathsf{\Omega }>0$, then

$$u_3(x,t)={\{-\frac{4(n+1)\mathsf{\Omega }(\rho -\lambda \sigma )}{n^2(\tau -\delta \omega )}{\csc }^2\left(2\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(51)

Here the $2D$ and $3D$ graphs, by taking $\kappa =1=\sigma =\delta$, $\omega =\mathsf{\Omega }=-1$, $\rho =0.5$ and $\tau =-2$ are displayed in Figure 3 and Figure 4 for selected solutions to visualized their dynamics.

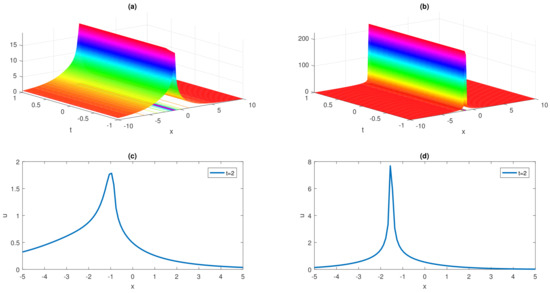
Figure 3. $2D$ and $3D$ wave simulations of singular soliton type solution (42) are presented in (a–d) for fractional parameter $\beta =0.75,1.0$ and $n=1.5$.

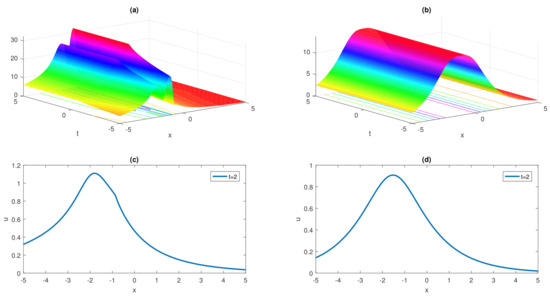
Figure 4. $2D$ and $3D$ wave simulations of bright soliton type solution (43) are presented in (a–d) for fractional parameter $\beta =0.75,1.0$ and $n=1.5$.

3.3. Quadratic-Cubic Law

For this law $G\left(u\right)=c_1\sqrt{u}+c_{2}u$, where $c_1$ and $c_2$ are constants. Equation (1) for PNLSE with Quadratic-cubic Law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau (c_1\left|u\right|+c_2{\left|u\right|}^2)u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2p}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2p})}{\partial x^{\beta }}.$$

(52)

Equation (10) changes into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U-\omega \delta U^{2p+1}+c_1{U}^2+c_2{U}^3=0$$

(53)

By using the homogeneous balance technique into the Equation (53), we get $m=1$. For $m=1$, Equation (5) reduces into:

$$U\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}.$$

(54)

Here ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ are unknown parameters. By using the Equations (16) and (6) into Equation (15) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ and other parameters. We now, with the use of symbolic software, we gain the following solution sets:

Set 1:

$$\begin{array}{c}\{{\alpha }_0=\frac{c_1}{3(\delta \omega -c_2)},{\alpha }_1=0,{\beta }_1=\mp \frac{c_1^2}{9\sqrt{2}\sqrt{(\delta \omega -c_2){}^3(\rho -\lambda \sigma )}},\theta =\frac{9\omega (\delta \omega -c_2)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)(\delta \omega -c_2)},\hfill \\ \hfill \mathsf{\Omega }=-\frac{c_1^2}{18(\delta \omega -c_2)(\rho -\lambda \sigma )}\}\end{array}$$

(55)

We now using the Equations (55) and (54) in Equation (7) and grab the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\frac{c_1}{3\left(\delta \omega -c_2\right)}\left(1\pm \frac{c_1\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{3\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}}\right)\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(56)

or

$$u_2(x,t)=\frac{c_1}{3\left(\delta \omega -c_2\right)}\left(1\pm \frac{c_1\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{3\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}}\right)\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(57)

If $\mathsf{\Omega }>0$, then

$$u_3(x,t)=\frac{c_1}{3\left(\delta \omega -c_2\right)}\left(1\mp \frac{c_1\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{3\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}}\right)\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(58)

or

$$u_4(x,t)=\frac{c_1}{3\left(\delta \omega -c_2\right)}\left(1\pm \frac{c_1\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{3\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}}\right)\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(59)

Set 2:

$$\left\{{\alpha }_0=\frac{c_1}{3(\delta \omega -c_2)},{\alpha }_1=\mp \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}},{\beta }_1=0,\theta =\frac{9\omega (\delta \omega -c_2)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)(\delta \omega -c_2)},\mathsf{\Omega }=-\frac{c_1^2}{18(\delta \omega -c_2)(\rho -\lambda \sigma )}\right\}$$

(60)

We now using the Equations (60) and (54) in Equation (7) and set to the below cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)=\{\frac{c_1}{3\delta \omega -3c_2}\pm \frac{\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(61)

or

$$u_2(x,t)=\{\frac{c_1}{3\delta \omega -3c_2}\pm \frac{\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(62)

If $\mathsf{\Omega }=0$, then

$$u_3(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}\pm \frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\eta \sqrt{\delta \omega -c_2}}\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(63)

If $\mathsf{\Omega }>0$, then

$$u_4(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}\mp \frac{\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(64)

or

$$u_5(x,t)=\{\frac{c_1}{3\delta \omega -3c_2}\pm \frac{\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(65)

Set 3:

$$\begin{array}{c}\{{\alpha }_0=\frac{c_1}{3\left(\delta \omega -c_2\right)},{\alpha }_1=-\frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}},{\beta }_1=-\frac{c_1^2}{18\sqrt{2}\left(\delta \omega -c_2\right){}^{3/2}\sqrt{\rho -\lambda \sigma }},\theta =\frac{9\omega \left(\delta \omega -c_2\right)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)\left(\delta \omega -c_2\right)},\hfill \\ \hfill \mathsf{\Omega }=\frac{c_1^2}{36\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}\}\end{array}$$

(66)

We now using the Equations (66) and (54) in Equation (7) and secure the consequent cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(67)

or

$$\begin{array}{c}{u}_2(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta ))\end{array}$$

(68)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(69)

or

$$\begin{array}{c}{u}_4(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(70)

Set 4:

$$\begin{array}{c}\{{\alpha }_0=\frac{c_1}{3\left(\delta \omega -c_2\right)},{\alpha }_1=-\frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}},{\beta }_1=-\frac{c_1^2}{36\sqrt{2}\left(\delta \omega -c_2\right){}^{3/2}\sqrt{\rho -\lambda \sigma }},\theta =\frac{9\omega \left(\delta \omega -c_2\right)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)\left(\delta \omega -c_2\right)},\hfill \\ \hfill \mathsf{\Omega }=-\frac{c_1^2}{72\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}\}\end{array}$$

(71)

We now using the Equations (71) and (54) in Equation (7) and set to the below cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(72)

or

$$\begin{array}{c}{u}_2(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(73)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(74)

or

$$\begin{array}{c}{u}_4(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(75)

Set 5:

$$\begin{array}{c}\{{\alpha }_0=\frac{c_1}{3\left(\delta \omega -c_2\right)},{\alpha }_1=\frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}},{\beta }_1=\frac{c_1^2}{36\sqrt{2}\left(\delta \omega -c_2\right){}^{3/2}\sqrt{\rho -\lambda \sigma }},\theta =\frac{9\omega \left(\delta \omega -c_2\right)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)\left(\delta \omega -c_2\right)},\hfill \\ \hfill \mathsf{\Omega }=-\frac{c_1^2}{72\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}\}\end{array}$$

(76)

We now using the Equations (76) and (54) in Equation (7) and grab the below cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(77)

or

$$\begin{array}{c}{u}_2(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{-\mathsf{\Omega }}\left(\delta \omega -c_2\right)\sqrt{\delta \omega -c_2}\sqrt{\rho -\lambda \sigma }}-\frac{\sqrt{2}\sqrt{-\mathsf{\Omega }}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta )).\end{array}$$

(78)

If $\mathsf{\Omega }=0$, then

$$\begin{array}{c}{u}_3(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\eta }{36\sqrt{2}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\eta \sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta )).\end{array}$$

(79)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_4(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{\mathsf{\Omega }}\left(\delta \omega -c_2\right)\sqrt{\delta \omega -c_2}\sqrt{\rho -\lambda \sigma }}+\frac{\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(80)

or

$$\begin{array}{c}{u}_5(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{36\sqrt{2}\sqrt{\mathsf{\Omega }}\left(\delta \omega -c_2\right)\sqrt{\delta \omega -c_2}\sqrt{\rho -\lambda \sigma }}-\frac{\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(81)

Set 6:

$$\begin{array}{c}\{{\alpha }_0=\frac{c_1}{3\delta \omega -3c_2},{\alpha }_1=\frac{\sqrt{2}\sqrt{\rho -\lambda \sigma }}{\sqrt{\delta \omega -c_2}},{\beta }_1=\frac{c_1^2}{18\sqrt{2}\left(\delta \omega -c_2\right){}^{3/2}\sqrt{\rho -\lambda \sigma }},\theta =\frac{9\omega \left(\delta \omega -c_2\right)(\kappa +\rho \omega )-2c_1^2}{9(\sigma \omega -1)\left(\delta \omega -c_2\right)},\hfill \\ \hfill \mathsf{\Omega }=\frac{c_1^2}{36\left(\delta \omega -c_2\right)(\rho -\lambda \sigma )}\}\end{array}$$

(82)

We now using the Equations (82) and (54) in Equation (7) and set the following results.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(83)

or

$$\begin{array}{c}{u}_2(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(84)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}+\frac{c_1^2\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}+\frac{\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(85)

or

$$\begin{array}{c}{u}_4(x,t)=\{\frac{c_1}{3\left(\delta \omega -c_2\right)}-\frac{c_1^2\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{18\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\delta \omega -c_2}\left(\delta \omega -c_2\right)\sqrt{\rho -\lambda \sigma }}-\frac{\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(\sqrt{2}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{\sqrt{\delta \omega -c_2}}\}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(86)

Here the $2D$ and $3D$ graphs, by taking $\kappa =1$, $\delta =2=\rho =\sigma$ and $\omega =-0.5$ are displayed in Figure 5 and Figure 6 for selected solutions to visualized their dynamics.

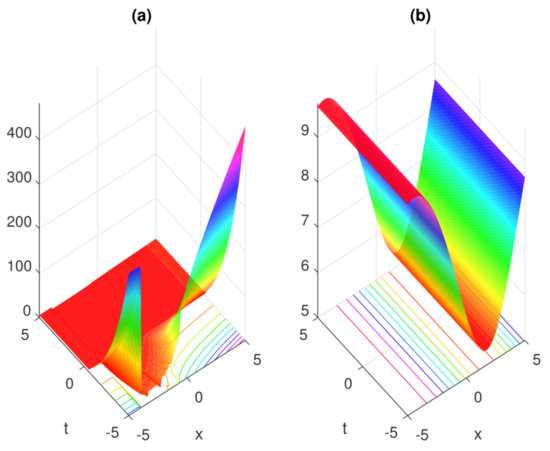
Figure 5. $2D$ and $3D$ wave simulations of singular soliton solution (56) are presented in (a,b), for fractional parameter $\beta =0.75,1.0$ and $c_1=0.5=c_2$.

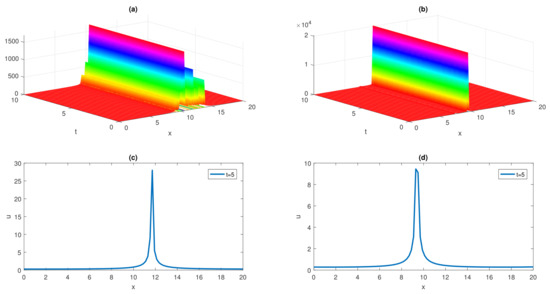
Figure 6. $2D$ and $3D$ wave simulations of dark soliton solution (57) are presented in (a–d) for fractional parameter $\beta =0.75,1.0$ and $c_1=1$, $c_2=0.2$.

3.4. Anti-Cubic Law

For this law $G\left(u\right)=\frac{c_1}{u^2}+c_{2}u+c_3{u}^2$, where $c_1$, $c_2$ and $c_3$ are constants. Equation (1) for PNLSE with Anti-cubic Law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau (c_1{\left|u\right|}^{-4}+c_2{\left|u\right|}^2+c_3{\left|u\right|}^4)u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2p}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2p})}{\partial x^{\beta }}.$$

(87)

Equation (10) reduces into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U-\omega \delta U^{2p+1}+c_1{U}^{-3}+c_2{U}^3+c_3{U}^5=0$$

(88)

To get the solutions in retrieve form, we use the transformation $U\left(\eta \right)=V^{\frac{1}{2}}\left(\eta \right)$. The above Equation (88) reduces into:

$$(\rho -\sigma \lambda )(2V{V}^{″}-4(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)V^2-4\omega \delta V^{2p+2}+4(c_1+c_2{V}^3+c_3{V}^4=0$$

(89)

By using the homogeneous balance technique onto the Equation (89), we get $m=1$. For $m=1$, Equation (5) reduces into:

$$V\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}.$$

(90)

Here ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ are unknown parameters. By putting the Equations (90) and (6) into Equation (89) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ and other parameters. We now, with the use of symbolic software and taking $p=1$, we attain the following solution sets:

Set 1:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8(\delta \omega -c_3)},{\alpha }_1=\mp \frac{1}{8}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3\delta \omega \mathsf{\Omega }{\mathrm{c}}_2^2-9c_3^2\mathsf{\Omega }{\mathrm{c}}_2^2-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},{\beta }_1=0,\hfill \\ \theta =\frac{1}{48{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(16\right(-9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2-9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2+9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2-3c_3^3\kappa \omega {\mathsf{\Omega }}^2\\ -3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-4\mathsf{\Gamma }{\omega }^2+3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2+3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2+2\mathsf{\Omega }\mathsf{\Gamma })-9c_2^2\mathsf{\Omega }({\omega }^2+\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =-\frac{16(9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+4\mathsf{\Gamma }-3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{48{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(91)

We now using the Equations (91) and (90) in Equation (7) and grab the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \mathsf{\Omega }\omega -9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(92)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(93)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\mp \frac{1}{8}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(94)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{\mathsf{\Omega }\left(c_3-\delta \omega \right){}^4}}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(95)

Set 2:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=0,{\beta }_1=\mp \frac{1}{8}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{(c_3-\delta \omega ){}^4}},\hfill \\ \theta =-\frac{1}{48{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(16\right(9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2+9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2-9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2\\ +3c_3^3\kappa \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-4\mathsf{\Gamma }{\omega }^2+2\mathsf{\Gamma }\mathsf{\Omega }-3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2-3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }({\omega }^2+\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =\frac{16(-9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2-3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+4\mathsf{\Gamma }+3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)-9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{48{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(96)

We now using the Equations (96) and (90) in Equation (7) and secure the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8\sqrt{-\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(97)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8\sqrt{-\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(98)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\mp \frac{1}{8\sqrt{\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(99)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8\sqrt{\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(100)

Set 3:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=0,{\beta }_1=\mp \frac{1}{8}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{(c_3-\delta \omega ){}^4}},\hfill \\ \theta =\frac{1}{48{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(16\right(-9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2-9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2+9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2\\ -3c_3^3\kappa \omega {\mathsf{\Omega }}^2-3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-4\mathsf{\Gamma }{\omega }^2+2\mathsf{\Gamma }\mathsf{\Omega }+3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2+3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2)-9c_2^2\mathsf{\Omega }({\omega }^2+\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =-\frac{16(9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+4\mathsf{\Gamma }-3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{48{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(101)

We now using the Equations (101) and (90) in Equation (7) and grab the subsequent cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}\pm \frac{1}{8\sqrt{-\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(102)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8\sqrt{-\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(103)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\mp \frac{1}{8\sqrt{\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(104)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8\sqrt{\mathsf{\Omega }}}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{\left(c_3-\delta \omega \right){}^4}}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(105)

Set 4:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=\mp \frac{1}{8}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},{\beta }_1=0,\hfill \\ \theta =-\frac{1}{48{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(16\right(9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2+9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2-9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2\\ +3c_3^3\kappa \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-4\mathsf{\Gamma }{\omega }^2+2\mathsf{\Gamma }\mathsf{\Omega }-3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2-3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }({\omega }^2+\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =\frac{16(-9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2-3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+4\mathsf{\Gamma }+3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)-9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{48{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(106)

We now using the Equations (106) and (90) in Equation (7) and get the consequent cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(107)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(108)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\mp \frac{1}{8}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(109)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{8}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(110)

Set 5:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=\mp \frac{1}{16}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},\hfill \\ {\beta }_1=\mathsf{\Omega }\pm \frac{1}{16}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},\\ \theta =-\frac{1}{192{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(64\right(9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2+9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2-9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2\\ +3c_3^3\kappa \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-\mathsf{\Gamma }{\omega }^2+2\mathsf{\Gamma }\mathsf{\Omega }-3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2-3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }({\omega }^2+4\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =\frac{64(-9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2-3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+\mathsf{\Gamma }+3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)-9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{192{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(111)

We now using the Equations (111) and (90) in Equation (7) and secure the following results.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8\delta \omega -8c_3}\pm \frac{1}{16}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}}(\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)+\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right))\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(112)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8\left(\delta \omega -c_3\right)}+\frac{1}{16}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }+64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\left(\mp \tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\pm \cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(113)

Set 6:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=\mp \frac{1}{16}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},\hfill \\ {\beta }_1=\mathsf{\Omega }\pm \frac{1}{16}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}},\\ \theta =\frac{1}{192{\mathsf{\Omega }}^2(\sigma \omega -1)(\delta \omega -c_3){}^3}\left(64\right(-9c_3{\delta }^2\kappa {\omega }^3{\mathsf{\Omega }}^2-9c_3{\delta }^2\lambda \sigma {\omega }^4{\mathsf{\Omega }}^2+9c_3^2\delta \kappa {\omega }^2{\mathsf{\Omega }}^2+9c_3^2\delta \lambda \sigma {\omega }^3{\mathsf{\Omega }}^2\\ -3c_3^3\kappa \omega {\mathsf{\Omega }}^2-3c_3^3\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-\mathsf{\Gamma }{\omega }^2+2\mathsf{\Gamma }\mathsf{\Omega }+3{\delta }^3\kappa {\omega }^4{\mathsf{\Omega }}^2+3{\delta }^3\lambda \sigma {\omega }^5{\mathsf{\Omega }}^2)-9c_2^2\mathsf{\Omega }({\omega }^2+4\mathsf{\Omega })(c_3-\delta \omega ){}^2),\\ \rho =-\frac{64(9c_3{\delta }^2\lambda \sigma {\omega }^2{\mathsf{\Omega }}^2-9c_3^2\delta \lambda \sigma \omega {\mathsf{\Omega }}^2+3c_3^3\lambda \sigma {\mathsf{\Omega }}^2+\mathsf{\Gamma }-3{\delta }^3\lambda \sigma {\omega }^3{\mathsf{\Omega }}^2)+9c_2^2\mathsf{\Omega }(c_3-\delta \omega ){}^2}{192{\mathsf{\Omega }}^2(\delta \omega -c_3){}^3},\\ \hfill \mathsf{\Gamma }=\sqrt{3}\sqrt{c_1{\mathsf{\Omega }}^2(\delta \omega -c_3){}^7}\}\end{array}$$

(114)

We now using the Equations (114) and (90) in Equation (7) and get the following results.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{3c_2}{8(\delta \omega -c_3)}\pm \frac{1}{16}\sqrt{-\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2(c_3-\delta \omega ){}^4}}(\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)+\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right))\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(115)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_2(x,t)={\{\frac{3c_2}{8(\delta \omega -c_3)}+\frac{1}{16}\sqrt{\mathsf{\Omega }}\sqrt{\frac{-9c_2^2{\delta }^2{\omega }^2\mathsf{\Omega }+18c_3{c}_2^2\delta \omega \mathsf{\Omega }-9c_3^2{c}_2^2\mathsf{\Omega }-64\mathsf{\Gamma }}{{\mathsf{\Omega }}^2\left(c_3-\delta \omega \right){}^4}}\left(\mp \tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\pm \cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\right)\}}^{\frac{1}{2}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(116)

Set 7:

$$\begin{array}{c}\{{\alpha }_0=\frac{3c_2}{8\delta \omega -8c_3},{\alpha }_1=\mp \frac{\sqrt{27c_2^4-4096c_1\left(\delta \omega -c_3\right){}^3}}{16\sqrt{3}\sqrt{c_2^2\mathsf{\Omega }\left(c_3-\delta \omega \right){}^2}},{\beta }_1=\mp \frac{\mathsf{\Omega }\sqrt{27c_2^4-4096c_1\left(\delta \omega -c_3\right){}^3}}{16\sqrt{3}\sqrt{c_2^2\mathsf{\Omega }\left(c_3-\delta \omega \right){}^2}},\hfill \\ \theta =\frac{9c_2^2\left(64\omega \mathsf{\Omega }\left(\delta \omega -c_3\right)(\kappa +\lambda \sigma \omega )+3c_2^2\left({\omega }^2-5\mathsf{\Omega }\right)\right)-4096c_1\left({\omega }^2+\mathsf{\Omega }\right)\left(\delta \omega -c_3\right){}^3}{576c_2^2\mathsf{\Omega }(\sigma \omega -1)\left(\delta \omega -c_3\right)},\\ \hfill \rho =\frac{9c_2^2\left(64\lambda \sigma \mathsf{\Omega }\left(\delta \omega -c_3\right)+3c_2^2\right)-4096c_1\left(\delta \omega -c_3\right){}^3}{576c_2^2\mathsf{\Omega }\left(\delta \omega -c_3\right)}\}\end{array}$$

(117)

We now using the Equations (117) and (90) in Equation (7) and secure the subsequent results.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)={\{\frac{9c_2^2-\sqrt{3}\iota \sqrt{27c_2^4-4096c_1\left(\delta \omega -c_3\right){}^3}\csc \mathrm{h}\left(2\eta \sqrt{-\mathsf{\Omega }}\right)}{24c_2\left(c_3-\delta \omega \right)}\}}^{\frac{1}{2}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(118)

If $\mathsf{\Omega }>0$, then

$$u_2(x,t)={\{\frac{\sqrt{3}\sqrt{27c_2^4-4096c_1\left(\delta \omega -c_3\right){}^3}\csc \left(2\eta \sqrt{\mathsf{\Omega }}\right)+9c_2^2}{24c_2\left(\delta \omega -c_3\right)}\}}^{\frac{1}{2}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(119)

3.5. Dual Power Law

For this law, $G\left(u\right)=\frac{c_1}{u^n}$, where $c_1$ and $c_2$ are constants. Equation (1) for PNLSE with dual power law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau (c_1{\left|u\right|}^{2n}+c_2{\left|u\right|}^{4n})u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2n}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2n})}{\partial x^{\beta }}.$$

(120)

here $p=n$ as in the case of power law. Moreover, if $n=1$ dual power law becomes to the parabolic law. Equation (10) changes into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U+(c_1-\omega \delta )U^{2n+1}+c_2{U}^{4n+1}=0$$

(121)

To get the solutions in retrieve form, we use the transformation $U\left(\eta \right)=V^{\frac{1}{2n}}\left(\eta \right)$. The above Equation (121) reduces into:

$$(1-2n)(\rho -\sigma \lambda ){\left(V^{\prime }\right)}^2+2n(\rho -\sigma \lambda )V{V}^{″}-4n^2(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)V^2+4n^2(c_1-\omega \delta )V^3+4n^2{c}_2{V}^4=0$$

(122)

By using the homogeneous balance technique into the Equation (122), we get $m=1$. For $m=1$, Equation (5) reduces to:

$$V\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}.$$

(123)

Here ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ are unknown parameters. By putting the Equations (123) and (6) into Equation (122) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ and other parameters. We now, with the use of symbolic software and taking $p=1$, we attain the following solution sets:

Set 1:

$$\begin{array}{c}\{{\alpha }_0=\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)},{\alpha }_1=0,{\beta }_1=\mp \frac{\sqrt{-\frac{n^2{(2n+1)}^3\left(c_1-\delta \omega \right){}^4}{c_2(\rho -\lambda \sigma )}}}{8c_2{(n+1)}^2},\mathsf{\Omega }=\frac{n^2(2n+1)\left(c_1-\delta \omega \right){}^2}{4c_2{(n+1)}^2(\rho -\lambda \sigma )},\hfill \\ \hfill \theta =\frac{\omega \left(4c_2{(n+1)}^2(\kappa +\rho \omega )+{\delta }^2(2n+1)\omega \right)-2c_1\delta (2n+1)\omega +c_1^2(2n+1)}{4c_2{(n+1)}^2(\sigma \omega -1)}\}\end{array}$$

(124)

We now using the Equations (124) and (123) in Equation (7) and secure the following results.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{\left((2n+1)\left(\delta \omega -c_1\right)\right)}{4c_2(n+1)}\left(1\pm \frac{\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(n\sqrt{-(2n+1)}\left(\delta \omega -c_1\right)\right)}{2(n+1)\sqrt{-\mathsf{\Omega }}\sqrt{c_2(\rho -\lambda \sigma )}}\right)\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(125)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{\left((2n+1)\left(\delta \omega -c_1\right)\right)}{4c_2(n+1)}\left(1\pm \frac{\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\left(n\sqrt{-(2n+1)}\left(\delta \omega -c_1\right)\right)}{2(n+1)\sqrt{-\mathsf{\Omega }}\sqrt{c_2(\rho -\lambda \sigma )}}\right)\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(126)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{\left((2n+1)\left(\delta \omega -c_1\right)\right)}{4c_2(n+1)}\left(1\mp \frac{\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(n\sqrt{-(2n+1)}\left(\delta \omega -c_1\right)\right)}{2(n+1)\sqrt{\mathsf{\Omega }}\sqrt{c_2(\rho -\lambda \sigma )}}\right)\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(127)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{\left((2n+1)\left(\delta \omega -c_1\right)\right)}{4c_2(n+1)}\left(1\pm \frac{\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(n\sqrt{-(2n+1)}\left(\delta \omega -c_1\right)\right)}{2(n+1)\sqrt{\mathsf{\Omega }}\sqrt{c_2(\rho -\lambda \sigma )}}\right)\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(128)

Set 2:

$$\begin{array}{c}\{{\alpha }_0=\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)},{\alpha }_1=\mp \frac{i\sqrt{2n+1}\sqrt{\rho -\lambda \sigma }}{2\sqrt{c_2}n},{\beta }_1=0,\mathsf{\Omega }=\frac{n^2(2n+1)\left(c_1-\delta \omega \right){}^2}{4c_2{(n+1)}^2(\rho -\lambda \sigma )},\hfill \\ \hfill \theta =\frac{\omega \left(4c_2{(n+1)}^2(\kappa +\rho \omega )+{\delta }^2(2n+1)\omega \right)-2c_1\delta (2n+1)\omega +c_1^2(2n+1)}{4c_2{(n+1)}^2(\sigma \omega -1)}\}\end{array}$$

(129)

We now using the Equations (129) and (123) in Equation (7) and get the following cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{(2n+1)(\delta \omega -c_1)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(130)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(131)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)}\mp \frac{\left(i\sqrt{2n+1}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(132)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(133)

Set 3:

$$\begin{array}{c}\{{\alpha }_0=\frac{(2n+1)(\delta \omega -c_1)}{4c_2(n+1)},{\alpha }_1=\mp \frac{i\sqrt{2n+1}\sqrt{\rho -\lambda \sigma }}{2\sqrt{c_2}n},{\beta }_1=\pm \frac{in{(2n+1)}^{3/2}(c_1-\delta \omega ){}^2}{32c_2^{3/2}{(n+1)}^2\sqrt{\rho -\lambda \sigma }},\hfill \\ \hfill \mathsf{\Omega }=\frac{n^2(2n+1)(c_1-\delta \omega ){}^2}{16c_2{(n+1)}^2(\rho -\lambda \sigma )},\theta =\frac{\omega (4c_2{(n+1)}^2(\kappa +\rho \omega )+{\delta }^2(2n+1)\omega )-2c_1\delta (2n+1)\omega +c_1^2(2n+1)}{4c_2{(n+1)}^2(\sigma \omega -1)}\}\end{array}$$

(134)

We now using the Equations (134) and (123) in Equation (7) and get the following cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{\frac{(2n+1)(\delta \omega -c_1)}{4c_2(n+1)}+\frac{(i\sqrt{2n+1})(\pm \sqrt{\rho -\lambda \sigma }\sqrt{-\mathsf{\Omega }}\tanh (\eta \sqrt{-\mathsf{\Omega }})\mp \frac{\coth (\eta \sqrt{-\mathsf{\Omega }})(n^2(2n+1)(c_1-\delta \omega ){}^2)}{16c_2{(n+1)}^2\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(135)

or

$$\begin{array}{c}{u}_2(x,t)={\{\frac{(2n+1)(\delta \omega -c_1)}{4c_2(n+1)}+\frac{(i\sqrt{2n+1})(\pm \sqrt{\rho -\lambda \sigma }\sqrt{-\mathsf{\Omega }}\coth (\eta \sqrt{-\mathsf{\Omega }})\mp \frac{\tanh (\eta \sqrt{-\mathsf{\Omega }})(n^2(2n+1)(c_1-\delta \omega ){}^2)}{16c_2{(n+1)}^2\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(136)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\mp \sqrt{\rho -\lambda \sigma }\sqrt{\mathsf{\Omega }}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\pm \frac{\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(n^2(2n+1)\left(c_1-\delta \omega \right){}^2\right)}{16c_2{(n+1)}^2\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(137)

or

$$\begin{array}{c}{u}_4(x,t)={\{\frac{(2n+1)\left(\delta \omega -c_1\right)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\pm \sqrt{\rho -\lambda \sigma }\sqrt{\mathsf{\Omega }}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\mp \frac{\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\left(n^2(2n+1)\left(c_1-\delta \omega \right){}^2\right)}{16c_2{(n+1)}^2\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))\end{array}$$

(138)

3.6. Triple Power Law

For this law, $G\left(u\right)=\frac{c_1}{u^n}+c_2{u}^{2n}+c_3{u}^{3n}$, where $c_1$, $c_2$ and $c_3$ are constants. Equation (1) for PNLSE with triple power law nonlinearity becomes:

$$\iota \frac{{\partial }^{\beta }u}{\partial t^{\beta }}+\sigma \frac{{\partial }^{2\beta }u}{\partial t^{\beta }\partial x^{\beta }}+\rho \frac{{\partial }^{2\beta }u}{\partial x^{2\beta }}+\tau (c_1{\left|u\right|}^{2n}+c_2{\left|u\right|}^{4n}+c_3{\left|u\right|}^{6n})u=\iota \kappa \frac{{\partial }^{\beta }u}{\partial x^{\beta }}+\delta \frac{{\partial }^{\beta }{\left(\right|u|}^{2n}u)}{\partial x^{\beta }}+\varrho u\frac{{\partial }^{\beta }{\left(\right|u|}^{2n})}{\partial x^{\beta }}.$$

(139)

Equation (10) changes into the following form:

$$(\rho -\sigma \lambda )U^{″}-(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)U-\omega \delta U^{2p+1}+c_1{U}^{2n+1}+c_2{U}^{4n+1}+c_3{U}^{6n+1}=0$$

(140)

To get the solutions in retrieve form, we use the transformation $U\left(\eta \right)=V^{\frac{1}{2n}}\left(\eta \right)$. The above Equation (88) reduces into:

$$(\rho -\sigma \lambda )((1-2n){\left(V^{\prime }\right)}^2+2nV{V}^{″})-4n^2(\theta +\kappa \omega -\sigma \theta \omega +\rho {\omega }^2)V^2-4n^2\omega \delta V^{\frac{p}{n}+2}+4n^2(c_1{V}^3+c_2{V}^4+c_3{V}^5)=0$$

(141)

By using the homogeneous balance technique onto the Equation (141), one secure $m=1$ and for $m=1$, Equation (5) reduces to:

$$V\left(\eta \right)={\alpha }_0+{\alpha }_1\varphi \left(\eta \right)+\frac{{\beta }_1}{\varphi \left(\eta \right)}.$$

(142)

Here ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ are unknown parameters. By putting the Equations (142) and (6) into Equation (141) and collecting the coefficients of each power of $\varphi \left(\eta \right)$, we get the algebraic expressions involving ${\alpha }_0$, ${\alpha }_1$ and ${\beta }_1$ and other parameters. We now, with the use of symbolic software and taking $p=3n$, we gain the following solution sets:

Set 1:

$$\begin{array}{c}\{{\alpha }_0=-\frac{c_1(2n+1)}{4c_2(n+1)},{\alpha }_1=\mp \frac{i\sqrt{2n+1}\sqrt{\rho -\lambda \sigma }}{2\sqrt{c_2}n},{\beta }_1=0,\theta =-\frac{c_1^2{\delta }^2(2n+1)+4c_2{c}_3{(n+1)}^2\left(c_3\rho +\delta \kappa \right)}{4c_2\delta {(n+1)}^2\left(\delta -c_3\sigma \right)},\hfill \\ \hfill \mathsf{\Omega }=\frac{c_1^2{n}^2(2n+1)}{4c_2{(n+1)}^2(\rho -\lambda \sigma )},\omega =\frac{c_3}{\delta }\}\end{array}$$

(143)

We now using the Equations (143) and (142) in Equation (7) and secure the following cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{2\sqrt{c_2}n}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(144)

or

$$u_2(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{2\sqrt{c_2}n}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp (\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }(\beta )})}^{\beta }+\vartheta ))$$

(145)

If $\mathsf{\Omega }=0$, then

$$u_3(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}\pm \frac{i\sqrt{2n+1}\sqrt{\rho -\lambda \sigma }}{\eta \left(2\sqrt{c_2}n\right)}\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(146)

If $\mathsf{\Omega }>0$, then

$$u_4(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}\mp \frac{\left(i\sqrt{2n+1}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{2\sqrt{c_2}n}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(147)

or

$$u_5(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}\pm \frac{\left(i\sqrt{2n+1}\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }\right)}{2\sqrt{c_2}n}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(148)

Set 2:

$$\begin{array}{c}\{{\alpha }_0=-\frac{c_1(2n+1)}{4c_2(n+1)},{\alpha }_1=\mp \frac{i\sqrt{2n+1}\sqrt{\rho -\lambda \sigma }}{2\sqrt{c_2}n},{\beta }_1=\pm \frac{i{c}_1^{2}n{(2n+1)}^{3/2}}{32c_2^{3/2}{(n+1)}^2\sqrt{\rho -\lambda \sigma }},\hfill \\ \hfill \theta =-\frac{c_1^2{\delta }^2(2n+1)+4c_2{c}_3{(n+1)}^2\left(c_3\rho +\delta \kappa \right)}{4c_2\delta {(n+1)}^2\left(\delta -c_3\sigma \right)},\mathsf{\Omega }=\frac{c_1^2{n}^2(2n+1)}{16c_2{(n+1)}^2(\rho -\lambda \sigma )},\omega =\frac{c_3}{\delta }\}\end{array}$$

(149)

We now using the Equations (149) and (142) in Equation (7) and secure the following cases.

If $\mathsf{\Omega }<0$, then

$$\begin{array}{c}{u}_1(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\pm \sqrt{\rho -\lambda \sigma }\sqrt{-\mathsf{\Omega }}\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)\mp \frac{\left(c_1^2{n}^2(2n+1)\right)\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{16c_2{(n+1)}^2\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)\end{array}$$

(150)

or

$$\begin{array}{c}{u}_2(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\pm \sqrt{\rho -\lambda \sigma }\sqrt{-\mathsf{\Omega }}\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)\mp \frac{\left(c_1^2{n}^2(2n+1)\right)\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{16c_2{(n+1)}^2\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)\end{array}$$

(151)

If $\mathsf{\Omega }>0$, then

$$\begin{array}{c}{u}_3(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\mp \sqrt{\rho -\lambda \sigma }\sqrt{\mathsf{\Omega }}\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)\pm \frac{\left(c_1^2{n}^2(2n+1)\right)\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{16c_2{(n+1)}^2\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)\end{array}$$

(152)

or

$$\begin{array}{c}{u}_4(x,t)={\{-\frac{c_1(2n+1)}{4c_2(n+1)}+\frac{\left(i\sqrt{2n+1}\right)\left(\pm \sqrt{\rho -\lambda \sigma }\sqrt{\mathsf{\Omega }}\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)\mp \frac{\left(c_1^2{n}^2(2n+1)\right)\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{16c_2{(n+1)}^2\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }}\right)}{2\sqrt{c_2}n}\}}^{\frac{1}{2n}}\hfill \\ \hfill \times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)\end{array}$$

(153)

Set 3:

$$\begin{array}{c}\{{\alpha }_0=-\frac{c_1(2n+1)}{4c_2(n+1)},{\alpha }_1=0,{\beta }_1=\mp \frac{i{c}_1^{2}n{(2n+1)}^{3/2}}{8\sqrt{c_2}\sqrt{n+1}\sqrt{c_2^2{(n+1)}^3(\rho -\lambda \sigma )}},\hfill \\ \hfill \theta =-\frac{c_1^2{\delta }^2(2n+1)+4c_2{c}_3{(n+1)}^2\left(c_3\rho +\delta \kappa \right)}{4c_2\delta {(n+1)}^2\left(\delta -c_3\sigma \right)},\mathsf{\Omega }=\frac{c_1^2{n}^2(2n+1)}{4c_2{(n+1)}^2(\rho -\lambda \sigma )},\omega =\frac{c_3}{\delta }\}\end{array}$$

(154)

Now using the Equations (154) and (142) in Equation (7), one can get the following cases.

If $\mathsf{\Omega }<0$, then

$$u_1(x,t)={\left\{\frac{c_1(2n+1)}{4c_2(n+1)}(-1\pm \frac{\left(i{c}_{1}n\sqrt{2n+1}\right)\coth \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{2\sqrt{c_2}(n+1)\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})\right\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(155)

or

$$u_2(x,t)={\left\{\frac{c_1(2n+1)}{4c_2(n+1)}(-1\pm \frac{\left(i{c}_{1}n\sqrt{2n+1}\right)\tanh \left(\eta \sqrt{-\mathsf{\Omega }}\right)}{2\sqrt{c_2}(n+1)\sqrt{-\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})\right\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(156)

If $\mathsf{\Omega }>0$, then

$$u_3(x,t)={\left\{\frac{c_1(2n+1)}{4c_2(n+1)}(-1\mp \frac{\left(i{c}_{1}n\sqrt{2n+1}\right)\cot \left(\eta \sqrt{\mathsf{\Omega }}\right)}{2\sqrt{c_2}(n+1)\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})\right\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(157)

or

$$u_4(x,t)={\left\{\frac{c_1(2n+1)}{4c_2(n+1)}(-1\pm \frac{\left(i{c}_{1}n\sqrt{2n+1}\right)\tan \left(\eta \sqrt{\mathsf{\Omega }}\right)}{2\sqrt{c_2}(n+1)\sqrt{\mathsf{\Omega }}\sqrt{\rho -\lambda \sigma }})\right\}}^{\frac{1}{2n}}\times \exp \left(\iota (-\frac{\omega }{\beta }{(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\frac{\theta }{\beta }{(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{\beta }+\vartheta )\right)$$

(158)

Here the $3D$ graphs, by taking $c_1=1$, $\kappa =1=\sigma =\delta$ and $n=1.5$ are displayed in Figure 7, Figure 8 and Figure 9 for selected solutions to visualized their dynamics.

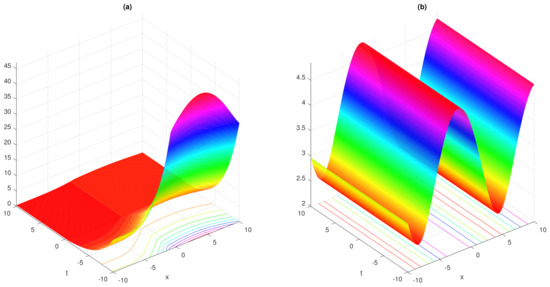
Figure 7. $3D$ wave simulations of complex solitary solution (144) are presented in (a,b) for fractional parameter $\beta =0.5,1.0$ and $c_2=-2$, $c_3=-1$.

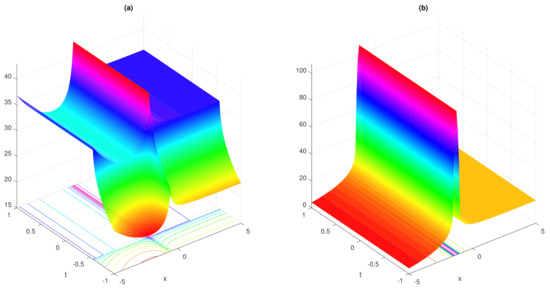
Figure 8. $3D$ wave simulations of complex solitary solution (145) are presented in (a,b) for fractional parameter $\beta =0.5,1.0$ and $c_2=-2$, $c_3=-0.5$.

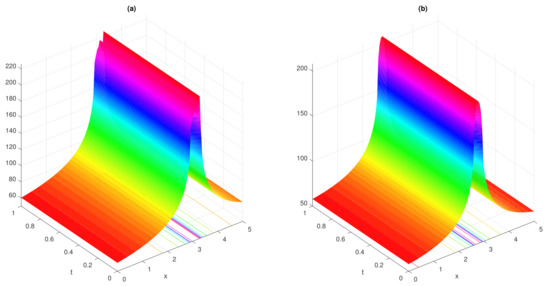
Figure 9. $3D$ wave simulations of complex periodic solution (147) are presented in (a,b) for fractional parameter $\beta =0.75,1.0$ and $c_2=2$, $c_3=-0.25$.

4. Conclusions

We have produced the different types of solitary wave solutions of the perturbed nonlinear Schrödinger equation with different nonlinearities successfully. The novel beta derivative operator and the modified extended tanh expansion method have been employed to retrieve dark, singular and combined solitary wave solutions. The obtained solutions have been verified through some symbolic mathematical tools. The obtained solutions have been demonstrated via numerical simulation by taking suitable values for physical and arbitrary parameters. The novelty of this paper has been proved by investigating the perturbed nonlinear Schrödinger equation for the first time in the generalized form of classical derivative sense.