Using Fractional Bernoulli Wavelets for Solving Fractional Diffusion Wave Equations with Initial and Boundary Conditions
Abstract
:1. Introduction
- (I)
- For , and , Equation (1) is the Time Fractional Generalized Cattaneo Equation (TFGCE), which is widely used in modelling both heat and mass transfer and the fractional Ficks laws, which are written in terms of space and/or time fractional derivatives and lead to the space and/or time fractional diffusion equations [8,9,10].
- (II)
- For , the linear Time Fractional Klein–Gordon Equation (TFKGE) is obtained for and the linear Time Fractional Dissipative Klein–Gordon Equation (TFDKGE) for . We observe that linear and nonlinear Klein–Gordon equations model many problems in classical and quantum mechanics, solitons and condensed matter physics. For example, nonlinear sine Klein–Gordon equation models a Josephson junction, the motion of rigid pendula attached to a stretched wire, dislocations in crystals and DNA dynamics [11,12,13,14].
2. Preliminaries on Fractional Calculus
3. Main Results
3.1. BWs and FBWs
3.2. Function Approximation by FBWs
3.3. Operational Matrix of Riemann–Liouville Fractional Integration for FBWs
3.4. Operational Matrix of Derivative for FBWs
4. Numerical Implementation
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Basel, Switzerland; Philadelphia, PA, USA, 1993. [Google Scholar]
- Riewe, F. Mechanics with fractional derivatives. Phys. Rev. E 1997, 55, 3581. [Google Scholar] [CrossRef]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 462. [Google Scholar] [CrossRef]
- Klimek, M. Fractional sequential mechanics-models with symmetric fractional derivative. Czech. J. Phys. 2001, 51, 1348–1354. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ghazizadeh, H.R.; Maerefat, M.; Azimi, A. Explicit and implicit finite difference schemes for fractional Cattaneo equation. J. Comput. Phys. 2010, 229, 7042–7057. [Google Scholar] [CrossRef]
- Wang, L.Q.; Zhou, X.S.; Wei, X.H. Heat Conduction, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Batiha, B.; Noorani, M.S.M.; Hashim, I. Numerical solution of sine-Gordon equation by variational iteration method. Phys. Lett. A 2007, 370, 437–440. [Google Scholar] [CrossRef]
- El-Sayed, S. The decomposition method for studying the Klein–Gordon equation. Chaos Soliton Fract. 2003, 18, 1025–1030. [Google Scholar] [CrossRef]
- Nagy, A.M. Numerical solution of time fractional nonlinear Klein–Gordon equation using Sinc-Chebyshev collocation method. Appl. Math. Comput. 2017, 310, 139–148. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh method: Exact solutions of the sine-Gordon and the sinh-Gordon equations. Appl. Math. Comput. 2005, 167, 1196–1210. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Doha, E.H.; Baleanu, D.; Ezz-Eldien, S.S. A spectral Tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 2015, 295, 142–156. [Google Scholar] [CrossRef]
- Heydari, M.H.; Hooshmandasl, M.R.; Ghaini, F.M.; Cattani, C. Wavelets method for the time fractional diffusion-wave equation. Phys. Lett. A 2015, 379, 71–76. [Google Scholar] [CrossRef]
- Mohammad, M.; Trounev, A.; Alshbool, M. A Novel Numerical Method for Solving Fractional Diffusion-Wave and Nonlinear Fredholm and Volterra Integral Equations with Zero Absolute Error. Axioms 2021, 10, 165. [Google Scholar] [CrossRef]
- Ghafoor, A.; Haq, S.; Hussain, M.; Kumam, P.; Asif Jan, M. Approximate Solutions of Time Fractional Diffusion Wave Models. Mathematics 2019, 7, 923. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Dai, L.; Kamran, K.; Nazeer, W. Numerical solution of multi-term time fractional wave diffusion equation using transform based local meshless method and quadrature. AIMS Math. 2020, 5, 5813–5838. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Huang, Y.; Wei, H. Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Comput. Math. Appl. 2017, 73, 1218–1232. [Google Scholar] [CrossRef]
- Yaseen, M.; Abbas, M.; Nazir, T.; Baleanu, D. A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation. Adv. Differ. Equ. 2017, 2017, 274. [Google Scholar] [CrossRef] [Green Version]
- Singh, H.; Kumar, D.; Singh, J.; Singh, C.S. A reliable numerical algorithm for the fractional Klein–Gordon equation. Eng. Trans. 2019, 67, 21–34. [Google Scholar] [CrossRef]
- Singh, H.; Kumar, D.; Singh, J.; Singh, C.S.; Nosrati Sahlan, M.; Afshari, H. Three new approaches for solving a class of strongly nonlinear two-point boundary value problems. Bound. Value Probl. 2021, 2021, 61. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Model. 2014, 38, 6038–6051. [Google Scholar] [CrossRef]
- Ismail, M.; Saeed, U.; Alzabut, J.; Rehman, M. Approximate Solutions for Fractional Boundary Value Problems via Green-CAS Wavelet Method. Mathematics 2019, 7, 1164. [Google Scholar] [CrossRef] [Green Version]
- Nosrati Sahlan, M. Four computational approaches for solving a class of boundary value problems arising in chemical reactor industry. Appl. Math. Comput. 2019, 355, 253–268. [Google Scholar] [CrossRef]
- Saker, S.H.; Alzabut, J.; O’Regan, D.; Agarwal, R.P. Self-improving properties of weighted Gehring classes with applications to partial differential equations. Adv. Differ. Equ. 2021, 2021, 397. [Google Scholar] [CrossRef]
- Rehman, M.; Baleanu, D.; Alzabut, J.; Ismail, M.; Saeed, U. Green-Haar wavelets method for generalized fractional differential equations. Adv. Differ. Equ. 2020, 2020, 515. [Google Scholar] [CrossRef]
- Hedayati, V.; Samei, M.E. Positive solutions of fractional differential equation with two pieces in chain interval and simultaneous dirichlet boundary conditions. Bound. Val. Prob. 2019, 2019, 141. [Google Scholar] [CrossRef]
- Samei, M.E.; Hedayati, V.; Rezapour, S. Existence results for a fraction hybrid differential inclusion with caputo-hadamard type fractional derivative. Adv. Diff. Equ. 2019, 2019, 163. [Google Scholar] [CrossRef]
- Flandrin, P. Time-frequency and chirps. Proc. SPIE 2001, 4391, 161–175. [Google Scholar] [CrossRef]
- Mendlovic, D.; Zalevsky, Z.; Mas, D.; Garca, J.; Ferreira, C. Fractional wavelet transform. Appl. Opt. 1997, 36, 4801–4806. [Google Scholar] [CrossRef] [PubMed]
- Rahimkhani, P.; Ordokhani, Y. A numerical scheme based on Bernoulli wavelets and collocation method for solving fractional partial differential equations with Dirichlet boundary conditions. Numer. Meth. Partial Differ. Equ. 2019, 35, 34–59. [Google Scholar] [CrossRef] [Green Version]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Fractional-order Bernoulli wavelets and their applications. Appl. Math. Model. 2016, 40, 8087–8107. [Google Scholar] [CrossRef]
- Chouhan, D.; Mishra, V.; Srivastava, H.M. Bernoulli wavelet method for numerical solution of anomalous infiltration and diffusion modeling by nonlinear fractional differential equations of variable order. Res. Appl. Math. 2021, 10, 100146. [Google Scholar] [CrossRef]
- Podlubny. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier Science: San Diego, CA, USA, 2006. [Google Scholar]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Numerical solution of ractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J. Comput. Appl. Math. 2017, 3098, 493–510. [Google Scholar] [CrossRef]
- Khader, M.M.; Adel, M.H. Numerical solutions of fractional wave equations using an efficient class of FDM based on the Hermite formula. Adv. Differ. Equ. 2016, 34, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Zhang, L. On finite difference methods for fourth-order fractional diffusion-wave and subdiffusion systems. Appl. Math. Comput. 2012, 218, 5019–5034. [Google Scholar] [CrossRef]
- Mohebbi, A.; Abbaszadeh, M.; Dehghan, M. High-order difference scheme for the solution of linear time fractional Klein-gordon equations. Numer. Meth. Part D E 2014, 2014, 1–20. [Google Scholar] [CrossRef]
- Kanwal, A.; Phang, C.; Iqbal, U. Numerical solution of fractional diffusion Wave equation and fractional Klein–Gordon equation via two-dimensional Genocchi polynomials with a Ritz-Galerkin method. Computation 2018, 6, 40. [Google Scholar] [CrossRef] [Green Version]

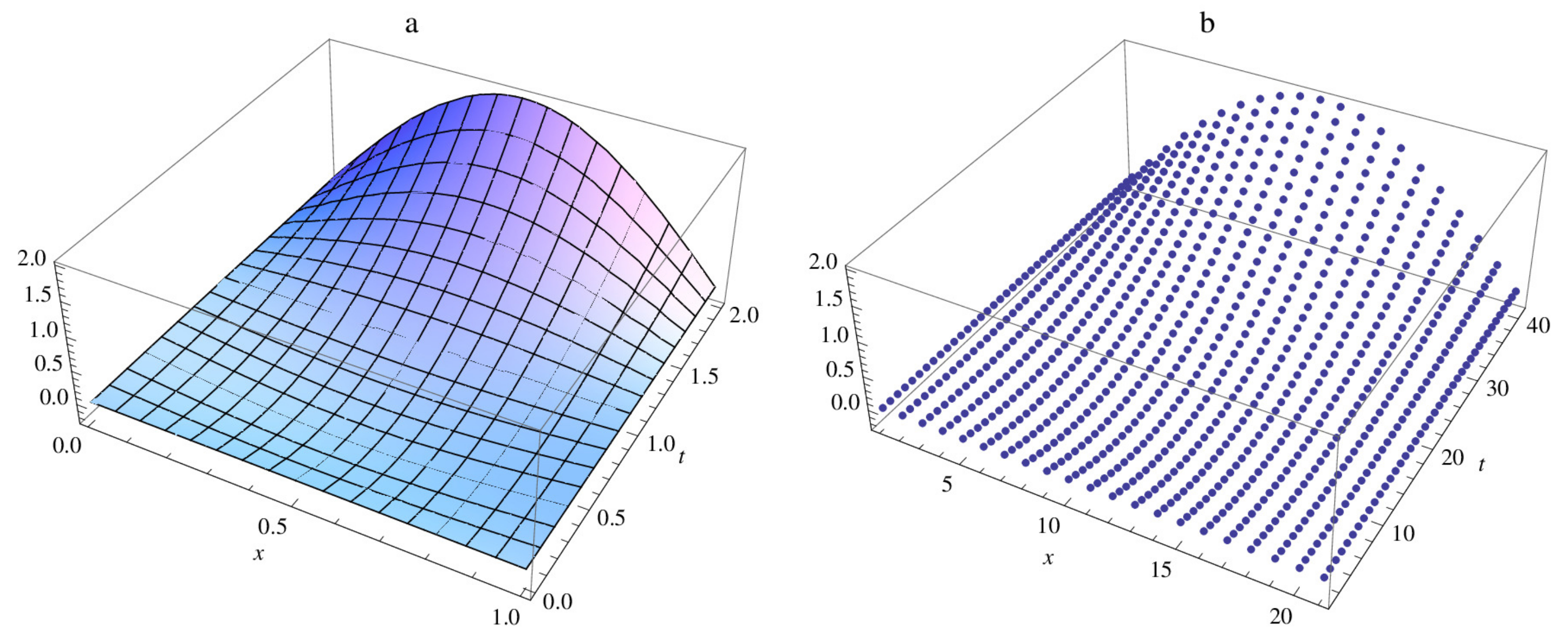
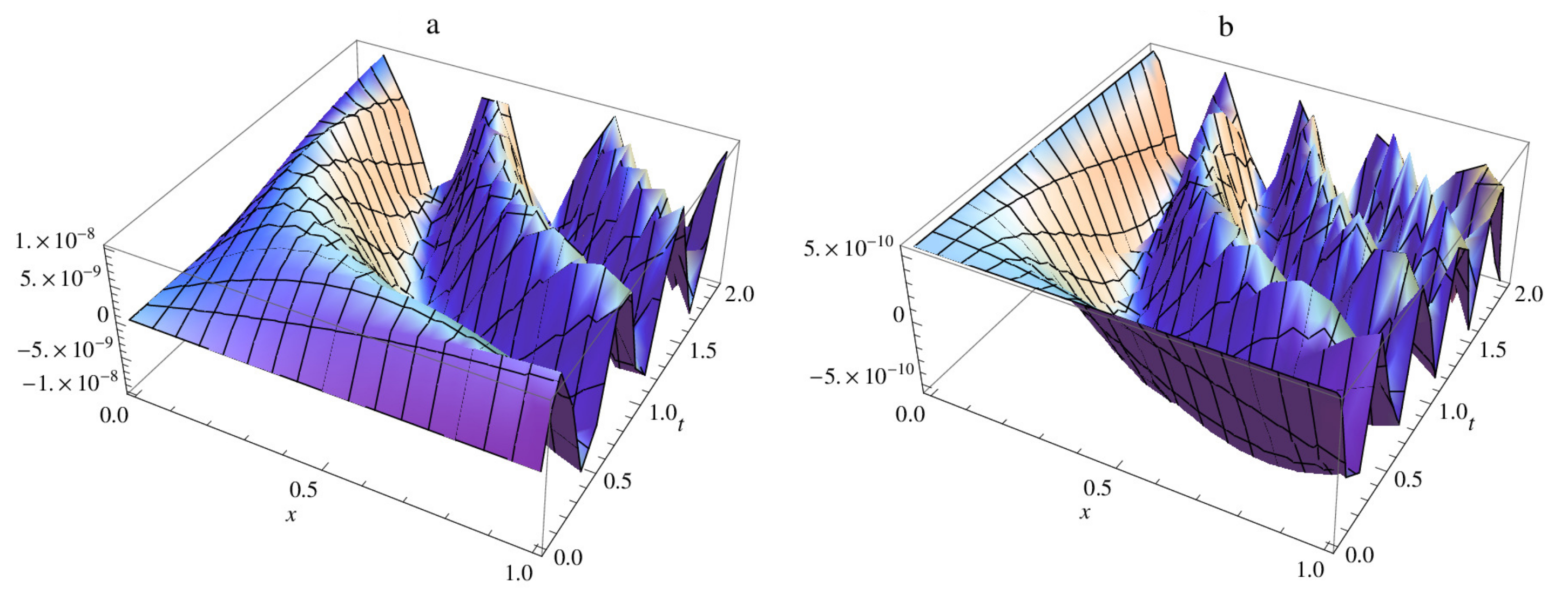
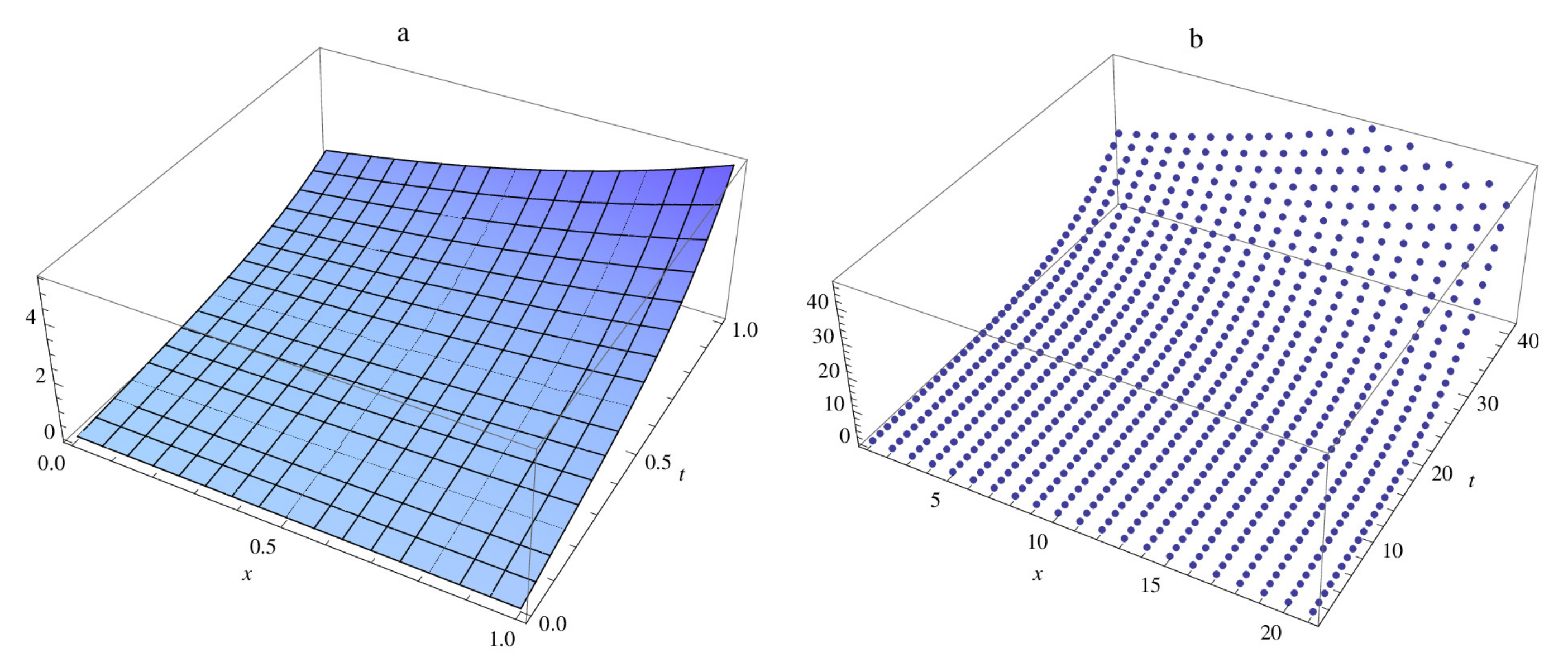
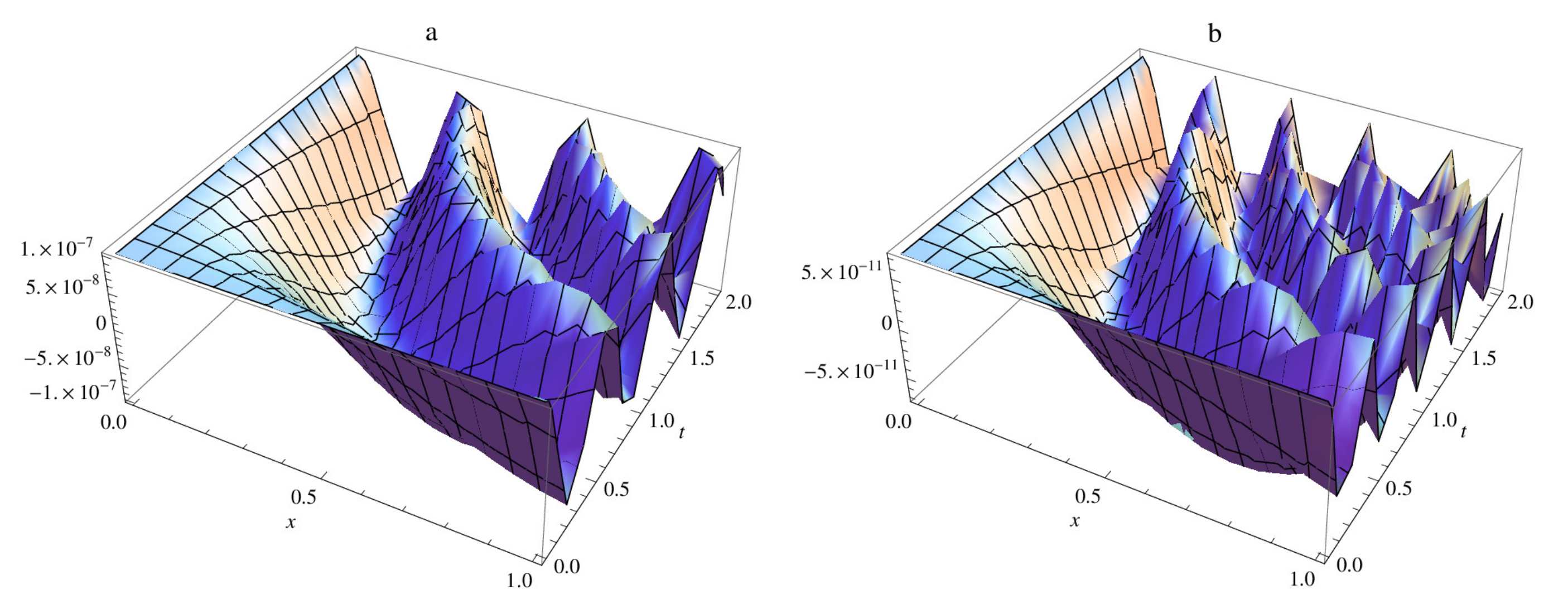
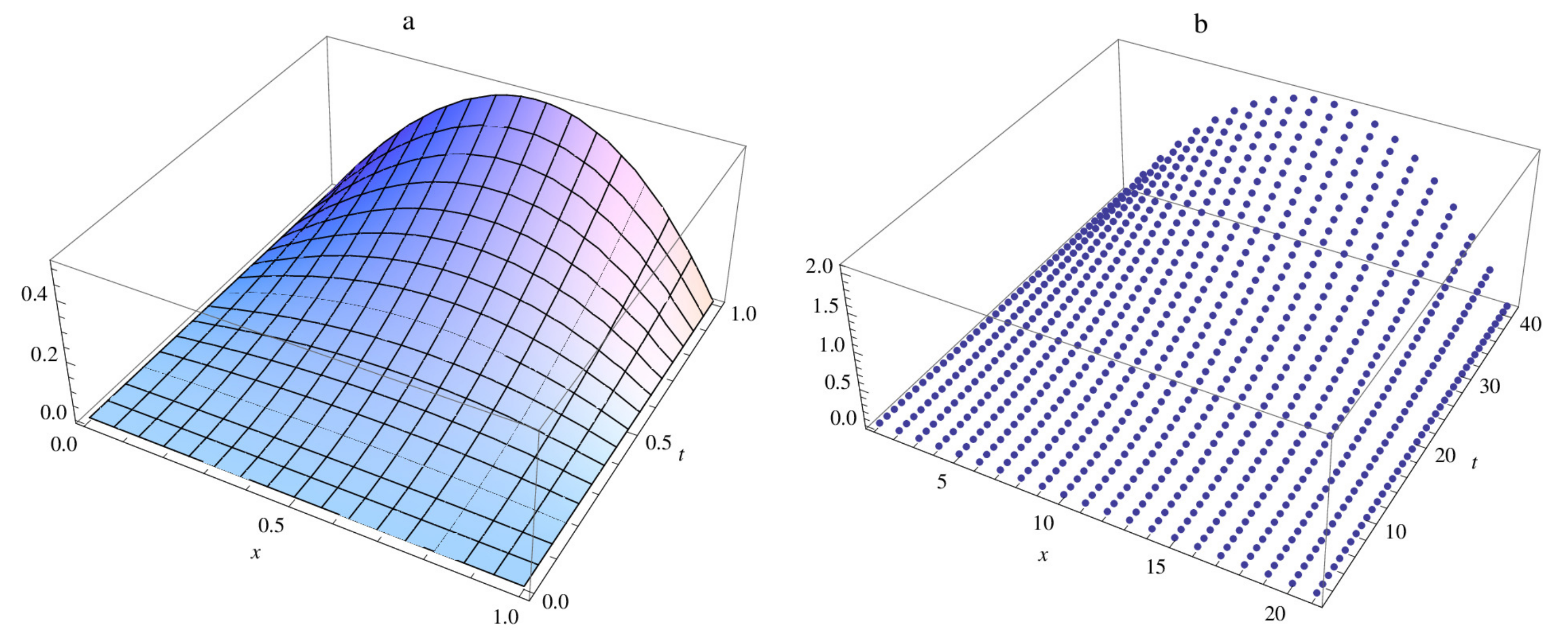
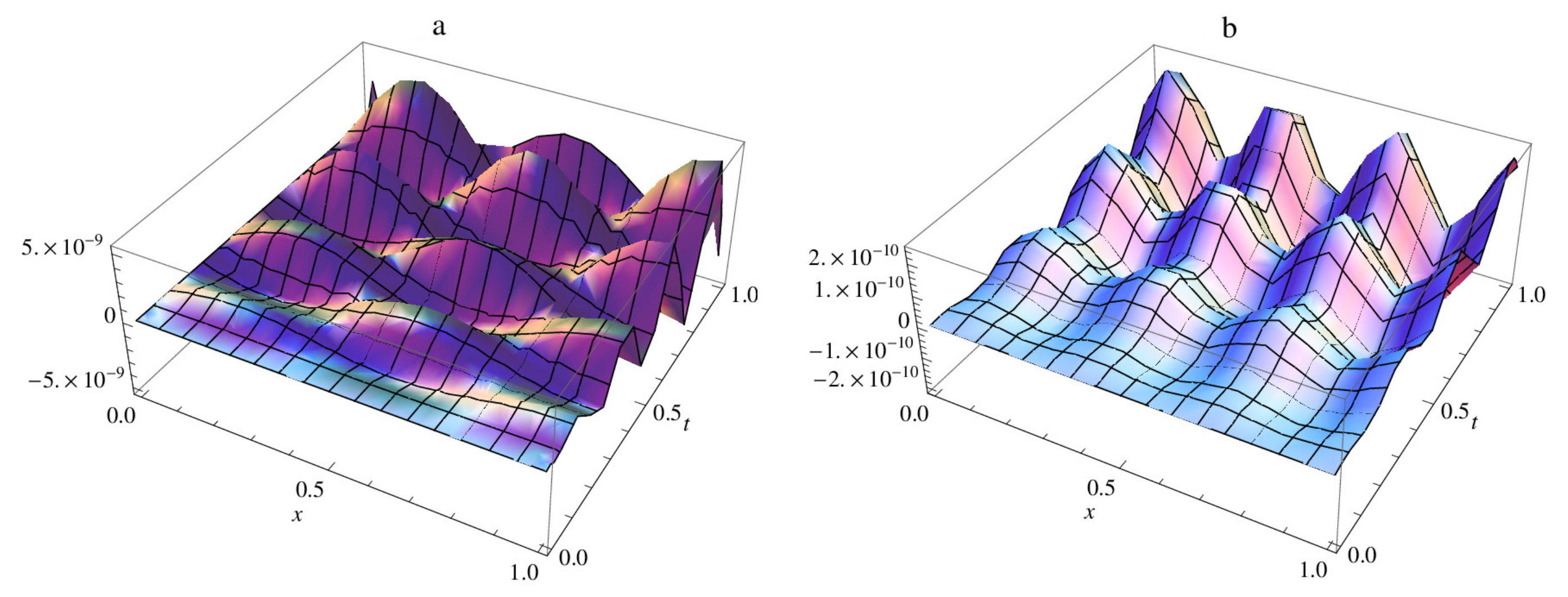
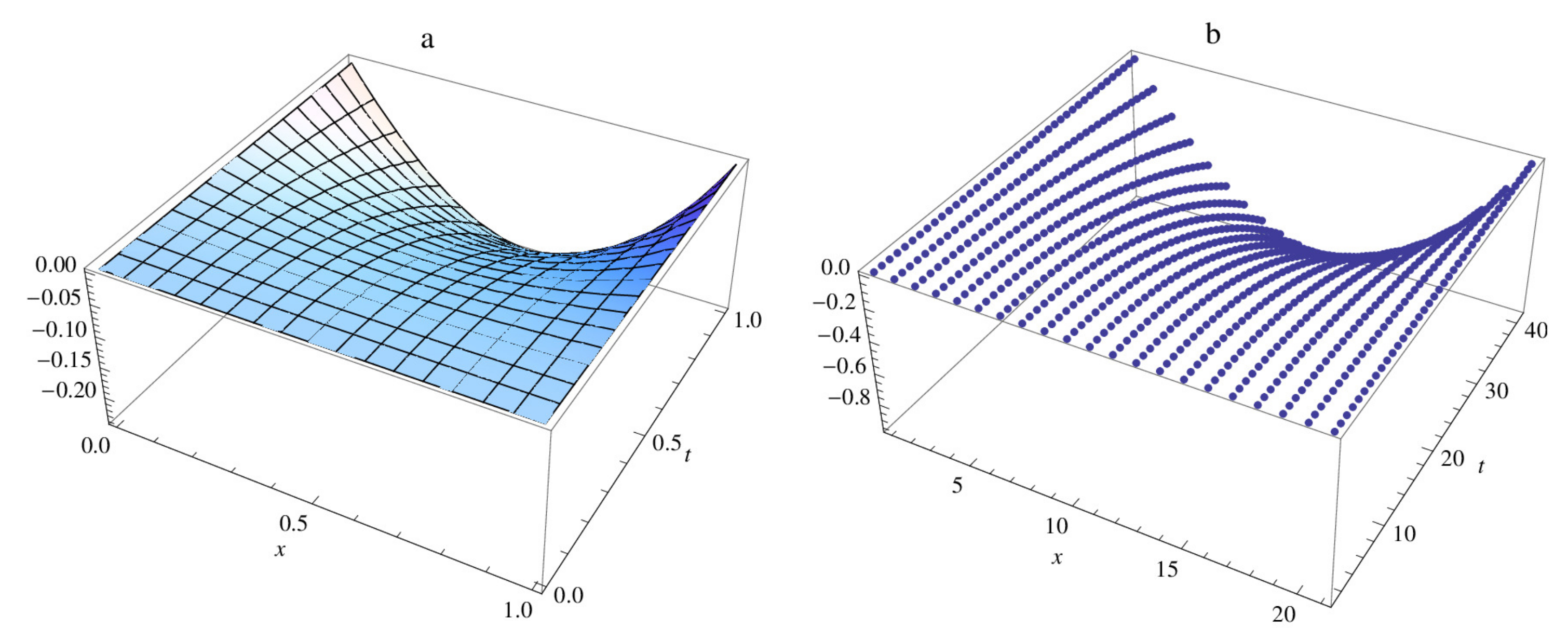


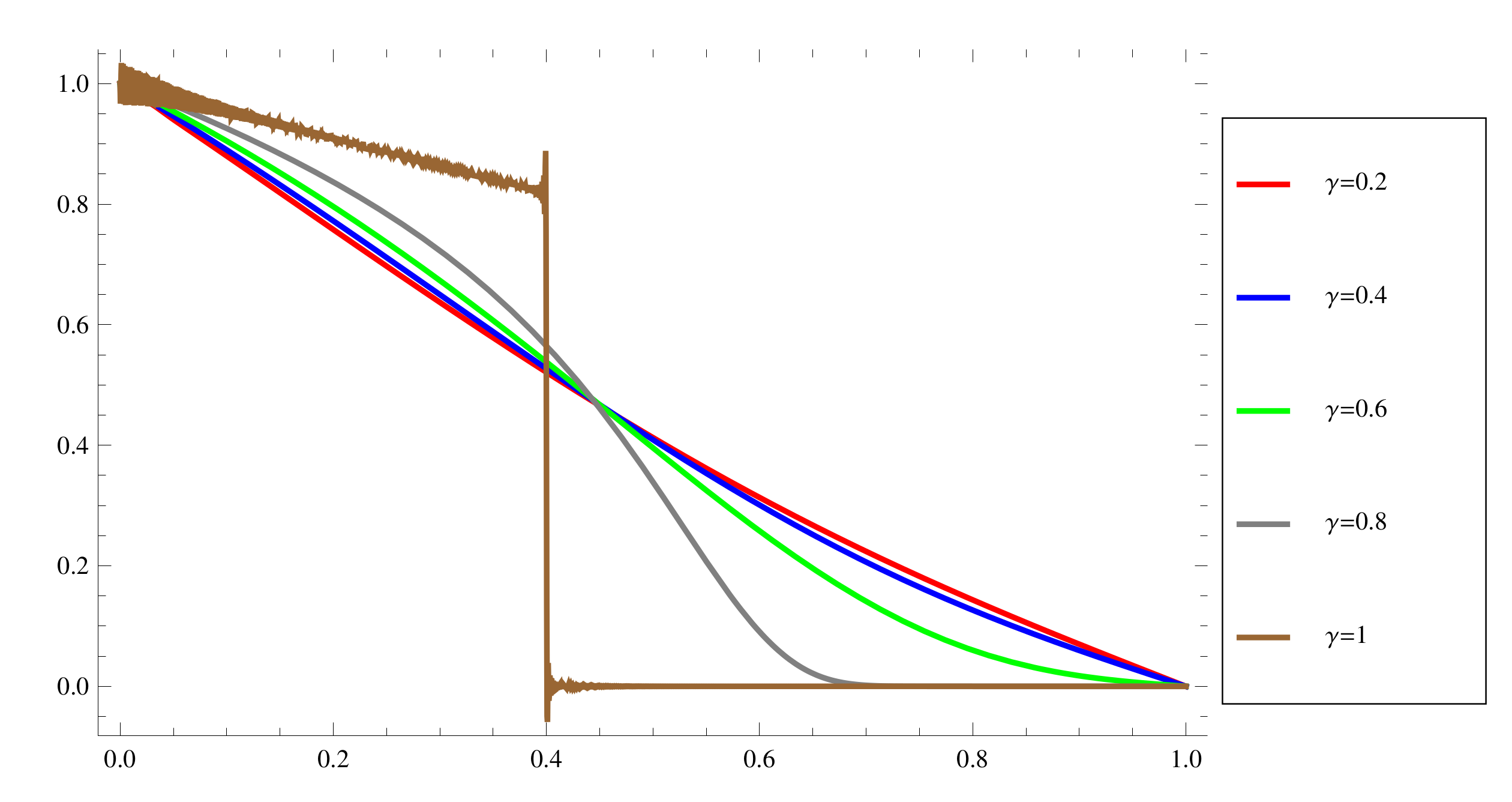
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | |||||||||
| 4 | |||||||||
| [42] | – | – | |||||||
| – | – |
| M | |||||||
|---|---|---|---|---|---|---|---|
| 3 | |||||||
| 4 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nosrati Sahlan, M.; Afshari, H.; Alzabut, J.; Alobaidi, G. Using Fractional Bernoulli Wavelets for Solving Fractional Diffusion Wave Equations with Initial and Boundary Conditions. Fractal Fract. 2021, 5, 212. https://doi.org/10.3390/fractalfract5040212
Nosrati Sahlan M, Afshari H, Alzabut J, Alobaidi G. Using Fractional Bernoulli Wavelets for Solving Fractional Diffusion Wave Equations with Initial and Boundary Conditions. Fractal and Fractional. 2021; 5(4):212. https://doi.org/10.3390/fractalfract5040212
Chicago/Turabian StyleNosrati Sahlan, Monireh, Hojjat Afshari, Jehad Alzabut, and Ghada Alobaidi. 2021. "Using Fractional Bernoulli Wavelets for Solving Fractional Diffusion Wave Equations with Initial and Boundary Conditions" Fractal and Fractional 5, no. 4: 212. https://doi.org/10.3390/fractalfract5040212
APA StyleNosrati Sahlan, M., Afshari, H., Alzabut, J., & Alobaidi, G. (2021). Using Fractional Bernoulli Wavelets for Solving Fractional Diffusion Wave Equations with Initial and Boundary Conditions. Fractal and Fractional, 5(4), 212. https://doi.org/10.3390/fractalfract5040212







