Solutions of Bernoulli Equations in the Fractional Setting

Abstract

We present a general series representation formula for the local solution of the Bernoulli equation with Caputo fractional derivatives. We then focus on a generalization of the fractional logistic equation and present some related numerical simulations.

1. Introduction

Interest in time fractional evolutive systems has progressively grown in recent years. Models arising with aspects related to non-local behavior need to be studied in the fractional setting; see [1,2] for an overview and [2,3] for fractional growth models for social and biological dynamics. The fractional derivatives are indeed non-local operators, that is, convolution-type operators. In the applied sciences, the main interest in fractional models is due to the fact that such models introduce the so-called memory effect. This effect is mainly justified by the non-locality of the time-fractional derivative, and it seems to be relevant in the characterization of many applied models. A second reading is given in terms of the delaying effect. Indeed, the time-fractional derivative introduces a different clock for the underlying model, as in the case of the relaxation equation. When the order of the fractional derivative is one, the underlying model emerges.

Here, we locally solve the following Cauchy system, involving a fractional Bernoulli equation of the form

$${{}^{C}D}_t^{\beta }u+a_{0}u=a_1{u}^{p+1},u\left(0\right)=u_0$$

(1)

where $p\in \mathbb{N}$, with $p\ge 1$, $a_0$ and $a_1$ are real numbers and ${{}^{C}D}_t^{\beta }$ denotes the Caputo derivative. If $\beta =1$ then ${{}^{C}D}_t^{\beta }u=u^{\prime }$ and (1) is the Bernoulli equation, studied by Jacob Bernoulli (1695). We remark that Bernoulli equations (with $\beta =1$) arise in non-linear models of production and capital accumulation, in particular when polynomial production functions are considered, see ([4] Chapter 6.3). As an example of an application to mathematical bio-medicine, we refer to ([5] Chapter 4), where the parameter p is associated with the exponential growth rate of a homogeneous avascular tumor.

As a particular case, the exact solution in the case $a_0=a_1=-1$ and $\beta =1$ is given by

$$u\left(t\right)=\frac{e^t}{\sqrt[p]{c_0+e^{pt}}};\mathrm{where}{c}_0:=u_0^{-p}-1.$$

Moving to the fractional setting, we have similar approaches that cannot be followed. As it is well known, the solution of the fractional logistic equation—corresponding to $p=1$ and $a_0=a_1=-1$ in (1)—was an open problem, and in [6], the first and the third author were able to solve the fractional logistic equation by series representation, giving a detailed formula involving Euler numbers for $u_0=1/2$. The use of a logistic equation to model population dynamics dates back to the mid-19th century when Pierre François Verhulst devoted a series of papers [7,8,9] to the description of a model of population growth. Since then, the logistic equation is largely used in bio-mathematical modeling, for instance, to describe cancer growth models and epidemic models. In the particular case of social dynamics, the need to model memory effects and non-local behavior lead to a decline of the above models in a fractional setting. At this early stage, the problem of addressing non-linear dynamics and series expansions proved, at least in a local setting, to be a viable approach. This methodology was applied to SIS epidemic models in [10] (a compartmental epidemic model in which the population is split into susceptible and infective individuals) and also further investigated in [11]. The present study extends the result in [6] to general initial data and to Bernoulli equations of general degree $p+1$: we present a recursive formula for the coefficients of the solutions and explicit closed formulas for the first terms. Note that the relation with Euler numbers for general initial data, even in the logistic case $p=1$, appears to be lost, but the general recursive formula preserves its structure, based on generalized binomial coefficients that were introduced in [6] and further investigated in [12]. Then the proposed method is applied to the particular case $a_0=a_1=\pm 1$, related to the fractional logistic equation, and we present a qualitative analysis of the solutions based on numerical simulations—see Figure 1.

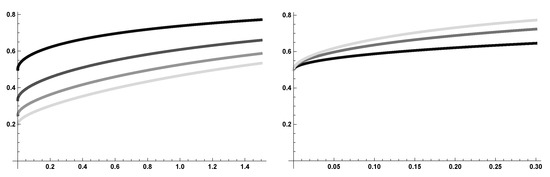
Figure 1. On the (left), solutions of the logistic equation ${}^C{D}^{\beta }u-u=-u^2$ (on the left) with $\beta =1/2$ and $u_0=1/2,1/3,1/4,1/5$; darker lines correspond to bigger $u_0$s. On the (right), solutions of the logistic equation ${}^C{D}^{\beta }u-u=-u^{p+1}$ with $\beta =u_0=1/2$ and $p=1,2,3$; darker lines correspond to bigger ps.

Preliminaries on Fractional Calculus

Let us consider the set $AC\left(\right[a,b\left]\right)$ of continuous functions with a derivative in $L_1\left([a,b]\right)$. Thus, $v\in AC\left(\right[a,b\left]\right)$ is continuous and such that $v^{\prime }=g\in L_1\left([a,b]\right)$, that is, v has the representation

$$\begin{array}{c}\hfill v\left(t\right)=v\left(a\right)+{\int }_a^{t}g\left(s\right)ds,t\in [a,b].\end{array}$$

(2)

We notice that the space $AC\left(\right[a,b\left]\right)$ coincides with the Sobolev space

$$\begin{array}{c}\hfill W^{1,1}\left([a,b]\right)=\{v\in L_1\left([a,b]\right):v^{\prime }\in L_1\left([a,b]\right)\}\end{array}$$

endowed with the norm

$$\begin{array}{c}\hfill {\parallel v\parallel }_{W^{1,1}}={\parallel v\parallel }_{L_1}+{\parallel v^{\prime }\parallel }_{L_1}.\end{array}$$

For $v\in AC\left(\right[a,b\left]\right)$ and $\beta \in (0,1)$, we introduce the Riemann–Liouville derivative of v,

$$\begin{array}{c}\hfill {\mathcal{D}}_t^{\beta }v\left(t\right):=\frac{1}{\Gamma (1-\beta )}\frac{d}{dt}{\int }_a^{t}v\left(s\right){(t-s)}^{-\beta }ds,t\in [a,b]\end{array}$$

(3)

and the Caputo derivative of v,

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }v\left(t\right):=\frac{1}{\Gamma (1-\beta )}{\int }_a^t{v}^{\prime }\left(s\right){(t-s)}^{-\beta }ds,t\in [a,b].\end{array}$$

(4)

Further on, we use the following relation between derivatives

$$\begin{array}{cc}\hfill {\mathcal{D}}_t^{\beta }v\left(t\right)=& \frac{1}{\Gamma (1-\beta )}\frac{v\left(a\right)}{{(t-a)}^{\beta }}+{{}^{C}D}_t^{\beta }v\left(t\right).\hfill \end{array}$$

(5)

The relation (5), together with the existence of the derivatives (3) and (4), hold a.e. on $[a,b]$ and ${\mathcal{D}}_t^{\beta }v\in L_q\left([a,b]\right)$ with $1\le q\le 1/\beta$ (see for example ([13] page 28)).

In this study, we consider the fractional equations on $[0,b)$. Let us emphasize that if $v\left(0\right)=0$, then Formula (5) gives the equivalence

$$\begin{array}{c}\hfill {\mathcal{D}}_t^{\beta }v={{}^{C}D}_t^{\beta }v.\end{array}$$

2. Fractional Bernoulli Equations

Let us introduce

$$\begin{array}{c}\hfill u\left(t\right)=\sum _{n\ge 0}{c}_n^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)},t\in (0,r)\end{array}$$

(6)

where $r>0$ is the radius of convergence and $c_n^{\left(1\right)}$ are real coefficients.

Next, we introduce the generalized binomial coefficient

$$\begin{array}{c}\hfill {\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }=\frac{\Gamma (n\beta +1)}{\Gamma (k\beta +1)\Gamma \left(\right(n-k)\beta +1)},0\le k\le n,k,n\in \mathbb{N},\beta \in (0,1).\end{array}$$

Theorem 1.

The unique continuous solution on $[0,b)\subset [0,r)$ to

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u+a_{0}u=a_1{u}^{p+1},u\left(0\right)=u_0,p\in \mathbb{N},a_0,a_1\in \mathbb{R},\beta \in (0,1)\end{array}$$

has the series representation (6) on $[0,b)$ where

$$\begin{array}{cc}\hfill & c_0^{\left(1\right)}=u_0\hfill \\ \hfill & c_{n+1}^{\left(1\right)}=-a_0{c}_n^{\left(1\right)}+a_1\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}forn\ge 0.\hfill \end{array}$$

(7)

Proof. 

We consider

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u+a_{0}u=a_1{u}^{p+1},u\left(0\right)=u_0\end{array}$$

where ${{}^{C}D}_t^{\beta }$ denotes the Caputo derivative. Let us denote the power of u as follows

$$\begin{array}{c}\hfill u\left(t\right)=\sum _{n\ge 0}{c}_n^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)},\\ \hfill \\ \hfill u^2\left(t\right)=\sum _{n\ge 0}{c}_n^{\left(2\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)},\end{array}$$

(8)

$$\begin{array}{c}\hfill u^3\left(t\right)=\sum _{n\ge 0}\left(\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(2\right)}{c}_{n-k}^{\left(1\right)}\right)\frac{t^{\beta n}}{\Gamma (\beta n+1)}=\sum _{n\ge 0}{c}_n^{\left(3\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)},\end{array}$$

where

$$\begin{array}{c}\hfill c_k^{\left(2\right)}=\sum _{s=0}^k{\left[\begin{array}{c}k\\ s\end{array}\right]}_{\beta }{c}_s^{\left(1\right)}{c}_{k-s}^{\left(1\right)}\Rightarrow c_n^{\left(3\right)}=\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(2\right)}{c}_{n-k}^{\left(1\right)}\end{array}$$

and, by further iterations,

$$\begin{array}{c}\hfill u^{p+1}\left(t\right)=\sum _{n\ge 0}{c}_n^{(p+1)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\end{array}$$

where

$$\begin{array}{c}\hfill c_n^{(p+1)}=\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}.\end{array}$$

(9)

Note that for $p\in \mathbb{N}$

$$c_0^{\left(p\right)}={\left(c_0^{\left(1\right)}\right)}^p.$$

Therefore,

$$\begin{array}{cc}\hfill a_{0}u-a_1{u}^{p+1}=& u(a_0-a_1{u}^p)=\sum _i{c}_i^{\left(1\right)}\frac{t^{\beta i}}{\Gamma (\beta i+1)}·\left(a_0-a_1\sum _j{c}_j^{\left(p\right)}\frac{t^{\beta j}}{\Gamma (\beta j+1)}\right)\hfill \\ \hfill =& a_0\sum _i{c}_i^{\left(1\right)}\frac{t^{\beta i}}{\Gamma (\beta i+1)}-a_1\sum _i{c}_i^{\left(1\right)}\frac{t^{\beta i}}{\Gamma (\beta i+1)}\sum _j{c}_j^{\left(p\right)}\frac{t^{\beta j}}{\Gamma (\beta j+1)}\hfill \\ \hfill =& a_0\sum _j{c}_j^{\left(1\right)}\frac{t^{\beta j}}{\Gamma (\beta j+1)}-a_1\sum _n{c}_n^{(p+1)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\hfill \\ \hfill =& \sum _n\left(a_0{c}_n^{\left(1\right)}-a_1{c}_n^{(p+1)}\right)\frac{t^{\beta n}}{\Gamma (\beta n+1)}\hfill \\ \hfill =& \sum _n\left(a_0{c}_n^{\left(1\right)}-a_1\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}\right)\frac{t^{\beta n}}{\Gamma (\beta n+1)}.\hfill \end{array}$$

On the other hand, from (5), we have that

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u\left(t\right)=-u_0\frac{t^{-\beta }}{\Gamma (1-\beta )}+{\mathcal{D}}_t^{\beta }\sum _{n\ge 0}{c}_n^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\end{array}$$

where, after some calculation, from (3),

$$\begin{array}{c}\hfill {\mathcal{D}}_t^{\beta }\frac{t^{\beta n}}{\Gamma (\beta n+1)}=\frac{t^{\beta (n-1)}}{\Gamma \left(\beta \right(n-1)+1)},t\in [0,b).\end{array}$$

Thus, we obtain

$$\begin{array}{cc}\hfill {{}^{C}D}_t^{\beta }u\left(t\right)=& -u_0\frac{t^{-\beta }}{\Gamma (1-\beta )}+\sum _{n\ge 0}{c}_n^{\left(1\right)}\frac{t^{\beta (n-1)}}{\Gamma \left(\beta \right(n-1)+1)}\hfill \\ \hfill =& -u_0\frac{t^{-\beta }}{\Gamma (1-\beta )}+c_0^{\left(1\right)}\frac{t^{-\beta }}{\Gamma (-\beta +1)}+\sum _{n\ge 1}{c}_n^{\left(1\right)}\frac{t^{\beta (n-1)}}{\Gamma \left(\beta \right(n-1)+1)}.\hfill \end{array}$$

From the fact that $u_0=c_0^{\left(1\right)}$ by construction, we write

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u\left(t\right)=\sum _{n\ge 0}{c}_{n+1}^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)},t\in [0,b].\end{array}$$

Then the solution to

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u=-a_{0}u+a_1{u}^{p+1}=-u(a_0-a_1{u}^p)\end{array}$$

can be written in terms of the coefficients $c_n^{\left(1\right)}$, $n\in \mathbb{N}$ given by

$$\begin{array}{cc}\hfill c_{n+1}^{\left(1\right)}& =-a_0{c}_n^{\left(1\right)}+a_1{c}_n^{(p+1)}\hfill \\ \hfill & =-c_n^{\left(1\right)}\left(a_0-a_1{c}_0^{\left(p\right)}\right)+a_1\sum _{k=1}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)},\hfill \\ \hfill & =-a_0{c}_n^{\left(1\right)}+a_1\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}\mathrm{for}n\ge 0.\hfill \end{array}$$

□

Some Closed Formulas

The first few elements of the sequence $c_n^{\left(p\right)}$, $p\in \mathbb{N}$ (over the index p) are

$$\begin{array}{cc}\hfill & c_n^{\left(1\right)},n\in \mathbb{N}\hfill \\ \hfill & c_n^{\left(2\right)}=\sum _{s=0}^n{\left[\begin{array}{c}n\\ s\end{array}\right]}_{\beta }{c}_s^{\left(1\right)}{c}_{n-s}^{\left(1\right)}\hfill \\ \hfill & c_n^{\left(3\right)}=\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }\sum _{s=0}^k{\left[\begin{array}{c}k\\ s\end{array}\right]}_{\beta }{c}_s^{\left(1\right)}{c}_{k-s}^{\left(1\right)}{c}_{n-k}^{\left(1\right)}.\hfill \end{array}$$

We compute the first terms of $c_n^{\left(1\right)}$. Fix $p\ge 1$ and note that $c_0^{\left(1\right)}=u_0$ and if $n=1$ then

$$c_1^{\left(1\right)}=-u_0(a_0-a_1{u}_0^p).$$

(10)

To compute $c_2^{\left(1\right)}$ we need $c_1^{\left(h\right)}$ for $h=1,\dots ,p$. By (9) one can prove by induction that for $h\in \mathbb{N}$

$$c_1^{\left(h\right)}=-h{u}_0^h(a_0-a_1{u}_0^p).$$

Hence, we apply (7) and we get

$$\begin{array}{cc}\hfill c_2^{\left(1\right)}& =-c_1^{\left(1\right)}\left(a_0-a_1{c}_0^{\left(p\right)}\right)+a_1{\left[\begin{array}{c}1\\ 1\end{array}\right]}_{\beta }{c}_1^{\left(p\right)}{c}_0^{\left(1\right)}\hfill \end{array}$$

from which we deduce by a direct computation

$$c_2^{\left(1\right)}=u_0(a_0-a_1{u}_0^p)(a_0-a_1(p+1)u_0^p).$$

(11)

To compute $c_3^{\left(1\right)}$, we also need $c_2^{\left(h\right)}$ for $h=1,\dots ,p$. Using (9), we obtain

$$c_2^{\left(h\right)}=\sum _{k=0}^2{\left[\begin{array}{c}2\\ k\end{array}\right]}_{\beta }{c}_k^{(h-1)}{c}_{2-k}^{\left(1\right)}$$

and, by an inductive argument, using also the fact that $c_0^{\left(p\right)}=u_0^p$ for all $p\ge 1$, one can prove the closed formula for all $h\ge 1$

$$c_2^{\left(h\right)}=u_0^h(a_0-a_1{u}_0^p)\left(h(a_0-a_1(p+1)u_0^p)+\frac{h(h-1)}{2}{\left[\begin{array}{c}2\\ 1\end{array}\right]}_{\beta }(a_0-a_1{u}_0^p)\right).$$

Then

$$\begin{array}{cc}\hfill c_3^{\left(1\right)}=& -a_0{c}_2^{\left(1\right)}+a_1{c}_2^{(p+1)}\hfill \\ \hfill =& -a_0{u}_0(a_0-a_1{u}_0^p)(a_0-a_1(p+1)u_0^p)\hfill \\ \hfill & +a_1{u}_0^{p+1}(a_0-a_1{u}_0^p)((p+1)(a_0-a_1(p+1)u_0^p)\hfill \\ \hfill & +\frac{p(p+1)}{2}{\left[\begin{array}{c}2\\ 1\end{array}\right]}_{\beta }(a_0-a_1{u}_0^p))\hfill \\ \hfill =& -u_0(a_0-a_1{u}_0^p){(a_0-a_1(p+1)u_0^p)}^2\hfill \\ & +\frac{p(p+1)}{2}{\left[\begin{array}{c}2\\ 1\end{array}\right]}_{\beta }{a}_1{u}_0^{p+1}{(a_0-a_1{u}_0^p)}^2\hfill \\ \hfill =& -u_0(a_0-a_1{u}_0^p)({(a_0-a_1(p+1)u_0^p)}^2\hfill \\ \hfill & -\frac{p(p+1)}{2}{\left[\begin{array}{c}2\\ 1\end{array}\right]}_{\beta }{a}_1{u}_0^p(a_0-a_1{u}_0^p)).\hfill \end{array}$$

(12)

3. Fractional Logistic Equations

Here, we extend some of the results established in [6] for the fractional logistic equation with initial datum $u_0=1/2$ to the case of general initial data $u_0\in (0,1)$. Applying the above method, if $p=1$ and $a_0=a_1=-1$, then the solution of

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u=u-u^2;u\left(0\right)=u_0\end{array}$$

(13)

can be represented in series form

$$\begin{array}{c}\hfill u\left(t\right)=\sum _{n\ge 0}{c}_n^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\end{array}$$

where

$$c_0^{\left(1\right)}=u_0;c_{n+1}^{\left(1\right)}=c_n^{\left(1\right)}-\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(1\right)}{c}_{n-k}^{\left(1\right)}.$$

Note that, as shown in [6], when $u_0=1/2$, the above formula reduces to

$$\left\{\begin{array}{c}{c}_0^{\left(1\right)}={\displaystyle \frac{1}{2}};c_1^{\left(1\right)}={\displaystyle \frac{1}{4}};\hfill \\ \\ {\displaystyle c_{2n}^{\left(1\right)}=0;c_{2n+1}^{\left(1\right)}=-\sum _{k=0}^n{\left[\begin{array}{c}2n\\ 2k+1\end{array}\right]}_{\beta }{c}_{2k+1}^{\left(1\right)}{c}_{2(n-k)-1}^{\left(1\right)}}\hfill & \mathrm{for}n\ge 1.\hfill \end{array}\right.$$

Keeping $a_0=a_1=-1$ and considering the equation with generic p, we have that the solution of

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u=u-u^{p+1};u\left(0\right)=u_0\end{array}$$

(14)

can be represented in series form

$$\begin{array}{c}\hfill u\left(t\right)=\sum _{n\ge 0}{c}_n^{\left(p\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\end{array}$$

where

$$\left\{\begin{array}{c}{c}_0^{\left(1\right)}=u_0{c}_1^{\left(1\right)}=u_0(1-u_0^p);\hfill \\ \hfill \\ {\displaystyle c_{n+1}^{\left(1\right)}=c_n^{\left(1\right)}-\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}.}\hfill \end{array}\right.$$

Remark 1

(On the null coefficients in the general case). Note that if $u_0=\sqrt[p]{1/(p+1)}$ then, in view of (11), $c_2^{\left(1\right)}=0$, in agreement with the case $p=1$. However, it is not possible to deduce that $c_{2n}^{\left(1\right)}\equiv 0$ as in the case $p=1$, because even for $p=2$, choosing $u_0=\sqrt{1/3}$ one can numerically verify that $c_2^{\left(1\right)}=0$ and $c_4^{\left(1\right)}\ne 0$. Then, one may look for some other generalization, for instance imposing $c_{p+1}^{\left(1\right)}=0$ and guess whether $c_{n(p+1)}^{\left(1\right)}=0$ for some $n\ge 1$. Furthermore, in this case, the answer is negative. Indeed, using the last equality (12) to solve the equation $c_3^{\left(1\right)}=0$ with respect to the initial datum $u_0$, we get by a direct computation that if $u_0=\frac{12+6\pi +\sqrt{144+96\pi }}{24+18\pi }$ and if $p=2$ then $c_3^{\left(1\right)}=0$, but symbolic numerical computations yield $c_n^{\left(1\right)}\ne 0$ for $n=3,\dots ,30$.

Consider now the case $a_0=a_1=1$. Then the solution of

$$\begin{array}{c}\hfill {{}^{C}D}_t^{\beta }u=u-u^2;u\left(0\right)=u_0\end{array}$$

(15)

can be represented as

$$\begin{array}{c}\hfill u\left(t\right)=\sum _{n\ge 0}{\overline{c}}_n^{\left(p\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}\end{array}$$

where

$$\begin{array}{cc}\hfill c_0^{\left(1\right)}& =u_0{c}_1^{\left(1\right)}=-u_0(1-u_0^p),\hfill \\ \hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill c_{n+1}^{\left(1\right)}& =-c_n^{\left(1\right)}+\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{\beta }{c}_k^{\left(p\right)}{c}_{n-k}^{\left(1\right)}.\hfill \end{array}$$

(17)

We compare the coefficients $c_n^{\left(1\right)}$ and ${\overline{c}}_n^{\left(1\right)}$. We have ${\overline{c}}_0^{\left(1\right)}=c_0^{\left(1\right)}$, ${\overline{c}}_1^{\left(1\right)}=-c_1^{\left(1\right)}$ and, by induction, ${\overline{c}}_1^{\left(p\right)}=-c_1^{\left(p\right)}$. Moreover, ${\overline{c}}_2^{\left(1\right)}=-c_2^{\left(1\right)}$. However, this symmetry breaks as soon as we consider ${\overline{c}}_2^{\left(2\right)}$; indeed, we have

$${\overline{c}}_2^{\left(2\right)}=-c_2^{\left(2\right)}+2{\left[\begin{array}{c}2\\ 1\end{array}\right]}_{\beta }{\left(c_1^{\left(1\right)}\right)}^2.$$

Numerical Simulations

Our tests rely on a direct application of the above explicit formulas. Coefficients are calculated via Wolfram Mathematica software. In our tests, we focused on the logistic case $a_0=a_1=-1$ and on the case $a_0=a_1=1$. We computed the coefficients $c_n^{\left(1\right)}$ using the recursive Formulas (9) and (10), and we approximated the solution of (1) with the partial sum

$$u\left(t\right)=\sum _{n=0}^N{c}_n^{\left(1\right)}\frac{t^{\beta n}}{\Gamma (\beta n+1)}$$

with $N=200$, the parameter N was tuned so that no appreciable difference can be noted with respect to higher-order approximations. The method was validated by comparison with the exact solutions of (1), which can be explicitly computed in the ordinary case $\beta =1$.

In Figure 2, we evaluated $u\left(t\right)$ with fixed initial datum $u_0=1/2$ and $p=1$ and several orders of fractional derivatives. We may note the expected damping effect of fractional derivation.

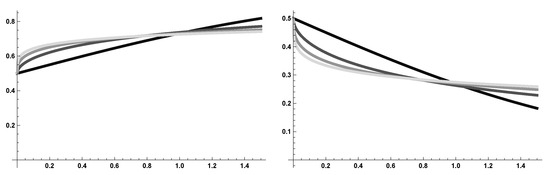
Figure 2. Numerical solutions of ${}^C{D}^{\beta }u-u=-u^2$ (on the left) and of ${}^C{D}^{\beta }u=-u+u^2$ (on the right) with $u_0=1/2$ and $\beta =1,1/2,1/3,1/4$. Darker lines correspond to bigger $\beta$’s.

Figure 3 compares the solutions $u\left(t\right)$ with different initial data, setting $\beta =1/2$ and $p=1$. The resulting set of ordered curves suggests the local uniqueness of the solutions; however, the investigation of this is beyond the purpose of the present paper.

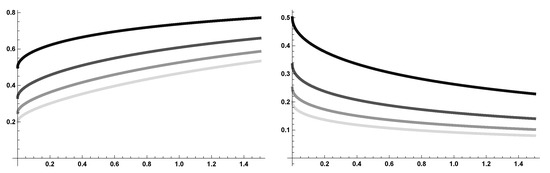
Figure 3. Solutions of ${}^C{D}^{\beta }u-u=-u^2$ (on the left) and of ${}^C{D}^{\beta }u+u=u^2$ (on the right) with $\beta =1/2$ and $u_0=1/2,1/3,1/4,1/5$. Darker lines correspond to bigger $u_0$’s.

We then investigated higher degree fractional Euler equations, setting $\beta =u_0=1/2$ and letting p vary between 1 and 3, see Figure 4. At least near 0, from a qualitative point of view, the solutions display a similar behavior, and no intersections between the solutions are detected.

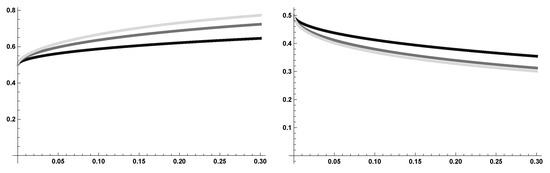
Figure 4. Solutions of ${}^C{D}^{\beta }u-u=-u^{p+1}$ (on the left) and of $D^{\beta }u+u=u^{p+1}$ (on the right) with $\beta =u_0=1/2$ and $p=1,2,3$. Darker lines correspond to bigger p’s.

For the sake of comparison, we collected some of the above results in Figure 5, showing the combined effect of varying initial data $u_0$ and degrees p.

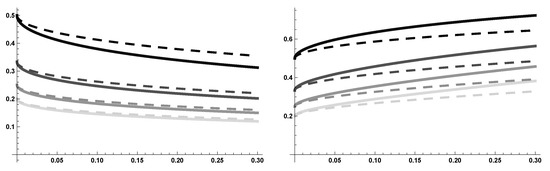
Figure 5. Solutions of ${}^C{D}^{\beta }u+u=u^{p+1}$ (on the left) and of ${}^C{D}^{\beta }u=u-u^{(p+1)}$ (on the right) with $\beta =1/2$ and $u_0=1/2,1/3,1/4,1/5$ and $p=1,2$. Darker lines correspond to bigger $u_0$’s; continuous lines correspond to $p=2$ and dashed lines correspond to $p=1$.

Finally we propose some numerical estimations for the radius of convergence of the series (8), by computing the sequence

$$r_n:={\left(\frac{\Gamma (\beta n+1)}{|c_n^{\left(1\right)}|}\right)}^{\frac{1}{\beta n}}.$$

In Figure 6 and Figure 7, we plotted the first 300 terms of $r_n$ with varying degrees p and orders of derivation $\beta$. The asymptotic behavior of $r_n$ suggests an exponential increase for the series coefficients $c_n^{\left(1\right)}$ in all the cases under exam. Furthermore, their comparison shows the radius of convergence $r:=lim{r}_n$ to be decreasing with respect to both the degree p (Figure 6) and order of derivation $\beta$ (Figure 7). Finally, no substantial difference between the case $a_0=a_1=-1$ and the case $a_0=a_1=1$ emerged.

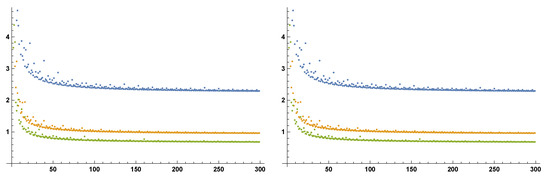
Figure 6. Asymptotic behavior of the sequence approximating the radius of convergence $r_n$ for $a_0=a_1=-1$ (on the left) and $a_0=a_1=1$ (on the right) with $\beta =1/2$, $u_0=1/3$ and $p=1,2,3$ in blue, orange, and green, respectively.

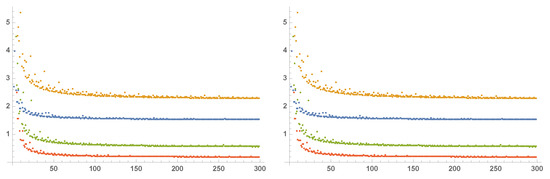
Figure 7. Asymptotic behavior of the sequence approximating the radius of convergence $r_n$ for $a_0=a_1=-1$ (on the left) and $a_0=a_1=1$ (on the right) with $u_0=1/3$, $p=1$, and $\beta =1,1/2,1/3,1/4$ in blue, orange, green, and red, respectively.

4. Conclusions

Although the fractional differential calculus is as old as the ordinary one (the first introduction of a fractional derivative dates back to Leibniz in 1695), the complexity of the computations involved still prevents a full exploitation of its applicative potential. Here, we consider the Caputo fractional derivative. The presence of a singular kernel introduces a memory, and it gives a non-local character to the dynamics. These non-local aspects are realistic in the applications. By introducing fractional derivatives, we obtain a global effect, which may slow down the underlying dynamics. In particular, for non-linear equations, we still observe the classical delaying effect introduced by the fractional derivative for linear equations. This motivates our analysis. Further directions include estimations of the radius of convergence, global existence results, and possible generalization to other non-linear fractional dynamics.