Solutions of Bernoulli Equations in the Fractional Setting
Abstract
1. Introduction
Preliminaries on Fractional Calculus
2. Fractional Bernoulli Equations
Some Closed Formulas
3. Fractional Logistic Equations
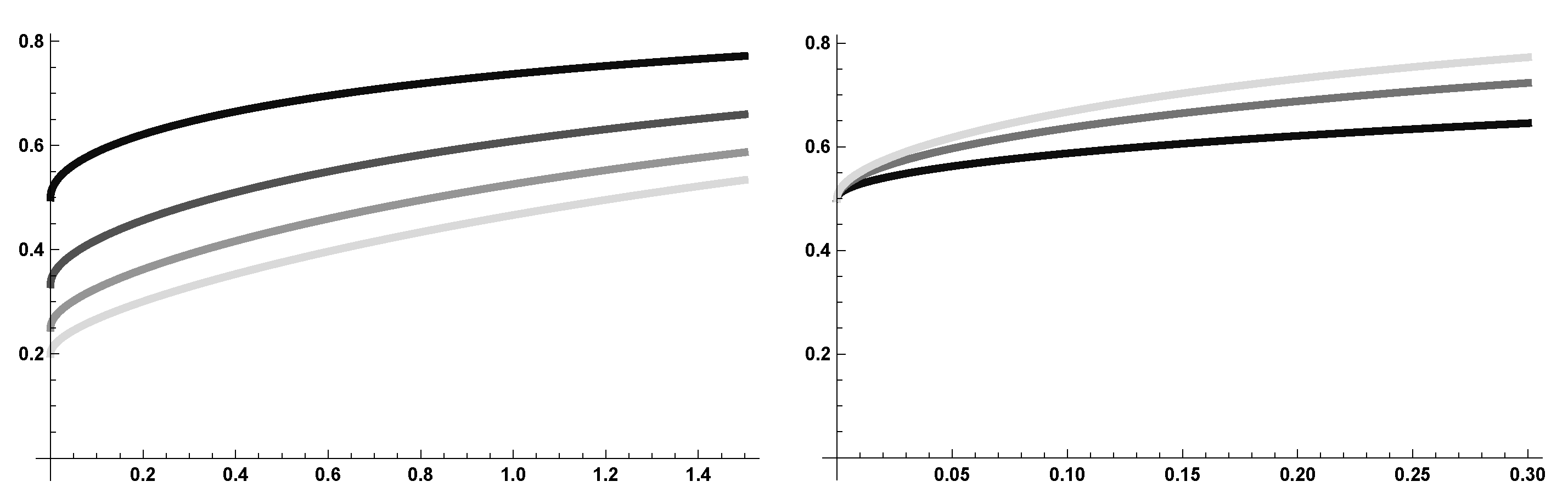
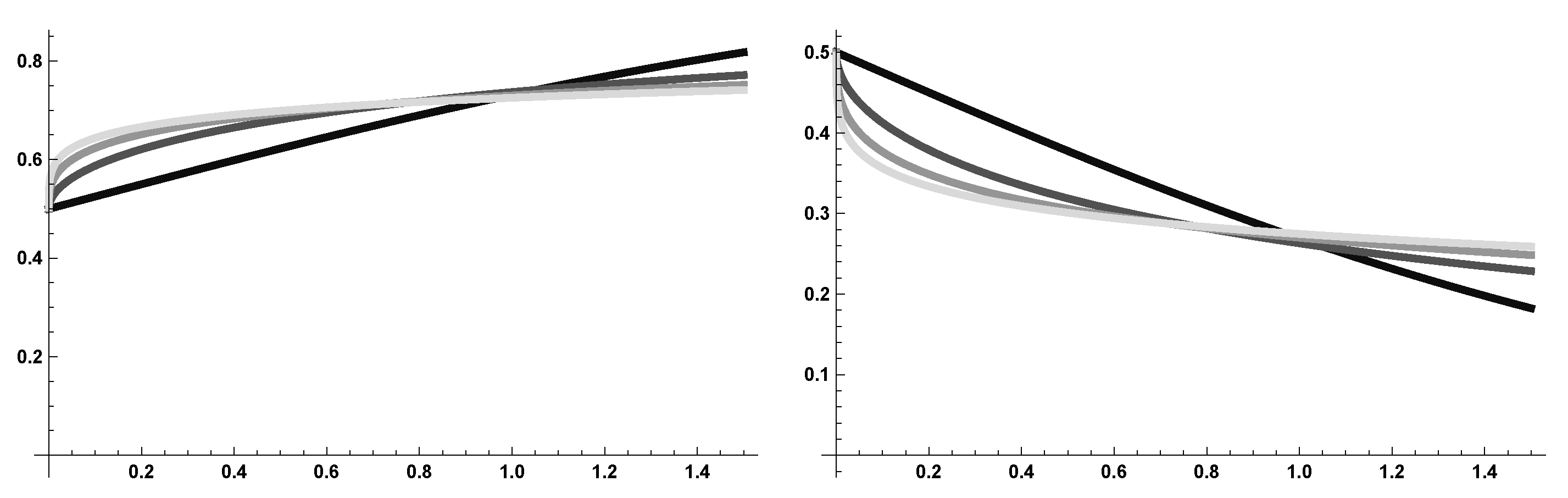
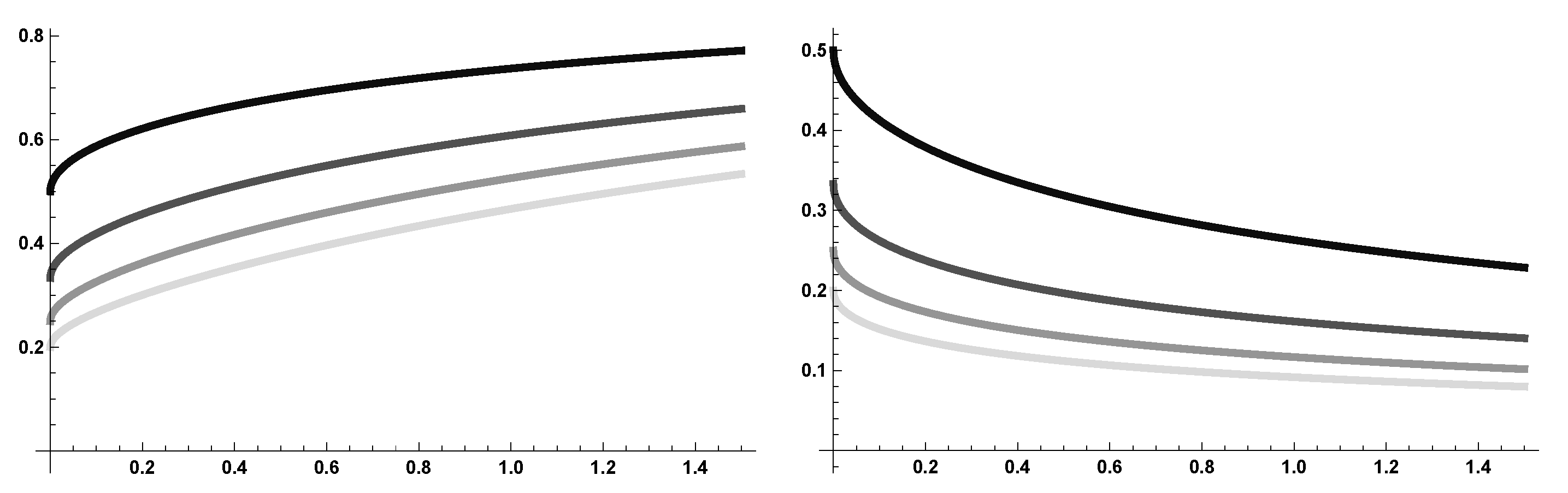
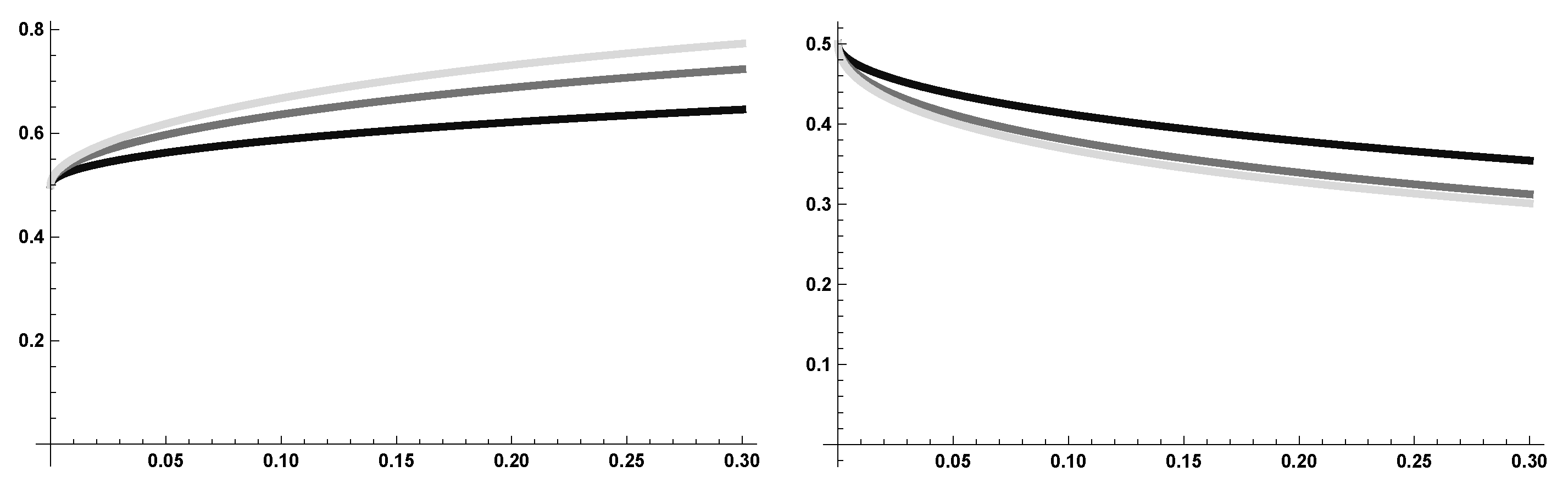
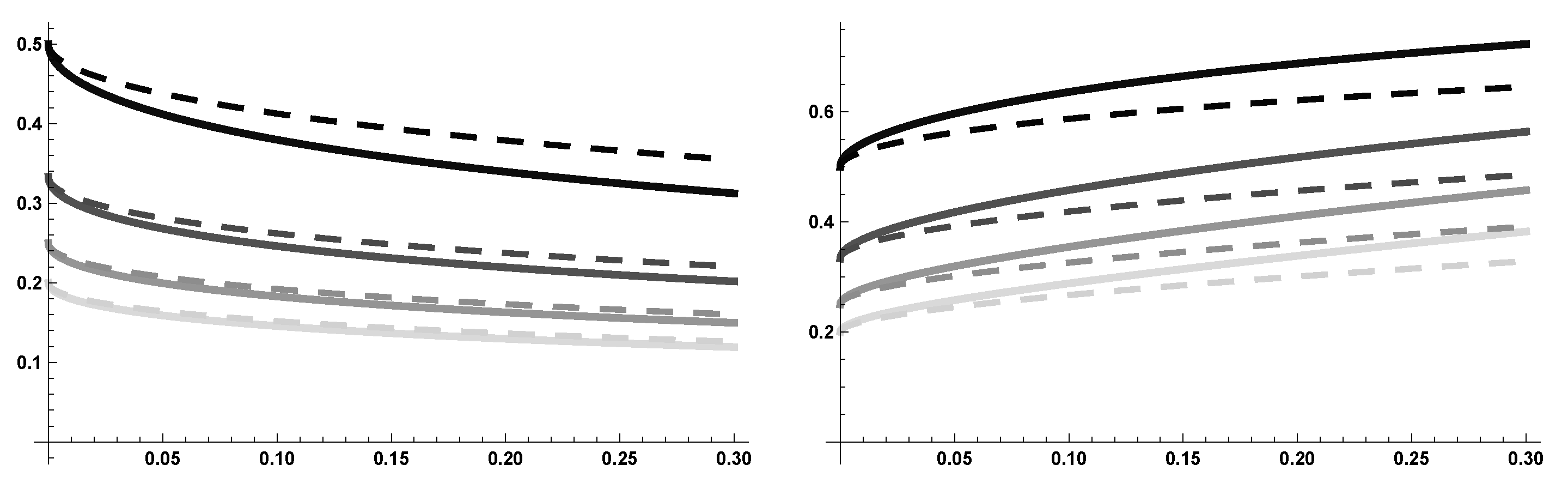
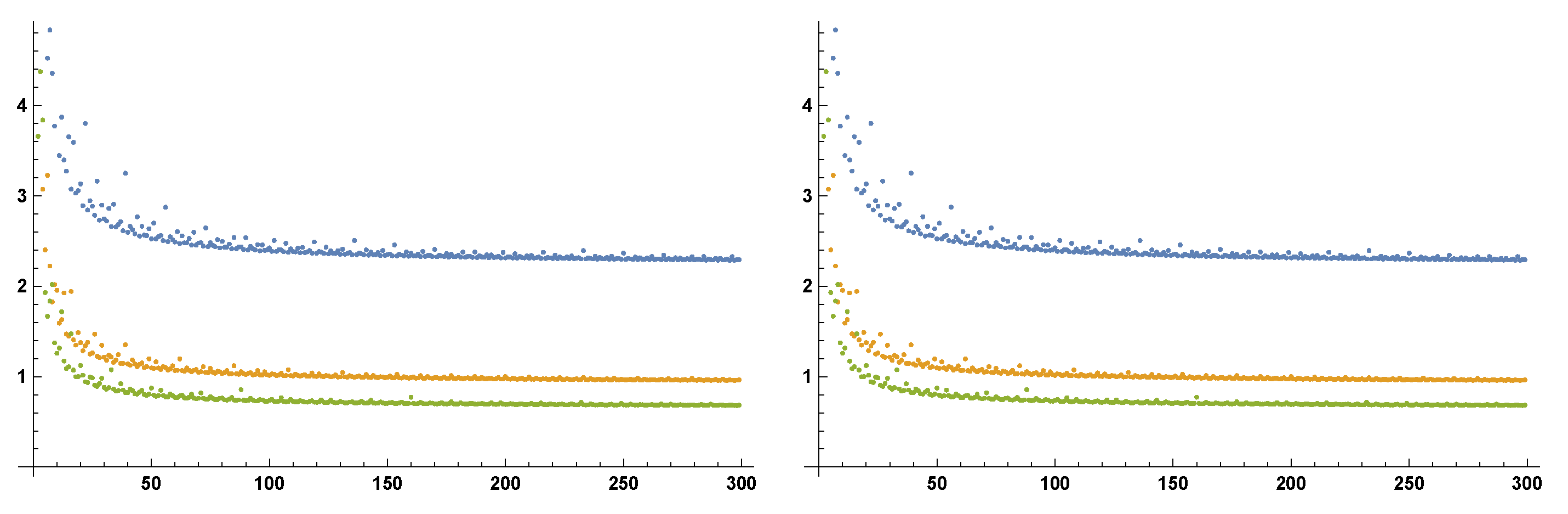
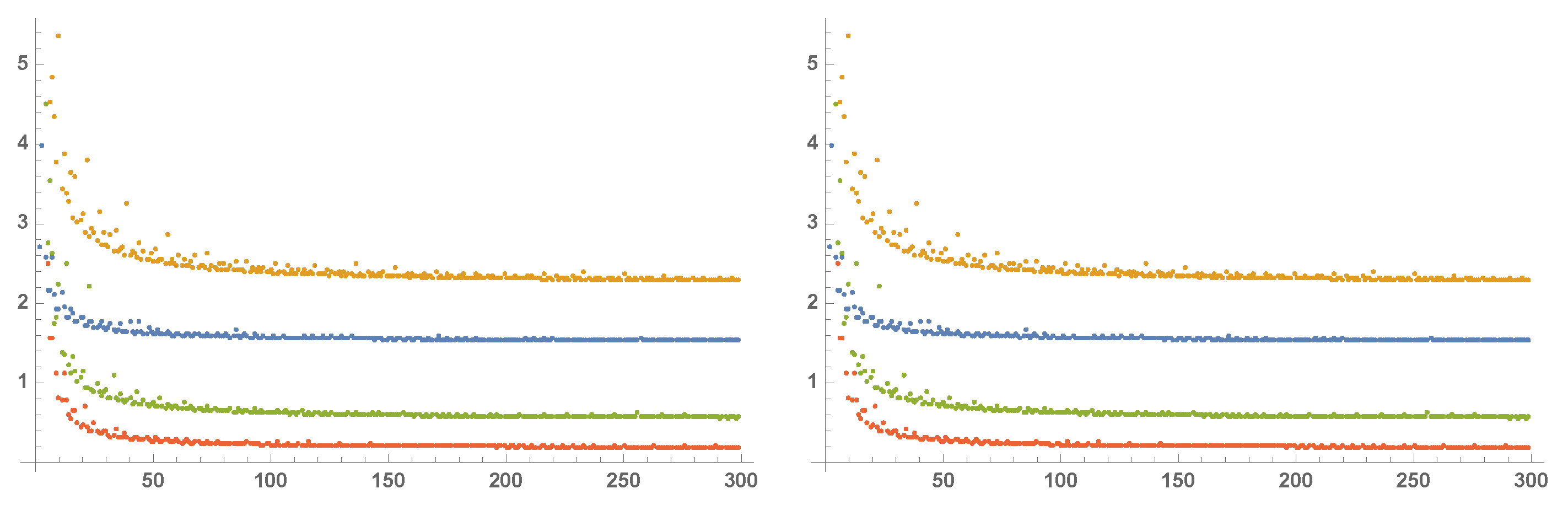
Numerical Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1999; Volume 198. [Google Scholar]
- Valentim, C.A., Jr.; Oliveira, N.A.; Rabi, J.A.; David, S.A. Can fractional calculus help improve tumor growth models? J. Comput. Appl. Math. 2020, 379, 112964. [Google Scholar] [CrossRef]
- Yang, X.J.; Tenreiro Machado, J. A new insight into complexity from the local fractional calculus view point: Modelling growths of populations. Math. Mod. Meth. Appl. Sci. 2017, 40, 6070–6075. [Google Scholar] [CrossRef]
- Haavelmo, T. A Study in the Theory of Economic Evolution; North-Holland: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Helen, M. Byrne, Modelling Avascular Tumour Growth. In Cancer Modelling and Simulation; Preziosi, L., Ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- D’Ovidio, M.; Loreti, P. Solutions of fractional logistic equations by Euler’s numbers. Phys. A Stat. Mech. Appl. 2018, 506, 1081–1092. [Google Scholar] [CrossRef]
- Verhulst, P.-F. Notice sur la loi que la population poursuit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Verhulst, P.-F. Recherches mathématiques sur la loi d’accroissement de la population. Nouv. Mémoires L’Académie R. Sci. Belles Lett. Brux. 1845, 18, 8. [Google Scholar]
- Verhulst, P.-F. Deuxième mémoire sur la loi d’accroissement de la population. Mémoires L’Académie R. Sci. Lett. Beaux-Arts Belg. 1847, 20, 1–32. [Google Scholar]
- Balzotti, C.; D’Ovidio, M.; Loreti, P. Fractional SIS Epidemic Models. Fractal Fract. 2020, 4, 44. [Google Scholar] [CrossRef]
- Area, I.; Nieto, J.J. Power series solution of the fractional logistic equation. Phys. A Stat. Mech. Appl. 2021, 573, 125947. [Google Scholar] [CrossRef]
- D’Ovidio, M.; Lai, A.C.; Loreti, P. Generalized binomials in fractional calculus. arXiv 2020, arXiv:2010.05610. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ovidio, M.; Lai, A.C.; Loreti, P. Solutions of Bernoulli Equations in the Fractional Setting. Fractal Fract. 2021, 5, 57. https://doi.org/10.3390/fractalfract5020057
D’Ovidio M, Lai AC, Loreti P. Solutions of Bernoulli Equations in the Fractional Setting. Fractal and Fractional. 2021; 5(2):57. https://doi.org/10.3390/fractalfract5020057
Chicago/Turabian StyleD’Ovidio, Mirko, Anna Chiara Lai, and Paola Loreti. 2021. "Solutions of Bernoulli Equations in the Fractional Setting" Fractal and Fractional 5, no. 2: 57. https://doi.org/10.3390/fractalfract5020057
APA StyleD’Ovidio, M., Lai, A. C., & Loreti, P. (2021). Solutions of Bernoulli Equations in the Fractional Setting. Fractal and Fractional, 5(2), 57. https://doi.org/10.3390/fractalfract5020057






