Extraction Complex Properties of the Nonlinear Modified Alpha Equation

Abstract

This paper applies one of the special cases of auxiliary method, which is named as the Bernoulli sub-equation function method, to the nonlinear modified alpha equation. The characteristic properties of these solutions, such as complex and soliton solutions, are extracted. Moreover, the strain conditions of solutions are also reported in detail. Observing the figures plotted by considering various values of parameters of these solutions confirms the effectiveness of the approximation method used for the governing model.

1. Introduction

In the last three decades, we have seen an enthralling research topic on the real world problems expressed by using mathematical models. Qi et al. have investigated some important models used to describe the certain waves in physics [1,2]. In this sense, an interesting model for investigating numerically the nonlinear weakly singular models has been presented by Ray et al. [3]. Syam has worked on the Bernoulli sub-equation method [4]. He has also obtained a lot of different interesting results for the governing model. A few years ago, Mendo has studied the series of wave forces connected with Bernoulli structures [5]. He has also produced a different Bernoulli variable algorithm. Rani et al. have studied on a special matrix that could be solved by Bernoulli polynomials [6]. Jeon et al. have investigated the generalized hypergeometric differential [7]. In 2019, Arqub et al. have studied the Riccati and Bernoulli properties to find new and different solutions for the governing model [8]. Ordokhani et al. have observed some important properties the Bernoulli wavelets with their special cases [9]. Yang has proved a new form of high order Bernoulli polynomials in 2008 [10], which obtained many new special cases about the Bernoulli model. In 2016, Dilcher has searched for identities of the Bernoulli polynomial properties in a physical aspect [11,12]. Furthermore, they have given more detailed information regarding these special functions. Ordokhani et al. have defined an original rational relation based on the Bernoulli wavelet [13]. Tian et al. have worked on the solution of beam problem by using an ansatz method based on the Bernoulli polinomials [14], and so on [15,16,17,18,19,20,21,22,23,24,25,26,27].

More general properties of auxiliary and sub-equation function methods have been comprehensively introduced in the literature [28,29]. Moreover, there are many published methods for solving similar equations using different techniques and methods [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49].

In the organization of this paper, in Section 2, we give some preliminaries about the method. In Section 3, we discuss the application of projected method to the nonlinear modified alpha equation (MAE) defined as [21]

$$u_t-u_{xxt}+(\alpha +1)u^2{u}_x-\alpha u_x{u}_{xx}-u{u}_{xxx}=0,$$

(1)

in which $\alpha$ is real constant and non-zero. Islam et al., have applied the modified simple equation method to Equation (1) for getting some important properties [21]. Wazwaz investigated the physical meaning of Equation (1) in a previous study [22].

Comparison and discussion related to the solutions obtained in this paper are presented in Section 4. After the graphical simulations, a conclusion completes the paper.

2. Fundamental Facts of BSEFM

This section presents the general properties of BSEFM [23] based on the four steps defined as follows:

Step 1. We consider the following nonlinear partial differential equation (NLPDE) given as

$$P\left(u,u_x,u_{xt},u_{xx},u^2,\dots \right)=0,$$

(2)

which is taking into account the travelling wave transformation

$$u\left(x,t\right)=U\left(\eta \right),\hspace{0.17em}\hspace{0.17em}\eta =kx-ct,$$

(3)

where $k\ne 0,c\ne 0$. Substituting Equation (3) into Equation (2) yields the following ordinary differential equation:

$$N\left(U,U^{\prime },U^{″},U^2,\dots \right)=0,$$

(4)

$$\mathrm{where} U=U\left(\eta \right),U^{\prime }=\frac{dU}{d\eta },U^{″}=\frac{d^{2}U}{d{\eta }^2},\dots .$$

Step 2. In this step, we take the following trial solution equation to the Equation (4):

$$U\left(\eta \right)={\displaystyle \sum _{i=0}^n{a}_i{F}^i}=a_0+a_{1}F+a_2{F}^2+\dots +a_n{F}^n,$$

(5)

and

$$F^{\prime }=bF+d{F}^M,\hspace{0.17em}\hspace{0.17em}b\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}d\ne 0,\hspace{0.17em}\hspace{0.17em}M\in R-\left\{0,1,2\right\},$$

(6)

where $F\left(\eta \right)$ is Bernoulli differential polynomial. Substituting Equation (5) along with Equation (6) into Equation (4), it produces an algebraic equation of polynomial $\mathsf{\Omega }\left(F\right)$ as follows:

$$\mathsf{\Omega }\left(F\right)={\rho }_s{F}^s+\dots +{\rho }_{1}F+{\rho }_0=0.$$

(7)

We can find more than one solution by obtaining a relation between $M$ and $n$ via the balancing principle and then using this relation.

Step 3. If we take into account that all the coefficients of $\mathsf{\Omega }\left(F\right)$ are zero:

$${\rho }_i=0,\hspace{0.17em}\hspace{0.17em}i=0,\dots ,s.$$

If we solve this system, we will find and control the values of

$$a_0,a_1,a_2,\dots ,a_n$$

(8)

Step 4. Solving Equation (6), we find the following according to $b$ and $d$:

$$F\left(\eta \right)={\left[\frac{-d}{b}+\frac{\epsilon }{e^{b\left(M-1\right)\eta }}\right]}^{\frac{1}{1-M}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}b\ne d,$$

(9)

$$F\left(\eta \right)={\left[\frac{\left(\epsilon -1\right)+\left(\epsilon +1\right)\tanh \left(\frac{b\left(1-M\right)\eta }{2}\right)}{1-\tanh \left(\frac{b\left(1-M\right)\eta }{2}\right)}\right]}^{\frac{1}{1-M}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}b=d,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon \in R.$$

Using a complete discrimination system for polynomial parameters, we find the solutions to Equation (4), using some computational programs, and organize the exact solutions to Equation (4). In order to better understand the results obtained in this way, we can draw the two and three dimensional surfaces of the solutions by considering the appropriate parameter values.

3. Implementation of the BSEFM

This section of the manuscript applies the BSEFM to the MAE to obtain new complex and exponential solutions. Using

$$u\left(x,t\right)=U\left(\eta \right),\eta =kx-ct$$

where $c,k$ are real constants and non-zero, we obtain the nonlinear ordinary equation as follows:

$$6c{k}^2{U}^{″}-6k^{3}U{U}^{″}+3k^3\left(1-\alpha \right){\left(U^{\prime }\right)}^2-6cU+2k\left(\alpha +1\right)U^3=0.$$

(10)

With the help of the balance principle, it is obtained a relationship between $n$ and $M$ as follows:

$$2M=n+2.$$

(11)

This gives some new analytical solutions for the governing model being Equation (1).

Case 1: Considering as $n=4$ and $M=3$ produce the following trial solution for Equation (10):

$$U=a_0+a_{1}F+a_2{F}^2+a_3{F}^3+a_4{F}^4,$$

(12)

$$U^{\prime }=a_{1}bF+a_{1}d{F}^3+2a_{2}b{F}^2+2a_{2}d{F}^4+3a_{3}b{F}^3+3a_{3}d{F}^5+4a_{4}b{F}^4+4a_{4}d{F}^6,$$

(13)

and

$$\begin{array}{l}{U}^{″}=a_1{d}^{2}F+4a_{1}bd{F}^3+3a_1{b}^2{F}^5+4a_2{d}^2{F}^2+12a_{2}bd{F}^4+8a_2{b}^2{F}^6+9a_3{d}^2{F}^3\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+24a_{3}bd{F}^5+15a_3{b}^2{F}^7+16a_4{d}^2{F}^4+40a_{4}bd{F}^6+24a_4{b}^2{F}^8.\end{array}$$

(14)

where $a_4\ne 0,\hspace{0.17em}\hspace{0.17em}b\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}d\ne 0.$ Putting Equations (12)–(14) into Equation (10), it gives a system of algebraic equations of $F$. With the help of powerful computational programs, we get the following coefficients and solutions.

Case 1.1. If it is selected follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill & a_0=-\frac{3d^2\alpha +\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}}{2d^2\left(1+\alpha \right)},a_1=a_3=0,\hfill \\ \hfill & k=-\frac{1}{2}\sqrt{-\frac{d^2\left(2+a\right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}}{d^4\left(1+\alpha \right)\left(2+\alpha \right)}},\hfill \\ \hfill & a_2=-\frac{6b}{d^3{\left(1+\alpha \right)}^2}\left(d^2\left(2+a\right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}\right),\hfill \\ \hfill & a_4=-\frac{6b^2}{d^4{\left(1+\alpha \right)}^2}\left(d^2\left(2+a\right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}\right),\hfill \\ \hfill & c=-\frac{1}{4d^2\left(1+\alpha \right)}\sqrt{-\frac{d^2\left(2+a\right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}}{d^4\left(1+\alpha \right)\left(2+\alpha \right)}}\hfill \\ \hfill & \times \left(\alpha \sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}+d^2\left(2+{\alpha }^2\right)\right),\hfill \end{array}\end{array}\end{array}$$

(15)

we find the following new singular soliton solution for the governing model being Equation (1):

$$u_1\left(x,t\right)=\sigma -\frac{\omega }{d^4{\left(1+\alpha \right)}^2{\left(-\frac{b}{d}+e^{-2d\left(-\frac{1}{2}x\tau +t\tau \varpi \right)}\epsilon \right)}^2}-\frac{\omega }{b{d}^3{\left(1+\alpha \right)}^2\left(-\frac{b}{d}+e^{-2d\left(-\frac{1}{2}x\tau +t\tau \varpi \right)}\epsilon \right)},$$

(16)

in which

$$\begin{gathered} \tau =\sqrt{-\frac{d^2\left(2+\alpha \right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}}{d^4\left(1+\alpha \right)\left(2+\alpha \right)}},\omega =6b^2\left(d^2\left(2+\alpha \right)\left(-1+2\alpha \right)+\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}\right), \\ \varpi =\frac{\left(\sqrt{3}\alpha \sqrt{-d^4\left(-4+{\alpha }^2\right)}+d^2\left(2+{\alpha }^2\right)\right)}{4d^2\left(1+\alpha \right)},\sigma =-\frac{3d^2\alpha +\sqrt{3}\sqrt{-d^4\left(-4+{\alpha }^2\right)}}{2d^2\left(1+\alpha \right)},-2<\alpha <-1 \end{gathered}$$

for validity of Equation (16). Choosing the suitable values of parameters in Equation (16), we plot various figures as follows as being in Figure 1 and Figure 2.

Figure 1. The 3D and contour surfaces of Equation (16) under the values of $d=0.1,\alpha =-1.8,b=0.5,\epsilon =0.4.$

Figure 2. The 2D graph of Equation (16) under the values of $d=0.1,\alpha =-1.8,b=0.5,\epsilon =0.4,t=0.5,-5<x<5.$

Case 1.2. For $b\ne d$, when they are considered as follows:

$$a_0=a_1=a_3=0,a_2=\frac{-24bc}{1+\alpha },a_4=\frac{96b^2{c}^2}{2+3a+{\alpha }^2},k=\frac{2c}{2+\alpha },d=-\frac{2+\alpha }{4c},$$

(17)

This produces a new singular soliton solution for the governing model as:

$$u_2\left(x,t\right)=-\frac{24bc}{1+a}{\left(\frac{4bc}{2+a}+\epsilon e^{\frac{2+a}{2c}\left(-ct+\frac{2c}{2+a}x\right)}\right)}^{-1}+\frac{96b^2{c}^2}{{\alpha }^2+3a+2}{\left(\frac{4bc}{2+a}+\epsilon e^{\frac{2+a}{2c}\left(-ct+\frac{2c}{2+a}x\right)}\right)}^{-2}.$$

(18)

The strain condition is also given as $\alpha \ne -1,\alpha \ne -2$. We can observe the wave surfaces of Equation (18) as being in Figure 3 and Figure 4.

Figure 3. 3D and contour graphs of Equation (18) for $\alpha =0.2,b=0.3,c=-0.5,\epsilon =0.4,d=0.1,-15<x<15,-15<t<15.$

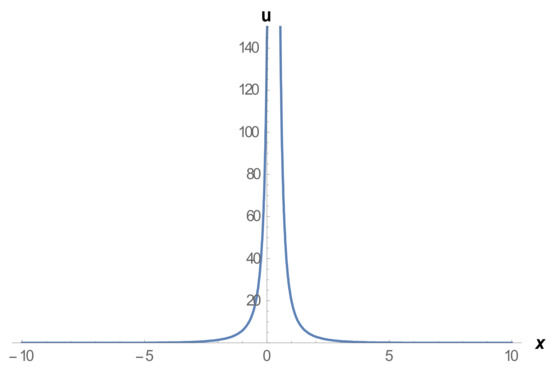
Figure 4. 2D graph of Equation (18) for $\alpha =0.2,b=0.3,c=-0.5,\epsilon =0.4,d=0.1,t=0.6,-10<x<10.$

Case 1.3. If we select the following complex coefficient together with $b\ne d$,

$$\begin{array}{l}{a}_4=4,k=1,a_0=i,a_1=a_3=0,a_2=4\sqrt{-1+3i},b=-\frac{1}{10}\sqrt{11-2i},c=\frac{-7}{13}+\frac{4i}{13},\\ d=-\frac{1}{2}\sqrt{\frac{-1}{5}+\frac{7i}{5}},\alpha =\frac{8}{13}-\frac{12i}{13},\end{array}$$

(19)

it produces a complex soliton solution for the governing model as:

$$\begin{array}{l}{u}_3\left(x,t\right)=i+4{\left(-\frac{1}{\sqrt{-1+7i}}\sqrt{\frac{11}{5}-\frac{2i}{5}}+\epsilon e^{\sqrt{\frac{-1}{5}+\frac{7i}{5}}\left(x+\left(\frac{7}{13}-\frac{4i}{13}\right)t\right)}\right)}^{-2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+4\sqrt{-1+3i}{\left(-\frac{1}{\sqrt{-1+7i}}\sqrt{\frac{11}{5}-\frac{2i}{5}}+\epsilon e^{\sqrt{\frac{-1}{5}+\frac{7i}{5}}\left(x+\left(\frac{7}{13}-\frac{4i}{13}\right)t\right)}\right)}^{-1}.\end{array}$$

(20)

Wave surfaces of Equation (20) can be observed in Figure 5, Figure 6 and Figure 7.

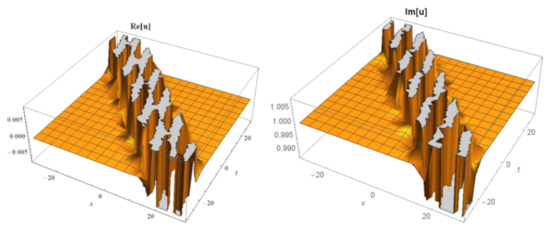
Figure 5. The 3D surfaces of Equation (20) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

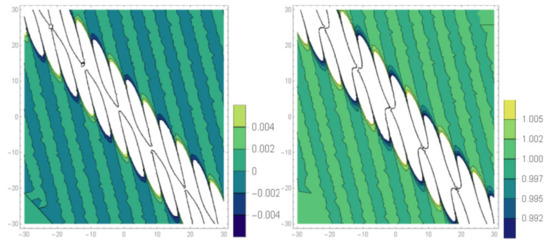
Figure 6. The contour surfaces of Equation (20) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

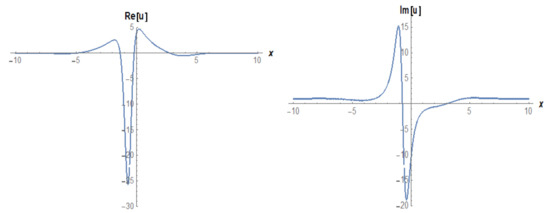
Figure 7. The 2D surfaces of Equation (20) under the values of $\epsilon =0.4,t=0.5,-10<x<10.$

Case 1.4. When choosing the following other complex coefficients and also $b\ne d$,

$$\begin{array}{l}{a}_4=4,k=1,a_0=i,a_1=a_3=0,a_2=-4\sqrt{-1+3i},b=-\frac{1}{10}\sqrt{11-2i},\\ d=\frac{1}{2}\sqrt{\frac{-1}{5}+\frac{7i}{5}},\alpha =\frac{8}{13}-\frac{12i}{13},c=\frac{-7}{13}+\frac{4i}{13},\end{array}$$

(21)

it produces another complex soliton solution to the governing model as:

$$\begin{array}{l}{u}_4\left(x,t\right)=i+4{\left(\frac{1}{\sqrt{-1+7i}}\sqrt{\frac{11}{5}-\frac{2i}{5}}+\epsilon e^{-\sqrt{\frac{-1}{5}+\frac{7i}{5}}\left(x+\left(\frac{7}{13}-\frac{4i}{13}\right)t\right)}\right)}^{-2}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-4\sqrt{-1+3i}{\left(\frac{1}{\sqrt{-1+7i}}\sqrt{\frac{11}{5}-\frac{2i}{5}}+\epsilon e^{-\sqrt{\frac{-1}{5}+\frac{7i}{5}}\left(x+\left(\frac{7}{13}-\frac{4i}{13}\right)t\right)}\right)}^{-1}.\end{array}$$

(22)

Under the suitable choosing of the values of these parameters, we plot various graphs as being Figure 8, Figure 9 and Figure 10.

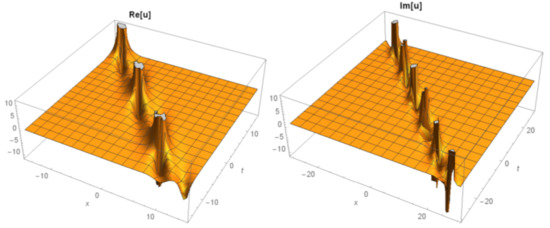
Figure 8. The 3D surfaces of Equation (22) under the values of $\epsilon =0.4,-15<x<15,-15<t<15.$

Figure 9. The contour surfaces of Equation (22) under the values of $\epsilon =0.4,-15<x<15,-15<t<15.$

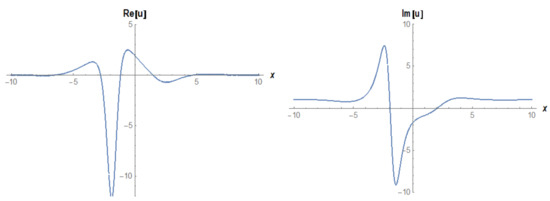
Figure 10. The 2D surfaces of Equation (22) under the values of $\epsilon =0.4,t=0.5,-15<x<15.$

Case 1.5. Choosing the following other complex coefficients by considering $b\ne d$,

$$\begin{array}{l}{a}_4=-i,k=1,a_0=2,a_1=0,a_2=\left(-2+2i\right)\sqrt{5},a_3=0,b=\frac{1}{10}-\frac{i}{10},d=\frac{-2}{\sqrt{5}},\\ \alpha =\frac{-1}{13},c=\frac{16}{13},\end{array}$$

(23)

gives another complex exponential function solution as:

$$u_5\left(x,t\right)=2-i{\left(\frac{1-i}{4\sqrt{5}}+\epsilon e^{\frac{4}{\sqrt{5}}\left(x-\frac{16}{13}t\right)}\right)}^{-2}-\left(2-2i\right)\sqrt{5}{\left(\frac{1-i}{4\sqrt{5}}+\epsilon e^{\frac{4}{\sqrt{5}}\left(x-\frac{16}{13}t\right)}\right)}^{-1}.$$

(24)

Choosing the suitable values of these parameters, we present several simulations as Figure 11, Figure 12 and Figure 13.

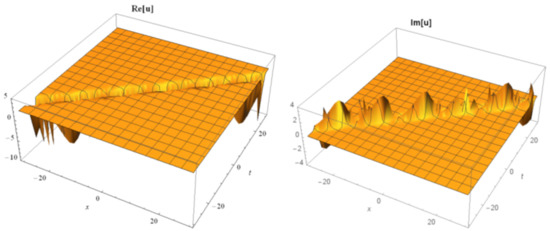
Figure 11. The 3D simulations of Equation (24) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

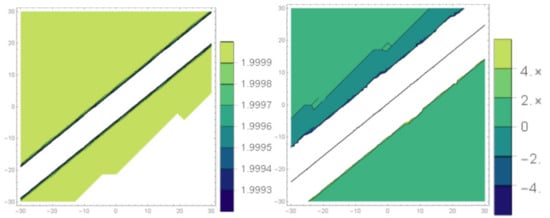
Figure 12. The contour graphs of Equation (24) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

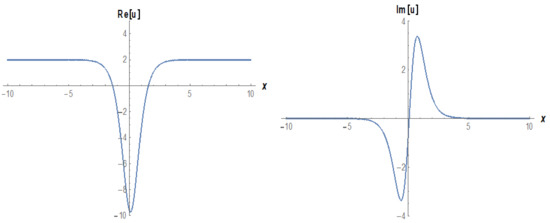
Figure 13. The 2D graphs of Equation (24) under the values of $\epsilon =0.4,t=0.5,-10<x<10.$

Case 1.6. Taking the following other complex coefficients with $b\ne d$,

$$\begin{array}{l}{a}_4=-i,k=1,a_0=2,a_1=0,a_2=\left(2-2i\right)\sqrt{5},a_3=0,b=-\frac{1}{10}+\frac{i}{10},d=\frac{-2}{\sqrt{5}},\\ \alpha =\frac{-1}{13},c=\frac{16}{13},\end{array}$$

(25)

gives another complex exponential function solution as:

$$u_6\left(x,t\right)=2-i{\left(\frac{-1+i}{4\sqrt{5}}+\epsilon e^{\frac{4}{\sqrt{5}}\left(x-\frac{16}{13}t\right)}\right)}^{-2}+\left(2-2i\right)\sqrt{5}{\left(\frac{-1+i}{4\sqrt{5}}+\epsilon e^{\frac{4}{\sqrt{5}}\left(x-\frac{16}{13}t\right)}\right)}^{-1}.$$

(26)

Various simulations of Equation (26) may be observed in Figure 14, Figure 15 and Figure 16.

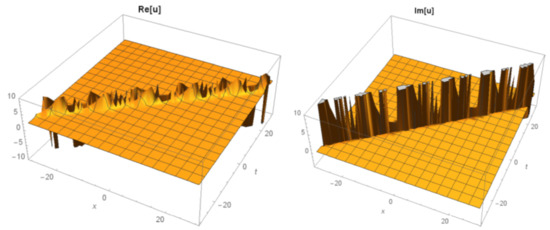
Figure 14. The 3D simulations of Equation (26) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

Figure 15. The contour graphs of Equation (26) under the values of $\epsilon =0.4,-30<x<30,-30<t<30.$

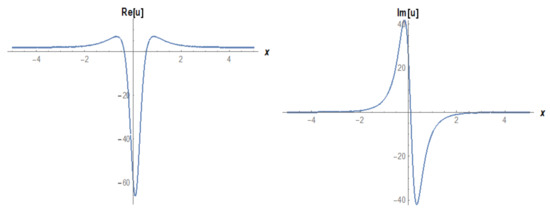
Figure 16. The 2D graphs of Equation (26) under the values of $\epsilon =0.4,t=0.5,-5<x<5.$

Case 2. Taking $n=6$ and $M=4$, we can write as follows:

$$U=a_0+a_{1}F+a_2{F}^2+a_3{F}^3+a_4{F}^4+a_5{F}^5+a_6{F}^6,$$

(27)

and

$$\begin{array}{l}{U}^{\prime }=a_1{F}^{\prime }+2a_{2}F{F}^{\prime }+3a_3{F}^2{F}^{\prime }+4a_4{F}^3{F}^{\prime }+5a_5{F}^4{F}^{\prime }+6a_6{F}^5{F}^{\prime },\\ U^{″}=\dots .\end{array}$$

(28)

where $a_6\ne 0,\hspace{0.17em}\hspace{0.17em}b\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}d\ne 0$. Putting Equations (27) and (28) into Equation (10) produces some entirely new analytical solutions for the governing model as follows.

Case 2.1: When

$$\begin{array}{l}d=2,a_0=a_1=\hspace{0.17em}{a}_2=a_4=a_5=0,a_3=\left(-1+i\right)\sqrt{3/5},a_6=i,b=\left(1-i\right)\sqrt{5/3},\\ k=1/6,\alpha =-11/6,c=1/72,\end{array}$$

(29)

another new complex soliton solution is extracted as:

$$u_7\left(x,t\right)=i{\left(\frac{i\sqrt{5}-\sqrt{5}}{2\sqrt{3}}+\epsilon e^{-x+\frac{t}{12}}\right)}^{-2}+\left(i-1\right)\frac{\sqrt{3}}{\sqrt{5}}{\left(\frac{i\sqrt{5}-\sqrt{5}}{2\sqrt{3}}+\epsilon e^{-x+\frac{t}{12}}\right)}^{-1},$$

(30)

in which $\epsilon$ is a real constant with non-zero. Under the suitable chosen of parameters, we can presents various graphs as in Figure 17, Figure 18 and Figure 19.

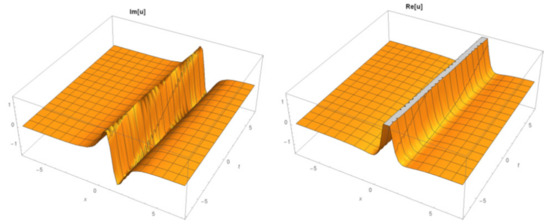
Figure 17. The 3D surfaces of Equation (30) under the values of $\epsilon =5,-7<x<7,-7<t<7$.

Figure 18. The contour surfaces of Equation (30) under the values of $\epsilon =5,-70<x<70,-70<t<70.$

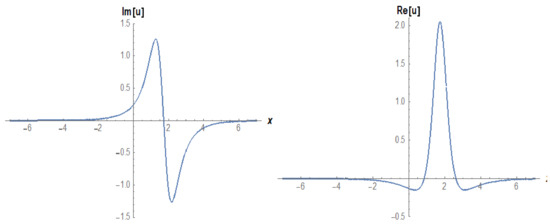
Figure 19. The 2D surfaces of Equation (30) under the values of $\epsilon =5,t=0.3,-7<x<7.$

Case 2.2. Considering the following:

$$\begin{array}{l}d=2,a_0=a_1=\hspace{0.17em}{a}_2=a_4=a_5=0,a_3=\left(\sqrt{6}\left(1+\alpha \right)\sqrt{2+\alpha }\right)/{\left(i\left(1+\alpha \right)\right)}^{3/2},a_6=i,\\ k=1/6,b=\left(-\sqrt{2/3}\sqrt{i\left(1+\alpha \right)}\right)/\sqrt{2+\alpha },c=\left(2+\alpha \right)/12,\end{array}$$

(31)

another new complex mixed dark soliton solution is extracted as:

$$u_8\left(x,t\right)=i{\left(\frac{1-Tanh\left(f\left(x,t\right)\right)}{\varpi +\epsilon +\left(\epsilon -\varpi \right)Tanh\left(f\left(x,t\right)\right)}\right)}^2+\frac{1-Tanh\left(f\left(x,t\right)\right)}{\varpi +\epsilon +\left(\epsilon -\varpi \right)Tanh\left(f\left(x,t\right)\right)},$$

(32)

in which $\epsilon ,\alpha$ are real constants and non-zero and also

$$\begin{gathered} \varpi =\frac{\sqrt{i\left(1+\alpha \right)}}{\sqrt{12+6\alpha }},\sigma =\frac{\sqrt{6}\left(1+\alpha \right)\sqrt{2+\alpha }}{{\left(i\left(1+\alpha \right)\right)}^{3/2}}, \\ f\left(x,t\right)=\frac{2+\alpha }{4}t-\frac{x}{2}. \end{gathered}$$

We plot its surfaces in Figure 20, Figure 21 and Figure 22.

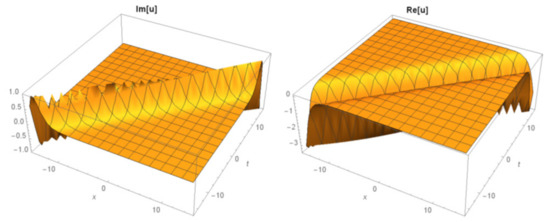
Figure 20. The 3D surfaces of Equation (32) for $\epsilon =0.4,\alpha =0.1,-15<x<15,-15<t<15.$

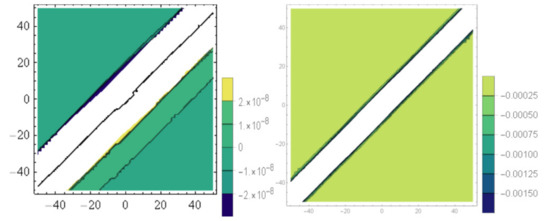
Figure 21. The contour surfaces of Equation (32) for $\epsilon =0.4,\alpha =0.1,-50<x<50,-50<t<50.$

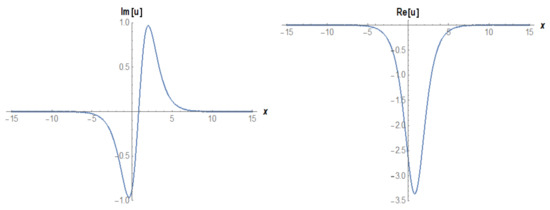
Figure 22. The 2D surfaces of Equation (32) for $\epsilon =0.4,\alpha =0.1,t=0.5,-15<x<15.$

4. Comparison and Discussion

In a previous research [21], Asaduzzman et al., have studied the special cases of Equation (1) by considering $\alpha =2$. In this paper, we have extracted the general solutions of MAE according to $\alpha$ as being in the solutions of Equations (16), (18), and (32). Moreover, we have also investigated other values of $\alpha$ such as complex and rations in the coefficients of Equations (19), (21), (23), (25) and (29). When we compare these solutions with the solutions presented in the previous study [21], it may be observed that they are an entirely new solution for the governing model of MAE.

Moreover, if we consider more values of $n,M$ as $n=8$ and $M=5$, we obtain another new solution for the governing model as:

$$U=a_0+a_{1}F+a_2{F}^2+a_3{F}^3+a_4{F}^4+a_5{F}^5+a_6{F}^6+a_7{F}^7+a_8{F}^8,$$

(33)

in which $a_8\ne 0,\hspace{0.17em}\hspace{0.17em}b\ne 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}d\ne 0$. By getting the necessary derivations of Equation (33) for Equation (10), we report more new complex and rational wave solutions to the MAE, which these solutions produced by BSEFM. In this regard, this projected technique is a powerful tool for obtaining new analytical solutions for the nonlinear partial differential equations.

In the physical sense, if we consider the solution of $u_8\left(x,t\right)$ being Equation (32), this is a complex mixed dark soliton solution for the governing model. Such reported results in this manuscript have some important properties. To illustrate this, the hyperbolic tangent (dark soliton) arises in the calculation of magnetic moment and rapidity of special relativity [50]. In this regard, it is estimated that this solution may help to better understanding of the meaning of MAE physically.

5. Conclusions

In this article, we have successfully applied BSEFM to the MAE. We obtained many entirely new complex and exponential characteristic properties of MAE. We observed that the results obtained with the help of the projected algorithm are new deeper investigations and a generalized version according to $\alpha .$ Moreover, we have reported the strain conditions for the validity of solutions. Various wave behaviors in many simulations from Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 have been also presented to observe wave distributions of solutions. All figures are clearly commented, which give the idea of effectiveness of the proposed schemes. The method proposed in this paper can be used to seek more travelling wave solutions of such governing models, because the method has some advantages such as easily calculations, writing programme for obtaining coefficients, and many others.