A Collocation Method Based on Discrete Spline Quasi-Interpolatory Operators for the Solution of Time Fractional Differential Equations
Abstract
1. Introduction
2. Materials and Methods
2.1. Linear Fractional Differential Problems
2.2. B-Spline Spaces
2.3. Refinable Spline Quasi-Interpolatory Operators
3. Numerical Method
3.1. The Fractional Derivative of the Refinable B-Spline Basis
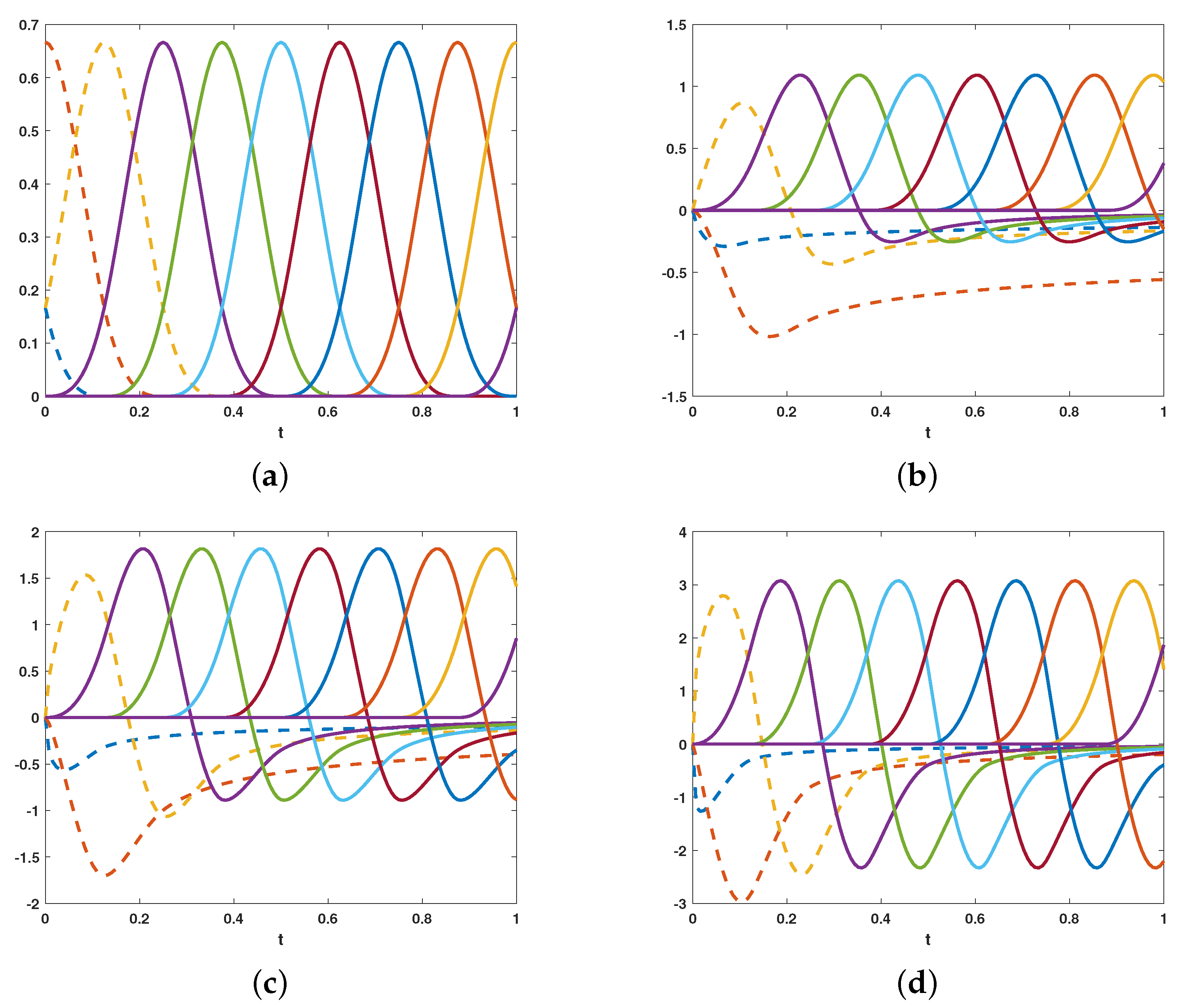
4. Numerical Results
4.1. Example 1
4.2. Example 2
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Sabatier, J.; Agrawal, O.; Tenreiro Machado, J.A. Advances in Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science (North-Holland): Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics; Nonlinear Physical Science; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Diethelm, K.; Garrappa, R.; Giusti, A.; Stynes, M. Why fractional derivatives with nonsingular kernels should not be used. Fract. Calc. Appl. Anal. 2020, 23, 610–634. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, J.M.; Ford, N.J.; Weilbeer, M. Pitfalls in fast numerical solvers for fractional differential equations. J. Comput. Appl. Math. 2006, 186, 482–503. [Google Scholar] [CrossRef]
- Li, C.; Chen, A. Numerical methods for fractional partial differential equations. Int. J. Comput. Math. 2018, 95, 1048–1099. [Google Scholar] [CrossRef]
- Schumaker, L. Spline Functions: Basic Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Unser, M.; Blu, T. Fractional splines and wavelets. SIAM Rev. 2000, 42, 43–67. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A fractional spline collocation-Galerkin method for the time-fractional diffusion equation. Commun. Appl. Ind. Math. 2018, 9, 104–120. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 2018, 147, 210–219. [Google Scholar] [CrossRef]
- Pitolli, F. A fractional B-spline collocation method for the numerical solution of fractional predator-prey models. Fractal Fract. 2018, 2, 13. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E. On the convergence of spline collocation methods for solving fractional differential equations. J. Comput. Appl. Math. 2011, 235, 3502–3514. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E. Numerical solution of nonlinear fractional differential equations by spline collocation methods. J. Comput. Appl. Math. 2014, 255, 216–230. [Google Scholar] [CrossRef]
- Dadkhah, E.; Shiri, B.; Ghaffarzadeh, H.; Baleanu, D. Visco-elastic dampers in structural buildings and numerical solution with spline collocation methods. J. Appl. Math. Comput. 2020, 63, 29–57. [Google Scholar] [CrossRef]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Differential Equations; Cambridge University Press: Cambridge, UK, 2004; Volume 15. [Google Scholar]
- Lyche, T.; Schumaker, L.L. Local spline approximation methods. J. Approx. Theory 1975, 15, 294–325. [Google Scholar] [CrossRef]
- Gori, L.; Santi, E. Refinable quasi-interpolatory operators. In Constructive Theory of Functions, Varna 2002; Bojanov, B., Ed.; DARBA: Sofia, Bulgaria, 2003; pp. 288–294. [Google Scholar]
- Sablonnière, P. Recent progress on univariate and multivariate polynomial and spline quasi-interpolants. In Trends and Applications in Constructive Approximation, ISNM; De Bruin, M., Mache, D., Szabados, J., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; Volume 177, pp. 229–245. [Google Scholar]
- Pellegrino, E.; Pezza, L.; Pitolli, F. A collocation method in spline spaces for the solution of linear fractional dynamical systems. Math. Comput. Simul. 2020, 176, 266–278. [Google Scholar] [CrossRef]
- Pellegrino, E.; Pezza, L.; Pitolli, F. Quasi-interpolant operators and the solution of fractional differential problems. In Approximation Theory XVI. Nashville 2019; Fasshauer, G.E., Ed.; Springer Nature: Switzerland, 2020. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag–Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014; Volume 2. [Google Scholar]
- de Boor, C. A Practical Guide to Splines; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Schoenberg, I.J. On spline functions. In Inequalities; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1967; pp. 255–291. [Google Scholar]
- de Boor, C.; Fix, G.J. Spline approximation by quasiinterpolants. J. Approx. Theory 1973, 8, 19–45. [Google Scholar] [CrossRef]
- Goodman, T.N.T.; Sharma, A. A modified Bernstein-Schoenberg operator. In Constructive Theory of Functions 87; Sendov, B., Ed.; Bulgarian Academy Sciences: Sofia, Bulgaria, 1988. [Google Scholar]
- Lee, B.G.; Lyche, T.; Mørken, K. Some examples of quasi-interpolants constructed from local spline projectors. In Mathematical Methods for Curves and Surfaces. Oslo 2000; Lyche, T., Schumaker, L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 2001; pp. 243–252. [Google Scholar]
- Gori, L.; Santi, E. Convergence properties of certain refinable quasi-interpolatory operators. Appl. Numer. Math. 2005, 55, 312–321. [Google Scholar] [CrossRef]
- Ascher, U. Discrete least squares approximations for ordinary differential equations. SIAM J. Numer. Anal. 1978, 15, 478–496. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Evaluation of generalized Mittag–Leffler functions on the real line. Adv. Comput. Math. 2013, 39, 205–225. [Google Scholar] [CrossRef]
- Pitolli, F. Optimal B-spline bases for the numerical solution of fractional differential problems. Axioms 2018, 7, 46. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behaviour of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]



| 3 | 17 | 3.33 | 4.44 | 4.44 | 2.10 | 7.77 | 1.26 |
| 4 | 33 | 1.33 | 1.89 | 6.88 | 2.00 | 2.22 | 1.78 |
| 5 | 65 | 7.80 | 3.84 | 4.71 | 1.78 | 1.95 | 1.84 |
| 6 | 129 | 7.17 | 1.06 | 1.71 | 3.04 | 1.14 | 2.95 |
| 3 | 17 | 1.13 | 1.65 | 2.35 | |||
| 4 | 33 | 1.63 | 2.800 | 2.38 | 2.800 | 3.37 | 2.800 |
| 5 | 65 | 2.34 | 2.800 | 3.41 | 2.800 | 4.84 | 2.800 |
| 6 | 129 | 3.35 | 2.800 | 4.90 | 2.800 | 6.96 | 2.800 |
| 3 | 17 | 7.77 | 9.07 | 1.20 | |||
| 4 | 33 | 1.12 | 2.800 | 1.30 | 2.800 | 1.72 | 2.800 |
| 5 | 65 | 1.60 | 2.800 | 1.87 | 2.800 | 2.47 | 2.800 |
| 6 | 129 | 2.30 | 2.800 | 2.69 | 2.800 | 3.55 | 2.800 |
| 3 | 97 | 1.61 | 5.97 | 1.40 | |||
| 4 | 193 | 1.41 | 0.191 | 4.29 | 0.475 | 8.33 | 0.744 |
| 5 | 385 | 1.23 | 0.199 | 3.07 | 0.482 | 4.97 | 0.746 |
| 6 | 769 | 1.07 | 0.206 | 2.19 | 0.488 | 2.96 | 0.747 |
| 3 | 97 | 1.12 | 4.28 | 1.03 | |||
| 4 | 193 | 9.52 | 0.236 | 2.93 | 0.546 | 5.88 | 0.808 |
| 5 | 385 | 7.98 | 0.253 | 1.95 | 0.588 | 3.27 | 0.847 |
| 6 | 769 | 6.61 | 0.272 | 1.24 | 0.651 | 1.72 | 0.926 |
| 3 | 5.65 | 3 | 3.39 | ||
| 4 | 2.89 | 0.965 | 4 | 1.15 | 1.564 |
| 5 | 1.48 | 0.971 | 5 | 3.87 | 1.566 |
| 6 | 7.50 | 0.977 | 6 | 1.30 | 1.577 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellegrino, E.; Pezza, L.; Pitolli, F. A Collocation Method Based on Discrete Spline Quasi-Interpolatory Operators for the Solution of Time Fractional Differential Equations. Fractal Fract. 2021, 5, 5. https://doi.org/10.3390/fractalfract5010005
Pellegrino E, Pezza L, Pitolli F. A Collocation Method Based on Discrete Spline Quasi-Interpolatory Operators for the Solution of Time Fractional Differential Equations. Fractal and Fractional. 2021; 5(1):5. https://doi.org/10.3390/fractalfract5010005
Chicago/Turabian StylePellegrino, Enza, Laura Pezza, and Francesca Pitolli. 2021. "A Collocation Method Based on Discrete Spline Quasi-Interpolatory Operators for the Solution of Time Fractional Differential Equations" Fractal and Fractional 5, no. 1: 5. https://doi.org/10.3390/fractalfract5010005
APA StylePellegrino, E., Pezza, L., & Pitolli, F. (2021). A Collocation Method Based on Discrete Spline Quasi-Interpolatory Operators for the Solution of Time Fractional Differential Equations. Fractal and Fractional, 5(1), 5. https://doi.org/10.3390/fractalfract5010005







