A Verifiable, Privacy-Preserving, and Poisoning Attack-Resilient Federated Learning Framework

Abstract

Federated learning is the on-device, collaborative training of a global model that can be utilized to support the privacy preservation of participants’ local data. In federated learning, there are challenges to model training regarding privacy preservation, security, resilience, and integrity. For example, a malicious server can indirectly obtain sensitive information through shared gradients. On the other hand, the correctness of the global model can be corrupted through poisoning attacks from malicious clients using carefully manipulated updates. Many related works on secure aggregation and poisoning attack detection have been proposed and applied in various scenarios to address these two issues. Nevertheless, existing works are based on the trust confidence that the server will return correctly aggregated results to the participants. However, a malicious server may return false aggregated results to participants. It is still an open problem to simultaneously preserve users’ privacy and defend against poisoning attacks while enabling participants to verify the correctness of aggregated results from the server. In this paper, we propose a privacy-preserving and poisoning attack-resilient federated learning framework that supports the verification of aggregated results from the server. Specifically, we design a zero-trust dual-server architectural framework instead of a traditional single-server scheme based on trust. We exploit additive secret sharing to eliminate the single point of exposure of the training data and implement a weight selection and filtering strategy to enhance robustness to poisoning attacks while supporting the verification of aggregated results from the servers. Theoretical analysis and extensive experiments conducted on real-world data demonstrate the practicability of our proposed framework.

1. Introduction

Data breaches are a general concern, and various governments have created regulations to safeguard users’ data. Some of such established regulations include the European Union General Data Protection Regulation (GDPR) [1], the California Consumer Privacy Act (CCPA) in the United States [2], and Singapore’s Personal Data Protection Act (PDPA) [3]. Organizations face high penalties for breaching these regulations, and under the above circumstances, preserving the users’ private data is paramount. Traditional machine learning (ML) approaches typically employ a centralized architecture where data are stored and processed centrally. In addition to the high cost and unacceptable latency associated with such practices, data privacy and security remain the major concerns. With central data storage and processing, sensitive data are exposed to leaks and attacks. An alternative solution that can preserve data privacy is a distributed and on-device ML technique known as federated learning (FL).

FL is a concept introduced by Google that can be used to support the privacy preservation of data. FL allows for the distributed and on-device collaborative training of devices or servers without sharing raw data. The privacy and security issues associated with centralizing data in a single location are solved using FL because it allows individual participants to process data locally and only share model weights. As a distributed ML technique, it can operate with a coordinating central server or without a server orchestrating the training in a fully distributed approach [4]. FL enables decentralized computing by utilizing edge devices’ computational power, reducing reliance on centralized servers. Moreover, there is a reduction in bandwidth usage and minimization of network load because only model updates are transmitted. Due to its numerous advantages, it has been applied in different areas, such as healthcare [5], finance [6], vehicle networks [7], and cyberattack detection [8]. A standard FL framework typically comprises a coordinating (central) server, participating devices, and a communication–computation framework to train the model [9]. The operating technique is such that the central server sends a pre-trained or global model to participating devices for global model training. The participating devices upload weights generated from local training data to the central server for aggregation. The central server aggregates these weights to generate an updated global model. To achieve model convergence or attain a specific number of rounds, there is a continuous client–server interaction [10].

Recent studies have identified specific challenges around the FL approach to model training regarding privacy preservation, security, and integrity [3,4,5,6,7,8]. A malicious server can indirectly obtain sensitive information such as local training data [11], class representatives [12], and labels [13] through shared weights. On the other hand, poisoning attacks by malicious clients through manipulated updates can corrupt the correctness of the global model [14,15,16]. Also, a malicious server may return incorrectly aggregated results to participants [17], precipitating the need to verify the correctness of the aggregated model. To tackle the above challenges, several works focusing on privacy preservation, security, and integrity of aggregation in FL have been proposed. To address the issue of privacy preservation in FL, Refs. [18,19] proposed using secure multiparty computation to enable secure aggregation. To tackle poisoning attacks, Refs. [20,21] implemented a statistical approach using Euclidean distance. Additionally, to prove the correctness of model aggregation, Ref. [22] proposed using a homomorphic hash function.

These research works either solved the problem of privacy preservation or poisoning attacks but failed to tackle either two or all the three issues identified simultaneously. It is particularly challenging to preserve privacy in FL and ensure robustness against poisoning attacks because the techniques employed for privacy preservation hide the exchanged weights, making it difficult to query them for anomaly [23]. To simultaneously preserve user privacy while defending against poisoning attacks, Ref. [24] proposed using two servers to detect poisoning attacks based on Euclidean distance and secure multiparty computation (SMC) for privacy preservation. Similarly, Ref. [25] adopted K-nearest weight to detect poisoning attacks and secret sharing for privacy preservation. Moreso, [26] proposed a distributed trust architecture for poisoning attack resilience and malformed update defense. Nonetheless, none of the solutions mentioned support the verification of the correctness of aggregated results from the server. The tendency to compromise participants’ privacy increases once a malicious server can manipulate the data returned to participants. Research carried out in [17] proposed using a double-masking protocol for privacy preservation and a homomorphic hash function to verify aggregated results from the server. However, they failed to provide a mechanism to defend against poisoning attacks from the participants. None of these solutions implemented a framework for simultaneously preserving privacy and security while supporting the verification of aggregated results. In addition, as mentioned earlier, these solutions have an element of trust in their framework. As stated in [27], a zero-trust architectural framework can transform the FL network into a robust defense system that will prevent an authorized party or compromised clients from acting. In an FL environment, there is a need for simultaneous preservation of privacy, security, and zero-trust verification of aggregated results.

This paper proposes a simultaneous privacy-preserving, poisoning attack-resilient, and zero-trust verification FL framework. Our privacy preservation technique and prevention of poisoning attacks while supporting the verification of aggregated results enhance the confidentiality, integrity, and authentication of device–server communication in FL. Our contributions can be summarized as follows:

• To eliminate the single point of exposure of the training data and ensure that all parties are equally blind to the complete training data, we exploit additive secret sharing with an oblivious transfer protocol by splitting the training data between the two servers. This minimizes the risk of exposing the training data, enhances protection against reconstruction attacks, and enables privacy preservation even if one server is compromised.
• To enhance robustness against poisoning attacks by malicious participants, we implement a weight selection and filtering strategy that identifies the coherent cores of benign updates and filters out boosted updates based on their L2 norm. The weight selection, filtering, and cross-validation across servers achieve a synergy that creates a resilient barrier against poisoning attacks.
• To reduce reliance on trusting a single party and ensure that all participant contributions are proportionally represented, we utilize our dual-server architecture to exploit the additive secret-sharing scheme. Specifically, this allows each server to provide proof of aggregation and enables the participants to verify the correctness of the aggregated results returned by the servers. This helps to foster a zero-trust architecture and maintain data integrity and confidentiality throughout the training process.

The rest of this paper is organized as follows. In Section 2, we review related studies. Section 3 comprises preliminaries. Section 4 shows the system architecture, threat model, design goals, and system interpretation. In Section 5, we present our secret-sharing schemes and a method for detecting poisoning attacks. Section 6 shows the security analysis of our framework. Section 7 outlines the experimental setup and discusses the results. We conclude our work in Section 8.

2. Related Studies

In this section, we will review state-of-the-art (SOTA) research carried out on FL in areas such as data privacy preservation, security, and the correctness of aggregation.

FL is a distributed learning paradigm that enables the joint training of a machine learning (ML) model by multiple participants without exchanging local data [9]. The participants are the beneficiaries of FL and also the data owners. Depending on the settings, they are termed cross-device [28] or cross-silo [29]; the former can be an Internet-of-Things device, while the latter can be an organization. The participants’ local data for model training must be preserved to encourage participation and foster a secure, privacy-preserved FL environment. To this end, Ref. [30] proposed using optimized differential privacy to preserve individual local data while extracting valuable information. The aim is to achieve heightened privacy by analyzing the integration of FL with differential privacy. Similarly, to defend against gradient inversion and reconstruction attacks while preserving the privacy of local data, Refs. [31,32] proposed differential privacy where random noise is added to the model parameters of the data holder to preserve the privacy of local data. The above works achieved privacy preservation of local data; however, there is a trade-off in the model’s accuracy.

To achieve better accuracy while still preserving the privacy of local data, several works have proposed the use of homomorphic encryption (HE) [33,34,35] and a secure multiparty computation (SMC) protocol [36,37]. HE is implemented in FL for privacy preservation and to allow computations on encrypted data without decrypting it. When decrypted, the computation results match the operations carried out on the original data. To support unlimited computation in ciphertexts, Hijazi et al. [33] proposed a secure FL using full HE (FHE) for data security and privacy preservation. The integration of FL with FHE provided unlimited computations on ciphertexts and allowed multiparty collaborative training of the model. To preserve the privacy of local data, Zhang et al. [34] implemented an HE-based FL that prevents model inversion and reconstruction attacks. The proposed method supports a tolerable dropout scheme that would not terminate the model learning process if there were a drop in the number of online participants that is not less than the preset threshold. To prevent the interception and decryption of ciphertexts from malicious users, Cai et al. [35] proposed SecFed, a multikey HE that combines its operations with a trusted execution environment (TEE) to preserve user privacy within an FL environment. Similarly to the scheme mentioned above, their proposed scheme supports the continuous operation of the model learning process with disconnected users. SMC is a protocol that enables collaborative computing using multiparty computing (MPC) without disclosing information about the parties. SMC enhances the performance of the learning scheme by combining data from various parties. To simultaneously achieve efficiency, security, and accuracy, Cao et al. [36] proposed MSBLS, an SMC interactive protocol combined with a neural network that generates mapped features of two encrypted datasets and uses the same to determine the ML model parameters in a privacy-preserved manner. To limit communication costs while preventing the reconstruction of the original data used to train the model, Sotthiwat et al. [37] proposed a partially encrypted MPC for FL. In their scheme, sensitive parts of the gradients prone to privacy attacks were encrypted to lessen communication and computational overheads. Additionally, Mbonu et al. [38] implemented a combination of a blockchain network and aggregator servers to enable transparency and privacy preservation while reducing the computation cost of aggregating with the blockchain network. To preserve the privacy of user data, [39] proposed a secure aggregation in FL using SMC protocol to ensure that the server learns nothing except the aggregated model updates.

Besides the computational overheads incurred by using these cryptographic schemes, participants in FL can return poisoned updates. To this end, several works [24,25,26,40,41,42,43,44,45] have proposed solving the problem of poisoning attacks while preserving the privacy of local data. To prevent privacy compromise in the distance between two updates used to detect poisoning attacks, Li et al. [24] proposed EPPRFL. This poisoning attack detection scheme utilizes Euclidean distance filtering and clipping. Using additive secret sharing, they customized an SMC protocol for privacy preservation. To prevent Byzantine adversaries while protecting users’ privacy, Zhang et al. [25] proposed LSFL, a lightweight secure FL that guarantees Byzantine robustness and preserves the privacy of participant data during model aggregation. They implemented a non-colluding dual-server architecture for Byzantine robustness and a secret-sharing scheme for privacy preservation. Rathee et al. [26] proposed ELSA, a distributed trust secure aggregation protocol for FL that filters out boosted gradients by employing an L2 gradient resilient to poisoning attacks. Their architectural framework is based on two-server architecture. This scheme preserves the privacy of honest participants’ updates in the presence of collusion between, at most, one malicious server and malicious clients. To detect poisoning behaviors in ciphertexts while preserving privacy, Liu et al. [43] proposed PEFL, a framework based on HE. Their proposed scheme established a benchmark score using the median of the coordinates value. It utilized a logarithmic gradient extraction function to filter out malicious gradients that differ from the benchmark. Similarly, Ma et al. [40] proposed SheildFL, a two-trapdoor HE FL scheme. Their scheme provides resilience against an encrypted poisoned model that measures the distance between two encrypted gradients. Moreover, Lim et al. [41] proposed a poisoning-detectable privacy-preserving FL scheme that utilized a cosine similarity function to detect poisonous gradients. In their bid to exclude malicious participants’ updates, a benchmark value was established from the previous aggregated update. A cosine similarity was computed between the update and the benchmark value. Sakazi et al. [45] proposed using a semi-supervised transfer learning approach to detect phishing attacks. Liu et al. [46] proposed a semi-supervised client selection method that aids the server in selecting clients with good label information and quality updates to guard against poisoning attacks within an FL environment. Khazbak et al. [42] proposed MLGuard, a distributed collaborative system that utilized a lightweight secret-sharing scheme for privacy preservation and a cosine similarity function that measures each parameter updates angular distance. Lastly, Li et al. [44] proposed PFLS, a privacy-preserving dynamic adaptive poisoning detection scheme that prevents the impact of poisonous updates. Nevertheless, an assumption is made that poisonous gradients would deviate from the bulk of honest gradients; however, this is not always true.

Nevertheless, none of the works described above supports the verification of the correctness of the aggregated result from the server. To this end, Xu et al. proposed VerifyNet [17], a privacy-preserved and verifiable FL. In their scheme, they argued that the correctness of the aggregated results from the server is closely related to the privacy of users’ updates. They further stated that there is a high tendency to compromise the users’ privacy once an adversary can falsify the data returned to participants. This assertion holds because unverified aggregated results from malicious servers could compromise users’ privacy. In their scheme, they utilized a homomorphic hash function to verify the correctness of aggregated results from the server while preserving participants’ privacy using a double-masking protocol. Besides incurring high computation costs, malicious participants can poison the global model. This paper proposes a privacy-preserved secure aggregation protocol supporting verification and proof of aggregation, symbolizing a zero-trust FL environment. Moreover, our framework is lightweight and does not incur high computational burdens on either the servers or the participants. A comparison of our framework with existing SOTA research is described in Table 1.

Table 1. COMPARISON BETWEEN OUR FRAMEWORK AND EXISTING SOTA RESEARCH.

Solution	Privacy Preserved	Poisoning Attack Resilience	PoA	Techniques/Strategy Adopted	Server Architecture
[47] TAPFed	✓	✓	✗	Decisional Diffie–Hellman	Multi
Yazdinejad et al. [48]	✓	✓	✗	Additive homomorphic encryption, Gaussian mixture model (GMM), Mahalanobis distance	Single
[26] ELSA	✓	✓	✗	L2 defense, additive secret sharing, oblivious transfer protocol	Dual
[17] VerifyNET	✓	✗	✓	Homomorphic hash function, pseudorandom technology, secret sharing	Single
[24] EPPRFL	✓	✓	✗	Euclidean distance filtering and clipping, additive secret sharing, secure multiplication protocol	Dual
[25] LSFL	✓	✓	✗	Euclidean distance, additive secret sharing, Gaussian noise	Dual
[45] STFL	✓	✓	✗	Minmax optimization	Single
[49] SecureFL	✓	✓	✗	Additive homomorphic encryption, multiparty computation, FLTrust	Dual
[50] FLOD	✓	✓	✗	Multiparty computation, Sign-SGD, FLTrust	Dual
Our Framework	✓	✓	✓	Euclidean distance, L2 norm, additive secret sharing, oblivious transfer protocol	Dual

The symbol ✓ indicates achieved while ✗ indicates not achieved.

3. Preliminaries

(1)

FL System

For this study, our framework is based on a scalable FL system, and we adopted the Horizontal FL (HFL) method in which participants with the same data structure train an ML model using a parameter.

A brief description of the significant steps involved in the HFL is as follows:

• The server randomly selects participants for model training and distributes the global model for training.
• Participants selected for model training use their local data to train the model, compute their model weights, and individually send their updates to the servers for aggregation.
• The servers use the agreed protocol to collectively aggregate the updates to form a new global model without knowing the participants’ private data.
• The aggregator server sends the aggregated new global model to the participants for another round of training.

(A)

Local training dataset ($D_x)$: Within an FL process, assume that there are M participants and each participant $P_i$ holds a local training dataset:

$$D_x=\left\{⟨U_y^x,V_y^x⟩|y\in \left[d_x\right]\right\}$$

(1)

where $U_y^x=Input$ data at index y in $P_i$ dataset;

$V_y^x$ = Label or ground truth for the input $U_y^x$;

$d_x$ = The total number of data samples available in the local training dataset $D_x$ of $P_i$;

$D_x$ = Local training dataset;

(B)

Global dataset (D): This is the union of all individual datasets from M participants consisting of the training data from all the participants in an FL setting. Let the global dataset be:

$$D=U_{x=1}^M{D}_x$$

(2)

(C)

Neural Network (NN) and Loss Function ($L_F$): For an NN function defined as f(U, N) where the model input is still $U$ and the trainable parameters (weight and biases) are represented as $N$. As a Mean Squared Error (MSE), the loss function $L_F\left(D,N\right)$ can be defined as:

$$L_F\left(D,N\right)={\displaystyle \frac{1}{\left|D\right|}}\sum ⟨U_y^x,V_y^x⟩\in D{\left(V_y^x-f\left(U_y^x,N\right)\right)}^2$$

(3)

where $f\left(U_y^x,N\right)$ = the predicted output of the NN;

${\left(V_y^x-f\left(U_y^x,N\right)\right)}^2$ = the squared error for each data point.

Here, the goal is to find the optimal parameters to minimize the loss function. If $N$ is updated using SGD optimizer, iteratively, each parameter is calculated as:

$$N^{i+1}=N^i-\eta \Delta L_F\left(D^i,N^i\right)$$

(4)

where

$N^i$ = ith iterative parameter;

$\eta$ = Learning rate (predefined);

$D^i$ = A random subset of D.

(2)

Proof of Aggregation (PoA) [51]

PoA is considered a vital component in FL systems, providing a need to authenticate, validate, and ensure the integrity of the aggregated process and result [52]. Conventional FL relies on the trust assumption that the central server will perform its aggregation function effectively and faithfully. This may not be true because a malicious server, in reality, could manipulate aggregated results by carefully injecting false participants into the training process or replacing participant’s training models. Therefore, the aggregator server should provide proof of aggregation for each round to demonstrate to the participants that the aggregation process was executed faithfully and to ensure the correctness of the aggregated result [53]. In other words, it demonstrates the certainty of a result to another party without exposing any data beyond the result’s authenticity [54].

(3)

Zero-Trust Architecture

Participants in FL involve devices with few security measures and could pose weak points of entry to critical assets. In the same vein, the privacy of participants’ local updates is closely related to the correctness of results returned by the server. Manipulated results returned to participants by a malicious server tend to increase the risk of participants’ privacy being compromised. Consequently, carefully manipulated results in white-box attacks could incite participants to unleash sensitive information [55]. A zero-trust architecture is the assumption that every entity within an FL framework could be at some point malicious or compromised by external attackers, and amid an attack, the initial point of contact is often not the intended target [56].

4. System Architecture

This section describes the components of the system’s architectural framework, a description of the threat model, a design goal, and a detailed interpretation of the system architecture.

A.

Description of components

Server $\left(S_a\right)$: This server is tasked with the responsibilities of generating the global model, the distribution of the model, the prevention of poisoning attacks by a malicious participant’s update, and the aggregation of combined results in collaboration with the server $\left(S_b\right)$. Furthermore, it provides PoA after every iteration and sends the results to $S_b$ and the participants.

Server $\left(S_b\right)$: Similarly to all the responsibilities associated with $S_a$, it validates the correctness of the aggregated results from $S_a$ and also provides PoA to all entities within the framework.

Participants: They are multiple devices or organizations $\left(P_1 \mathrm{t}\mathrm{o} P_n\right)$ that communicate with the servers for model computations and training.

B.

Threat Model

All entities in the framework are considered to be honest-but-curious entities [17], which implies that the entities could use an agreed arrangement to execute the protocol but may try to infer other entities’ private data. Similarly to related schemes [24,25], we consider the following threat model in this framework:

• The two servers $\left(S_a \mathrm{a}\mathrm{n}\mathrm{d} S_b\right)$ will not collude with each other and will use the agreed arrangement to execute the protocol but may independently try to infer the data privacy of the participants.
• Poison attacks from malicious participants corrupt the global model through the exchange of malicious local updates. We consider a strong threat model with diverse attack rates (10% to 40%) of participants in the FL process to be malicious. The assumption is that the participants may launch poisoning attacks such as label flipping, sign flipping, gradient manipulation, backdoor, and backdoor embedding attacks.
• Modifying aggregated results and forging proof of aggregated results from any server to deceive other entities within the framework.

Specifically, there is no collusion between any entities in the framework.

C.

Design Goal

Our design goal is to preserve the privacy of local data and prevent poisoning attacks from malicious participants while supporting the correctness of the aggregated model. Consequently, our framework should simultaneously achieve privacy preservation, robustness, and proof of the correctness of the aggregated model and enable a zero-trust architectural framework. Specifically, our scheme guarantees the following design goal:

• Privacy: The scheme should prevent an attacker or a malicious server from interfering with the privacy of the exchanged gradients and further ensure that there is no privacy leakage of the information used to detect poisoning attacks.
• Fidelity: The accuracy of the global model should not be compromised due to the robustness of the framework. As a baseline, we use FedAVG [57], a standard algorithm resilient to poisoning attacks with no privacy preservation method. Therefore, the framework should achieve a level of accuracy comparable to FedAvg.
• Robustness: The framework should ensure the robustness of the global model by preventing malicious participants from poisoning the global model. Specifically, the framework should be resilient to poisoning attacks from malicious participants.
• Efficiency: Our framework should minimize the computation and communication overheads by enabling the preservation of the privacy of participants with limited computational resources.

In addition, the framework should ensure a zero-trust architectural framework capable of transforming the FL network into a solid defense system where no malicious entity can successfully act.

D.

System Interpretation

Figure 1 depicts a distributed ML framework. Similarly to [24,25,26], our framework utilizes a dual-server architecture $\left(S_a \mathrm{a}\mathrm{n}\mathrm{d} S_b\right)$. This dualistic approach provides a robust, secure, decentralized data processing, and zero-trust framework. The server ($S_a$) initiates the training process by randomly selecting participants for model training. The global model is sent to selected participants for model training through a secured channel. It is worth noting that both servers can initiate the model training.

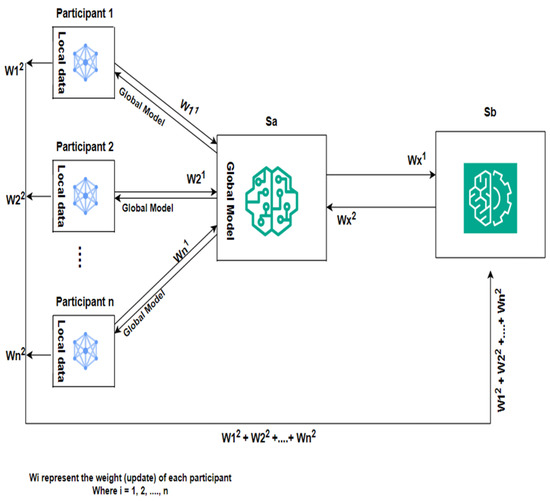
Figure 1. System architecture.

On receiving the global model, the participants individually perform local computations using their local data to train the model. They try to solve the loss function using optimal parameters. After local computation and training of the model with their local data, each participant splits their updates to obtain $W_i^a \mathrm{a}\mathrm{n}\mathrm{d} W_i^b$, and sends it to the two servers $S_a \mathrm{a}\mathrm{n}\mathrm{d} S_b$, respectively, using additive secret sharing. No server receives the full participants’ update, but the splitting is at the discretion of individual participants. The splitting is such that $W_i^a \mathrm{a}\mathrm{n}\mathrm{d} { W}_i^b$ add up to give a complete update of each participant. In this framework, the oblivious transfer (OT) protocol transfers the split weights, and there is no collusion between entities within the framework. The OT protocol is explained in Section 5.

On receiving the updates, the servers collaboratively check for malicious updates to prevent poisoning of the global model. Servers $S_a \mathrm{and} S_b$ individually aggregate their results to compute a weighted average and combine their aggregated results to obtain a complete model update. Each server individually sends its partial aggregated result and complete model update to all the entities within the framework to show PoA and ensure a zero-trust architecture. Participants reject a round if the aggregated results from both servers do not add up to give the complete model update without splitting the updates.

5. Secret Sharing Schemes

5.1. Secret Sharing for Privacy Preservation

Using Lagrange polynomial interpolation over finite fields, Shamir’s Secret Sharing (SSS) [58] is an optimal and ideal $\left(t, n\right)$ threshold method where $t$ is the threshold, and $n$ is the number of participants in our framework. SSS is a protocol that can be used to achieve dropout robustness [59]. In such a method, the objective is to split a confidential secret $S$ into fragments of shares $S_1, S_2, S_3,\dots , S_i$ (where $i=1,$ 2, 3, …, n) in such a manner that the following applies:

• The learning knowledge of $t$ or more shares $S_i$ permits the computation of the original confidential secrets $S$. That is, the complete reconstruction of the secret $S$ has a combination of at least $t$ shares.
• The learning knowledge of $t-1$ or fewer shares $S_{i },$ makes $S$ completely unknown. That is, the potential value of the secret $S$ remains unknown when aware of up to $t-1$ shares, just as there would be knowledge of zero shares. It is vital to note that the reconstruction of the secret $S$ requires the presence of at least $t$ shares. If $n=t,$ then the complete shares are required for the reconstruction of the secret $S$.

5.2. Mathematical Formulation of SSS

Assume a value $S$ which is secret-shared, a vector of $\left(n, t\right)$. This value $S$ is not known to anyone and is individually shared with each participant in the training process. As an element of the finite field $A_p$, let $S$ be represented as $a_0$. $A_p$ is an array of large prime $p$ where $0<t\le n<p$.

Picking a random polynomial $A\left(x\right)$ with a degree of $t$ (where $t\le 1)$ and a constant term of $S$, the secret holder randomly picks $a_1, \dots , a_{t-1}$ from $A_p$ where $==S$. This polynomial can be defined as:

$$A\left(x\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{a}_0+a_{1}x+a_2{x}^2+a_3{x}^3+\dots a_{t-1}{x}^{t-1}mod p$$

(5)

$$A\left(x\right)={\in }_r{P}^{s,t}$$

(6)

The evaluations are happening at ${\alpha }_1, {\alpha }_2, \dots , {\alpha }_n$ which are distinct, non-zero, and publicly known elements. These evaluations are fixed for all instances of the sharing method. $A\left(x\right)$ is evaluated at $x=\left({\alpha }_1, a_1\right), \left({\alpha }_2, a_2\right), \left({\alpha }_3, a_3\right), \dots , \left({\alpha }_n,a_n\right)$. The value of $S$ is unknown, and no participant has the full vector. Instead, component-wise, each participant has the corresponding component of this vector.

To share the secret, the secret holder computes $S^{\left(i\right)}=A\left(i\right) \mathrm{f}\mathrm{o}\mathrm{r} i \in \left(\mathrm{1,2},3,\dots ,n\right)$ and each participant receives $\left(i, S^{\left(i\right)}\right)$.

To reconstruct the secret, any subset of $t$ of $\left(i, S^{\left(i\right)}\right)$ pairs will be able to reconstruct the secret using the Lagrange interpolation formula:

$$a_0=S={\sum }_{j=1}^t{S}^{\left(j\right)}.{\prod }_{m=0,m\ne j}^t{\displaystyle \frac{x_m}{x_m-x_j}}mod p$$

(7)

5.3. Additive Secret Sharing (ASS)

ASS [60] is an n-out-of-n scheme that requires all shares to reconstruct the secret. It is typically an SMC technology with additive homomorphism, as illustrated in Algorithm 1. ASS is a simple secret-sharing scheme, and our framework considers an ASS of 2-out-of-2. The recovered value would be random if there is a lack of any share. Without any collusion, it supports linear computation and protocol. Consequently, a secret $w_i\in Z_L$ is additively shared between two servers in a manner that $S_a$ and $S_b$, respectively, possess the random shares $w_i^a \mathrm{a}\mathrm{n}\mathrm{d} w_i^b$ such that $w_i^a+w_i^b=W_i$.

As a privacy-preserving protocol in FL, it naturally aids the addition of the weights as $W_1+W_2=\left(W_1^1+W_2^1\right)+\left(W_1^2+W_2^2\right)$. It is simple, practicable, and the communication cost of clients in multiple-server architectures is much less than in a single-server architecture [61]. In ASS, the privacy of participants’ updates is guaranteed as long as these two conditions are satisfied. Firstly, the servers do not collude with each other, or in the case of multiple servers, at least one server does not collude with other servers. This means that if the two servers collude in a dual-server architecture, the secret shares can be reconstructed because each server can access one share. In multiple-server architectures, the secret reconstruction will be impossible because the secret share of the non-colluding server will be missing. Secondly, at least two participants do not collude with the rest. Suppose all participants collude with each other except one; the colluding participants can compute the weight of the non-colluding participants by subtracting its weight from the total weight of all participants (colluding and non-colluding). The computation will reveal the original weight of the non-colluding participant.

Nevertheless, ASS could introduce rounding errors and compromise precision [62]. Moreover, it could lead to information loss during splitting because there may exist more significant digits in the original weight than the split can accommodate [63]. Additionally, finite bit representation may result in rounding errors during weight reconstruction. However, these vulnerabilities are prevalent in single-server architecture.

Algorithm 1: Additive Secret Sharing

Given $W_x\in Z_L$ Split $W_x$ into ${Wi}^1 , {Wi}^2$ Such that ${Wi}^1+{Wi}^2=W \left(mod L\right)$ Apply Oblivious Transfer ${Wi}^1\leftarrow Z_L$ ${Wi}^1\equiv Wi-{Wi}^2\left(mod L\right)$ Send ${Wi}^1 \mathrm{to} S_a$ and ${Wi}^2 \mathrm{to} S_b$ Given two secret values ${Wx}^1 \mathrm{and} {Wy}^1$ Shares of $Z\equiv {Wx}^1+{Wx}^2\left(mod L\right)$ can be computed locally by each server $S_a$ setting $Z^a\leftarrow {Wx}^1+{Wy}^1 \left(mod L\right)$ $S_b$ setting $Z^b\leftarrow {Wx}^2+{Wy}^2 \left(mod L\right)$ Where L = 2

5.4. Oblivious Transfer (OT)

An OT protocol [64] is a very important cryptographic primitive that involves sending data only one part of which will arrive, but the sender is unaware of the part that will arrive. The receiver selects what they can read. The most basic protocol, and the one we considered for this work, is 1-out-of-2 OT [65]. The sender (OTS) has two private inputs $\left(w_0. w_1\right)$ and the receiver (OTR) has a selection bit $z\left( 0, 1\right)$. After the execution of the protocol by both parties, the OTR obtains the message $w_z$ from messages held by the OTS, with the latter receiving no output.

The security execution of the protocol requires that the OTS learns nothing about the choice of the OTR while the OTR learns only its choice. The practical implementation is in the privacy preservation of data and has been widely used in secure two-party computation. Assume participant P₁ $\in$ P_n as the sender and Server $S_a$ as the receiver. P₁ splits its weight into two and then interacts with $S_a.$ As a result, $S_a$ only acquires the weight selected and nothing more, while P₁ learns nothing about $S_a$’s chosen weight. In a 1-out-of-2 OT protocol, P₁ takes $W_1^1, W_1^2\in \left\{0, 1\right\}$ as an input and $S_a$ takes $x_y\left(y=1, 2\right)$ as an input. As a result of running the protocol, $S_a$ receives a challenged weight $W_{x_y}$ and $P_1$ is unaware of $S_a$’s choice. As such, the protocol satisfies the privacy properties of $S_a$, the privacy of $P_1$, and the correctness of OT. Other variants of the OT protocol include Cut-and-Choose OT (CCOT) [66] and Outsourced OT (OOT) [67]. CCOT has proven to be secure in the presence of malicious adversaries [68]. In CCOT, the receiver receives the sender’s output values differently. Similarly, OOT has been used in cloud-assisted models involving three entities known as the sender, receiver, and cloud. The cloud obtains the receiver’s choice output values, and this protocol allows participants to preserve their privacy while outsourcing their work to the cloud. A high level of system interpretation is illustrated with Algorithm 2.

Algorithm 2: Dual Server Secure Aggregation and PoA Protocol

Input: Servers Sa and Sb, Participants Pi = ($P_1,P_2,\dots ,P_n$), Global model WG, Local data LD, number of participants n, update W, number of training rounds K, Additive Secret-Shared (ASS) update of current round ${Wi}^1$, ${Wi}^2$, Shamir’s Secret Sharing SSS, Selected Participants SP, Proof of Aggregation PoA. Output: Aggregated final model W. 1  Initialization N: 2  Procedure 3  for k = 1 ≤ k: 4     (I) Participants 5     for Pi Є Pn do: 6        (a) Split LD between Pi Є Pn using SSS 7  (b) Train WG using LD 8        // Weight Splitting 9  (c) Split each participant W using ASS into $W_1$ and $W_2$ 10     Participants $P_i\left(i \in \left[1,n\right]\right)$ splits $W_i$ into $W_i^a \mathrm{and} W_i^b$ subject to $W_i^a+W_i^b=W_i$ 11     Such that $W_1+W_2=\left(W_1^1+W_2^1\right)+\left(W_1^2+W_2^2\right)$ 12  // OT Protocol 13         (d) Use OT protocol to send $W_i^a$ to Sa and $W_i^b$ to Sb 14     $S_a$ holds the weight $W_i^a$ but does not know of $W_i^{1-a}$ 15     $S_b$ holds $W_i^b$ and no knowledge of $W_i^{1-b}$ 16     end 17     // Poisoning attack detection 18     (II) Sa and Sb 19     for Sa do: 20  (a) Compute ${Wx}^1\leftarrow \sum _{i=1}^n{Wi}^1$ 21  (b) Send ${Wx}^1$ to Sb 22     end 23     for Sb do: 24  (a) Compute ${Wx}^2\leftarrow \sum _{i=1}^n{Wi}^2$ 25  (d) Send ${Wx}^2$ to Sa 26     end 27     // Both servers recover weight ${\mathit{W}\mathit{i}}^{12}$ 28     Sa, Sb performs ${Wi}^{12}={\displaystyle \frac{1}{2n}}\left({Wx}^1+{Wx}^2\right)$ 29     Sb sends the computation of ${\displaystyle \frac{1}{2}}{Wi}^2-{Wi}^{12}$ to Sa 30     Sa sends the computation of ${\displaystyle \frac{1}{2}}{Wi}^1-{Wi}^{12}$ to Sb 31     // Distance (D) computation on both servers 32     for all $\mathit{w}\mathit{i}\in \mathit{w}$ do 33       Sa via $D_i={\displaystyle \frac{1}{2}}{Wi}^1+{\displaystyle \frac{1}{2}}{Wi}^2-{Wi}^{12}$ 34       Sb via $D_i={\displaystyle \frac{1}{2}}{Wi}^2+{\displaystyle \frac{1}{2}}{Wi}^1-{Wi}^{12}$ 35       $D\left(i\right)\leftarrow \left|D_i\right|$ 36     end 37     // Determination of median (M) 38     Sa and Sb gets the median M of $D_i$ via $D_i^I=\left[D\left(W_1\right),D\left(W_2\right), \dots , D\left(W_n\right)\right]$ 39     for all $\mathit{W}\mathit{i}\in \mathit{W}$do: 40       Sa and Sb computes $D_i^{II}$= $\left|D\left(W_i\right)-M\right|$ 41     end 42     // Participants N with the smallest similarity are selected 43     $S{P}_i\leftarrow \left\{{SP}_1, {SP}_2, \dots , {SP}_N\right\}$ 44     // Secure aggregation and proof of PoA 45     Sa computes $W_1={\displaystyle \frac{1}{2N}}\sum _{i=1}^N{Wi}^1, P_i\in SP$ 46     Sb computes $W_2={\displaystyle \frac{1}{2N}}\sum _{i=1}^N{Wi}^2, P_i\in SP$ 47     Sa sends $W_1$ to Sb and SP; Sb sends $W_2$ to Sa and SP 48     Sa and Sb computes $W=W_1+W_2$ 49     Sa updates global model and sends W to Sb and (W, $W_2)$ to SP for PoA 50     Sb updates its global model and sends W to Sa and (W, $W_1)$ to SP for PoA 51     if $\mathit{W}\ne {\mathit{W}}_1+{\mathit{W}}_2$: 52       reject PoA 53     else: 54       accept PoA 55  end 56  return Aggregated final model W

5.5. Poisoning Attack Detection

Our focus is on data poisoning [69] and model poisoning attacks [68] that are implemented in the training phase. In this scenario, attackers intentionally modify the weight parameters to poison the global model. We adopt the strategy deployed in [25] with modifications. We mitigated poisoning attacks using a weight selection and filtering scheme. In our approach, we computed the median value of the distances between the individual participants’ models and the average model after transforming it from a vector to a weight value. The difference between the weighted distance and the median is utilized as a similarity judging criterion. This process is used to identify poisoned updates based on their distance from their nearest neighbors, and it uses distance metrics. Considering a dataset $d=\left\{\left(U_1,V_1\right),\left(U_2,V_2\right),\dots ,\left(U_n,V_n\right)\right\}$ where $U_i$ and $V_i$ are the feature vector and corresponding label, respectively. The process is as follows:

Distance metrics calculation: This involves the use of Euclidean distance to calculate the distance between test point $U$ and all other training points. It also measures the deviation of each participant’s update from some central tendency measure (such as the mean or median) of all updates. A participant’s update is considered an anomaly if the update is too far from the central tendency.

Assume we have $n$ participants, and each participant provides an updated vector $W_i$ for $i-\mathrm{1,2},\dots ,n$

i.

Central Tendency Calculation

Using the median (M) as a central tendency measure, the median update vector ($\forall )$ can be computed as $M=x_{\left({\displaystyle \frac{n}{2 }}+1\right)}$ for an odd number of observations and $M=x_{\left({\displaystyle \frac{n}{2}}\right)}+$ $x_{\left({\displaystyle \frac{n}{2 }}+1\right)}$ for an even number of observations.

ii.

Euclidean Distance Calculation

The Euclidean distance (D) of each update from the median could be calculated as:

$$D\left(U,U_i\right)=\sqrt{{\sum }_{j=1}^q{\left(U_j-U_{ij}\right)}^2}$$

(8)

where q = the number of features.

iii.

Malicious Threshold

A threshold τ needs to be determined. This threshold could be a fixed value or function of the distances beyond which an update is considered malicious. The threshold τ could also be determined by a percentile.

iv.

Malicious Update Detection

An update is considered malicious if $D_i>\tau .$

A participant’s update, whose distance from the median is greater than this threshold, would be considered an anomaly that could be investigated further or potentially discarded. For each participant update, a similarity measure using Euclidean distance is computed. This computation is the distance between the participant’s update and the median update from other participants. The purpose is to determine the proximity of each update to the central update that represents the median of all updates. This central update invariably represents the consensus of honest participants. Moreover, a baseline threshold is defined based on initial runs, signifying the highest permissible deviation from the central update. A similarity measure of the threshold for each participant update is carried out to determine potentially honest or suspicious participants. However, this does not truly represent the criteria for judging similarity, as outliers from large weights may exist. The basic criterion for judging similarity is explained in the next section. In high-dimensional data settings, iteratively, the dynamic adjustment of the threshold can be carried out over time. That is to say, if too few or too many updates are labeled malicious, the threshold can be adjusted based on the latest distribution.

Locate Nearest Weights: Identify the closest K training points to U based on the distance metrics.

(1)

Classification: Classify U as a poisoned update if a significant proportion of outliers within its K nearest weights exist.

5.6. Application in Federated Learning

To demonstrate its application in FL, let us consider a scenario where multiple participants train a global model with their local data. We aim to detect poisoned updates from the participants before aggregation.

Let W represent the global model.

Let i index each participant,

where $P_i$ Є $\left\{1,2,\dots ,n\right\}$.

Let the local model updates sent by each participant be represented by $w$. This is a vector that represents the change they propose to W.

Let the median of the updates be represented as $M$.

Let the Euclidean distance for each update be represented as $D_i$.

For the local updates $W_i$ collection, poisoning attack detection, and aggregation by the server, the following steps ensued:

Step 1: Collection of local updates with privacy preserved.

Each participant trains the model locally and individually sends their updates $W_i$ to the servers using the ASS protocol.

Let the computed weight at $S_a$ be ${wx}^1=\sum _{i=1}^n{wi}^1$ and $S_b$ be ${wx}^2=\sum _{i=1}^n{wi}^2$, respectively.

$S_a$ sends ${wx}^1$ to $S_b$ while $S_b$ sends ${wx}^2$ to $S_a$.

To recover the weight ${wi}^{12}$, both $S_a$ and $S_b$ each perform computation ${wi}^{12}={\displaystyle \frac{1}{2n}}\left({wx}^1+{wx}^2\right)$.

$S_b$ sends the computation of ${\displaystyle \frac{1}{2}}{wi}^2-{wi}^{12}$ to $S_a$ and $S_a$ sends the computation ${\displaystyle \frac{1}{2}}{wi}^1-{wi}^{12}$ to $S_b$.

Step 2: Poisoning attack detection.

Distance (D) computation on both servers.

$S_a$ via $D_i={\displaystyle \frac{1}{2}}{wi}^1+{\displaystyle \frac{1}{2}}{wi}^2-{wi}^{12}$

$S_b$ via $D_i={\displaystyle \frac{1}{2}}{wi}^2+{\displaystyle \frac{1}{2}}{wi}^1-{wi}^{12}$

Selecting a baseline model (m), the similarity between participants’ updates $\left(w_i\right)$ can be calculated by each server [$D\left(wi,m\right)=$ $w_i-m].$ To filter out boosted weight using the L2 norm, each participant provides a weight $D_i\in n^d$, with d as the dimension of the model parameter space. The two servers can compute the L2 norm of each participant’s update as ${‖D_i‖}_2={\displaystyle \frac{1}{2n}}\sqrt{\sum _{k=1}^d{D}_{i,k}^2}$, where k is the index from 1 to d. This computed L2 norm gives a scalar measure of the overall magnitude of the updates. To define a suitable threshold ($\tau )$ that distinguishes normal updates from outliers, we computed the median (M) as $M=\left(\left\{{‖D_i‖}_2 :i=\mathrm{1,2},\dots ,n\right\}\right)$ and median deviation ($M_d$) as $M_d=\left(\left|{‖D_i‖}_2-M\right| :i=\mathrm{1,2},\dots ,n\right)$. Thus, $\tau =M+\left(C.M_d\right)$, where C is a constant $\left(C>0\right)$. This represents the true criterion to judge similarity and updates larger than $\tau$ are flagged as malicious. The threshold ($\tau$) is also used to obtain the deviation of each participant’s update from the average model with new benign participants selected for secure aggregation.

Step 3: Secure aggregation and PoA

Let new selected participants (SP) be $S{P}_i=\left\{{SP}_1,{SP}_2,\dots ,{SP}_N\right\}$.

$$S_a \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{s}{ W}_1={\displaystyle \frac{1}{2N}}{\sum }_{i=1}^N{wi}^1,P_i\in SP$$

(9)

$$S_b \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{s} W_2={\displaystyle \frac{1}{2N}}{\sum }_{i=1}^N{wi}^2,P_i\in SP$$

(10)

$S_a$ sends $W_1$ to $S_b$ and SP while $S_b$ sends $W_2$ to $S_a$ and SP. $S_a$ and $S_b$ compute the new aggregated weight $W=W_1+W_2$.

$S_a$ updates the global model and sends W to $S_b$, and (W, $W_2)$ to SP for PoA. Similarly, $S_b$ updates its global model and sends W to $S_a$, and (W, $W_1)$ to SP for PoA. The participants reject the result if $W\ne W_1+W_2$.

6. Security Analysis

In this section, we analyze the security of our framework and showcase that it meets the security goals and design objectives.

Theorem 1. 

Servers$\left(S_a and S_b\right)$know no information about the local data used to train the model.

Proof of Theorem 1. 

To securely share data, we adopt a dual-server architecture $S_y \left(y \in \left[a, b\right]\right)$. For the weight $W_i$ and dataset $D_i$, each participant $P_i\left(i \in \left[1,n\right]\right)$ splits $W_i$ into $W_i^a \mathrm{and} W_i^b$ subject to $W_i^a+W_i^b=W_i$. $P_i$ sends $W_i^y, D_i$ to the y-th server. Server $S_a$ is required to compute $W_i^a={\displaystyle \frac{\sum _{i=1}^n{W}_i^a{D}_i}{\sum _{i=1}^n{D}_i}}$ and server $S_b$ is required to compute $W_i^b={\displaystyle \frac{\sum _{i=1}^n{W}_i^b{D}_i}{\sum _{i=1}^n{D}_i}}$. Consequently, $S_a$ holds the weight $W_i^a$ but does not know of $W_i^{1-a}$ while $S_b$ holds $W_i^b$ and no knowledge of $W_i^{1-b}$. Suppose $S_a$ is malicious, it sees only $\left\{W_i^a:i=1, 2,\dots n\right\}$. Knowing of $W_i^a$ alone does not reveal $W_i$ because, for any given $W_i^b$, there is a different $W_i$. The confidentiality or integrity cannot be broken if one server is compromised. During poisoning attack detection, the weight at both servers = ${\displaystyle \frac{1}{2n}}\left(W_i^a+W_1^b\right)$. Distance computation at both servers reveals that each server obtains ${\displaystyle \frac{1}{2}}{W}_i^a+{\displaystyle \frac{1}{2}}{W}_i^b-W_i^{ab}$. Without collision, no server has the full weight of any participant. □

Theorem 2. 

Our framework shows robustness against malicious participants.

Proof of Theorem 2. 

Each participant splits their weight vector $W_i$ into $W_i^a \mathrm{and} W_i^b$ such that $W_i^a+W_i^b=W_i$. Each server would ideally compute partial aggregation. Server $S_a$ computes $W_1={\displaystyle \frac{\sum _{i=1}^n{W}_i^a{D}_i}{\sum _{i=1}^n{D}_i}}$ and server $S_b$ computes $W_2={\displaystyle \frac{\sum _{i=1}^n{W}_i^b{D}_i}{\sum _{i=1}^n{D}_i}}$. The final global weight $W_G$ is reconstructed as $W_G=$ $W_1+W_2$. To influence $W_G$, a malicious participant aims to upload the poisoned weight $W_P$. $W_P$ is split as $W_P^a \mathrm{a}\mathrm{n}\mathrm{d} W_P^b$ such that $W_P^a+W_P^b=W_P$. The visibility of the full poisoned vector at any single server is reduced because of the splitting of the poisoned weights. Selecting a baseline model $m$, each server computes the nearest weight based on Euclidean distance [$D\left(w_i,m\right)=$ $w_i-m]$.

For legitimate participants, $D\left(W_i^a,m\right)\approx D\left(W_i^b,m\right)$, ensures coherent weights across servers. For malicious participants, $D\left(W_P^a, m\right)\gg D\left(W_i^a,m\right)$, suggests a deviation. Furthermore, the L2 norm of each participant’s update at both servers is computed as ${‖D_i‖}_2={\displaystyle \frac{1}{2n}}\sqrt{\sum _{k=1}^d{D}_{i,k}^2}$. A threshold ($\tau )$ is computed as $\tau =M+\left(C.M_d\right)$, with median (M) as $M=\left(\left\{{‖D_i‖}_2 :i=\mathrm{1,2},\dots ,n\right\}\right)$, median deviation ($M_d$) as $M_d=\left(\left|{‖D_i‖}_2-M\right| :i=\mathrm{1,2},\dots ,n\right)$, and C as a constant $\left(C>0\right)$. The threshold ($\tau )$ represents the criterion for judging similarity and the deviation of each participant’s update from the average model. At both servers, new participants are selected ${SP}_i\in \left[1, N\right]$, and outliers excluded from aggregation as: $W_i^a={\displaystyle \frac{{\sum }_{i\ne P}{D}_i{W}_i^a}{{\sum }_{i\ne P}{D}_i}}$ and $W_i^b={\displaystyle \frac{{\sum }_{i\ne P}{D}_i{W}_i^b}{{\sum }_{i\ne P}{D}_i}}$. The influence of $W_P$ is entirely removed, and our framework shows robustness to poisoned updates. □

Theorem 3. 

Our framework satisfies PoA.

Proof of Theorem 3. 

After filtering malicious updates, a new participant ${SP}_i\in \left[1, N\right]$ is selected for model training. During training, each participant splits their weight $W_i$ subject to $W_i^a+W_i^b=W_i$. $S_a$ would aggregate weight as follows: $W_1={\displaystyle \frac{\sum _{i=1}^N{W}_i^a{D}_i}{\sum _{i=1}^N{D}_i}}$ and $S_b$ as $W_2={\displaystyle \frac{\sum _{i=1}^N{W}_i^b{D}_i}{\sum _{i=1}^N{D}_i}}$. The final global aggregation would be $W_G=$ $W_1+W_2$. The computation would result in $W_G={\displaystyle \frac{\sum _{i=1}^N{W}_i^a{D}_i}{\sum _{i=1}^N{D}_i}}+{\displaystyle \frac{\sum _{i=1}^N{W}_i^b{D}_i}{\sum _{i=1}^N{D}_i}}$ which equates to $W_G={\displaystyle \frac{\sum _{i=1}^N{W}_i{D}_i}{\sum _{i=1}^N{D}_i}}$. □

For PoA, let ${\delta }_i\epsilon \left[\mathrm{0,1}\right]$ be the proportion that determines the split such that:

$$W_i^a={\delta }_i{w}_i\mathrm{and} W_i^b=\left(1-{\delta }_i\right)w_i$$

$$W_G={\displaystyle \frac{\sum _{i=1}^N{W}_i^a{D}_i}{\sum _{i=1}^N{D}_i}}+{\displaystyle \frac{\sum _{i=1}^N{W}_i^b{D}_i}{\sum _{i=1}^N{D}_i}}$$

Substitution would result in:

$$W_G={\displaystyle \frac{\sum _{i=1}^N{D}_i\left({\delta }_i{w}_i\right)}{\sum _{i=1}^N{D}_i}}+{\displaystyle \frac{\sum _{i=1}^N{D}_i\left(\left(1-{\delta }_i\right)w_i\right)}{\sum _{i=1}^N{D}_i}}$$

$$W_G={\displaystyle \frac{\sum _{i=1}^N{D}_i\left({\delta }_i{w}_i\right)+\sum _{i=1}^N{D}_i\left(\left(1-{\delta }_i\right)w_i\right)}{\sum _{i=1}^N{D}_i}}$$

$$W_G={\displaystyle \frac{\sum _{i=1}^N{D}_i\left({\delta }_i+1-{\delta }_i\right)w_i}{\sum _{i=1}^N{D}_i}}$$

$$W_G={\displaystyle \frac{\sum _{i=1}^N{W}_i{D}_i}{\sum _{i=1}^N{D}_i}}$$

A participant would reject the result if $W_G\ne$ $W_1+W_2$. If all entities within the framework correctly execute the protocol, each selected participant will receive $W_G$, partial aggregation at $S_a$ $\left(W_1\right)$ and $S_b$ $\left(W_2\right)$. This will provide the participants with all specific and reconfirmation details to investigate the correctness of aggregation.

Theorem 4. 

Our framework exhibits a zero-trust architecture.

Proof of Theorem 4. 

As previously stated, a zero-trust architecture ensures no malicious entity acts within a federated learning environment. We have established that partial aggregation from $S_a$ is $W_1={\displaystyle \frac{\sum _{i=1}^N{W}_i^a{D}_i}{\sum _{i=1}^N{D}_i}}$, at $S_b$ is $W_2={\displaystyle \frac{\sum _{i=1}^N{W}_i^b{D}_i}{\sum _{i=1}^N{D}_i}}$, and the global aggregated model is $W_G=$ $W_1+W_2$. No single entity is trusted within the framework, and each entity is treated as potentially compromised. Through structural guarantees, security is achieved, and no server has full information. Consequently, $S_a$ holds only $\left\{W_i^a\right\}$ and $S_b$ only holds $\left\{W_i^b\right\}$. The zero-trust principle can be seen as a requirement that a subset of the framework cannot compute the final. Hence, the final global model is a function of $F\left(\left\{W_i\right\}\right)=W_G$. Let us define $G_1\left(\left\{W_i^a\right\}\right)=W_i^a$, $G_2\left(\left\{W_i^b\right\}\right)=W_i^b$. Then, $F\left(\left\{W_i\right\}\right)=$ $G_1\left(\left\{W_i^a\right\}\right)+$ $G_2\left(\left\{W_i^b\right\}\right).$ Without both servers’ output, there is no transformation of $H_1$ or $H_2$ that permits $H_1\left(G_1\left(\left\{W_i^a\right\}\right)\right)=W_G$ or $H_2\left(G_2\left(\left\{W_i^b\right\}\right)\right)=W_G$. No single entity within the framework is privileged to control the global result independently. To reinforce zero trust and prevent undetected attacks during the training process, each participant’s update must be audited for anomalies during each round of training. No incentive is given for performance, and equal scrutiny is applied to all participants. Moreover, the aggregated results from the two servers should be added to give the total aggregated weight (W). Furthermore, the protocol should ensure that each server sends its weight and the corresponding weight of the other server to the participants for verification and reconfirmation. A round is terminated if there is a variation in the weights received from the servers or if the weights were not added to give the total aggregated weight. □

7. Evaluation

In this section, we experimentally evaluate our framework to verify that it meets the design goals. Specifically, we have evaluated our framework for fidelity, robustness, and efficiency.

A.

Implementation

All experiments were run on a High-Performance Computing (HPC) cluster configured with Linux CentOS. A Dell C6420 PowerEdge with compute nodes of 2 Intel Xeon Platinum, 48 cores per node, 8640 compute cores, 2.9 GHz 24-core processor, 180 nodes, 192 GB RAM per node, and 4 GB RAM per core. The experiment is implemented in Python 3.12 using TensorFlow Federated (TFF) libraries.

B.

Experimental Setup

(1)

Datasets: We evaluated our framework with two different domain benchmark datasets, which are MNIST [70] and CIFAR [71].

• MNIST dataset: The MNIST dataset is among the most popular datasets used in ML and computer vision. As a standardized dataset, it consists of handwritten digits 0–9 as grayscale images sized 28 × 28 pixels. It has training and test sets of 60,000 and 10,000 images, respectively. We utilize CNN and MLP models to experiment with the IID and non-IID datasets.
• CIFAR-10 dataset: The CIFAR-10 dataset is a 32 × 32-pixel image consisting of 10 different classes of color images of objects with a training set of 50,000 and a test set of 10,000 images. It has a total of 3072 pixels per image (32 × 32 × 3) with integer values of 0–9 representing the object class. We also use CNN and MLP models

(2)

Data Splits: We experimented by splitting each participant’s dataset into IID and non-IID. For IID, the total number of MNIST and CIFAR dataset samples were shuffled and divided evenly among participants. For non-IID, the data distribution is based on class where each participant may possess data from a few classes. To create class-specific data distributions, we utilized a stratified sampling method based on class labels.

(3)

Baselines: As benchmarks, we utilized a standard aggregation rule, a poisoning attack detection scheme, an SMC protocol with filtering and clipping method, and a secret-sharing secure aggregation scheme resilient to poisoning attacks.

• FedAvg [57]: This standard algorithm is used in FL and is resistant to poisoning attacks without any privacy preservation method.
• Krum [72]: A poisoning attack detection method in FL that optimally selects an update from returned post-trained models and uses the updates’ Euclidean distance as a baseline of comparison with other received updates.
• EPPRFL [24]: A resistant poisoning attack privacy preservation scheme that utilizes SMC protocols for filtering and clipping poisoned updates.
• LSFL [25]: An ASS scheme for privacy preservation as well as a K-nearest weight selection aggregation method that is robust to Byzantine participants.

(4)

Hyper-Parameters: In our setup, we conducted experiments to test our framework using the following cases: MNIST CNN IID, MNIST CNN non-IID, MNIST MLP IID, MNIST MLP non-IID, CIFAR CNN IID, CIFAR CNN non-IID, CIFAR MLP IID, and CIFAR MLP non-IID. The learning rate for local training was set at 0.0001, an epoch as 5, and a batch size of 32 was chosen while the server learning rate was set to 0.5. For each round of training in FL, we had at least 70% of selected participants N for model training.

(5)

Poisoning Attack: We considered the following poisoning attacks such as sign-flipping, label-flipping, backdoor, backdoor embedding, and gradient manipulation attacks. We carried out experiments to demonstrate the resilience and robustness of our framework to these attacks and conducted a comparison with some SOTA research

C.

Experimental Results

We performed experiments using the hyperparameters listed above to evaluate our framework in terms of fidelity, robustness, and efficiency.

(1)

Fidelity Evaluation: We compared FedAvg and our framework in terms of accuracy and loss to evaluate the fidelity goal when there are no poisoning attackers. In this experiment, the number of participants and communication rounds was set to 100, respectively, with the evaluation carried out using the MNIST and CIFAR-10 datasets over the CNN and MLP models in both IID and non-IID settings. The convergence of our framework and the FedAvg are shown in Figure 2 and Figure 3, using the MNIST and CIFAR-10 datasets over the CNN and MLP models in both IID and non-IID settings, respectively. The two figures illustrate the comparable convergence performance of our framework and a standard FedAvg in terms of training loss and the number of training rounds using both the MNIST and CIFAR-10 datasets over the CNN and MLP models in IID and non-IID settings. In terms of convergence, our framework has no impact on the model’s performance and, as observed, it yields approximately the same result as a standard FedAVG without any privacy-preserving mechanisms or poisoning attack-resilient methods. The results show that our framework does not impact model performance but performs equally well as a standard FedAvg offering additional benefits such as stability and robustness.

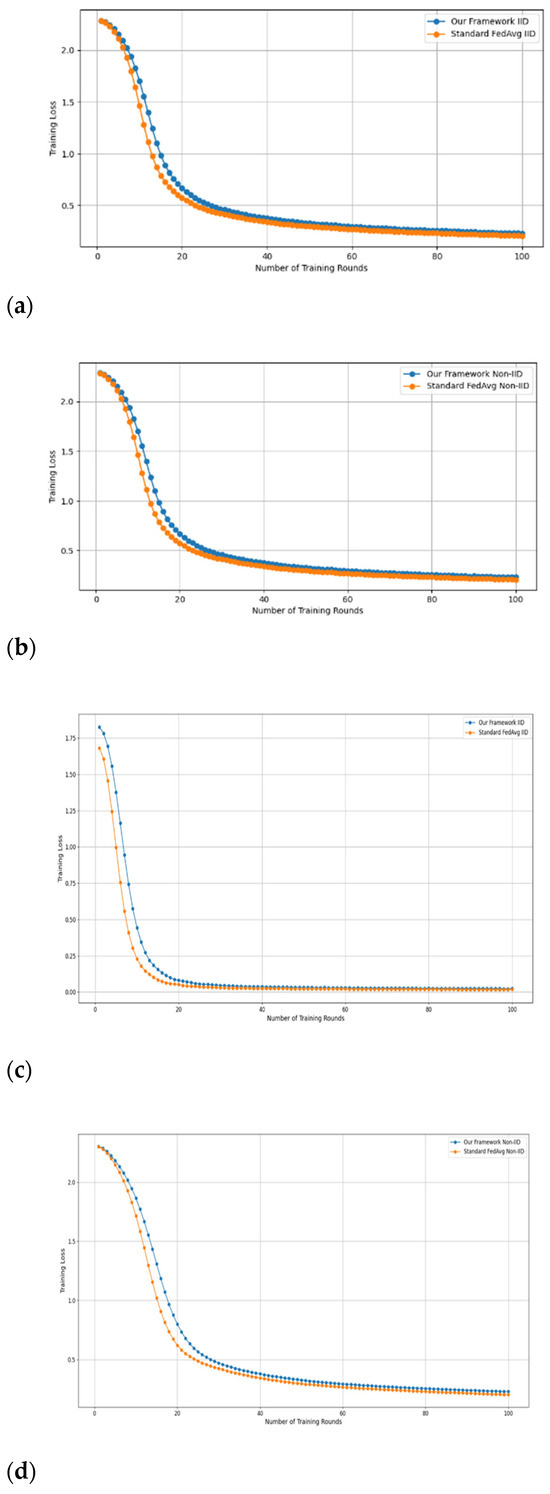Figure 2. The convergence of our framework and the FedAvg on MNIST (CNN and MLP) in IID and non-IID settings. (a) MNIST CNN IID, (b) MNIST CNN non-IID, (c) MNIST MLP IID, and (d) MNIST MLP non-IID.

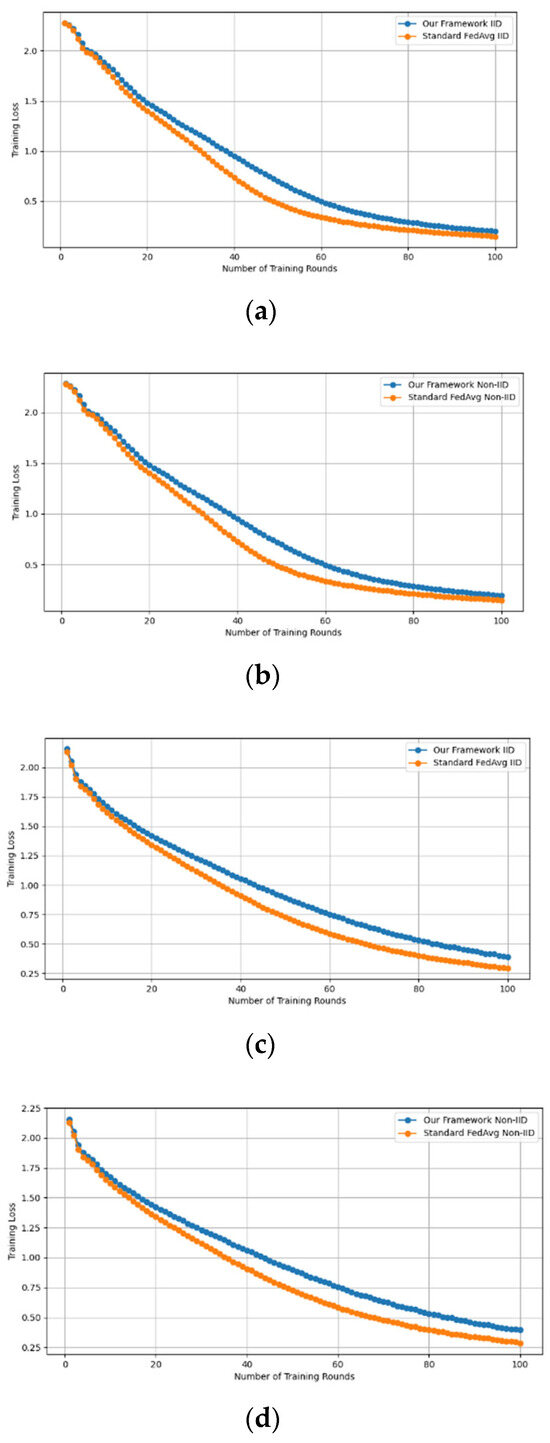Figure 3. The convergence of our framework and the FedAVG on CIFAR-10 (CNN and MLP) in IID and non-IID settings. (a) CIFAR-10 CNN IID, (b) CIFAR-10 CNN non-IID, (c) CIFAR-10 MLP IID, and (d) CIFAR-10 MLP non-IID.

Similarly, we demonstrate that the accuracy of our framework is approximately consistent with that of FedAVG, as shown in Figure 4 and Figure 5. using the MNIST and CIFAR-10 datasets over CNN and MLP models in both IID and non-IID settings, respectively. Our framework has no effect on accuracy, as it is consistent with that of FedAVG on both the MNIST (CNN and MLP) and CIFAR10 (CNN and MLP) datasets across IID and non-IID settings with both methods converging to the same accuracy. These figures demonstrate that our framework has no impact on the model’s accuracy and effectively preserves participants’ privacy.

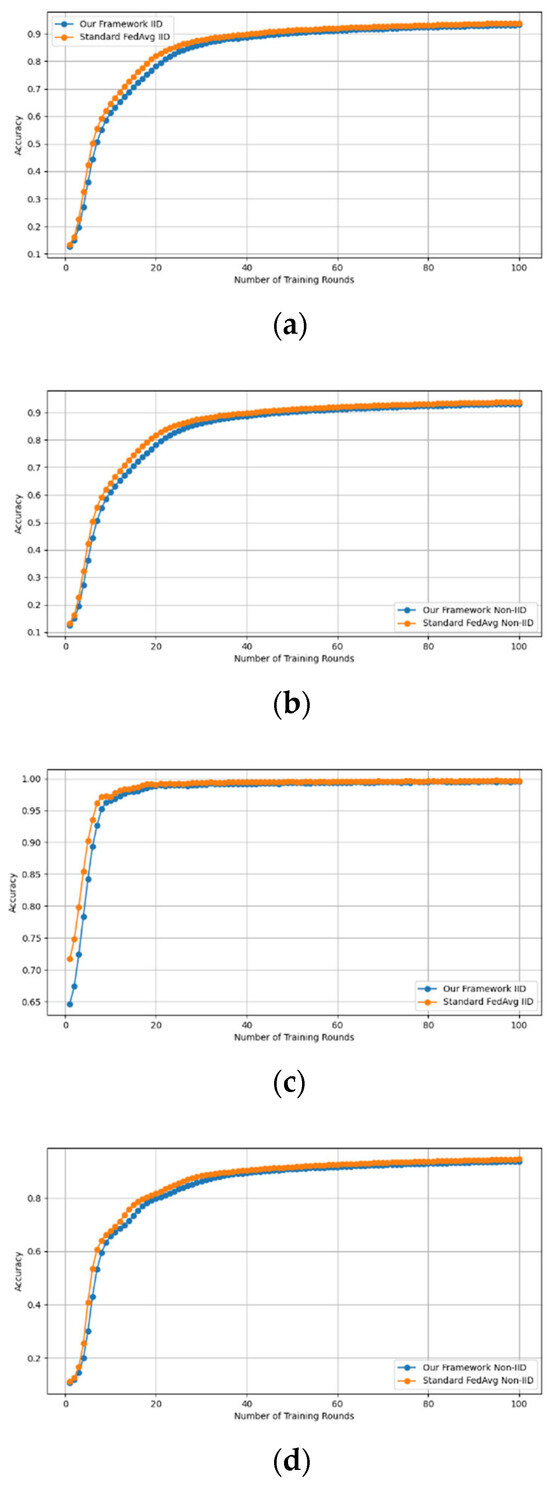
Figure 4. Accuracy curves of our framework and FedAvg on MNIST CNN (IID and non-IID) and MNIST MLP (IID and non-IID). (a) MNIST CNN IID, (b) MNIST CNN non-IID, (c) MNIST MLP IID, and (d) MNIST MLP non-IID.

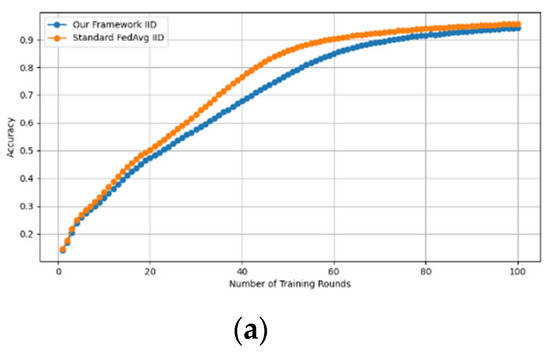
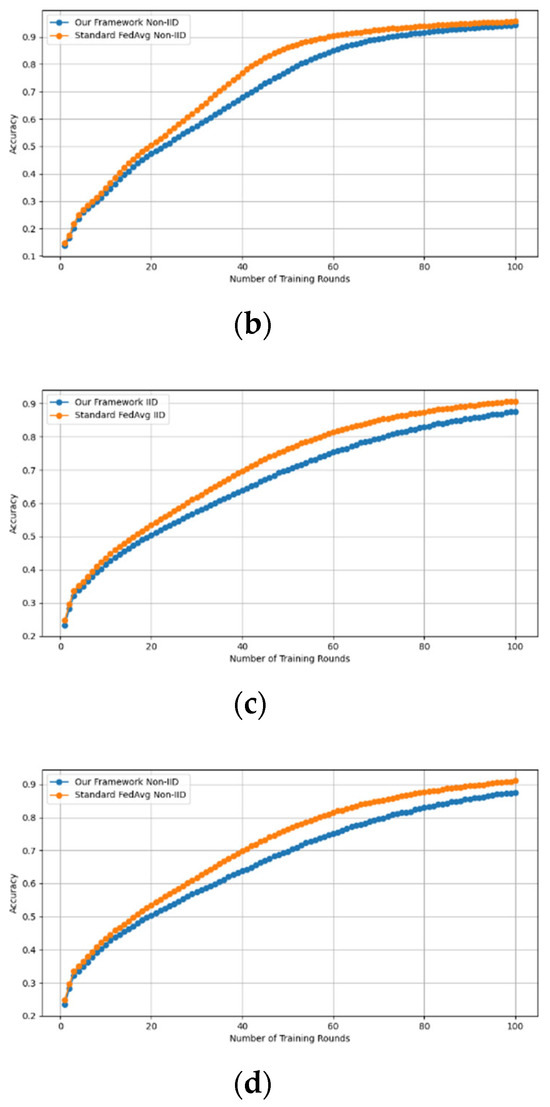
Figure 5. Accuracy curves of our framework and FedAvg on CIFAR10 CNN (IID and non-IID) and MLP (IID and non-IID). (a) CIFAR10 CNN IID, (b) CIFAR10 CNN non-IID, (c) CIFAR10 MLP IID, and (d) CIFAR10 MLP non-IID.

(2)

Robustness Evaluation: We considered label flipping, sign flipping, backdoor, backdoor embedding, and gradient manipulation attacks on the MNIST and CIFAR-10 datasets in both IID and non-IID settings. The effectiveness of these attacks was evaluated by their impact on the model’s accuracy. First, we considered the attacks in situations where 10%, 20%, 30%, and 40% of the participants were poisoning attackers and evaluated the impact on the model’s accuracy. Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 illustrate the accuracy of our framework with varying numbers of label flipping, sign flipping, backdoor, backdoor embedding, and gradient manipulation attacks, respectively, using the MNIST and CIFAR-10 datasets in both IID and non-IID settings. Our framework demonstrated graceful degradation in accuracy as the attack fraction increased, maintaining an accuracy level of above 60% on all attacks, even at a 40% attack fraction, suggesting that the model is resilient to data heterogeneity and robust to poisoning attacks.

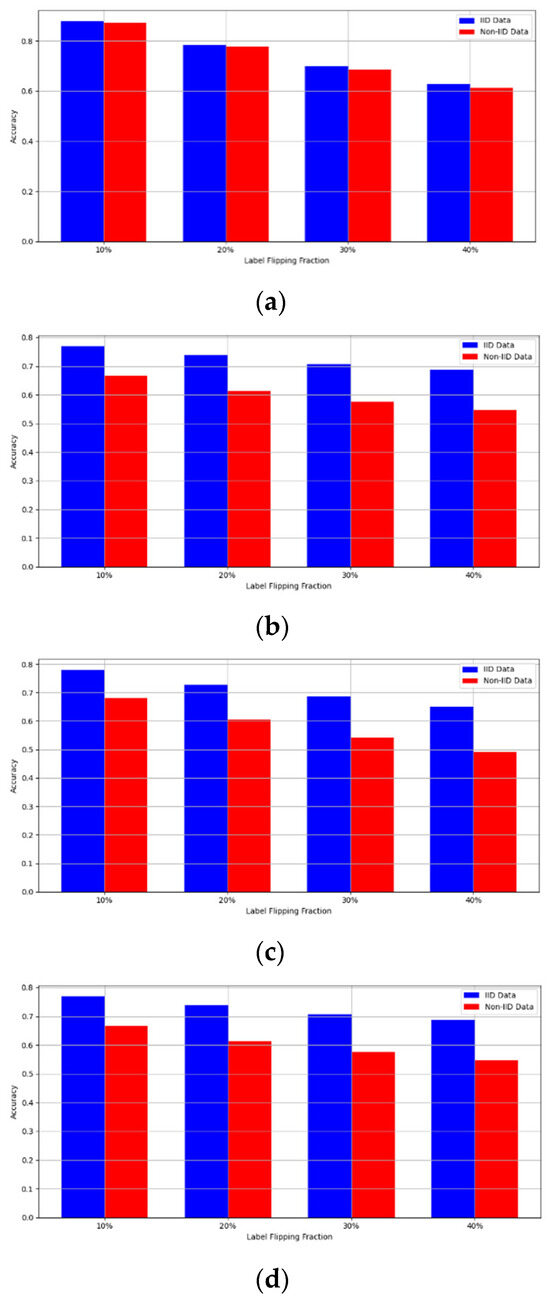Figure 6. Accuracy with label flipping attack. (a) Label flipping attack MNIST CNN. (b) Label flipping attack MNIST MLP. (c) Label flipping attack CIFAR10 CNN (d) Label flipping attack CIFAR10 MLP.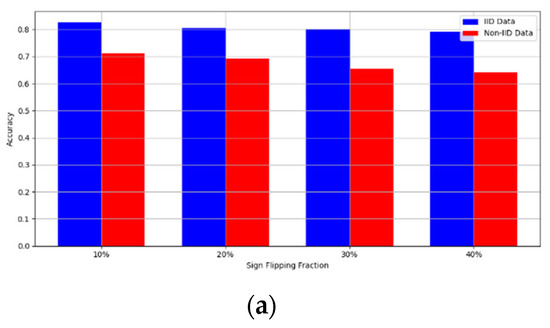

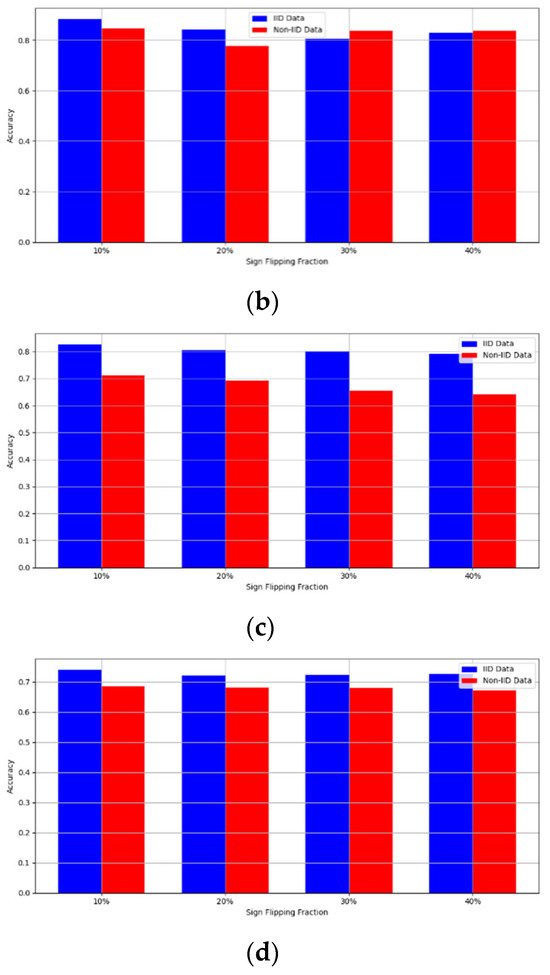Figure 7. Accuracy with sign flipping attack. (a) Sign flipping attack MNIST CNN (b) Sign flipping attack MNIST MLP (c) Sign flipping attack CIFAR10 CNN (d) Sign flipping attack CIFAR10 MLP.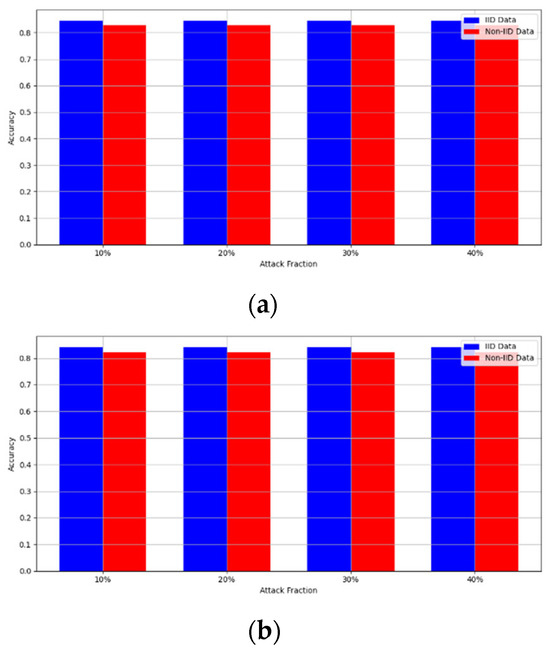

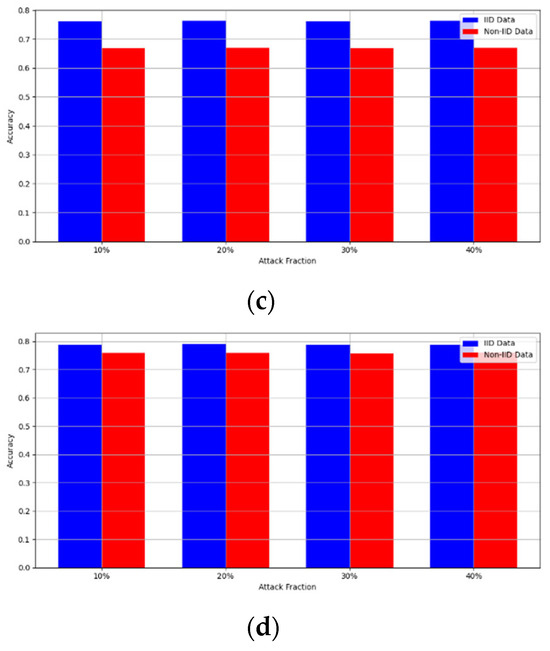Figure 8. Accuracy with backdoor attack. (a) Backdoor attack MNIST CNN (b) Backdoor attack MNIST MLP (c) Backdoor attack CIFAR10 CNN (d) Backdoor attack CIFAR10 MLP.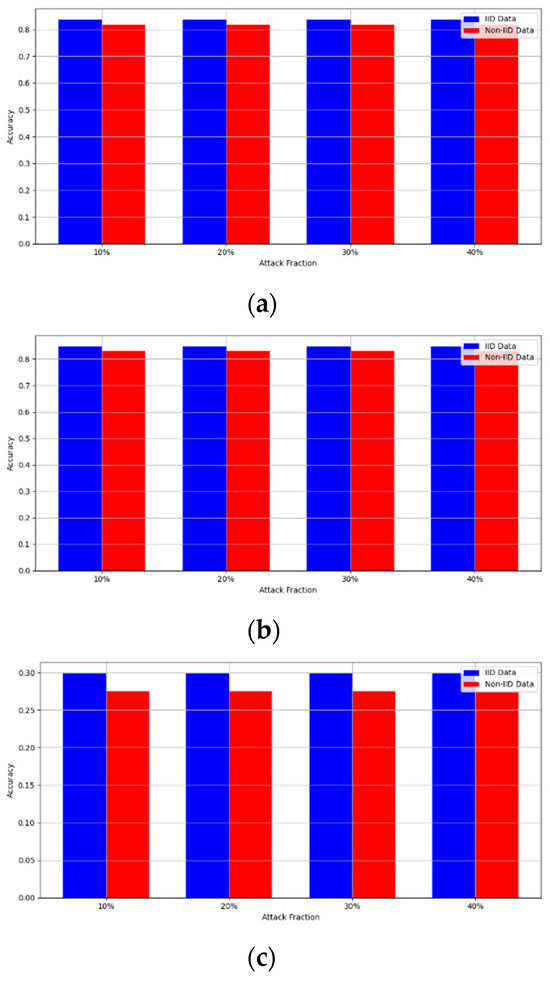

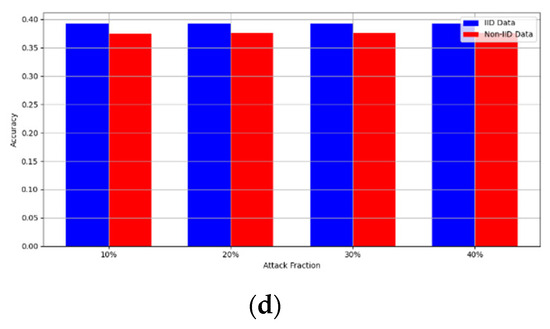Figure 9. Accuracy with backdoor embedding attack. (a) Backdoor embedding MNIST CNN; (b) backdoor embedding MNIST MLP; (c) backdoor embedding CIFAR10 CNN; (d) backdoor embedding CIFAR10 MLP.

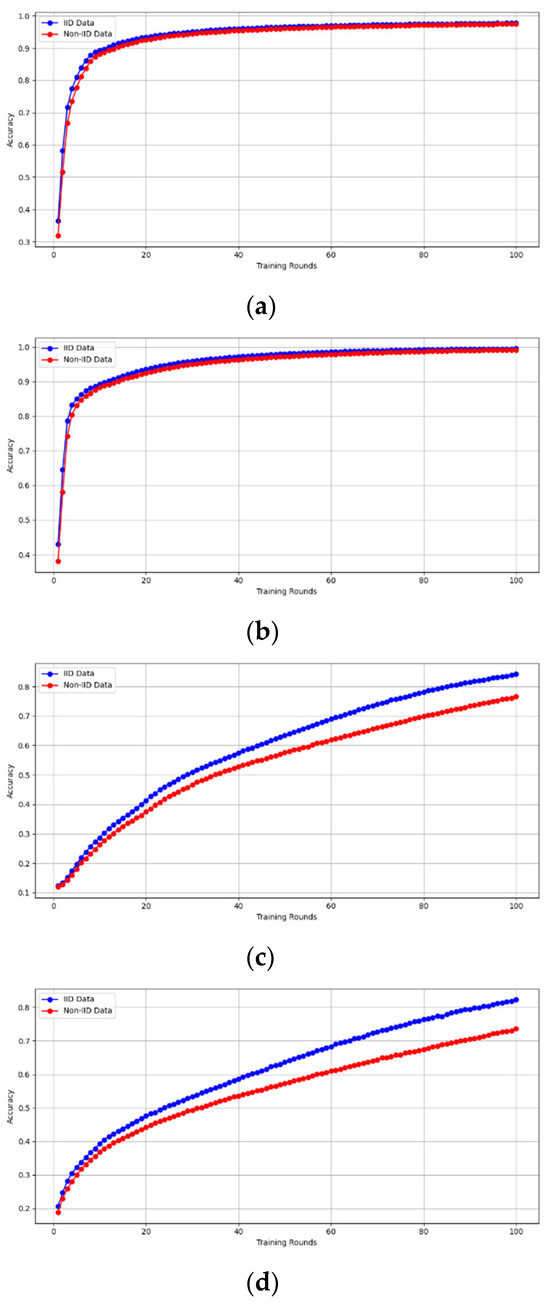Figure 10. Accuracy with gradient manipulation attack. (a) Gradient manipulation MNIST CNN; (b) gradient manipulation MNIST MLP; (c) gradient manipulation CIFAR10 CNN; and (d) gradient manipulation CIFAR10 MLP.

Secondly, we compared our framework with schemes such as EPPRFL, LSFL, and KRUM using various attack fractions, as previously stated. We maintained the number of participants at 100 and the number of training rounds at 100. The results show that our framework achieves higher accuracy in most instances, even in the presence of varying attack fractions, as shown in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

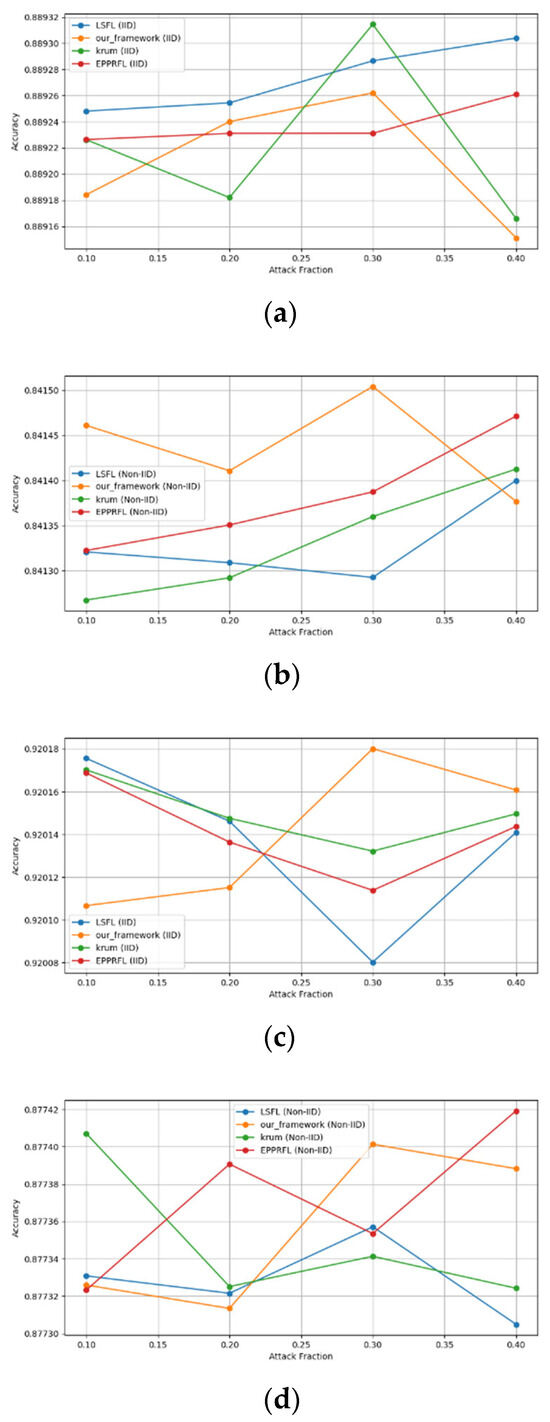
Figure 11. Label flipping attack over MNIST dataset in IID and non-IID settings. (a) MNIST CNN (IID), (b) MNIST CNN (non-IID), (c) MNIST MLP (IID), and (d) MNIST MLP (non-IID).

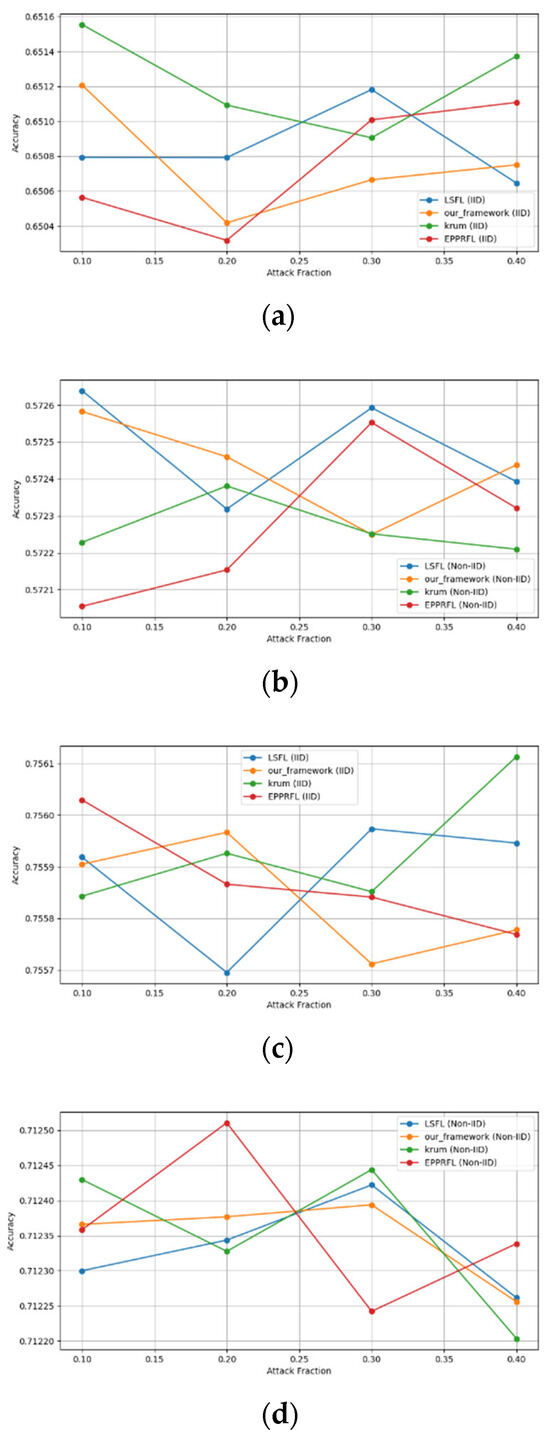
Figure 12. Label flipping attack over CIFAR-10 dataset in IID and non-IID settings. (a) CIFAR10 CNN (IID), (b) CIFAR10 CNN (non-IID), (c) CIFAR10 MLP (IID), and (d) CIFAR10 MLP (non-IID).

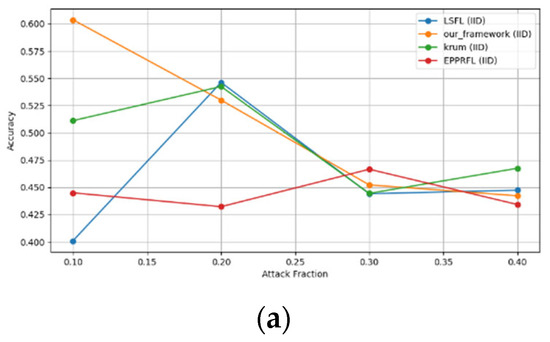
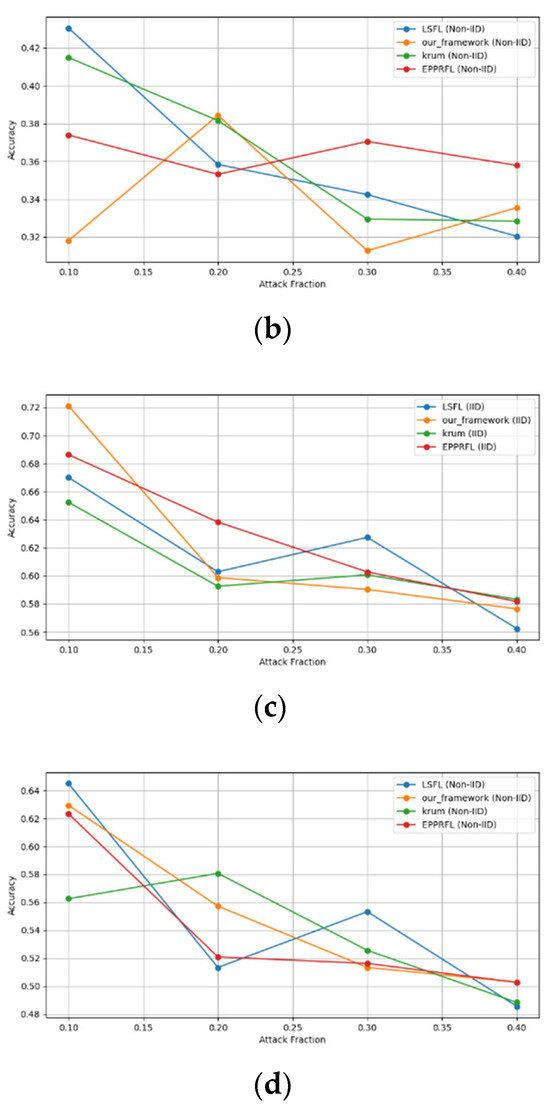
Figure 13. Sign flipping attack over MNIST dataset in IID and non-IID settings. (a) MNIST CNN (IID), (b) MNIST CNN (non-IID), (c) MNIST MLP (IID), and (d) MNIST MLP (non-IID).

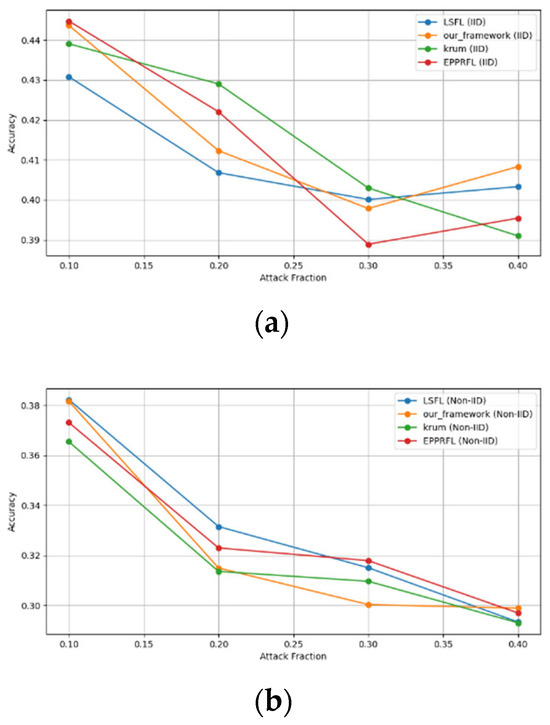
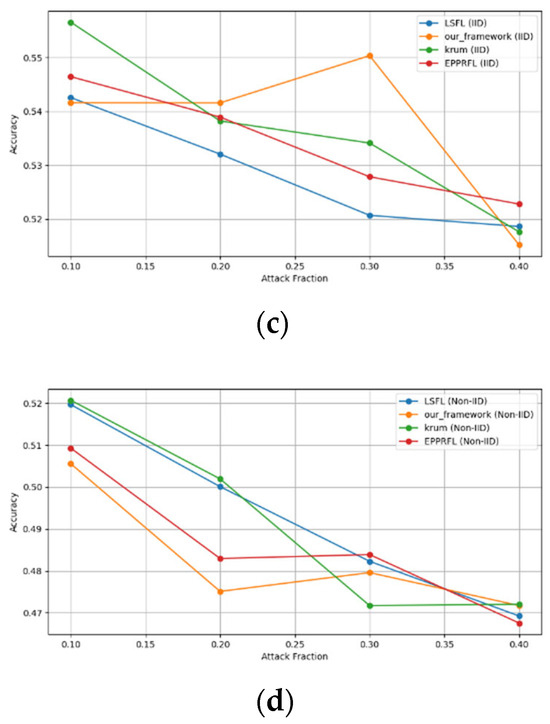
Figure 14. Sign flipping attack over CIFAR-10 dataset in IID and non-IID settings. (a) CIFAR-10 CNN (IID), (b) CIFAR-10 CNN (non-IID), (c) CIFAR-10 MLP (IID), and (d) CIFAR-10 MLP (non-IID).

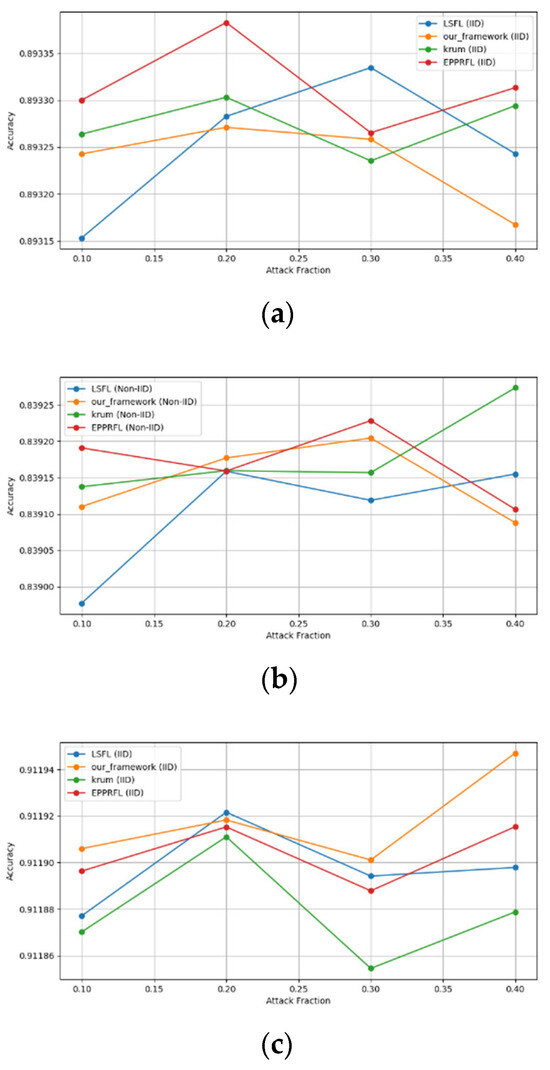
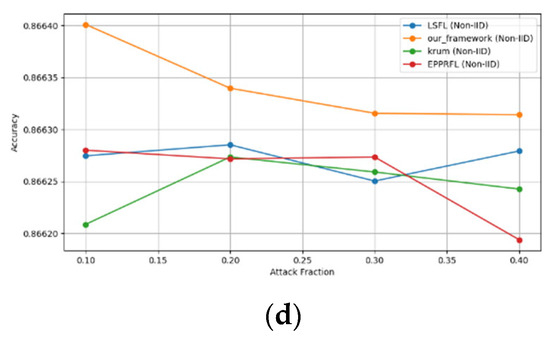
Figure 15. Backdoor attack over MNIST dataset in IID and non-IID settings. (a) Backdoor CNN (IID), (b) Backdoor CNN (non-IID), (c) Backdoor MLP (IID), and (d) Backdoor MLP (non-IID).

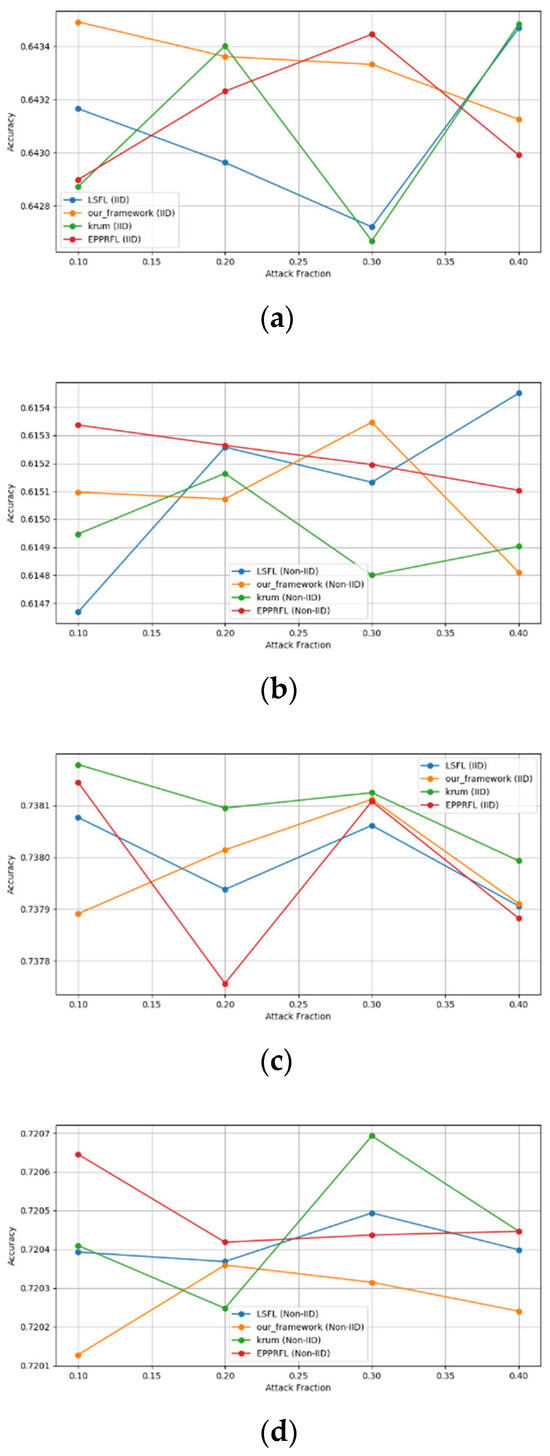
Figure 16. Backdoor attack over CIFAR-10 dataset (a) CNN (IID), (b) CNN (non-IID), (c) MLP (IID), and (d) MLP (non-IID).

The experimental results regarding label flipping, sign flipping, and backdoor attacks over MNIST and CIFAR-10 datasets in IID and non-IID settings are shown in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. We compared our results with LSFL, KRUM, and EPPRFL in cases where 10%, 20%, 30%, and 40% of participants were subjected to poisoning attacks, respectively. The experimental results indicate that our framework outperforms LSFL, KRUM, and EPPRFL in certain cases while maintaining relatively stable model accuracy in situations involving high levels of poisoning attacks. The performance of our framework is attributed to the use of the median and median deviation as metric information, which is robust to outliers. Both metrics were used to compute a suitable threshold that distinguishes normal updates from outliers. This represents the true criterion for judging similarity and updates larger than the threshold are flagged as malicious. The results indicate that our framework can detect varying fractions of poisoning attacks in both IID and non-IID settings.

(3)

Efficiency Evaluation: To evaluate the efficiency of our framework, we measured and compared the latency of FedAVG and our framework for various participants, providing a real-world efficiency comparison. Therefore, we tested FedAVG and our framework with varying numbers of participants (10, 50, 100, 150, and 200), and the result showed no difference despite the robustness of our framework. Figure 17 shows latency iteration over a varying number of participants. The average latency per round is the ratio of the total time to the number of rounds. This is conducted using MNIST and CIFAR10 datasets over the CNN model in an IID setting with the number of rounds set at 20. Moreover, we demonstrate that the communication overheads of our framework do not result in a drastic increase as the number of participants increases. Instead, it linearly increases with an increased number of participants, as shown in Figure 18. This implies that our framework would work with large-scale deployments. Finally, we show our framework’s computation cost per round in Figure 19 to reflect real-world performance.

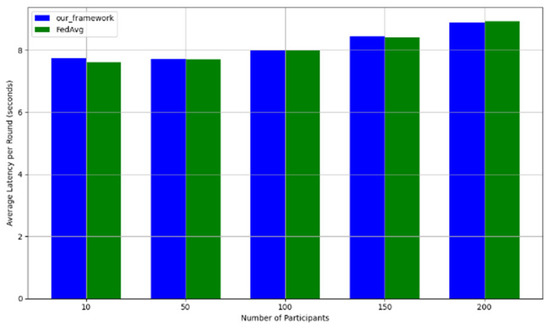Figure 17. Latency comparison between FedAvg and our framework.

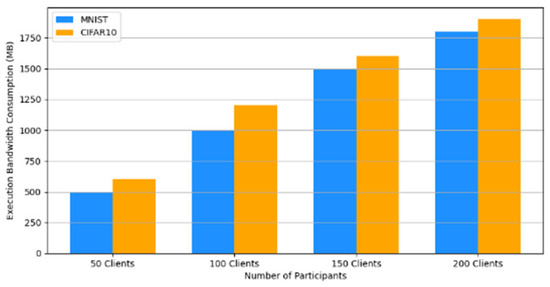Figure 18. Communication costs for different numbers of participants.

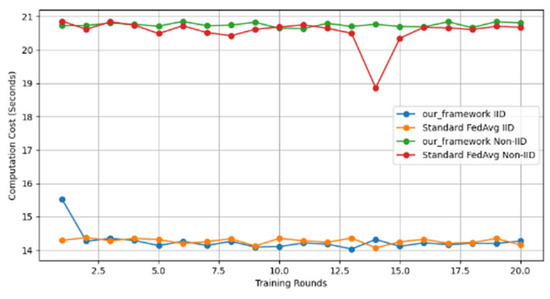Figure 19. Computation cost per round.

Additionally, participant diversity has no significant impact on our framework performance regarding privacy preservation and poisoning attack resilience. Our framework performed optimally when compared to FedAvg and other SOTA schemes in terms of privacy and robustness against diverse poisoning attacks.

8. Conclusions

In this paper, we propose a framework for privacy preservation, defense against poisoning attacks, and verification of the correctness of aggregation in the federated learning environment. The framework’s robustness tends to ensure that no malicious entity acts successfully, thereby satisfying a zero-trust architectural framework. The privacy of the local data used to train the model is preserved by additive secret sharing that splits the weights between the two servers. The splitting is carried out using oblivious transfer protocol, which guarantees that a malicious server cannot infer the private data used to train the model. Our poisoning attack detection method is based on a weight selection and filtering scheme that uses distance metrics and L2 defense. We provided a means of verifying the correctness of aggregated results from the servers. Participants are to reject and terminate a round if there is a discrepancy in the aggregated results returned by the servers, guaranteeing a zero-trust architecture. Theoretical analysis and experimental results show that our framework can achieve an accuracy level almost the same as FedAvg with the privacy of the local data preserved and not incurring additional computational burden. Therefore, our framework demonstrates a robust defense system that prevents malicious parties from acting, enhancing confidentiality, integrity, and the authentication of device–server communication in a federated learning environment. Future directions would be to preserve privacy and improve poisoning attack resilience in the potential collusion of two entities within the framework.