Uncertainty-Aware δ-GLMB Filtering for Multi-Target Tracking
Abstract
1. Introduction
2. Background
2.1. Labelled Random Finite Sets (RFS)
2.1.1. Bernoulli RFS
2.1.2. Multi-Bernoulli RFS
2.1.3. Labelled Multi-Bernoulli RFS
2.2. Generalised Labelled Multi-Bernoulli RFS
2.3. Bayesian Multi-Target Filtering
2.4. Measurement Likelihood Function
2.5. Delta-Generalised Labelled Multi-Bernoulli
2.6. N-Scan GM-PHD Filter
3. Proposed Methods
3.1. Uncertainty Effects on -GLMB
3.2. N-Scan -GLMB
3.2.1. Initialisation
3.2.2. Prediction
3.2.3. Update
3.2.4. Pruning and Extraction
| Algorithm 1: Summary of N-scan pruning algorithm. |
 |
3.3. Enhanced Update Phase
3.4. Enhanced Predict Phase
3.5. Refined -GLMB
4. Experimental Results and Discussion
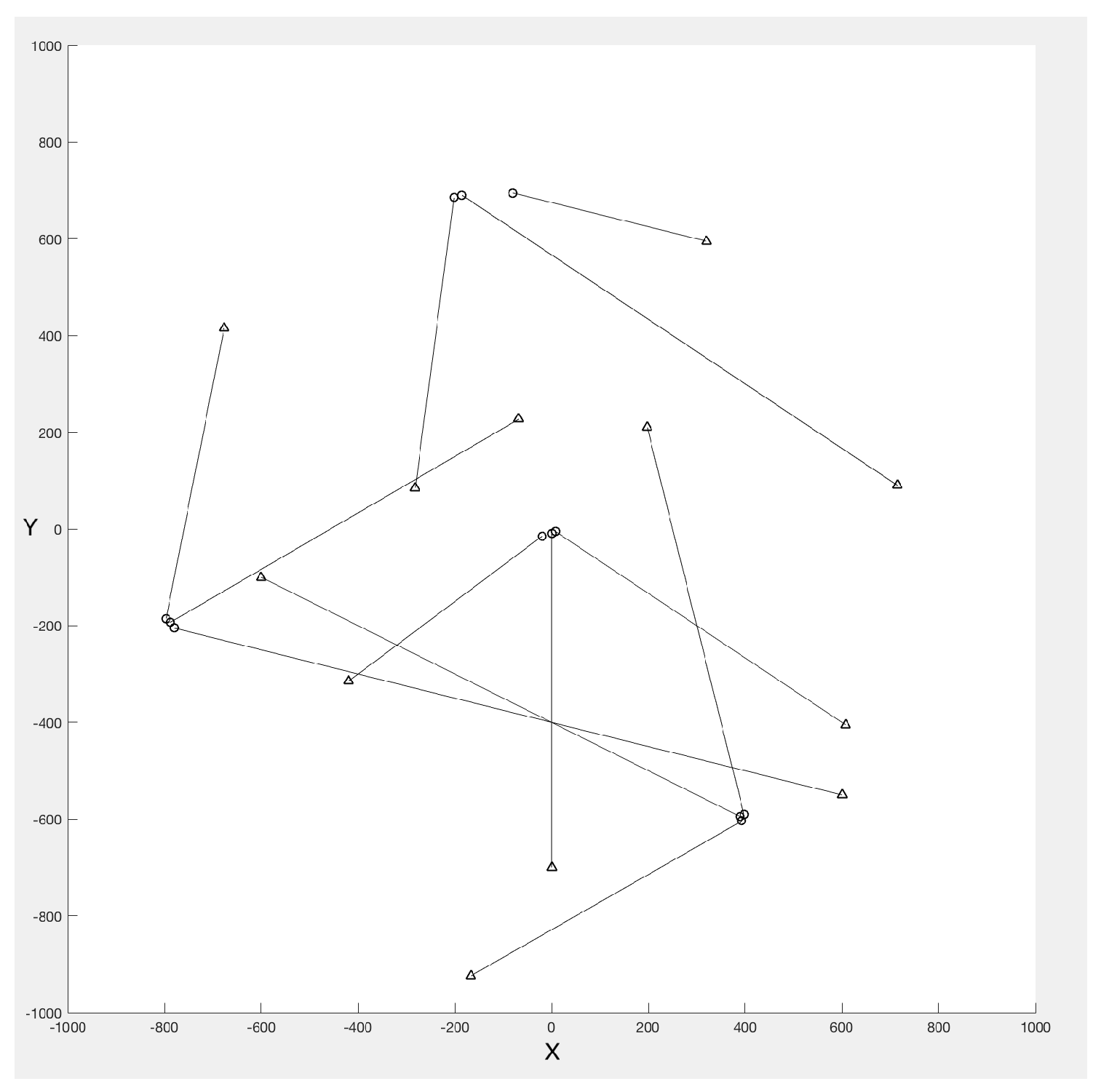
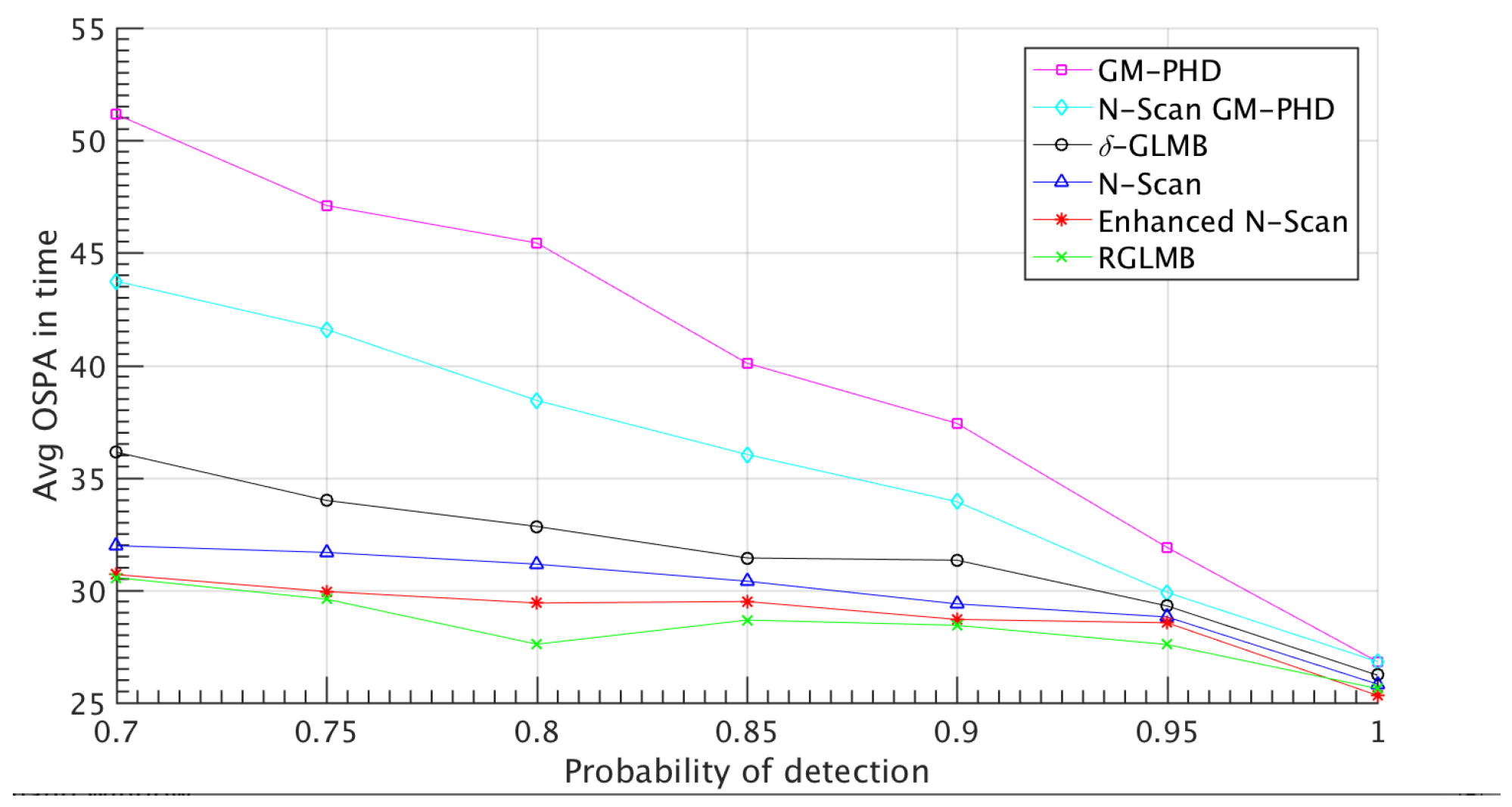
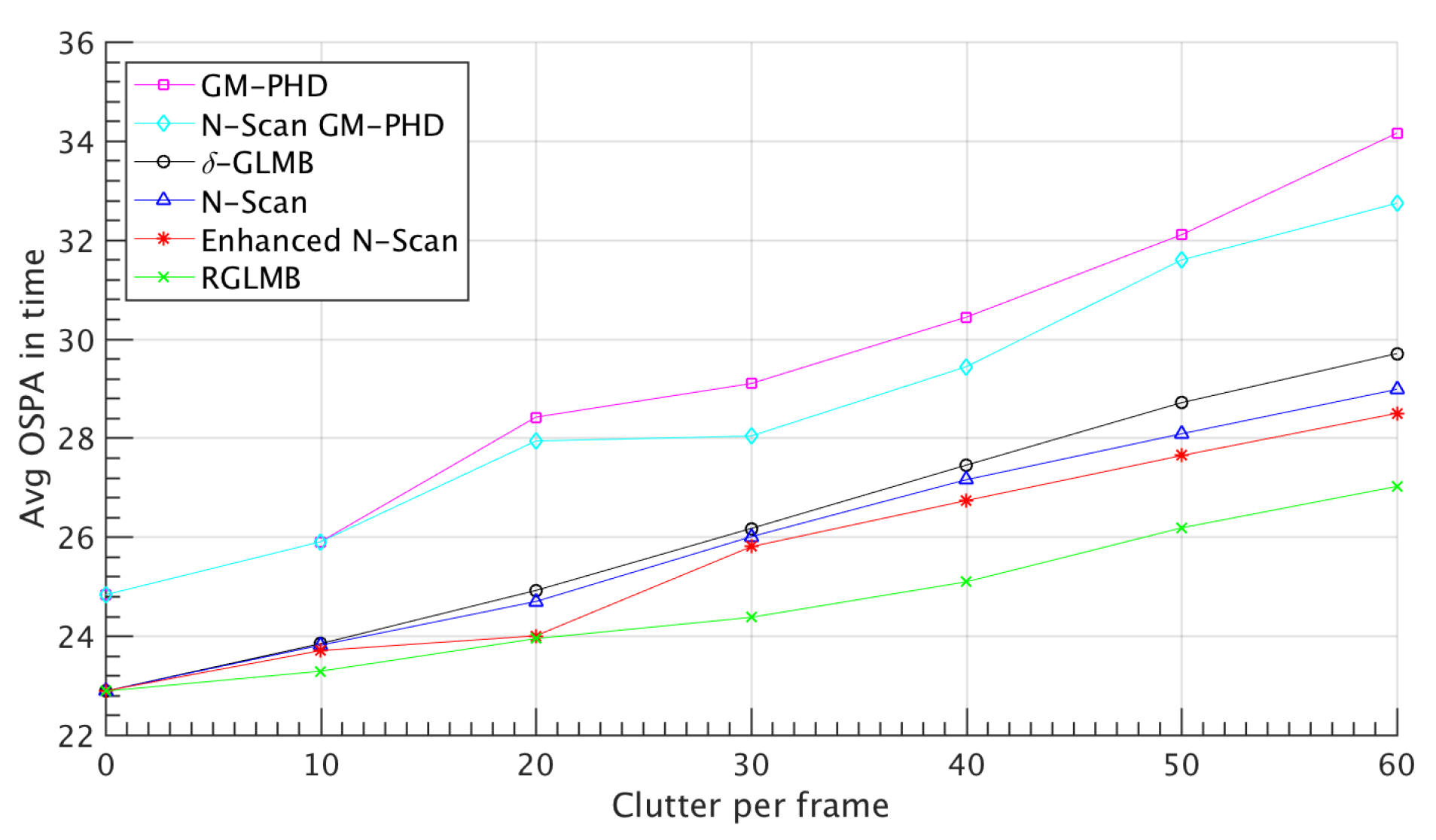
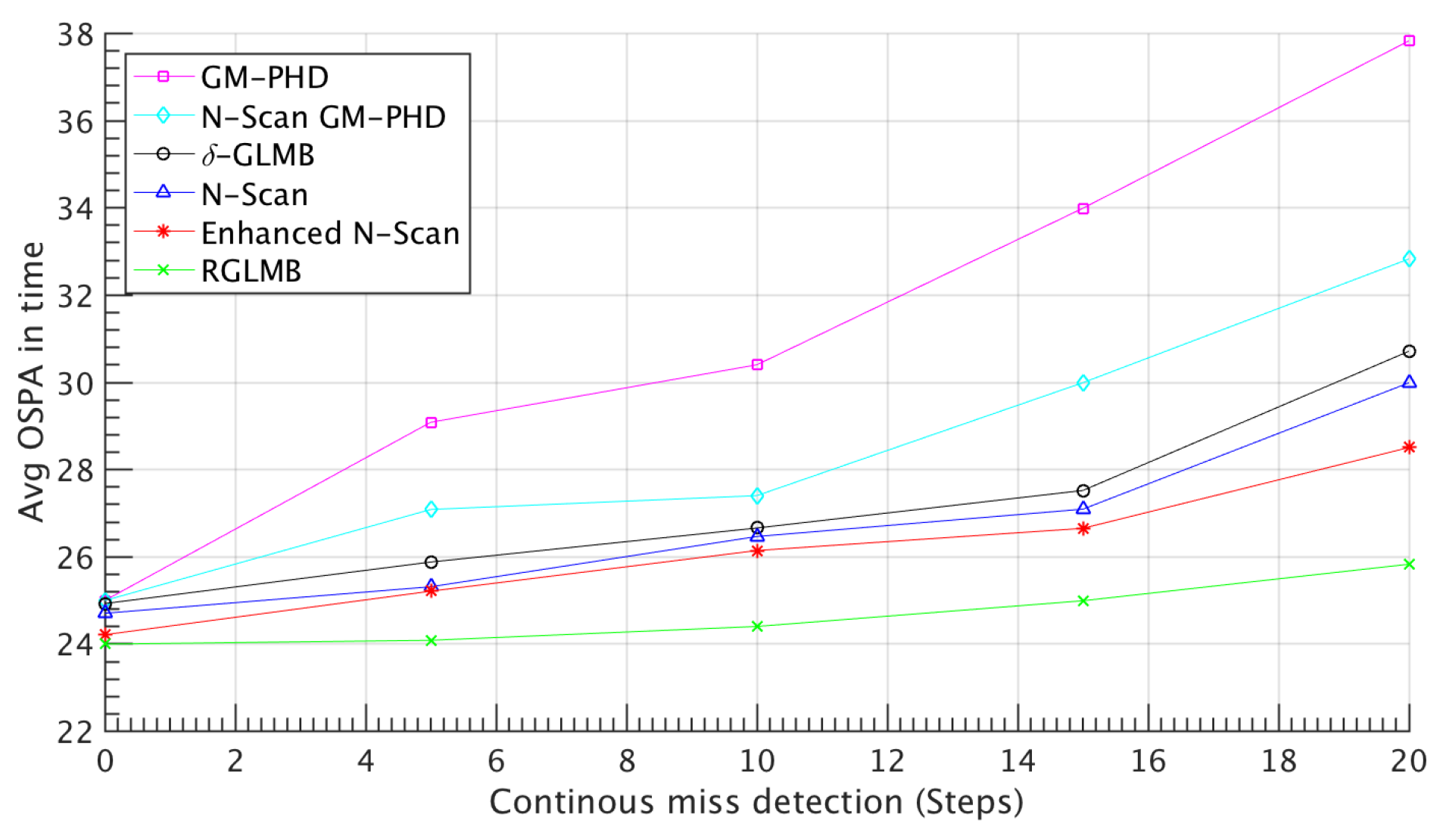
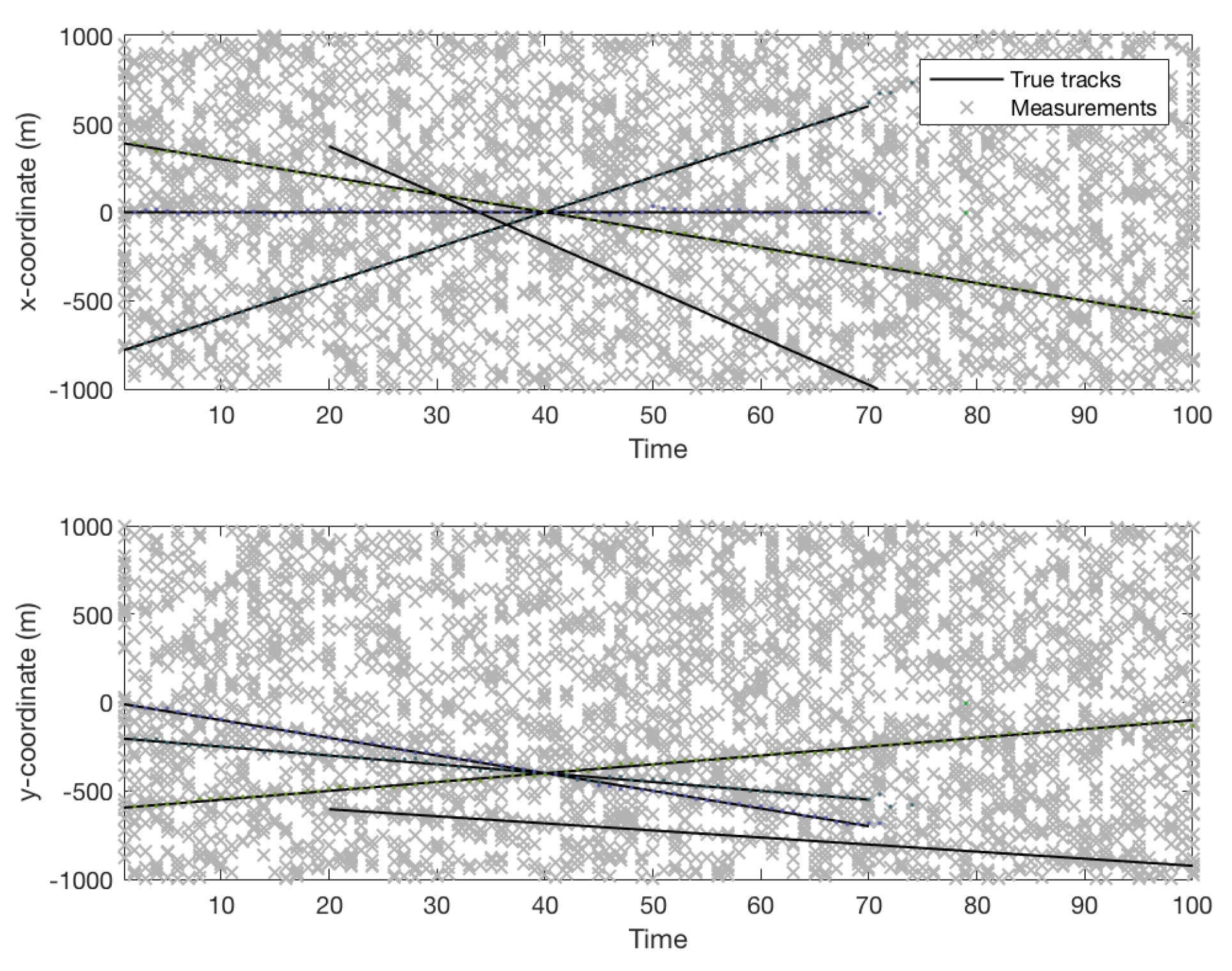
4.1. Simulated Dataset Results
4.2. Visual Dataset Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Supplementary Background
Appendix B. The L1-Error of N-Scan Method and Traditional Method of Discarding
References
- Bar, S.Y.; Fortmann, T. Tracking and Data Association. Ph.D. Thesis, Academic Press, Cambridge, UK, 1988. [Google Scholar]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems (Artech House Radar Library); Artech House: London, UK, 1999. [Google Scholar]
- Alhadhrami, E.; Seghrouchni, A.E.F.; Barbaresco, F.; Zitar, R.A. Testing Different Multi-Target/Multi-Sensor Drone Tracking Methods Under Complex Environment. In Proceedings of the 2024 International Radar Symposium (IRS), Wroclaw, Poland, 2–4 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 352–357. [Google Scholar]
- Hong, J.; Wang, T.; Han, Y.; Wei, T. Multi-Target Tracking for Satellite Videos Guided by Spatial-Temporal Proximity and Topological Relationships. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5614020. [Google Scholar] [CrossRef]
- Wang, X.; Li, D.; Wang, J.; Tong, D.; Zhao, R.; Ma, Z.; Li, J.; Song, B. Continuous multi-target tracking across disjoint camera views for field transport productivity analysis. Autom. Constr. 2025, 171, 105984. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, T.; Shen, J.; Sun, G.; Tian, Z.; Ju, W. Multi-Hypothesis Tracking Algorithm for Missile Group Targets. In Proceedings of the 2024 IEEE International Conference on Unmanned Systems (ICUS), Nanjing, China, 18–20 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 745–750. [Google Scholar]
- Yang, Z.; Nie, H.; Liu, Y.; Bian, C. Robust Tracking Method for Small and Weak Multiple Targets Under Dynamic Interference Based on Q-IMM-MHT. Sensors 2025, 25, 1058. [Google Scholar] [CrossRef]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Ocean. Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, P.; Wei, H. An algorithm for multi-target tracking in low-signal-to-clutter-ratio underwater acoustic scenes. AIP Adv. 2024, 14, 105121. [Google Scholar] [CrossRef]
- Gu, Z.; Cheng, S.; Wang, C.; Wang, R.; Zhao, Y. Robust Visual Localization System With HD Map Based on Joint Probabilistic Data Association. IEEE Robot. Autom. Lett. 2024, 9, 9415–9422. [Google Scholar] [CrossRef]
- Mahler, R. Random set theory for target tracking and identification. In Data Fusion Hand Book; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Daley, D.J.; Vere-Jones, D. An Introduction to the Theory of Point Processes: Volume II: General Theory and Structure; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Forti, N.; Millefiori, L.M.; Braca, P.; Willett, P. Random finite set tracking for anomaly detection in the presence of clutter. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Yao, X.; Qi, B.; Wang, P.; Di, R.; Zhang, W. Novel Multi-Target Tracking Based on Poisson Multi-Bernoulli Mixture Filter for High-Clutter Maritime Communications. In Proceedings of the 2024 12th International Conference on Information Systems and Computing Technology (ISCTech), Xi’an, China, 8–11 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar]
- Si, W.; Wang, L.; Qu, Z. Multi-target tracking using an improved Gaussian mixture CPHD Filter. Sensors 2016, 16, 1964. [Google Scholar] [CrossRef]
- Li, C.; Bao, Q.; Pan, J. Multi-target Tracking Method of Non-cooperative Bistatic Radar System Based on Improved PHD Filter. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar]
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T. Visual tracking in background subtracted image sequences via multi-Bernoulli filtering. IEEE Trans. Signal Process. 2013, 61, 392–397. [Google Scholar] [CrossRef]
- Wu, W.; Sun, H.; Zheng, M.; Huang, W. Target Tracking with Random Finite Sets; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Lee, C.S.; Clark, D.E.; Salvi, J. SLAM with dynamic targets via single-cluster PHD filtering. IEEE J. Sel. Top. Signal Process. 2013, 7, 543–552. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Li, S.; Zeng, J.; Wang, Y.; Yan, S. Multi-target tracking in multi-static networks with autonomous underwater vehicles using a robust multi-sensor labeled multi-Bernoulli filter. J. Mar. Sci. Eng. 2023, 11, 875. [Google Scholar] [CrossRef]
- Chen, J.; Xie, Z.; Dames, P. The semantic PHD filter for multi-class target tracking: From theory to practice. Robot. Auton. Syst. 2022, 149, 103947. [Google Scholar]
- Jeong, T. Particle PHD filter multiple target tracking in sonar image. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 409–416. [Google Scholar]
- Zeng, Y.; Wang, J.; Wei, S.; Zhang, C.; Zhou, X.; Lin, Y. Gaussian mixture probability hypothesis density filter for heterogeneous multi-sensor registration. Mathematics 2024, 12, 886. [Google Scholar] [CrossRef]
- Liang, G.; Zhang, B.; Qi, B. An augmented state Gaussian mixture probability hypothesis density filter for multitarget tracking of autonomous underwater vehicles. Ocean Eng. 2023, 287, 115727. [Google Scholar]
- Leach, M.J.; Sparks, E.P.; Robertson, N.M. Contextual anomaly detection in crowded surveillance scenes. Pattern Recognit. Lett. 2014, 44, 71–79. [Google Scholar]
- Blair, A.; Gostar, A.K.; Bab-Hadiashar, A.; Li, X.; Hoseinnezhad, R. Enhanced Multi-Target Tracking in Dynamic Environments: Distributed Control Methods Within the Random Finite Set Framework. arXiv 2024, arXiv:2401.14085. [Google Scholar]
- Meißner, D.A.; Reuter, S.; Strigel, E.; Dietmayer, K. Intersection-Based Road User Tracking Using a Classifying Multiple-Model PHD Filter. IEEE Intell. Transport. Syst. Mag. 2014, 6, 21–33. [Google Scholar]
- Zhang, Y.; Zhang, B.; Shen, C.; Liu, H.; Huang, J.; Tian, K.; Tang, Z. Review of the field environmental sensing methods based on multi-sensor information fusion technology. Int. J. Agric. Biol. Eng. 2024, 17, 1–13. [Google Scholar]
- Gruden, P.; White, P.R. Automated extraction of dolphin whistles—A sequential Monte Carlo probability hypothesis density approach. J. Acoust. Soc. Am. 2020, 148, 3014–3026. [Google Scholar] [CrossRef] [PubMed]
- Rezatofighi, S.H.; Gould, S.; Vo, B.N.; Mele, K.; Hughes, W.E.; Hartley, R. A multiple model probability hypothesis density tracker for time-lapse cell microscopy sequences. In Proceedings of the International Conference on Information Processing in Medical Imaging, Asilomar, CA, USA, 28 June–3 July 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 110–122. [Google Scholar]
- Ben-Haim, T.; Raviv, T.R. Graph neural network for cell tracking in microscopy videos. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 610–626. [Google Scholar]
- Kim, D.Y. Multi-Bernoulli filtering for keypoint-based visual tracking. In Proceedings of the 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Republic of Korea, 27–29 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 37–41. [Google Scholar]
- Baker, L.; Ventura, J.; Langlotz, T.; Gul, S.; Mills, S.; Zollmann, S. Localization and tracking of stationary users for augmented reality. Vis. Comput. 2024, 40, 227–244. [Google Scholar] [CrossRef]
- Mahler, R.P. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: London, UK, 2014. [Google Scholar]
- Mahler, R.P. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.T.; Suter, D. Joint detection and estimation of multiple objects from image observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, D.; Yuan, J.; Chen, A.; Li, H.; Zhou, C.; Chen, W.; Liu, Q. δ-GLMB Filter Based on Multiple Model Multiple Hypothesis Tracking. In Proceedings of the 2022 14th International Conference on Signal Processing Systems (ICSPS), online, 18–20 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 249–258. [Google Scholar]
- Yazdian-Dehkordi, M.; Azimifar, Z. Novel N-scan GM-PHD-based approach for multi-target tracking. IET Signal Process. 2016, 10, 493–503. [Google Scholar] [CrossRef]
- Mahler, R.P. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: London, UK, 2007. [Google Scholar]
- Vo, B.N.; Ma, W.K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091. [Google Scholar] [CrossRef]
- Sepanj, M.H.; Azimifar, Z. N-scan δ-generalized labeled multi-bernoulli-based approach for multi-target tracking. In Proceedings of the Artificial Intelligence and Signal Processing Conference (AISP), Shiraz, Iran, 25–27 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 103–106. [Google Scholar]
- Miller, M.L.; Stone, H.S.; Cox, I.J. Optimizing Murty’s ranked assignment method. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 851–862. [Google Scholar] [CrossRef]
- Murty, K.G. Letter to the editor—An algorithm for ranking all the assignments in order of increasing cost. Oper. Res. 1968, 16, 682–687. [Google Scholar]
- Punchihewa, Y.G.; Vo, B.T.; Vo, B.N.; Kim, D.Y. Multiple Object Tracking in Unknown Backgrounds With Labeled Random Finite Sets. IEEE Trans. Signal Process. 2018, 66, 3040–3055. [Google Scholar] [CrossRef]
- Yazdian-Dehkordi, M.; Azimifar, Z. Refined GM-PHD tracker for tracking targets in possible subsequent missed detections. Signal Process. 2015, 116, 112–126. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Tang, T.; Wang, P.; Zhao, P.; Zeng, H.; Chen, J. A novel multi-target TBD scheme for GNSS-based passive bistatic radar. IET Radar Sonar Navig. 2024, 18, 2497–2512. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Zhao, J.; Han, X. Improved GM-PHD Filter for Multi-target Tracking with Dense Clutter and Low Detection Probability. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 3505–3510. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Hoang, H.G. An efficient implementation of the generalized labeled multi-Bernoulli filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Guerrero-Gomez-Olmedo, R.; Lopez-Sastre, R.J.; Maldonado-Bascon, S.; Fernandez-Caballero, A. Vehicle Tracking by Simultaneous Detection and Viewpoint Estimation. In Proceedings of the IWINAC 2013, Mallorca, Spain, 10–14 June 2013; Part II, LNCS 7931. pp. 306–316. [Google Scholar]
- Bernardin, K.; Stiefelhagen, R. Evaluating multiple object tracking performance: The CLEAR MOT metrics. J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Putra, H.; Nuha, H.H.; Irsan, M.; Putrada, A.G.; Hisham, S.B.I. Object Tracking in Surveillance System Using Particle Filter and ACF Detection. In Proceedings of the 2024 International Conference on Decision Aid Sciences and Applications (DASA), Hybrid, Bahrain, 11–12 December 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar]
- Sepanj, H.; Fieguth, P. Context-Aware Augmentation for Contrastive Self-Supervised Representation Learning. J. Comput. Vis. Imaging Syst. 2023, 9, 4–7. [Google Scholar]
- Sepanj, H.; Fieguth, P. Aligning Feature Distributions in VICReg Using Maximum Mean Discrepancy for Enhanced Manifold Awareness in Self-Supervised Representation Learning. J. Comput. Vis. Imaging Syst. 2024, 10, 13–18. [Google Scholar]
- Sepanj, M.H.; Fiegth, P. SinSim: Sinkhorn-Regularized SimCLR. arXiv 2025, arXiv:2502.10478. [Google Scholar]
- Sepanj, M.H.; Ghojogh, B.; Fieguth, P. Self-Supervised Learning Using Nonlinear Dependence. arXiv 2025, arXiv:2501.18875. [Google Scholar]


| Notation | Description |
|---|---|
| x | Single-target state |
| X | Multi-target state (set of targets) |
| State space | |
| Z | Multi-object measurement set |
| Label space | |
| ℓ | Unique label assigned to a target |
| Generalised Kronecker delta function | |
| Indicator function | |
| Probability of detection for target | |
| Likelihood of measurement z given target | |
| Multi-target probability density | |
| Distinct label indicator function | |
| Hypothesis weight | |
| Probability density of target state |
| Method () | OSPA (AVG) (# of Targets) |
|---|---|
| GM-PHD [53] | 47.46 (5.17) |
| N-scan GM-PHD [43] | 39.71 (5.88) |
| -GLMB | 33.4375 (6.13) |
| N-scan -GLMB | 31.1589 (6.71) |
| Enhanced N-scan -GLMB | 29.4330 (6.94) |
| Refined N-scan -GLMB | 27.0017 (7.26) |
| Method | OSPA (AVG) |
|---|---|
| GM-PHD [53] | 39.03 |
| N-scan GM-PHD [43] | 34.51 |
| -GLMB [42] | 32.28 |
| N-scan -GLMB (ours) | 28.67 |
| Enhanced N-scan -GLMB (ours) | 26.44 |
| Refined N-scan -GLMB (ours) | 24.10 |
| Method | MOTA | MOTP | ReR | FAR | MTR | MOR |
|---|---|---|---|---|---|---|
| GM-PHD [53] | 42.62 | 54.02 | 0.45 | 0.12 | 0.57 | 0.71 |
| N-scan GM-PHD [43] | 46.78 | 58.49 | 0.51 | 0.10 | 0.46 | 0.57 |
| -GLMB [42] | 51.05 | 63.62 | 0.57 | 0.10 | 0.42 | 0.64 |
| N-scan -GLMB (ours) | 54.53 | 65.28 | 0.62 | 0.07 | 0.34 | 0.42 |
| Enhanced N-scan -GLMB (ours) | 55.60 | 65.91 | 0.62 | 0.07 | 0.34 | 0.35 |
| Refined N-scan -GLMB (ours) | 56.79 | 66.38 | 0.71 | 0.05 | 0.26 | 0.28 |
| Method | MOTA | MOTP | ReR | FAR | MTR | MOR |
|---|---|---|---|---|---|---|
| GM-PHD [53] | 27.91 | 32.59 | 0.31 | 0.17 | 0.68 | 0.78 |
| N-scan GM-PHD [43] | 31.20 | 36.17 | 0.46 | 0.12 | 0.56 | 0.66 |
| -GLMB [42] | 30.83 | 37.55 | 0.48 | 0.14 | 0.53 | 0.64 |
| N-scan -GLMB (ours) | 35.41 | 40.06 | 0.58 | 0.07 | 0.46 | 0.56 |
| Enhanced N-scan -GLMB (ours) | 36.26 | 41.74 | 0.60 | 0.07 | 0.41 | 0.53 |
| Refined N-scan -GLMB (ours) | 39.32 | 43.45 | 0.68 | 0.04 | 0.34 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sepanj, M.H.; Moradi, S.; Azimifar, Z.; Fieguth, P. Uncertainty-Aware δ-GLMB Filtering for Multi-Target Tracking. Big Data Cogn. Comput. 2025, 9, 84. https://doi.org/10.3390/bdcc9040084
Sepanj MH, Moradi S, Azimifar Z, Fieguth P. Uncertainty-Aware δ-GLMB Filtering for Multi-Target Tracking. Big Data and Cognitive Computing. 2025; 9(4):84. https://doi.org/10.3390/bdcc9040084
Chicago/Turabian StyleSepanj, M. Hadi, Saed Moradi, Zohreh Azimifar, and Paul Fieguth. 2025. "Uncertainty-Aware δ-GLMB Filtering for Multi-Target Tracking" Big Data and Cognitive Computing 9, no. 4: 84. https://doi.org/10.3390/bdcc9040084
APA StyleSepanj, M. H., Moradi, S., Azimifar, Z., & Fieguth, P. (2025). Uncertainty-Aware δ-GLMB Filtering for Multi-Target Tracking. Big Data and Cognitive Computing, 9(4), 84. https://doi.org/10.3390/bdcc9040084







