Deep Learning-Based Method for a Ground-State Solution of Bose-Fermi Mixture at Zero Temperature

Abstract

A Bose-Fermi mixture, consisting of both bosons and fermions, exhibits distinctive quantum coherence and phase transitions, offering valuable insights into many-body quantum systems. The ground state, as the system’s lowest energy configuration, is essential for understanding its overall behavior. In this study, we introduce the Bose-Fermi Energy-based Deep Neural Network (BF-EnDNN), a novel deep learning approach designed to solve the ground-state problem of Bose-Fermi mixtures at zero temperature through energy minimization. This method incorporates three key innovations: point sampling pre-training, a Dynamic Symmetry Layer (DSL), and a Positivity Preserving Layer (PPL). These features significantly improve the network’s accuracy and stability in quantum calculations. Our numerical results show that BF-EnDNN achieves accuracy comparable to traditional finite difference methods, with effective extension to two-dimensional systems. The method demonstrates high precision across various parameters, making it a promising tool for investigating complex quantum systems.

1. Introduction

In modern quantum physics research, Bose-Fermi mixtures—a unique class of ultracold atomic systems—have attracted significant attention due to their distinct quantum degeneracy characteristics and rich physical phenomena [1,2,3]. This system, composed of bosons and fermions, exhibits pronounced quantum degeneracy behavior at ultracold temperatures. Bose-Fermi mixtures hold significant research value in quantum statistics and condensed matter physics, particularly serving as an ideal platform for studying novel quantum effects such as tunneling dynamics in double-well potentials [4,5]. With advancements in experimental techniques, laser cooling and trapping technologies have enabled the reliable preparation of Bose-Fermi mixtures by cooling alkali metal atoms (e.g., Na, K) to near absolute zero and confining them in engineered external potentials [6].

The ground-state properties of Bose-Fermi mixtures reveal the quantum interactions between bosons and fermions. To study these properties, various theoretical approaches have been developed, including Density Functional Theory (DFT), Bogoliubov approximation, and Hartree-Fock theory [7,8,9]. These methods exhibit distinct advantages: Hartree-Fock theory excels at capturing fermionic many-body effects, while DFT achieves higher precision in high-density systems. At zero temperature, the coupled Gross-Pitaevskii equations have become a standard mean-field approach for ground-state studies. However, their validity strictly requires fermions to be in a normal (non-superfluid) state. This model characterizes bosonic and fermionic components through effective wavefunctions ${\psi }_B$ and ${\psi }_F$ respectively, where fermionic degrees of freedom in the dilute gas limit can be approximated as single-particle wavefunctions [1,2]. It is crucial to note that when fermions form superfluid pairs or enter strongly correlated regimes, more rigorous theoretical frameworks such as the Bogoliubov-de Gennes equations must be employed. Although rigorous many-body descriptions better satisfy the Pauli exclusion principle, this mean-field approximation can accurately capture the essential physics of weakly interacting systems while maintaining computational efficiency.

However, determining the ground state solutions remains a key theoretical challenge. Conventional approaches predominantly use gradient flow with discrete normalization, specifically imaginary-time evolution techniques, which rely on classical spatial discretization methods such as finite difference and finite element schemes [1,10]. Nevertheless, such computations are still confined to lower dimensions. For high-dimensional GPEs or many-body Schrödinger equations, the curse of dimensionality severely limits their practical applicability. In recent years, deep learning techniques have gained traction in scientific computing [11]. Notably, the Deep Ritz method—a neural network-based variational approach—utilizes the nonlinear approximation capabilities of neural networks to represent solutions to partial differential equations as network outputs. By optimizing network parameters to minimize energy functionals, it has shown considerable potential for addressing high-dimensional challenges in complex scientific problems [12]. This method not only significantly improves calculation efficiency but also accelerates convergence speed [13].

Given the limitations of traditional numerical methods in solving ground state problems for Bose-Fermi mixtures, this work introduces a deep learning-based framework—the Bose-Fermi Energy-based Deep Neural Network (BF-EnDNN). By integrating three key innovations—Dynamic Symmetry Layers (DSL), pre-training with adaptive point sampling, and Positivity Preserving Layers (PPL)—the framework significantly enhances the precision and stability of neural networks in quantum ground state calculations. Compared to conventional finite difference methods (FDM), BF-EnDNN achieves high consistency in predictions of ground state energy and chemical potential, with relative errors maintained within acceptable thresholds. Extensive numerical experiments validate its effectiveness and accuracy across diverse parameter configurations, providing novel insights for solving complex quantum systems. The paper is structured as follows: Section 2 outlines the physical background of Bose-Fermi mixtures and the mathematical formulations of ground state problems. Section 3 details the BF-EnDNN methodology, including the network architecture, design principles of DSL, adaptive point sampling strategies, and the implementation of PPL. Section 4 demonstrates BF-EnDNN’s performance in 1D Bose-Fermi systems through numerical benchmarks against FDM, with in-depth analyses of the efficacy of innovations, network hyperparameter robustness, and comparisons of activation functions. Its applicability is further verified in 2D scenarios. Section 5 concludes with a summary of research findings and suggestions for future directions.

2. Physical Background and Problem Elicitation

In quantum physics, determining the ground state is crucial for understanding the properties of a system. The ground state represents the lowest energy of the system and is key to studying quantum phase transitions, quantum entanglement, and other related phenomena [14,15]. Here we specifically consider the scenario where fermions remain in a normal (non-superfluid) degenerate state, allowing their effective description through single-particle wavefunctions ${\psi }_F$ in the dilute limit. This treatment remains valid when fermionic pairing effects are negligible and the system resides in the weakly interacting regime. At zero temperature, the dynamics of Bose-Fermi mixed system is often described by the coupled Gross Pitaevskii (GP) equation. According to the literature [1], in dimensionless form, for d dimensional space ($d=1,2,3$), the equation is:

$$\begin{array}{ccc}\hfill i{\displaystyle \frac{\partial {\psi }_B}{\partial t}}& =& \left(-{\displaystyle \frac{{\nabla }^2}{2}}+V_B\left(x\right)+{\beta }_{11}|{\psi }_B{|}^2+{\beta }_{12}{N}_F{|{\psi }_F|}^2\right){\psi }_B,x\in {\mathbb{R}}^d,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill i{\displaystyle \frac{\partial {\psi }_F}{\partial t}}& =& \left(-{\displaystyle \frac{{\nabla }^2}{6\lambda }}+V_F\left(x\right)+{\beta }_{12}{N}_B|{\psi }_B{|}^2+{\beta }_{22}{|{\psi }_F|}^{4/3}\right){\psi }_F,x\in {\mathbb{R}}^d.\hfill \end{array}$$

(2)

Here, ${\psi }_B:={\psi }_B(x,t)$ and ${\psi }_F:={\psi }_F(x,t)$ represent the time-dependent wavefunctions of the bosons and fermions, respectively. It is important to note that the nonlinear term ${\beta }_{22}{|{\psi }_F|}^{4/3}$ arises from the chemical potential of a degenerate Fermi gas at zero temperature, where ${\mu }_F\propto n_F^{2/3}$ ($n_F={|{\psi }_F|}^2$). This result is a direct consequence of the Thomas-Fermi approximation.

In the dilute limit and weakly interacting regimes, a approach is commonly used, where fermionic density is described by effective wavefunctions ${\psi }_F\left(\mathbf{r}\right)=\sqrt{n_F\left(\mathbf{r}\right)}$. Although this method neglects the Weizsäcker gradient correction term, it simplifies the computational effort while maintaining the accuracy of bulk system properties.

The dimensionless energy per particle of the system (total particles $N=N_B+N_F$) is expressed as:

$$\begin{array}{ccc}\hfill E({\psi }_B,{\psi }_F)& =& {\displaystyle \frac{N_B}{N}}{\int }_{{\mathbb{R}}^d}\left({\displaystyle \frac{|\nabla {\psi }_B{|}^2}{2}}+V_B|{\psi }_B{|}^2+{\displaystyle \frac{{\beta }_{11}}{2}}{|{\psi }_B|}^4\right)dx\hfill \\ & +& {\displaystyle \frac{N_F}{N}}{\int }_{{\mathbb{R}}^d}\left({\displaystyle \frac{|\nabla {\psi }_F{|}^2}{6\lambda }}+V_F|{\psi }_F{|}^2+{\displaystyle \frac{3{\beta }_{22}}{5}}{|{\psi }_F|}^{10/3}\right)dx\hfill \\ & +& {\displaystyle \frac{N_B{N}_F}{N}}{\int }_{{\mathbb{R}}^d}{\beta }_{12}|{\psi }_F{|}^2{|{\psi }_B|}^{2}dx.\hfill \end{array}$$

(3)

Here, ${\displaystyle \frac{|\nabla {\psi }_B{|}^2}{2}}$ and ${\displaystyle \frac{|\nabla {\psi }_F{|}^2}{6\lambda }}$ are positive kinetic energy terms. In the Hamiltonian, the kinetic energy operator is $-{\nabla }^2/2m$ (for bosons) or $-{\nabla }^2/\left(6\lambda m_F\right)$ (for fermions). However, in the energy functional, the kinetic energy is expressed in positive form by calculating the expectation value. For instance, for the bosonic part, the expected kinetic energy is $\int {\psi }_B^{*}(-{\nabla }^2/2){\psi }_{B}dx$, which yields $\int |\nabla {\psi }_B{|}^2/2dx$ through partial integration (assuming the boundary term is zero). A similar treatment applies to the fermionic part, where the coefficient is adjusted to $\int |\nabla {\psi }_F{|}^2/6\lambda dx$. This symbolic transformation follows the standard procedure for energy calculation in quantum mechanics and represents the positive kinetic energy contribution of the system.

A key challenge in the study of Bose-Fermi mixtures is the determination of their ground state solutions. The ground state solution $({\varphi }_B^g\left(x\right),{\varphi }_F^g\left(x\right))$ is a time-independent wave function, which is obtained by minimizing the energy functional subject to the constraint conditions $E({\psi }_B,{\psi }_F)$:

$$\begin{array}{c}\hfill E({\varphi }_B^g\left(x\right),{\varphi }_F^g\left(x\right))=\underset{({\varphi }_B,{\varphi }_F)\in S_d}{min}E({\varphi }_B,{\varphi }_F).\end{array}$$

(4)

Here, $E({\psi }_B,{\psi }_F)$ represents the energy functional for any wave function, while $E({\varphi }_B^g,{\varphi }_F^g)$ corresponds to the ground state energy. The wave functions ${\varphi }_B$ and ${\varphi }_F$ are those that minimize the energy functional. The non-convex set $S_d$ is defined as:

$$\begin{array}{c}\hfill S_d=\left\{({\varphi }_B,{\varphi }_F)\mid {\int }_{{\mathbb{R}}^d}|{\varphi }_B\left(x\right){|}^{2}dx=1,{\int }_{{\mathbb{R}}^d}{|{\varphi }_F\left(x\right)|}^{2}dx=1,E({\varphi }_B,{\varphi }_F)<\infty \right\}.\end{array}$$

(5)

To find the steady-state solution, it is assumed that the bosonic and fermionic wave functions take separate forms: ${\psi }_B(x,t)=e^{-i{\mu }_{B}t}{\varphi }_B\left(x\right)$ and ${\psi }_F(x,t)=e^{-i{\mu }_{F}t}{\varphi }_F\left(x\right)$, where ${\mu }_B$ and ${\mu }_F$ are the chemical potentials of the bosons and fermions, respectively. The functions ${\varphi }_B\left(x\right)$ and ${\varphi }_F\left(x\right)$ are time-independent real functions that satisfy the definition of the non-convex set, i.e., Equation (5). Substituting these into Equations (1) and (2), we eliminate the terms $e^{-i{\mu }_{B}t}$ and $e^{-i{\mu }_{F}t}$, leading to the following nonlinear eigenvalue problem for the ground state solution:

$$\begin{array}{ccc}\hfill {\mu }_B{\varphi }_B& =& \left(-{\displaystyle \frac{{\nabla }^2}{2}}+V_B\left(x\right)+{\beta }_{11}|{\varphi }_B{|}^2+{\beta }_{12}{N}_F{|{\varphi }_F|}^2\right){\varphi }_B,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\mu }_F{\varphi }_F& =& \left(-{\displaystyle \frac{{\nabla }^2}{6\lambda }}+V_F\left(x\right)+{\beta }_{12}{N}_B|{\varphi }_B{|}^2+{\beta }_{22}{|{\varphi }_F|}^{4/3}\right){\varphi }_F.\hfill \end{array}$$

(7)

Multiplying both sides of Equation (6) by ${\varphi }_B\left(x\right)$ and integrating over ${\mathbb{R}}^d$ gives:

$$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^d}{\mu }_B{\varphi }_B^{2}dx={\mu }_B{\int }_{{\mathbb{R}}^d}{|{\varphi }_B|}^{2}dx={\mu }_B,\end{array}$$

On the right-hand side, we have:

$$\begin{array}{ccc}& & {\int }_{{\mathbb{R}}^d}{\varphi }_B\left(-{\displaystyle \frac{{\nabla }^2}{2}}+V_B+{\beta }_{11}|{\varphi }_B{|}^2+{\beta }_{12}{N}_F{|{\varphi }_F|}^2\right){\varphi }_{B}dx\hfill \\ & =& {\int }_{{\mathbb{R}}^d}\left[-{\displaystyle \frac{1}{2}}{\varphi }_B{\nabla }^2{\varphi }_B+V_B|{\varphi }_B{|}^2+{\beta }_{11}|{\varphi }_B{|}^4+{\beta }_{12}{N}_F|{\varphi }_F{|}^2{|{\varphi }_B|}^2\right]dx.\hfill \end{array}$$

For the kinetic energy term, we use partial integration (assuming ${\varphi }_B\to 0$ as $|x|\to \infty$):

$$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^d}-{\displaystyle \frac{1}{2}}{\varphi }_B{\nabla }^2{\varphi }_{B}dx={\displaystyle \frac{1}{2}}{\int }_{{\mathbb{R}}^d}{|\nabla {\varphi }_B|}^{2}dx,\end{array}$$

Thus, we obtain the following equation:

$$\begin{array}{ccc}\hfill {\mu }_B& =& {\int }_{{\mathbb{R}}^d}\left({\displaystyle \frac{|\nabla {\varphi }_B{|}^2}{2}}+V_B|{\varphi }_B{|}^2+{\beta }_{11}|{\varphi }_B{|}^4+{\beta }_{12}{N}_F|{\varphi }_F{|}^2{|{\varphi }_B|}^2\right)dx,\hfill \end{array}$$

(8)

For the fermionic chemical potential ${\mu }_F$, it can be deduced from Equation (7) as:

$$\begin{array}{ccc}\hfill {\mu }_F& =& {\int }_{{\mathbb{R}}^d}\left({\displaystyle \frac{|\nabla {\varphi }_F{|}^2}{6\lambda }}+V_F|{\varphi }_F{|}^2+{\beta }_{12}{N}_B|{\varphi }_F{|}^2|{\varphi }_B{|}^2+{\beta }_{22}{|{\varphi }_F|}^{10/3}\right)dx.\hfill \end{array}$$

(9)

When studying the ground state solution, the symmetry of the potential functions $V_B\left(x\right)$ and $V_F\left(x\right)$ plays a crucial role in determining the symmetry of the wave functions. For instance, if $V_B\left(x\right)$ exhibits point symmetry or axial symmetry, quantum mechanics theory predicts that the ground state wave function ${\varphi }_B\left(x\right)$ will exhibit corresponding symmetry [1]. This provides theoretical support for subsequent calculations and simplifies the solution process [16].

3. Neural Network Method

3.1. Neural Network Architecture

In order to solve the ground state problem of Bose-Fermi mixtures, this paper proposes a Bose-Fermi Energy-based Deep Neural Network (BF-EnDNN) framework based on the energy functional. Although our method follows the general framework of energy-minimization neural networks (such as the Deep Ritz method and PINNs), it incorporates several problem-specific architectural and training innovations that distinguish it from standard approaches.

In particular, two network components—the Dynamic Symmetry Layer (DSL) and the Positivity Preserving Layer (PPL)—act as hard architectural constraints that directly enforce physical symmetry and non-negativity of the wave function, rather than soft penalty terms in the loss. This structural enforcement reduces the reliance on penalty weights and helps maintain physical consistency throughout training.

In addition, an adaptive pre-training and residual-based point addition strategy is employed to accelerate convergence and enhance training stability. These enhancements provide a more robust and physically consistent implementation of energy-minimization neural networks for the Bose–Fermi ground-state problem.

The network architecture is shown in Figure 1. The input to the network is the spatial coordinate $x\in {\mathbb{R}}^d$ ($d=1,2,3$), and the output consists of the normalized boson and fermion wave functions ${\varphi }_B\left(x\right)$ and ${\varphi }_F\left(x\right)$. The network structure primarily consists of the input layer, hidden layer, positivity-preserving layer, and normalization layer, as described below:

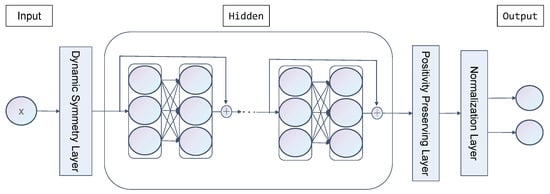
Figure 1. BF-EnDNN Network Architecture.

Input Layer: This layer receives the spatial coordinates x and passes them to the Dynamic Symmetry Layer (DSL) for pre-processing. The processed results are then input into the hidden layer.

Hidden Layer: The hidden layer adopts a residual block structure. Each residual block consists of two fully connected layers with a skip connection. The calculation formula is:

$$y_l=y_{l-1}+\sigma \left(W_{l,2}\sigma \left(W_{l,1}{y}_{l-1}+b_{l,1}\right)+b_{l,2}\right),$$

where $y_{l-1}$ is the input to the l-th residual block, $y_l$ is the output of the l-th residual block, $W_{l,1}$ and $b_{l,1}$ are the weight matrix and bias vector of the first fully connected layer in the residual block, and $W_{l,2}$ and $b_{l,2}$ are the weight matrix and bias vector of the second fully connected layer in the residual block. The index l denotes the residual block number. This structure effectively mitigates the issue of vanishing gradients, enhances the stability of the network training process, and accelerates convergence speed [17]. The hidden layer uses the sin function as the activation function [18]. This choice is motivated by the complex interactions between particles in the Bose-Fermi mixture, which lead to diverse wavefunction distributions in space. The oscillatory nature of the sin function allows the network to capture multi-frequency components in the wavefunction variations, with rapid oscillations enhancing the ability to resolve wavefunction profiles in high-gradient regions.

Positivity-Preserving Layer: This layer employs the Softplus activation function to ensure the non-negativity of the wavefunction. Specifically, the Positivity-Preserving Layer enforces non-negative values across the entire spatial domain by applying a monotonic transformation to the network’s outputs.

Normalization Layer: This layer ensures that the wave functions meet the normalization condition: $\int |{\varphi }_B{|}^{2}dx=1$ and $\int |{\varphi }_F{|}^{2}dx=1$, providing stable physical constraints for the model and ensuring the physical consistency of the computation results.

3.2. Loss Function

The training process in this study is divided into two phases: pre-training and formal training. In these two phases, the loss functions differ.

In the pre-training phase, the standard Gaussian function is used as the initial guess, and the initial shape of the wave functions is quickly obtained by minimizing the residual between the predicted wave function and the Gaussian distribution. The loss function is defined as:

$${\mathcal{L}}_{\mathrm{pre}}={\displaystyle \frac{1}{N_x}}\sum _{j=1}^{N_x}\left(|{\varphi }_B\left(x_j\right)-{\varphi }_{\mathrm{Gauss},B}\left(x_j\right){|}^2+{|{\varphi }_F\left(x_j\right)-{\varphi }_{\mathrm{Gauss},F}\left(x_j\right)|}^2\right),$$

where ${\varphi }_{\mathrm{Gauss},B}\left(x\right)={\varphi }_{\mathrm{Gauss},F}\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{x^2}{2}}}$.

During the formal training phase, the loss function is constructed based on the coupled Gross-Pitaevskii equations and the system’s energy functional (Equation (3)). Computational implementation requires solving these equations over discrete spatial points. We denote ${\left\{x_j\right\}}_{j=1}^N$ as a set of N collocation points in the spatial domain ${\mathbb{R}}^d$. These points can be evenly distributed grid points or points obtained through other sampling strategies. The loss function is defined as:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{train}& ={\displaystyle \frac{N_B}{N}}{\displaystyle \frac{1}{N}}\sum _{j=1}^N\left({\displaystyle \frac{|\nabla {\varphi }_B\left(x_j\right){|}^2}{2}}+V_B\left(x_j\right)|{\varphi }_B\left(x_j\right){|}^2+{\displaystyle \frac{{\beta }_{11}}{2}}{|{\varphi }_B\left(x_j\right)|}^4\right)\hfill \\ \hfill & +{\displaystyle \frac{N_F}{N}}{\displaystyle \frac{1}{N}}\sum _{j=1}^N\left({\displaystyle \frac{|\nabla {\varphi }_F\left(x_j\right){|}^2}{6\lambda }}+V_F\left(x_j\right)|{\varphi }_F\left(x_j\right){|}^2+{\displaystyle \frac{3{\beta }_{22}}{5}}{|{\varphi }_F\left(x_j\right)|}^{{\displaystyle \frac{10}{3}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{N_B{N}_F}{N}}{\displaystyle \frac{1}{N}}\sum _{j=1}^N{\beta }_{12}|{\varphi }_F\left(x_j\right){|}^2{|{\varphi }_B\left(x_j\right)|}^2.\hfill \end{array}$$

We use the automatic differentiation functionality in the PyTorch 2.0.1 framework, torch.autograd.grad, to compute $\nabla {\varphi }_B\left(x_j\right)$ and $\nabla {\varphi }_F\left(x_j\right)$.

3.3. Dynamic Symmetry Layer

The symmetry of a quantum system (such as spatial reflection symmetry, rotational symmetry, etc.) is a key characteristic of the ground state wave function [19,20]. A common approach to incorporate symmetry is by introducing symmetry constraint terms into the loss function. However, this soft-constraint methodology requires manual parameter tuning, which often leads to cumbersome optimization processes and suboptimal training efficiency. To address these limitations, we propose the Dynamic Symmetry Layer, which automatically enforces physical symmetries through input data preprocessing prior to network propagation. This method embeds the symmetry of $V_B\left(x\right)$ directly into the network and imposes a hard constraint on the symmetry of the wave function during the training process.

Specifically, we replace the original coordinate x with the potential function value $x_{\mathrm{input}}=V_B\left(x\right)$. For symmetric points $x_1$ and $x_2$ satisfying the symmetry operation $x_2=T{x}_1$ (where T is a symmetry operation, such as $Tx=-x$), the symmetry of $V_B\left(x\right)$ implies that $V_B\left(x_1\right)=V_B\left(x_2\right)$ and $x_{1,\mathrm{input}}=x_{2,\mathrm{input}}$. Based on the mapping characteristics of the neural network, we then have ${\varphi }_B\left(x_1\right)={\varphi }_B\left(x_2\right)$, ensuring the symmetry of the wave function at symmetric points.

3.4. Pre Training Point Adding Strategy

In Physics-Informed Neural Networks (PINNs), the Residual-based Adaptive Refinement (RAR) strategy has been extensively studied to improve model training efficiency and solution accuracy. This approach dynamically allocates new training points to regions with large PDE residuals, thereby optimizing the distribution of training points and significantly enhancing model performance [21,22].

Building upon this idea, we introduce a residual-based point addition strategy during the pre-training phase of the neural network. By analyzing the residuals of the neural network during pre-training, the strategy dynamically selects points with larger residuals as new training points. This method allows the model to quickly focus on regions with large prediction errors, reduces the number of required training samples, and accelerates the convergence process, thus significantly improving computational efficiency when dealing with complex physical systems.

The specific implementation steps are as follows:

• Residual Calculation: For each discrete point $x_j$, calculate the loss functions for bosons and fermions, ${\mathrm{Loss}}_B\left(x_j\right)$ and ${\mathrm{Loss}}_F\left(x_j\right)$, respectively. The total loss is defined as:

  $$\mathrm{Loss}\left(x_j\right)={\mathrm{Loss}}_B\left(x_j\right)+{\mathrm{Loss}}_F\left(x_j\right).$$
• Dynamic Point Addition: After every K-th round of training, select the first M points with the largest loss values and add them to the training set.

3.5. Positivity-Preserving Layer

The Softplus activation function is employed in the positivity-preserving layer to ensure that the wave function remains non-negative. The Softplus function is defined as:

$$\mathrm{Softplus}\left(x\right)=log(1+e^x).$$

This function is applied to the non-normalized wave functions ${\varphi }_B^{*}\left(x\right)$ and ${\varphi }_F^{*}\left(x\right)$ as follows:

$${\varphi }_B\left(x\right)=\mathrm{Softplus}\left({\varphi }_B^{*}\left(x\right)\right),{\varphi }_F\left(x\right)=\mathrm{Softplus}\left({\varphi }_F^{*}\left(x\right)\right).$$

The output of the Softplus function is non-negative, which helps suppress high-frequency oscillations of the sin function, thereby improving the stability of the training process.

3.6. Normalization Layer

The normalization layer enforces the conservation of particle number by ensuring that the wave functions are normalized [23]. Specifically, ${\varphi }_B\left(x\right)$ and ${\varphi }_F\left(x\right)$ are normalized as follows:

$$\begin{array}{cccc}\hfill {\varphi }_B\left(x\right)& ={\displaystyle \frac{{\varphi }_B\left(x\right)}{\sqrt{{\int }_{{\mathbb{R}}^d}{|{\varphi }_B\left(x\right)|}^{2}dx}}},\hfill & \hfill {\varphi }_F\left(x\right)& ={\displaystyle \frac{{\varphi }_F\left(x\right)}{\sqrt{{\int }_{{\mathbb{R}}^d}{|{\varphi }_F\left(x\right)|}^{2}dx}}}.\hfill \end{array}$$

3.7. Program Implementation Details

This section provides the implementation details of the neural network, including data sampling and model construction. The experiments were conducted using the PyTorch 2.0.1 framework on a server equipped with a 14-core Intel Xeon (R) Platinum 8362 CPU (Intel Corporation, Santa Clara, CA, USA) and an NVIDIA RTX 3090 GPU (24 GB of video memory) (Nvidia Corporation, Santa Clara, CA, USA).

This study employs an unsupervised learning approach based on the Deep Ritz method. The training data is generated by uniformly sampling points within the spatial domain ${\mathbb{R}}^d$. In one dimension, 3000 points are uniformly sampled, and in two dimensions, a $100\times 100$ grid is used. For the model architecture, BF-EnDNN consists of three residual blocks, each with 70 neurons in the hidden layers. The training process is divided into pre-training (3000 iterations) and formal training (20,000 iterations), with a batch size of 3000. Adam is used as the optimizer, with an initial learning rate of 0.01. The learning rate is reduced every 500 iterations using a StepLR scheduler, with an attenuation factor of 0.95.

Through this design, BF-EnDNN significantly enhances the efficiency and accuracy of determining the ground state solution for the Bose-Fermi mixture system while adhering to physical constraints. The code used in this study is available upon request by contacting the author.

4. Numerical Experiment

This section presents a systematic series of numerical experiments comparing BF-EnDNN with the finite difference method (FDM) in one-dimensional (1D) scenarios. The study evaluates the practical impact of each technical innovation, assesses the model’s robustness to parameter variations, and compares the performance of different activation functions. Additionally, BF-EnDNN is extended to two-dimensional (2D) configurations. The results provide comprehensive empirical validation, reinforcing the advantages and application potential of BF-EnDNN in quantum system studies.

4.1. One-Dimensional Numerical Experiment

4.1.1. Parameter Settings and Description

In the one-dimensional numerical experiments, a series of key parameters is chosen to simulate the ground state solution of the Bose–Fermi mixture system. The angular frequencies are set to ${\omega }_B={\omega }_F=2\pi \times 200\mathrm{Hz}$, the Boson mass is $m_B=7.016u$, and the Fermion mass is $m_F=6.0151u$ (where $u=1.6605\times {10}^{-27}\mathrm{kg}$ is the atomic mass unit). The Planck constant is $\hslash =1.0546\times {10}^{-34}\mathrm{Js}$, and the mass ratio is $\lambda =m_F/m_B=0.8573$. The external trapping potentials are set as $V_B\left(x\right)=0.5x^2$ and $V_F\left(x\right)=\lambda V_B\left(x\right)$.

These parameter selections are based on typical experimental setups in cold atomic physics [1], where $m_B$ and $m_F$ correspond to the masses of ${}^7\mathrm{Li}$ (boson) and ${}^6\mathrm{Li}$ (fermion), respectively. The value $\lambda =0.8573$ is the experimental mass ratio, which is commonly used in studies of the ground state properties of Bose–Fermi mixtures [1,2]. The angular frequency ${\omega }_B={\omega }_F=2\pi \times 200\mathrm{Hz}$ simulates the resonance potential in optical trapping, reflecting typical conditions in actual cold atom experiments.

For the neural network, the hidden layers consist of 6 layers, with each layer containing 70 neurons, and the model is trained using 3000 uniformly sampled points.

In the 1D numerical experiments, BF-EnDNN is compared to the traditional finite difference method (FDM). The FDM discretizes the spatial and temporal domains, transforming continuous equations into numerical problems on discrete grids. Key steps in the FDM include defining spatial grid points, calculating nonlinear terms, constructing coefficient matrices, solving systems of linear equations, and iteratively normalizing and updating wave functions until convergence is achieved.

4.1.2. Comparison with the Results of Traditional Methods

Figure 2, Figure 3 and Figure 4 show the results of Examples 1 to 3, where subfigures (a), (d), and (g) of each graph display the boson and Fermi wave functions obtained using the BF-EnDNN solution. Subfigures (b), (e), and (h) compare the BF-EnDNN results with the Bose wave functions solved using the finite difference method, while subfigures (c), (f), and (i) compare the BF-EnDNN results with the Fermi wave functions solved using the finite difference method.

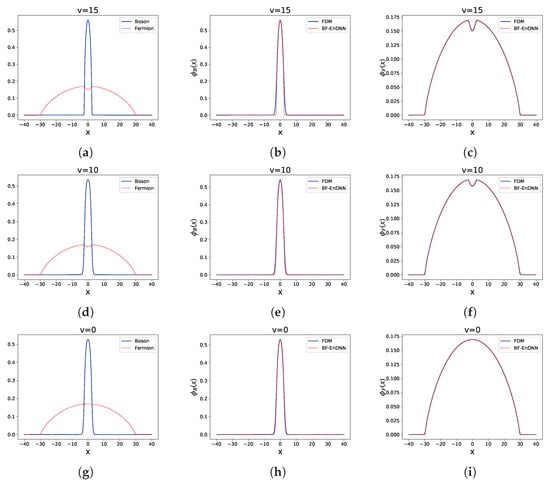
Figure 2. Example 1: Comparison of results for different interaction strengths v.

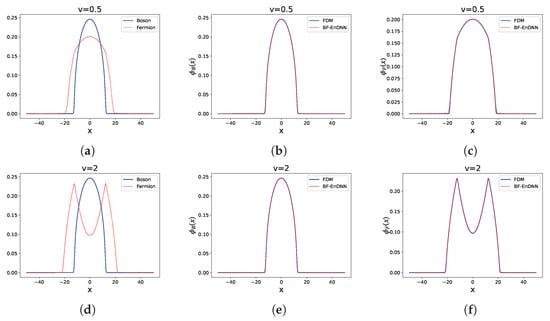
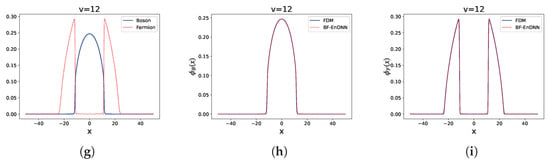
Figure 3. Example 2: Comparison of results for different interaction strengths v.

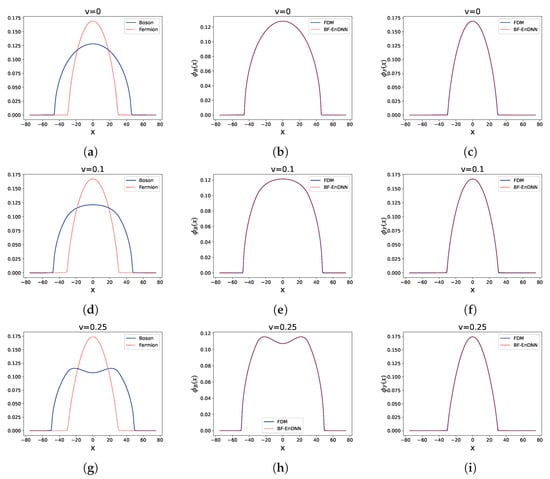
Figure 4. Example 3: Comparison of results for different interaction strengths v.

The specific parameter settings and result analyses for each example are as follows:

Example 1: The parameters were set as: ${\beta }_{11}=12.6418$, ${\beta }_{12}{N}_F=12.6418\times \nu$, ${\beta }_{12}{N}_B=12.6418\times \nu$, ${\beta }_{22}=4028.2$ ($N_B=N_F={10}^4$). The spatial range is $[-40,40]$, and the ratio $\nu$ varies from 15 to 0. This setting aims to study the effect of different boson–fermion interaction strengths (adjusted by $\nu$) on the ground state of the system. The results are shown in Figure 2 and Table 1. In Figure 2, subfigures (a), (b), and (c) show the results when $v=15$, subfigures (d), (e), and (f) show the results when $v=10$, and subfigures (g), (h), and (i) show the results when $v=0$.

Table 1. Comparison of Results between Finite Difference Method and BF-EnDNN.

Example	v	FDM			BF-EnDNN
		$\mathit{E}$	${\mathit{\mu }}_{\mathit{B}}$	${\mathit{\mu }}_{\mathit{F}}$	$\mathit{E}$	${\mathit{\mu }}_{\mathit{B}}$	${\mathit{\mu }}_{\mathit{F}}$
1	15	129.227	8.250	380.882	129.229	8.261	380.874
	10	128.445	6.844	379.597	128.437	6.868	379.599
	0	126.732	3.544	376.937	126.727	3.558	376.895
2	0.5	46.559	76.821	142.380	46.559	76.841	142.411
	2	47.071	77.178	193.143	47.071	77.159	193.191
	12	47.342	77.160	234.527	47.340	77.159	234.551
3	0	437.538	1039.641	376.937	437.598	1034.873	376.710
	0.1	484.011	1107.844	464.340	484.020	1107.953	464.350
	0.25	546.854	1206.396	573.569	546.861	1206.410	573.527

From Figure 2, when $\nu =15$, BF-EnDNN shows a slight deviation from the Bose wave function obtained using the finite difference method. However, in other cases, the results from both methods are highly consistent, with both methods accurately capturing the increasing trend of the central density of the boson condensate as $\nu$ decreases. Table 1 shows that in Example 1, the relative error of the ground state energy is between 0.0015% and 0.0041%, and the relative error of the chemical potentials ${\mu }_{\mathrm{B}}$ and ${\mu }_{\mathrm{F}}$ ranges from 0.0205% to 0.3950%.

Example 2: The parameters were set as: ${\beta }_{11}=1264.18$, ${\beta }_{12}{N}_F=12.6418\times \nu$, ${\beta }_{12}{N}_B=1264.18\times \nu$, ${\beta }_{22}=886.0764$ ($N_B={10}^6$, $N_F={10}^4$). The spatial range is $[-50,50]$, and the ratio $\nu$ varies from 0.5 to 12. This setting focuses on studying the influence of large boson numbers $N_B$ and the effect of $\nu$ on the ground state of the system. The results are shown in Figure 3 and Table 1. In Figure 3, subfigures (a), (b), and (c) show the results when $v=0.5$, subfigures (d), (e), and (f) show the results when $v=2$, and subfigures (g), (h), and (i) show the results when $v=12$.

From Figure 3, it can be seen that the boson and Fermi wave functions calculated by both BF-EnDNN and the finite difference method are highly consistent at all values of $\nu$, accurately capturing the characteristic that as $\nu$ increases, the Fermi wave function forms a “shell” around the boson condensate. Table 1 shows that in Example 2, the relative error of the ground state energy is between 0.0000% and 0.0042%, and the relative errors of the chemical potentials ${\mu }_{\mathrm{B}}$ and ${\mu }_{\mathrm{F}}$ range from 0.0013% to 0.0260%.

Example 3: The parameters were set as: ${\beta }_{11}=63209$, ${\beta }_{12}{N}_F=63209\times \nu$, ${\beta }_{12}{N}_B=63209\times \nu$, ${\beta }_{22}=4028.2$ ($N_B=N_F={10}^4$). The spatial range is $[-75,75]$, and the ratio $\nu$ varies from 0 to 0.25. This setting aims to investigate the influence of a larger ${\beta }_{11}$ on the ground state solution of the system. The results are shown in Figure 4 and Table 1. In Figure 4, subfigures (a), (b), and (c) show the results when $v=0$, subfigures (d), (e), and (f) show the results when $v=0.1$, and subfigures (g), (h), and (i) show the results when $v=0.25$.

As shown in Figure 4, at all values of $\nu$, the results from BF-EnDNN are highly consistent with the boson and Fermi wave functions calculated by the finite difference method, accurately capturing the characteristic that the central peak of the boson condensate gradually decreases as $\nu$ increases. Table 1 shows that in Example 3, the relative error of the ground state energy is between 0.0012% and 0.0137%, and the relative errors of the chemical potentials ${\mu }_{\mathrm{B}}$ and ${\mu }_{\mathrm{F}}$ range from 0.0021% to 0.4993%.

The three case studies collectively demonstrate that the BF-EnDNN method accurately captures the variations in ground state wave functions across diverse parameter configurations. Furthermore, the method achieves high precision in calculating ground state energies (relative errors: 0.0012% to 0.0137%) and chemical potentials (${\mu }_{\mathrm{B}}$ and ${\mu }_{\mathrm{F}}$: 0.0013% to 0.4993%). These results confirm the reliability and effectiveness of BF-EnDNN in solving ground state problems for Bose–Fermi mixtures.

The sources of relative error may include the following aspects: firstly, the randomness in neural network training may introduce fluctuations, especially under high interaction strengths (such as in Example 3 when $\nu =0$, where the error in ${\mu }_{\mathrm{B}}$ is large). The network may not fully converge to the global optimal solution. Secondly, the integration of the energy functional in BF-EnDNN is discretized through 3000 uniform sampling points, which may lead to numerical integration errors, especially in areas where the wave function changes rapidly. In contrast, the finite difference method, using denser grids (such as over 10,000 points), may have higher accuracy in these regions. These factors collectively contribute to the slight deviations between the BF-EnDNN and FDM results.

In addition to the above error sources, it is also worth noting that the two methods are conceptually different in nature. Since the coupled Bose–Fermi equations considered in this work do not admit closed-form analytical solutions except in very special cases, the finite difference method (FDM) is commonly adopted as a reference numerical solver. In this study, FDM serves as the benchmark for evaluating the accuracy of the proposed BF-EnDNN approach.

The FDM is a deterministic numerical scheme that relies on structured spatial grids. It provides high accuracy for low-dimensional problems when a sufficiently fine mesh is used, and its convergence behavior is well understood. However, its reliance on grid-based discretization can limit its scalability and flexibility, particularly in problems with complex geometries or higher dimensionality. Extending FDM often requires problem-specific meshing and fine-tuning, which reduces its generalizability across different parameter regimes.

In contrast, BF-EnDNN employs a mesh-free formulation based on sampling and stochastic optimization. Thanks to its physics-informed network structure and the incorporation of symmetry and positivity constraints, BF-EnDNN exhibits good flexibility and generalization capability. Once trained, the model can be adapted to different parameter settings without redesigning discretization schemes. Furthermore, its scalability makes it more suitable for problems where structured grids are less practical, such as high-dimensional or irregular domains.

Therefore, the two methods offer complementary advantages. FDM remains an efficient and accurate tool for structured low-dimensional problems, whereas BF-EnDNN provides a flexible and generalizable alternative that can achieve comparable accuracy in more general and challenging settings.

4.1.3. Analysis of the Effect of the Pre-Training Point Strategy

To explore the impact of the pre-training point addition strategy, this study compares the cases with and without point addition under the same number of training epochs.

Figure 5 shows a comparison of loss curves during the pre-training phase, with and without the addition of points, for different network sizes. The experimental results indicate that when using the residual-based point addition strategy, the model experiences greater fluctuations in the loss during the early stages of training as it adapts to new data. However, once point addition stops and training continues, the model is able to learn richer features, leading to a significant improvement in accuracy. Moreover, fewer epochs are required to reach the lowest loss value.

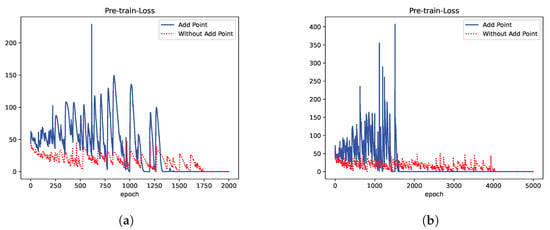
Figure 5. Pre-training phase: comparison of loss curves for residual-based point addition and non-point addition. (a) The network has 6 hidden layers with 100 units each. (b) The network has 8 hidden layers with 100 units each.

As shown in Figure 5a,b, as the network depth increases from 6 to 8, the residual-based point addition strategy significantly reduces the number of epochs needed to achieve stability during the pre-training phase. This gap becomes more pronounced as the model size increases. These results suggest that the point addition strategy can more effectively accelerate the training process and reduce training time, especially for larger models.

4.1.4. Analysis of the Effect of Dynamic Symmetric Layer (DSL)

We evaluate the role of the dynamic symmetric layer (DSL) in BF-EnDNN by comparing its training performance with and without DSL.

• Comparison of Symmetric Fitting Performance: Figure 6 and Figure 7 show a significant deviation on both sides of the symmetry axis in the model output without DSL, with a noticeable difference from the symmetry distribution fitted by traditional methods. This indicates that the model struggles to accurately capture the symmetry characteristics of quantum systems. After incorporating DSL, the wave function output by the model exhibits high symmetry on both sides of the axis and is highly consistent with the fitting results from traditional methods.
  

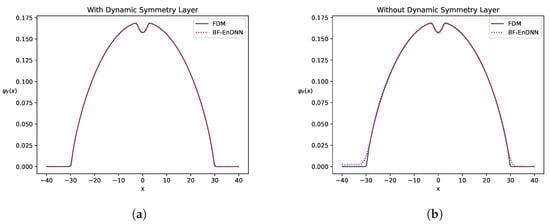  Figure 6. Fermion wave function plots with and without DSL for Example 1 ($v=10$) under the $0.5\times x^2$ potential. (a) With DSL. (b) Without DSL.
  

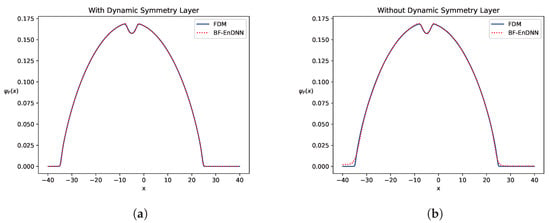  Figure 7. Fermion wave function plots with and without DSL for Example 1 ($v=10$) under the $0.5\times {(x+5)}^2$ potential. (a) With DSL. (b) Without DSL.
• Generalization performance validation: Figure 7 shows that when dealing with the external potential field $a{(x+b)}^2$, the model with DSL accurately adapts to the offset of the symmetry axis and stably outputs the wave function.

From Table 2, we can see that without DSL, the relative error range for ground state energy is 0.00% to 0.01%, for chemical potential ${\mu }_B$ is 0.35% to 0.70%, and for chemical potential ${\mu }_F$ is 0.011% to 0.03%. After incorporating DSL, the relative error range for ground state energy is 0.00% to 0.01%, for chemical potential ${\mu }_B$ is 0.00% to 0.39%, and for chemical potential ${\mu }_F$ is 0.0005% to 0.022%. This suggests that the model incorporating DSL can more accurately predict the values of energy E and chemical potentials ${\mu }_B$ and ${\mu }_F$ in all cases, bringing it closer to the results from the finite difference method (FDM).

Table 2. Comparison of Results with and without DSL.

Ex.	v				BF-EnDNN
		FDM			With DSL			Without DSL
		$\mathit{E}$	${\mathit{\mu }}_{\mathit{B}}$	${\mathit{\mu }}_{\mathit{F}}$	$\mathit{E}$	${\mathit{\mu }}_{\mathit{B}}$	${\mathit{\mu }}_{\mathit{F}}$	$\mathit{E}$	${\mathit{\mu }}_{\mathit{B}}$	${\mathit{\mu }}_{\mathit{F}}$
1	10	128.445	6.844	379.597	128.437	6.868	379.599	128.451	6.884	379.858
1	0	126.732	3.544	376.937	126.727	3.558	376.895	127.732	3.575	3.575
2	0.5	46.559	76.821	142.380	46.559	76.841	142.411	46.561	76.982	142.509
2	2	47.071	77.178	193.142	47.071	77.159	193.191	47.141	77.415	199.117

4.1.5. Analysis of the Importance of Positivity Preserving Layer (PPL)

In quantum physics, the non-negativity of wavefunctions is a fundamental requirement for physical consistency. The square of the wavefunction represents the probability density of particle presence at a given position, which necessitates strictly non-negative wavefunction values to preserve the non-negativity of probabilities. To enforce this constraint, we implement a Positivity Preserving Layer (PPL) using the Softplus activation function, which rigorously confines the wavefunction output to non-negative values. This design not only guarantees the physical validity of the model’s predictions but also enhances training stability and convergence by suppressing high-frequency oscillations inherent in conventional sin-based functions.

4.1.6. Evaluation of Network Robustness to Parameter Adjustments

To evaluate the robustness of the neural network under parameter adjustments, we constructed BF-EnDNN models with varying network depths (number of hidden layers) and widths (neurons per layer). Using the benchmark case from Example 2 ($v=12$) with fixed hyperparameters, we conducted multiple independent training trials and assessed model performance based on the converged minimum energy values. The experimental configurations are summarized in Table 3.

Table 3. Effects of Different Network Architectures.

	Width	10	20	30	70
Depth
2		47.426	47.381	47.373	47.386
4		47.347	47.345	47.349	47.349
6		47.347	47.343	47.343	47.343

As shown in Table 3, the performance of the BF-EnDNN model varies with the number of hidden layers and neurons per layer. Increasing the depth of hidden layers generally improves the model’s capacity to capture complex features, leading to enhanced performance and stability. On the other hand, increasing the number of neurons in fixed-depth architectures initially improves accuracy, but the gains plateau as excessive neurons introduce training difficulties or overfitting due to the increased model complexity. Across all configurations tested, the BF-EnDNN model converged stably to physically valid ground state solutions, demonstrating robust adaptability to parameter variations.

4.1.7. Activation Function Comparison Experiment

This experiment was conducted to compare the performance of the sin function, used as the hidden layer activation function in this paper, with the commonly used ReLU activation function. The experiment was based on the parameter settings of Example 1, with ${\beta }_{12}=50$, simulating a strong boson–fermion interaction scenario. The training loss curves during the formal training phase are shown in Figure 8.

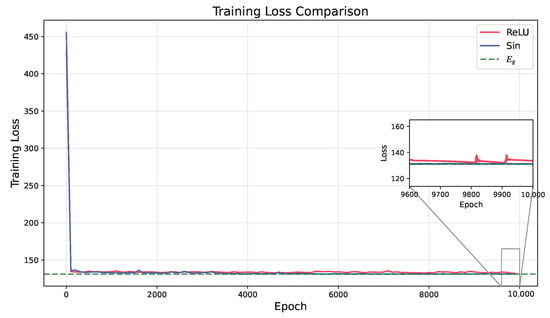
Figure 8. Comparison of activation functions: training loss curves for sin and ReLU.

In most cases, the choice of activation function has minimal impact on training. Both sin and ReLU can stably converge to similar loss values. However, as shown in Figure 8, under the strong interaction condition of ${\beta }_{12}=50$, the final loss for sin is slightly lower than that for ReLU, with a corresponding higher energy accuracy. In the ground state solution of Bose–Fermi hybrid systems, strong interactions may induce significant spatial variations in the wave function. The harmonic characteristics of the sin function make it more adaptable to these features, while ReLU’s piecewise linearity may be more limited. This result indicates that sin has certain advantages under specific conditions.

4.2. Two-Dimensional Numerical Experiment

In this section, we extend and verify the application of the BF-EnDNN method to 2D scenarios. The physical parameters used in the two-dimensional setting are as follows: angular frequencies ${\omega }_B={\omega }_F=2\pi \times 200\mathrm{Hz}$, boson mass $m_B=7.016u$, fermion mass $m_F=6.0151u$, Planck constant $\hslash =1.0546\times {10}^{-34}\mathrm{Js}$, and mass ratio $\lambda =m_F/m_B=0.8573$. The spatial range is set to $[-20,20]\times [-20,20]$. The external trapping potentials are defined as $V_B(x,y)=0.5(x^2+y^2)$ and $V_F(x,y)=\lambda V_B(x,y)$. For the neural network, the depth of the hidden layers is set to 6, with a width of 70. $100\times 100$ uniform sampling points are used to better capture the distribution characteristics of the wave functions in the plane.

4.2.1. Specific Parameter Settings and Experiment

In the two-dimensional scene, the following two experiments were conducted:

Example 4: The parameters were set as: ${\beta }_{11}=63209$, ${\beta }_{12}{N}_F=63209\times \nu$, ${\beta }_{12}{N}_B=63209\times \nu$, ${\beta }_{22}=4028.2$ ($N_B=N_F={10}^4$), and $\nu$ varies from 0.5 to 0.75. This setting mainly investigates the effect of a large ${\beta }_{11}$ (achieved by adjusting the scattering length $a_{BB}$) on the ground state solution of the system. The experimental results are shown in Figure 9 and Figure 10, where Figure 9 shows the scenario when $v=0.5$, and Figure 10 shows the scenario when $v=0.75$.

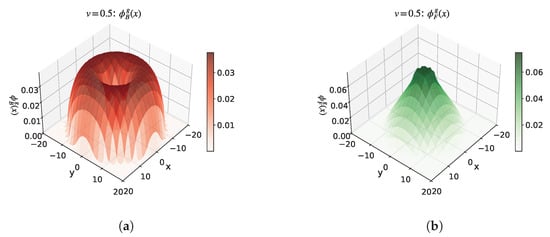
Figure 9. Example 4: Wave functions when $v=0.5$. (a) Example 4 ($v=0.5$)—Bose wave function. (b) Example 4 ($v=0.5$)—Fermi wave function.

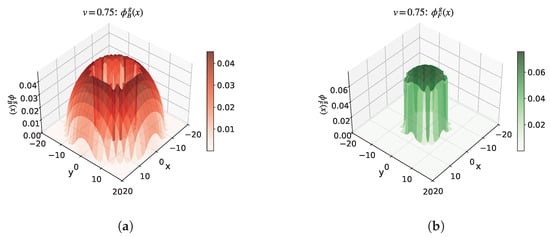
Figure 10. Example 4: Wave functions when $v=0.75$. (a) Example 4 ($v=0.75$)—Bose wave function. (b) Example 4 ($v=0.75$)—Fermi wave function.

From Figure 9 and Figure 10, we observe that as $\nu$ increases, the Bose condensate first forms an envelope around the Fermi condensate, and with further increases in $\nu$, the Fermi condensate gradually forms a dense region in the center of the Bose gas.

Example 5: The parameters were set as: ${\beta }_{11}=12.6418$, ${\beta }_{12}{N}_F=1264.18\times \nu$, ${\beta }_{12}{N}_B=12.6418\times \nu$, ${\beta }_{22}=88608$, $N_B={10}^4$, $N_F={10}^6$, and $\nu$ varies from 0 to 1.5. This setting focuses on the effect of different $\nu$ values on the ground state of the system at a large fermion number $N_F$. The experimental results are shown in Figure 11 and Figure 12, where Figure 11 shows the situation when $v=5$, and Figure 12 shows the situation when $v=50$.

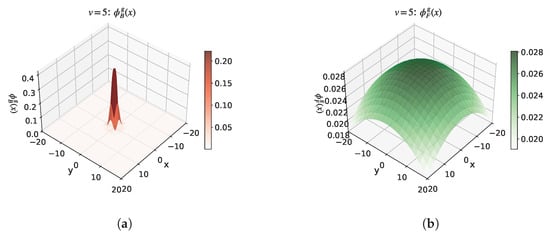
Figure 11. Example 5: Wave functions when $v=5$. (a) Example 5 ($v=5$)—Bose wave function. (b) Example 5 ($v=5$)—Fermi wave function.

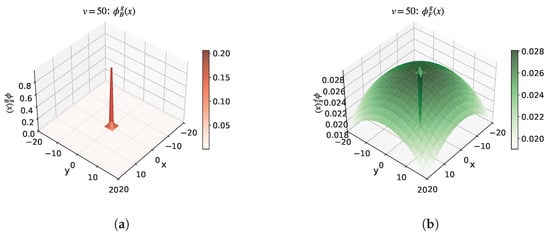
Figure 12. Example 5: Wave functions when $v=50$. (a) Example 5 ($v=50$)—Bose wave function. (b) Example 5 ($v=50$)—Fermi wave function.

From Figure 11 and Figure 12, we observe that as $\nu$ increases, the Bose condensate is gradually squeezed to form a single peak within the Fermi gas, and the center of the Fermi gas becomes increasingly concave.

4.2.2. Experimental Results and Analysis

The experimental results demonstrate that the BF-EnDNN method effectively solves the ground state problems for Bose-Fermi mixtures in 2D scenarios. The model-generated 2D wave functions accurately capture the particle distribution characteristics in planar geometries. Furthermore, under varying parameter configurations—such as changes in interaction strength and particle numbers—the model consistently converges to physically reasonable ground states, highlighting its robust performance and reliable solution capability in 2D systems.

5. Conclusions

This paper presents a deep learning-based approach, BF-EnDNN, for solving the ground states of Bose-Fermi mixtures at zero temperature. By introducing three key components—Dynamic Symmetry Layers (DSL), pretraining with a point-adding strategy, and Positive-definite Penalty Layers (PPL)—the method significantly enhances both the efficiency and accuracy of calculations in complex quantum systems. Numerical experiments confirm the effectiveness and robustness of BF-EnDNN across a variety of parameter settings. The results show excellent agreement with the traditional finite difference method (FDM) in calculating ground state energy and chemical potential, with relative errors remaining within acceptable ranges. Notably, the DSL component excels in preserving the symmetries of the quantum system, thereby improving both accuracy and stability. The combination of the pretraining strategy and PPL accelerates training convergence and ensures the physical validity of the wavefunctions. Future work will extend BF-EnDNN to 3D systems and non-equilibrium quantum states, and will explore adaptive network architectures and hybrid quantum Monte Carlo integration to further enhance its applicability in many-body quantum problems.