Detached Eddy Simulation of a Radial Turbine Operated with Supercritical Carbon Dioxide †
Abstract
1. Introduction
2. Mathematical Model and Solution Method
2.1. Governing Equations
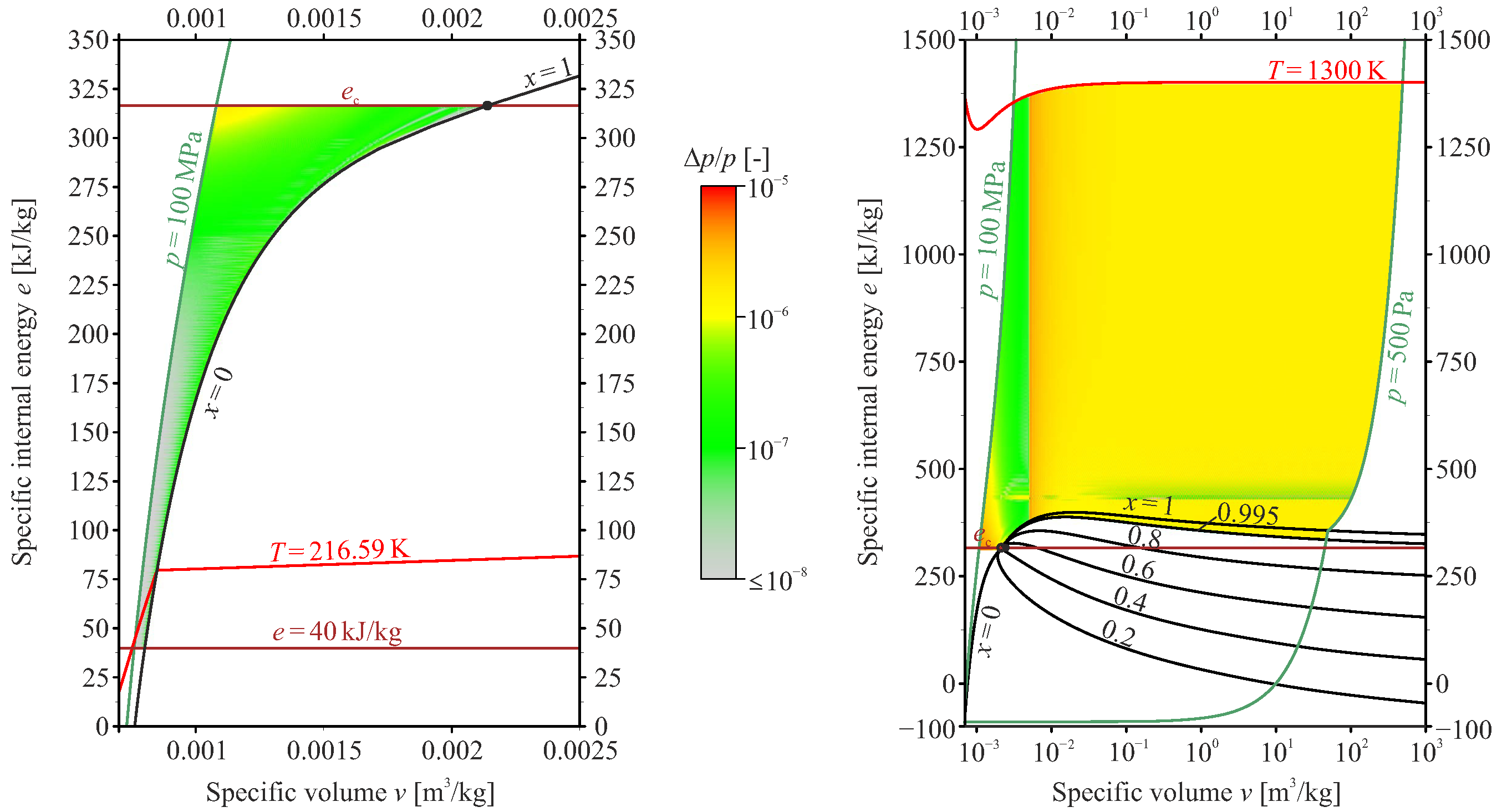
2.2. Thermodynamic Model
2.3. Turbulence Model
2.4. Spatial Discretization
3. IDDES Model Validation
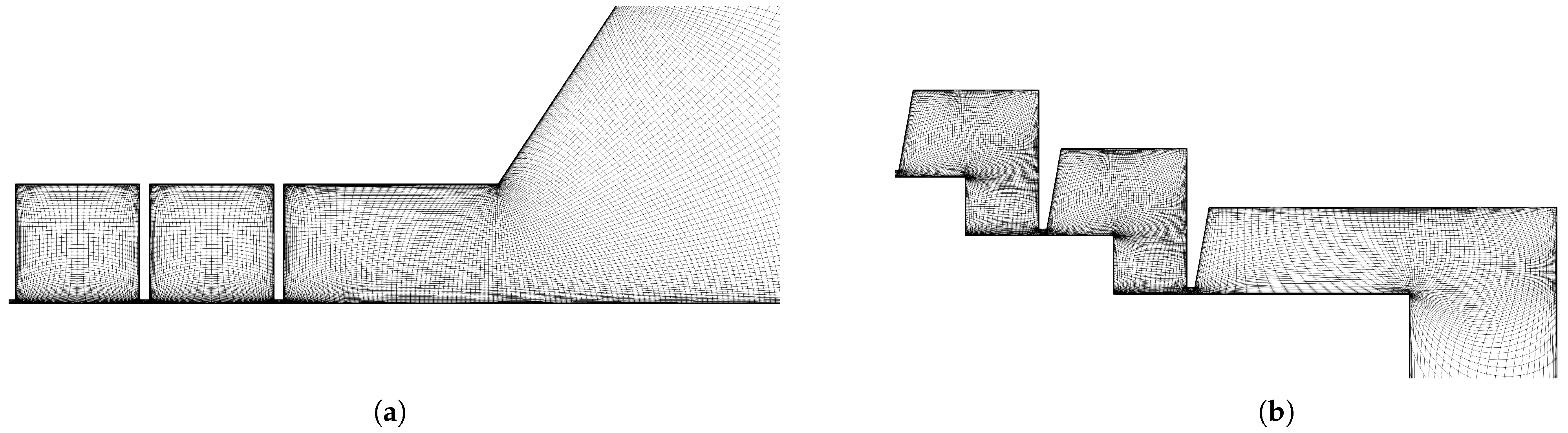
3.1. Computational Setup
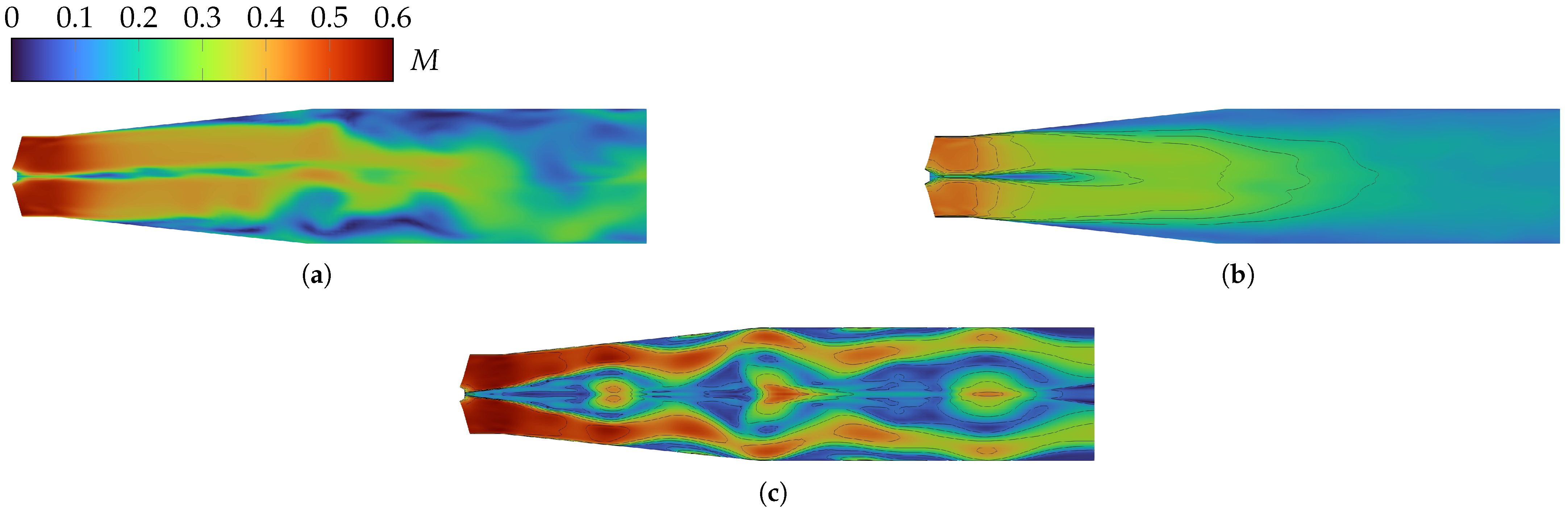
3.2. Instantaneous Flow Field
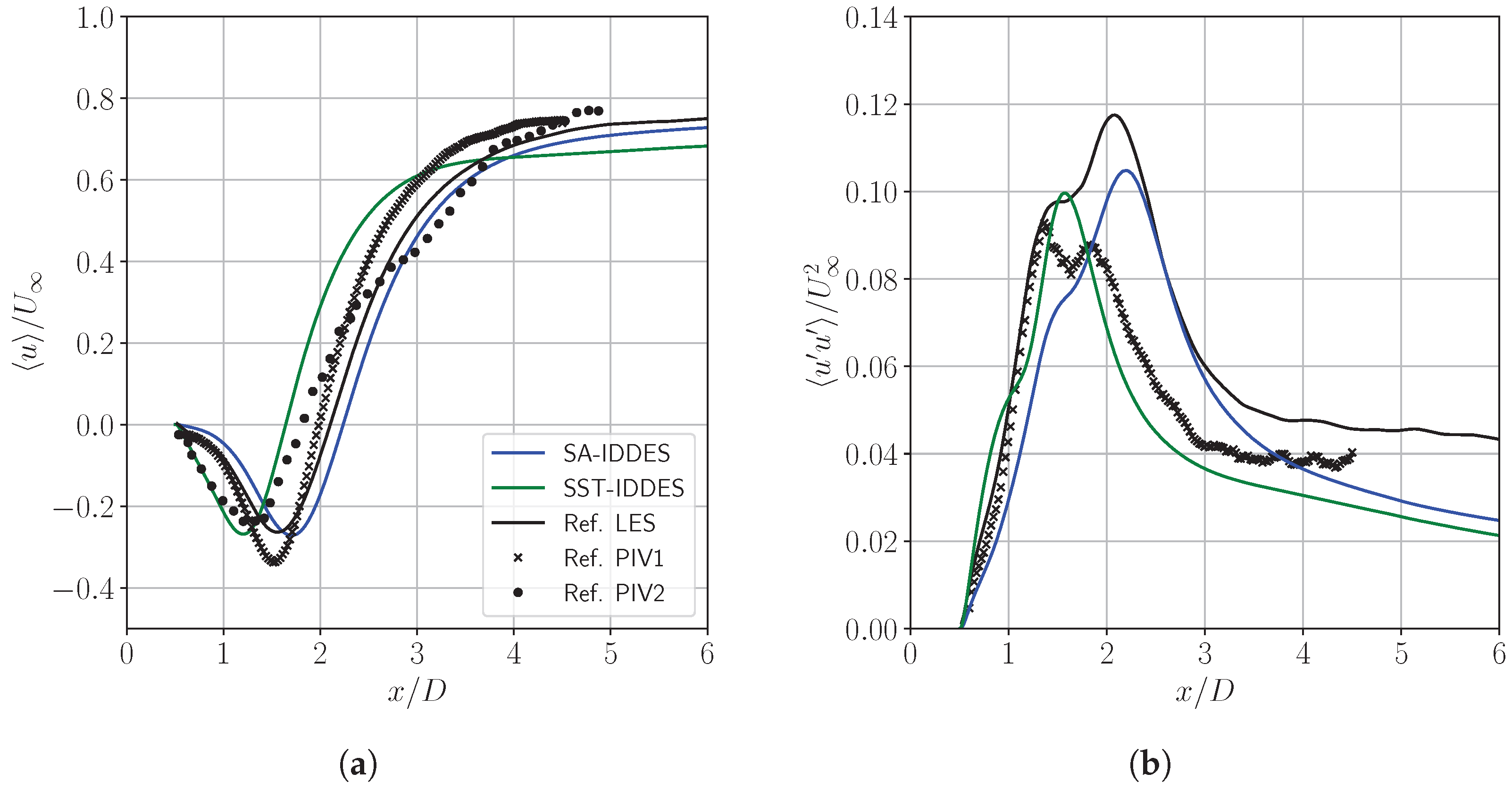
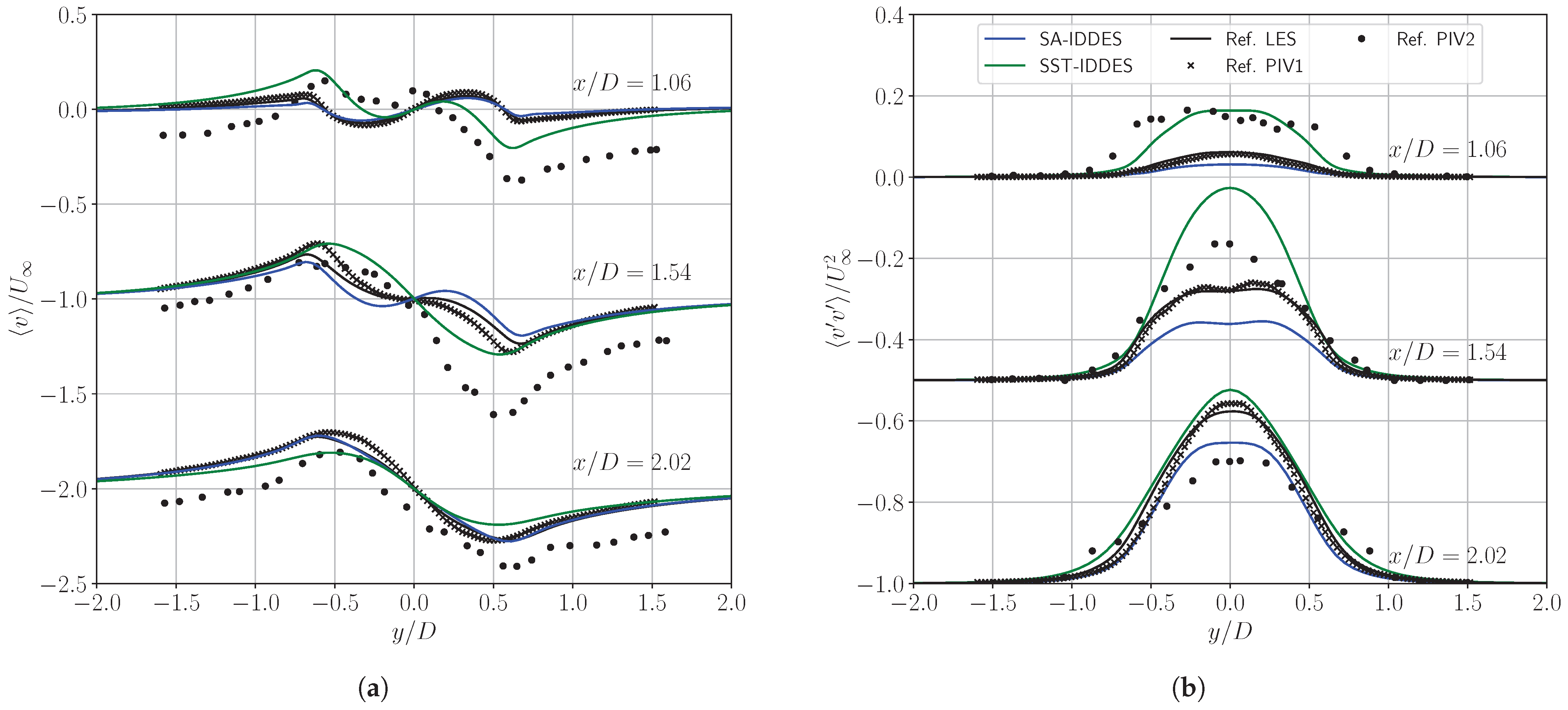
3.3. First- and Second-Order Statistics
4. Detached Eddy Simulation of sCO2 Turbine
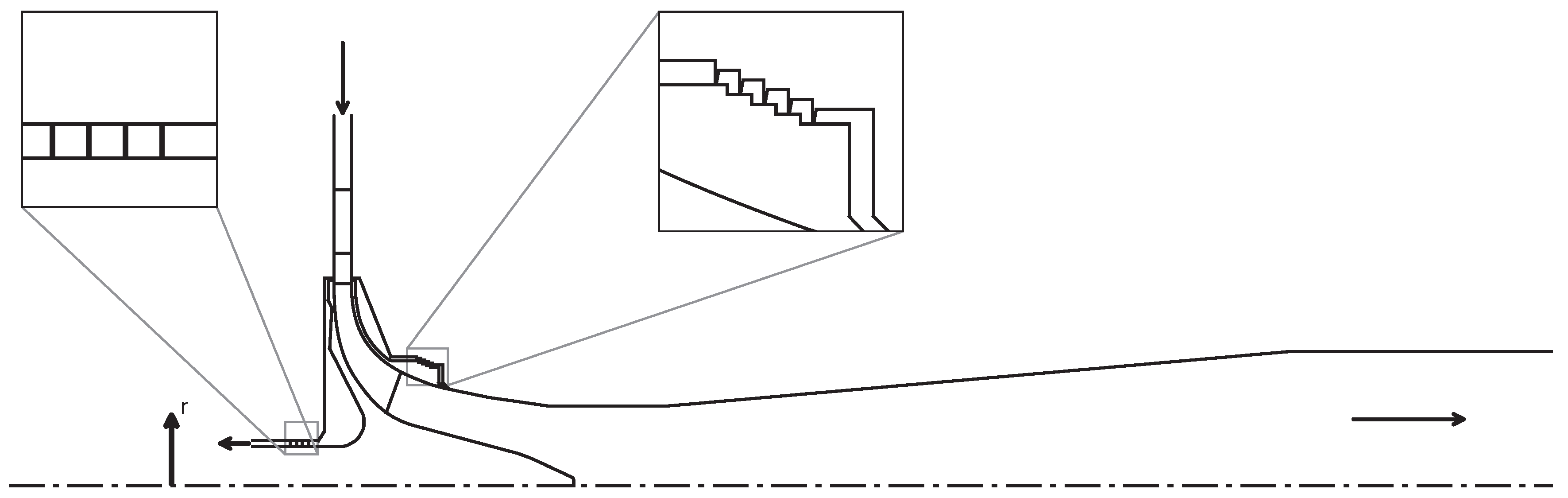
4.1. Computational Setup
4.2. Instantaneous Flow Field
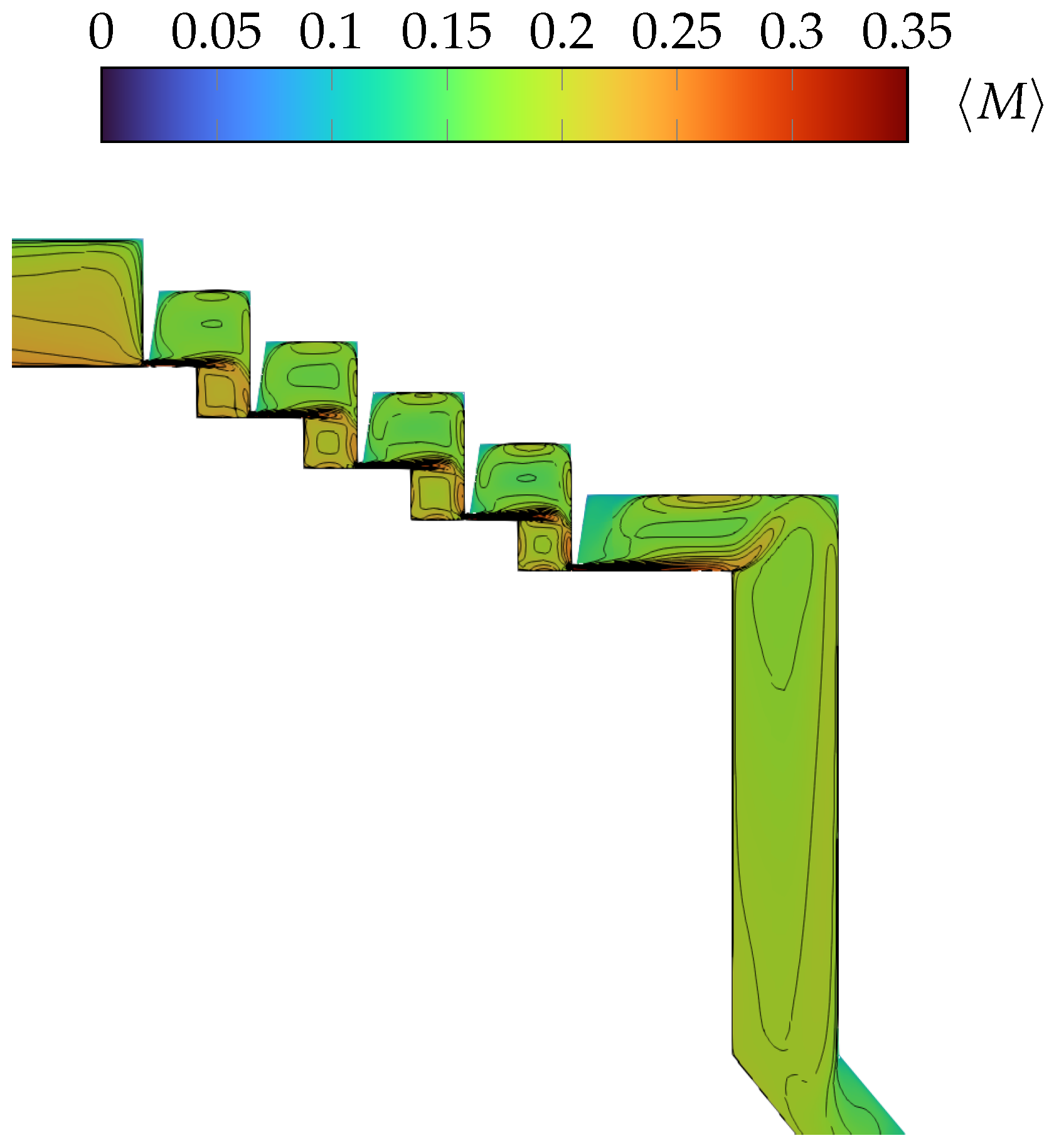
4.3. Time-Averaged Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Angelino, G. Carbon Dioxide Condensation Cycles For Power Production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Guardone, A.; Colonna, P.; Pini, M.; Spinelli, A. Nonideal Compressible Fluid Dynamics of Dense Vapors and Supercritical Fluids. Annu. Rev. Fluid Mech. 2024, 56, 241–269. [Google Scholar] [CrossRef]
- White, M.T.; Bianchi, G.; Chai, L.; Tassou, S.A.; Sayma, A.I. Review of Supercritical CO 2 Technologies and Systems for Power Generation. Appl. Therm. Eng. 2021, 185, 116447. [Google Scholar] [CrossRef]
- Brun, K.; Dennis, R.; Friedman, P. Fundamentals and Applications of Supercritical Carbon Dioxide (Sco2) Based Power Cycles, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Qi, J.; Reddell, T.; Qin, K.; Hooman, K.; Jahn, I.H.J. Supercritical CO2 Radial Turbine Design Performance as a Function of Turbine Size Parameters. J. Turbomach. 2017, 139, 081008. [Google Scholar] [CrossRef]
- Post, P.; Winhart, B.; di Mare, F. Large Eddy Simulation of a Condensing Wet Steam Turbine Cascade. J. Eng. Gas Turbines Power 2021, 143, 021016. [Google Scholar] [CrossRef]
- Boudin, A.; Dombard, J.; Duchaine, F.; Gicquel, L.; Odier, N.; Lavagnoli, S.; Lopes, G.; Simonassi, L. Analysis of Rotor/Stator Interactions in a High-Speed Low-Pressure Turbine Cascade Using Large-Eddy Simulations. In Proceedings of the European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Budapest, Hungary, 24–28 April 2023. [Google Scholar] [CrossRef]
- Piomelli, U.; Radhakrishnan, S.; Zhong, L.; Li, M. Wall-Layer Models for Large-Eddy Simulations of High Reynolds Number Non-Equilibrium Flows. In Advances in Turbulence XI; Palma, J., Lopes, A.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 117, pp. 47–54. [Google Scholar] [CrossRef]
- Al-Am, J.; Giauque, A.; Clair, V.; Boudet, J.; Gea-Aguilera, F. Direct-Noise of an Ultrahigh-Bypass-Ratio Turbofan: Periodic-Sector vs. Full-Annulus Large-Eddy Simulations. AIAA J. 2024, 62, 2831–2845. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Sadowski, W.; Lo Presti, F.; Di Mare, F. Assessment of Hybrid Turbulence Models for the Simulation of Ribbed Channel with Heat Transfer. In Proceedings of the European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Budapest, Hungary, 24–28 April 2023. [Google Scholar] [CrossRef]
- Karaefe, R.E.; Post, P.; Sembritzky, M.; Schramm, A.; Di Mare, F.; Kunick, M.; Gampe, U. Numerical Investigation of a Centrifugal Compressor for Supercritical CO2 Cycles. In Proceedings of the Volume 11: Structures and Dynamics: Structural Mechanics, Vibration, and Damping; Supercritical CO2, Virtual, Online, 21–25 September 2020; p. V011T31A011. [Google Scholar] [CrossRef]
- Lea, B.; Lo Presti, F.; Sadowski, W.; di Mare, F. Detached Eddy Simulation of a Radial Turbine operated with supercritical Carbon Dioxide. In Proceedings of the 16th European Turbomachinery Conference, Hannover, Germany, 24–28 March 2025; American Society of Mechanical Engineers: New York, NY, USA, 2025. [Google Scholar]
- Keep, J.A.; Jahn, I.H.J. Numerical Loss Investigation of a Small Scale, Low Specific Speed Supercritical CO2 Radial Inflow Turbine. J. Eng. Gas Turbines Power 2019, 141, 091003. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, J.; Xia, J.; Guo, Y.; Zhao, P.; Dai, Y. Design and Performance Analysis of a Supercritical CO2 Radial Inflow Turbine. Appl. Therm. Eng. 2020, 167, 114757. [Google Scholar] [CrossRef]
- Iim, H.; Chen, X.Y.; Zha, G. Detached-Eddy Simulation of Rotating Stall Inception for a Full-Annulus Transonic Rotor. J. Propuls. Power 2012, 28, 782–798. [Google Scholar] [CrossRef]
- Gan, J.; Im, H.S.; Zha, G.C. Delayed Detached Eddy Simulation of Rotating Stall for a Full Annulus Transonic Axial Compressor Stage. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. American Society of Mechanical Engineers Digital Collection, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Menter, F.R. Improved Two-Equation k-Omega Turbulence Models for Aerodynamic Flows. Technical Report A-92183; 1 October 1992. [Google Scholar]
- Spalart, P.; Jou, W.H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Laesecke, A.; Muzny, C.D. Reference Correlation for the Viscosity of Carbon Dioxide. J. Phys. Chem. Ref. Data 2017, 46, 013107. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.L.; Sykioti, E.A.; Assael, M.J.; Perkins, R.A. Reference Correlation of the Thermal Conductivity of Carbon Dioxide from the Triple Point to 1100 K and up to 200 MPa. J. Phys. Chem. Ref. Data 2016, 45, 013102. [Google Scholar] [CrossRef] [PubMed]
- Kunick, M. Fast Calculation of Thermophysical Properties in Extensive Process Simulations with the Spline-Based Table Look-Up Method (SBTL); VDI Verlag: Düsseldorf, Germany, 2018. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A Hybrid RANS-LES Approach with Delayed-DES and Wall-Modelled LES Capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Travin, A.K.; Shur, M.L.; Strelets, M.; Spalart, P.R. Physical and Numerical Upgrades in the Detached-Eddy Simulation of Complex Turbulent Flows. In Advances in LES of Complex Flows: Proceedings of the Euromech Colloquium 412, Munich, Germany, 4–6 October 2000; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES Formulations for the K-ω Shear Stress Transport Model. Flow, Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- van Albada, G.D.; van Leer, B.; Roberts, W.W. A Comparative Study of Computational Methods in Cosmic Gas Dynamics. In Upwind and High-Resolution Schemes; Hussaini, M.Y., van Leer, B., Van Rosendale, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 95–103. [Google Scholar] [CrossRef]
- Liou, M.S. A sequel to AUSM, Part II: AUSM+-up for all speeds. J. Comput. Phys. 2006, 214, 137–170. [Google Scholar] [CrossRef]
- Spalart, P.; Shur, M.; Strelets, M.; Travin, A. Sensitivity of Landing-Gear Noise Predictions by Large-Eddy Simulation to Numerics and Resolution. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Breuer, M. Towards Technical Application of Large Eddy Simulation. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 2001, 81, 461–462. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Lourenco, L.M.; Shih, C. Characteristics of the plane turbulent near wake of a cylinder, A particle image velocimetry study. Unpublished.
- Ong, L.; Wallace, J.M. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Ma, X.L.; Karamanos, G.S.; Karniadakis, G.E. Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 2000, 410, 29–65. [Google Scholar] [CrossRef]
- Beaudan, P.; Moin, P. Numerical Experiments on the Flow Past A Circular Cylinder at Sub-Critical Reynolds Number; Stanford University: Stanford, CA, USA, 1994. [Google Scholar]
- Mahesh, K.; Constantinescu, G.; Moin, P. A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 2004, 197, 215–240. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Franke, J.; Frank, W. Large eddy simulation of the flow past a circular cylinder at ReD = 3900. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1191–1206. [Google Scholar] [CrossRef]
- D’Alessandro, V.; Montelpare, S.; Ricci, R. Detached–eddy simulations of the flow over a cylinder at Re = 3900 using OpenFOAM. Comput. Fluids 2016, 136, 152–169. [Google Scholar] [CrossRef]
- Pereira, F.S.; Vaz, G.; Eça, L.; Girimaji, S.S. Simulation of the flow around a circular cylinder at Re=3900 with Partially-Averaged Navier-Stokes equations. Int. J. Heat Fluid Flow 2018, 69, 234–246. [Google Scholar] [CrossRef]
- Lodato, G.; Domingo, P.; Vervisch, L. Three-dimensional boundary conditions for direct and large-eddy simulation of compressible viscous flows. J. Comput. Phys. 2008, 227, 5105–5143. [Google Scholar] [CrossRef]
- Spalart, P.R.; Streett, C. Young-Person’s Guide to Detached-Eddy Simulation Grids; Technical report; Langley Research Center: Hampton, VA, USA, 2001. [Google Scholar]
- Lea, B.; di Mare, F.; Franz, H. Numerical Investigation of the Axial Thrust Load of a Prototype Radial Turbine for Supercritical CO2 Cycles. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, London, UK, 24–28 June 2024; American Society of Mechanical Engineers: New York, NY, USA, 2024; Volume 88049, p. V011T28A010. [Google Scholar]
- Yoon, S.; Jameson, A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef]




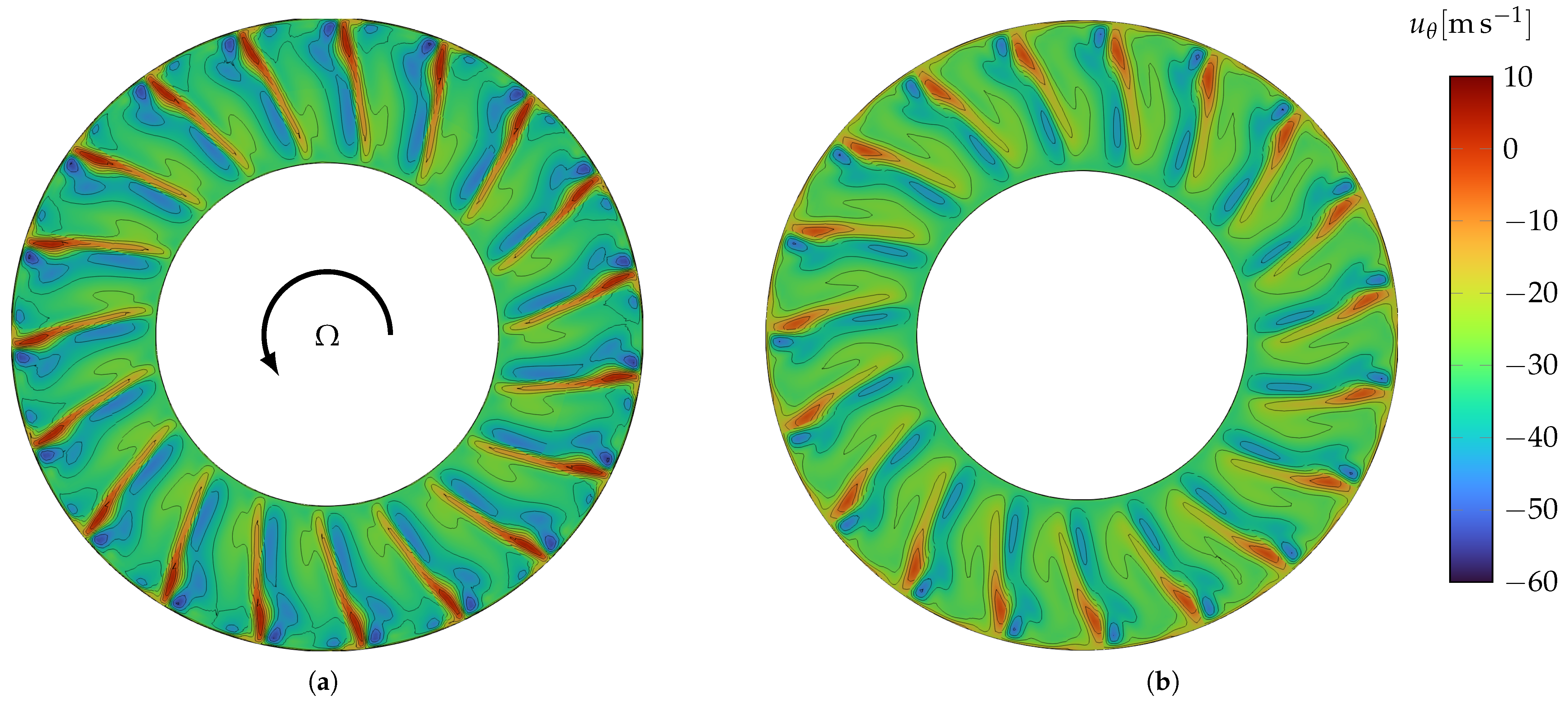

| SBTL Function | Liquid Region | Gas Region | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Lea, B.; Lo Presti, F.; Sadowski, W.; di Mare, F. Detached Eddy Simulation of a Radial Turbine Operated with Supercritical Carbon Dioxide. Int. J. Turbomach. Propuls. Power 2025, 10, 43. https://doi.org/10.3390/ijtpp10040043
Lea B, Lo Presti F, Sadowski W, di Mare F. Detached Eddy Simulation of a Radial Turbine Operated with Supercritical Carbon Dioxide. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):43. https://doi.org/10.3390/ijtpp10040043
Chicago/Turabian StyleLea, Benedikt, Federico Lo Presti, Wojciech Sadowski, and Francesca di Mare. 2025. "Detached Eddy Simulation of a Radial Turbine Operated with Supercritical Carbon Dioxide" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 43. https://doi.org/10.3390/ijtpp10040043
APA StyleLea, B., Lo Presti, F., Sadowski, W., & di Mare, F. (2025). Detached Eddy Simulation of a Radial Turbine Operated with Supercritical Carbon Dioxide. International Journal of Turbomachinery, Propulsion and Power, 10(4), 43. https://doi.org/10.3390/ijtpp10040043





